Similar presentations:
Общие методы решения уравнений
1.
Общие методы решенияуравнений
2.
1 методЗамена
уравнения
h( f ( x)) h( g ( x))
уравнением
f ( x) g ( x)
3.
При решении показательных уравненийа
f ( x)
a
g ( x)
(а 0, а ≠1)
f ( x) g ( x)
При решении логарифмических уравнений
log
f ( x) log g ( x)
a
a
f ( x) g ( x)
При решении иррациональных уравнений
n f ( x) n g ( x)
f ( x) g ( x)
Этот метод можно применять только тогда,
когда y = h(x) – монотонная функция
4.
2 методРазложения на множители
Уравнение
f ( x ) g ( x ) h( x ) 0
заменить
совокупностью уравнений
f ( x) 0, g ( x) 0, h( x) 0
Необходима проверка корней
5.
3 методВведения новой переменной
f ( x) 0
•Уравнение
•преобразуем к виду:
p( g ( x)) 0
•вводим новую переменную:
u g (x)
•решаем совокупность уравнений
g ( x) u1 ; g ( x) u2 ;...; g ( x) un
6.
4 методФункционально - графический
для решения уравнения
f ( x) g ( x)
строим графики функций
y f (x),
y g (x)
7.
Пример 1 :(2 x 2) (5 x 9)
7
2 x 2 5x 9
11
x
3
Ответ:
11
3
7
8.
Пример 2 :( x 2 3) ln( x 8) 0
x 2 3 0; ln( x 8) 0
x 2 3
x 2 9
x 7
ОДЗ:
x 8 1
x 9
x 2 0
x 8 0
С учётом ОДЗ:
Ответ:
9
x 9
9.
Пример 3 :2 sin 2 x 13 sin x 11 0
t sin x, t 1
2t 2 13t 11 0
t1 1 t2 5,5
sin x 1
x
2
2 n, n Z
Ответ:
2
2 n, n Z
не удовл.
10.
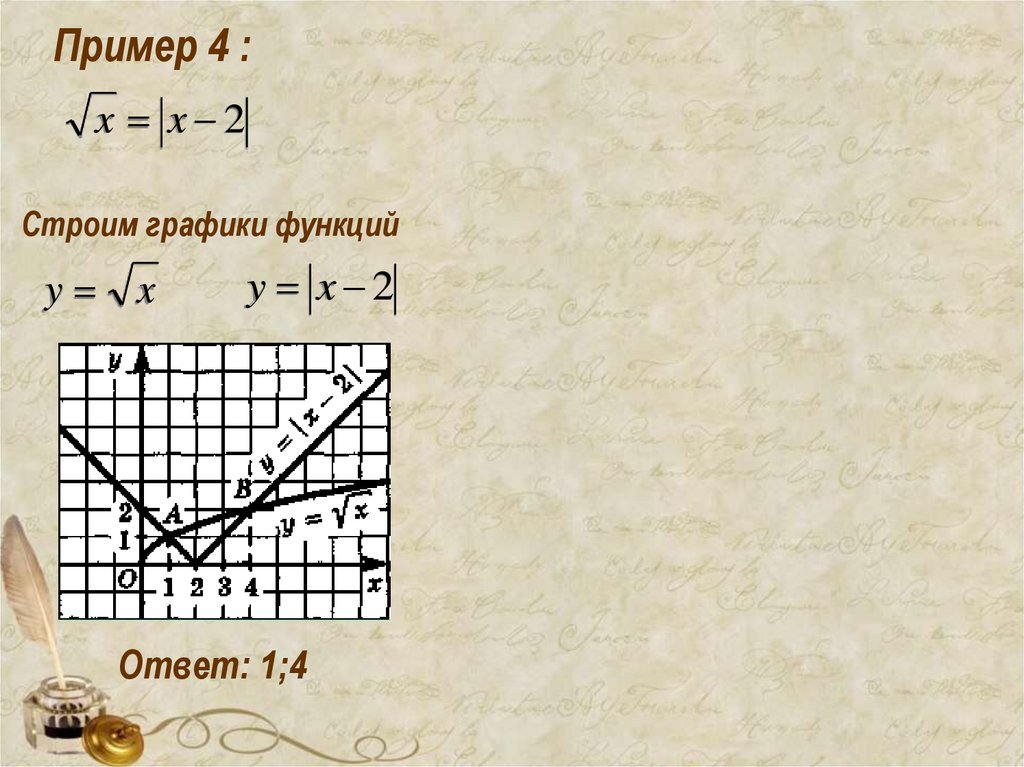
Пример 4 :x x 2
Строим графики функций
y x
y x 2
Ответ: 1;4









 mathematics
mathematics








