Similar presentations:
Одноосный силовой гиростабилизатор
1. Одноосный силовой гиростабилизатор
2.
3. Уравнения движения ОСГС
A0 D H M xA0 p 2 D p Hp M x
J 0 D H k p M yB1
J 0 p 2 D p Hp k p M yB1
Определитель системы:
Hp
( J 0 p 2 D p)
(A0 p 2 D p)
(Hp k p )
Характеристическое уравнение
A0 J 0 p 4 ( J 0 D A0 D ) p3 ( H 2 D D ) p 2 k p Hp 0
4.
A0 J 0 p 4 ( A0 D J 0 D ) p3 ( H 2 D D ) p 2 k p Hp 0По критерию Гурвица:
1. a j 0,
a4 0( p 0 )
2. j 0
Т.е. силовой ГС неустойчив, но с инженерной т. зрения эта неустойчивость нас
устраивает, хотя и не стремится к нулю, но и не увеличивается (остается
постоянной малой величиной)
Исследуем устойчивость по скорости. Заменим
p
A0 J 0 p3 ( A0 D J 0 D ) p 2 ( H 2 D D ) p k p H 0
По критерию Гурвица:
1. a j 0,
kp 0
a1 a3 0
2. j a0 a2 0 , a1a2 a0 a3
0
a1 a3
5.
( A0 D J 0 D )( H 2 D D ) A0 J 0k p HИзменять ничего нельзя кроме
kp
kp
( A0 D J 0 D )( H 2 D D )
HA0 J 0
Учитывая, что
D 0,
Условие устойчивость Силового ГС
kp
HD
J0
Силовые ГС редко применяются для стабилизации больших объектов.
Пример.
H 104 cHсмс, D 1000cHсмс, J 0 1000cHсмс 2
104103
4
kp
10
cHсм / рад
3
10
При
Т.о. силовые ГС применяют при малых
J 0 100cHсмс 2 , k p 105
J0
6. Частотный метод с помощью ЛАЧХ и ЛФЧХ
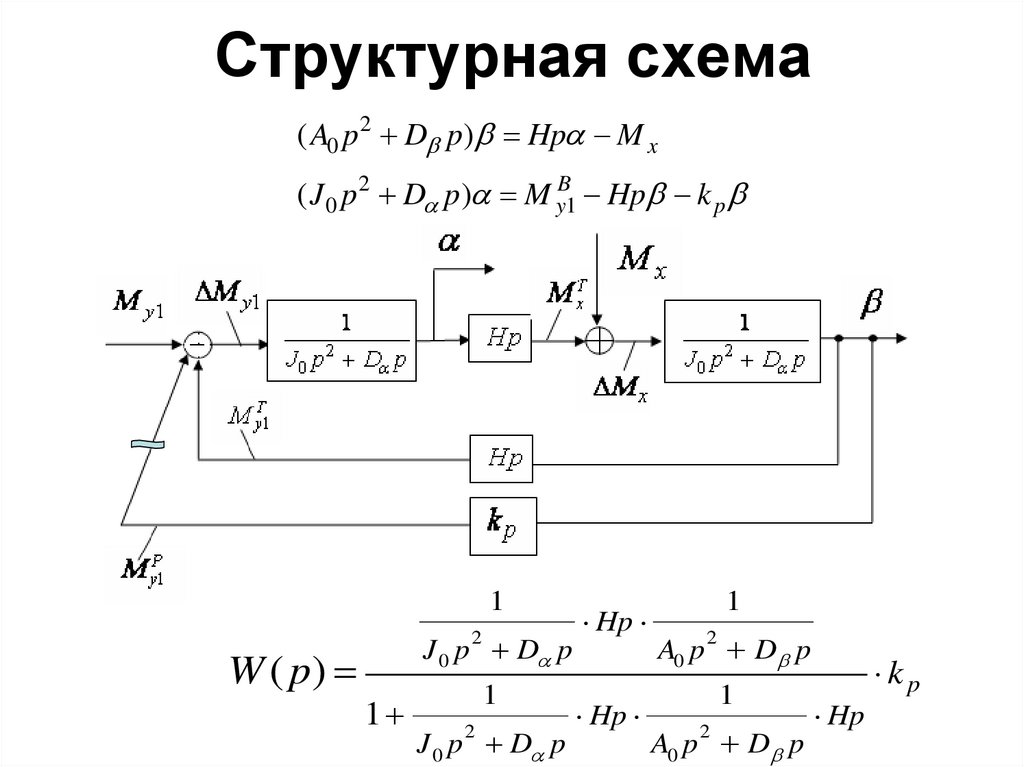
7. Структурная схема
( A0 p 2 D p) Hp M x( J 0 p 2 D p) M yB1 Hp k p
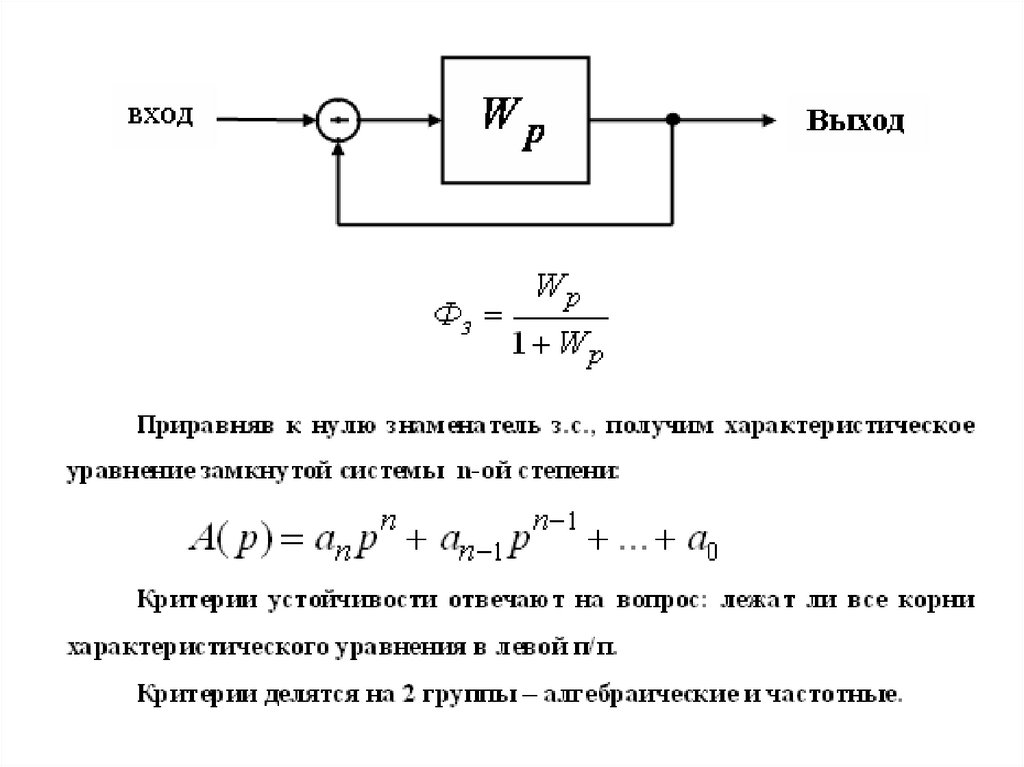
1
W ( p)
J 0 p D p
2
1
1
J 0 p D p
2
Hp
Hp
1
A0 p D p
2
1
A0 p D p
2
Hp
kp
8.
W ( p)Hk p p
J 0 A0 p 4 ( J 0 D A0 D ) p3 D D p 2 H 2 p 2
W ( p)
Hk p
p
D 0
W ( p)
kp
1
J 0 A0 p 2 ( J 0 D A0 D ) p ( D D H 2 )
W ( p)
Hk p
1
Hp T p 2 Tp 1
T
2
2
p
1
J 0 A0 p 2 A0 D p H 2
передаточная ф-ия разомкнутой системы
J 0 A0
1 A0 D 1
,
2
2
2T H
2
H
Пост. Врем. нут.кол.
A0 D
J0 H
Отн. Коэфф. Затух. Нут. Кол.
(0.01 0.1)
9.
1, M y1 ( p )
J 0 p D p
2
1
1
J 0 p D p
2
1
Hp
Hp
2
A0 p D p
1
A0 p D p
2
( Hp k p )
Hp
J 0 A0 p 4 ( A0 D J 0 D ) p 3 ( H 2 D D ) p 2 Hk p p
1
J 0 p D p
, M y 1 ( p )
1
1
1
Hp
( Hp k p )
2
2
J 0 p D p
A0 p D p
2
A0 p D
J 0 A0 p 3 ( A0 D J 0 D ) p 2 ( H 2 D D ) p Hk p
10.
W ( p)kp
1
Hp T p 2 Tp 1
2
2
11.
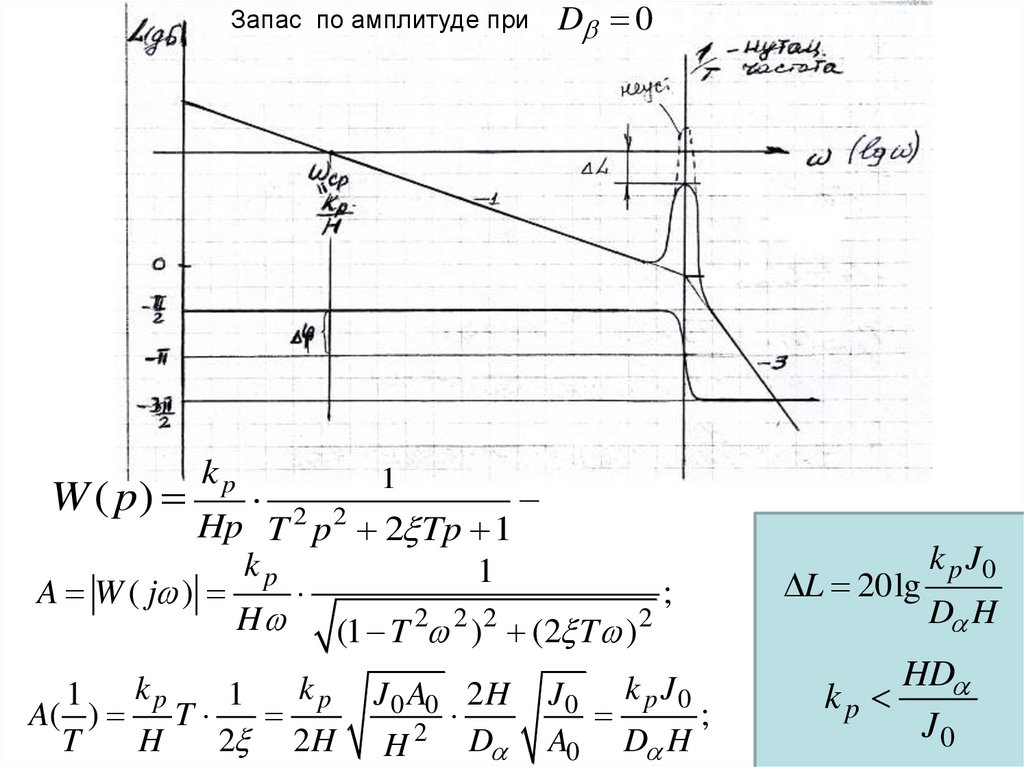
Запас по амплитуде приW ( p)
kp
1
D 0
Hp T p 2 Tp 1
kp
1
A W ( j )
;
H (1 T 2 2 )2 (2 T )2
2
2
kp
kp
1
1
A( ) T
T
H
2 2 H
J 0 A0 2 H
2
D
H
J0 k p J0
;
A0 D H
L 20lg
k p J0
D H
HD
kp
J0
12. Устойчивость
13.
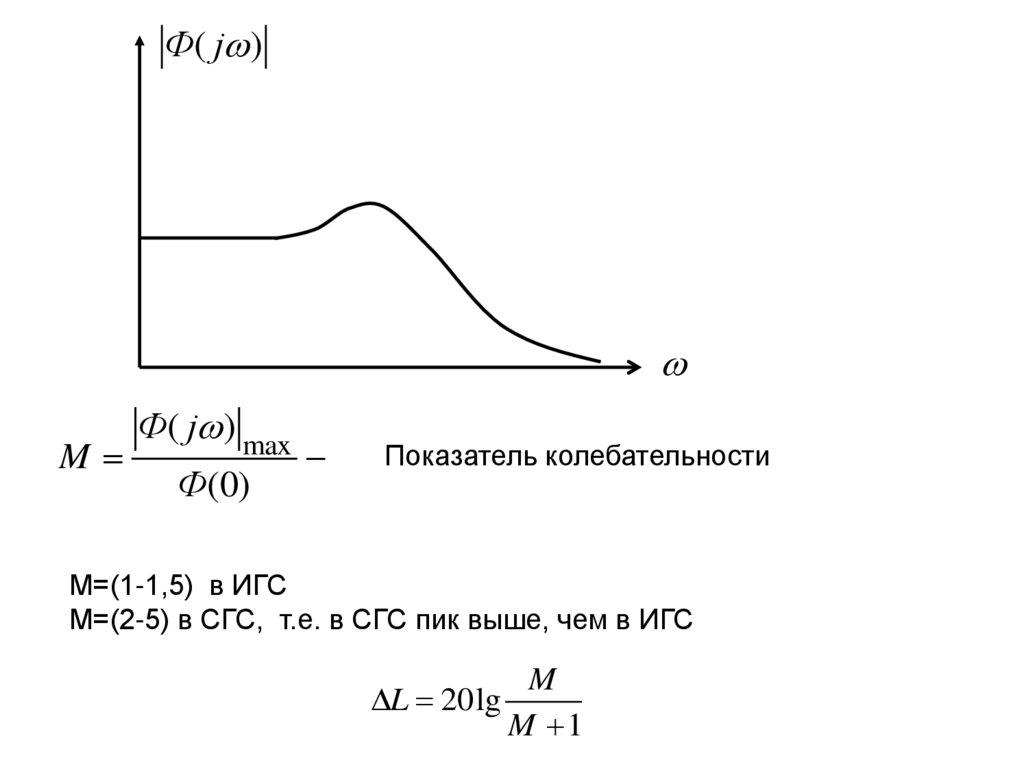
Ф( j )M
Ф( j ) max
Ф(0)
Показатель колебательности
М=(1-1,5) в ИГС
М=(2-5) в СГС, т.е. в СГС пик выше, чем в ИГС
L 20lg
M
M 1
14.
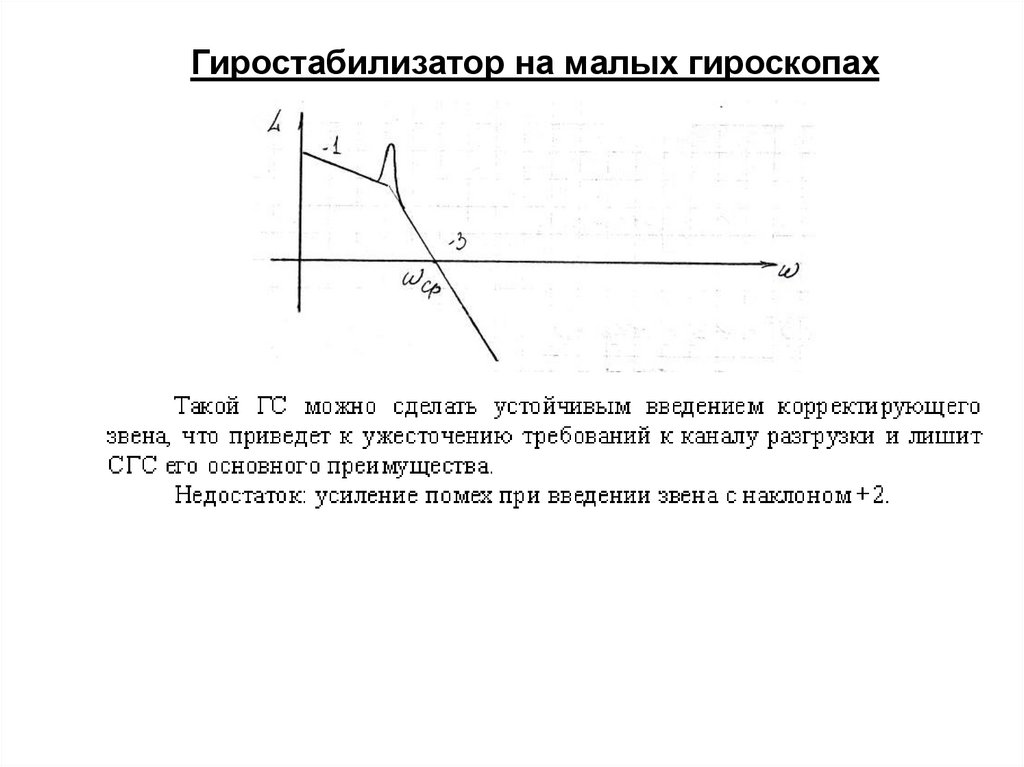
Гиростабилизатор на малых гироскопах15.
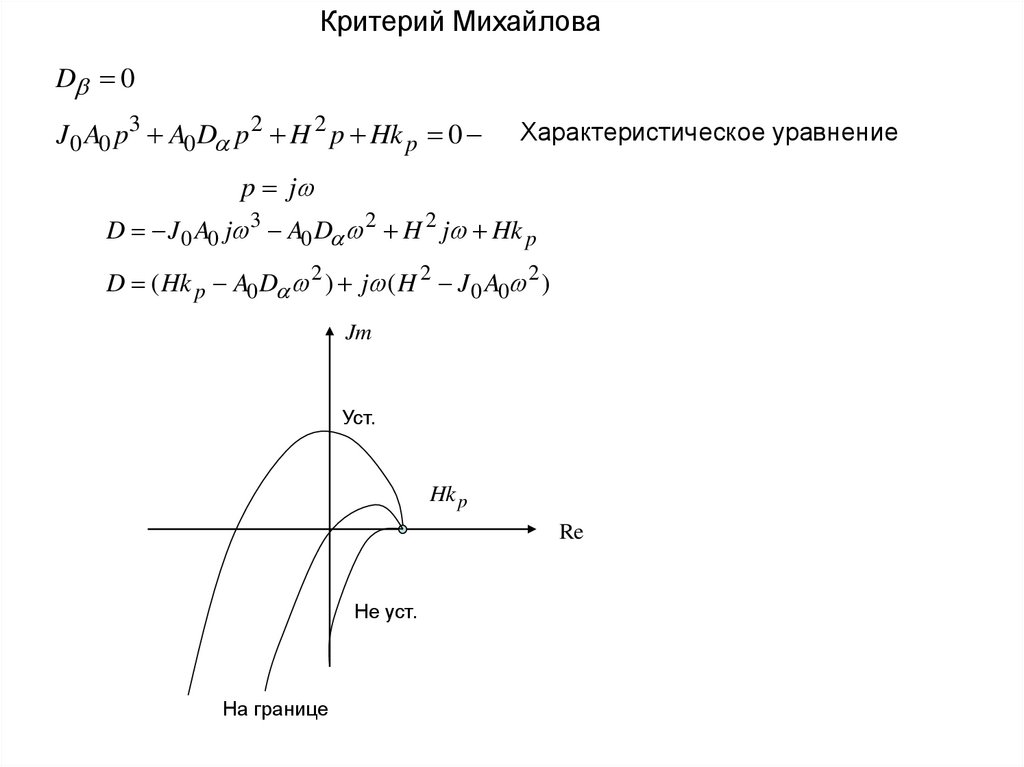
Критерий МихайловаD 0
J 0 A0 p3 A0 D p 2 H 2 p Hk p 0
Характеристическое уравнение
p j
D J 0 A0 j 3 A0 D 2 H 2 j Hk p
D ( Hk p A0 D 2 ) j ( H 2 J 0 A0 2 )
Jm
Уст.
Hk p
Re
Не уст.
На границе
16.
TaH
kp
постоянная времени системы разгрузки
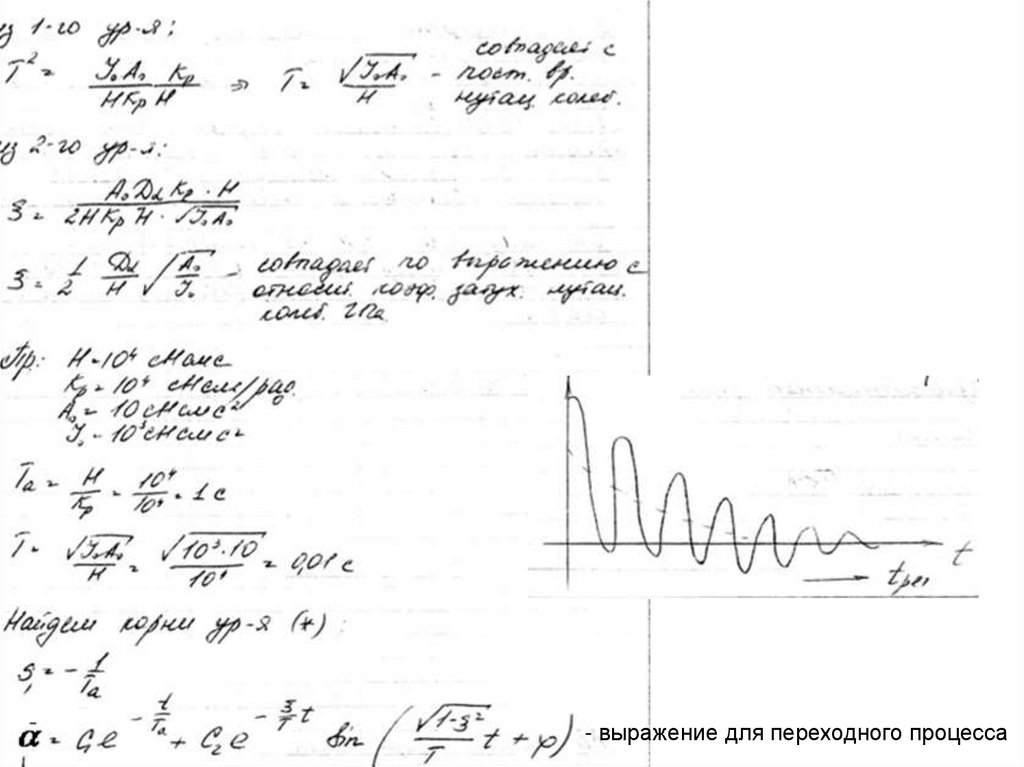
17.
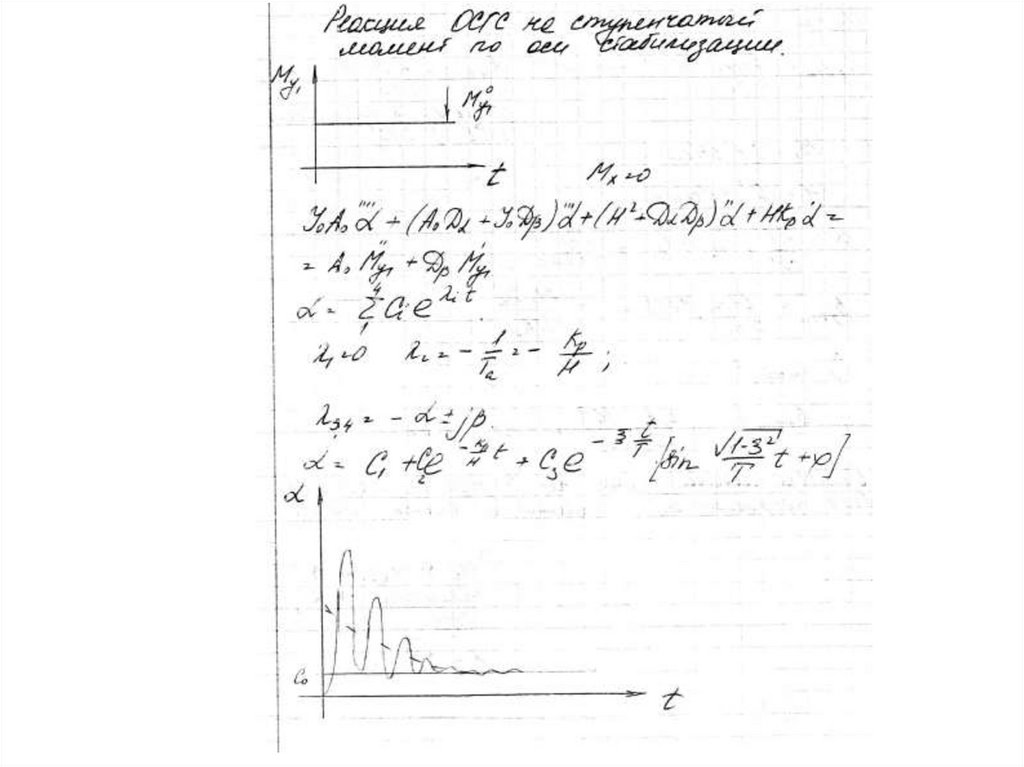
- выражение для переходного процесса18.
Таким образом, переходной процесс содержит экспоненту, определяемуюпараметрами канала разгрузки, и наложенную на нее затухающую гармонику,
определяемую параметрами только гироскопа.
Обычно экспонента затухает быстрее, чем колебательный процесс.
Таким образом. Время регулирования
t рег
гироскопа.
малый
А
демпфирования
т.к.
гироскоп
регулирования – плохое.
имеет
определяется параметрами
относительный
коэффициент
, то время регулирования – большое, а качество
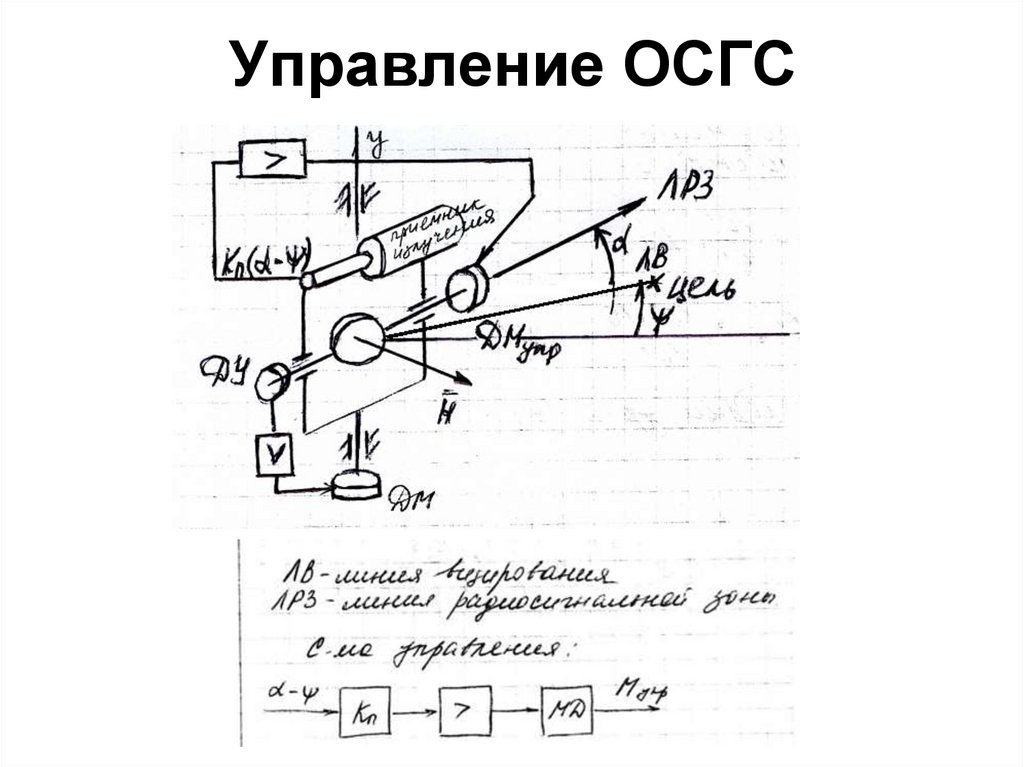
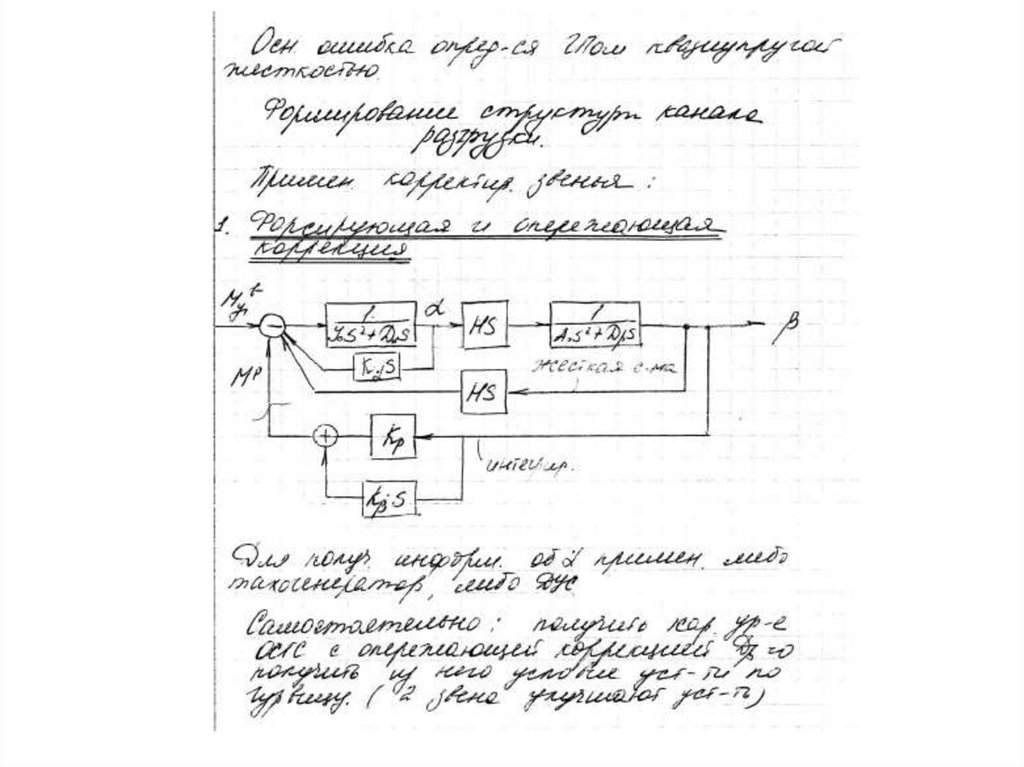
19. Управление ОСГС
20.
21.
22.
Точность стабилизацииA0 p 2 D p Hp M x
J 0 p 2 D p Hp k p M y
Hp
J 0 p 2 D p
A 0 p 2 D p
Hp k p
M x
A 0 p 2 D p
M y1
Hp k p
Hp
J 0 p 2 D p
Mx
M y1
23.
M x ( Hp k p ) M y1 ( A0 p 2 D p)( p)
J 0 A0 p 4 ( J 0 D A0 D ) p3 ( H 2 D D ) p 2 Hk p p
M y1 Hp M x ( J 0 p 2 D p)
( p)
J 0 A0 p 4 ( J 0 D A0 D ) p3 ( H 2 D D ) p 2 Hk p p
Зная изображения моментов, подставляем их в уравнения и получаем
( p)
и
( p)
Установившиеся ошибки под действием постоянных моментов
по оси стабилизации
1. Моменты:
M y1 const ,
Mx 0
уст lim ( p)
p 0
M y1D
Hk p
0
Т.к. демпфирование мало, то ошибка тоже мала. С ростом k p
еще падает.
ошибка
24.
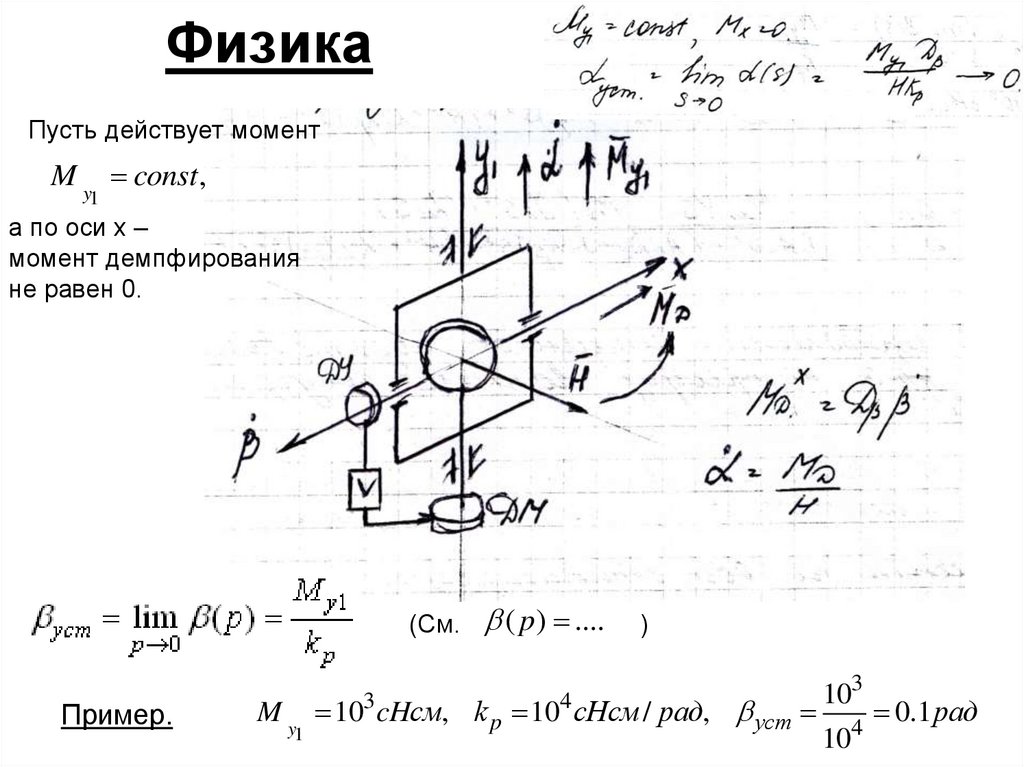
25. Физика
Пусть действует моментM y const ,
1
а по оси х –
момент демпфирования
не равен 0.
(См.
Пример.
( p) ....
)
M y 10 cHсм, k p 10 cHсм / рад, уст
3
1
4
103
10
4
0.1 рад
26.
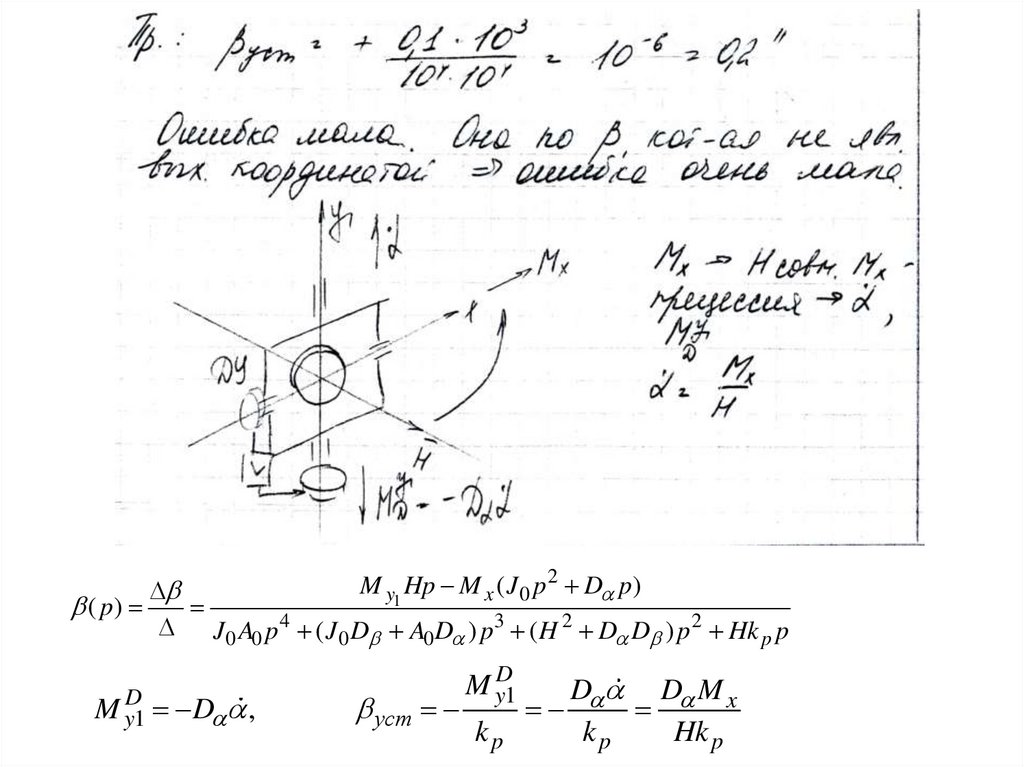
Установившиеся ошибки под действием момента по оси прецессии:M x ( Hp k p ) M y1 ( A0 p 2 D p)
( p)
J 0 A0 p 4 ( J 0 D A0 D ) p3 ( H 2 D D ) p 2 Hk p p
Mx
уст (t ) lim p 0 ( p) lim p 0
Hp
2.
M y1 0,
M x const
уст lim ( p) ,
p 0
Mx
уст lim ( p)
H
p 0
Т.е. это собственная скорость прецессии гироскопа.
Пример. M x 0,1сНсм,
H 104 сНсмс
5 1
10
2 град / час
4
c
10
M D
уст lim ( p) x
Hk p
p 0
0,1
kp
надо увеличивать
27.
M y1 Hp M x ( J 0 p 2 D p)( p)
J 0 A0 p 4 ( J 0 D A0 D ) p3 ( H 2 D D ) p 2 Hk p p
M yD1 D ,
уст
M yD1
kp
D D M x
kp
Hk p
28.
29.
30.
31.
32.
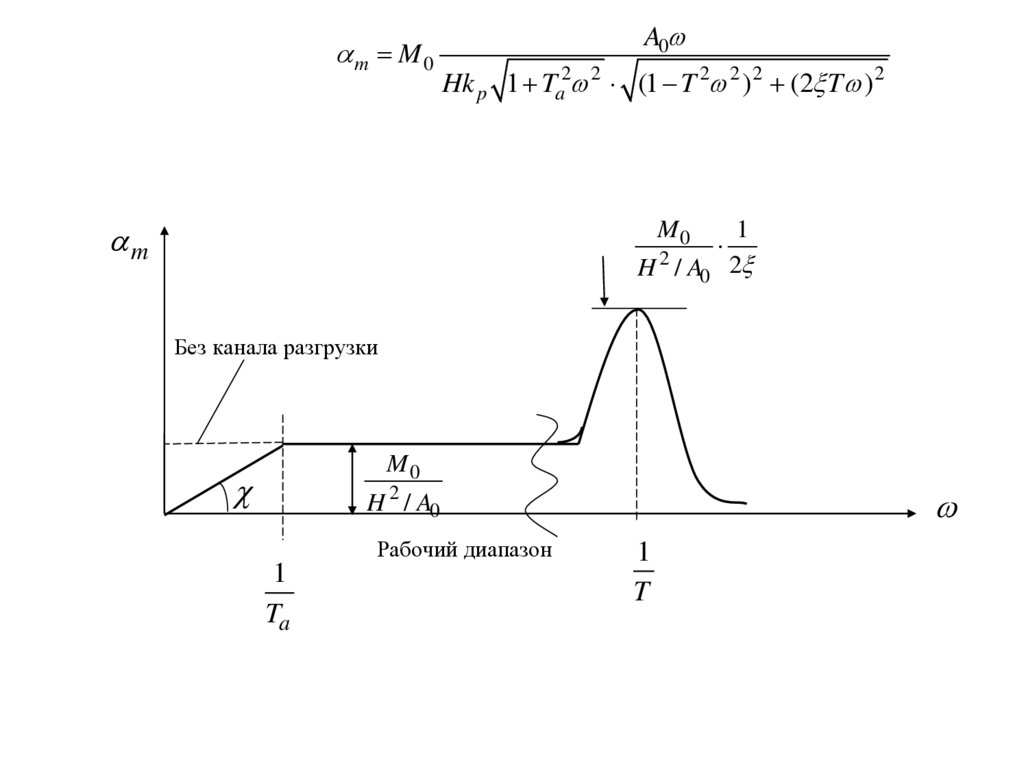
m M 0A0
Hk p 1 Ta2 2 (1 T 2 2 )2 (2 T )2
m
M0
H 2 / A0
1
2
Без канала разгрузки
M0
H 2 / A0
Рабочий диапазон
1
Ta
1
T
33.
m M 01. m M 0
A0
Hk p
A0
Hk p 1 Ta2 2 (1 T 2 2 )2 (2 T )2
tg M 0
2.
3.
4.
(Ta ) 2 1
, т.к.
и
(T ) 2 1
A0
Hk p
A0
M 0 A0 M 0 A0k p M 0 A0
m M 0
Hk pTa Hk pTa
Hk p H
H2
m
M0
2
2
H / A0
m (J0 / 2 ) M 0
34.
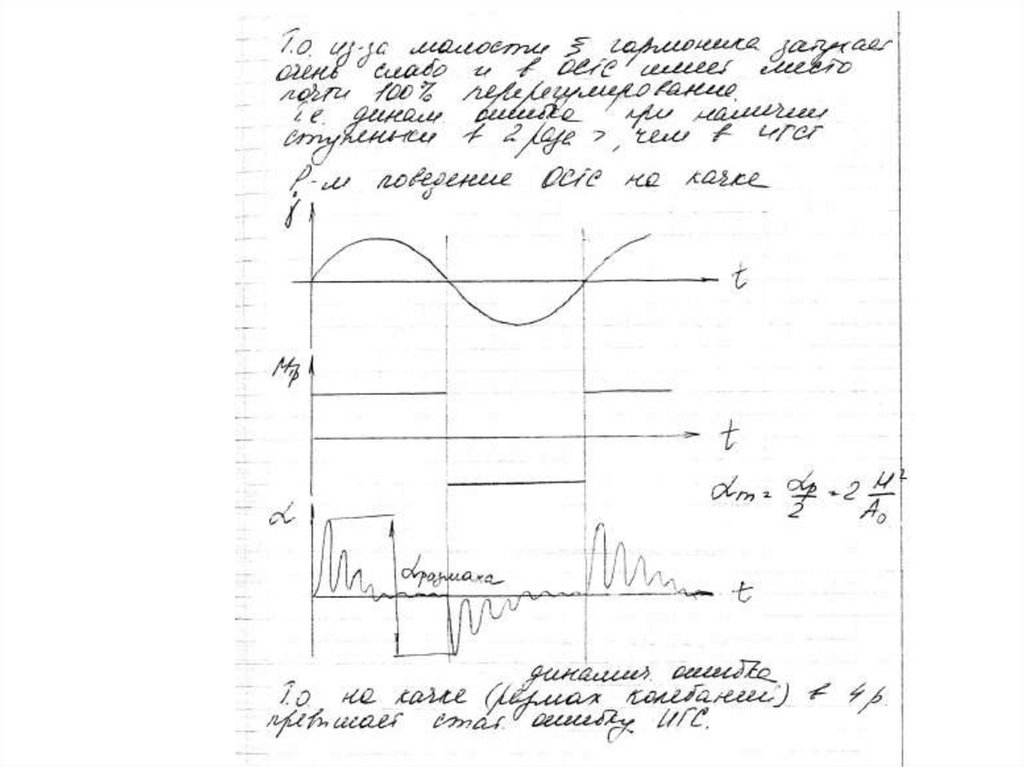
На 1 этапе работает система разгрузки (есть kp) и гироскоп.На 2 этапе ошибка определяется квазиупругой жесткостью гироскопа,
система разгрузки не работает. Величина ошибки мала, т.к. H 2 стоит
в знаменателе.
На 3 этапе – резонанс, амплитуда в десятки раз возрастает, что может
привести к поломке.
На 4 этапе – 2-ой закон Ньютона, работает инерционный момент платформы.
Пример
1 k p 104
4 1[1/ с]
Ta H 10
1
T
H
104
102[1/ c]
J 0 A0
103 10











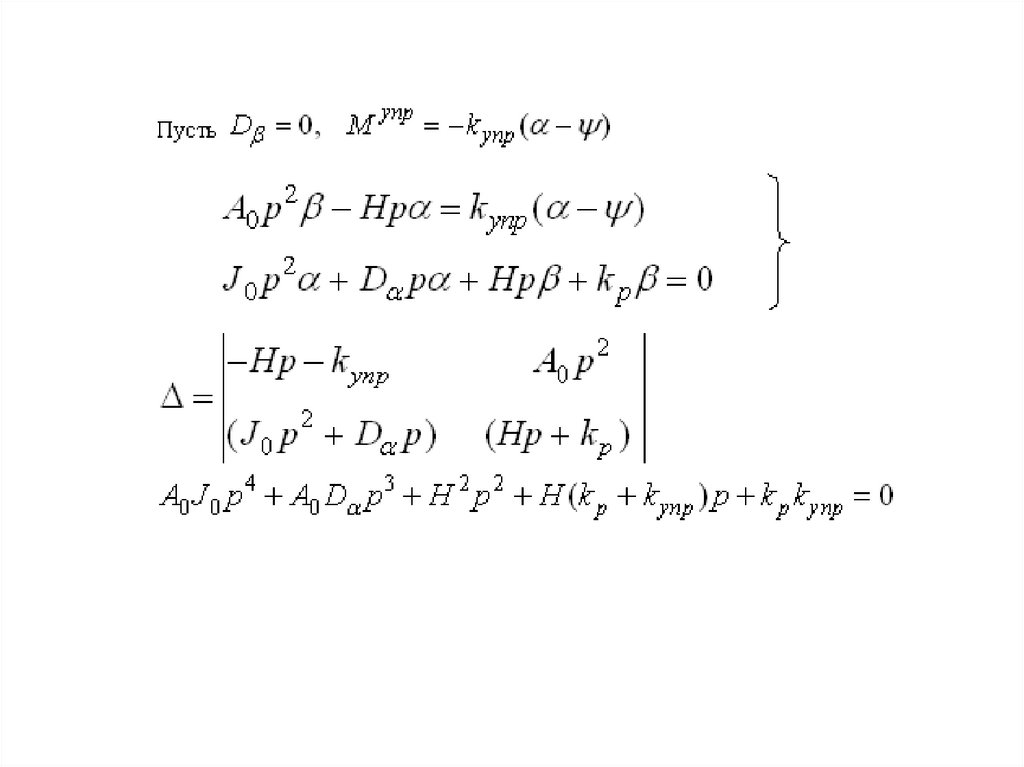









 industry
industry








