Similar presentations:
Физические основы технологических процессов
1.
Литература:1.Кушнер В.С. Технологические процессы в машиностроении: учебник для
студ.высш.учеб.заведений/ В.С.Кушнер, А.С.Верещака, А.Г.Схиртладзе.М.:Издательский центр «Академия», 2011.-416 с.
2. Кушнер В.С. Технологические процессы в машиностроении.
Часть1:Металлургия, литейное производство и обработка резанием: Учеб для
машиностроительных направлений и специальностей технических
университетов /В.С.Кушнер, А.С.Верещака, А.Г.Схиртладзе, Д.А.Негров, Омск, Изд-во ОмГТУ,2005.- 200 с.
3. Кушнер В.С. Технологические процессы в машиностроении.
Часть2:Обработка давлением и сварочное производство Учеб для
машиностроительных направлений и специальностей технических
университетов /В.С.Кушнер, А.С.Верещака, А.Г.Схиртладзе, Д.А.Негров, Омск, Изд-во ОмГТУ,2005.-200 с.
4. Кушнер В.С. Технологические процессы в машиностроении. Часть3: Тесты
для контроля остаточных знаний и текущего контроля знаний: Учеб.для вузов
/В.С.Кушнер, А.С.Верещака, А.Г.Схиртладзе, Д.А.Негров, -Омск, Изд-во
ОмГТУ,2006.-172 с.
4. Способы обработки конструкционных материалов: -обработка
резанием:Кушнер В.С. и др. Метод.указ.к лабор.работам- Омск, Изд-во
ОмГТУ,2011
5. Способы обработки конструкционных материалов: -обработка литьем
Кушнер В.С. и др. Метод.указ.к лабор.работам- Омск, Изд-во ОмГТУ, .
Способы обработки конструкционных материалов: -обработка давлением
Кушнер В.С. и др. Метод.указ.к лабор.работам- Омск, Изд-во ОмГТУ,
2. Лекция №1
ВведениеОсновными задачами дисциплины «Физические основы
технологических процессов» являются :
- научиться обосновывать и выбирать технические
характеристики технологического оборудования при
применении металлургических и машиностроительных
технологий, основанных на изменении агрегатного
состояния материала , а также на формоизменении
заготовок и деталей путем механической обработки
- назначать рациональные технологические режимы обработки
материалов и получения заготовок и деталей в различных
металлургических и машиностроительных производствах
- научиться анализировать и моделировать механические,
тепловые и термомеханические физические явления ,
составляющие суть разнообразных технологических
процессов , на основе общих фундаментальных физических
законов
3.
По особенностям формообразования различают литейныетехнологии, основанные на изменении агрегатного состояния,
технологии обработки материалов давлением , резанием ,
сварочные технологии и др.
Физические процессы разнообразных металлургических и
машиностроительных технологий
в значительной
мере
основаны на закономерностях нагрева или
охлаждения
материалов с целью изменения агрегатного состояния
(плавления,
кристаллизации),изменения
механических
свойств и сопротивления
пластическим
деформациям,
способности к соединению различных частей заготовок
(сварке), составляющих два крупных научных направления:
теплофизику и механику технологических процессов.
Изучение физических основ технологических процессов
и способов производства и обработки важно для более
глубокого понимания изучаемых процессов и технологий.
4.
Следуя традициям, заложенным в теоретической механике,основными разделами механики считают кинематику
(твердого тела и сплошной среды), статику и динамику.
С позиций кинематики обычно классифицируют и
схематизируют различные технологические процессы
(способы).
Иллюстрацией этого является классификация и
схематизация способов лезвийной обработки материалов
резанием.
5.
Схема продольного точения6.
Основная плоскость перпендикулярна скоростидействительного главного движения (рис.а)
в основной плоскости измеряют действительный угол в
плане : между проекцией режущей кромки и рабочей
плоскостью (направлением подачи). В этой же плоскости
измеряют и радиус r при вершине (радиус закругления
вершины).
Рабочая плоскость содержит векторы скорости резания v
и подачи s (рис. б)
в рабочей плоскости измеряют действительный задний угол
: как угол между задней поверхностью и скоростью резания
Плоскость резания содержит режущую кромку и скорость
резания v.
Если режущая кромка криволинейная, то плоскость резания
касается режущего лезвия в рассматриваемой точке
7.
В плоскости резания измеряют угол наклона режущейкромки : между режущей кромкой и основной плоскостью.
Положительным считается угол , если вершина резца –
самая низкая точка режущей кромки
Плоскость стружкообразования перпендикулярна режущей
кромке в данной точке режущей кромки (для элементарного
участка стружки шириной b).
В плоскости стружкообразования определяют
действительный передний угол : между основной
плоскостью и направлением схода стружки (при отсутствии
нароста – передней поверхностью)
Считается, что закономерности деформации, силы резания,
температуры в плоскости стружкообразования одинаковы
для различных способов лезвийной обработки резанием.
Благодаря этому можно создать теорию стружкообразования,
общую для различных способов резания.
8.
Условие непрерывности и усадка стружкиv sin y v1 cos y
v cos y
,
v1
sin y
v t L рез
G
l
v1 t Lстр st Lстр
vab v1a1b1
a1
а
a cos
у arc tg
sin
b1
а l, b 1
b
9.
Относительный сдвигУсловие контакта
инструмента со
стружкой:
v cos v2 cos y
cos
v2 v
cos( y )
v2
cos
vn cos y sin y
1 2 sin
ctg y tg y
.
cos
10.
Скаляр, векторСкаляр величина , значение которой может быть выражено одним числом
Примером скалярной величины является температура в конкретной точк
пространства в конкретный момент времени.
Вектор - величина , для которой любому направлению в пространстве
может быть поставлен в соответствие скаляр посредством
соотношения, линейного относительно направляющих косинусов :
3
x x1e1 x2e2 x3e3 xi ei
3
i ei ,
i 1
i 1
1 cos , e1 , 2 cos , e2 , 3 cos , e3
x x1 cos , e1 x2 cos , e2 x3 cos , e3
Примерами векторных величин являются тепловой поток , сила,
скорость .
11.
Тензор (второго ранга)Тензор (второго ранга) - величина , для которой любому
направлению в пространстве может быть поставлен в соответствие
вектор посредством соотношения, линейного относительно
направляющих косинусов :
T T1 cos , e1 T2 cos , e2 T3 cos , e3
T1 T11e1 T12e2 T13e3
T2 T21e1 T22e2 T23e3
T3 T31e1 T32e2 T33e3
T11 T12 T13
T T21 T22 T23
T
T
T
31 32 33
Примерами тензорных величин являются деформации
и напряжения
Деформа́ция (от лат. deformatio — «искажение») —
изменение взаимного положения частиц тела, связанное с
их перемещением друг относительно друга.
12.
Деформации. Характеристики деформацииДеформации среды характеризуются симметричным тензором деформаци
x xy xz
ij yx y yz .
zx zy z
x, y, z
1
xy yx xy
2
zy yz
xz zx
1
zx
2
1
yz
2
- Линейные деформации по осям x, y, и z,
xy , xz , yz - Угловые деформации
(деформации сдвига)
.
При повороте осей координат компоненты тензора деформации
изменяются. Существует одно положение системы координат, при
котором угловые деформации равны нулю. Оно описывыется
уравнением:
x xy
xz
yx y yz 0
zx
zy
z
I1 I 2 I 3 0
3
2
13.
Тензор деформации можно представить в виде суммы шарового тензораи девиатора:
0
0
T 0 0
0
0
0
x 0
xy
0 , D yx
y 0
0
0
zx
zy
xz
yz
z 0
где
0
x y z
3
Первый инвариант тензора деформации используется для условия
постоянства деформируемого объема (несжимаемости материала):
I1 x y z 0
Второй инвариант девиатора деформации используется для
характеристики деформации - интенсивности деформации .
Интенсивностью деформаций называют величину, пропорциональную
квадратному корню из второго инварианта девиатора деформаций
4
I 2 D
3
2
2
2
2 3 2
2
2
i
x y y z z x xy yz
zx
3
2
i
Интенсивность
деформаций сдвига
Г 4 I 2 D 3 i
14.
Для малых деформаций компоненты тензора деформаций можновычислить по формулам Коши:
1 дU i дU j
ij
2 дx j
дxi
(i = 1,2,3; j = 1,2,3).
1 x, 2 y , 3 z
дU y
дU x
дU z
x
, y
, z
,
дx
дy
дz
дU y дU z
дU x дU y
дU z дU x
xy
, yz
, zx
.
дy
дx
дz
дy
дx
дz
Тензор скоростей деформации
дVi дV j
ij
дx j дxi
(i = 1,2,3; j = 1,2,3).
15.
Л.3.Схема зоны деформации при образовании сливной
стружки с зоной стружкообразования с параллельными
границами и областями пластических деформаций на передней
поверхности и в застойных зонах
A – зона стружкообразования с параллельными границами;
Б – застойная зона адиабатических деформаций;
В и Г – зоны контактных
деформаций на передней и задней
поверхностях.
16.
Распределение деформаций в зоне стружкообразованияи в застойных зонах
17.
Поле скоростей в зонепараллельными границами
стружкообразования
y
v x y v v 2
H
v y vn .
с
n
,
18.
Скорости деформации при резании1 дvi дv j
ij
2 дx j дxi
xy
yx
(i = 1, 2, 3; j = 1, 2, 3).
1
1 дv x y 1 v 2
xy
n
2
2 дy
2 H
y
H
n 1
Для : = 2,5, v = 1 м/с, у=30 о, n = 5, H = (0,2–0,5)a, a=0,2 мм,
6
xy H 0,6 1,5 10
, c–1
- Резание
- Растяжение
истинные деформации в зоне стружкообразования
0, 018 1/с
и y
y / vn
0
v2 y
n
H H
n 1
y
d
vn
v2 y
y
.
H
vn H
n
n
19.
Деформации при растяженииl1 l0 l
z
l0
l0
l
*100, %
l0
х y
1 l
2 l0
ij 0
0
0
1 l
2 l0
0
0
l
l0
Относительное удлинение
х y ,
2 Z 0,
1
1 l
Z
2
2 l0
Истинные деформации
l
l0 l
dl
l1
Zu ln ln
ln 1
l0
l0
l0
0
l0 l
i z
l
Истинные деформации сдвига: u 3 ln 1
l0
l1
20.
СТАТИКАНапряженное состояние , напряжение
Напряжение является мерой
внутренних сил, возникающих в теле
под влиянием внешних воздействий
(нагрузок, изменения температуры и
др.).
Напряжение T зависит только от
положения точки А и направления
нормали , то есть каждому
направлению соответствует свое
напряжение T
21.
Соответствие напряжений T любому направлению устанавливается наоснове принципа равновесия с помощью тензора напряжений.
ij (i = 1, 2. 3; j = 1, 2, 3).
x
ij yx
zx
xy xz
y yz
zy z
xy yx , xz zx , yz zy.
22.
Имеется такое положение системы координат, при котором вдоль одной из осейнормальное напряжение максимально, а вдоль другой - минимально, причем
касательные напряжения на площадках, перпендикулярных этим осям,
равны нулю. Эти направления называют главными.
напряжения 1, 2, 3; вдоль главных направлений называют главными
1 всегда обозначает наибольшее нормальное напряжение, а 3
- наименьшее.
-
Наибольшее касательное напряжение лежит в плоскости, нормаль к
которой делит угол между минимальным и максимальным
нормальными напряжениями пополам, и равно:
max
1
1 3
2
Три инварианта I1, I2, I3 определяют главные направления
тензора напряжений и сами находятся из условия
равенства нулю касательных напряжений при повороте
системы координат
23.
Сумму нормальных напряжений называют первыминвариантом I1 тензора напряжений:
I1 x y z 3 0 .
x y z
называют гидростатическим давлением
0
3
S x xy xz S x x 0 , S y y 0 , S z z 0
S yx S y yz называют девиатором напряжений
S
zy
z
zx
Второй инвариант определяется следующим выражением
I 2 y z z x x y
i 3I 2 (S )
2
yx
2
zx
2
zy .
интенсивность нормальных напряжений i
i I 2 (S ) интенсивность касательных напряжений
24.
Упругость, прочность , пластичностьE
закон Гука:
где E – модуль упругости
при растяжении (модуль Юнга)
предел упругости
y
предел пропорциональности пц.
предел текучести Т
Pmax
b
.
F0
- условный предел прочности
S b b 1
-действительный
предел прочности Sb
0, 2
F0 dz Fdz 1
F0
F
1
25.
Условия пластичностипластические деформации происходят, когда значение второго инварианта
девиатора напряжений достигает некоторой постоянной (для данных
условий деформирования ) величины :
2
1 2
I 2 S1 S22 S32 Т .
2
3
Условие пластичности Мизеса может быть записано в виде:
i I2 Т .
Т характеризует сопротивление материала деформации в данных
условиях деформирования и называется пределом текучести на сдвиг
Для интенсивности нормальных напряжений
условие пластичности Мизеса примет вид :
i 3 i
i Т
26.
Влияние условий деформирования на сопротивлениематериалов пластическим деформациям
Идеально пластическое тело
Т 0
Т 0
Отношение абсолютной температуры к
абсолютной температуре плавления
называют гомологической температурой
Повышение температуры деформации способствует возвращению металла
структурно-неустойчивого состояния, полученного в результате пластических
деформаций, в более устойчивое структурное состояние
Абсолютная температура, при которой отдых и рекристаллизация
происходят более интенсивно, чем искажение кристаллической решетки и
упрочнение пропорциональна абсолютной температуре плавления
Для металлов обычной
Т рек
T
0,3 0,4
технической чистоты
Т пл
Горячей называют деформацию при температуре, равной или выше
температуры рекристаллизации. при горячей деформации при постоянной
температуре и постоянной скорости деформации имеют вид прямой,
параллельной оси деформации
27.
для свинца, имеющего температуру плавления Тпл=600 К при комнатнойтемпературе гомологическая температура равна: Т 0,49
для стали , имеющей температуру плавления 1800 К, идеальная
пластичность может быть при температуре около 700 - 900 К
(400 - 600 град. Цельсия)
Схема к определению удельных касательных сил при резании
P sin y v2 cos y
AW
y
*
ab
v cos
u
28.
Простое нагружение, теория теченияХолодной называют деформацию при температуре ниже температуры
рекристаллизации. T Т рек
Пластические деформации вызывают повышение плотности дислокаций,
искажение кристаллической решетки и приводят к увеличению напряжения
m
p
p 0
0
29.
Влияние температуры деформации при растяженииТ 0 exp B T
Т Т 0
Т 0 1
1 Т 0
Влияние температуры на предел прочности стали 45
B
30.
Влияние скорости деформации при растяженииВлияние скорости деформации и температуры на предел прочности стали 45
при относительном удлинении = 20
Коэффициент динамичности
0
k Т
K
31.
Влияние скорости деформации при резаниирезание сталей 00, 10, 20Х,
Х18Н9Т
Со скоростью резания
v = 0,2 м/мин a = 0,22 мм и
о, Н.Н.Зорев
cp
m
1 u Sb p
d p
0
u
3 0
AS b m
u ,
m 1
обобщенное определяющее уравнение :
Т 0
0
m
0
k Т
exp B Т ,
32.
Сопротивлениематериалов
большим
пластическим
деформациям в адиабатических условиях деформирования
Aw S b
T
Aw A1
СV Tпл
и
Aw
o
AW
dAw
AK pm exp B * A1 AW
d p
p
Sb
y
Sb
p
dAw
S b d p
d p
u
0
k Т
K
exp B * A1 AW dAw AK pm d p
33.
Удельная работа деформацииA
AA1 BK 1 m
Sb
1
Aw
ln 1
p A1
СV Tпл
BA1
1 m
3 3 ln 1 100
3,5
Удельная работа
1
m
Расчет сталь
С45 -резание
3
2,5
Эксперимент
сталь С45 резание
растяжение
сталь 45
2
1,5
1
0,5
0
0
1
2
3
4
5
Экстраполяция
растяжение,
сталь С45
Текущий истинный сдвиг
Гипотеза о равенстве удельных работ при сжатии и резании
А.М.Розенберга использовалась для расчета сил резания
34.
Удельная работа3
Расчет сталь
35Х3МН резание
2,5
2
1,5
Эксперимент
сталь 35Х3МН
- резание
1
0,5
0
0
1
2
3
4
5
Без учета
локализации
Текущий истинный сдвиг
Влияние локализации деформаций в узкой зоне на зависимости
удельной работы от деформации при резании стали 35Х3МН
35.
Кривая течения для адиабатических условия деформированияp
p
Отношение предела текучести к
действительному пределу
прочности
dAW
S b d p
Sb
m
AK p 1
AA1 BK 1 m
p
1 m
1
средний предел текучести
на сдвиг при растяжении
1
0,9
0,8
0,7
0,6
Экстраполированное
среднее значение
предела текучести на
сдвиг при растяжении
Средний предел текучести
на сдвиг в зоне
стружкообразования
0,5
0,4
0,3
0,2
0,1
0
0
1
2
3
4
Текущий истинный сдвиг
5
Расчетный средний
предел текучести резание стали С45
Гипотеза о единой кривой течения использовалась Зоревым Н.Н.
36.
Действительные характеристики сопротивления материалапластическим деформациям в адиабатических условиях
AK ~ m
,
Sb
1 m
~
1
m 1 m 1 m
~
AK
A
B
1
B 1,25;
K 1,3;
K q 1,6
q
Sb
A K q qm
1 m
m 1 m
q
A K q A1 B
условие локализации деформаций:
d p
d p
1
1 m
0
37.
Влияние локализации деформаций на кривую теченияp p при p p p и
p p
p и при p p p u
Отношение предела
текучести к
действительному
пределу прочности
0,8
0,7
0,6
0,5
0,4
0,3
0,0
0,5
1,0
1,5
2,0
2,5
3,0
3,5
4,0
Текущий и конечный истинный сдвиг
без учета локализации
конечный истинный сдвиг 4
Конечный истинный сдвиг 3
Конечный истинный сдвиг 2
Удельные касательные силы в плоскости сдвига, эксперимент
4,5
38.
Л.1.ТЕПЛОФИЗИКА ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
1.1.Виды теплообмена. Температурное поле. Градиент
температуры.
три основных вида теплообмена: теплопроводность,
конвекция и тепловое излучение.
Теплопроводность — это молекулярный перенос теплоты
между непосредственно соприкасающимися телами или
частицами одного тела с различной температурой, при
котором происходит обмен энергией движения структурных
частиц (молекул, атомов, свободных электронов).
Конвекция осуществляется путем перемещения в
пространстве неравномерно нагретых объемов среды. При
этом перенос теплоты неразрывно связан с переносом самой
среды.
Тепловое излучение характеризуется переносом энергии от
одного тела к другому электромагнитными волнами.
Передача теплоты теплопроводностью связана с наличием
разности температур тела.
39.
Совокупность значений температур всех точек тела в данныймомент времени называется температурным полем.
x, y, z,
- нестационарное объемное температурное по
Если температура тела не изменяется с течением времени,
то температурное поле называется стационарным.
д
x, y, z ,
0.
д
Температурное поле может быть также плоским или одномерны
Точки тела с одинаковой температурой образуют
изотермическую поверхность (для объемного
температурного поля) или изотермическую линию
(изотерму) (для двухмерного температурного поля .
40.
Градиент температуры.Интенсивность изменения температуры T характеризуется производной
по направлению s, принимающей наибольшее значение в направлении
нормали к изотермической поверхности .
Вектор, направленный по нормали к изотермической поверхности в
сторону возрастания температуры, модуль которого равен производной
температуры
по
этому
направлению, называется
градиентом
температурного поля.
дТ
дТ
grad T
дs max дn
дТ
ex ,
для одномерного температурного поля T(x, ) grad T
дх
Для двухмерного нестационарного температурного поля
дТ
дТ
gradT
ex
ey
дх
дy
дТ
дТ
дТ
а для трехмерного поля: grad T
ex
ey
ez
дх
дy
дz
41.
1.2. Основные законы теплопроводности (Фурье) итеплоотдачи.(Ньютона – Рихмана)
Основной закон теплопроводности, коэффициент
теплопроводности
Количество
тепла,
поступившее
через
изотермическую поверхность площадью F за единицу
времени, называют тепловым потоком Ф:
Тепловой поток, отнесенный к единице
площади изотермической поверхности,
называют плотностью теплового потока
Ф
1 dQ
qф
F d
dQ
, Вт
d
Вт / м2
Основной закон теплопроводности (Закон Фурье):
дT x,
q ф gr a dТ
ex
дx
плотность теплового потока пропорциональна градиенту
температуры
42.
Основной закон теплоотдачи (Ньютона-Рихмана) ,коэффициент теплоотдачи
Основной закон теплоотдачи (Ньютона-Рихмана) гласит:
количество теплоты, передаваемое конвективным
теплообменом прямо пропорционально разности температур
поверхности тела (Тп) и окружающей среды (Тс):
Ф= α · (Тп - Тс )·F ,
или
q = α · (Тп - Тс ) ,
где: коэффициент теплоотдачи [Вт/(м2К)], характеризует
интенсивность теплообмена между поверхностью тела и
окружающей средой.
43.
СредаКоэффициент
теплоотдачи
Вт/(м*м*К)
Спокойная вода – металлическая 300 – 580
стенка
Текущая вода – металлическая 350+2100* v
стенка
Кипящая вода – металлическая
стенка
3500 - 5800
V – в м/с
Ф * * F
Например, при
1000 Вт /( м 2 К ),
100К ,
F 5 *10 6 м 2
Ф 0,5 Вт
Влияние охлаждения путем теплоотдачи в воздух или в жидкую
среду эффективно в тех случаях, когда мощности источников
теплоты близки к мощности теплоотдачи. С увеличением мощности
тепловыделения эффективность охлаждения теплоотдачей
снижается
44.
1.3. Теплофизические характеристики материаловкоэффициент пропорциональности плотности теплового потока градиенту
температуры, называется коэффициентом теплопроводности.
Коэффициент теплопроводности равен количеству тепла,
протекающему за единицу времени через единицу поверхности
при перепаде температуры на единицу длины, равном одному градусу.
Теплопроводность Вт/(м*К)
380
Размерность
коэффициента
теплопроводности определяется
отношением
размерностей
плотности теплового потока и
градиента температуры:
330
280
230
180
130
80
30
300
400
500
600
700
800
900
Температура, К
Железо
Кобальт
Магний
Медь
Никель
1000
q
ф
gradT
ватт на метр-кельвин (Вт/(м К)).
45.
ТеплоёмкостьТеплоёмкость тела - отношение бесконечно малого количества теплоты
полученного телом, к соответствующему приращению его температуры:
Q dQ
.
dT
T 0 T
C lim
Единица измерения теплоёмкости в —Дж/К.
Уде́льная теплоёмкость —
1
Q 1 dQ
отношение теплоемкости
с
lim
.
к массе
М T 0 T М dT
Дж/(кг*К)
Объемная теплоемкость — это количество теплоты,
которое необходимо подвести к единице объема
вещества, чтобы нагреть его на единицу температуры.
1 dQ
с СV
Дж /( м3 / К )
V dT
46.
Теплоемкости различных металлов (Fe, Co, Cu, Ni) взависимости от температуры.
1000
950
Теплоемкость Дж/(кг*К)
900
850
800
750
700
650
600
550
500
450
400
350
400
600
800
1000
1200
1400
Температура, К
Железо
Кобальт
Медь
Никель
47.
МатериалыСV МДж
Вт
м К
м3 К
Чугун (СЧ 12-28)
40
3.5
11.4
Углеродистые стали
40
5
8
Стали на аустенитной основе
22.5
4.5
5
Титановые сплавы (ВТ3 и др.)
13.2
2.7
4.9
Никелевые сплавы (ХН77ТЮ и др.)
19.7
4.8
4.1
Медь
360
3.6
100
Алюминий
223
2.7
84
Латунь (ЛС-59)
147.3
3.7
39.8
Полистерол, фторопласт
0.25
2.5
0.1
Быстрорежущая сталь (Р18)
27
5.1
5.3
Твердый сплав ВК8
54
2.2
24.5
Твердый сплав Т5К10
38.3
2.7
14.2
Твердый сплав Т15К6
27.1
2.7
10
Алмаз
146
1.75
83.4
мм 2
с
48.
Теплофизические характеристики песчаной формовочной смесии некоторых литейных сплавов
Вид песчаной ,
с,
Сv,
3 кДж /(кг К )
Смеси
кг / м
МДж / м3 К
,
Песок сухой
1600
0,84
1,344
0,87
1,0813
Смесь сырая
1800
1,05
1,89
0,29
0,7403
Смесь сухая
1700
0,84
1,428
0,17
0,4927
1,7
0,51
0,07
0,1889
7200
0,84
6,048
29
13,24
7000
0,77
5,39
40
16,68
Алюминиевые
2600
сплавы
1,15
2,99
290
29,44
Сырая
опилками
Сталь
Чугун серый
с 300
Вт / м К
,
кДж
м 2 К с1 2
49.
Удельная теплота плавления металловУдельная теплота плавления количество теплоты ,
которое необходимо сообщить одной единице массы
кристаллического вещества в равновесном изобарноизотермическом процессе, чтобы перевести его из
твёрдого состояния в жидкое
Металл
Алюминий
Вольфрам
Железо
Золото
Магний
Медь
Натрий
Олово
Удельная
теплота
Металл
плавления
кДж/кг
393
Платина
184
Ртуть
270
Свинец
67
Серебро
370
Сталь
213
Тантал
113
Цинк
59
Чугун
Удельная
теплота
плавления
кДж/кг
113
12
24,3
87
84
174
112,2
96-140
50.
1.4. Уравнение теплопроводностиКоличество тепла, поступившего за время через
единичную площадь поверхности, может быть
определено через приращение плотности теплового
потока
дq
Q1 qф
Здесь линейная часть
приращения плотности
теплового потока :
дqФ
qФ
дx
ф
дx
x .
x,
дТ
q
С учетом основного закона Ф
дx
теплопроводности приращение количества
тепла равно:
Q1
д 2Т
дx
2
x .
51.
Изменение энтальпии (теплосодержания) равно:дТ
Q2 CV Т x CV
x
д
При передаче тепла теплопроводностью количество тепла,
поступившее в рассматриваемый элементарный объем за
время (или отведенное из этого объема) изменяет
теплосодержание этого объема ровно на эту величину
Q1 Q2
Приравнивая
Q1 и Q2 , получим:
дТ
д 2Т
CV
x 2 x
д
дx
дТ
д 2Т
д 2Т
д CV дx 2
дx 2
52.
Т.о. уравнение теплопроводности для одномерногонестационарного температурного поля
дТ
д 2Т
2
где
- Коэффициент температуд
дx
СV ропроводности м2 / с
Уравнение теплопроводности для двухмерного
нестационарного температурного поля
д 2Т д 2Т
дТ
2 2
дx
д
дy
Уравнение теплопроводности для трехмерного
нестационарного температурного поля
д 2Т д 2Т д 2Т
дТ
2 2 2
дx
д
дy
дz
53.
1.5. Начальные и граничные условияДля получения частного решения дифференциального уравнения
теплопроводности задают начальные и граничные условия.
Начальное условие задает распределение температуры внутри тела
(для одномерного поля - в стержне) в начальный момент времени:
Т x ,0 f x где f(x) - известная функция.
Важным частным случаем является равномерное распределение температуры
в начальный момент времени:
T x,0 T0 .
Граничные условия задают различными способами:
раничные условия первого рода задают в виде распределения температуры
а поверхности тела (на торце стержня) в любой момент времени :
Тп f .
Важным частным случаем является задание постоянной температуры:
Т п Tс .
54.
Граничные условия второго рода задают в виде распределения плотносттеплового потока для каждой точки поверхности как функции времени :
qп f
и, в частности, - постоянную во времени плотность теплового потока :
qп q0 .
граничные условия третьего рода характеризуют конвективный
теплообмен между поверхностью тела и движущейся окружающей средой
при постоянном потоке тепла
Плотность теплового потока qn, уносящегося средой, считают
пропорциональной разности температур поверхности тела и среды:
qn = (Tп - T с ), где - коэффициент теплообмена, Вт/(м2К):
При этом условия теплообмена на поверхности:
дТ
Tn Tc 0.
дn n
граничные условия четвертого рода для двух твердых тел в контакте
дТ с
дT
.
Tn Tc n , c
дn n
дn n
55.
1.6. Температура от точечного мгновенного источникатепла для трехмерного, двухмерного и одномерного
нестационарных полей
Температура стержня от мгновенного точечного источника тепла
G x, ,
x 2
x 2
Q
exp
exp
4 CV 4
4
4
B
д x,
0.
lim
дx
x
Распределения температуры
вдоль
стержня
от
мгновенного
точечного
источника
теплоты,
вспыхнувшего в точке х= =0 в
момент времени =0 при
Q CV
=5 К/м, =0,000008 м 2 с
56.
Свойства функции точечного источника:1. При бесконечном удалении от вспыхнувшего источника
теплоты приращение температуры стремится к нулю:
дG x, ,
0.
lim
дx
x
2. функция G(x, , ) имеет максимум в точке x= ,
3. количество тепла Q в любой момент времени остается
неизменным
4. Величина B Q CV
представляет собой площадь,
ограниченную функцией (x, ) и осью x.
5. Функция G(x, , ) интерпретируется как частное решение
для распределения температуры в неограниченном
однородном и изотропном стержне от мгновенного точечного
источника теплоты
57.
Для трехмерного нестационарного температурного полятемпература от точечного источника, вспыхнувшего
в начале координат:
R2
Q
2
2
2
2
R,
exp
R
x
y
z
CV 4 3 2
4
Температурное поле от точечного источника на плоскости
описывается функцией :
r2
Q
R,
exp
CV 4
4
r 2 x2 y 2
С учетом теплоотдачи граничных плоскостей:
r2
Q
R,
exp
b где
CV 4
4
2
b
CV
58.
1.7. Температурное поле в стержне при граничныхусловиях первого рода
С помощью линейной суперпозиции решений для точечного
источника можно сконструировать частное решение
уравнения теплопроводности для граничных условий
площадь под графиком распределения
первого рода.
температуры на элементарном участке d
равна отношению теплосодержания Q
к удельной объемной теплоемкости CV
f d Q / CV B
Приращение температуры d на
этом интервале представим в виде:
x 2
f d
d lim
exp
,
4
0 4
а начальные условия, заданные известной функцией
x 2
в виде: x,0
d .
lim
f exp
4
0 4
1
x,0 f x
59.
записанное в виде интеграла выражениеx 2
x,0 lim
d .
f exp
4
0 4
1
при 0 стремится к f(x).
Для доказательства заменим переменную интегрирования
новой переменной u :
x 2 u.
1
2
f
x
2
u
exp
u
du
lim
0
f x
1
2
exp
u
du f x .
60.
Из этого следует, что функцияx 2
x,
d
f exp
4
4
удовлетворяет начальному условию:
x,0 f x
1
Поскольку функция (x, ) удовлетворяет уравнению
теплопроводности и начальным условиям,
она является решением для выравнивания температуры
в неограниченном стержне от заданного распределения
температуры в начальный момент времени.
61.
По аналогии для плоской задачи :x 2 y 2
x, y ,
f , exp
d d ,
4
4
1
а для пространственной задачи :
x, y, z,
1
4
x 2 y 2 z 2
d d d ,
f , , exp
4
3
62.
Л.21.8. Температура полуограниченного стержня при
постоянной температуре торца стержня
Пусть в начальный момент времени температура
полуограниченного стержня задана функцией f(x ) ,
а торец стержня имеет температуру , постоянную в
течение всего периода теплообмена.
Рассмотрим задачу охлаждения стержня, поскольку
задача нагревания может быть описана этим же
решением с помощью замены переменной.
Для упрощения расчета примем . 0
c
Поставленная задача математически формулируется
следующим образом:
63.
Найти решение уравненияд x,
д 2 x,
.
2
д
дx
0,
0 x
при краевых условиях:
x,0 f x ,
0, c 0,
д ,
0.
дx
Решение этой задачи может быть получено как следствие
x 2
x,
d
f exp
4
4
1
64.
Для этого продолжим стержень в область отрицательныхзначений x , т.е. будем считать его неограниченным, а
распределение температуры в начальные момент времени
зададим нечетной функцией: f(x) = - f(-x)
При этом при x=0
температуры
0, c 0
, т.е. граничное условие
на поверхности
выполняется
65.
решение для температуры полуограниченного стержняс нулевой температурой на торце примет вид:
2
2
0
x
x
f exp
d f exp
d
4
4
4
0
x,
1
1
4
0
x 2
x 2
f exp
exp
d
4
4
66.
1.9. Температура полуограниченного стержня припостоянной температуре торца стержня и постоянной
начальной температуре
При постоянной начальной температуре полуограниченного
стержня
x,0 0 const
Решение можно упростить, подставив в первую часть
подынтегральной функции
x 2u
а во вторую:
x 2u
x, 0
1
x
2
x
2
exp u du.
2
67.
Поскольку подынтегральная функция - четная, то в силусимметрии
x,
2
0
x
2
0
x
exp u du erf
2
- функция ошибок Гаусса .
2
erf 0 0, erf 1
Практически erf 2,7 0,9999 1
Если торец стержня поддерживается не при нулевой
температуре, а при постоянной температуре с, то решение
получим с помощью замены переменной x, x,
x, c
2
0 c
x
2
0
x
x
exp u du Ф
erf
.
2
2
2
c
68.
Распределения температуры по длине стержня приразличных значениях времени нагрева при
CV 5 МДж / м К , 8 *10
3
6
2
м /с
69.
Плотность теплового потока на торце стержня приграничных условиях первого рода
на основании закона Фурье найдем плотность теплового
потока
с 0
д x,
qФ 0,
С
V
дx
x 0
СV
- Коэффициент
аккумуляции тепла,
кДж
м 2 К с1 2
Зависимость плотности теплового потока на торце стержня от времени
поддержания на торце температуры 1000 С при
CV 5 МДж / м3 К , 8 *10 6 м 2 / с
70.
1.10. Тепловой поток и количество теплоты поступившейв стержень при нагреве (или отведенное при охлаждении)
Количество тепла Q , поступившего через торец стержня
площадью F при его нагреве:
Q F qф d F c 0
0
1 d
0
2
c 0 F .
Зависимость теплоты,
отведенной в стержень
поперечного сечения
1 мм2 при
с 0 1000 oС и
CV 5 МДж / м3 К ,
8 *10 6 м2 / с
71.
1.11. Температурное поле в полуограниченном или внеограниченном стержне при граничных условиях второго
рода (по А.В.Лыкову)
эта задача (рис.) может быть сведена к задаче об одномерном
нестационарном температурном поле при граничных условиях
первого рода
Зависимость
температуры в
точке действия
точечного
источника (а),
схемы действия
точечного
источника для
полуограниченного
стержня (б) и для
неограниченного
стержня (в)
72.
Математическая формулировка задачи:найти решение уравнения
дТ
д Т
2 ,
д
дx
2
удовлетворяющее краевым условиям:
(1)
дT 0,
qc 0,
T x,0 T0 const ,
дx
дТ х,
0.
T , T0 ,
lim
x
дх
Продифференцируем (1) по x:
д дТ x, д д 2Т x,
дx д дx
дx 2
73.
Изменим порядок дифференцированияд дТ x,
д 2 дТ x,
2
д дx
дx дx
Перейдем к новой переменной - плотности теплового потока:
дq x,
д 2 q x,
,
2
д
дx
дТ x,
1
q x,
дx
Начальные и граничные условия примут вид:
qф x,0 0, qф 0, qc const , qф , 0.
Воспользовавшись известным решением
x, c
2
0 c
x
2
0
exp u du erf (
2
x
2
)
74.
запишемqф x , q c
qc
qф x ,
qc
x
2 2
x
exp u du. Ф
2
0
2
x
x
1 Ф
2
2 2
x
2
1
exp
u
du
erfc
0
2
д х,
С учетом qФ x,
дх
qc
д х,
дх
x
1 Ф
2
qc
x
erfc
2
.
75.
Интегрируя , найдем решение для температурыполуограниченного стержня, на торце которого действует
источник теплоты постоянной плотности теплового потока:
x
qc
2 2
2
x, 1
exp
u
x
0
2q c
x
ierfc
. x 0 .
2
du
(1)
Из (1) , в частности, следует, что на торце стержня, т.е. при
x=0 температура описывается простой формулой
0,
2 qc
2 qc
CV
2 qc
76.
Для неограниченного стержня плотность теплового потокаследует принять вдвое меньшей, поскольку теплота будет
поступать не только в направлении положительной полуоси x
, но и в направлении отрицательной полуоси.
x ,
qc
ierfc
1 qc
0,
CV
x
2
.
x 0
77.
Температурное поле в полуограниченном или внеограниченном стержне при граничных условиях
второго рода (методом точечных источников)
еще один способ решения этой задачи
2
q d
x
d x,
exp
4
CV 4
2
q
1
x
x,
exp
d
0
CV
4
4
В частности при x= =0 получим формулу
2q 1
1 qc
0,
.
4 CV
CV
Для полуограниченного стержня плотность теплового
потока необходимо удвоить
78.
1.12. Температурное поле в стержне послепрекращения действия источника теплоты
Для расчета
температуры после
прекращения действия
источника продлим
источник тепла и
добавим сток той же
плотности теплового
потока
79.
Изменение температуры в интервале нагрева (0< < 1)и после прекращения действия источника тепла
( > 1) определим суперпозицией температур от
источника и стока по формулам:
1 qc
при 0 1
CV
0,
q
1
c
1
при 1
CV
80.
1.13. Численный метод расчета температурынеограниченного стержня от непрерывно действующего
точечного источника с изменяющейся в зависимости от
времени плотностью теплового потока
Схема замены
убывающей
зависимости
плотности
теплового потока
от времени
суперпозицией
источника и
стоков
81.
q0 q1 q0 q1K1 q 0
2
2
q0 q1 q1 q2 q0 q2
K2
,
2
2
2
q1 q2 q2 q3 q1 q3
K3
,
2
2
2
............
qi 2 qi
K i
.
2
82.
Приращение безразмерной (гомологической) температуры вконце первого интервала времени
q0
1
1
0, H N 1
A
.
T1
A0 q0 H N A0 K1 H N , 0
CV Т пл
Т
пл
На следующих интервалах, соответственно:
T2 A0 q0 2H N A0 K1 2H N A0 K 2 H N ,
T3 A0 q0 3H N A0 K1 3H N A0 K 2 2H N A0 K 3 H N ,
T4 A0 q0 4H N A0 K1 4H N A0 K 2 3H N A0 K 3 2H N A0 K 4 H N
................
i
Ti A0 q0 iH N A0 K j
J 1
i j 1 H N ,
83.
1.14. Свободное охлаждение равномерно нагретого тела,пластины, стержня (граничные условия третьего рода)
Элементарный объем стержня Fdx, нагретый до температуры
T, отдает за время d через боковую поверхность pdx (где pпериметр) в окружающую среду с нулевой температурой
количество тепла dQ = Tp dx d .
С учетом теплоотдачи уравнение теплового баланса
элементарного объема Fdx примет вид:
дT
д 2T
p
Q CV
x 2 x T x
д
F
дx
2
Или:
дT
д T
p
2 bT , где b
д
CV F
дx
Соответственно, для пластины толщиной :
2
2
дT
д T д T
2
bT
,
где
b
дx 2 дy 2
д
CV
84.
При постоянной по всему объему температуреи уравнение теплопроводности примет вид:
д 2T
дx
2
д 2T
дy
2
0
dT
bT
d
dT
bd
T
ln T b C
Начальные условия:
при T=T0
C ln T0
Следовательно:
T
ln b
T0
или
T T0e
b
85.
1.15. Температурное поле двух соприкасающихсяполуограниченных стержней (граничные условия
четвертого рода)
Два полуограниченных
теплоизолированных с
боков стержня,
имеющих постоянные
начальные температуры
T1 x,0 T0
T2 x,0 0
в начальный момент
времени приведены в
соприкосновение,
причем начало
координат находится
в месте
соприкосновения
86.
необходимо найти решение системы уравненийдT1 x,
д 2T1 x,
1
,
2
д
дx
дT2 x,
д 2T2 x,
2
,
2
д
дx
0, x 0 ,
0, x 0
При краевых условиях:
T1 x,0 T0 const , T2 x,0 0,
дT1 , дT2 ,
0,
дx
дx
T1 0, T2 0, ,
дT1 0,
2 дT2 0,
.
дx
1
дx
87.
Решение этой задачи имеет видK
T1 x,
1
T0
1 K
1
x
1
,
erf
K
2
1
x
K
T2 x,
erfc
.
T0
1 K
2 2
1CV 1
1
K
2
2 CV 2
При K 1
коэффициент тепловой активности .
и
T1 0,
T1 x,
T2 0, T2 x, 1
1
1
T0
T0
T0
T0
2
Т.е. на границе соприкосновения температура
устанавливается сразу же после соприкосновения тел и
остается постоянной все время выравнивания
88.
2. ДВИЖУЩИЕСЯ И НЕПОДВИЖНЫЕ НЕПРЕРЫВНОДЕЙСТВУЮЩИЕ ТОЧЕЧНЫЕ ИСТОЧНИКИ ТЕПЛА
2.1. Схематизация расчета температуры от
движущегося точечного источника
Для движущихся источников тепла координату источника
задают в виде функции: x x v
0
отрезок времени действия источника разбивают на
элементарные интервалы
d
и считают, что в каждом из этих интервалов в точке с абсциссой
x x0 v вспыхнул точечный
мгновенный источник тепла
89.
Результатом действия элементарного точечного источникаявляется приращения температуры
d
температура от движущегося источника определится
суперпозицией температурных полей от элементарных
источников теплоты
d .
0
Изменение температуры в какой-либо точке может быть
представлено суммой изменений температуры при
распространении тепла от отдельных элементарных
воздействий источника с учетом времени и места их
приложения
90.
2.2. Непрерывно действующий точечный источник внеограниченном теле
Неограниченное теплопроводящее тело находится при
нулевой начальной температуре. В момент времени в
точке О начинает непрерывно действовать точечный источник
постоянной мощностью q. Процесс распространения тепла
может быть описан уравнением:
q
d
R,
e
3
2
CV 0 4
R2
4
2
R
Rd
Подстановкой
z , dz
32 ,
4
2 4
выразим интеграл через функцию интеграла вероятности
q
2
R,
*
CV * 4 R
e
z2
R
4
dz
91.
2 z2Принимая во внимание, что
e dz Ф Ф u 1 Ф u
получим:
R,
u
R
* 1 Ф
4 R
4
q
Температуры всех точек тела во время действия источника
возрастают , стремясь к предельным значениям (R, ),
устанавливающимся при
Тогда
R
0, Ф(0) 0
4
и
R,
q
4 R
Т.е., в предельном состоянии температуры тела более не
меняются.Такое состояние процесса распространения
тепла называется стационарным: тепло, вводимое
источником, распространяется в неограниченном теле, не
изменяя его температуры
92.
2.3. Непрерывно действующий точечный источниктепла постоянной мощности, движущийся по поверхности
полубесконечного тела
R x y z
2
2
2
2
R x0 v 2 y02 z02
0
В момент времени
( )
в точке О` находится
точечный источник,
действовавший
( )
93.
Элемент теплаdQ qd
от точечного источника тепла, вспыхнувшего в момент времени
за время вызовет к моменту времени
приращение температуры
x0 v 2 y02 z02
d R,
exp
3
2
4
CV 4
2qd
(Чтобы учесть полупространство, мощность удваиваем)
Температуру R, найдем, интегрируя d R, :
x0 , y0 , z0 , d R,
0
x0 v 2 y02 z02
x0 , y0 , z0 ,
exp
3
4
0 CV 4 2
2qd
94.
В подвижной системе координат X, Y, Z,x x0 v , y y0 , z z0
связанной с источником, решение примет вид:
2
2
d
vx
v
R
(1)
x, y, z,
exp
exp
3
32
4 4
2
0
CV 4 2
2q
Здесь
- длительность процесса распространения тепла
элементарного источника, введенного в точке O
R2 x2 y 2 z 2
С течением времени область повышенных температур
достигает предельных размеров и только перемещается с
источником. Такое состояние процесса называется
предельным или установившимся, а температурное поле
– квазистационарным.
95.
2.4. Уравнение предельного состояния процессараспространения тепла точечного источника постоянной
мощности, движущегося с постоянной скоростью по
поверхности полубесконечного тела
R2
2
u
Интеграл (1) в пределах от 0 до подстановкой
4
приводится к известному определенному интегралу:
m2
u 2
u du
e
2
e 2m
(2)
2
После преобразований с учетом (2) уравнение предельного
состояния процесса распространения тепла точечного
источника постоянной мощности, движущегося с постоянной
скоростью по поверхности полубесконечного тела
принимает вид [Н.Н.Рыкалин]:
0
R, x
vx vR
exp
2 R
2 2
q
96.
Л. №6.2.5. Предельное состояние нагрева
полубесконечного тела неподвижным непрерывно
действующим источником тепла постоянной мощности
При длительном
нагреве полуограниченного
тела
непрерывно действующим источником теплоты процесс
распространения тепла стремится к предельному состоянию.
При этом решение для температуры в полубесконечном теле
от неподвижного источника теплоты постоянной мощности q
получим из ( ) при v=0
R
q
2 R
Т.е. температура в полуограниченном теле пропорциональна
мощности источника q и обратно пропорциональна
коэффициенту теплопроводности . При постоянных
мощности и коэффициенте теплопроводности температура
обратно пропорциональна расстоянию R от неподвижного
источника теплоты. При этом изотермические поверхности
представляют собой полусферы, а зависимости
97.
Неподвижный точечный источник на поверхностиполубесконечного тела . Температура при коротком
замыкании или точечной сварке.
Для неподвижного точечного источника (при v=0):
Ток короткого замыкания I= 250 А, а напряжение U=1 В.
Мощность точечного источника тепла Ne= 250 Вт.
Коэффициенты теплопроводности медной плиты:
Ne
R
= 360 Вт/(мК), Стальной плиты - 40 Вт/(м*К):
2 R
98.
2.6. Влияние скорости источника на распределениетемпературы
Ne
vx vR
exp
Согласно формуле R, x
2 R
2 2
температуры на поверхности полуограниченного тела в
направлении движения точечного источника за источником
тепла (x<0) и перед источником (x>0) - различные
Для x<0, т.е. при x=-R , получим:
Для x>0, т.е. при x=R из
уравнения следует :
Ne
R
2 R
Ne
vR
R
exp
2 R
Т.е. , с увеличением скорости температура убывает
быстрее
99.
Влияние скорости перемещения точечного источника на распределениетемпературы предельного состояния по оси x в полубесконечном теле
При N=250 Вт, =40 Вт/(м*К), =0,000008 м*м/с
100.
Распределение температуры от движущегося источникав направлении оси OY , перпендикулярном скорости,
получим при x=0:
Ne
Ne
v * 0 vR
vR
R
exp
exp
2 R
2 2 2 R
2
Т.е.
в
боковом
направлении
температура убывает
медленнее,
чем
перед
источником
в
направлении
его
движения, но
быстрее, чем за
источником.
1- сварочная ванна, 2 – изотермы, 3 – столбчатые кристаллиты.
101.
2.7. Непрерывно действующий точечный источниктепла
постоянной
мощности,
неподвижный
или
движущийся по поверхности неограниченной пластины
Граничные плоскости пластины
z0 0, z
отдают тепло в окружающую
среду с нулевой температуро
при коэффициенте теплоотда
В неподвижной системе
координат
x0 , y0
температурное поле имеет
вид:
x0 v y02
q d
x0 , y0 , exp
b
4
CV 4
0
102.
учитывает теплоотдачу поверхн. вМножитель e b окружающую среду с нулевой
температурой
Вводя время ( ) и переходя к подвижной системе
координат, получим:
2
2
q
vx
v
r
q d
x, y ,
exp exp (
b)
4
4
2 a 0
4
Здесь r 2 x 2 y 2 Для предельного состояния подстановкой
v2
b w
4
2
v
b
и обозначением u 2 r 2
4 2 получим:
2
u
exp w 2 K 0 u
4w
0 w
dw
K 0 u
Бесселева функция от мнимого аргумента
второго рода нулевого порядка
103.
С учетом выражения интеграла через бесселеву функцию2
q
v
b
vx
r , x
exp
K0 r
2
2 4 2
Здесь r
u r
v2
b
2
4
2
b
CV
x 2 y 2 -расстояние от точки А до мгновенного
положения О источника тепла
- аргумент функции K 0 u
- коэффициент, учитывающий понижение
температуры пластины в окружающую среду в 1/с
- коэффициент теплоотдачи
Вт м К
2
104.
Распределение температуры в стальной пластине = 3 мм1,2 кВт
105.
Распределение температуры в алюминиевой пластине = 3 мпри шовной сварке
1 кВт
106.
Значения функции K(u) могут быть определены по таблицам [8]или графикам
или численными методами.
Для неподвижного источника уравнение
примет вид
b
R, x
K 0 R
2
q
r, x при v=0
107.
Зависимость температуры от непрерывно действующего источникав стальном полуограниченном теле и в стальной пластине, q=330 Вт.
В пластине тепловой поток больше стеснен, чем в полубесконечном теле .
Поэтому с удалением от источника температура в пластине (кривая 2)
убывает медленнее, чем в полубесконечном теле (кривая 1)
108.
2.8. Метод быстродвижущихся источников теплаН.Н.Рыкалиным было замечено, что при перемещении
источника тепла с большой скоростью нагретая область
располагается узкой полосой вдоль скорости его
перемещения.
При этом теплота распространяется в основном в
направлении, перпендикулярном оси перемещения источника,
что позволяет существенно упростить расчетные схемы,
описывающие процесс распространения тепла.
В предельном случае v тепло источника распределено
равномерно по оси перемещения и будет распространяться
только перпендикулярно этой оси
109.
На каждой изотерме температурного полябыстродвижущегося источника можно выделить участок,
очертание которого приближается к прямой, параллельной
оси OX. На этом участке тепло распространяется практически
только в направлении, перпендикулярном оси OX. Тепловой
поток, параллельный оси OX незначителен и им можно
пренебречь. При этом производные в направлении осей OY и
OZ значительно больше, чем в направлении OX
дТ
ду
дТ
дТ
,
ду
дх
дТ
дТ
.
дz
дх
110.
Температура от непрерывно действующего источникатепла, движущегося по поверхности пластины.
Поведем в пластине две бесконечно близкие параллельные
плоскости, перпендикулярные оси OX, не пропускающие
тепла и выделим т.о. стержень толщиной dx (рис.)
Для неподвижного
точечного (линейного)
мгновенного источника
температура описывалась
уравнением:
x2
T x,
exp
1
4
CV 4 2
Q2
Так как тепло распространяется в направлении оси OY,
заменим x на y0
111.
Приращение количества тепла от точечного источника:x q
dQ qd qd dx
v v
q
При этом интенсивность источника тепла Q2
v
b ,учитывающего теплоотдачу
e
С учетом множителя
поверхности пластины, где b 2
CV
Уравнение процесса распространения тепла в пластине
от быстродвижущегося линейного источника будет:
y02
T y0 ,
exp
b
4w
v 4 CV
q
112.
2.9. Температурное поле в полуплоскости отдвижущегося равномерно распределенного источника
тепла
y v
x, x, y
Схема к расчету температуры в полуплоскости от
быстродвижущегося равномерно распределенного источника
тепла
113.
Нестационарное температурное поле стержняx
x, x erfc
2
qc
ierfcU
2q c
x
ierfc
dx
2
U erfcWdW
1 U 2
e
UerfcU
температура торца стержня
2 qc
2 qc
0,
CV
0,
2 qc
114.
29. Схема и расчет температуры на укороченнойпередней поверхности от
быстродвижущегося
равномерно распределенного источника тепла
y
v1
Для условий резания (f=1 мм,
v1 1 м / с )
время нагрева стержня
0,001 с
все тепло от источника поступает
только в стержень (в стружку)
115.
при определении приращения температуры в полуплоскостимощность источника тепла необходимо удвоить:
1 qф 1
T x, y
CV
y
v1
0
1
x2
exp
y
y
4
v1
v1
d y
v1
на контактной поверхности резца со стружкой приращение
температуры Т 0, y
2 qф
Т 0, y
CV
y
v1
q ф q F v1
Т 0, y
2 qF Sb
Т пл
S b CV Т пл
v1 v
va y 1
2 qF
A1 Pe ,
a
Sb
Sb
va
y1
Pe , A1
,
1
CV Т пл a
116.
2.10. Оценка погрешностей и области применения методабыстродвижущихся источников
x, y
X
U X , Y
Y ierfc
0, f
2 Y
,
v
X
x,
f
Y
y
f
0, f ,
x
f v ,
y f .
Поле относительных
температур U(X,Y)в
безразмерных
координатах X и Y
117.
6При 8 10 м c ,
2
v 1 м / c, f 1 мм
x 0.9 10 5 , y 1 10 3
Сопоставление изотерм температурного
поля в с учетом масштабных
коэффициентов
118.
Воспользовавшись формулойx
x, x erfc
2
qc
вычислим угол
2qc
x
ierfc
dx
2
Б
1
2 2
д дx
1 ierfcZ
Б arccos
arccos 1
Z
grad
vy erfcZ
x v
Z
.
2 y
,
119.
Глубина проникновениятепла
при X>3
U(X,Y) < 0,02
Зависимость погрешности вычисления
градиента температурного поля методом
быстродвижущихся источников тепла от
критерия Ре
L 3
f
v
.
120.
При8 10 6 м2 с , v 1 м / с, f 1 мм
x 0.9 10 5 , y 1 10 3
потоки вдоль оси y будут иметь место и
вызовут выравнивание температуры
(0,y), изотермы будут еще более
пологими.
p Б
Воспользовавшись формулой
x,
2qc
вычислим угол
ierfc
Б
x
2
121.
12 2
д дx
1 ierfcZ
Б arccos
arccos 1
Z
grad
vy erfcZ
где
x v
Z
.
2 y
При Z>1,45 тепловые потоки и
температуры менее 2% от потоков и
температур при Z=0
,
122.
2.11. Одномерное температурное поле от движущегосяисточника тепла
-время после начала нагрева
v
dQ qф d
время выравнивания тепла:
= .
Приращение температуры
x0 v 2
d x0 ,
exp
1
2
4
CV 4
qф d
Температура в точке x0 в момент времени
x 0 ,
qф
12
0 CV 4
x0 v 2
exp
d
4
123.
при и, соответственно, при = .qф
vx
exp , x 0,
vCV
x
qф
, x 0.
vCV
Зависимости температуры стержня
от расстояния от движущегося
источника тепла с плотностью
теплового потока q 6,57 МДж м
ф
124.
3. ЗАКОНОМЕРНОСТИ ТЕПЛООБМЕНА ПРИ ЛИТЬЕ,ОБРАБОТКЕ МЕТАЛЛОВ ДАВЛЕНИЕМ И СВАРКЕ
3.1. Закономерности кристаллизации и затвердевания
отливки в литейной форме
Q L X 1
Q qф ( ) ,
c 0
q ф ф
Схема распределения
температуры в расплавленном
металле и в литейной форме
125.
X qф ф с 0U lim
.
L
L
0
ф с 0 d
с 0
2
X
ф
L
L 0
Изменение плотности теплового потока и толщины затвердевшего
слоя отливки с течением времени (а) и распределение скорости
кристаллизации по толщине стенки отливки (б).
126.
3.2. Закономерности отвода теплоты в литейную формувремя остывания разобьем на три отрезка: 1) от
температуры заливки до температуры плавления , 2) от
начала до конца кристаллизации при температуре
плавления, 3) от конца кристаллизации до температуры
выбивки
127.
Для первого интервала примем температуру на торце стержня постояннойравной средней температуре:
З пл
1с
2
Количество теплоты, которое необходимо отвести для остывания расплава
до температуры плавления равно:
Q1 з пл VCV
Зависимость отводимого количества теплоты от времени :
Q1
2 ф
1с 0 F 1 CVфV 1с 0
2
ф 1
V
Приравнивая два выражения для количества теплоты ,
найдем время остывания до начала кристаллизации:
З пл 1
1
З пл 1 2 0 пл
2
V F
ф
2
СV
СV ,ф
2
F 2
128.
МатериалСV,
МДж/(м3К)
, Вт/(м*К)
106 , м2/*с
Песок
1,35
1
0,8
Сталь
5
40
8
x, 1 x, 2 x, 1 , 1
x
2
1 x, З З 0
exp u du,
2
0
2 x, 1с пл 1с пл 0
x
2 1
0
exp u 2 du,
129.
Q2 З пл VCV LV CV ,фV 1c 0CV ,фV 1c пл
2
Рис.
Зависимость
средней
температуры
расплава (отливки)
от времени при
толщине
стенки
отливки 10
мм,
Формовочная смесь
–
сырая
с
добавлением
опилок:
ф ( 2 1 )
V F
2
.
ф 0,14 *10 6 м 2 / с, СVф 0,51 МДж м3 К
3
, литейный сплав – сталь: СV 6 МДж м К
2
ф 2
V F
2
130.
при толщине стенкиотливки 10 мм,
формовочная смесь
– сырая с добавлением
опилок:
ф 0,14 10 6 м 2 / с,
СVф 0,51 МДж м3 К
литейный сплав
– сталь:
СV 6 МДж м 3 К
Закономерности отвода теплоты от заливки расплава до
начала остывания отливки после кристаллизации расплава.
Условия те же, что на рис. 1.6,– равномерная шкала времени.
Q V * CV ( З выб ) M * L
131.
Q V * CV ( З выб ) M * LЗакономерности отвода теплоты от заливки расплава
до начала остывания отливки после кристаллизации
расплава.
Условия те же, логарифмическая шкала
времени,
132.
Охлаждение отливок в литейных формах после заливки происходитот температуры заливки до рациональной температуры выбивки.
Продолжительность выдержки в форме определяется
толщиной стенки отливки, свойствами залитого сплава и
литейной формы, температурой выбивки.
Закономерности остывания стальной (а) и алюминиевой (б)
отливок пластин размерами 100*100*10 мм
133.
3.3. Влияние теплофизических характеристик материаловпесчаных
и
металлических
литейных
форм
на
кристаллизацию расплава и остывание отливок
. Схематизация отвода тепла в литейную песчаную форму:
1, 2 - верхняя и нижняя половины литейной формы, 3 стержень, 4 – полость (рабочая часть), 5,6 –верхняя и нижняя
опоки.
134.
Закономерности остывания стальной (а) и алюминиевой (б) отливокпластин размерами в сырую песчаную форму с добавлением опилок:
1 – зависимость количества отведенного тепла от времени,
2 – количество теплоты до полного затвердения,
3 – количество теплоты до выбивки отливки,
4 – количество теплоты до температуры плавления
135.
Теплофизические характеристики песчанойформовочной смеси и некоторых литейных сплавов
,
Сv,
,
1,05
1,89
0,29
0,740338
1700
0,84
1,428
0,17
0,492707
300
1,7
0,51
0,07
0,188944
7200
0,84
6,048
29
13,24356
Чугун серый
7000
0,77
5,39
40
16,68332
Алюминиевые
сплавы
2600
1,15
2,99
290
29,44656
Вид песчаной
смеси
кг/м3
Песок сухой
1600
Смесь сырая
1800
Смесь сухая
Сырая с
опилками
Сталь
с,
кДж
кДж / кг К МДж / м3 К
Вт / м К м 2 К с1 2
0,84
1,344
0,87
1,081333
Теплопроводность песчаной формовочной смеси значительно меньше
теплопроводности компактного кварца и сухого кварцевого песка.
Теплофизические характеристики формовочной смеси снижаются при
добавлении опилок.
136.
Влияние теплофизических характеристик смесиДля регулирования теплообмена в литейную форму
встраивают обладающие высокой теплопроводностью
элементы, называемые холодильниками. Холодильники
обычно изготавливают из чугуна, реже из графита,
магнезита.
137.
Температуропроводность стальной формы в 40 раз больше,чем формы из сухой песчаной смеси 4,8 *10 6 и 0,12 *10 6 .
время остывания при переходе от песчаной формы
к кокилю сокращается более, чем в 600 раз
138.
Зависимости толщины затвердевшего слоя от времени приЛитье в подогретый кокиль и в песчаные формы
литье алюминиевого кубика размерами 100 мм*100 мм*100 мм
139.
3.4. Теплообмен при литье под давлениемспособ получения отливок из сплавов цветных металлов и
сталей, максимально приближающий размеры и форму
отливки к размерам и форме готовой детали за счет
нагнетания расплава в камеру прессования под давлением
Схема процесса изготовления отливок на машинах
с горизонтальной холодной камерой прессования
140.
Зависимости количества отведенного тепла от времени прилитье под давлением
отливки из алюминиевого сплава размерами
10 мм*10мм*1 мм под давлением
141.
3.5. Теплообмен и температура при горячей прокаткеПри соприкосновении холодного прокатного валка, имеющего
начальную температуру с нагретой до температуры
з
0
заготовкой тепло из заготовки интенсивно поступает в валок
к
з 0
2
- температура на
поверхности
контакта валка с
заготовкой
з 0
qф CV
.
- плотность теплового
потока на торце стержня
142.
Время нагрева «стержня»1 0,16 c.
В частности, при D=0,6 м, =30 , v=1 м/с
1 0,16 c.
При 40 Вт м К СV 5 МДж м К
3
з 0 1000 0 С
средняя плотность теплового потока на участке контакта
валка с заготовкой равна:
qср
1
1
1
0
При b=2,3 м
з 0
2( з 0 )
CV
d CV
40 МДж м 2
1
площадь контакта валка с заготовкой:
F = r b (м ) 0,157 м
2
2
тепловой поток Ф, поступающий в валок:
Ф q ср F 6,3 МВт
143.
Количество тепла Q1, поступившее в валки при прокате однойзаготовки
Пусть масса заготовки равна М=50 000 кг, высота полосы h=0,35 м,
ширина b=2,3 м. Соответственно, длина полосы будет:
L
М
8 м
bh
Время прокатки заготовки при скорости v=1 м/с:
L
1 8 c
v
Количество тепла Q1
2( з 0 )r b L
Q1 qср F 1 CV
7 МДж.
v
в каждый из двух валков при прокате одной заготовки массой
50 тн поступит примерно по 7 МДж теплоты
144.
Температуру за пределами участка вычислим путемналожения (суперпозиции) решений от равномерного
источника плотностью, продленного за пределы участка и
стока тепла той же плотности, действующего за пределами
участка
в конце первого
y
y
y k
1
оборота
l
l
k
k
температура
поверхности валка
снизится с 500 до
до 73,5 С
( 12 11) k 0,147 k
Это вызовет
дополнительное
повышение
контактной
температуры
примерно на 37 С.
145.
Еще через оборот валка остаточная поверхностнаятемпература, вызванная первым контактом, снизится до
величины: ( 24 23 ) 0,1
k
k
однако появится повышение температуры от следующего
контакта и суммарное повышение температуры от подогрева
валка на втором обороте будет:
(( 12 11) ( 24 23 )) * k 0,247 k 123 С
Колебания контактной температуры в рассматриваемом
примере происходят с амплитудой около 400 С и с частотой
около 0,6 Гц.
146.
При непрерывной прокатке заготовки контактная температураувеличивается. Так, например, за 4 оборота валка,
необходимых для прокатки заготовки длиной 8 м и весом 50
тн, контактная температура возрастает от 500 до 620 С
Примерное изменение
начальной
температуры валка и
контактной
температуры с ростом
числа оборотов валка
при прокате одной
заготовки
после проката заготовки и нескольких следующих друг за
другом оборотов валка в контакте с заготовкой необходимо
делать небольшой перерыв для выравнивания температуры.
147.
При полном выравнивании этой теплоты по всей массевалка его начальная температура повысится на величину
Q1
7
0
0
2
C
2
2
CV D 4 l 5 3,14 0,6 4 2,5
Зависимость контактной температуры от числа прокатанных заготовок
С ростом количества прокатанных заготовок суммарное
увеличение температуры валка, вызванное тепловыми
потоками от нагретых заготовок, существенно увеличивается
148.
3.6. Нагрев и охлаждение штампов при горячей штамповкеПусть начальная температура штампа равна =200 ,
а начальная температура заготовки з= 1000 С.
При соприкосновении штампа с нагретой
з 0
заготовкой контактная температура равна
к
600 0С
2
полусумме температур заготовки и штампа:
b штамповых сталей
умеренной теплостойкости
при температуре 600 -700
С составляет около 350250 МПа при достаточно
высокой ударной вязкости
800 кДж/м2
Схема к определению
контактной температуры и
тепловых потоков в штамп
при горячей штамповке
149.
Распределение температуры в глубине штампаx, к к
2
x
2
0
exp u 2 du
три группы штампов : 1- для прессов, 2- для штамповочных молотов,
3- для скоростных молотов и гидровинтовых прессов
Средняя температура поверхностного слоя толщиной около 1 мм ниже,
чем контактная температура (порядка 300 – 500 С)
150.
Плотность теплового потокаПри
з 0
qф CV
.
40 Вт м К СV 5 МДж м 3 К з 0
qср
1
1
1
0
800 0 С
з 0
2( з 0 )
CV
d CV
1
Влияние времени контакта на среднюю плотность теплового потока:
1 - при высокоскоростной штамповке, 2 – при штамповке на молотах,
3- при штамповке на прессах и ГКМ
151.
Количество теплоты, поступившее в штамп (ГКМ) за 1штампование
Q
При
2 СV
c 0 F
c 0 800 1 0,3 с
CV 5 МДж /( м 3 * К )
D=0,2 м,
29 Вт /( м * К )
Q1 190 КДж, Q1000 190 МДж
Нагрев на 1000 штамповок - 300 с,
Выравнивание и охлаждение 25000 с
152.
3.7. Анализ теплового баланса при ручной дуговойсварке
Схема дуговой сварки.
1-деталь, 2 –сварной
шов, 3- шлаковая
корка, 4 – жидкая
шлаковая ванна, 5 –
газовая защитная
атмосфера, 6-обмазка
(покрытие) электрода,
7 – электрод, 8 –
электрическая дуга, 9 –
металлическая ванна.
На электрод и заготовку подается напряжение, между ними
зажигается устойчивый разряд электрического тока –
электрическая дуга, обеспечивающая плавление электрода
и заполнение сварного шва.
153.
Схематизация тепловых потоков в электрод и деталь приручной дуговой сварке
сварочные токи до 200 А, мощности источника ( до 3-4 кВт)
154.
Примерный тепловой баланс при ручной дуговой сварке(по Н.Н.Рыкалину)
155.
1. Тепловой поток Фпл, необходимый для плавления металлапри дуговой сврке
Пусть длина шва Lш , шов разделан фасками под 45
2
шириной f . Объем сварного шва равен:
V f Lш
4
Количество тепла, необходимое для нагрева этого объема металла
до температуры плавления:
Q1 VCV ( пл 0 ),
Количество тепла, необходимое для плавления этого объема металла
Время сварки
Q2 LV ,
Lш Lш v0
vсв
v0 vсв
тепловой поток Фпл, необходимый для плавления металла:
Q1 Q2 vсв VCV пл 0 LV vсв
Фпл
.
Lш v0 v0
Lш v0
v0
156.
2.Тепловой поток, поступающий в сварочный электрод придуговой сварке
Электрод - полуограниченный изолированный с поверхности стержень
торец которого находится при температуре плавления электрода.
2 CV
d э2
пл 0
QЭ
Количество теплоты :
4
Тепловой поток в электрод: ФЭ
d Э2
4
СV
пл 0
Lш
v0
3. Тепловой поток, поступающий в деталь при дуговой
сварке
F
длина источника тепла : l a 2 f
F y 2 fy 2vсв , dF 2 fvсв d
y
v св
v
v0
Ip
2 fI a
.
157.
Т.к.F
пл 0
qФ CV
.
Фд qФ dF
0
4
1
СV пл 0 2 fvсв
пл 0 f
la vсв
d
0
l a v0
vсв
.
v0
Израсходованная длина электрода: ls
V
d Э2
f2
4d Э2
Lш
скорость перемещения электрода вдоль него, необходимая
для сохранения постоянной длины дуги
ls
Vvсв
S 2 .
d Э Lш
158.
Баланс тепловыхпотоков при
ручной дуговой
сварке
Соотношение
скоростей
перемещения
и подачи электрода
159.
3.8. Тепловые балансы при различных термическихспособах сварки
Схема автоматической дуговой сварки
сварочные токи до 2000 А, мощности источника (до 30-40 кВт)
160.
Баланс тепловыхпотоков при
автоматической
дуговой сварке.
(Основная
мощность - на
плавление)
Соотношение
скоростей
перемещения
и подачи электрода
161.
Схема сварки в защитных газах неплавящимся электродомпри прямой полярности с присадочным прутком
1 – присадочный
пруток, 2- сопло, 3 –
токопроводящий
мундштук, 4 – корпус
горелки, 5неплавящийся
вольфрамовый
электрод, 6 – рукоять
горелки, 7атмосфера
защитного газа, 8 –
сварочная дуга, 9 –
ванна
расплавленного
металла.
162.
Баланс тепловыхпотоков при
сварке
алюминиевых
заготовок в
защитных газах
223 Вт м К ,
CV 2,7 МДж м 3 К ,
84 мм 2 с
(Основная мощность –
в деталь)
соотношение скоростей
перемещения и подачи
электрода
Напряжение U=10 В, ток I= 400 А, =0,6, N=2,4 кВт.
163.
Схемы получения плазменной струи, выделенной из дуги (а),и плазменной дуги, совмещенной с плазменной струей (б)
1 – дуга,
2 –вольфрамовый
электрод,
3 – керамическая
прокладка,
4 - корпус горелки,
5 – сопло,
6 – плазменная струя,
7 - заготовка
164.
Баланс тепловых потоков при плазменной сваркестальная заготовка, ток I= 10A, U=20 В, ширина фаски
сварного шва f=1 мм
почти вся мощность отводится в виде теплового потока в
деталь (из-за градиентов)
165.
Схема электрошлаковой сварки1-трубы ползуна,
2 – сварочная ванна
расплавленного
металла,
3 – шлаковая ванна,
4
–
сварочная
проволока,
5 – мундштук,
6 – основной металл
заготовок,
7 – ползуны
8
–
затвердевший
сварной шов,
9 – вводная планка,
10 - выходная планка
166.
Баланс тепловых потоков при электрошлаковой сваркеСтальная
заготовка
при токе I=
1000 A, U=20 В,
ширина и длина
cварного шва
B*H=300*150
мм
Соотношения между
скоростями подачи
электродной проволоки
(диаметром 3 мм пучком
из 3 шт.) и перемещения
ползунов
167.
3.9. Температура при электрической контактнойстыковой сварке
Схема контактной стыковой сварки
1 – неподвижная плита,
2, 3 – зажимы,
4 – подвижная плита,
5 – сварочный трансформатор
6, 7 – свариваемые заготовки
Электрическое напряжение
подается на зажимы 2 и 3
через сварочный
трансформатор 5.
Подвижная плита 4 перемещается в
направлении неподвижной плиты 1 до
осуществления контакта заготовок 6 и
7 и сжимает заготовки с усилием Р
168.
Температура в плоскости контакта (т.е. при x=0) согласноформуле (1.64):
1 qc
при 0 1
CV
0,
1 q c 1 при
1
CV
Зависимость
контактной
температуры при
сварке круглых
стальных,
алюминиевых и
медных прутков
диаметром D = 4 мм от
времени при
напряжении на входе
трансформатора 220 В,
токе в первичной
обмотке
трансформатора 4 А, и
к.п.д. сварочной сети
=0,75.
169.
Мощность при стыковой сварке при 1 и 3-х импульсахЗависимости тока I и усилия Р от времени
нагрева
При одном импульсе
тока, равном 3 :
1 Ne
пл
3 ,
F
F пл
Ne
1,73
при трех импульсах тока:
пл 0, 5
Ne
F
F пл
Ne
.
0,777
5 4 3 2 0,777
Ne
F
Мощность в 2,2 раз больше, чем при
одном импульсе
170.
3.10. Температура и количество теплотыпри конденсаторной сварке
Конденсаторная
сварка
осуществляется за
счет энергии,
накопленной в
батарее
конденсаторов при
их зарядке от
источника
постоянного тока:
Q CU 2
2
Схема конденсаторной сварки: 1 – пружина, 2, 3 –
свариваемые заготовки, 4 – защелка, 5 – направляющие, В –
выпрямитель, П – переключатель, С – конденсаторная батарея.
171.
Зависимости температуры от времени разряда приконденсаторной сварке стальных, медных и алюминиевых
проводов диаметром 0,2 мм при количестве тепла Q= 0,020,05 Дж и мощности разряда 40 – 80 Вт.
время разрядки конденсаторной батареи очень мало и
измеряется тысячными или десятитысячными долями
секунды
172.
Температура стыка свариваемых заготовок рассчитываетсяпо формулам
1 qc
при 0 1
CV
0,
q
1
c
1
при 1
CV
при небольшой энергии (Q=0,02-0,05 Дж) достигаются
необходимые мощности и, соответственно, большие
плотности теплового потока (600-1200 ) Вт мм 2
173.
Зависимостьколичества тепла
от времени
действия
источника,
необходимого для
нагрева торцов
стальной
проволоки
диаметром 0,2 мм
до температуры
плавления
при уменьшении времени действия источника тепла от 1 с до
0,001 с, количество теплоты, необходимой для разогрева
торцов заготовок до температуры плавления, уменьшается в
32 раза ( от 1,15 Дж до 0,036 Дж)
174.
3.11. Температура при сварке трениемСварка
трением
осуществляется
за счет адгезии
(схватывания)
контактируемых
поверхностей
. Принципиальные схемы сварки трением:
а)-вращение одной детали, б) – вращение
обеих деталей, в) – сварка неподвижных
деталей с вращающейся вставкой, г) –
сварка при возвратно-поступательном
движении одной детали
175.
Плотность теплового потока (или удельная мощностьтрения q) на поверхности вращающегося цилиндрического
образца определяется как произведение касательного
напряжения , возникающего при трении, на скорость резания
v:
q qF v , где v 2 n
При постоянном
радиусе температура
рассчитывается по
формулам:
1 qc
при 0 1
CV
0,
1 q c 1 при
1
CV
Схема распределения
температуры по торцу
заготовки при сварке трением
176.
Сила Ропределится по
формуле:
Ne
P
v
где -
Зависимости температуры от
времени нагрева при диаметрах
трущихся заготовок от 5 мм до 10
мм.
коэффициент
трения, v –
скорость трения (в
средней части
заготовки или на
ее периферии, P –
осевая сила
сдавливания
заготовок.
177.
3.12. Температура при электрической контактнойточечной сварке
Решение
R
R,
* 1 Ф
4 R
4
q
может быть применено, для оценки температурного поля
при точечной сварке толстых пластин.
Схемы
контактной точечной
сварки:
а) двусторонней,
б)
односторонней
178.
Вт40
,
м*К
8 мм 2 / с
Зависимости температуры от расстояния от источника тепла в
различные моменты времени.
Мощность источника q=0,22 кВт.
Сварка относительно толстых стальных пластин.
В некоторой окрестности точки, в которой действует точечный источник
тепла, температура превышает температуру плавления и излишнее тепло
идет не на повышение температуры, а на расплавление металла
179.
NeR,
При
2 R
Для полупространства
мощность удваиваем
Стремление
температуры от
точечного источника к
предельным значениям .
Условия те же
1) - при меньшей мощности источника осуществлять прогрев и
расплавление металла, ориентируясь на предельное
температурное состояние.
2) -при большей мощности сварку производить, на более
жестком режиме, но отключать подачу тока, не доводя
температуры до предельных значений.
180.
Зависимости температуры от расстояния от источника тепла вразличные моменты времени. Мощность источника q=2,2 кВт.
(в 10 раз больше, чем для стальных). Точечная сварка
Вт
медных пластин
360
, 100 мм 2 / с
м*К
181.
3.13. Температура при электрической контактной шовнойсварке
а) – двусторонней,
б) – односторонней;
1- заготовки, 2 – электроды, 3 – медная подкладка
182.
Температура в окрестности движущегося точечногоисточника может быть вычислена по формуле:
2
q
vx
v
b
r , x
exp
K
r
0
2
2 4 2
или без учета влияния охлаждения пластины путем
теплообмена с окружающей средой :
vx Rv
R, x
exp
K 0
2
2 2
q
183.
Распределение температуры в стальной пластине = 3 ммпри шовной сварке N=1,2 кВт
184.
Распределение температуры в алюминиевой пластине= 3 мм при шовной сварке N=1 кВт
185.
3. 14. Схема и температура при ультразвуковой сварке1 – магнитострикционный преобразователь, 2 – трансформатор
продольных упругих колебаний, 3 – рабочий инструмент,
4 – наконечник рабочего инструмента, 5 – свариваемые
заготовки, 6 – опора
186.
Температура от неподвижноготочечного источника на
поверхности пластины:
b
R, x
K 0 R
2
Ne
Установившееся распределение температуры в стальной
пластине =1 мм, b=0,0028 1/с, =8 мм2/с, =0,04 Вт/(мм*К).
187.
4. ЭЛЕМЕНТЫ ТЕПЛОФИЗИКИ РЕЗАНИЯ4.1.Схематизация теплообмена в зоне резания
Вся работа, затрачиваемая при резании на деформацию и
трение, превращается в теплоту.
Это было доказано еще в начале двадцатого века
(в 1905 г)
опытами Н.Н.Савина.
Он сверлил деталь, помещенную в калориметр, измеряя
крутящий момент (и мощность резания) с помощью
динамометра и количество образованной при сверлении
теплоты с помощью калориметра. Работа резания,
измеренная
с
помощью
динамометра,
оказалась
эквивалентной теплоте, измеренной калориметром.
Источники теплоты:
1. зона стружкообразования,
2. участок контакта стружки и режущего лезвия
на передней поверхности,
3. участок контакта застойной зоны и фаски износа
режущего лезвия по задней поверхности с деталью.
188.
Распределения температуры и тепловые потокирассматривают в плоскости стружкообразования
189.
Наибольшее количество теплоты при резании образуется взоне
стружкообразования.
Эта
теплота
равномерно
выделяется внутри материала, почти вся уносится нагретым
материалом в стружку.
В результате повышения теплосодержания (энтальпии) и с
учетом удельной объемной теплоемкости обрабатываемого
материала стружка равномерно прогревается до температуры
деформации д.
Для расчета температуры деформации необходимо оценить
мощность (удельную работу) тепловыделения и тепловой
поток из зоны стружкообразования в деталь.
При этом используются сведения об угле наклона зоны
стружкообразования (или усадке стружки), а также
эмпирические или теоретические сведения об удельных
касательных силах в зоне стружкообразования
190.
4.2. Анализ тепловых потоков, поступающих в стружку ив инструмент при точении
Для анализа соотношения
тепловых потоков стружку и в
режущее лезвие будем считать
температуру на передней
поверхности равномерно
распределенной и известной.
Плотность теплового потока,
поступающего в стержень
через его торец при
постоянной температуре
торца , обратно
пропорциональна времени
нагрева
с 0
д x,
qФ 0,
СV
дx x 0
191.
Время нагрева стержня , выделенного в стружке, выразимчерез усадку стружки , критерий Pe=(va)/ , коэффициент
температуропроводности и толщину срезаемого слоя a:
стр
c c
a
c
a 2
a 2
, где 2 .
v1 a v
v
Pe
a
2
2
2
Отношение плотностей тепловых потоков, поступающих в
резец и в стружку:
qp
qстр
CV p
CV ом
где K
c 0
1
a
2
c д
Pe
CV p
,
CV ом
2
c 0
K
c д
1
a2
K K 2
Pe
192.
Теплофизические характеристики обрабатываемого иинструментального материалов оказывают относительно
небольшое влияние на соотношение тепловых потоков.
Материал
, Вт/(м*К)
Cv,
МДж/(м3К
Т5К10
ВК8
Т15К6
Сталь
38
54
27
40
2,7
2,2
2,7
5
CV
10
11
8,5
14
K
0,7
0,8
0,6
Зависимость
отношения тепловых
оттоков в резец и в
стружку от времени
резания при
c 1000 0С , 0 0 0С ,
д 300 0С , 2, Ре 30
193.
. Схема к определению теплообмена между полуограниченнымстержнем и быстродвижущейся полуплоскостью по А.Н.Резнико
b
1
3 A
1
2 B
v1
l
.
Принимая для типичных условий
обработки сталей
твердосплавными инструментами
=1, v = 1 м/с, l = 1 мм, = 10 с,
находим, что b 0,0066.
194.
4.3. Тепловые потоки в инструмент и в стружку приторцовом фрезеровании
. Схема торцового
фрезерования:
а) – в основной
плоскости,
б) – в рабочей плоскости,
в) - в плоскости
стружкообразования
a S z sin sin cos
195.
D 2 * м D2e
p
arccos 1
v
2v
D
Схема к определению
максимального угла контакта зуба
фрезы с заготовкой
c
a
qфр
S z sin м
a
K K
K K * 2
D
qстр
D м
м
2
для D=60 мм, Sz=0,1 мм/зуб, м 4 и прочих условиях
резания, как и в примере для точения, получим:
qфр
qстр
0,18
Или поправочный коэффициент
Ки=0,82
196.
4.4. Тепловой поток от условной плоскости сдвига вобрабатываемую заготовку и температура деформации
источник тепла
плотностью
qФ v * AW
движется в направлении
оси х, перпендикулярном
условной плоскости
сдвига со скоростью
vn v sin y
Схема к расчету теплового
потока от условной плоскости
сдвига в обрабатываемую
заготовку
Пи этом формула для
установившейся
температуры стержня от
движущегося источника:
197.
qфvx
exp , x 0,
vCV
x
qф
, x 0.
vCV
Примет вид:
qф
vn x A
vn x
exp
д exp
, x 0,
vnCV
x
qф
д ,
x 0.
vnCV
W
где
y u
AW
qф AW v, д
CV
AW y u
198.
Тепловой поток в деталь от плоскости сдвигаy x1 cos y ,
vn
d x
vn x
dФд
dF д exp
bdy.
x
dx
x1
,
sin y
0
vn
vn x
Фд qф dF д exp
bctg y dx
a
L
dF bdy, dF b ctg y dx.
cos
y
va
Ф дb ctg y 1 exp tg y дb ctg y .
Фд дbctg y
д ctg y ctg y
.
y u va
Ф0
y u abv
Pe
СV CV
при ctg y 1,74 и
Pe = 40 – 140
Фд/Ф0= 0,044….0,012
va
AW abv д abvCV дbctg y 1 exp tg y
1
1 exp Pe * tg y
AW
va
д
K Pe , K Pe 1
. Pe
Pe * tg y
СV
199.
4.6. Калориметрический метод измерения тепловыхпотоков, поступающих в обрабатываемую заготовку
Схема калориметра:
1 - внешний сосуд; 2 термометр;
3 - калориметрический
стакан;
4 - мешалка;
5 – трансформаторное
масло;
6 – втулка после обработки
резанием
После обработки лопаточным резцом деталь помещают в
ядро калориметра.
200.
Работа сил на заднихповерхностях может быть
определена измерением
количества тепла,
поступившего в деталь.
Схема резания лопаточным
резцом с обратными срезами
для измерения тепловых
потоков, поступающих в деталь
(s>b)
Тепловой поток Ф,
поступивший в деталь,
определяется по
теплосодержанию детали
Q и времени резания р:
Ф
Q
р
201.
По истечении некоторого времени температуры ядракалориметра и детали выравниваются и становятся равными
температуре 1
Типичные кривые измерения температуры ядра калориметра
при помещении в него детали после опыта (а) и при
охлаждении (б)
202.
Теплосодержание Q детали (втулки) определяется поформуле:
Q K 1 0
MCV
1 2 ,
где K - теплоемкость калориметра, определяемая тарировкой;
0 и 2 - начальные температуры ядра калориметра и детали;
М - масса детали; - плотность материала детали; температурная поправка, учитывающая теплообмен
калориметра с окружающей средой.
Температурная поправка в ряде случаев может
достигать 10 - 15 % от 1 - 0 и поэтому для повышения
точности калориметрических измерений ее необходимо
обязательно учитывать. Это особенно важно при проведении
нескольких, следующих друг за другом измерений.
203.
Для оценки теплоотдачи калориметра в окружающую средув ядро калориметра вводится некоторое количество тепла, в
результате чего температура ядра повышается на 0 .
Экспериментально в течение 8-10 часов определяется кривая
охлаждения ядра 0 (рис. … б), кривая аппроксимируется
экспоненциальной функцией вида :
0 exp K1 , где K1 ln 0 .
1
1
Снижение температуры за время (см. рис. ):
d
K1 K1 3
d
204.
Средняя температура главного периода измерения1
1
d 1 1 0 exp d
0
0
1
1
1 1 0 exp 1 1 K 2 1 0 , где K 2 exp 1 .
1 1 0 exp
,
где - константа, определяемая из экспериментальной
кривой (рис. , а)
Если время опыта не менее 0.5 с, погрешностями
теплообмена можно пренебречь
205.
4.7. Результаты измерения тепловых потоков,поступающих в обрабатываемую заготовку
f
h2 tg tg f a.
a
Схема потоков тепла, поступающих в деталь при резании
инструментом с упрочняющей фаской на передней
поверхности
206.
Экспериментальные результаты (рис.) подтверждаютпредположения о том, что тепловой поток Ф0, поступающий в
изделие из зоны стружкообразования, близок к нулю
. Влияние скорости резания на тепловые потоки в деталь
при точении стали 45: МПа, резец - Т15К6,
а=0,35 мм, b=1 мм, 1- h=0,1 мм, 2 - h=0,2 мм, 3 - h = 0,35 мм
207.
Опыты по определению тепловых потоков от застойной зоныпроводились острыми резцами (т. е. при h3 =0) с упрочняющей
фаской f на передней поверхности, расположенной под
углом f .
Зависимости теплового потока Ф от высоты застойной зоны
при точении с толщиной среза a=0,35 мм :а) - сталь 45,
резец Т15К6, v: 1 - 50 м/мин, 2 - 100 м/мин, 3 - 200 м/мин, б) ХН67МВТЮ-ВД, резец ВК8,: 1 - 2,0 м/мин, 2 - 5,0 м/мин, 3 10 м/мин, 4 - 20 м/мин
208.
Опыты по определению тепловых потоков от фаски износа h3(рис. ) проводились при точении резцами с плоской передней
поверхностью - без упрочняющей фаски
Зависимости теплового потока Ф от ширины фаски износа при
точении с толщиной среза a=0,35 мм :а) - сталь 45, резец
Т15К6, v: 1 - 50 м/мин, 2 - 100 м/мин, 3 - 200 м/мин, б) ХН67МВТЮ-ВД, резец ВК8, v : 1 - 2,0 м/мин, 2 - 5.0 м/мин, 3 10 м/мин, 4 - 20 м/мин
209.
Плотности тепловых потоков qФ вычислялись графическимdФ 1 dФ
дифференцированием потока Ф по площади F:
qф
dF b dh
или в безразмерном виде: q 1 Ф .
bSb v h
Зависимости плотности теплового потока q от высоты
застойной зоны при точении с толщиной среза a=0,35 мм: а)
- Сталь 45, резец Т15К6, v: 50 - 200 м/мин, б) ХН67МВТЮ-ВД, резец ВК8, v: 1 - 5,0 м/мин, 2 - 10 м/мин, 3 20 м/мин
210.
Зависимости плотности теплового потока q от ширины фаскиизноса при точении с толщиной среза a=0,35 мм :а) - Сталь
45, резец Т15К6, v: 50 - 200 м/мин, б) - ХН67МВТЮ-ВД,
резец ВК8, v: 1 - 5,0 м/мин, 2 - 10 м/мин, 3 - 20 м/мин
211.
4.8. Температура контакта резца со стружкой и детальюот равномерно распределенного источника тепла
Ранее было широко
распространено
предположение о
равномерном
распределении
удельных касательных
сил (и плотностей
тепловых потоков) по
ширине фаски износа
резца с
Схема распределения удельных
обрабатываемой
касательных сил на участке
заготовкой, и на участке
пластического контакта передней пластического контакта
поверхности и упруго-пластического стружки с резцом
контакта по задней поверхности
212.
расчет температуры на участке пластического контактастружки с резцом и на фаске износа по задней поверхности
режущего лезвия сводился к расчету температуры в
полуплоскости, движущейся относительно равномерно
распределенного источника тепла постоянной плотности
теплового потока
Схема к расчету
температуры в
полуплоскости,
быстродвижущейся
относительно
равномерно
распределенного
источника тепла
постоянной
плотности
y
теплового потока
v
213.
температурное поле в полуплоскости описывается решениемqc
2 2
x ,
x 1
2
2qc
x
ierfc
.
где
2
2
exp u du
0
x
y
v
Или более простым решением :
q
x,
CV
0
x2
exp
4
4
1
d
y
где
v
плотность теплового потока может быть представлена как
произведение удельной касательной силы на скорость
движения полуплоскости v:
qc qF v
214.
Температуру торца стержня определим по формуле2 qc
0, y
CV
2 qc
CV
y
2 qF
v
CV
vy
схема к расчету
приращения
температуры на
укороченной передней
поверхности резца от
равномерно
распределенного
источника тепла
215.
Наибольшая температура на передней поверхности отравномерно распределенного источника
Наибольшая температура будет иметь место при y=f в точке
(0,f). С учетом температуры деформации :
2 qF
f 1
0, f AW А1 K PeTпл
А1 Ре
Tпл ,
а
Sb
где
y
Sb
Ре
, А1
, AW u .
CV Tпл
Sb
vа
при точении отожженных сталей, имеющих относительно
невысокую твердость:
y 0,8Sb и qF 0,6Sb .
216.
. Распределение температуры по укороченной переднейповерхности при точении стали 12ХН3А резцом Т15К6 ,
=0 , =70 , f=0,4 мм, v=100 м/мин, s=0,2 мм/об, t= 3 мм,
при =2.
217.
4.9. Температура на границе быстродвижущейсяполуплоскости от неравномерно распределенного
источника тепла
Схема к расчету температуры передней поверхности при
равномерном распределении плотности теплового потока
на участке пластического контакта и линейно убывающей
плотности теплового потока на участке упругого контакта
218.
Формулу (…..) преобразуем к виду:2
qF y
T
A1 Pe
A0 q0 ,
Т пл
Sb c1
Sb
2
qF
y
где A0
A1 Pe , A1
, q0
, .
CV Т пл
Sb
c1
Участок упругого контакта стружки с резцом разобьем на
N интервалов. При этом безразмерная координата
i 1 i
y
, i 1, 2...N
c c1
значения плотности теплового потока q
qi q0 2 i . i 1, 2...N
Равномерно распределенный по длине участка
пластического контакта (0, 1) источник теплоты продлим на
участок упругого контакта (1, 2) и аппроксимируем линейно
убывающий источник тепла равномерно распределенными
источником и стоками K i (i 1, 2... N )
219.
При этом :q0 q1
q0 q 2
K1
, K2
,
2
2
q1 q3
qi 2 qi
K3
.... K i
2
2
или
Схема замены линейно
убывающего источника теплоты
равномерно распределенными
источником и стоками
q0 qi
при i 2,
2
Ki
q q
i 2 i при i 2.
2
220.
значения гомологических температур :1 T A0 q0 .
1 H N T A0 q0 1 H N K1 A0 H N ,
1 2 H N T A0 q0 1 2 H N K1 A0 2 H N K 2 H N
Температуру передней поверхности вычислим по формуле:
i д Т i * Т пл
при точении стали 45 HB=1800 МПа, =0,2 , m=0,15, резцом
Т5К10 =10 , =70 , со скоростью резания v= 65 м/мин,
глубиной t=5 мм, подачей s=0,4 мм/об вычислим =756 МПа,
, примем (по экспериментальным данным) =2, ,
температуру деформации (по расчету) (см. табл.)
221.
Таблица к расчету температуры на участке упругогоконтакта
На участке пластического
I
0
1
2
3
4
i
1
1,25
1,5
1,75
2
qi
0,6
0,45
0,3
0,15
0
Ki
-
0,075 0,15
0,15
0,15
0,375 0,396 0,36
0,34
0,29
918
860
763
Ti
985
890
контакта значения
гомологической
температуры
рассчитывались по
формуле:
Т i A0 q0 i
Точение стали 45
HB=1800 МПа,
=0,2 , m=0,15,
резцом Т5К10
=10 , =70 , со
скоростью резания
v= 65 м/мин,
глубиной t=5 мм,
подачей s=0,4
мм/об.
222.
4.10. Температура задней поверхности от равномернораспределенных на участке застойной зоны и фаски
износа источников тепла
Для резца без упрочняющей
фаски длина участка
застойной зоны по данным [
Н.Н.Зорев ] при
рациональных режимах
резания (порядка 800 – 900
С) высота застойной зоны
приблизительно равна 0,3a.
что безразмерная плотность
теплового потока
определяется соотношением:
Схема тепловых потоков
q0 q~ Sb 1.
на задних поверхностях
застойной зоны и фаски
износа
223.
Температура на участке застойной зоны рассчитана поформуле :
y
Наибольшая температура
3 A0 q0
Tпл , 0 y h3 ,
H0
достигается в конце застойной
зоны, т.е. в окрестности режущей
vH 0
Sb
2
где A0
A1
, A1
. кромки.
C T
V пл
Зависимость температуры
режущей кромки от
толщины срезаемого
слоя при точении стали
HB=1800 МПа, =0,2 ,
m=0,15, резцом Т5К10
=10 , =70 , , со
скоростью резания v= 65
м/мин (кривая 1) и v=130
м/мин (кривая 2) ,
глубиной t=5 мм, подачей
224.
температуру на фаске износа определим суммируяприращения температуры от источника и стока
h33 y q3 y
3 A0q0Tпл
1
, 0 y h3.
q0 H 0
H0
Распределение
температуры по фаске
износа задней
поверхности при
точении стали
HB=1800 МПа, =0,2 ,
m=0,15, резцом Т5К10
=10 , =70 , со
скоростью резания v=
65 м/мин , глубиной
t=5 мм, подачей s=0,4
мм/об.
225.
Зависимость температуры заднейповерхности от ширины фаски износа при
точении стали 45 HB=1800 МПа, =0,2, резцом
Т5К10 =10 , =70 , со скоростью резания v=
65 м/мин, глубиной t=5 мм, подачей s=0,4
мм/об., при : 1 – с учетом застойной зоны ,
2- без учета застойной зоны.
Большие
расхождения в
расчетных
температурах с
учетом и без
учета источника
теплоты на
участке застойной
зоны имеют место
вблизи режущей
кромки, т.е. для
«острого» резца
226.
5. СОВЕРШЕНСТВОВАНИЕ РАСЧЕТА ТЕМПЕРАТУРЫ ПРИРЕЗАНИИ НА ОСНОВЕ ТЕРМОМЕХАНИЧЕСКОГО
ПОДХОДА
5.1. Анализ гипотез о постоянстве удельных касательных
сил и об их зависимости от температуры, деформации и
скорости деформации
Схема зон
пластических,
упругопластических и
упругих деформаций в
плоскости
стружкообразования
при резании
227.
m2,5
y A , y 0,8S b , q F 0,6S b , q F y 0,5 const
0
2
Pxy 2 1 tg y
q F F sin y Pxy
,
cos sin tg y
tg y
c
c
y
PZ
P PZ
a
a
cos
где tg y
.
sin
На основании
данных
Н.Н.Зорева [ ] о
силах резания и
усадке стружки
228.
Распределение расчетнойтемпературы по укороченной
передней поверхности при
точении стали 60 резцом Т5К10
, =10 , =70 , s=1,2 мм/об, t= 10
мм, при =2, ( ),: 1 - v=30 м/мин
(Ре=70), 2 - v=60 м/мин (Ре=140),
Резание стали с
наростом на режущем
лезвии при невысоких
температурах
229.
Распределение отношенияпредела текучести на сдвиг
к действительному пределу
прочности при растяжении по
длине пластического
контакта стружки с режущим
лезвием. Условия резания те
же, что для рис. 5.3 (кривая
2).
Распределение расчетной
температуры по укороченной
передней поверхности при
точении стали 60 резцом Т5К10
, =10 , =70 , s=1,2 мм/об, t=
10 мм, при =2 с учетом
влияния температуры на
удельные касательные силы
при скорости резания v=60
230.
Расчетныераспределения
температуры и
плотностей тепловых
потоков при точении
стали 1- при скорости
резания v=0,01 м/мин,
2 – при скорости
резания v=80 м/мин.
p
p 0
0
m
0
p
0 K K T
0
m
k T
exp B T
231.
5.2. Сопротивление материалов большим пластическимдеформациям в адиабатических условиях (удельная
работа деформации)
m
m
k T
p
p
p 0
exp B T 0 K K T
0 0
0
и
p dAw
p
y
Aw S b
T
Aw A1 Aw d p u ,
S b d p
СV Tпл
S
Sb
o b
10 8 e18, 4
0
K Ke18, 4 k T , K T e B T
dAw
1
m
AK p exp B * A1 AW , где A
m
d p
3 3 ln 1 100
exp B * A1 AW dAw AK mp d p
AA1 BK 1 m
1
Aw
ln 1
p
BA1
1 m
232.
Удельная работа3,5
Расчет сталь
С45 -резание
3
2,5
Эксперимент
сталь С45 резание
растяжение
сталь 45
2
1,5
1
0,5
0
0
1
2
3
4
5
Экстраполяция
растяжение,
сталь С45
Текущий истинный сдвиг
Зависимость удельной работы деформации в
адиабатических условиях деформирования от
деформации
233.
Зависимость предела текучести от деформации прирезании для адиабатических условий деформирования
p
Отношение предела текучести к
действительному пределу
прочности
dAW
AA1BK 1 m
m
AK p 1
p
Sb
d p
1 m
1
средний предел текучести
на сдвиг при растяжении
1
0,9
0,8
0,7
0,6
Экстраполированное
среднее значение
предела текучести на
сдвиг при растяжении
Средний предел текучести
на сдвиг в зоне
стружкообразования
0,5
0,4
0,3
0,2
0,1
0
0
1
2
3
4
Текущий истинный сдвиг
5
Расчетный средний
предел текучести резание стали С45
при u ~
Сопоставление
зависимостей
отношения
предела
текучести на
сдвиг к пределу
прочности при
резании и
растяжении от
деформации
234.
Максимальные значения предела текучести при резаниизависимость предела текучести на сдвиг от деформации
описывается выпуклой кривой, имеющей точку максимума:
~
~m
AK
,
1 m
m 1 m
1
1 m
~
Sb
AK
A
B
1
В зонах Б и Г (рис….) деформации более однородны
(более равномерно распределены), вследствие чего
влияние скорости деформации будет несколько более
высоким:
1
AA
BK
q
1
q 1 m
m
AK q p 1
p
Sb
1 m
Максимальных значений пределы текучести в зоне А
стружкообразования и в зонах Б и Г достигают в стационарны
точках
1
~m
~
1 m
AK
q
m
1
m
q q
~
q0
, q
Sb
1 m
AK q A1B
235.
Удельные касательные силы в плоскостистружкообразования при адиабатических условиях
Зависимость отношения предела текучести на сдвиг к
действительному пределу прочности при точении стали 45
HB 1800 МПа, 20 , 40 , v 60 м / мин, s 1,2 мм / об, t 5 мм,
~ 1,7 , 1,7
u
236.
AA1 BK 1 m1
AW
ln 1
u 1,44
BA1 u
1 m
K Pe
1 exp Pe * tg y
1
Pe * tg y
температура деформации:
1
0,985,
Sb
A1
0,0784
CV Tпл
д Aw A1K PeTпл 200 С
При этом отношение среднего предела текучести к
действительному пределу прочности равно
y
Sb
AW
u
0,84
После достижения стабилизации предела текучести, т.е.
при часть деформации локализуется в узкой области
вблизи конечной границы зоны стружкообразования
237.
При увеличениидеформации температура деформации
возрастает, а интенсивность упрочнения деформируемого
материала уменьшается.
Стабилизации зависимости предела текучести от
деформации
способствуют
уменьшение
показателя
деформационного упрочнения m , повышение прочности
материала (A1) .
При
достижении
максимума
предела
текучести
деформируемый материал не
упрочняется
с ростом
деформации,
т.е.
обладает
свойствами
идеально
пластического тела.
При этом дальнейшее увеличение деформации может
происходить в узкой зоне (в плоскости сдвига).
Таким образом, закономерности упрочнения и разупрочнения
связаны с изменением схемы зоны стружкообразования
238.
5.3. Влияние локализации деформаций у конечной границызоны стружкообразования на температуру и удельную
работу деформации
При достижении
условий локализации деформаций
зависимость предела текучести от текущего истинного
сдвига имеет вид:
Сталь 65, HB 2800 МПа,
0 , 40 , v 60 м / мин,
s 1,2 мм / об , t 5 мм,
~ 1,17 , 3,3
u
K Pe 0,97 , A1 0,12
239.
Локализация деформаций в узкой области приводит кстабилизации предела текучести на более низком уровне, что
приводит к уменьшению удельной работы деформации
Удельная работа
3
Расчет сталь
35Х3МН резание
2,5
2
1,5
Эксперимент
сталь 35Х3МН
- резание
1
0,5
0
0
1
2
3
4
5
Без учета
локализации
Текущий истинный сдвиг
Влияние локализации деформаций в узкой зоне на зависимости
удельной работы от деформации при резании стали 35Х3МН
240.
Еслиu ~
, то локализация деформаций начинается уже
при
p 0
Деформацию 0 вычислим, аппроксимируя кривую
течения параболой при пересечении ее с прямой
p
Sb
p
Sb
u 0 0,3
Удельная работа с учетом локализации будет:
AW AW 0 u * u 0 AW 0,23 0,77 * 3 2,5
Sb
y
Sb
AW
u
0,77
д Aw A1K PeTпл 530 С
241.
Расчетная температура для условий точения закаленнойстали 60 после отпуска до твердости HB=2800 МПа с
подачей s=1,2 мм/об, с глубиной резания t=10 мм q F 0,6 Sb
Распределен
ие
расчетной
температуры по
укороченной
передней
поверхности
при
точении
стали
60
резцом Т5К10
, =10 , =70 ,
s=1,2 мм/об, t= 10 мм, при =2, (): 1 - v=30 м/мин
(Ре=70), 2 - v=60 м/мин (Ре=140),
242.
Схема зонпластических, упругопластических и
упругих деформаций
в плоскости
стружкообразования
при резании
2,5
y A
0
m
[ ], y 0,8S b , q F 0,6S b [ ], q F y 0,5 const [ ]
5.1.
эмпирические соотношения (5.1) справедливы только для
относительно узкого конкретного диапазона условий резания
243.
Схема к заданию плотностей тепловых потоков напередней и задней поверхностях режущего лезвия при
расчете распределений температуры и плотности
тепловых потоков
244.
~mМаксимальное значение
AK
q q
~ q qF
q
c
0
безразмерного предела текучести :
Sb
1 m
1
~ tg c
~
c
tg
1 ~ 1 arctg 2
где
1
m
m 1 m
~q
, a tg ~ tg a
2
~
AK q A1B
Температуру в начале интервала разупрочнения примем
273 д
равной температуре деформации:
~
T c T0
Т пл
Определяющее уравнение для интервала разупрочнения
обрабатываемого материала на передней поверхности
представим в виде:
q T q0 e
k T B T
e
Bq
T T0
.
q0 exp k B T q0 1
1 T0
эмпирический показатель степени Bq
отражает и
непосредственное разупрочняющее влияние температуры и
косвенное упрочняющее влияние температуры через
скорость деформации
245.
В интервале разупрочнениядля
любой координаты y=v температуру
быстродвижущегося
«стержня»,
выделенного
вдоль
оси
x,
необходимо рассчитывать с учетом
зависимости
плотности
теплового
потока от температуры:
дТ
д 2Т
2 ,
д
дx
Bq
q T q 1 T T0 .
0
1 T0
плотность теплового потока при температуре деформации
равна максимальному пределу текучести , а при
стремлении температуры к температуре плавления
стремится к нулю:
lim q y q0 , lim q y 0
при T 1 T0
при T T0
Показатель степени B q j,обычно находится в пределах от 1
до 1,5 и должен быть уточнен по имеющимся
экспериментальным данным о температуре или об удельных
касательных силах.
246.
СХЕМАТИЗАЦИя РАСЧЕТА ТЕМПЕРАТУР И УДЕЛЬНЫХКАСАТЕЛЬНЫХ СИЛ ПРИ РЕЗАНИИ НА ОСНОВЕ
ТЕРМОМЕХАНИЧЕСКОГО ПОДХОДА
дТ
д 2Т
2
д
дx
273 д
~
при T c T0
Т пл
AK q ~qm
q
q c~ q0 F
Sb
1 m
q0 y Sb
lim q y q0
при T T0
lim q c1 0
при T (1 T0 )
T
q q0 1
1 T0
Bq
При q y Sb нарост
247.
Схема итераций при расчете температуры и пределатекучести на передней поверхности инструмента «ТЕРМ»)
T10 A0 q0 H N ,
A0
2
A1
c 1
Pe 1 1
a
~
c
,
a
Sb
A1
, Pe va .
CV T п л
q0 q10
K 10
,
2
T11 A0 q0 H N A0 K10 H N .
T0i A0 q0 iH N A0 K 1 p iH N , i 2 .
Bq
Ti, p 1
K
qip q0 1
, ip
273 д
1
Tп л
q A qip
2
,
Tip T0i A0 K ip H N , p 1,2... r
Bq
T10
q11 q0 1
.
1 T0
K 11
q0 q11
,
2
T11 T10 A0K11 H N .
248.
249.
h2c1 1 c~
A
1
,
13
A
Pe
A0 1,13 A1 Pe
1 ,0, П
1
a a
a
1,22815
0,6721
250.
251.
252.
Примерыраспределений
температуры и
плотностей
тепловых
потоков
Распределения
температуры и
предела текучести по
длине контакта
при точении стали
HB=2000 Мпа
S=0,15 мм/об, t=4 мм
=2
253.
254.
255.
Распределения температуры и безразм. плотности теплового потокапо задней грани при точении стали HB=2000 Мпа S=0,15 мм/об, t=4 мм,
hз=0,6 мм
, V=25 м/мин
V=250 м/мин
256.
Температура формоустойчивостиТ форм Т п, max Т 0 Т з,max Т 0 / 1,41 Т 0
2
2
257.
Метод полуискусственной (защемленной) термопарыЯ.Г.Усачева (1905 г.)
1 – резец,
2 – спай термопары с
резцом,
3 - термопара, 4 –
милливольтметр,
5 - изолятор
258.
Метод естественной термопары(предложен Е. Гербертом и К. Готвейном)
1- обрабатываемая деталь,
2 – режущая пластина,
3 – державка резца,
4 – щуп, 5 – милливольтметр,
6- усилитель, 7 – токосъемник,
8 – провода, 9 – изоляторы.
токосъемник
температура резания,
Тр
Т п,ср С Т 3,ср h3
С h3
259.
Сопоставление экспериментальных и расчетныхтемператур резания
Эксперимент Н.В.Талантова
Эксперимент А.Д.Макарова
260.
Сопоставление экспериментальных и расчетных температуррезания
Сталь 40, , 45
Эксперимент Н.Н.Зорева
261.
Сопоставление экспериментальных и расчетных температуррезания
Сталь 40, , 45
Эксперимент Н.Н.Зорева
262.
Сопоставление экспериментальных и расчетных температуррезания
Сталь 40, , 45
Эксперимент Н.Н.Зорева
263.
Сопоставление экспериментальных и расчетных температуррезания
Эксперимент Н.Н.Зорева при точении стали 20,
HB=1260 Мпа, b =450 МПа, =30%, , 60
264.
Сопоставление экспериментальных и расчетных температуррезания
265.
метод измерения температуры по структурнымпревращениям в инструментах из быстрорежущей стали
(Трент Е.М.)
Температурное поле в резце при точении низкоуглеродистой стали с
подачей 0,5 мм/об и скоростью 91 м/мин после 30 с резания
при температуре, превышающей 600 С, быстрорежущая
сталь «переотпускается». После резания в течение 10 – 30 с
под влиянием нагрева микротвердость быстрорежущей стали
уменьшается и структура стали претерпевает превращения,
которые можно проследить с помощью металлографического
или электронного микроскопов
266.
Сопоставление экспериментальных и расчетных температурИзмерение температуры по
инфракрасному излучению
267.
Измерение температуры методом разрезного резца268.
Скаляр, векторСкаляр величина , значение которой может быть выражено одним числом
Примером скалярной величины является температура в конкретной точк
пространства в конкретный момент времени.
Вектор - величина , для которой любому направлению в пространстве
может быть поставлен в соответствие скаляр посредством
соотношения, линейного относительно направляющих косинусов :
3
x x1e1 x2e2 x3e3 xi ei
3
i ei ,
i 1
i 1
1 cos , e1 , 2 cos , e2 , 3 cos , e3
x x1 cos , e1 x2 cos , e2 x3 cos , e3
Примерами векторных величин являются тепловой поток , сила,
скорость .
269.
Тензор (второго ранга)Тензор (второго ранга) - величина , для которой любому
направлению в пространстве может быть поставлен в соответствие
вектор посредством соотношения, линейного относительно
направляющих косинусов :
T T1 cos , e1 T2 cos , e2 T3 cos , e3
T1 T11e1 T12e2 T13e3
T2 T21e1 T22e2 T23e3
T3 T31e1 T32e2 T33e3
T11 T12 T13
T T21 T22 T23
T
T
T
31 32 33
Примерами тензорных величин являются деформации
и напряжения
270.
Деформации. Характеристики деформацииДеформации среды характеризуются симметричным тензором деформаци
x xy xz
ij yx y yz .
zx zy z
x, y, z
1
xy yx xy
2
zy yz
xz zx
1
zx
2
1
yz
2
- Линейные деформации по осям x, y, и z,
xy , xz , yz - Угловые деформации
(деформации сдвига)
.
При повороте осей координат компоненты тензора деформации
изменяются. Существует одно положение системы координат, при
котором угловые деформации равны нулю. Оно описывыется
уравнением:
x xy
xz
yx y yz 0
zx
zy
z
I1 I 2 I 3 0
3
2
271.
ГдеI1, I 2 , I 3 - Инварианты тензора деформации.
I1 x y z
Первый инвариант тензора деформации :
Второй инвариант тензора деформации :
I 2 x y y z z x
2
xy
4
2
yz
4
2
zx
4
Третий инвариант тензора деформации :
x xy xz
1
2
2
2
I 3 yx y yz x y z x yz
y zx
z xy
xy yz zx
4
zx zy z
Выражения инвариантов через главные деформации имеют вид:
I1 1 2 3
I 2 1 2 2 3 3 1
I 3 1 2 3
272.
Тензор деформации можно представить в виде суммы шарового тензораи девиатора:
0
0
T 0 0
0
0
0
x 0
xy
0 , D yx
y 0
0
0
zx
zy
xz
yz
z 0
где
0
x y z
3
Первый инвариант тензора деформации используется для условия
постоянства деформируемого объема (несжимаемости материала):
I1 x y z 0
Второй инвариант девиатора деформации используется для
характеристики деформации - интенсивности деформации .
Интенсивностью деформаций называют величину, пропорциональную
квадратному корню из второго инварианта девиатора деформаций
4
I 2 D
3
2
2
2
2 3 2
2
2
i
x y y z z x xy yz
zx
3
2
i
Интенсивность
деформаций сдвига
Г 4 I 2 D 3 i
273.
Для малых деформаций компоненты тензора деформаций можновычислить по формулам Коши:
1 дU i дU j
ij
2 дx j
дxi
(i = 1,2,3; j = 1,2,3).
1 x, 2 y , 3 z
дU y
дU x
дU z
x
, y
, z
,
дx
дy
дz
дU y дU z
дU x дU y
дU z дU x
xy
, yz
, zx
.
дy
дx
дz
дy
дx
дz
Тензор скоростей деформации
дVi дV j
ij
дx j дxi
(i = 1,2,3; j = 1,2,3).
274.
Л.3.Схема зоны деформации при образовании сливной
стружки с зоной стружкообразования с параллельными
границами и областями пластических деформаций на передней
поверхности и в застойных зонах
A – зона стружкообразования с параллельными границами;
Б – застойная зона адиабатических деформаций;
В и Г – зоны контактных
деформаций на передней и задней
поверхностях.
275.
Распределение деформаций в зоне стружкообразованияи в застойных зонах
276.
Поле скоростей в зонепараллельными границами
стружкообразования
y
v x y v v 2
H
v y vn .
с
n
,
277.
Скорости деформации при резании1 дvi дv j
ij
2 дx j дxi
yx
xy
(i = 1, 2, 3; j = 1, 2, 3).
1
1 дv x y 1 v2
xy
n
2
2 дy
2 H
y
H
n 1
Для : = 2,5, v = 1 м/с, у=30 о, n = 5, H = (0,2–0,5)a, a=0,2 мм,
6
xy H 0,6 1,5 10
, c–1
- Резание
- Растяжение
истинные деформации в зоне стружкообразования
0, 018 1/с
и y
y / vn
0
v2 y
n
H H
n 1
y
d
vn
v2 y
y
.
H
vn H
n
n
278.
Деформации при растяженииl1 l0 l
z
l0
l0
l
*100, %
l0
х y
1 l
2 l0
ij 0
0
0
1 l
2 l0
0
0
l
l0
Относительное удлинение
х y ,
2 Z 0,
1
1 l
Z
2
2 l0
Истинные деформации
l
l0 l
dl
l1
Zu ln ln
ln 1
l0
l0
l0
0
l0 l
i z
l
Истинные деформации сдвига: u 3 ln 1
l0
l1
279.
СТАТИКАНапряженное состояние , напряжение
Напряжение является мерой
внутренних сил, возникающих в теле
под влиянием внешних воздействий
(нагрузок, изменения температуры и
др.).
Напряжение T зависит только от
положения точки А и направления
нормали , то есть каждому
направлению соответствует свое
напряжение T
280.
Соответствие напряжений T любому направлению устанавливается наоснове принципа равновесия с помощью тензора напряжений.
ij (i = 1, 2. 3; j = 1, 2, 3).
x
ij yx
zx
xy xz
y yz
zy z
xy yx , xz zx , yz zy.
281.
Имеется такое положение системы координат, прикотором вдоль одной из осей нормальное
напряжение максимально, а вдоль другой минимально, причем касательные напряжения на
площадках, перпендикулярных этим осям,
равны нулю. Эти
направления
называют
главными.
Три инварианта I1, I2, I3 определяют главные
направления тензора напряжений и сами
находятся из условия равенства нулю касательных
напряжений при повороте системы координат
282.
Сумму нормальных напряжений называют первыминвариантом I1 тензора напряжений:
I1 x y z 3 0 .
x y z
называют гидростатическим давлением
0
3
S x xy xz S x x 0 , S y y 0 , S z z 0
S yx S y yz называют девиатором напряжений
S
zy
z
zx
Второй инвариант определяется следующим выражением
I 2 y z z x x y
i 3I 2 (S )
2
yx
2
zx
2
zy .
интенсивность нормальных напряжений i
i I 2 (S ) интенсивность касательных напряжений
283.
Упругость, прочность , пластичностьE
закон Гука:
где E – модуль упругости
при растяжении (модуль Юнга)
предел упругости
y
предел пропорциональности пц.
предел текучести Т
Pmax
b
.
F0
- условный предел прочности
S b b 1
-действительный
предел прочности Sb
0, 2
F0 dz Fdz 1
F0
F
1
284.
Условия пластичностипластические деформации происходят, когда значение второго инварианта
девиатора напряжений достигает некоторой постоянной (для данных
условий деформирования ) величины :
2
1 2
I 2 S1 S22 S32 Т .
2
3
Условие пластичности Мизеса может быть записано в виде:
i I2 Т .
Т характеризует сопротивление материала деформации в данных
условиях деформирования и называется пределом текучести на сдвиг
Для интенсивности нормальных напряжений
условие пластичности Мизеса примет вид :
i 3 i
i Т
285.
Изменение кривой течения при увеличении скоростидеформации и температуры
286.
Л.5Влияние условий деформирования на сопротивление
материалов пластическим деформациям
Идеально пластическое тело
Т 0
Т 0
Отношение абсолютной температуры к
абсолютной температуре плавления
называют гомологической температурой
Повышение температуры деформации способствует возвращению металла
структурно-неустойчивого состояния, полученного в результате пластических
деформаций, в более устойчивое структурное состояние
Абсолютная температура, при которой отдых и рекристаллизация
происходят более интенсивно, чем искажение кристаллической решетки и
упрочнение пропорциональна абсолютной температуре плавления
Для металлов обычной
Т рек
T
0,3 0,4
технической чистоты
Т пл
Горячей называют деформацию при температуре, равной или выше
температуры рекристаллизации. при горячей деформации при постоянной
температуре и постоянной скорости деформации имеют вид прямой,
параллельной оси деформации
287.
для свинца, имеющего температуру плавления Тпл=600 К при комнатнойтемпературе гомологическая температура равна: Т 0,49
для стали , имеющей температуру плавления 1800 К, идеальная
пластичность может быть при температуре около 700 - 900 К
(400 - 600 град. Цельсия)
Схема к определению удельных касательных сил при резании
P sin y v2 cos y
AW
y
*
ab
v cos
u
288.
Гипотеза о постоянстве удельных касательных сил прирезании
y Т ,ср const
у 0,8 Sb ;
F
qF
const
bc
qF 0,6Sb
289.
Простое нагружение, теория теченияХолодной называют деформацию при температуре ниже температуры
рекристаллизации. T Т рек
Пластические деформации вызывают повышение плотности дислокаций,
искажение кристаллической решетки и приводят к увеличению напряжения
m
p
p 0
0
290.
Модель идеально-пластического тела илитеория течения (деформационного упрочнения)?
m
2,5
у А A2,5
0
у
qF
const 0,5
по Н.Н.Зореву
у
1 u
u
p d p A
0
по М.Ф.Полетике и Н.Н.Зореву
um
m 1
291.
Влияние температуры деформации при растяженииТ 0 exp B T
Т Т 0
Т 0 1
1 Т 0
Влияние температуры на предел прочности стали 45
B
292.
Влияние скорости деформации при растяженииВлияние скорости деформации и температуры на предел прочности стали 45
при относительном удлинении = 20
Коэффициент динамичности
0
k Т
K
293.
Влияние скорости деформации при резаниирезание сталей 00, 10, 20Х,
Х18Н9Т
Со скоростью резания
v = 0,2 м/мин a = 0,22 мм и
о, Н.Н.Зорев
cp
m
1 u Sb p
d p
0
u
3 0
AS b m
u ,
m 1
обобщенное определяющее уравнение :
Т 0
0
m
0
k Т
exp B Т ,
294.
Сопротивлениематериалов
большим
пластическим
деформациям в адиабатических условиях деформирования
Aw S b
T
Aw A1
СV Tпл
и
Aw
o
AW
dAw
AK pm exp B * A1 AW
d p
p
Sb
y
Sb
p
dAw
S b d p
d p
u
0
k Т
K
exp B * A1 AW dAw AK pm d p
295.
Удельная работа деформацииA
AA1 BK 1 m
Sb
1
Aw
ln 1
p A1
СV Tпл
BA1
1 m
3 3 ln 1 100
3,5
Удельная работа
1
m
Расчет сталь
С45 -резание
3
2,5
Эксперимент
сталь С45 резание
растяжение
сталь 45
2
1,5
1
0,5
0
0
1
2
3
4
5
Экстраполяция
растяжение,
сталь С45
Текущий истинный сдвиг
Гипотеза о равенстве удельных работ при сжатии и резании
А.М.Розенберга использовалась для расчета сил резания
296.
Удельная работа3
Расчет сталь
35Х3МН резание
2,5
2
1,5
Эксперимент
сталь 35Х3МН
- резание
1
0,5
0
0
1
2
3
4
5
Без учета
локализации
Текущий истинный сдвиг
Влияние локализации деформаций в узкой зоне на зависимости
удельной работы от деформации при резании стали 35Х3МН
297.
Кривая течения для адиабатических условия деформированияp
p
Отношение предела текучести к
действительному пределу
прочности
dAW
S b d p
Sb
m
AK p 1
AA1 BK 1 m
p
1 m
1
средний предел текучести
на сдвиг при растяжении
1
0,9
0,8
0,7
0,6
Экстраполированное
среднее значение
предела текучести на
сдвиг при растяжении
Средний предел текучести
на сдвиг в зоне
стружкообразования
0,5
0,4
0,3
0,2
0,1
0
0
1
2
3
4
Текущий истинный сдвиг
5
Расчетный средний
предел текучести резание стали С45
Гипотеза о единой кривой течения использовалась Зоревым Н.Н.
298.
Действительные характеристики сопротивления материалапластическим деформациям в адиабатических условиях
AK ~ m
,
Sb
1 m
~
1
m 1 m 1 m
~
AK
A
B
1
B 1,25;
K 1,3;
K q 1,6
q
Sb
A K q qm
1 m
m 1 m
q
A K q A1 B
условие локализации деформаций:
d p
d p
1
1 m
0
299.
Влияние локализации деформаций на кривую теченияp p при p p p и
p p
p и при p p p u
Отношение предела
текучести к
действительному
пределу прочности
0,8
0,7
0,6
0,5
0,4
0,3
0,0
0,5
1,0
1,5
2,0
2,5
3,0
3,5
4,0
Текущий и конечный истинный сдвиг
без учета локализации
конечный истинный сдвиг 4
Конечный истинный сдвиг 3
Конечный истинный сдвиг 2
Удельные касательные силы в плоскости сдвига, эксперимент
4,5
300.
Деформации при прокаткеПрокатке подвергают до 90% всей выплавляемой стали
и большую часть цветных металлов
Прокатка представляет собой механическую обработку металлов
путем обжатия между вращающимися валками прокатного стан
с целью уменьшения сечения прокатываемого слитка или
заготовки и придания им заданной формы (профиля)
Схемы прокатки
По расположению валков различают прокатку продольную,
поперечную или винтовую
Наиболее распространенным в практике является процесс
продольной прокатки металла между двумя принудительно
вращающимися валками
301.
Схемы продольной (а), поперечной (б) и винтовой (в) прокатки:1- заготовка; 2, 3 - валки
302.
Схема устройства прокатного стана: 1- электродвигатель,2- упругая муфта, 3 –редуктор, 4- главная муфта,
5 – шестеренная клеть, 6 –шпиндели, 7-– рабочие валки
Основная часть прокатного стана - рабочая клеть.
В подшипниках станины рабочей клети вращаются рабочие
валки 7 . Подшипники верхнего валка могут перемещаться
303.
При прокатке металл осаживаетсявдоль оси z, получает удлинение
(вытяжку) вдоль оси x и уширение –
вдоль оси y
Схема деформации металла при
продольной прокатке
При продольной прокатке
одновременно пластической
деформации подвергается только
та часть металла, которая
находится в очаге деформации
304.
Очагом деформацииназывают область
АВВ1А1, заключенную
между валками и
сечениями входа АА1
металла в валки и выхода
ВВ1 металла из валков
Схема деформации
прямоугольной
координатной сетки
в плоскости xz при
прохождении металла
через очаг деформации
АВВ1А1
при продольной прокатке
305.
Отношение длин заготовки после и до деформации(или отношение площадей поперечного сечения до и после
деформации) называют вытяжкой:
F0
l
l0
В качестве одной из основных
характеристик линейной
деформации применяют
относительное обжатие
используются также
относительное удлинение:
и относительное уширение:
F
h1 h0 h
Z h
h0
h0
l1 l0 l
x l
l0
l0
b1 b0 b
y b
b0
b0
Относительное обжатие за 1 проход составляет 10—60%,
а иногда и больше (до 90%).
306.
Условие неизменности объема имеет вид:l h b
x y z
0
l 0 h0 b0
При вычислении работы и сил деформирования используют
истинные (логарифмические) деформации:
высотную
Zи
поперечную
продольную
h1
h1
dh
ln
h
h0
h0
yи
b1
b1
db
ln
b0 b0 b
xи
l1
l1
dl
ln
l0 l0 l
307.
Для истинных (логарифмических) деформаций условиеПостоянства объема имеет вид:
l1 h1 b1
l1
h1
b1
l1 h1 b1
0, или
ln ln
ln
ln
1.
l0
h0
b0
l0 h0 b0
l0 h0 b0
Кроме линейных деформаций имеют место и сдвиги:
xz zx , xy yx , yz zy .
Вблизи поверхностей контакта прокатанного металла с
валками деформация больше, чем в глубине металла
308.
y 0,xy yx ,
yz
zy
.
x, и
h1
l1
ln ln
h0
l0
Схематизация деформации при прокатке: а) – линейные
деформации, б) деформации неоднородного сдвига
309.
zx
h1
2
z
U x z
h1
1 дU x z
xz zx
.
2 дz
h1 h1
Тензор деформации при прокатке полосы
h1
ln 0
z
2
h1
h0
T
0
0
0
h1
z
0
ln
h0
h12
2
310.
2i
3
y y z z x
2
x
2
2 8 2 h1 2
ln 2 z
3 3 h0 h1
i,ср
4
h1 2
h1 3 0
2
2
i ,ср
2
3 2
xy yz2 zx2
2
8 2 h1 2
ln
2 Z dz
3
h0 h1
2
h1
h1 2
dz
i
0
311.
i , ср K z ,ипри
h0
К ln ,
h1
h1 0,1 м, h0 0,04 м
v1 h0 h1 1
с
L h0
где K=1,15
z,и 0,4 и i , ср 0,47
v1 скорость выхода
металла из валков, м/с
L- горизонтальная проекция дуги захвата, м
D
L sin .
2
D- диаметр рабочего валка, -угол захвата.
v1
при
10 с
=1 м/с, D=0,6 м, =30О, h1=0,1 м, h0=0,04 м
1
При прокатке скорости деформации могут
изменяться в широких пределах:
от 0,1 до 1000 1/с.
312.
Удельная работа деформации в элементарном объеме деформируемогоматериала может быть оценена как произведение интенсивности
деформации и интенсивности напряжений :
Awp pi i
Среднее по объему V0 значение удельной
1
A
pi i dV
wcp
работы найдем интегрированием:
V0 V
0
При горячей прокатке при температуре
предварительного подогрева 1000 С
(1000) * K
T (1000) 50 МПа
pi
T
При V1= 1 м/с, диаметре валка D=0,6 м, угле контакта 30 ,
h0=0,1 м, h1=0,04 м скорость деформации будет:
h0 h1 1
1
0,06
с
4 с 1
D
0,6 * 0,5 0,1
h
o
0
sin 30
2
2
v1
313.
С поправкой на скоростьдеформации
T 100 МПа
Вынося предел текучести за знак
h1 D
V
* sin * b1
0
интеграла и принимая ,
2 2
получим:
2 T h1 2
Awcp
i ( z )dz
h1 0
2
где: 2 8 ln 2 h1 2 z
i
3 3 h0 h12
Вычисляя, получим:
Awcp 50 МПа
314.
мощность и крутящий момент при прокаткемощность прокатки:
При AW 50 МПа
N e AW * h1b1v1
h1=0,1 м,
b1 2 м, v1 1 м / с
N e 10 МВт
При диаметре валков D=0,6 м частота вращения валков равна:
60v1
n
31,8 об / мин 3,3 1 / с
D
Ne
Крутящий момент на одном валке: М кр
1,5 МНм
.
2n
315.
усилия на валкиN e 2 М кр
F
5 МН
2v1
D
при =30
Р
F
0
19 МН
sin 15
при прокатке стальной проволок
узких стальных полос Р около
200—1000 кн, а при прокатке
листов шириной 2—2,5 м
доходит до 30— 60 Мн
316.
СИЛЫ РЕЗАНИЯСхема технологических осей x, y, z и физических составляющих силы резания при
свободном прямоугольном продольном точении
317.
Связь приращений физических и технологическихсоставляющих силы резания
1)
y , y , (или )
Угол трения
arc tg arc tg
F
N
F
Коэффициент
N
трения
Угол действия
318.
Удельные силы резания на передней поверхностипо Ф.Мерчанту
ab
P y
sin y
1
y
cos
Sb st sin arctg
,
Sb
sin
Отождествление условий контакта
с трением
Угол трения :
F
arc tg arc tg
N
y ab
R
cos y cos y sin y
y ab cos
R R cos
K Sb st
cos y sin y
P
Угол действия :
Удельная касатель.
сила
y ab sin
R R sin
K Sb st
cos y sin y
P
y
ab sin y
Предел текучести?
319.
Теоретическое определение углау по Ф.Мерчанту
из условия минимума мощности стружкообразования
при
const , y const
d R v
d y
0
cos y sin y sin y sin y cos y cos y
y
cos 2
y
0
y
4
1- по Мерчанту, 2 – эксперимент
Н.Н.Зорева, сталь 20Х, = 20
2
4
2
2
1- по Мерчанту, 2 – эксперимент
Н.Н.Зорева, резание меди, = 20
=20 30
320.
Зависимости удельных сил резания от удельныхкасательных сил и усадки стружки
y,
у
P y
y
1
u
1
u
u
0
p d p
AW
1
ab
cos
Sb st sin arctg
,
sin y Sb
sin
qF
c
F q F bc
S b st .
Sb
a
qF
c
f
c
,
2 .
a a cos д a
321.
Удельные силы резания на передней поверхности1
N P
Ftg y .
cos y
sin y
cos
R N cos F sin P
F
K S b st ,
cos y
cos y
y 1 2 sin qF c 1 y u
qF
qF
K
2
AW 2
Sb
cos
Sb a
Sb
Sb
Sb
cos y
sin
R F cos N sin F
P
K S b st ,
cos y
cos y
q F c 1 sin y 1 2 sin
q F sin
K
tg
2
AW tg
Sb a cos
Sb
cos
Sb
cos
322.
Теоретическое определение усадки при постоянныхкасательных напряжениях const , q const ;
y
F
1
1
1
N c P v2 Fv1 y abv 2 sin
qF bfv
min
cos
cos
dN c
0,
d
1
1
y a 1 2 qF f 2 0
qF f
f 1
y a
(1)
Точение стали 65Г:
1-v=0,4 м/с, 2-v=0,6 м/с,
3-v=0,8 м/с, 4-v=1,25 м/с,
5 – теория по формуле (1)
323.
схема технологических составляющих силы присвободном прямоугольном точении
R
K
,
S b st
K
R
S b st
;
R K Sb st ,
N1 qN1h3 t sin , qN1 HB 3 b ,
F1 1N1.
1 0,4
R K Sb st.
324.
Удельные силы на задней поверхностиВлияние ширины фаски износа
на силы Pxy и Pz
Pxy
hз b
qN1,
Pz
qF1
hз b
qF1
1
qN1
Сталь 40ХНМА, t=2 мм, Н.Н.Зорев
qN1 b , qF1 1qN1 , 1 0,4 0,6
325.
Расчет сил при свободном прямоугольном точенииt
Px R N1 sin K Sb St b h3
sin ,
sin
t
Py R N1 cos K Sb St b h3
cos ,
sin
Pz R F1 K Sb St 1 b h3 0,7 Sb H 0 t sin .
326.
Силы при несвободном прямоугольном точенииСхема приращений сил при несвободном точении резцом с закругленной
вершиной
327.
Приращения сил на участке криволинейной кромкиR = K Sb ax l;
R = K Sb ax l,
N1 = b hз l;
F1 = b hз l.
Px = R sin x + N1 sin x
Py = R cos x + N1cos x,
Pz = R + F1,
На участке
l
дуги окружности
y r r x ,
2
2
x
r 2 x2
sx
l
x, sin x , cos x
, ax .
2
2
r
r
r
r x
r
Интегрируя приращения сил от x1=0 до x2 t 2 r t
328.
Силы при точении резцом с закругленной режущей кромкоK S b S
Px
r
r2
t 2 r t
t 2 r t
arcsin
r t
2
r
2
K Sb S t 2 r t
b h3 t
r
2
K S b S t 2 r t
Py
b h3 t 2 r t
r
2
t 2 r t
Pz K Sb S t b h3 qF h1 r arcsin
r
329.
Л.8.Схема сил при свободном косоугольном продольном точении
330.
Расчет сил при свободном косоугольном точенииR x 0 R 0 sin
Ry 0 R 0 cos
R 0 R cos
R 0 R sin
R x R sin cos
Rμy R sin sin
R x Rx 0 Rμx R sin R sin cos ,
Ry Ry 0 Rμy R cos R sin sin .
1 arctg
Rx
.
Ry
Px K SbSt sin 1 b h3t,
S
Py K SbSt cos 1 b h3t ctg K s ,
t
Pz K SbSt cos 1 b h3 0,7Sb H0 t sin K s S ,
331.
Напряжения в клине под действием сосредоточенной силы,действующей на острие клина (по Мичелу)
касательные напряжения на
поверхности режущего клина
1, 1
P1
b
1 sin
sin
3
2
1
2
4
2
Радиальные (сжимающие)
напряжения
P2 sin
r
sin
br
2
2
332.
Силы на передней поверхности1
P
Sb St ,
Sb sin y
q F 2C1
F
Sb St.
Sb a
cos
R P
cos y
F
sin y
cos y
cos y
sin
R P
F
.
cos y
cos y
,
333.
В системе координат 1 1, повернутой на угол ( )относительно координат , силы на передней поверхности
R 1 R cos 2
R sin 2
cos 2
P
cos y
F
sin y 2
cos y
R 1 R sin 2 R cos 2
cos y 2
sin 2
P
F
cos y
cos y
,
334.
Силы на задней поверхности в координатах :q3 h3
1 h3
F1
S b st , N1
S b st ,
Sb a
1 Z a
в новых координатах 1 1
R 1 F1 cos 2 N1 sin 2 ,
R 1 F1 sin 2 N1 cos 2 .
для тангенциальной (перпендикулярной биссектрисе угла
заострения) и радиальной (по биссектрисе) проекций силы
резания
sin y 2
cos 2
P1 P
F
F1 cos 2 N 1 sin 2 ,
cos y
cos y
cos y 2
sin 2
P2 P
F
F1 sin 2 N 1 cos 2 .
cos y
cos y
335.
Наибольшие касательные напряжения на поверхности клинапри
2
2
1 c
, учитывая, что
1
tg
1
2
2
P1 tg 2 2 cos 4 2
P1
sin
1, 1
* 1
0 K1 ,
bc sin
2 sin
2
bc
1
2
2
2
sin 2
K1 0,57
.
( sin )
Радиальные (сжимающие) напряжения
где P1 ,
0
0,57bc
r
sin 2
1 sin 2
r
2 2
sin 2
P2
sin
P2 2 1 sin 2
r
br sin b tg 2 sin
2
2
336.
радиальное напряжение2
при ,
P2
P2 2 1 2 2
r
0,23
b
2 b 1
2
sin 2
K1 0,57
.
( sin )
2 1
1 sin 2
2
K 2
.
2 2 tg 2 sin
P2
1 sin 2
r 0,23 * 8,7
b
tg 2 sin
Т.о. уменьшение угла заострения (увеличение ) увеличивает
касательные и особенно нормальные напряжения. С увеличени
нормальные напряжения уменьшаются.
337.
Наиболее благоприятными значениями ширины фаски износаи толщины среза следует считать такие, которые обеспечиваю
Касательное напряжение,
МПа
минимальные или допускаемые
касательные напряжения.
Т.о. критерий затупления ширину фаски износа h*
следует назначать с учетом
уровня касательных напряжений
2000
1500
1000
500
0
-500
-1000
-1500
0,05
0,15
0,25
Толщина срезаемого слоя, мм
hз=0,1 мм
hз=0,4 мм
338.
ВЛИЯНИЕ толщины среза и радиальной силы Р2 на округлениережущей кромки при :
*
, cж
6000 МПа,
2
в 1250 МПа
P2
r 0,23 ;
b
2
P2
0,23
b
339.
Схема приращений сил при несвободномфрезеровании торцово-конической фрезой
прямоугольном
340.
силы при несвободномпрямоугольном
торцово-конической фрезой
фрезеровании
Pxi K SbtS z sin i sin b h3t ,
Sz
Pyi K SbtS z sin i cos b h3t ctg K s
t
Pzi K SbtS z sin i 1 b h3 t sin K s S ,
Zp
PH ( Pxi sin i Pzi cos i )
i 1
Zp
PV Pxi cos i Pzi sin i
i 1
Zp
PW Pyi
i 1
,
341.
Схема приращений сил при фрезеровании цилиндрическими фрезами342.
Приращение силы ΔR на передней поверхности как и при точении:R K Sb a b, где
a s z sin cos , b D
1
,
2 sin
sм
sz .
nz
Здесь D – диаметр, z – число зубьев, n – частота вращения фрезы, sм, sz –
минутная подача и подача на зуб
Приращения осевой ΔR 0 и окружной (тангенциальной) ΔR 0 сил:
R 0 R sin ,
R 0 R cos .
в рабочей плоскости (г) могут быть показаны приращения ΔP 0 и ΔPν,
включающие приращения сил на передней и задней поверхностях зуба
фрезы:
2
cos
1 D
,
P 0 K S b s z
sin 1 b hз
sin
sin 2
D
P K S b s z sin b hз ctg .
2
Приращение крутящего момента Мкр, соответственно, будет:
М кр
D 3
P 0 10 .
2
343.
Приращения технологических сил:PV ( Sb s z K sin 2 K sin cos
1
D
cos 1 sin ) ctg ,
b h3
cos
2
PH ( Sb s z K sin cos K sin 2
1
D
1 cos sin ) ctg .
b h3
cos
2
Проекции сил фрезерования на технологические оси и крутящий момент
на фрезе от i-того зуба находят, интегрируя приращения сил ΔPH, ΔPV, ΔPW
и крутящего момента Мкр по активной длине i-того зуба.
344.
1 sin 2 sin 2 1iK cos 1
1i
1
2
D
PVi Sb s z 1i ctg
2
2
1 cos 2 1 cos 2
K
1i
2
cos cos 1i
D
1 sin sin 1i
,
b h3 1i ctg
1
1i
2
cos 1i
cos 2 1 cos 2
K
1
D
2 ( 1i )
PHi Sb s z 1i ctg
2
2
sin 2 sin 2 1i
K 1
2 ( 1i )
D
1 sin sin 1 cos cos 1
1
,
b h3 1i ctg
1
1
2
cos
345.
cos 1i cosD
PWi K Sb s z 1i ctg sin
1
2
М кр
cos 1 cos
Sb s z cos K
1
3 D D
10
ctg
1
2 2
1
1 b h3
cos
N e k М кр k
n
30
346.
nZ30
Зависимости технологически
составляющих сил и
мощности от угла
поворота зуба при
фрезеровании стали 60
HB=2850 Мпа
цилиндрической фрезой
Т5К10, D=120 мм, Z = 16,
= 10 , = 15 , hз = 0,6 мм
v = 60 м/мин, B = 10 мм,
e = 4 мм, sм = 500 мм/мин,
sz = 0,2 мм/зуб: а) = 1 ,
б) = 15 .
Частота вынужденных
колебаний равна:
nZ
30
347.
Вынужденные колебания при фрезерованииУравнение вынужденных колебаний
mZ1" СZ1 kZ P sin pt
C / 2m
0
- Коэффициент демпфирования,1/с
k m Собственная частота свободных
колебаний
Решение :
Z
ст
2
2
2 2
p
4
p
1
4
2
Kд
1
2 2
2 2
p
4
p
1
4
2
348.
Автоколебания при резанииНеоднозначность силы от пути за период
колебания: при E>0 –раскачивание, при
при E<0 – демпфирование
Нелинейность E(A) играет роль клапа
регулирующего амплитуду
Физическая причина автоколебаний
- убывающая зависимость предела
текучести от температуры
Для передней и задней поверхностей
модели колебаний - разные.
349.
Для задней поверхности может быть использованамодель Ван-дер-Поля автоколебаний при трении:
Предполагается, что причиной
возникновения энергии автоколебаний при трении
является падающая зависимос
силы трения от скорости
Предполагаемая физическая причина автоколебаний на
передней поверхности - убывающая зависимость предела
текучести в зоне стружкообразования и на передней
поверхности от температуры



















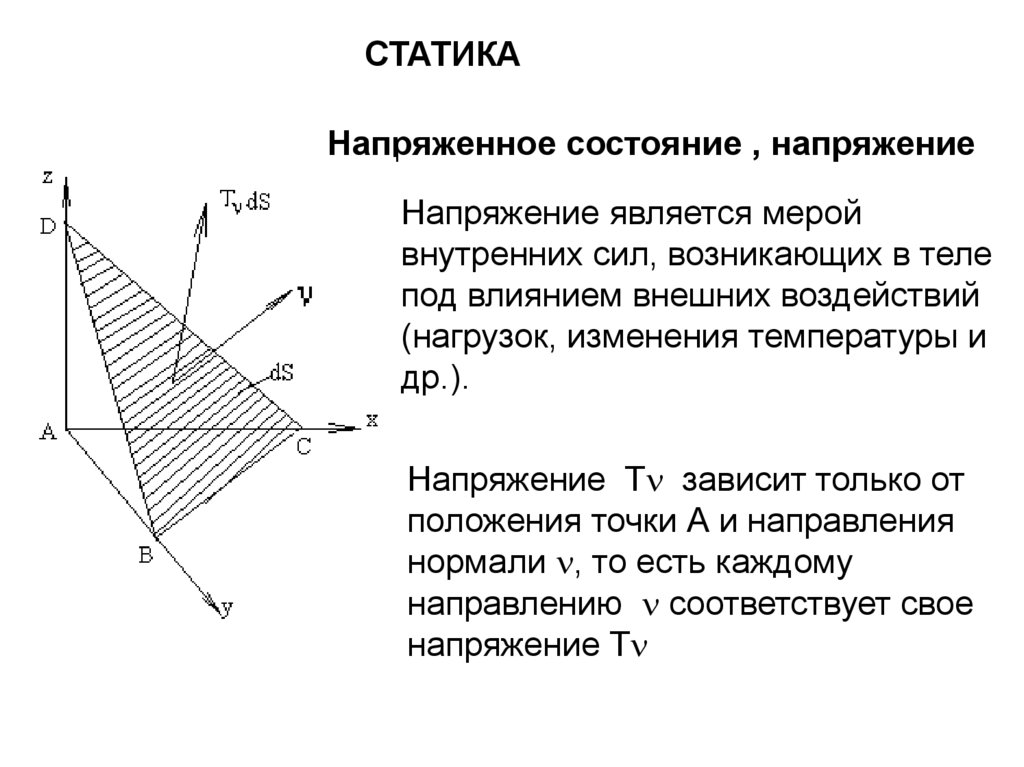








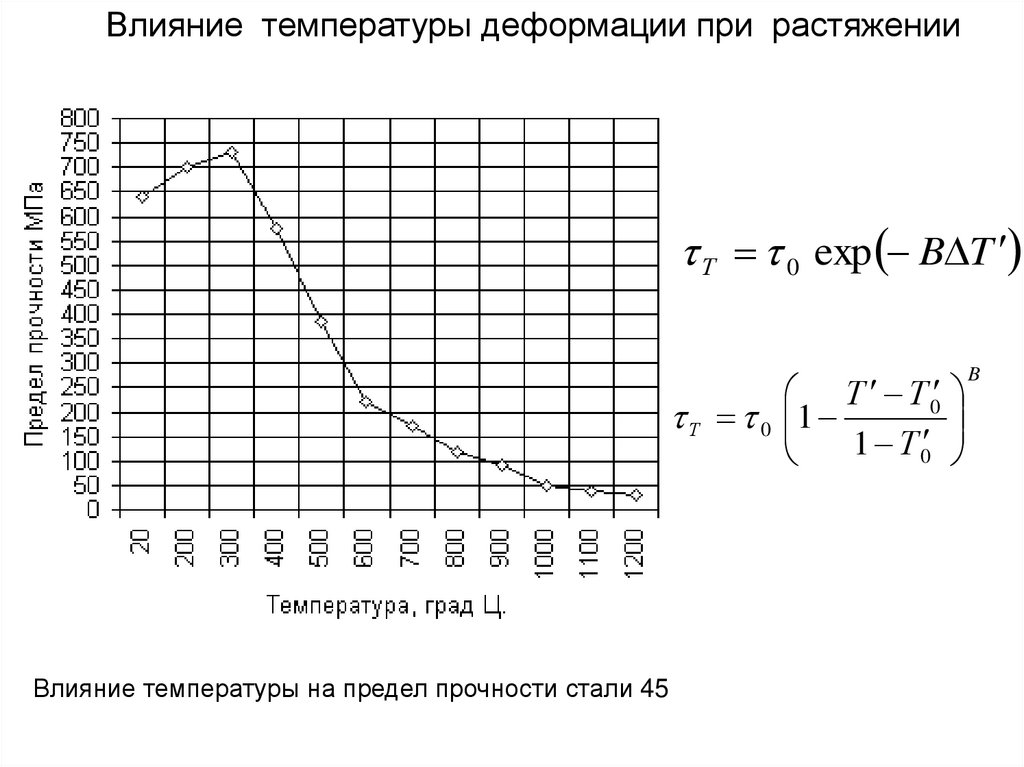
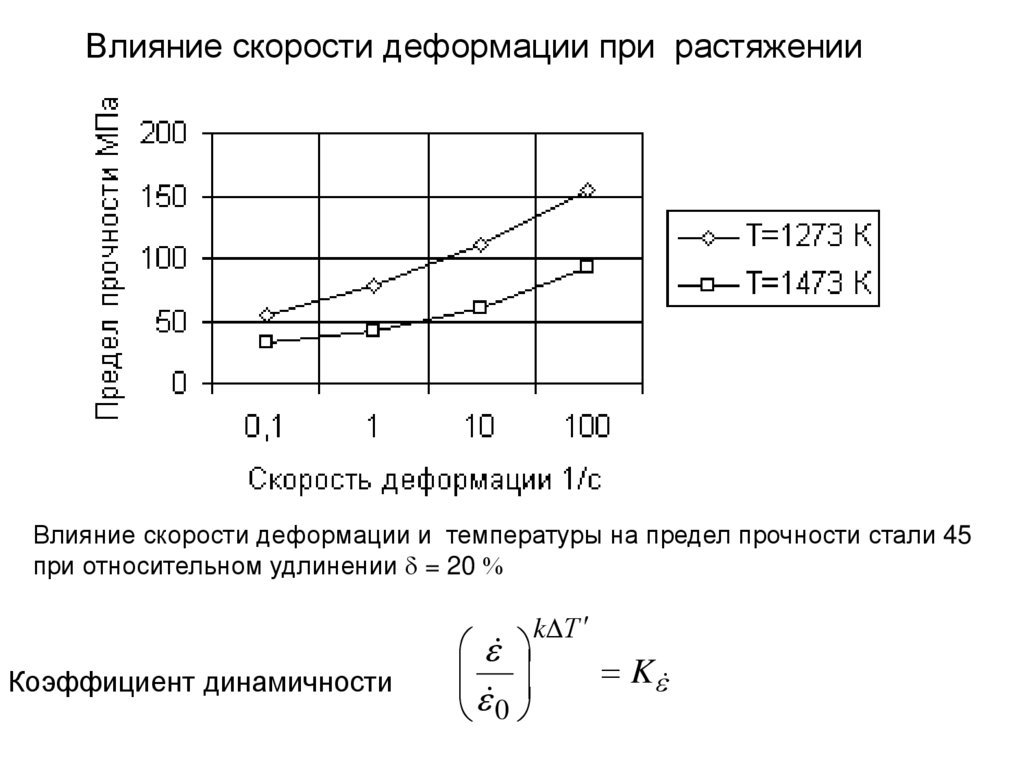


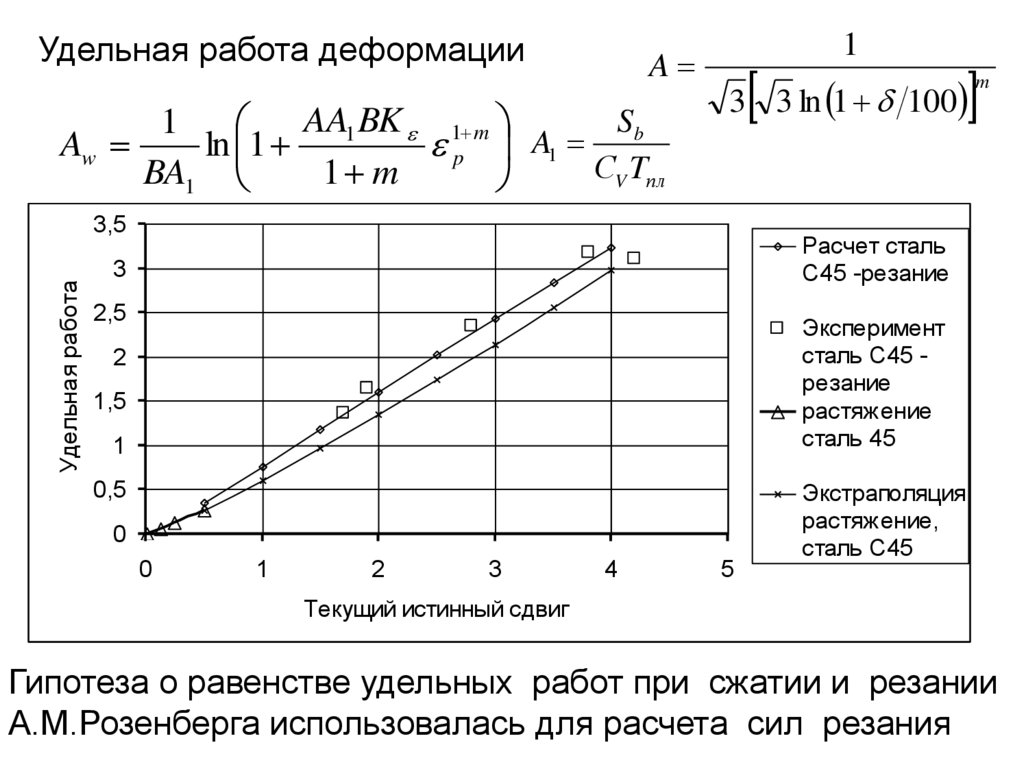
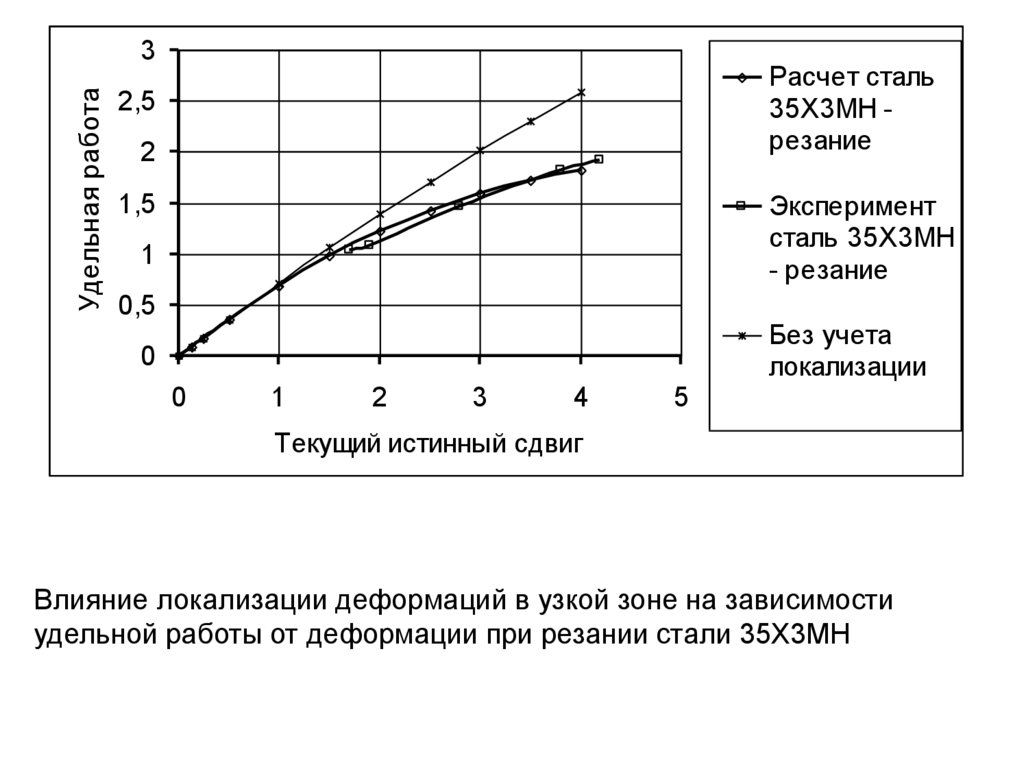


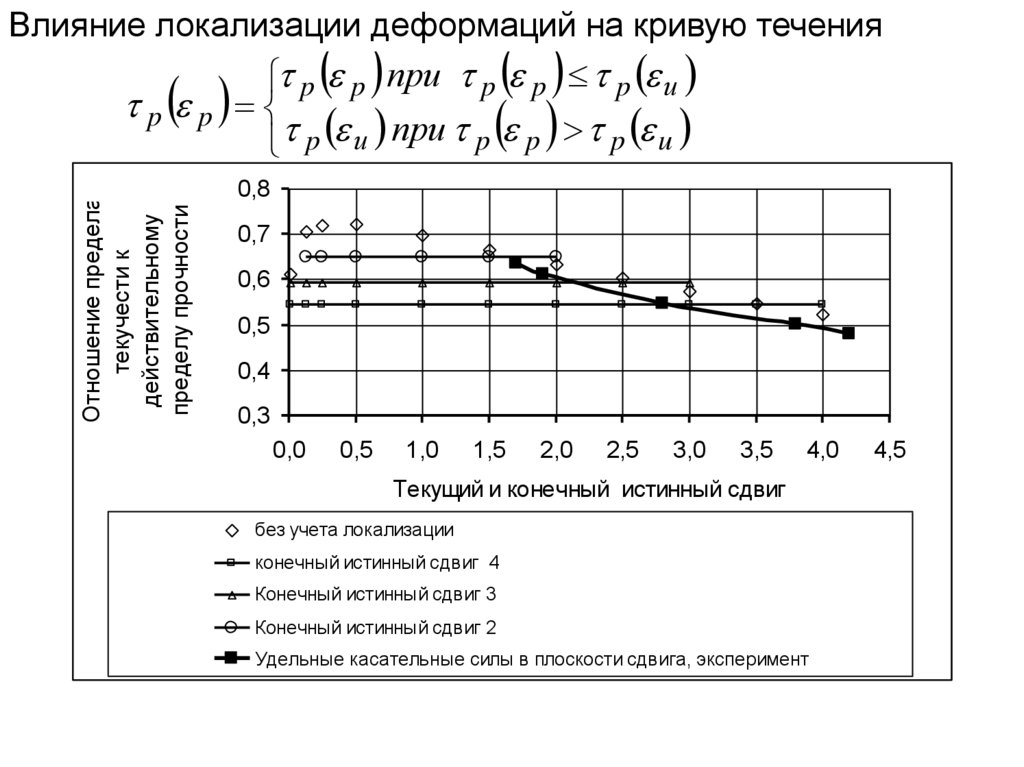






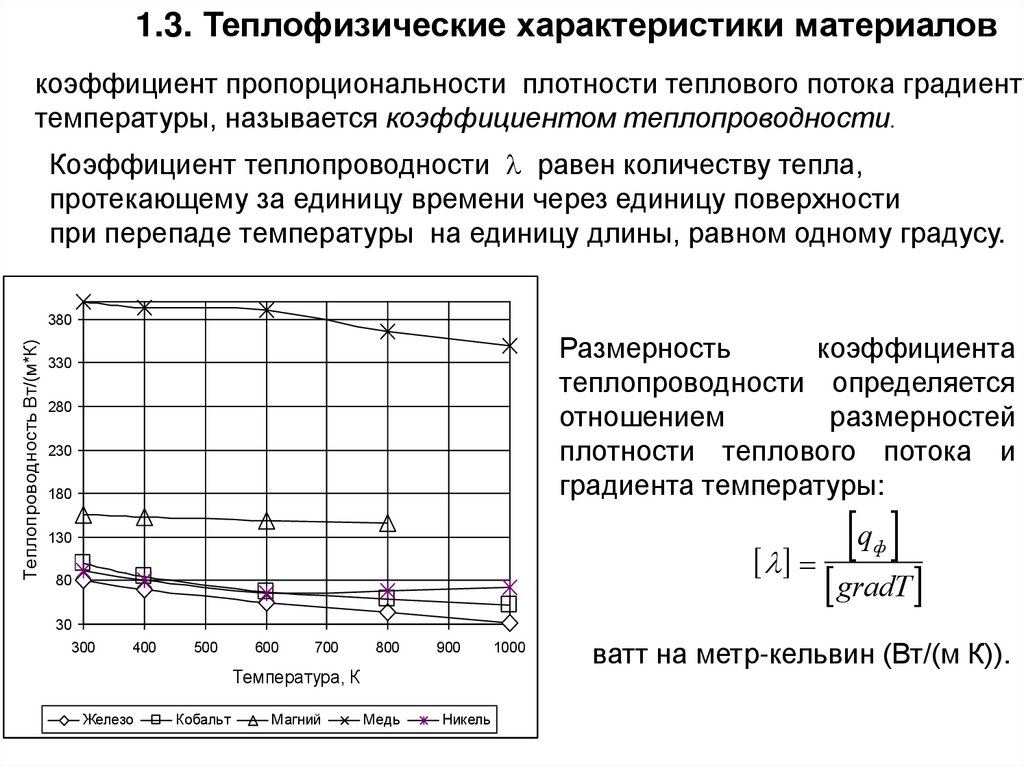

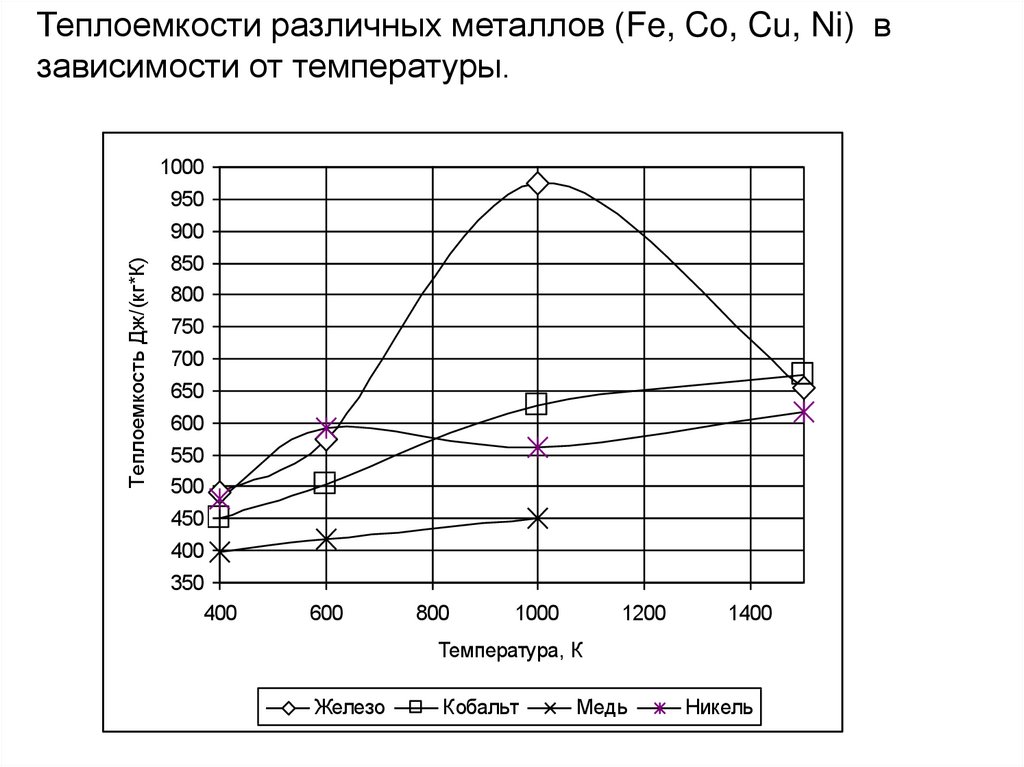
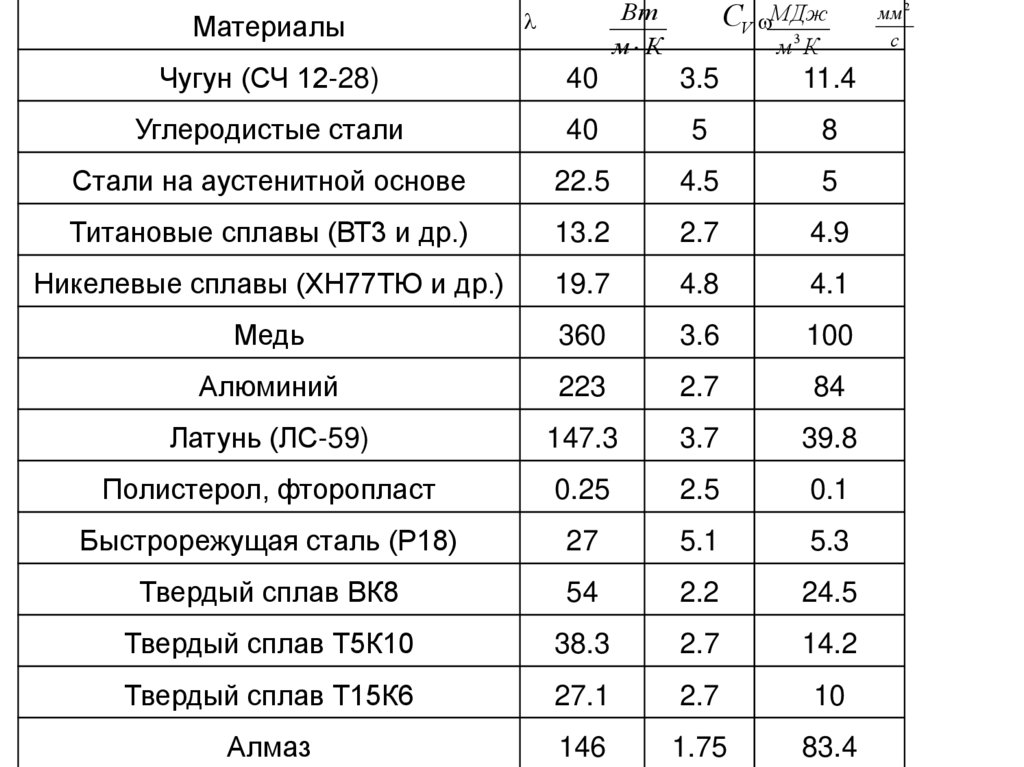


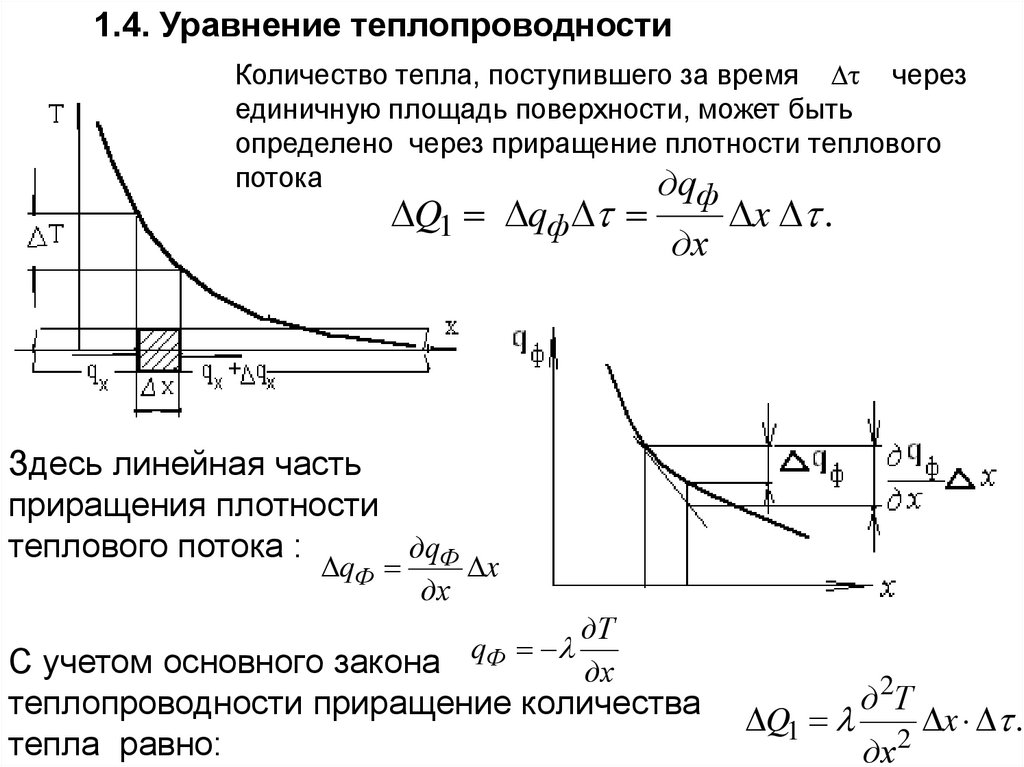



















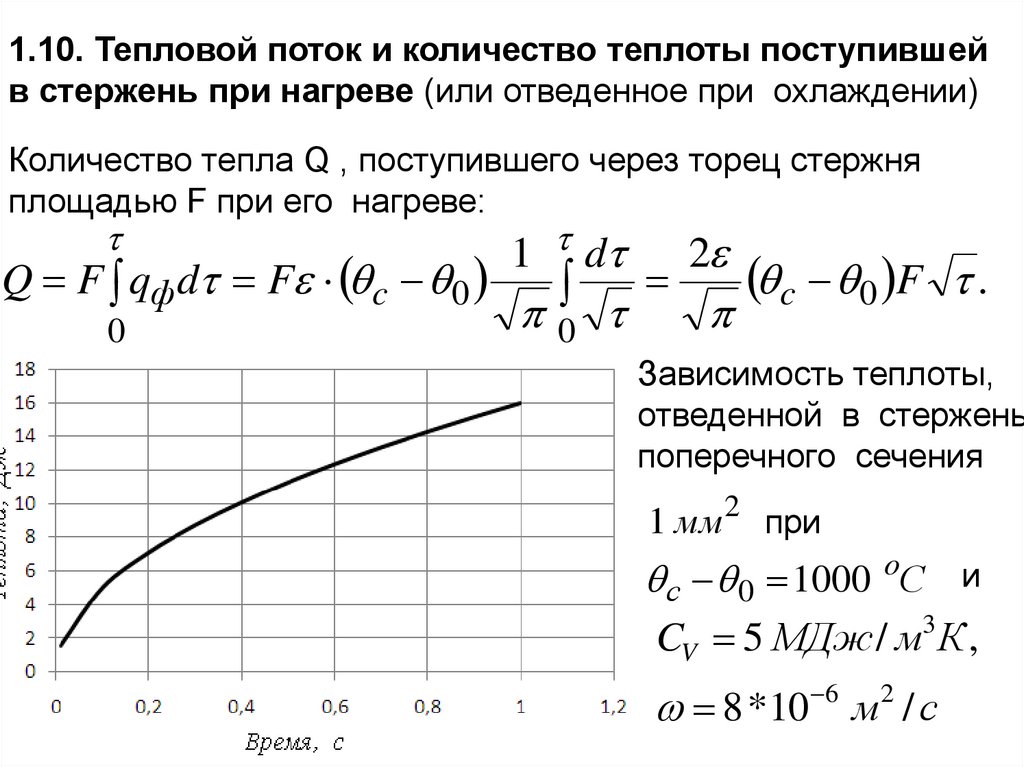



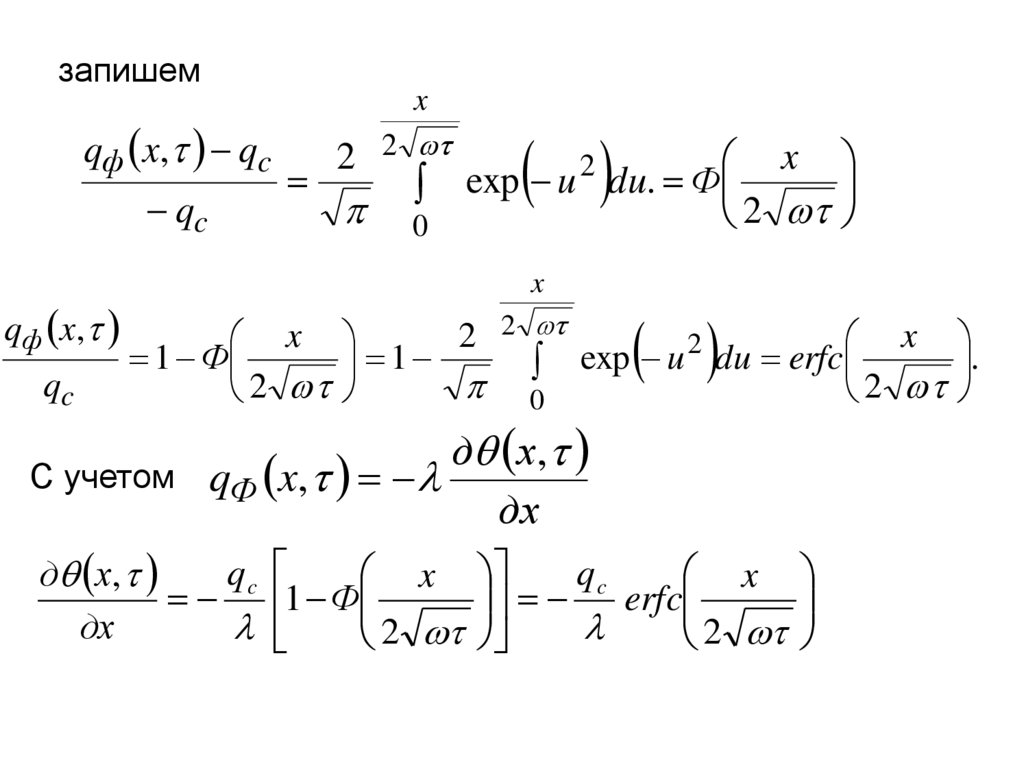





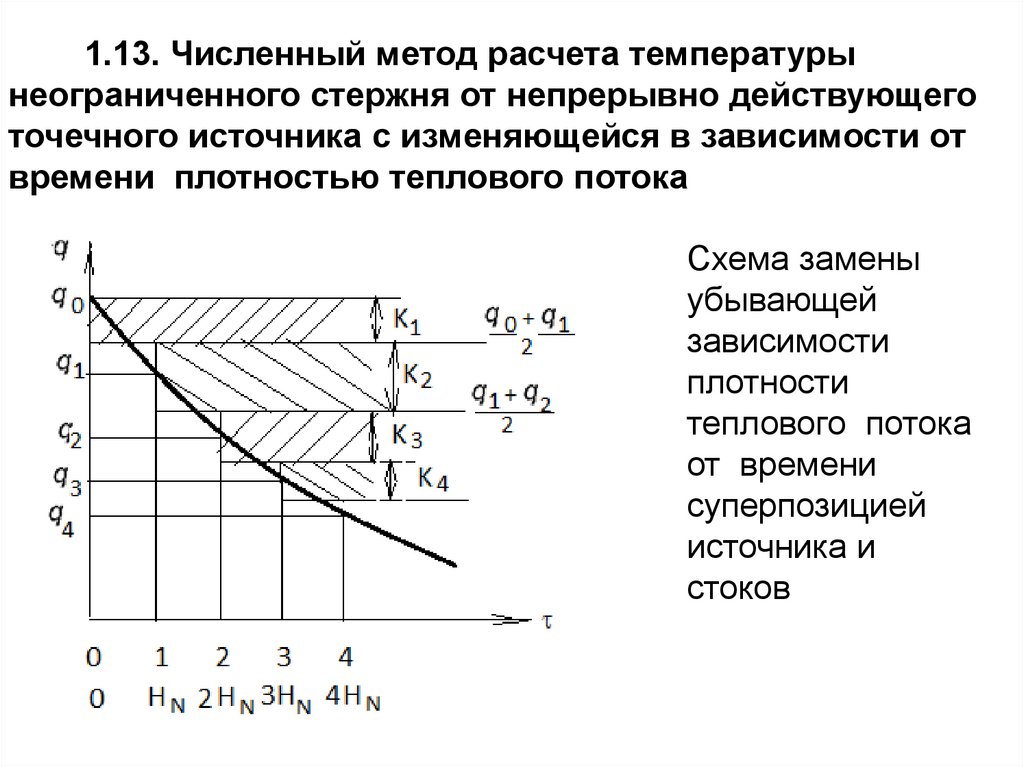



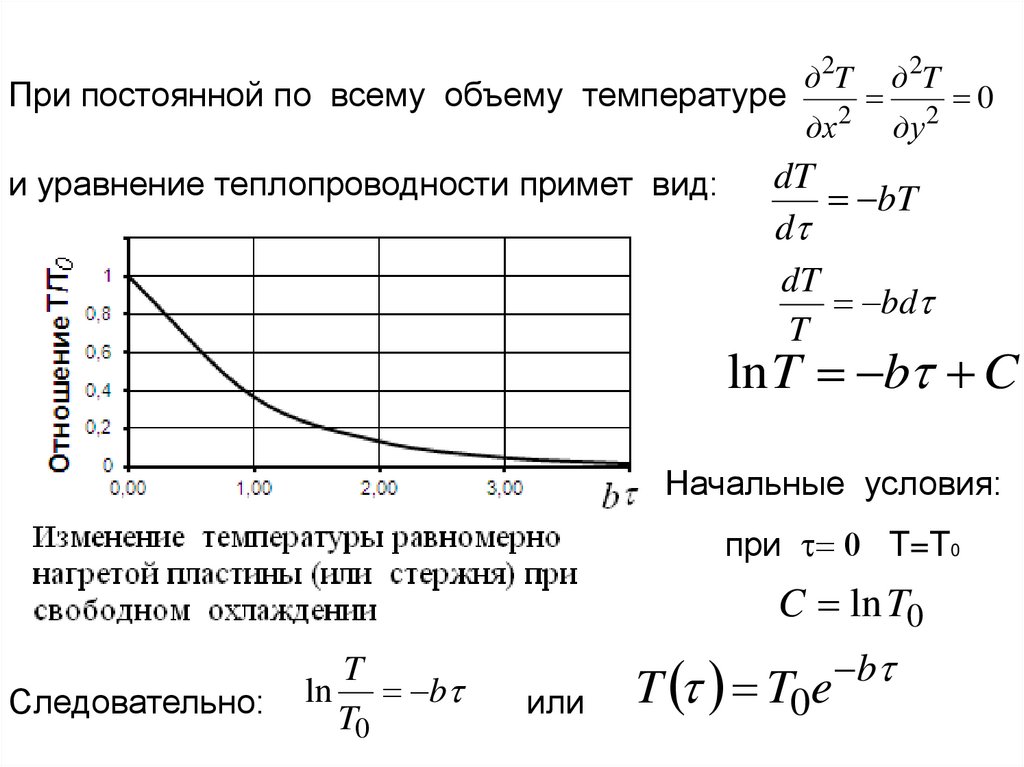







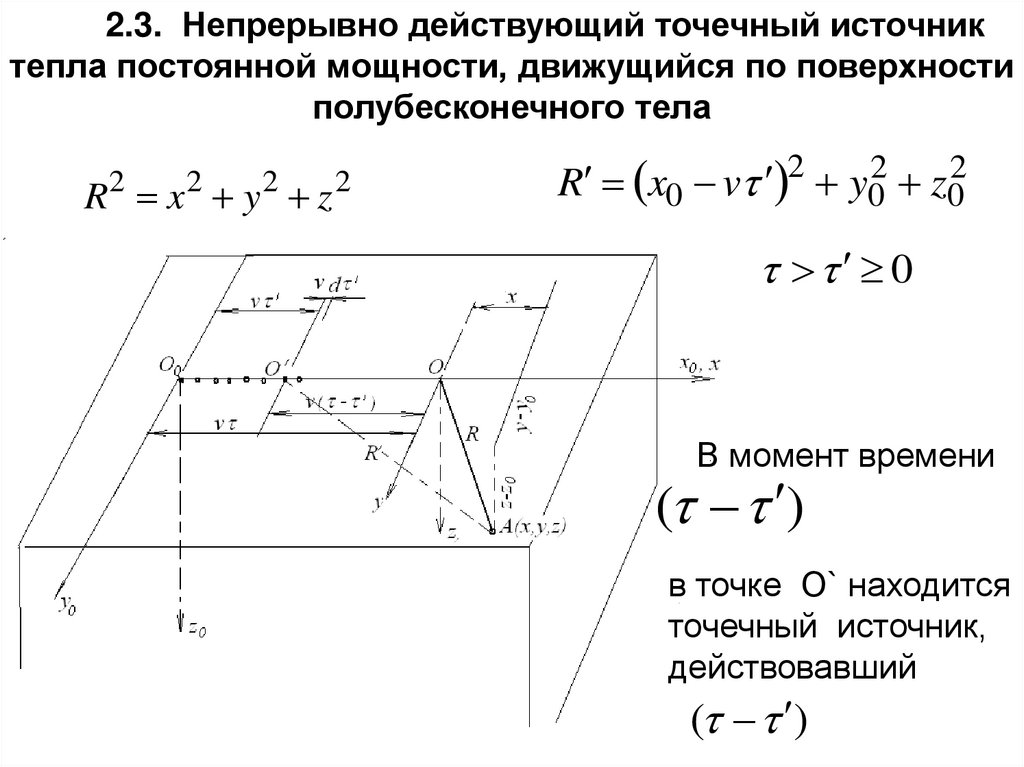












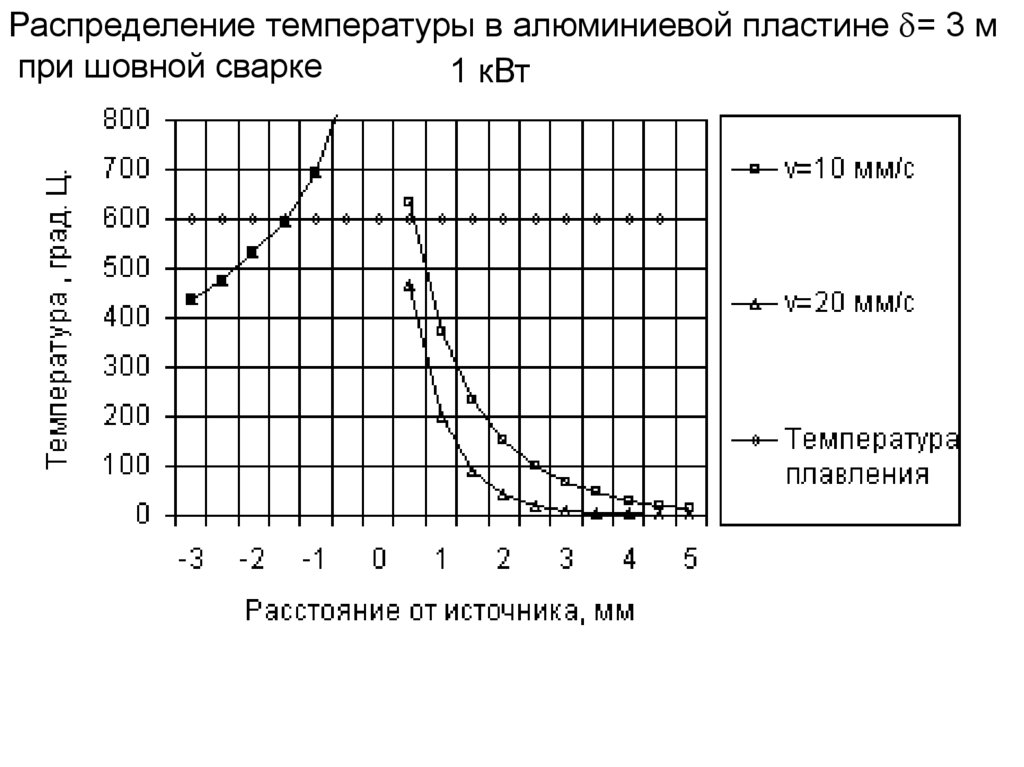
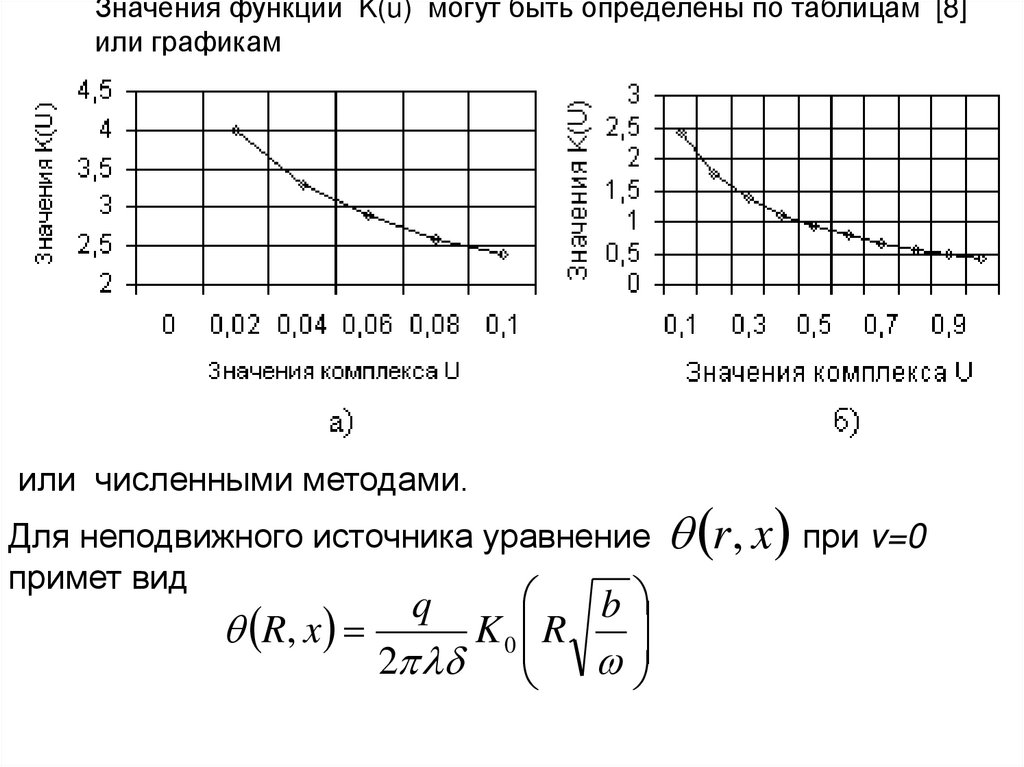


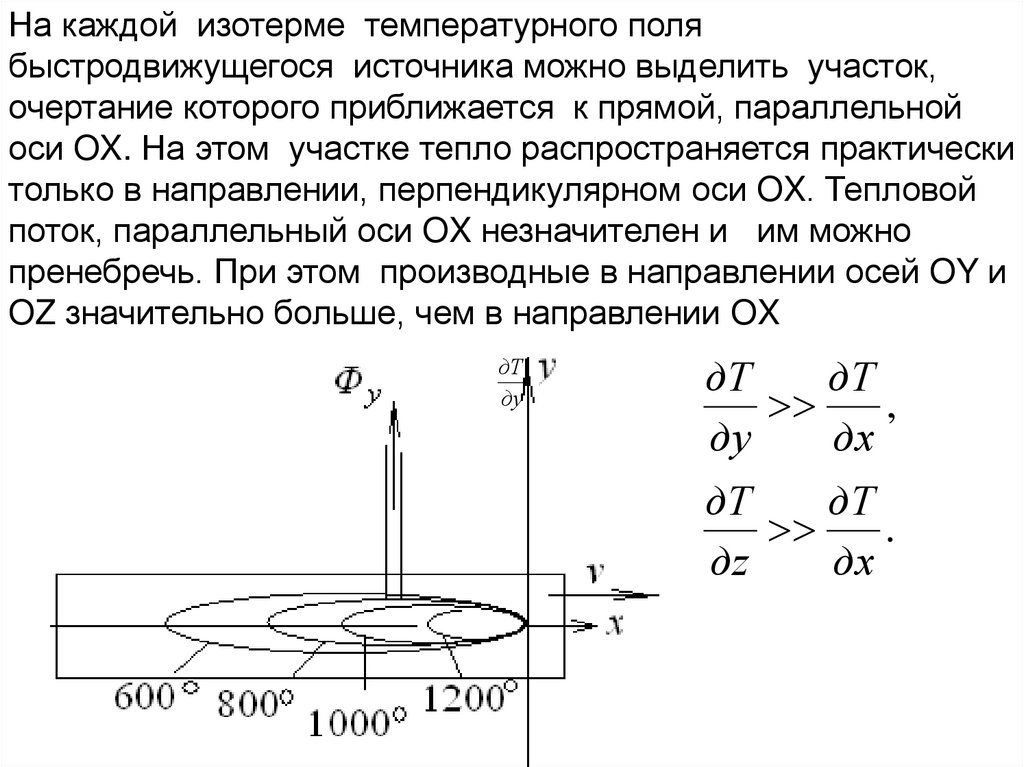




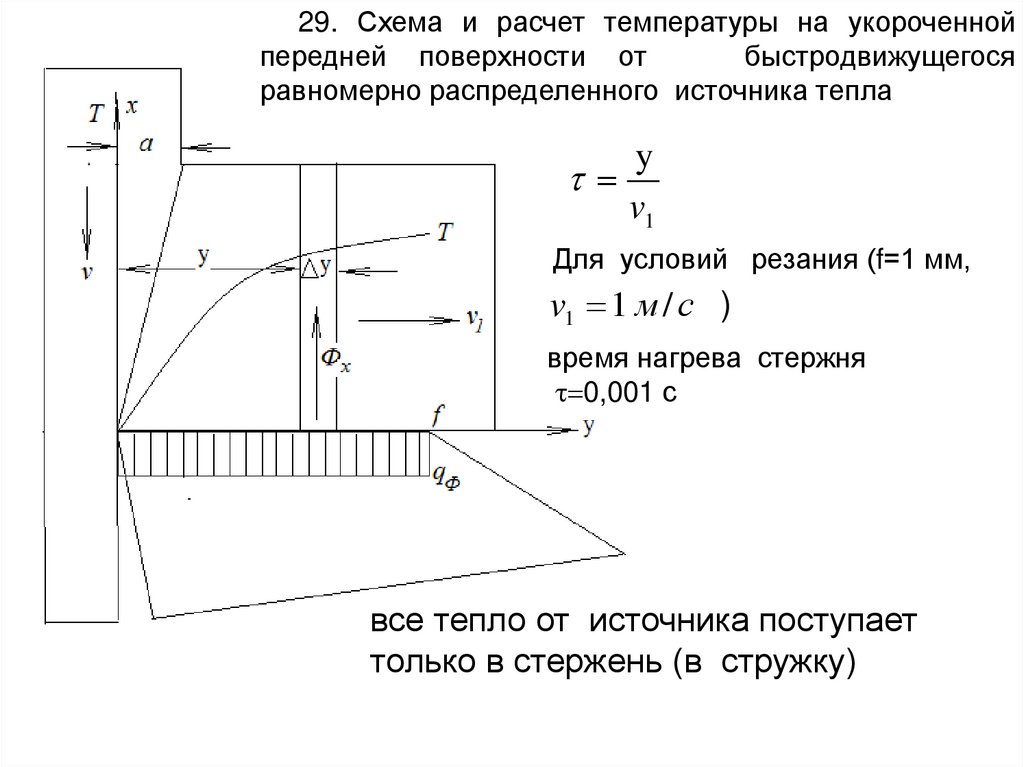

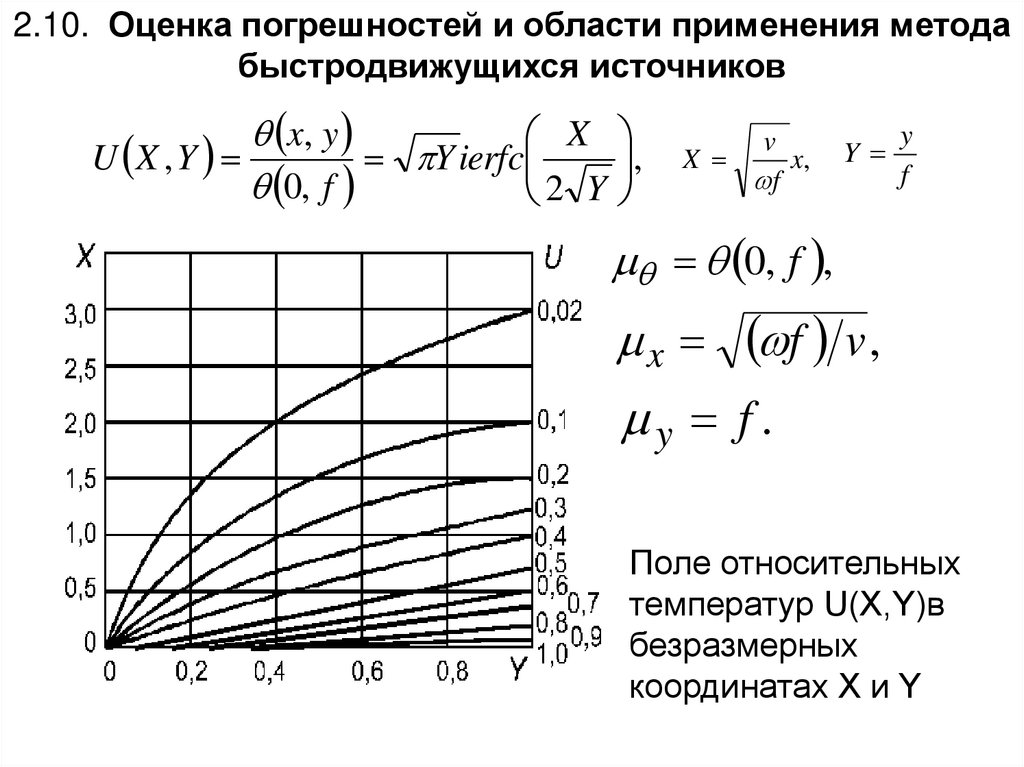
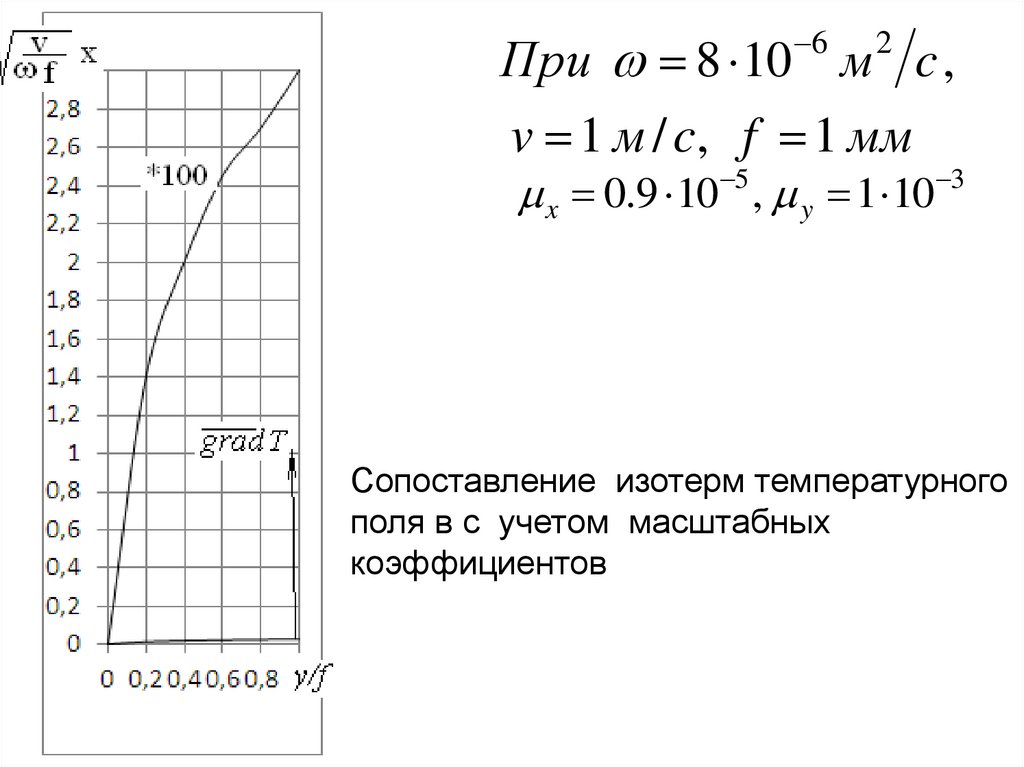



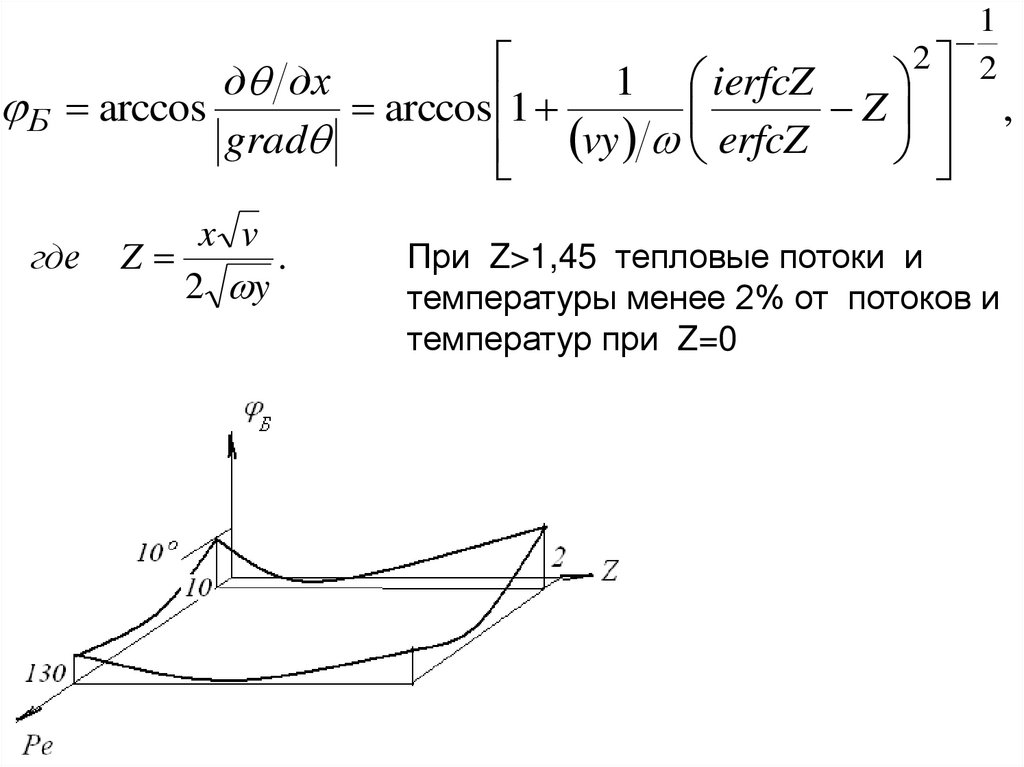


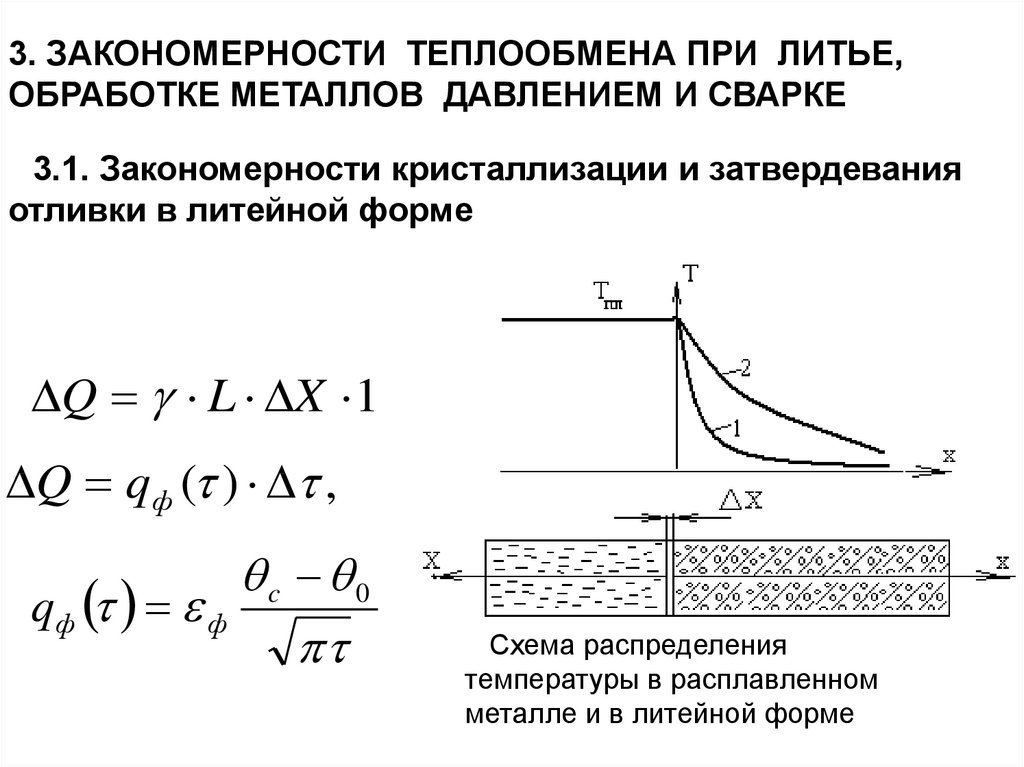

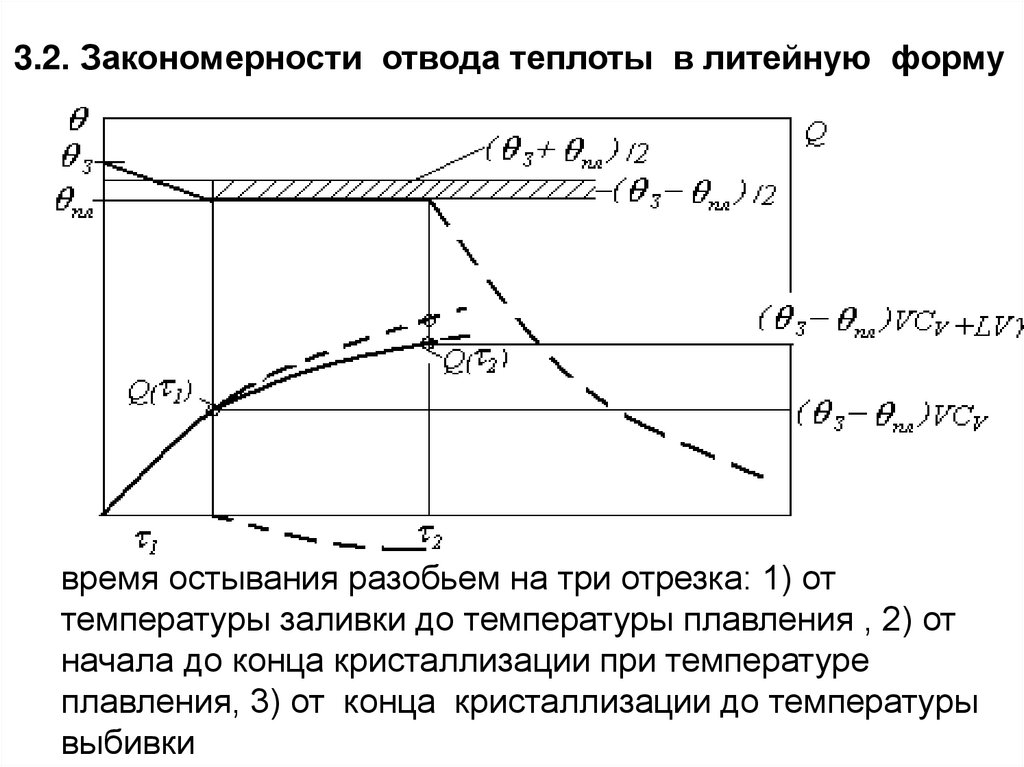


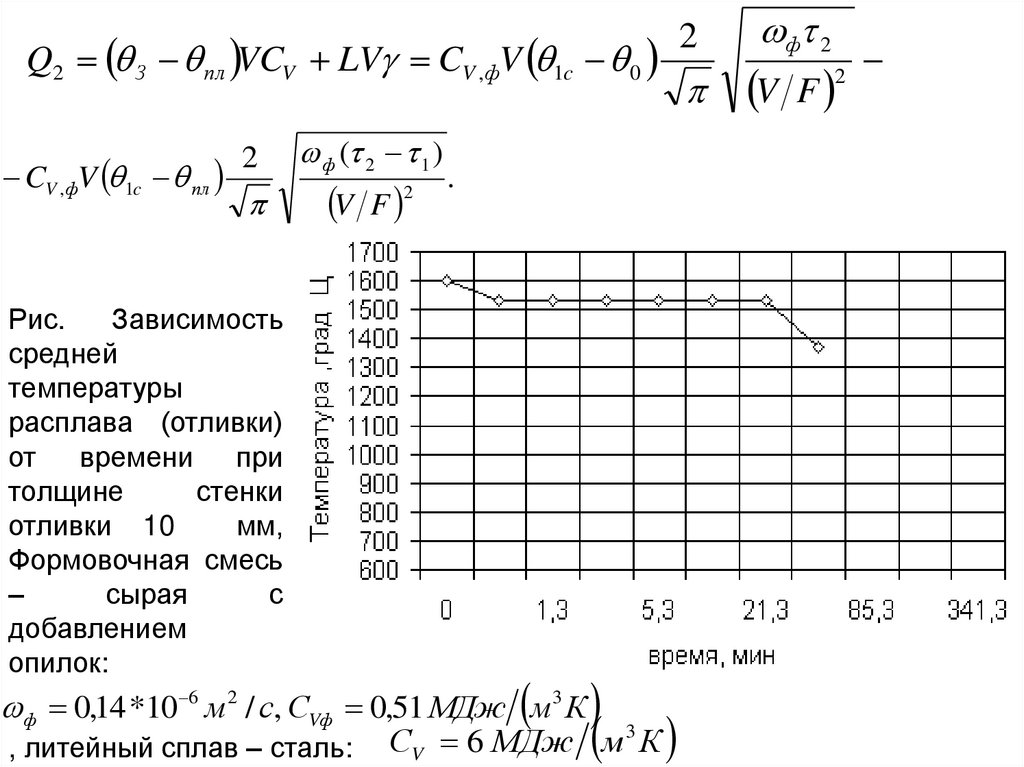




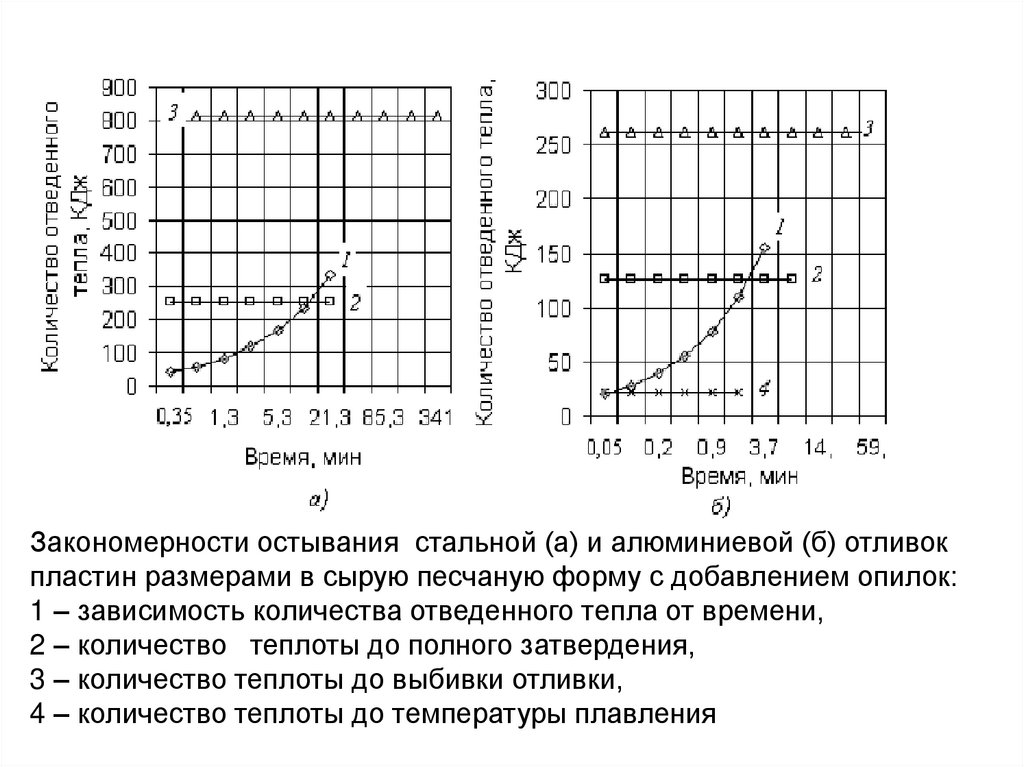



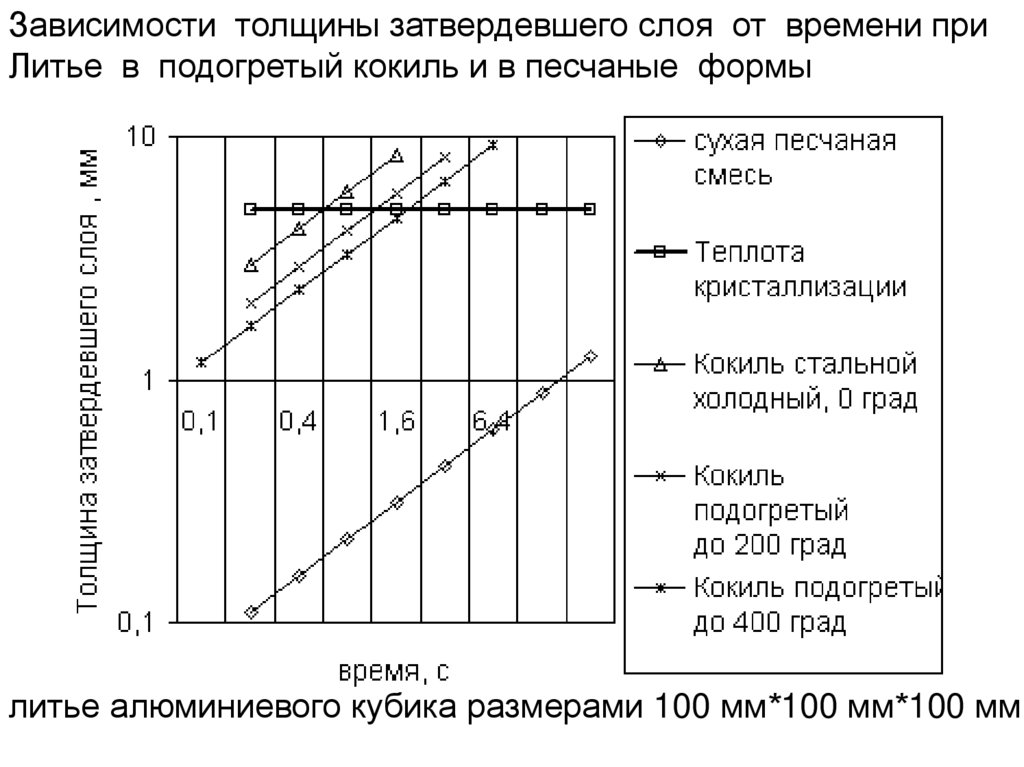

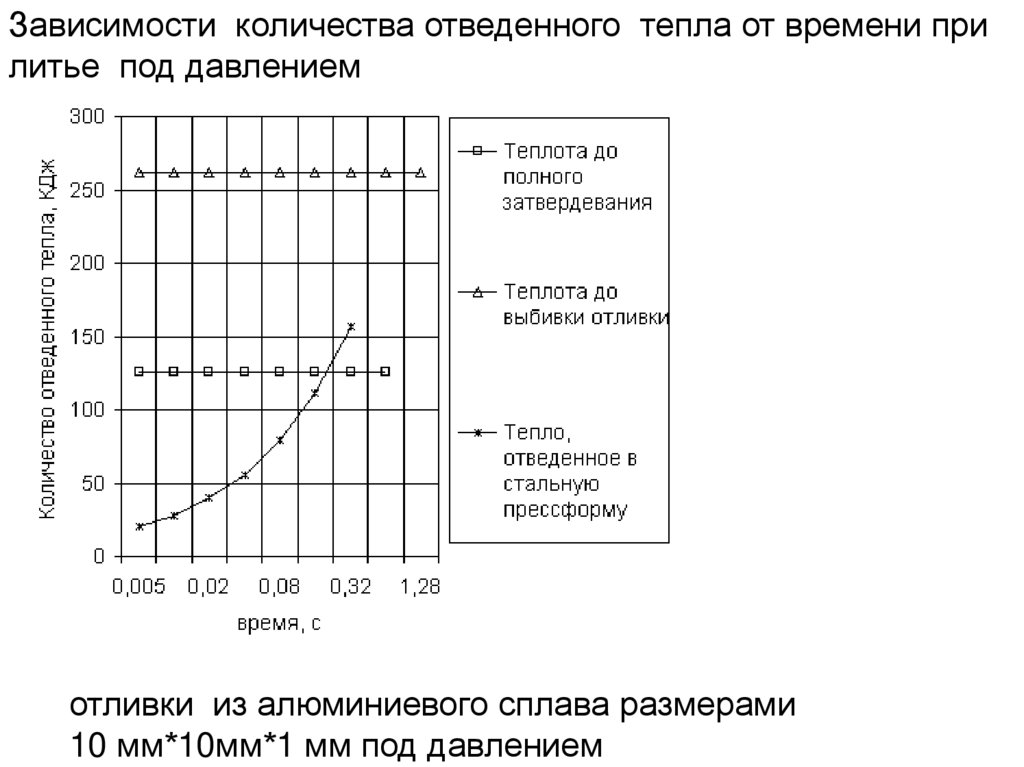











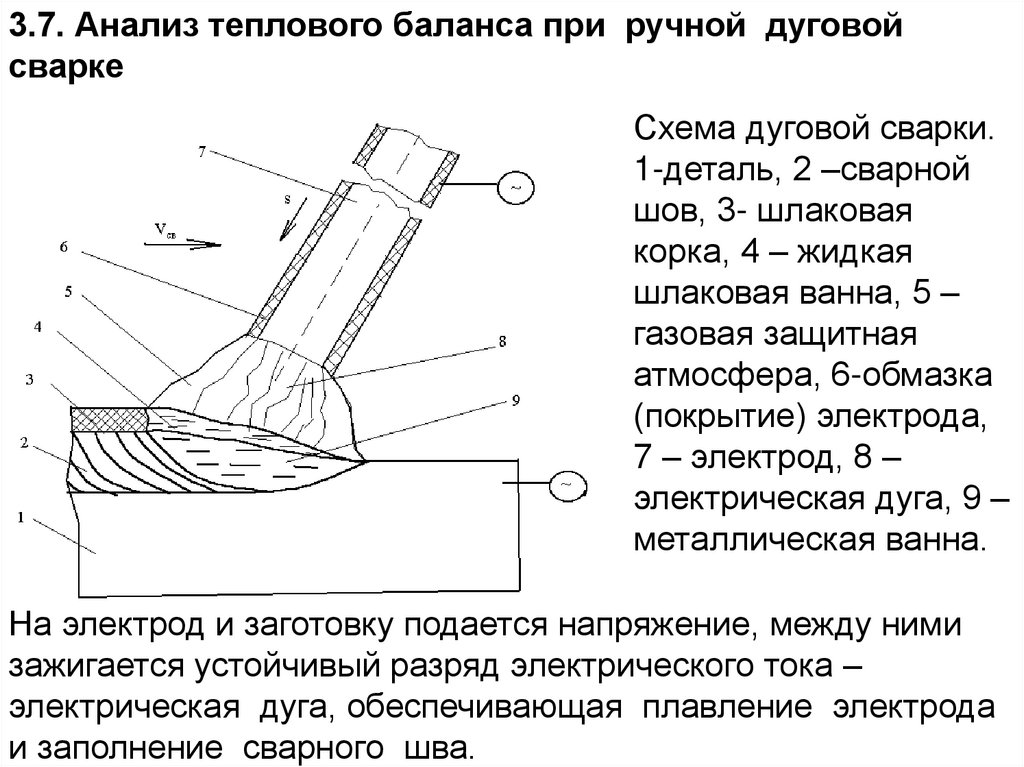








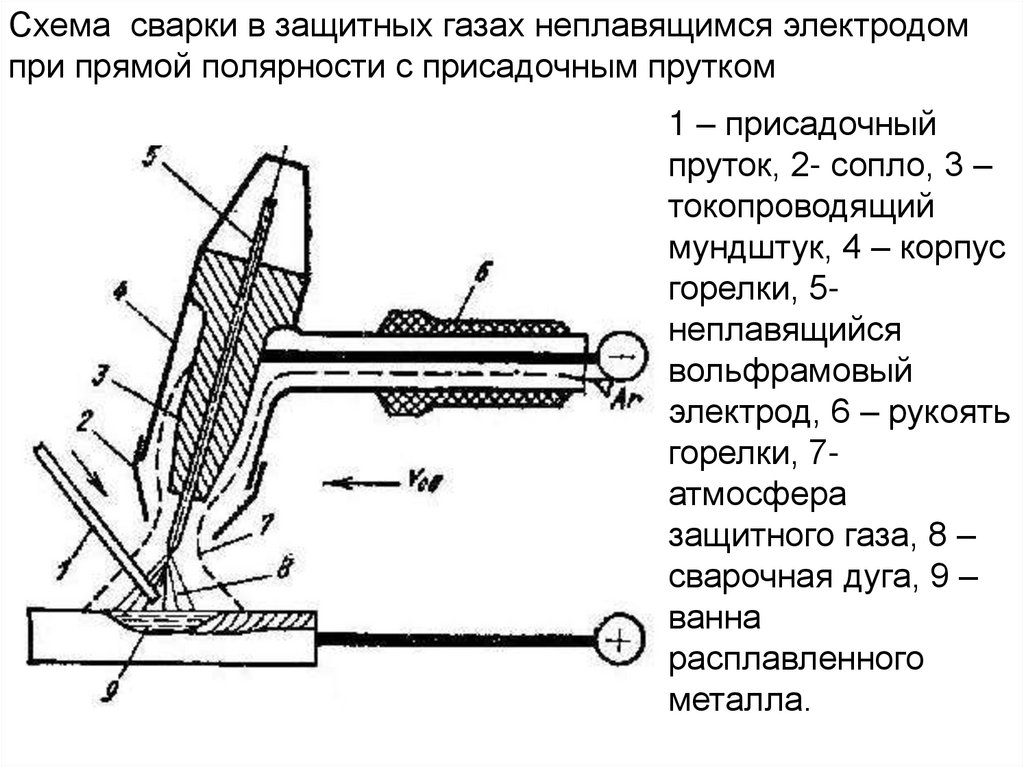



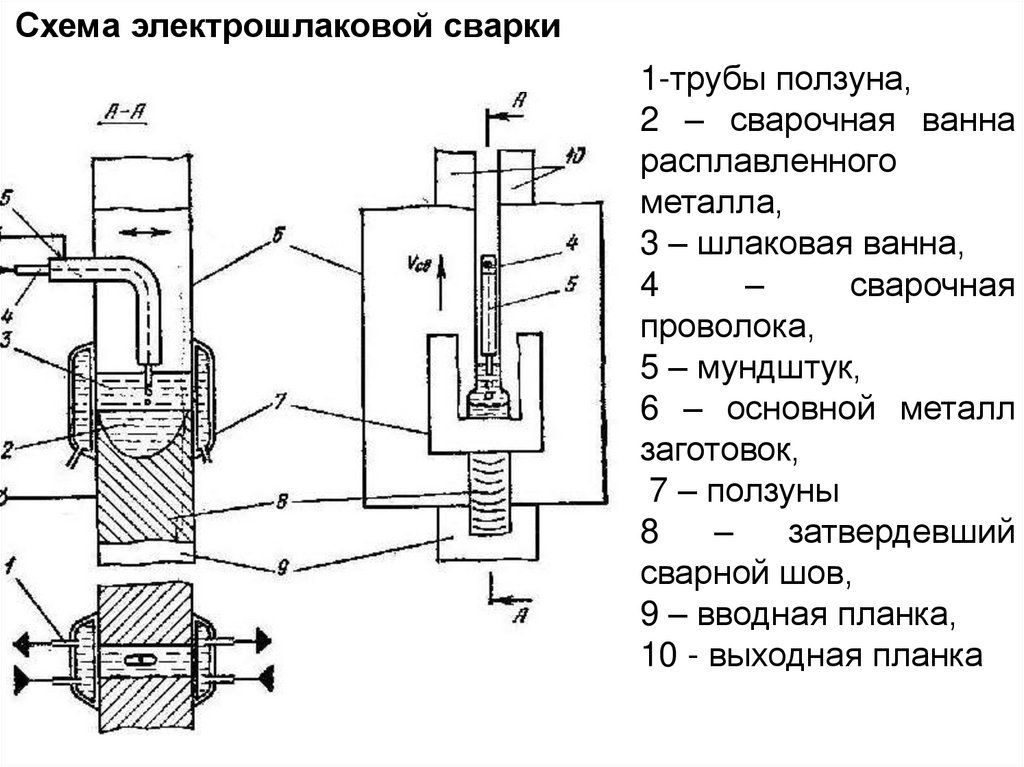



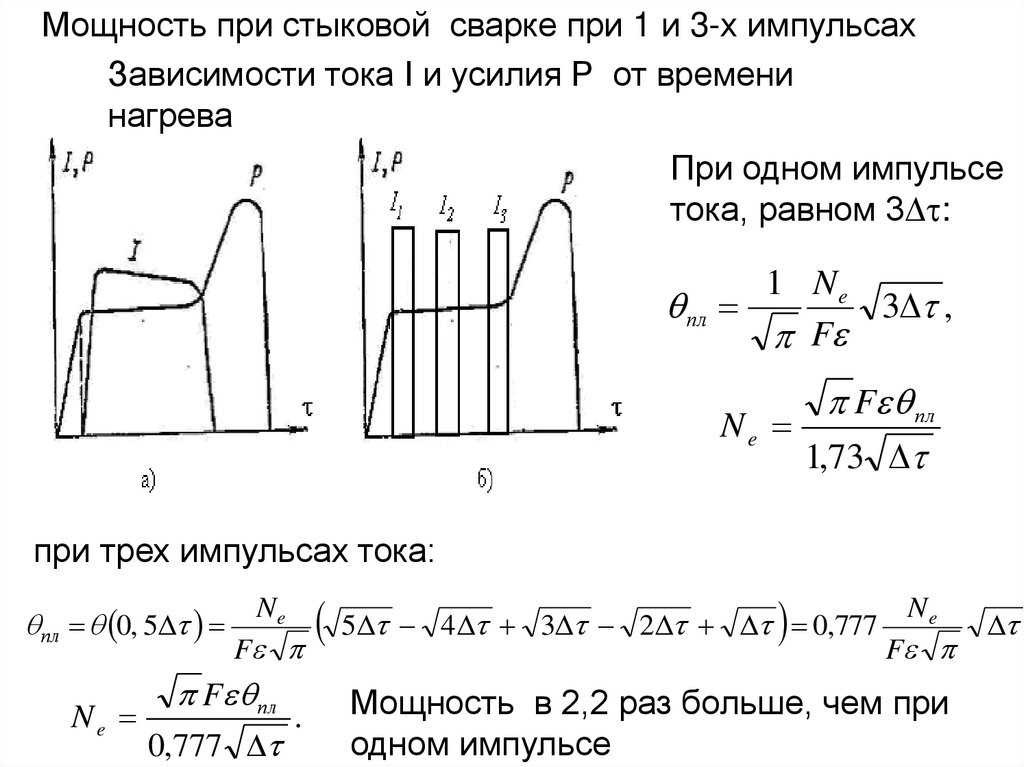




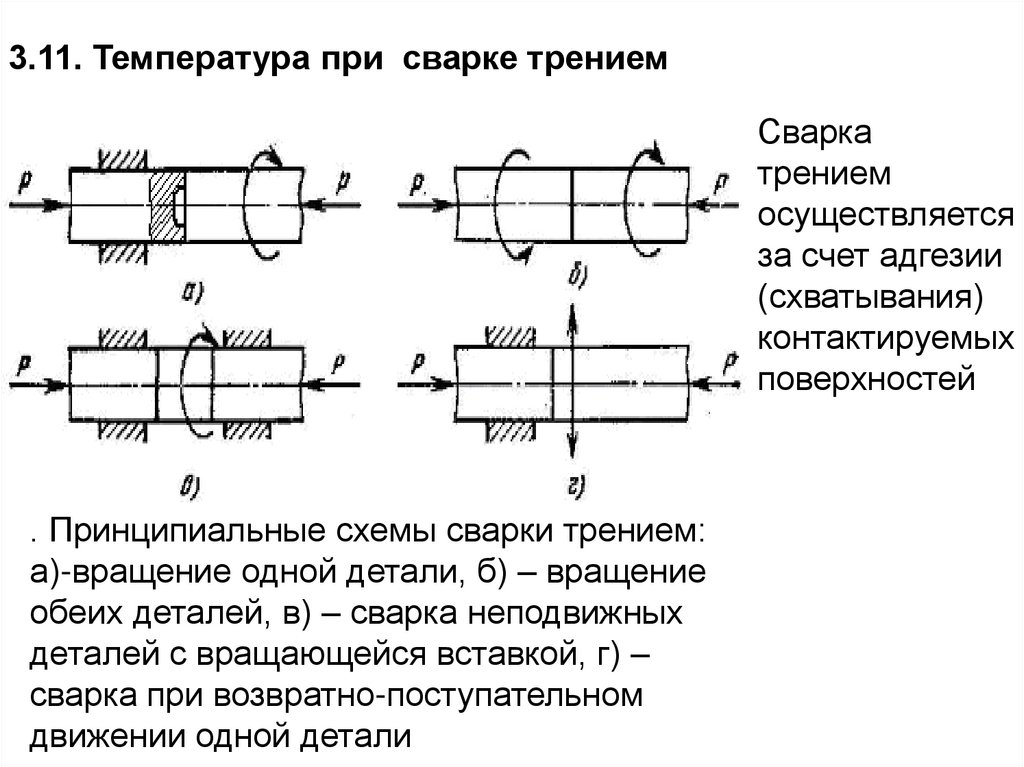

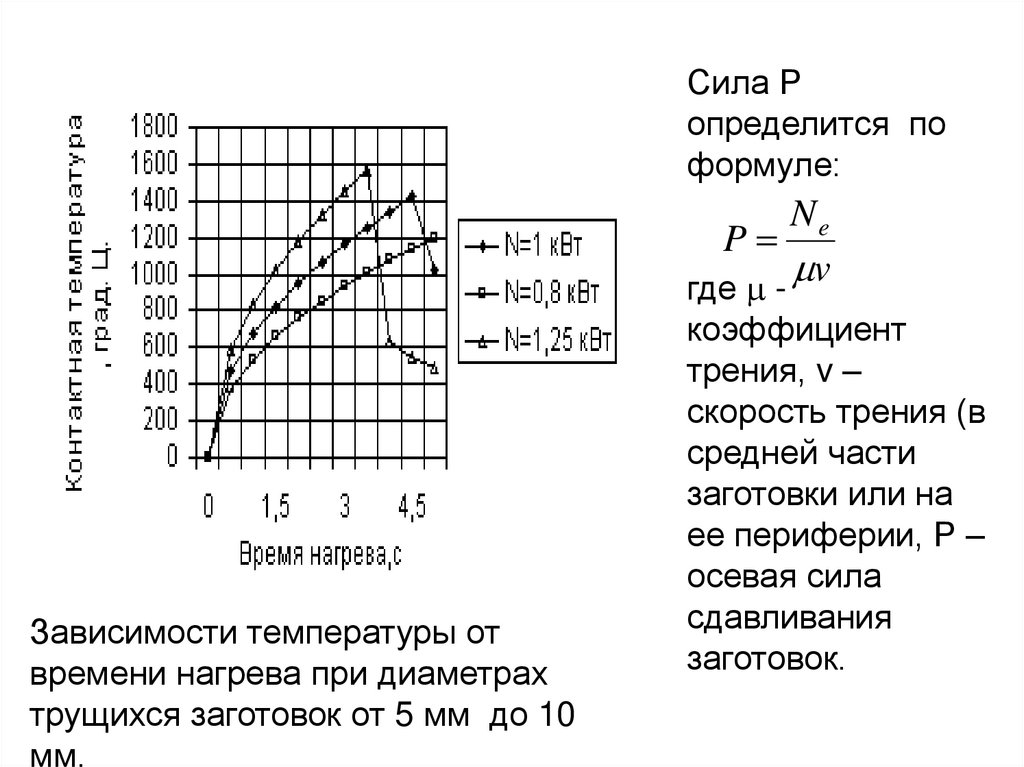
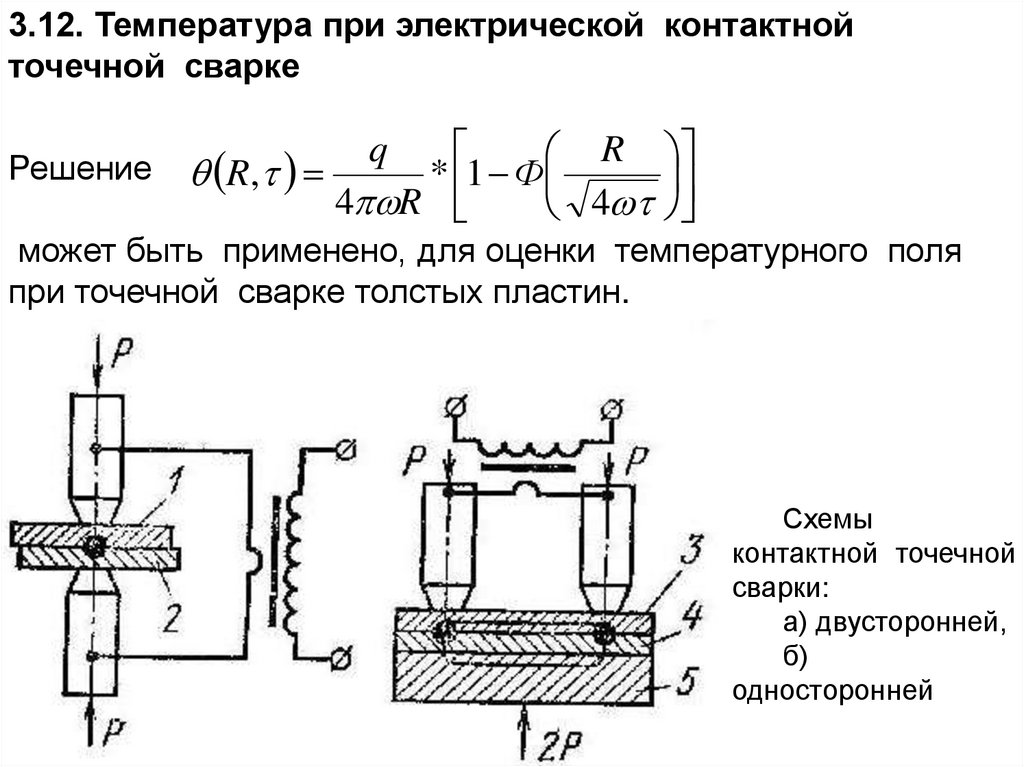







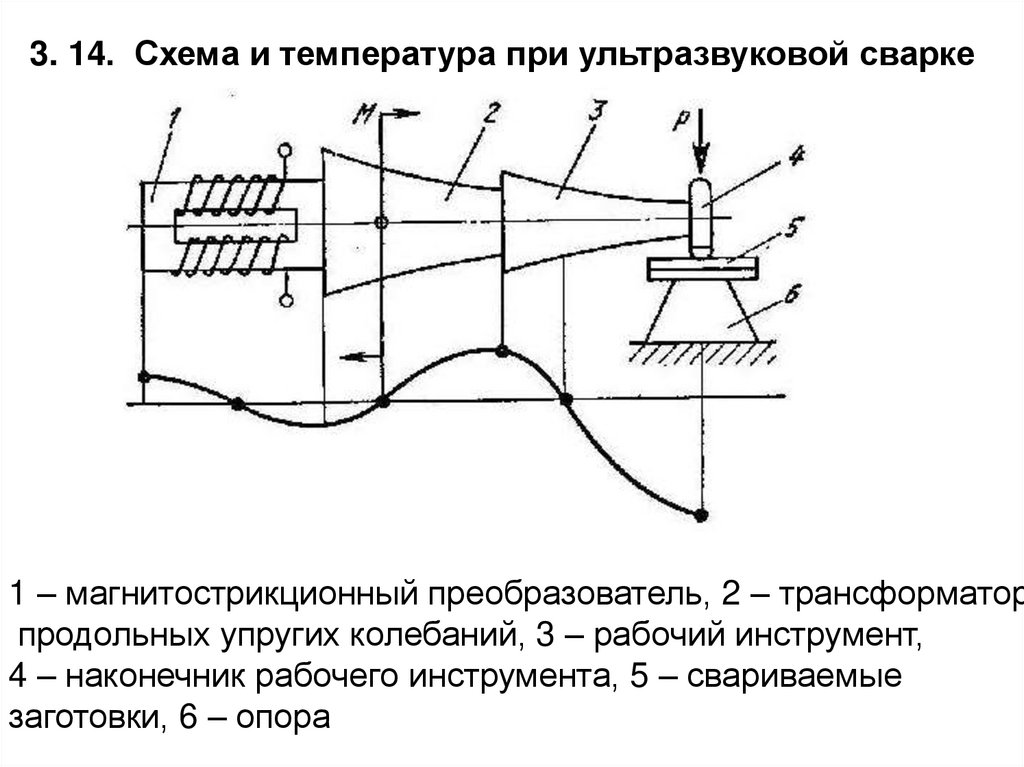


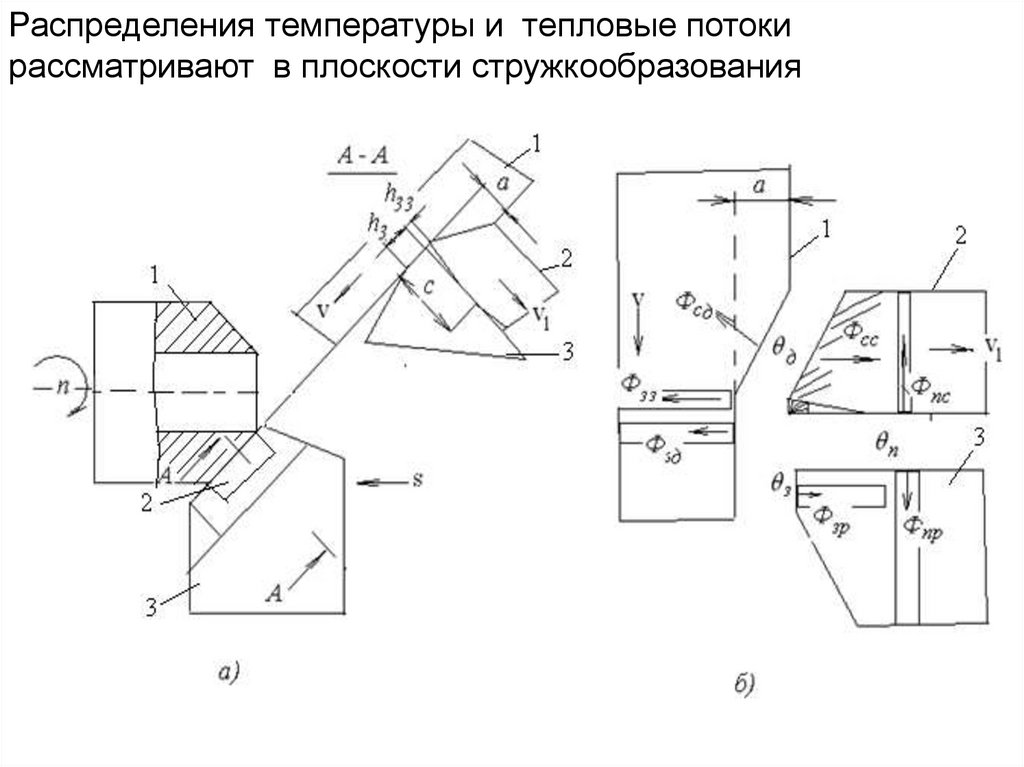




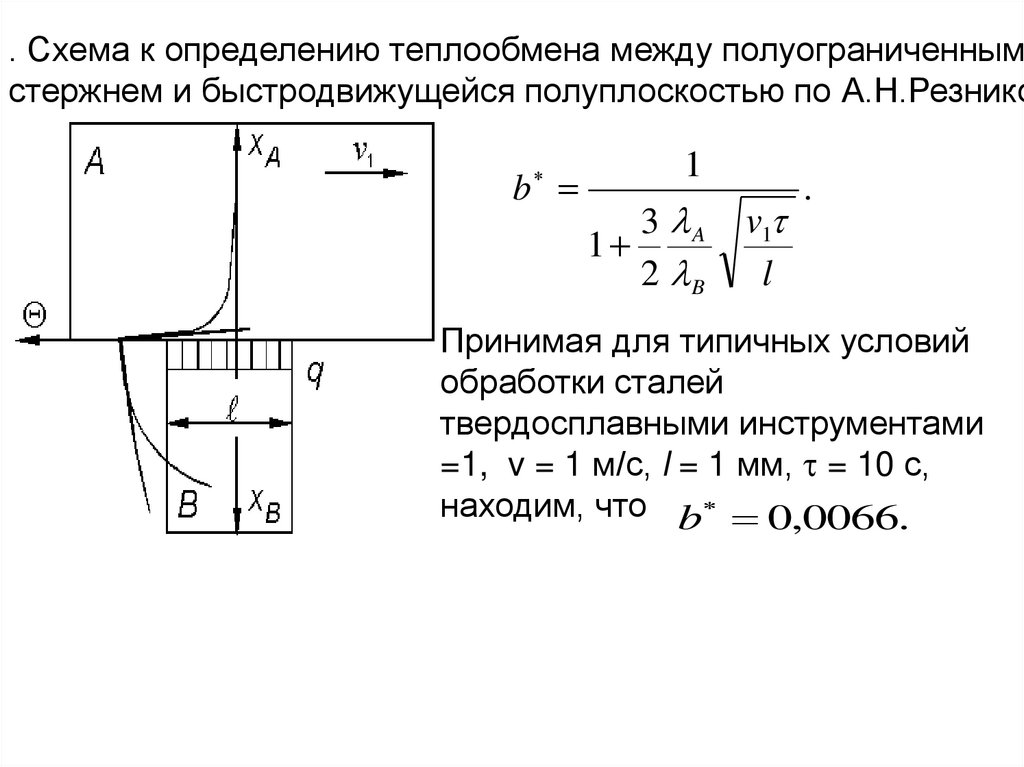













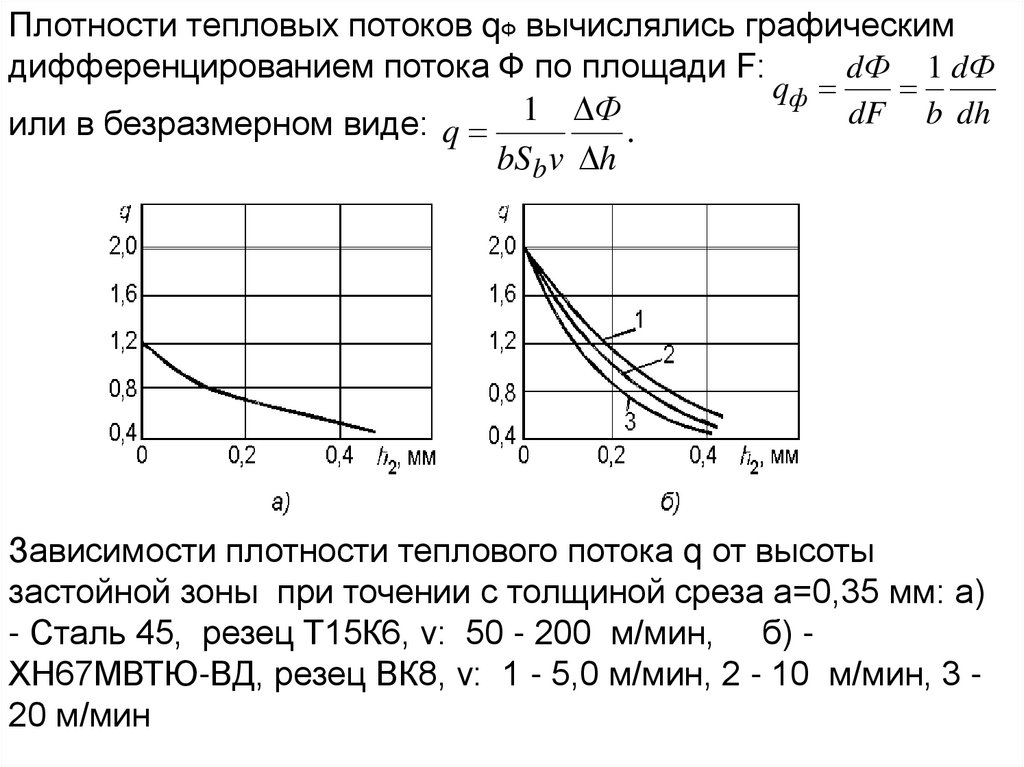

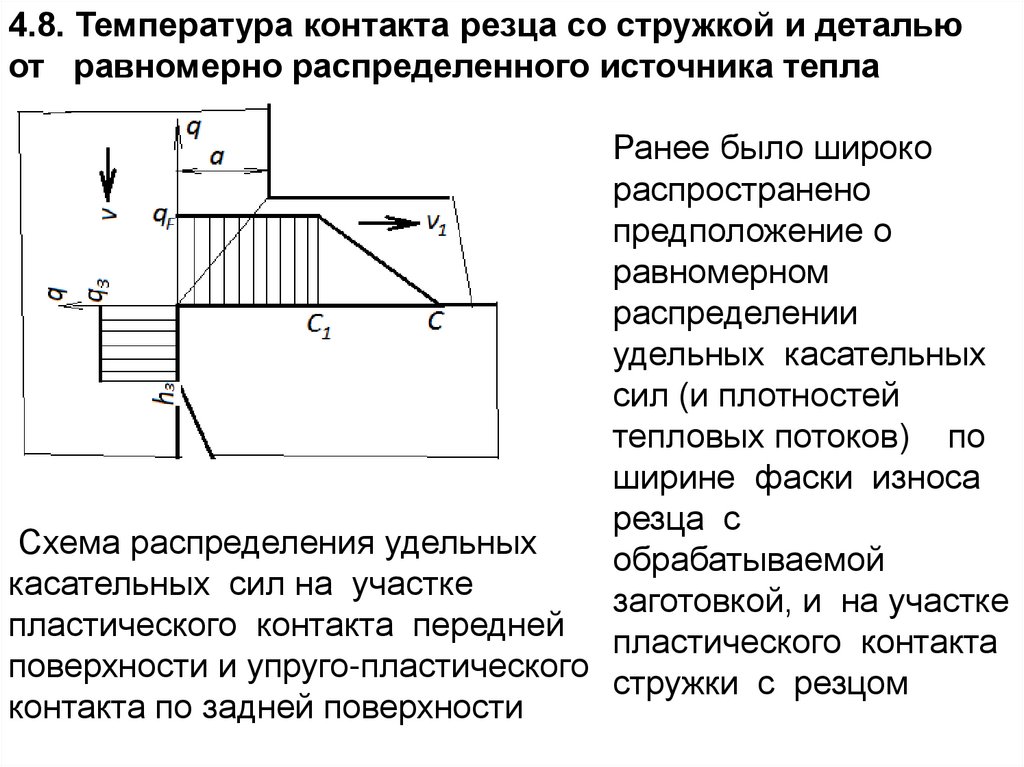


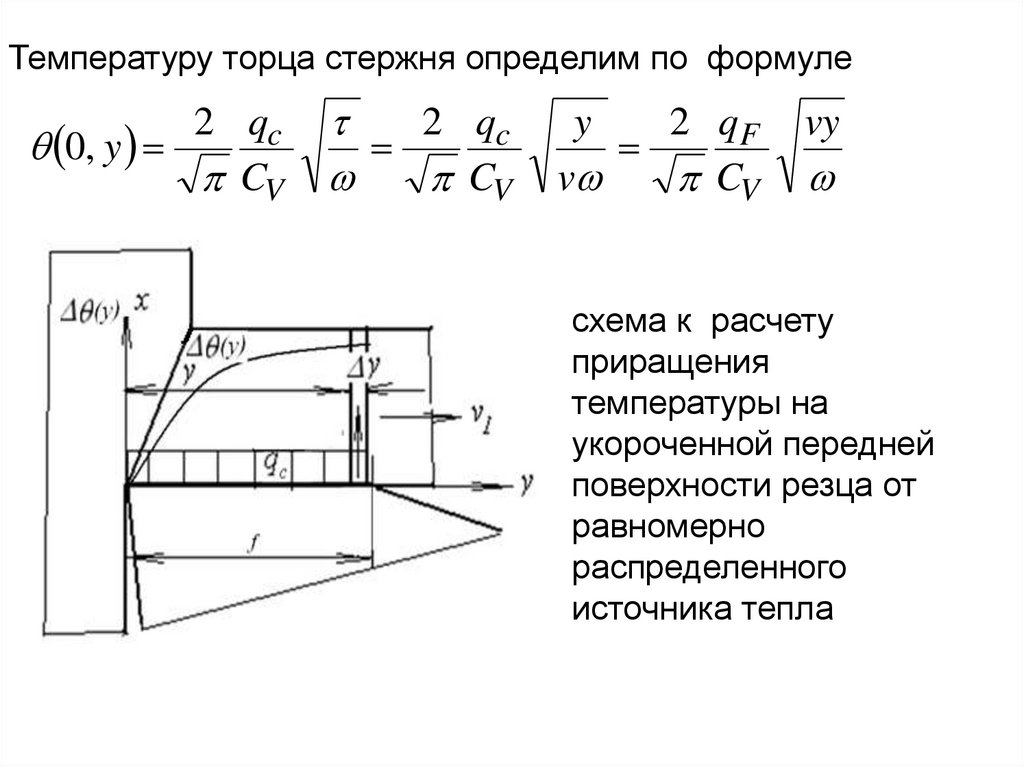


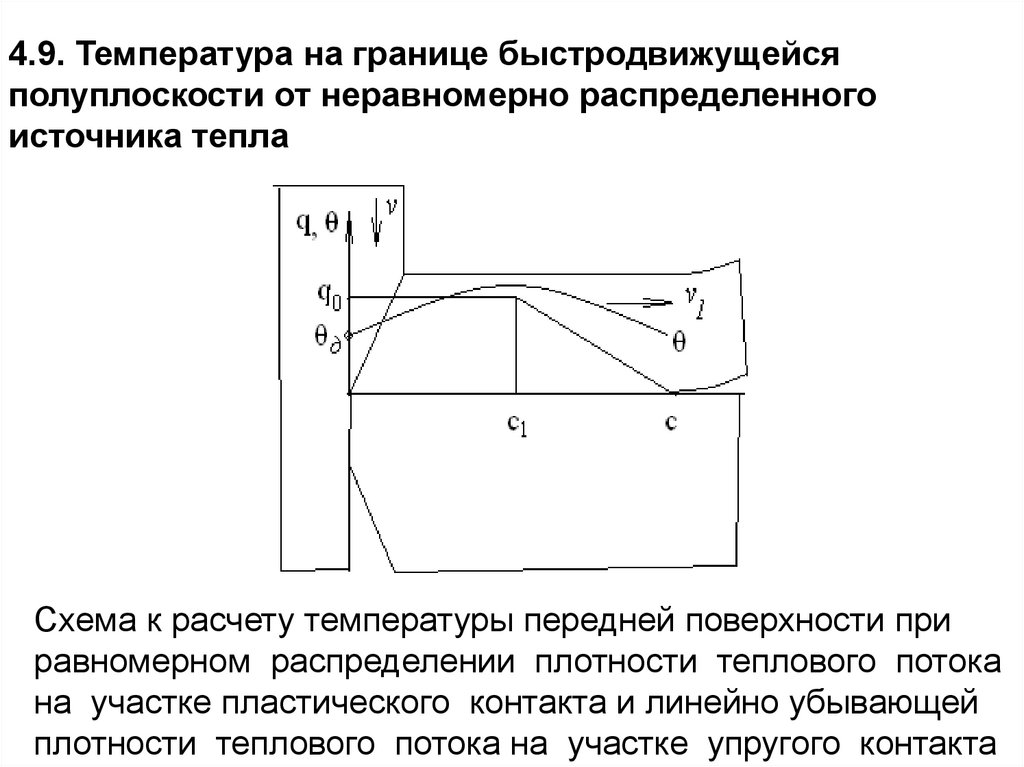





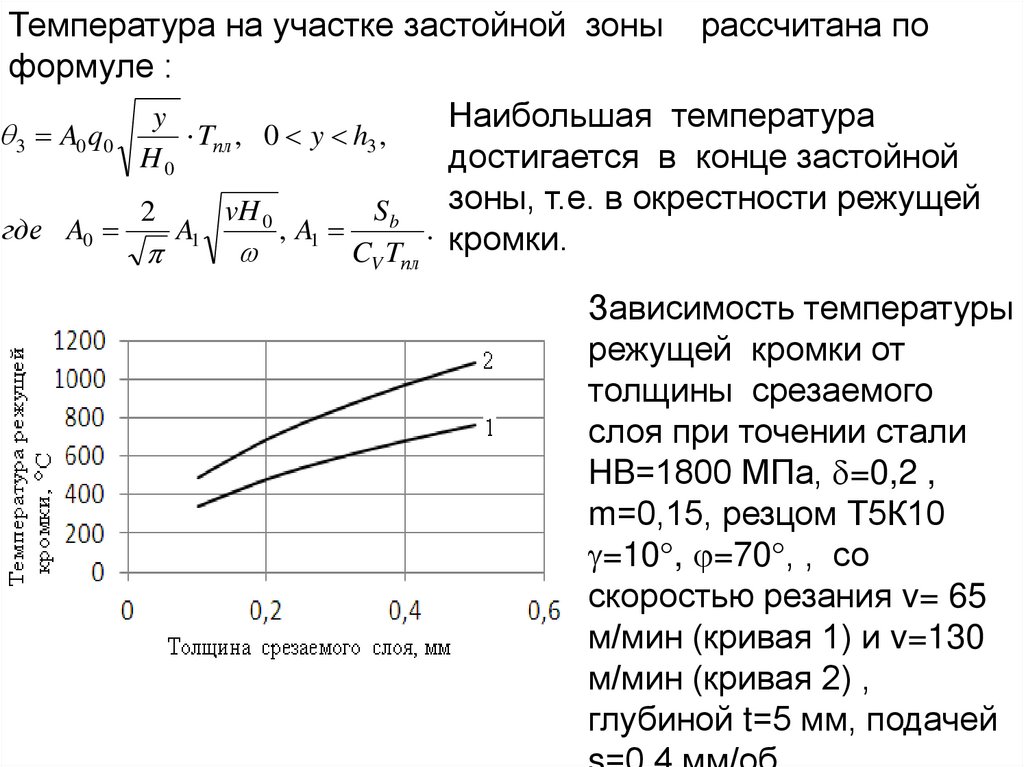
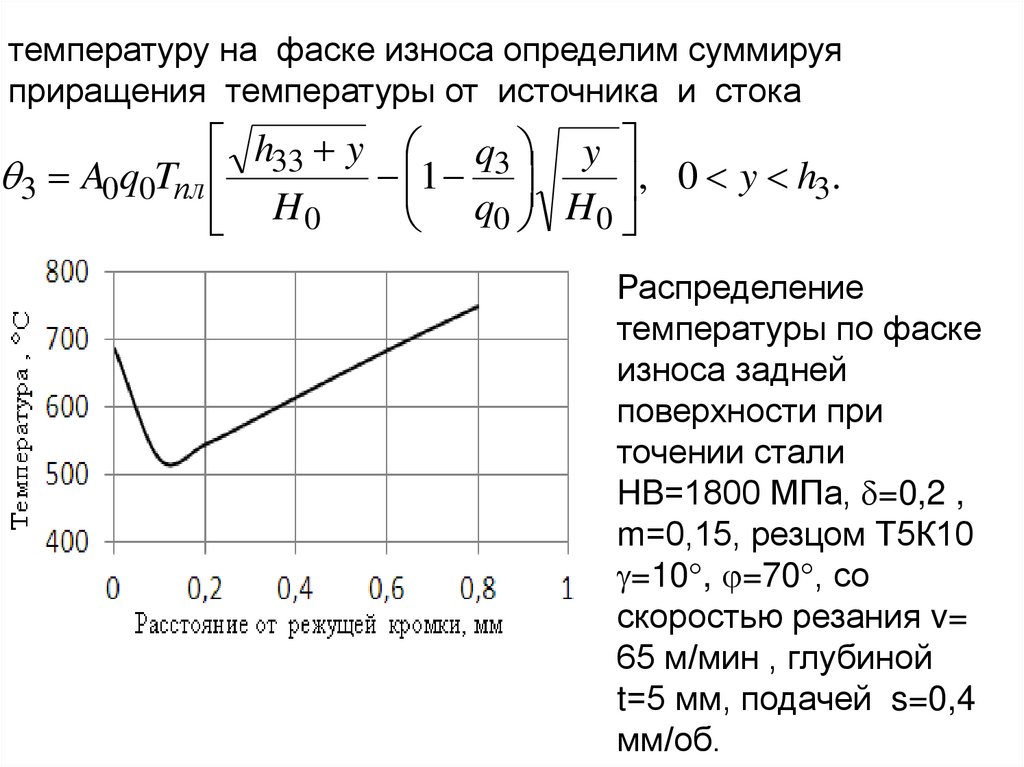
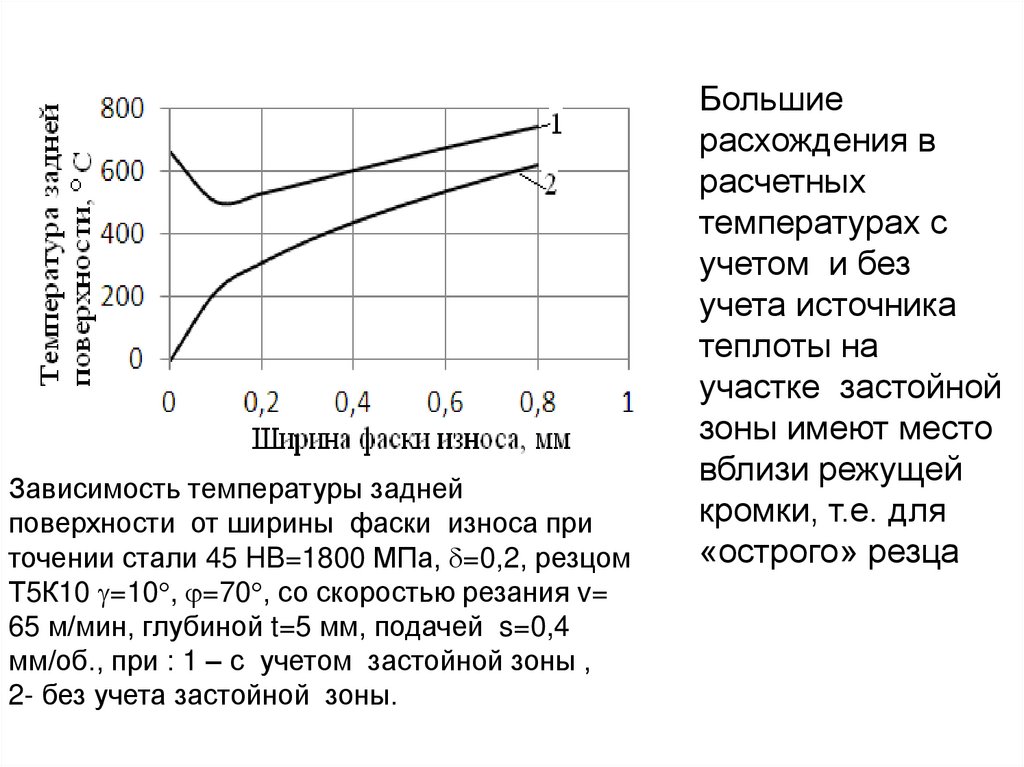


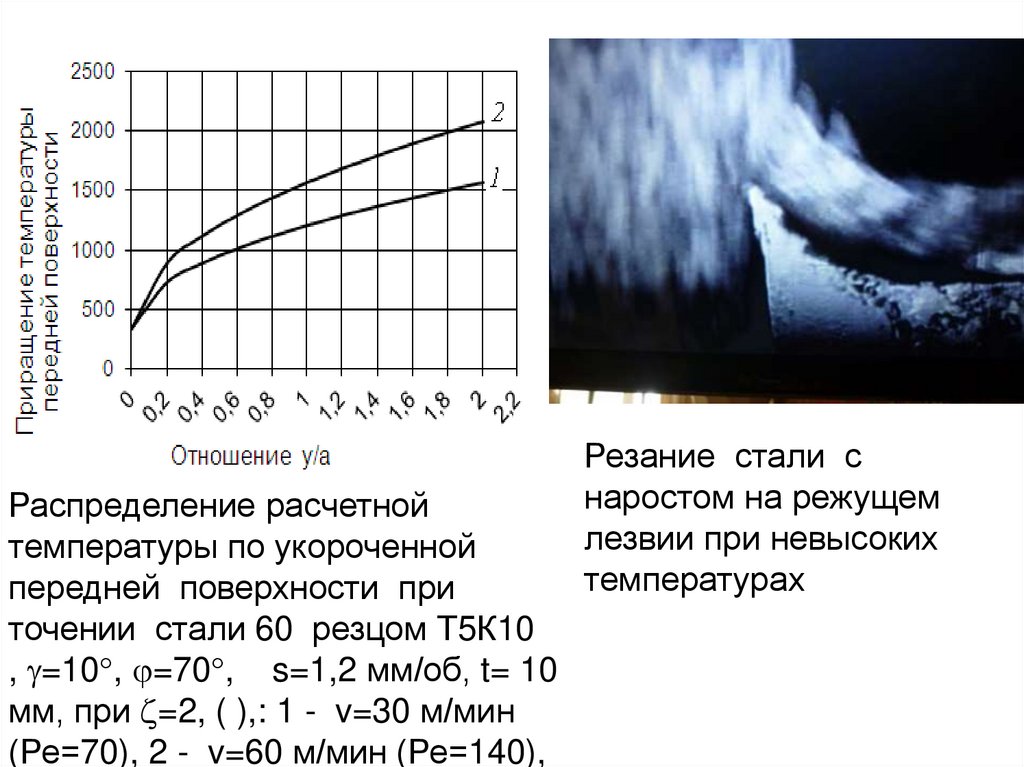
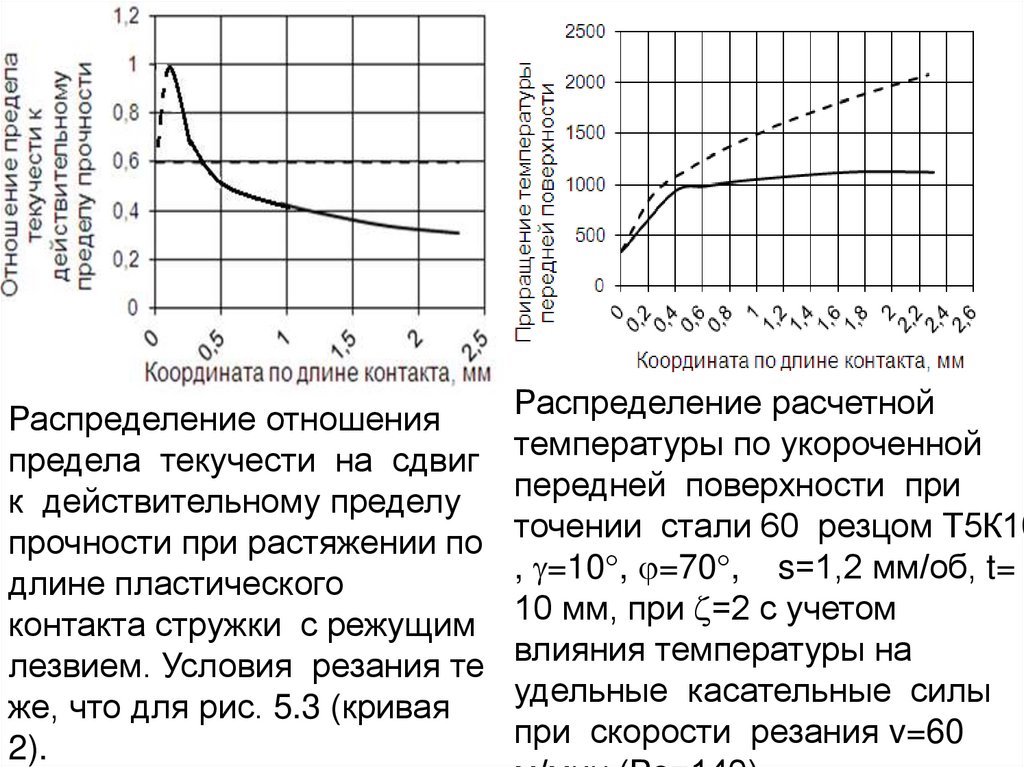








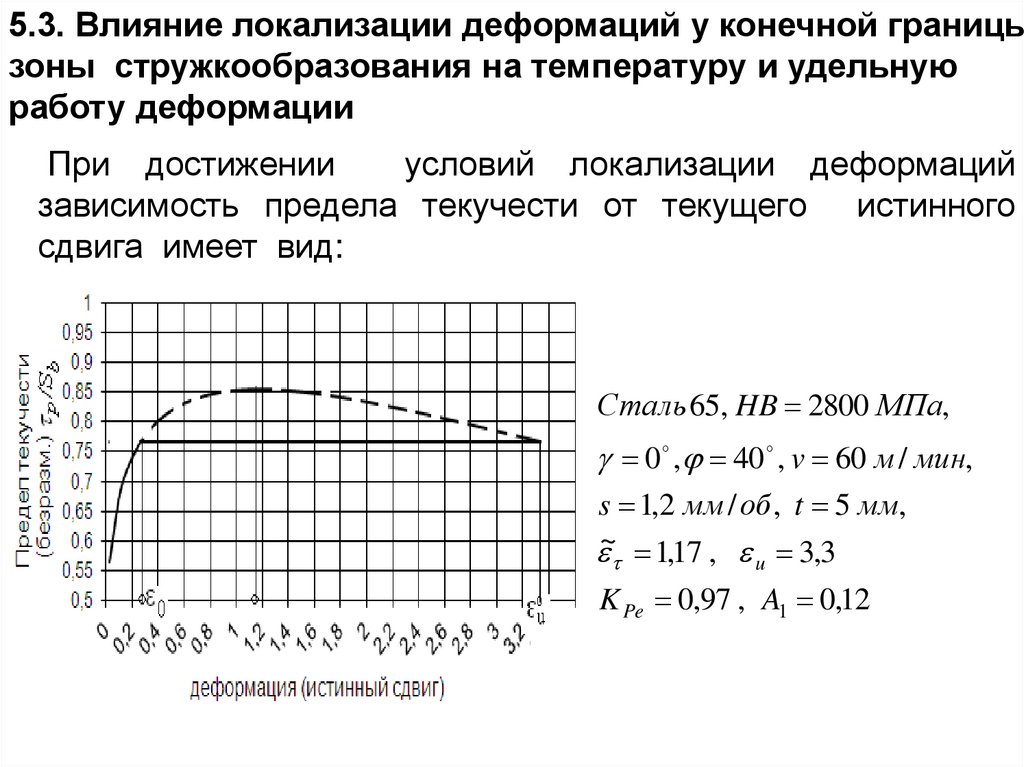



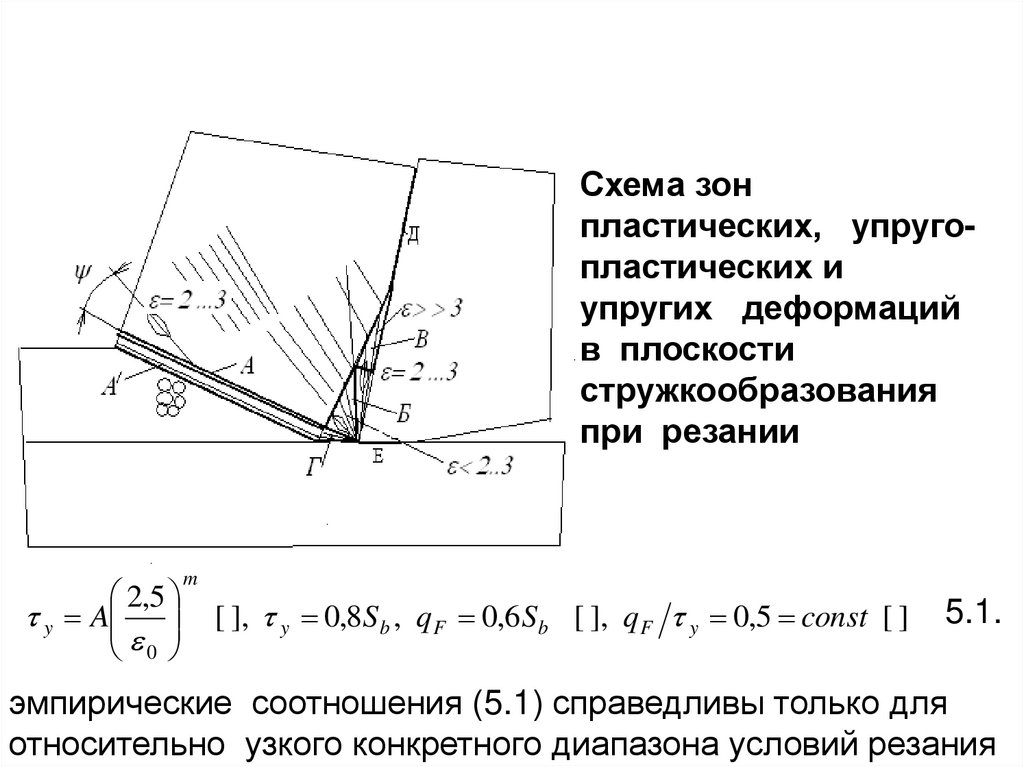
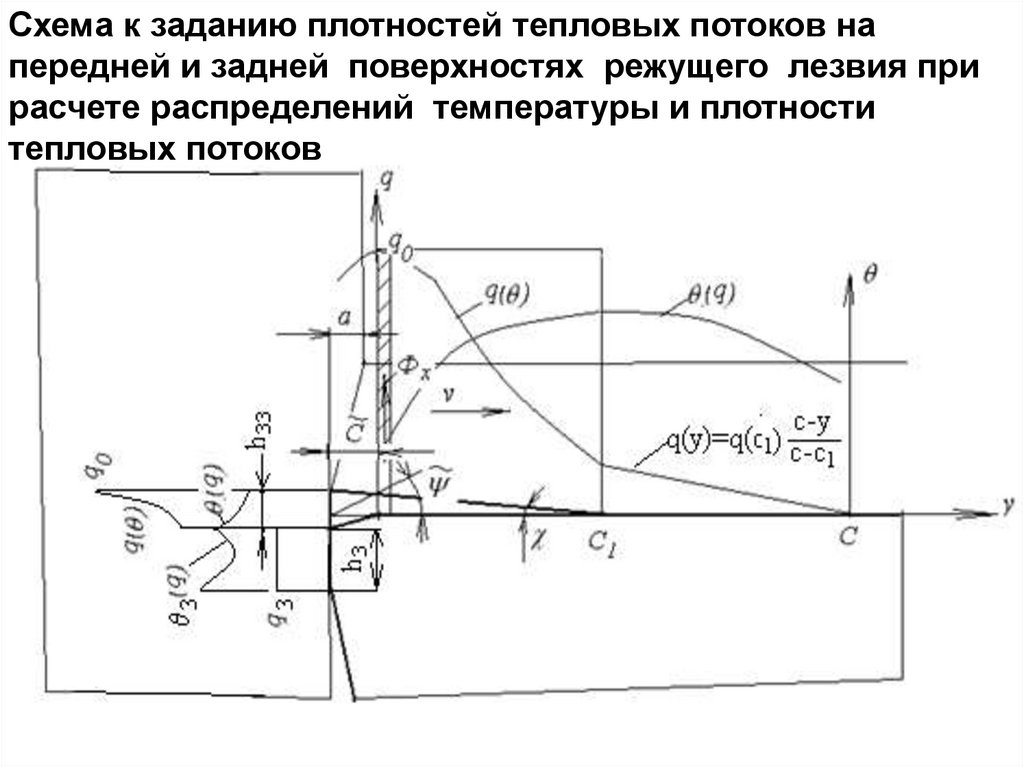






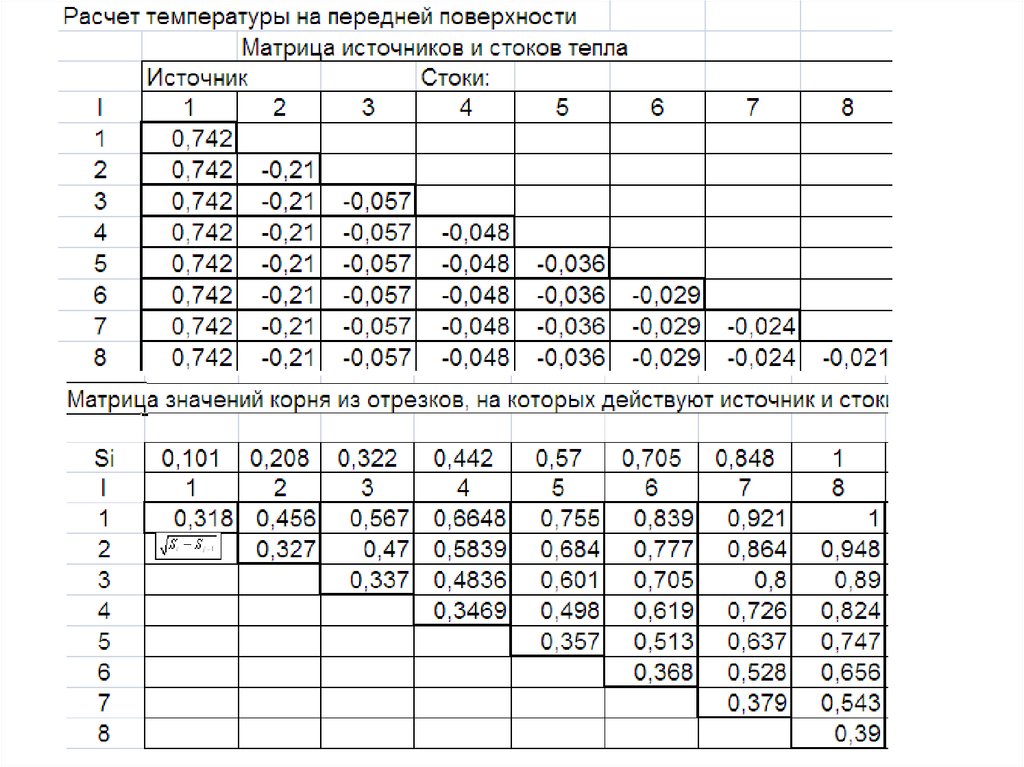
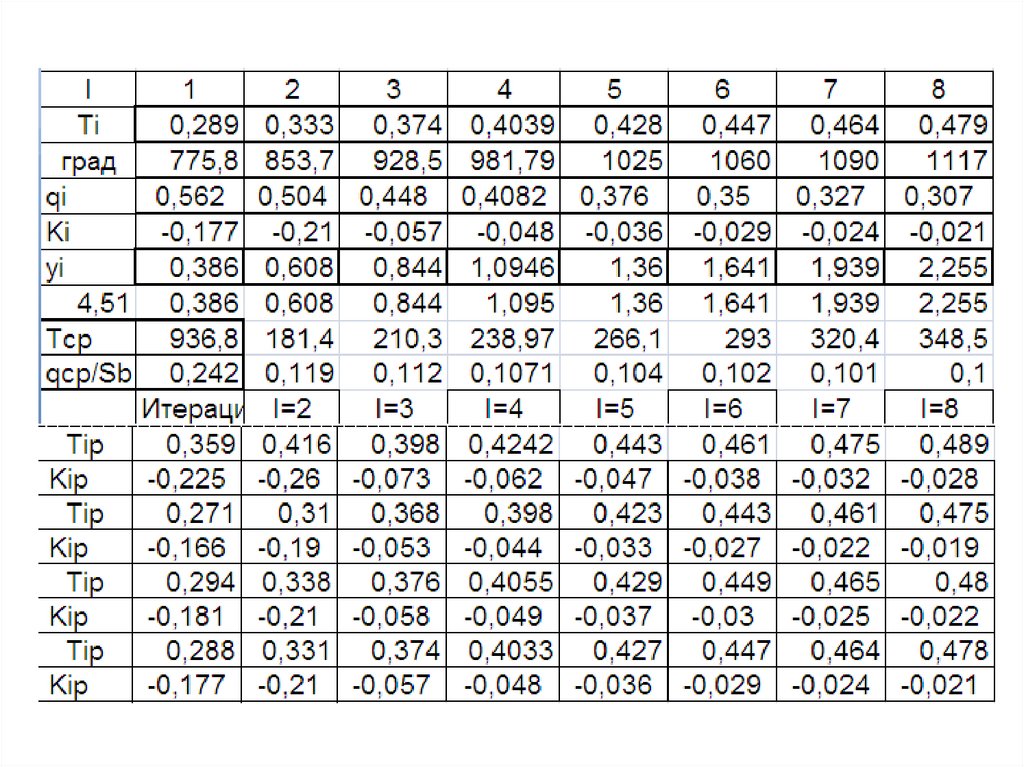


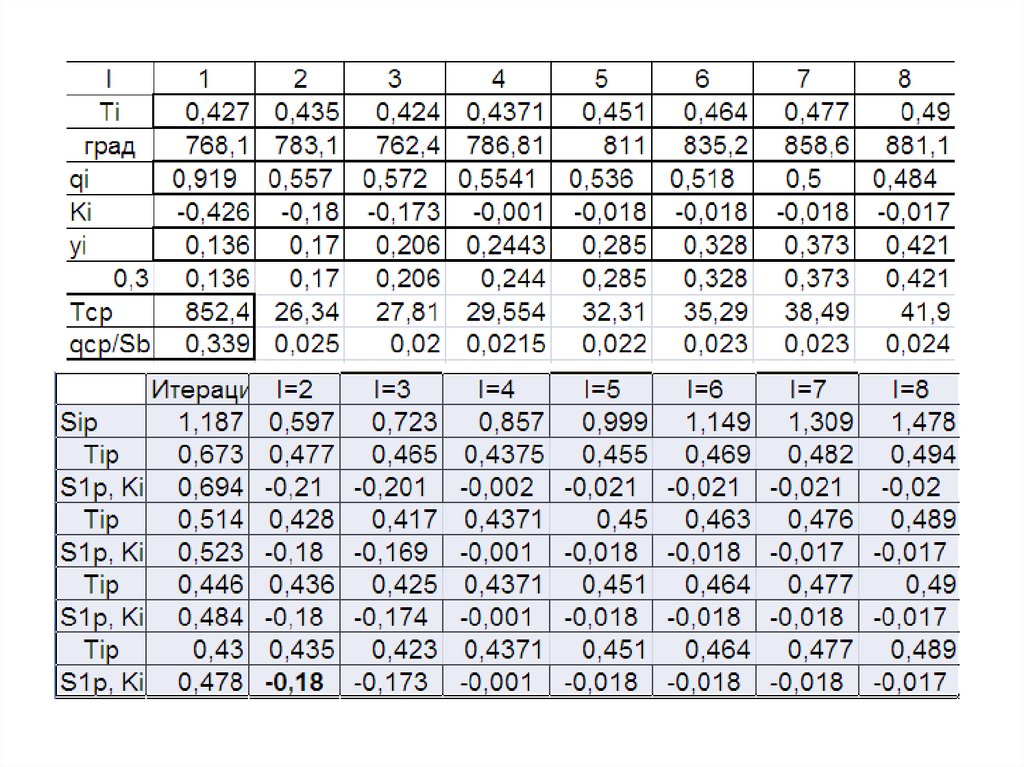

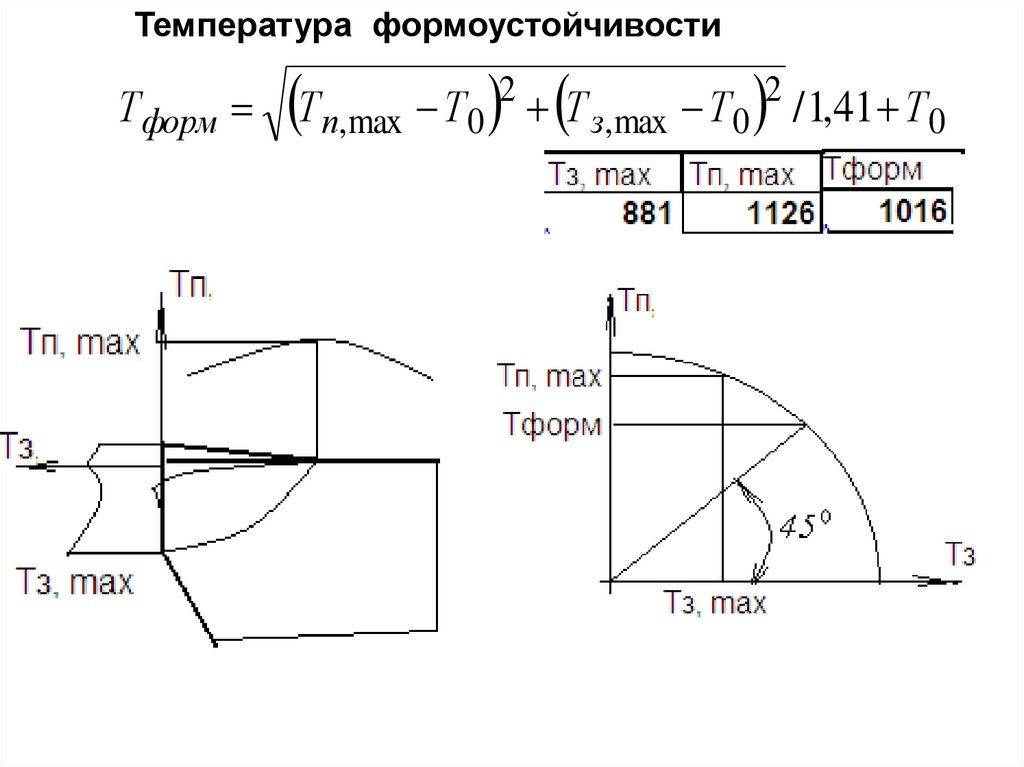

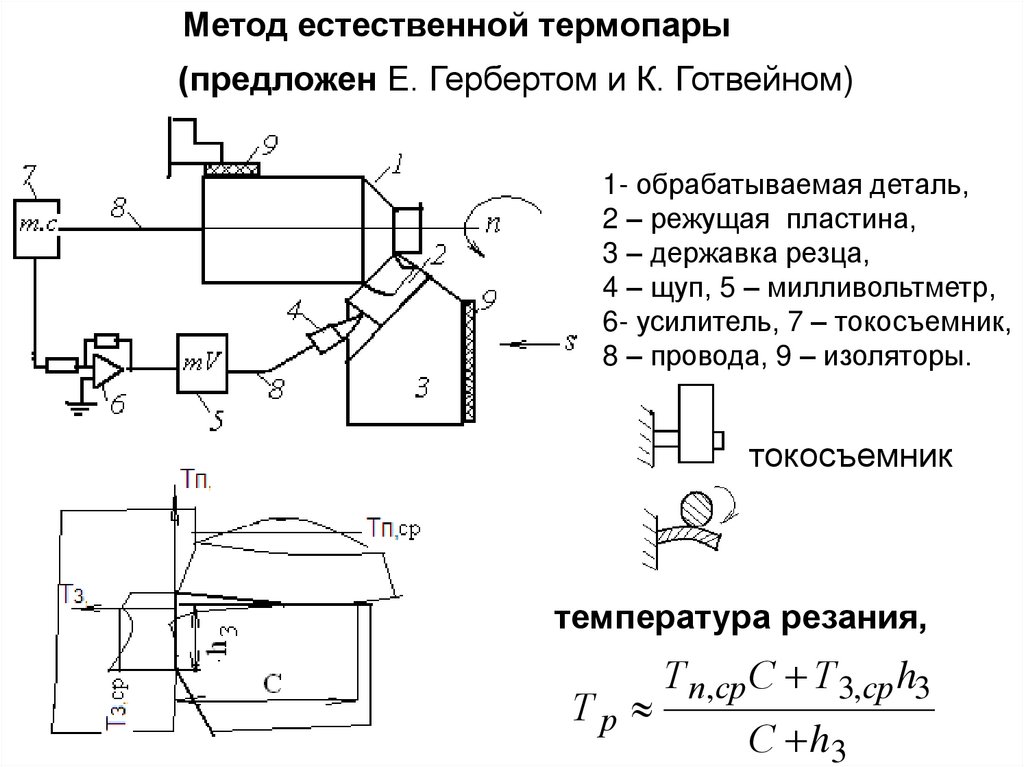





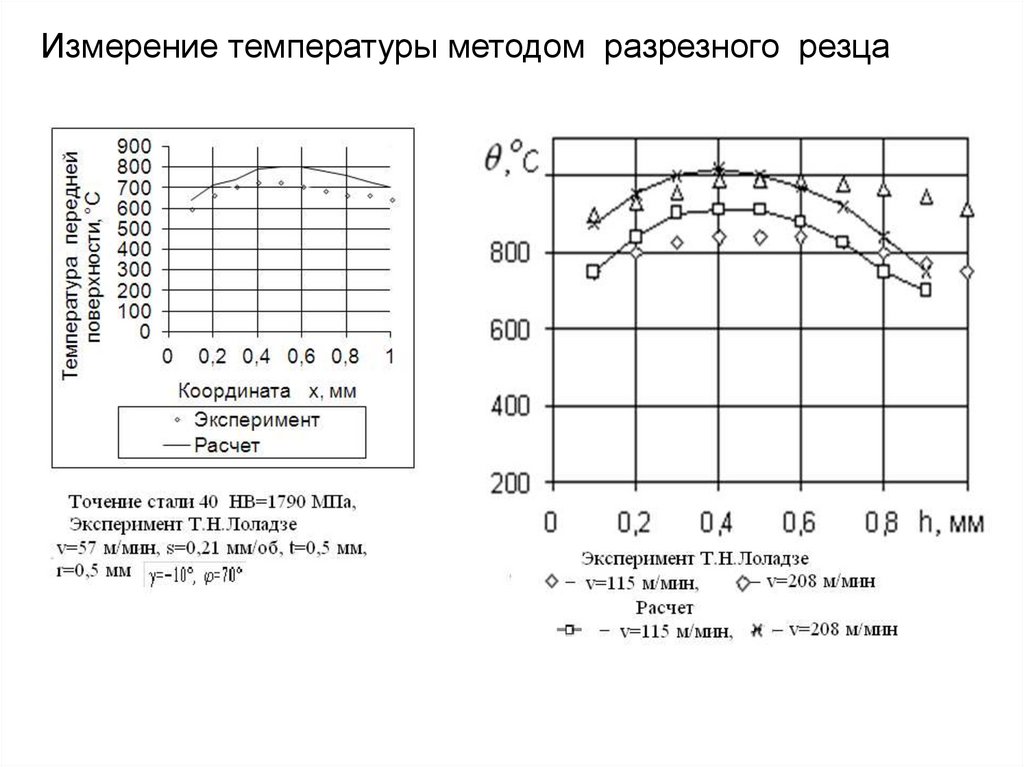







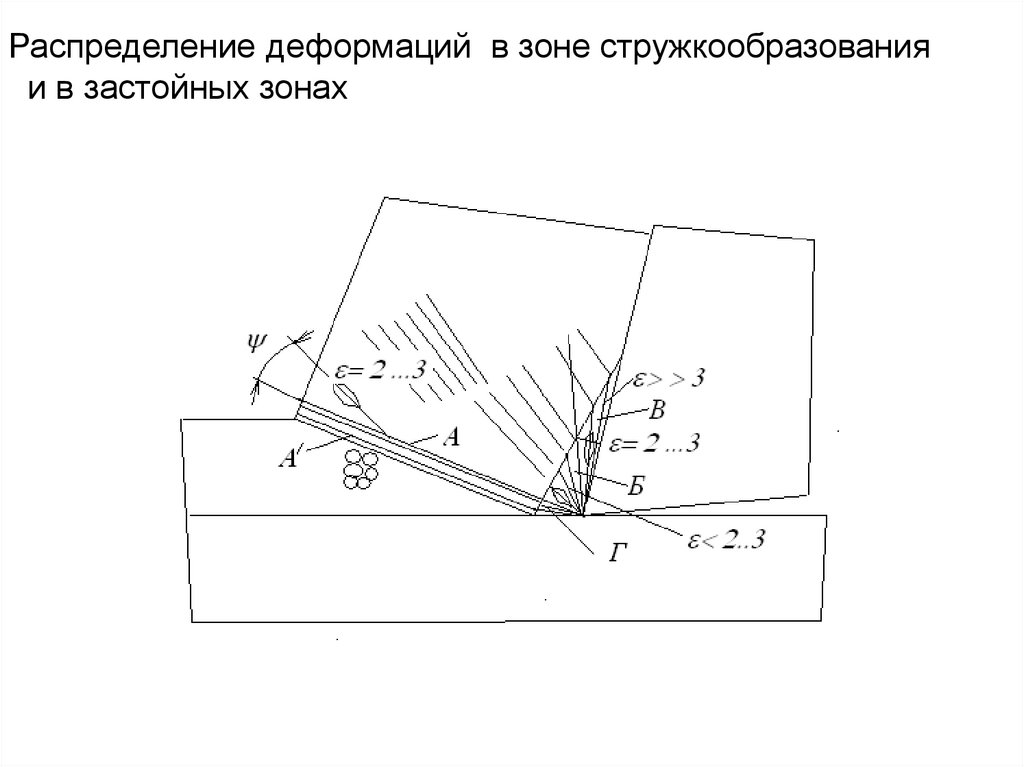
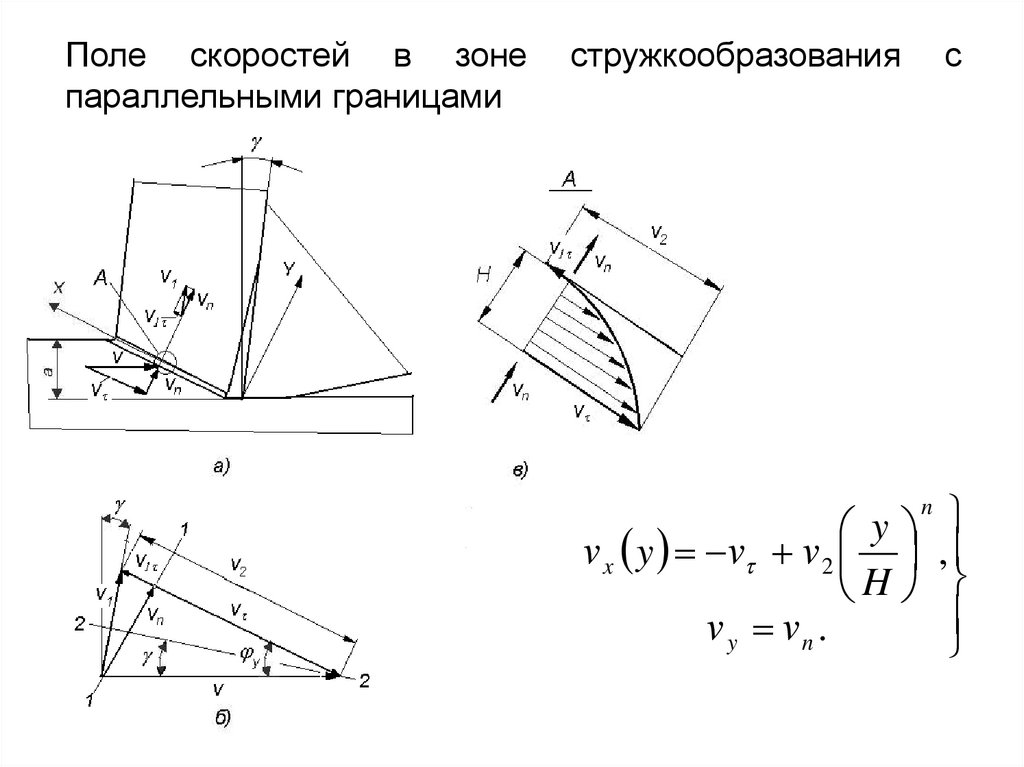


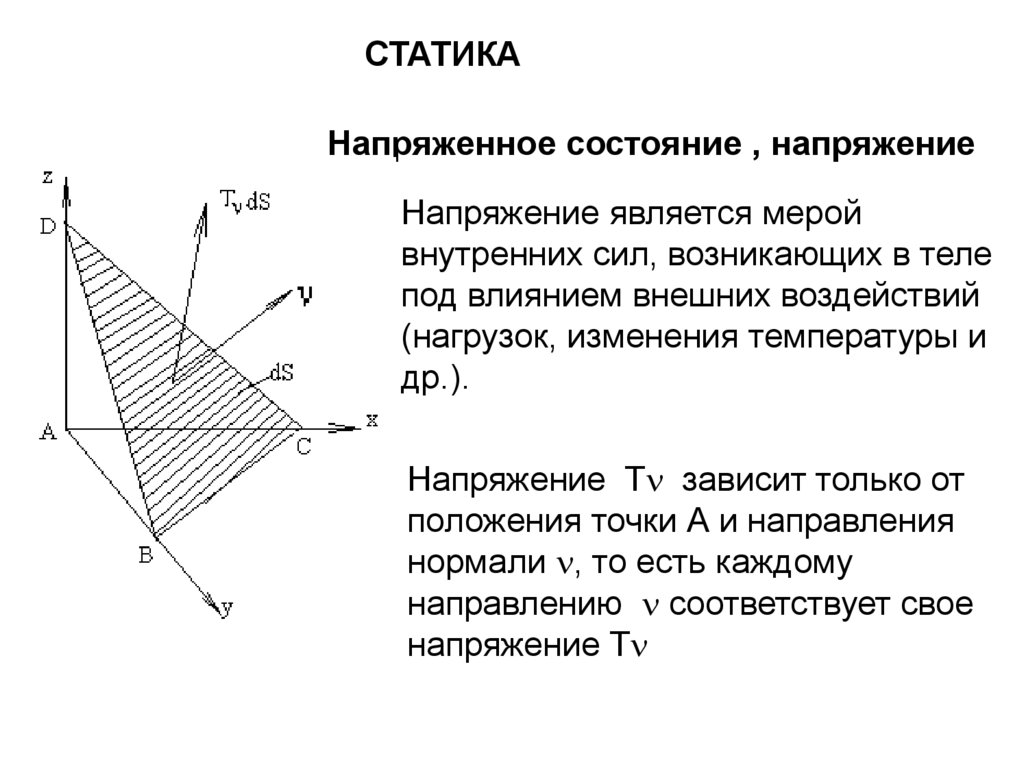
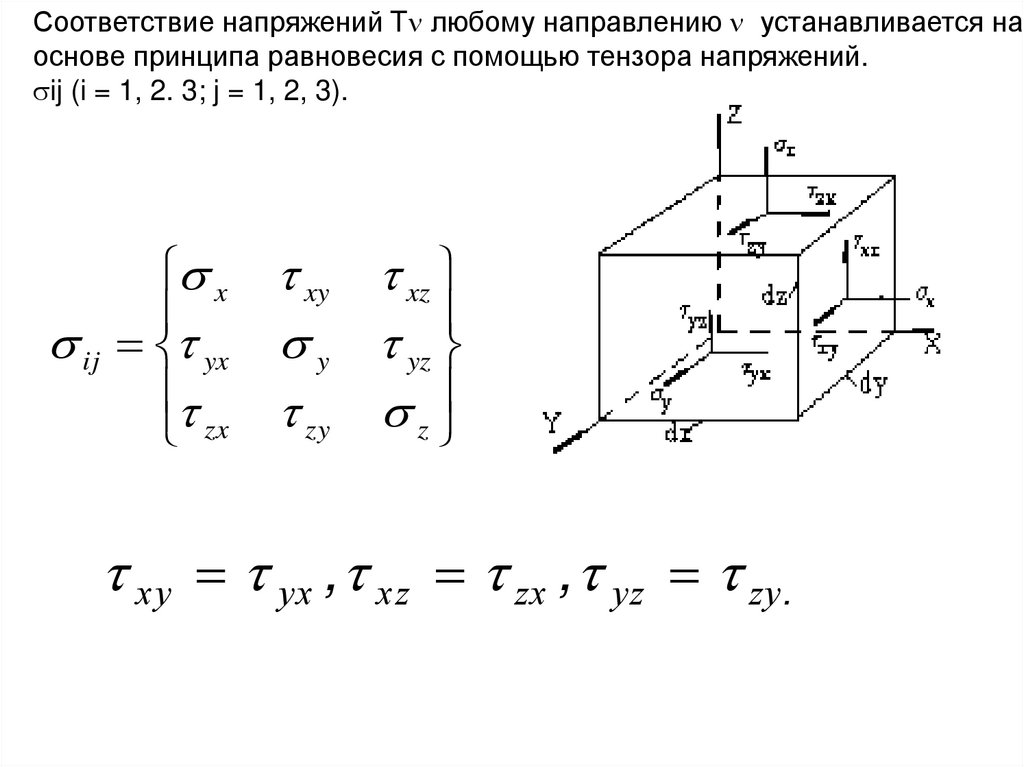




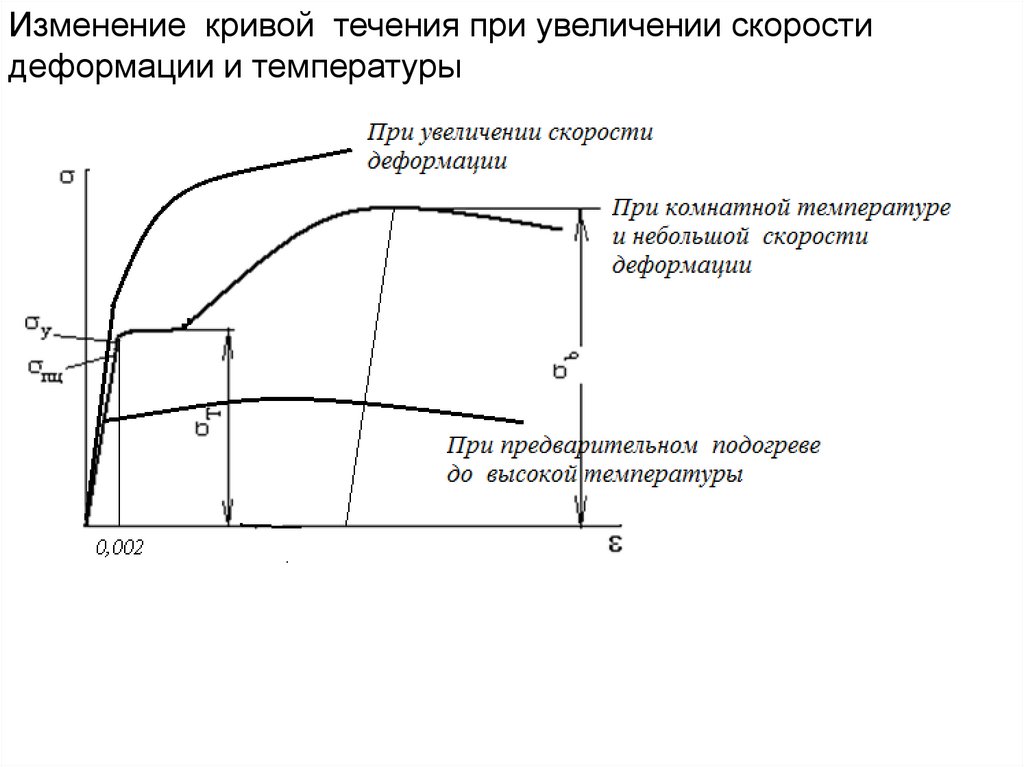

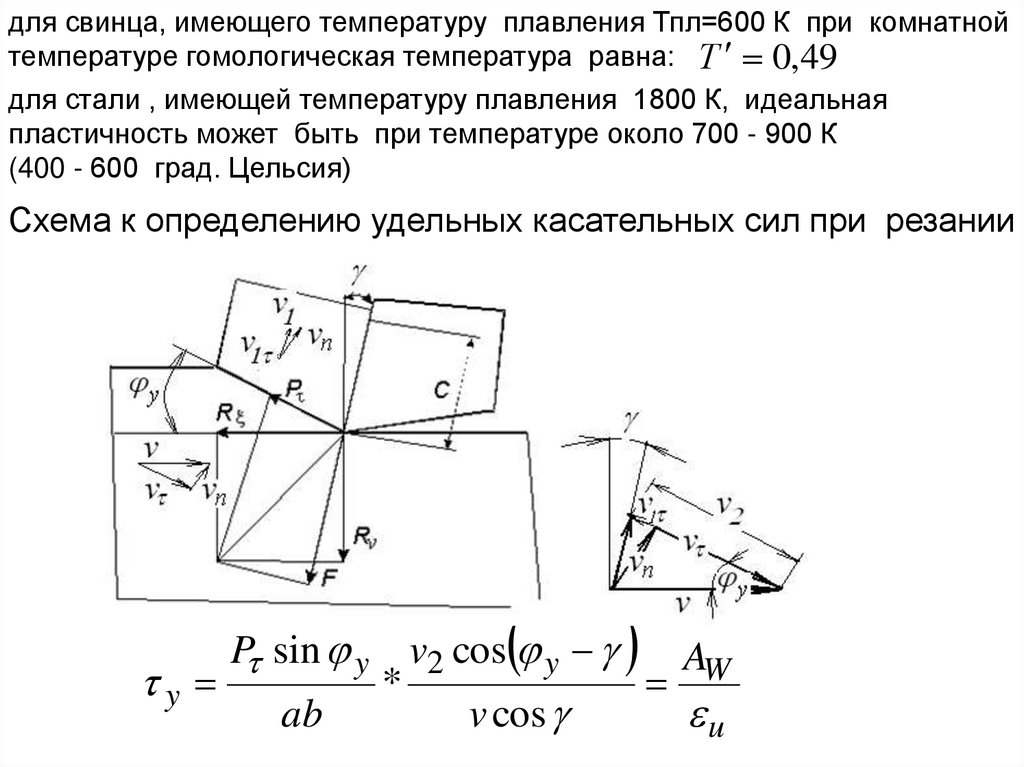

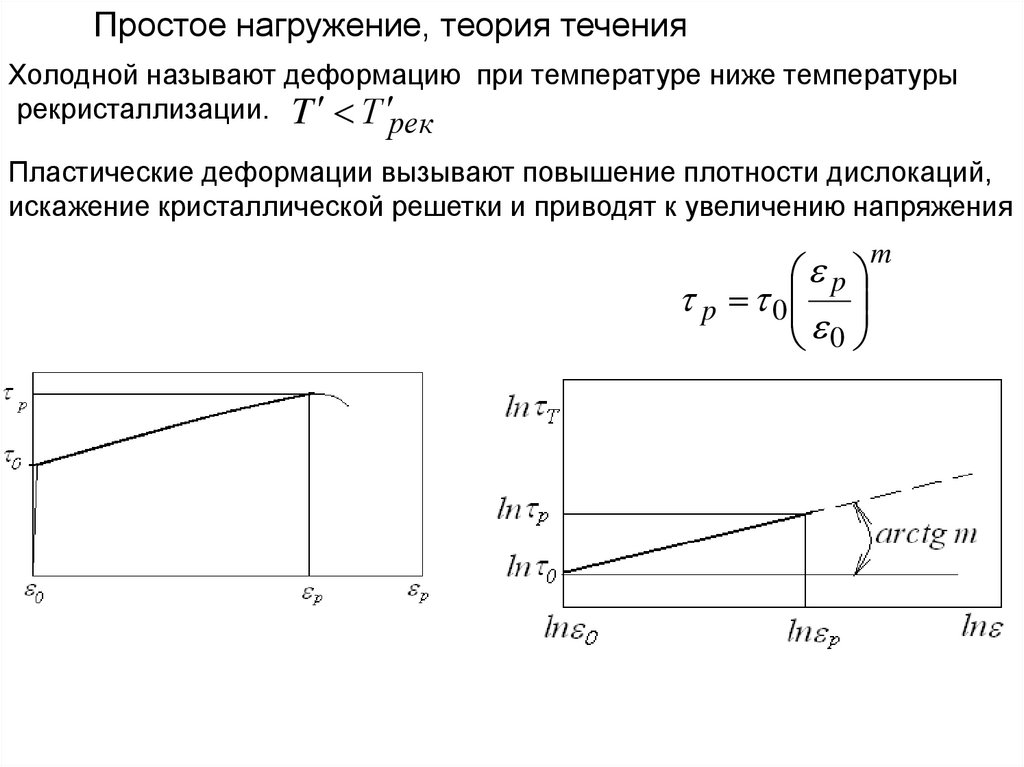


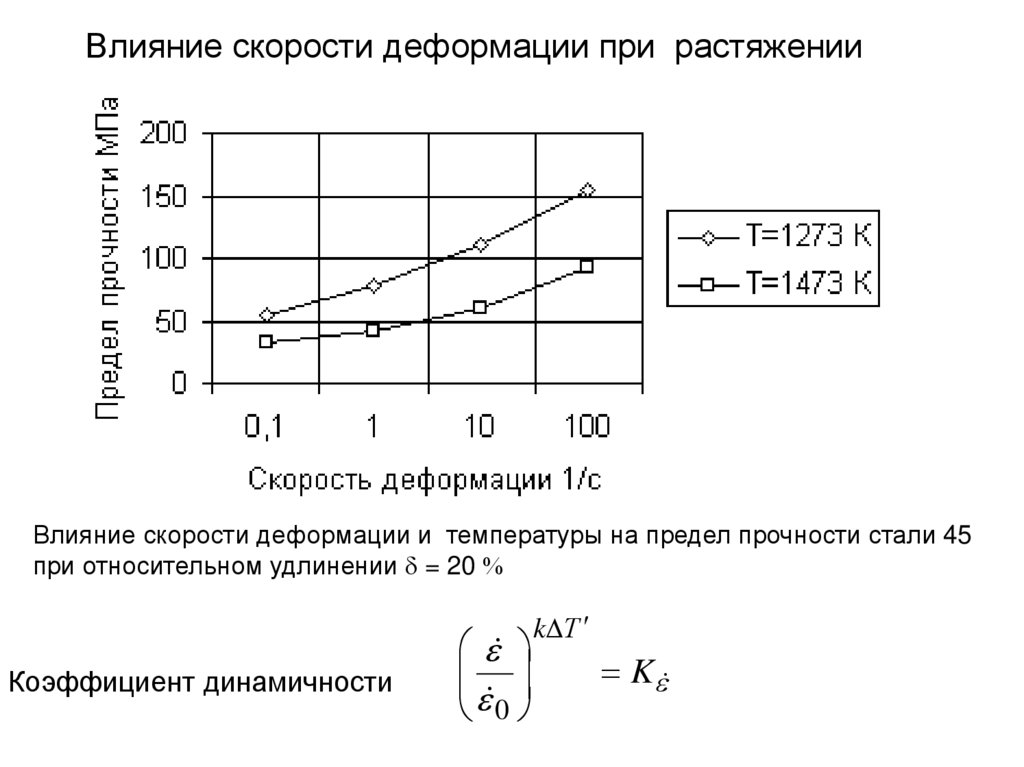





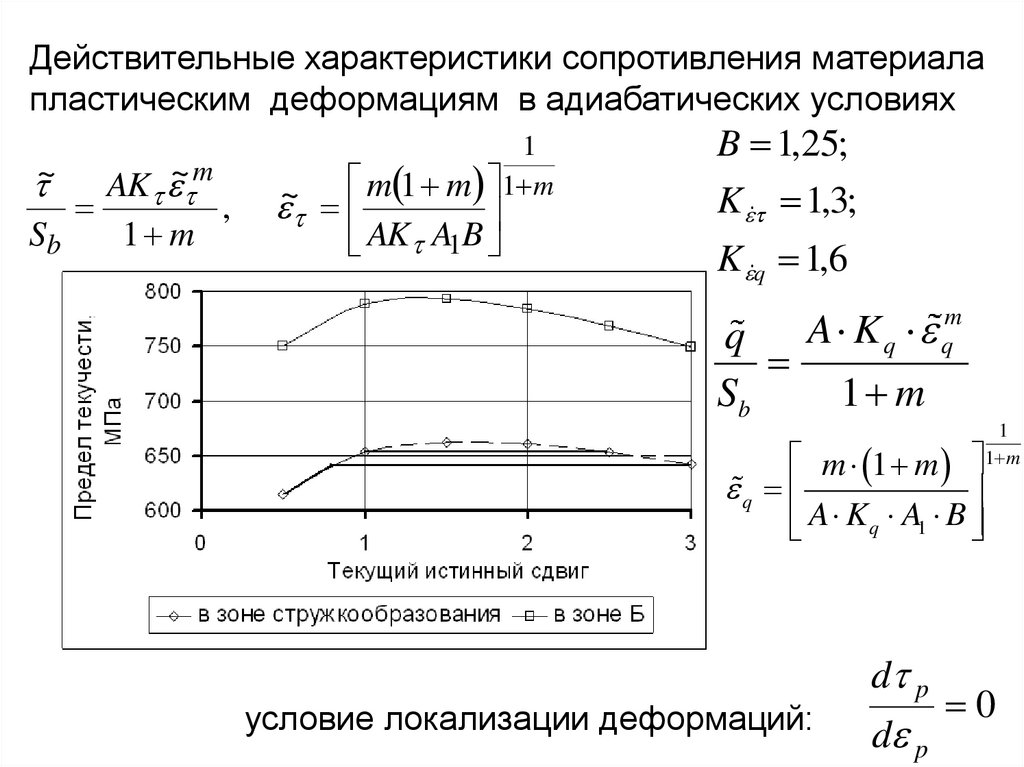
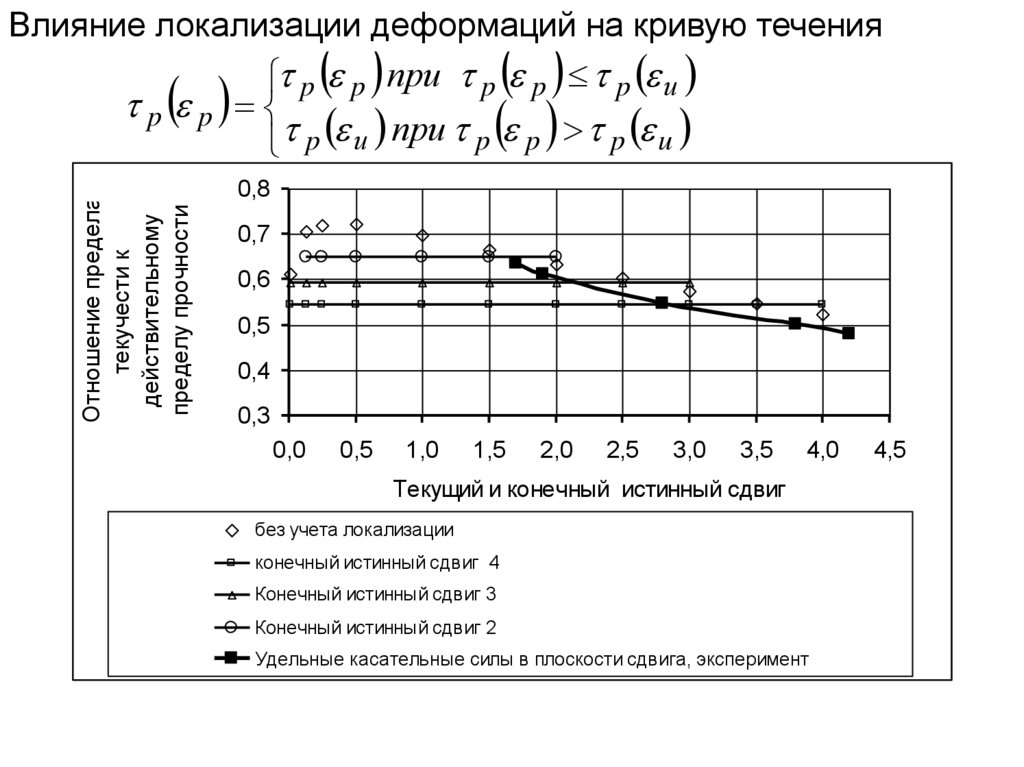















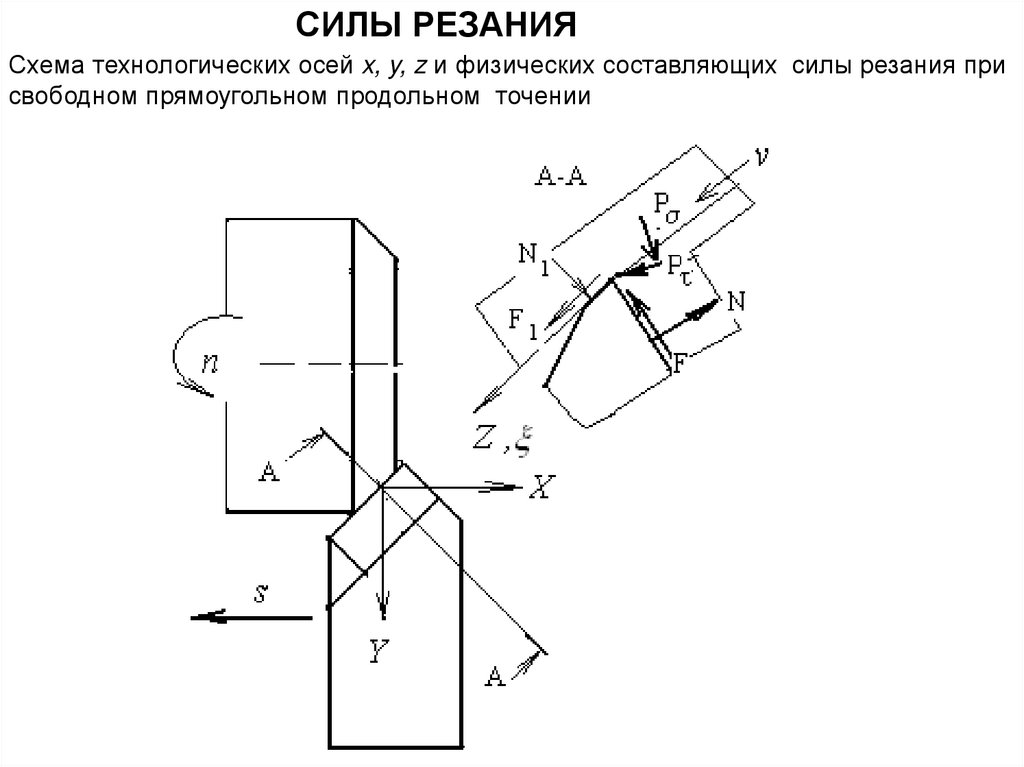
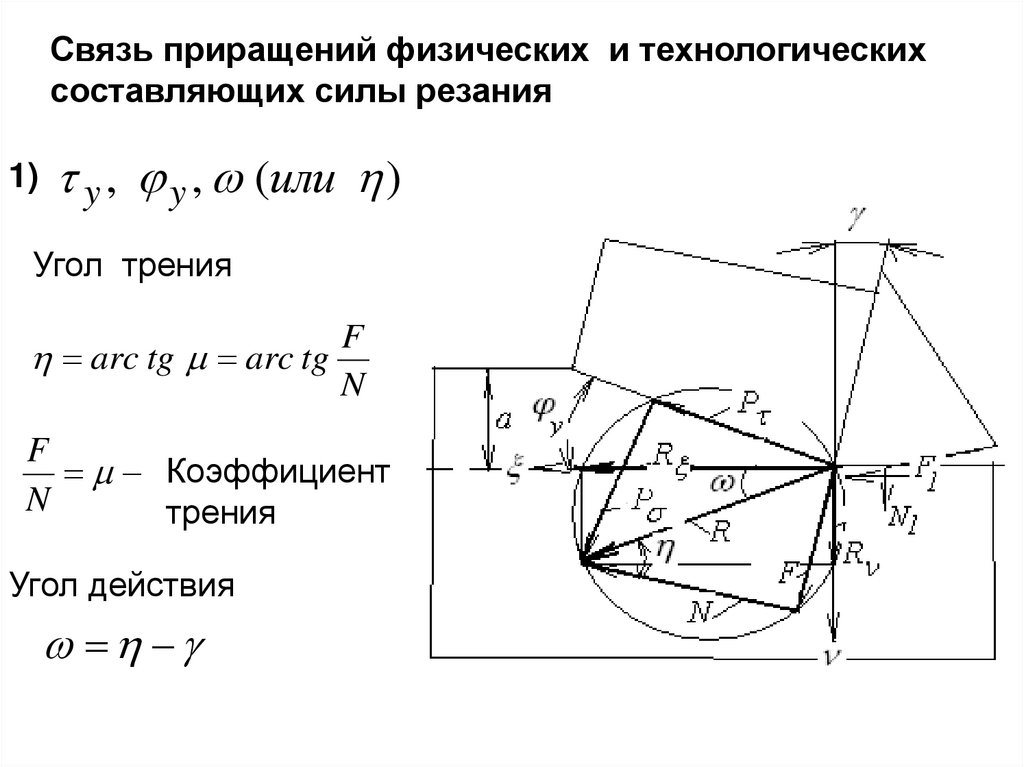

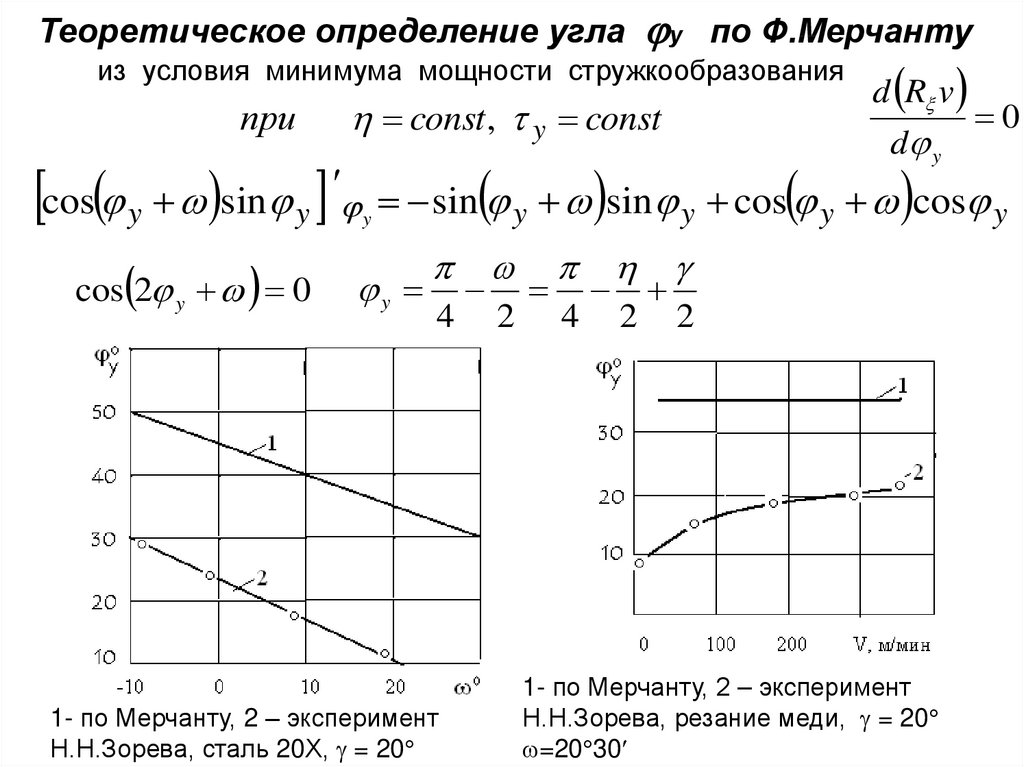
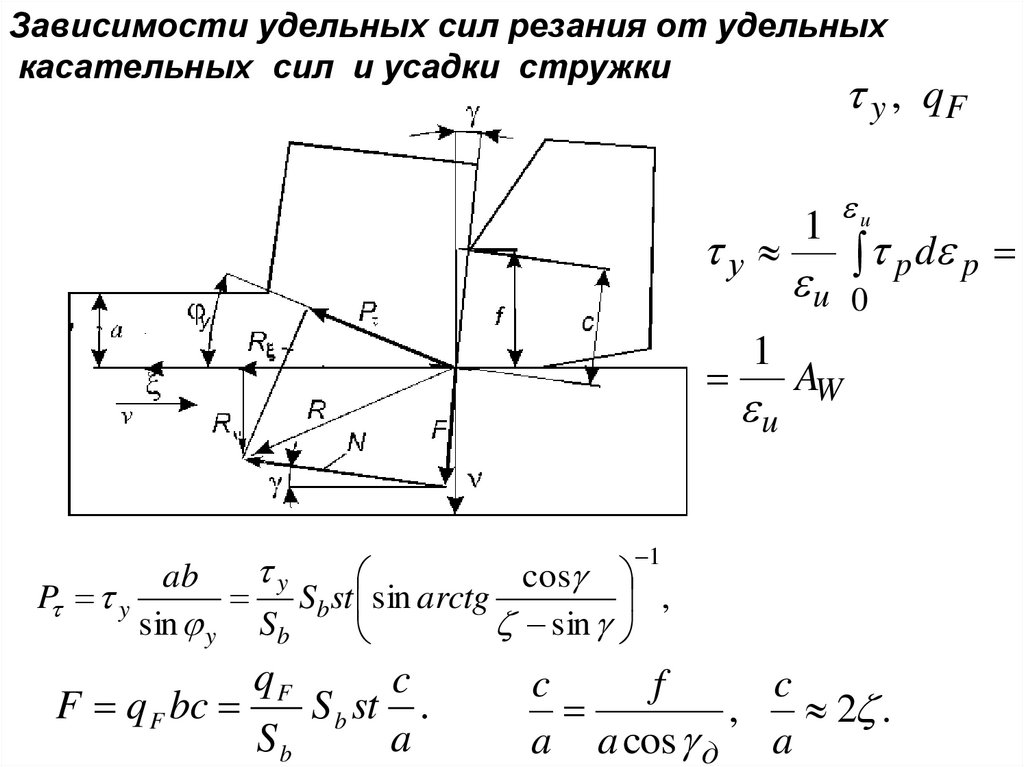

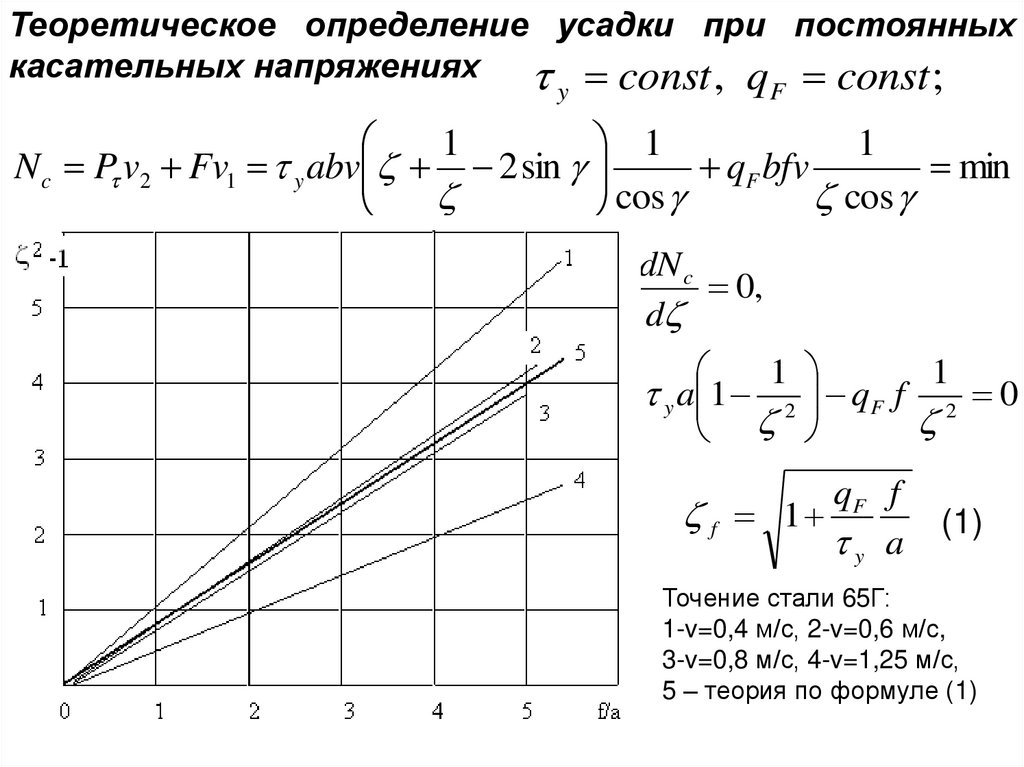
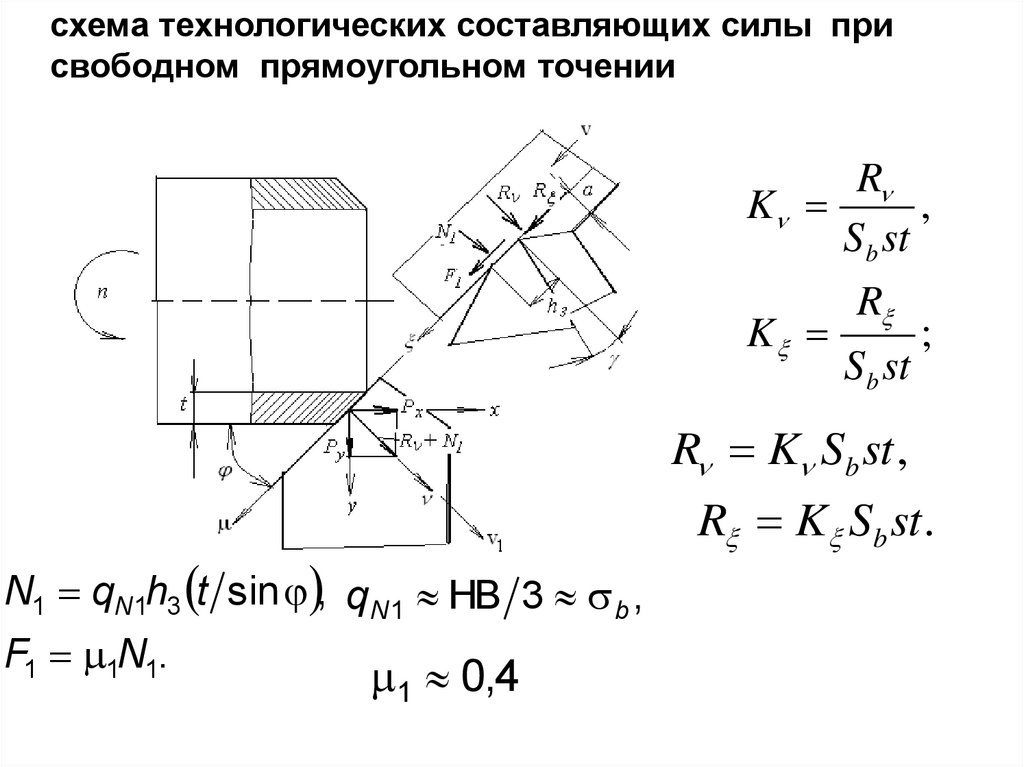







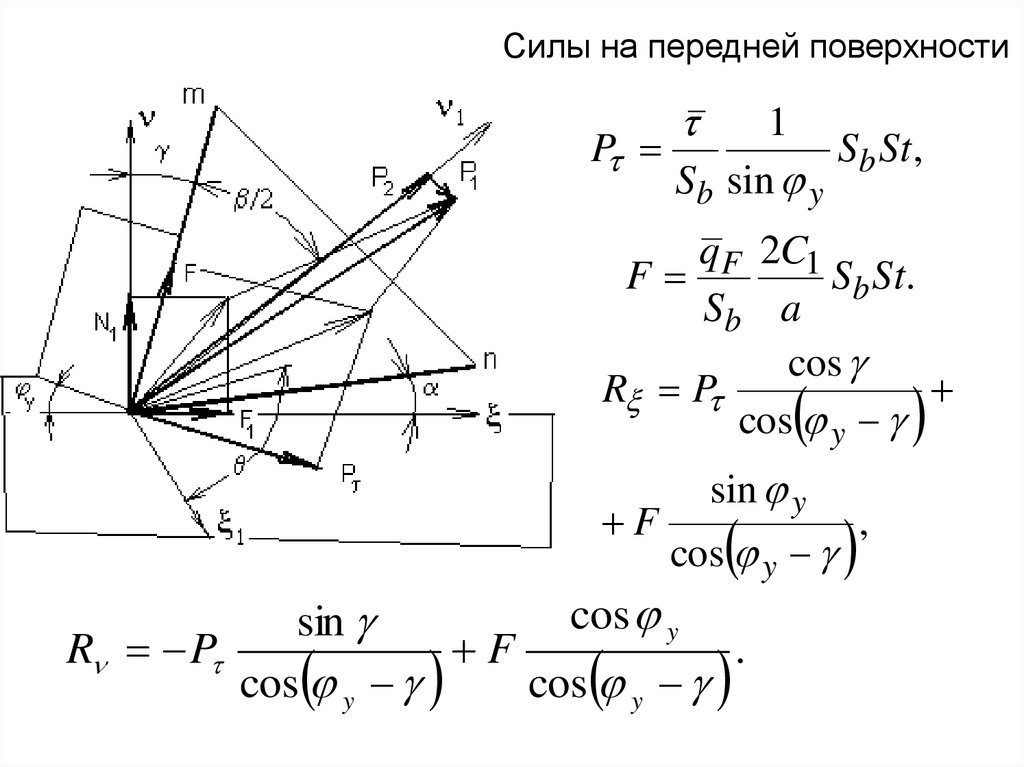





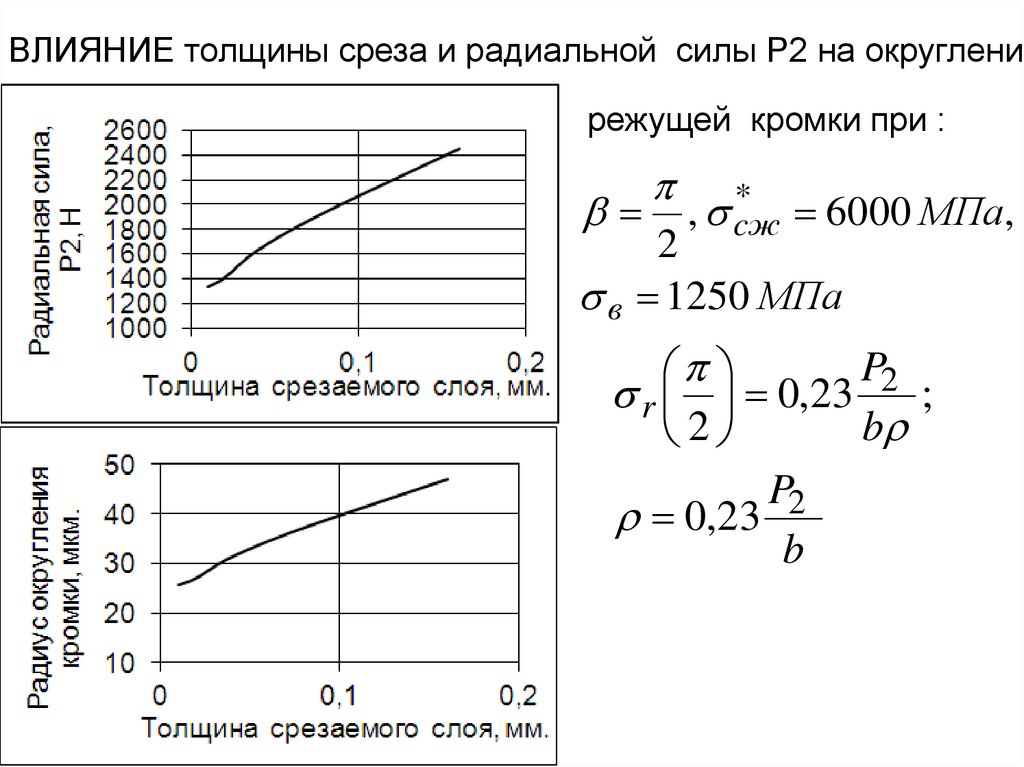









 industry
industry








