Similar presentations:
Лекция 11. Крутильные колебания стержня
1.
Лекция 11. Крутильные колебания стержняУравнение крутильных колебаний имеет вид
д
д
д 2
GJ к
J 0 2 ( x, t ) (7.22)
дx
дx
дt
Решение уравнения (7.22), удовлетворяющее на каждом конце одному из краевых
условий, должно также удовлетворять начальным условиям
д
( x,0) g ( x);
( x,0) g ( x) (7.23)
дt
2.
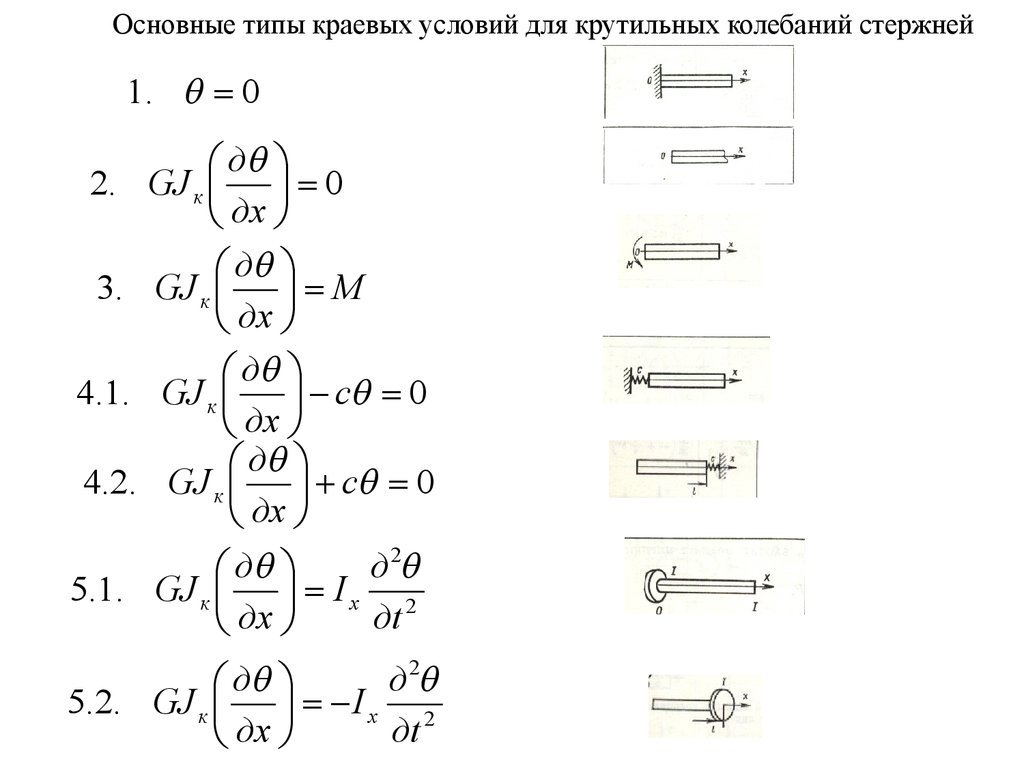
Основные типы краевых условий для крутильных колебаний стержней1. 0
д
2. GJ к 0
дx
д
3. GJ к M
дx
д
4.1. GJ к c 0
дx
д
4.2. GJ к c 0
дx
2
д
д
5.1. GJ к I x 2
дt
дx
д 2
д
5.2. GJ к I x 2
дt
дx
3.
В технической теории крутильные колебания стержня описываютуравнением при м = 0
2
д д
д
GJ к J 0 2 0 (8.11)
дx дx
дt
Если стержень имеет постоянные по длине характеристики
GJк = const,
рJ0 = const, то уравнение для исследования собственных колебаний будет
следующим:
GJ к
c0
J 0
д д J 0 д 2
0 (8.11а )
2
дx дx GJ к дt
д 2 1 д 2
2 2 0 (8.12а )
2
дx
c0 дt
- скорость распространения крутильных волн в стержне
( x, t ) на концах стержня должна удовлетворять краевым условиям,
соответствующим характеру закрепления концов стержня.
4.
Общее решение. Для стержня, совершающего собственные крутильныеколебания, переменные разделяют введением временного множителя,
гармонически изменяющегося со временем:
( x, t ) ( x) sin t
( 8.13)
д 2 1 д 2
2 2 0 (8.12а )
2
дx
c0 дt
Подстановка (8.13) в (8.12а) приводит к уравнению
2 0 (8.14) где
c0
(8.15)
Общее решение (8.14) можно представить в виде
( x) C1 sin x C2 cos x
( 8.16)
Определение собственных частот и форм продольных колебаний.
Подстановка (8.16) в краевые условия дает систему линейных
однородных уравнений для определения С1. и С2
Формы собственных колебаний определяются ненулевым решением Сj
при k (одной из собственных частот).





 mechanics
mechanics








