Решение вычислительных задач на компьютере (язык С++)

1. Решение вычислительных задач на компьютере (язык С++)

1
Решение
вычислительных задач
на компьютере
(язык С++)
§ 71. Дискретизация
К.Ю. Поляков, Е.А. Ерёмин, 2018-2019
http://kpolyakov.spb.ru

2. Вычисление длины линии

Решение вычислительных задач, 10 класс, C++
2
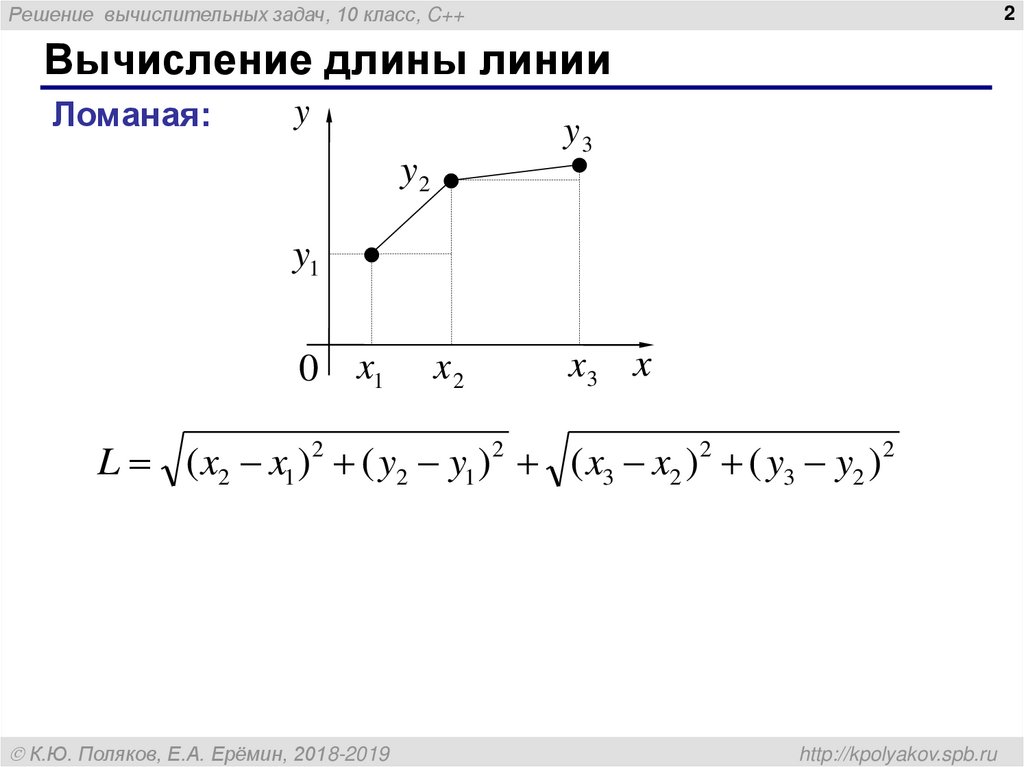
Вычисление длины линии
Ломаная:
y
y3
y2
y1
0
x1
x2
x3 x
L ( x2 x1 )2 ( y2 y1 )2 ( x3 x2 )2 ( y3 y2 )2
К.Ю. Поляков, Е.А. Ерёмин, 2018-2019
http://kpolyakov.spb.ru

3. Вычисление длины линии

Решение вычислительных задач, 10 класс, C++
3
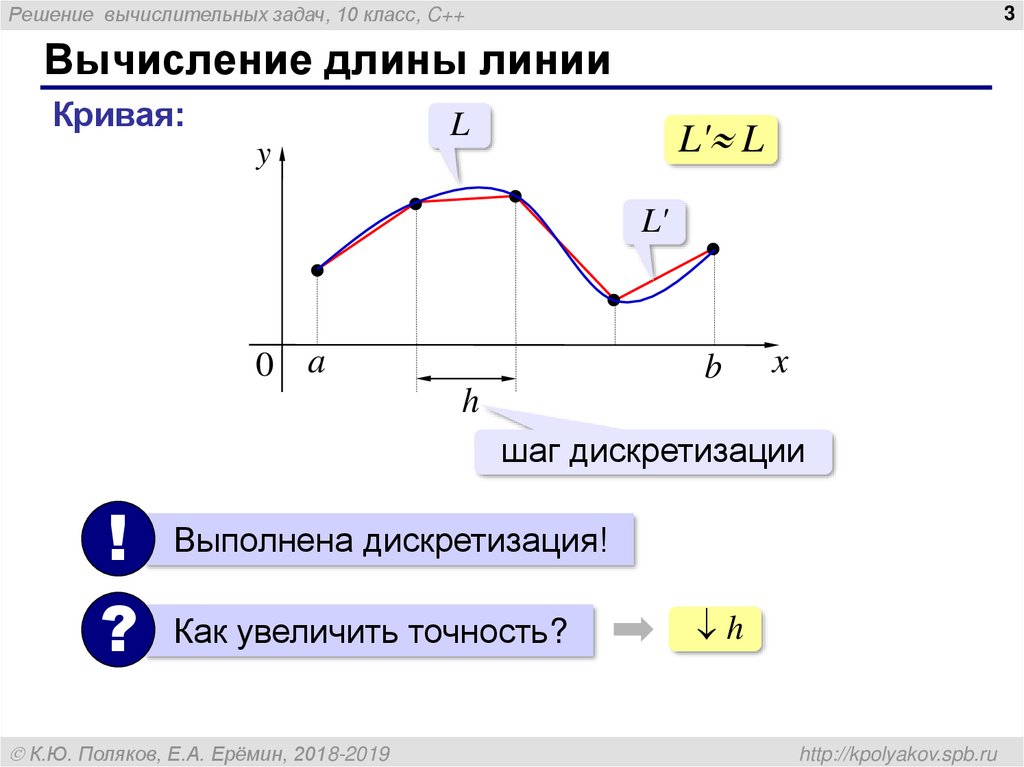
Вычисление длины линии
Кривая:
L' L
L
y
L'
0
a
b
x
h
шаг дискретизации
!
?
Выполнена дискретизация!
Как увеличить точность?
К.Ю. Поляков, Е.А. Ерёмин, 2018-2019
h
http://kpolyakov.spb.ru

4. Дискретизация

Решение вычислительных задач, 10 класс, C++
4
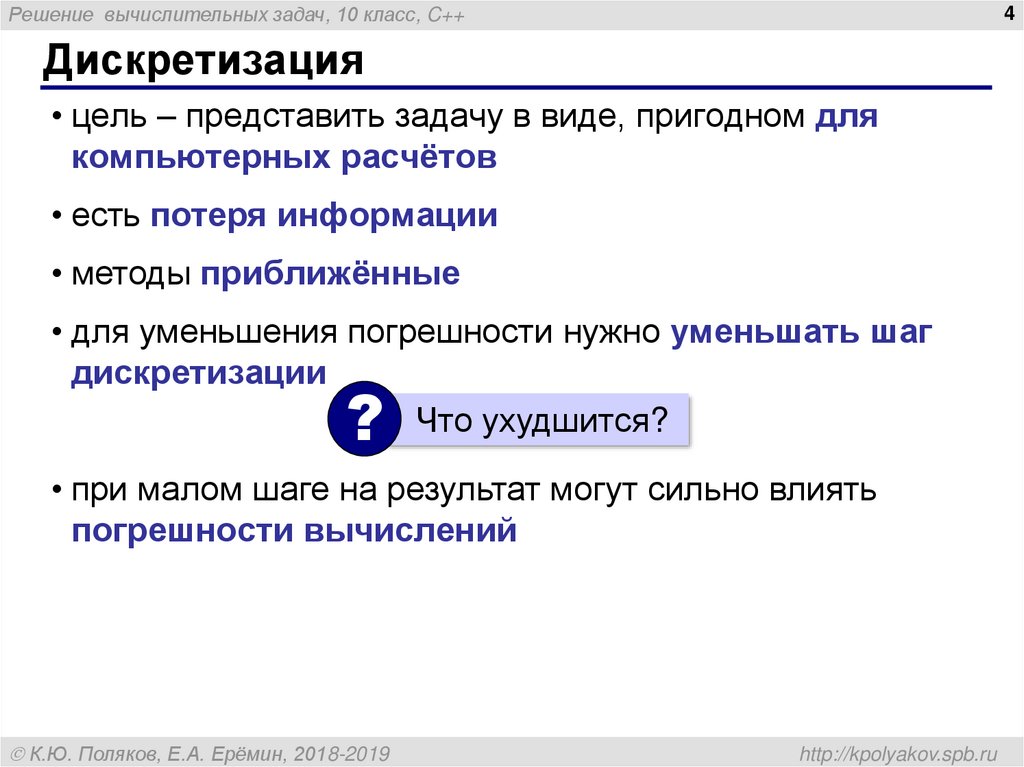
Дискретизация
• цель – представить задачу в виде, пригодном для
компьютерных расчётов
• есть потеря информации
• методы приближённые
• для уменьшения погрешности нужно уменьшать шаг
дискретизации
Что ухудшится?
?
• при малом шаге на результат могут сильно влиять
погрешности вычислений
К.Ю. Поляков, Е.А. Ерёмин, 2018-2019
http://kpolyakov.spb.ru

5. Вычисление длины кривой

Решение вычислительных задач, 10 класс, C++
5
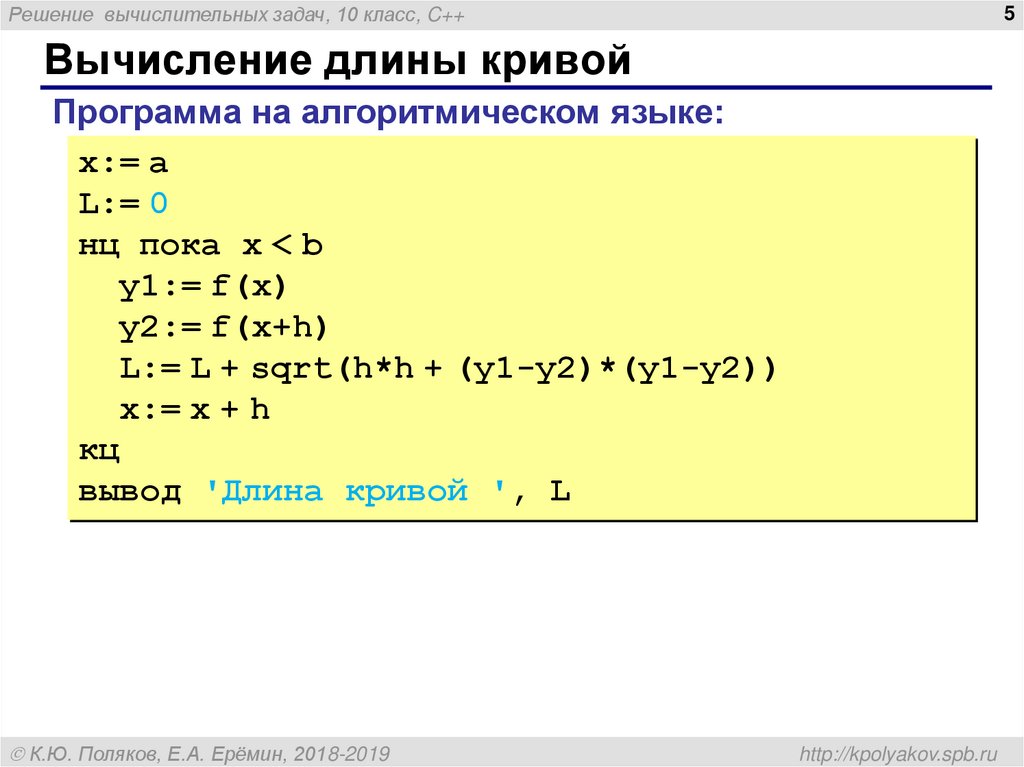
Вычисление длины кривой
Программа на алгоритмическом языке:
x:= a
L:= 0
нц пока x < b
y1:= f(x)
y2:= f(x+h)
L:= L + sqrt(h*h + (y1-y2)*(y1-y2))
x:= x + h
кц
вывод 'Длина кривой ', L
К.Ю. Поляков, Е.А. Ерёмин, 2018-2019
http://kpolyakov.spb.ru

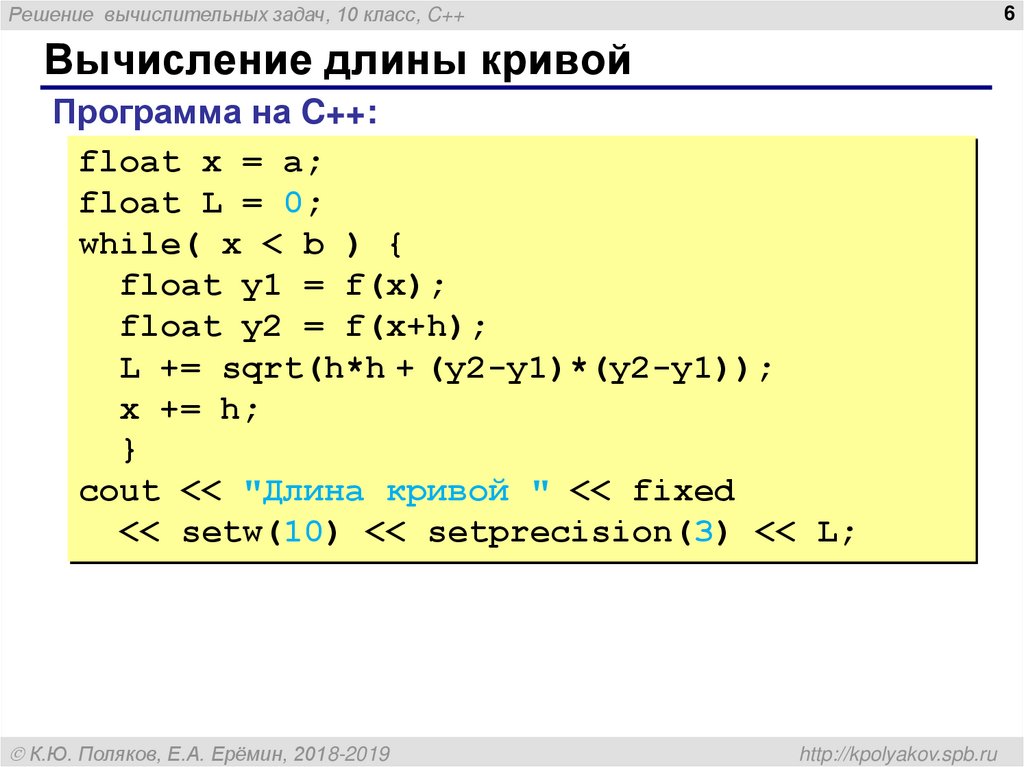
6. Вычисление длины кривой

Решение вычислительных задач, 10 класс, C++
6
Вычисление длины кривой
Программа на C++:
float x = a;
float L = 0;
while( x < b ) {
float y1 = f(x);
float y2 = f(x+h);
L += sqrt(h*h + (y2-y1)*(y2-y1));
x += h;
}
cout << "Длина кривой " << fixed
<< setw(10) << setprecision(3) << L;
К.Ю. Поляков, Е.А. Ерёмин, 2018-2019
http://kpolyakov.spb.ru

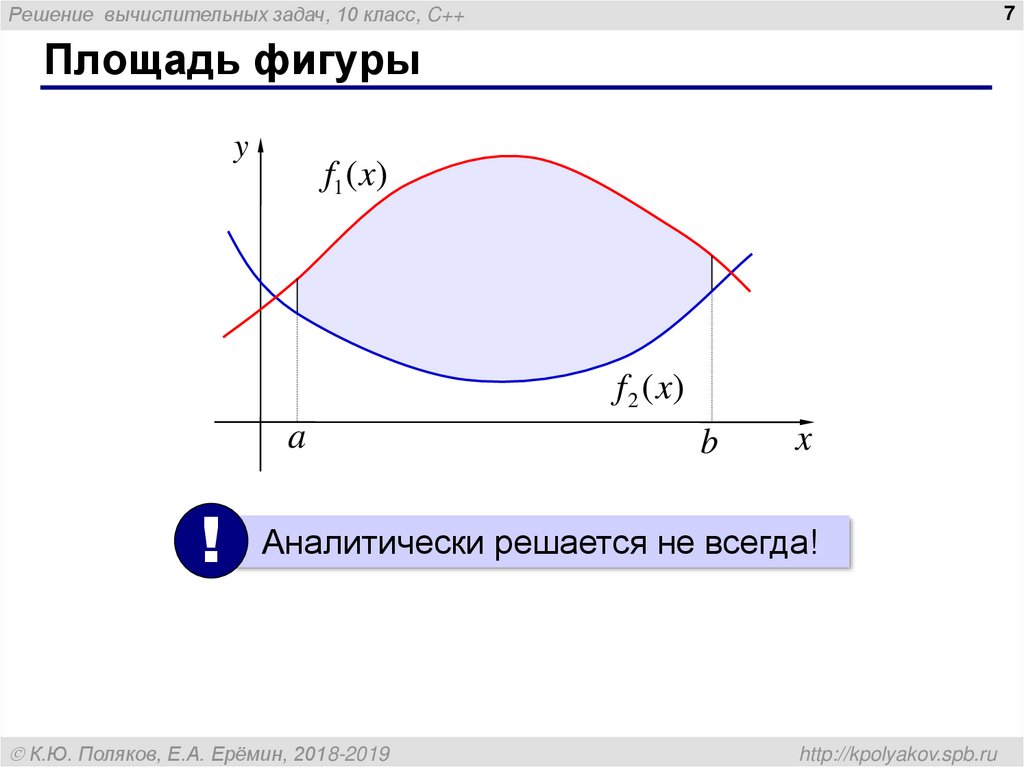
7. Площадь фигуры

Решение вычислительных задач, 10 класс, C++
7
Площадь фигуры
y
f1 ( x)
f 2 ( x)
a
!
b
x
Аналитически решается не всегда!
К.Ю. Поляков, Е.А. Ерёмин, 2018-2019
http://kpolyakov.spb.ru

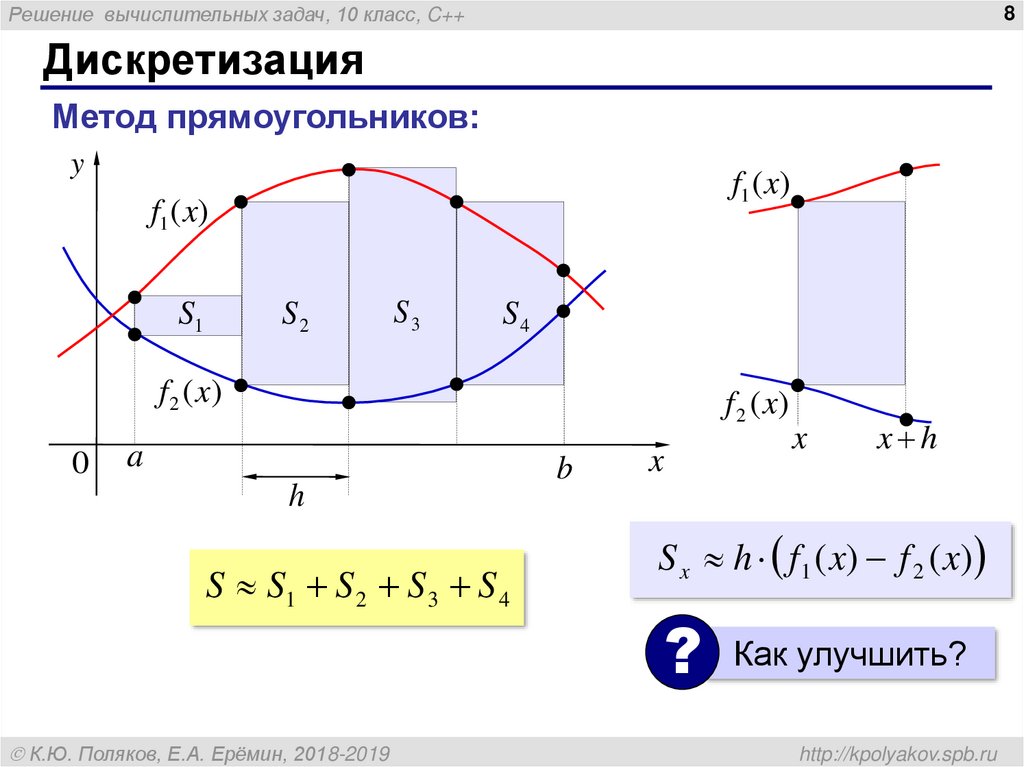
8. Дискретизация

Решение вычислительных задач, 10 класс, C++
8
Дискретизация
Метод прямоугольников:
y
f1 ( x)
f1 ( x)
S2
S1
S3
S4
f 2 ( x)
0
f 2 ( x)
a
h
S S1 S 2 S 3 S 4
К.Ю. Поляков, Е.А. Ерёмин, 2018-2019
b
x
x
x h
S x h f 1 ( x) f 2 ( x)
?
Как улучшить?
http://kpolyakov.spb.ru

9. Метод прямоугольников

Решение вычислительных задач, 10 класс, C++
9
Метод прямоугольников
Алгоритмический язык:
S:= 0; x:= a
нц пока x < b
S:= S + f1(x+h/2) - f2(x+h/2)
x:= x + h
кц
в середине
S:= h*S
отрезка [x, x+h]
вывод 'Площадь ', S
C++:
float S = 0, x = a;
while( x < b ) {
S += f1(x+h/2)- f2(x+h/2);
x += h;
}
S *= h;
cout << "Площадь " << fixed
<< setw(8) << setprecision(3) << S;
К.Ю. Поляков, Е.А. Ерёмин, 2018-2019
http://kpolyakov.spb.ru

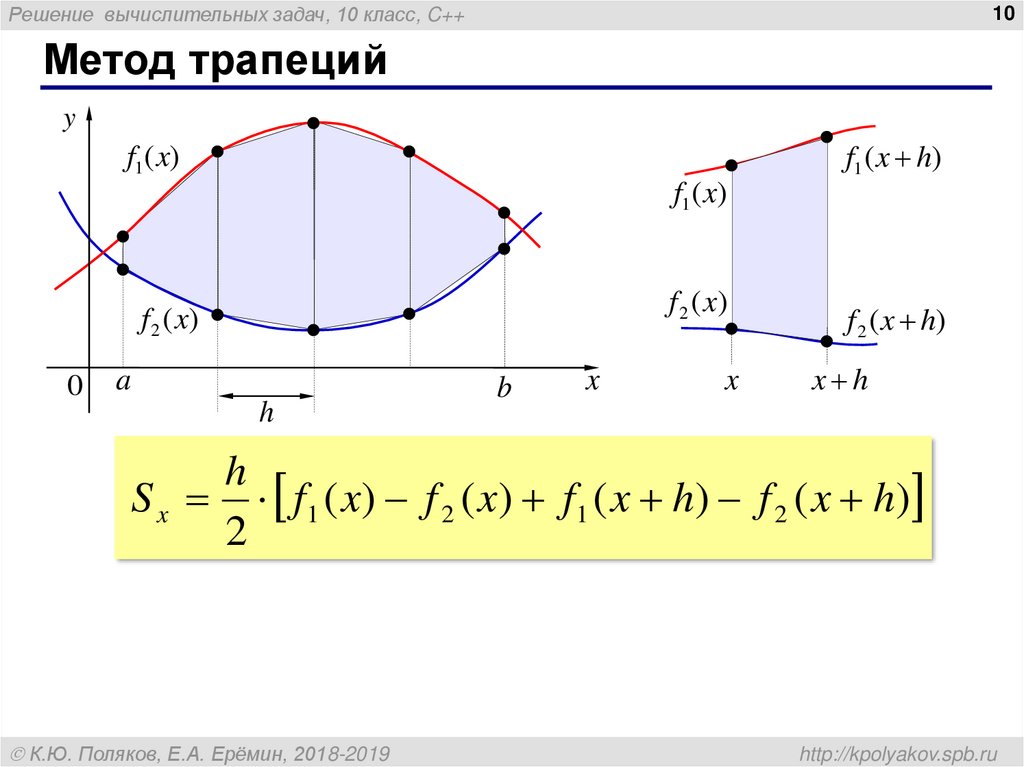
10. Метод трапеций

Решение вычислительных задач, 10 класс, C++
10
Метод трапеций
y
f1 ( x h)
f1 ( x)
f1 ( x)
f 2 ( x)
f 2 ( x)
0
a
h
b
x
x
f 2 ( x h)
x h
h
S x f 1 ( x ) f 2 ( x ) f 1 ( x h) f 2 ( x h)
2
К.Ю. Поляков, Е.А. Ерёмин, 2018-2019
http://kpolyakov.spb.ru

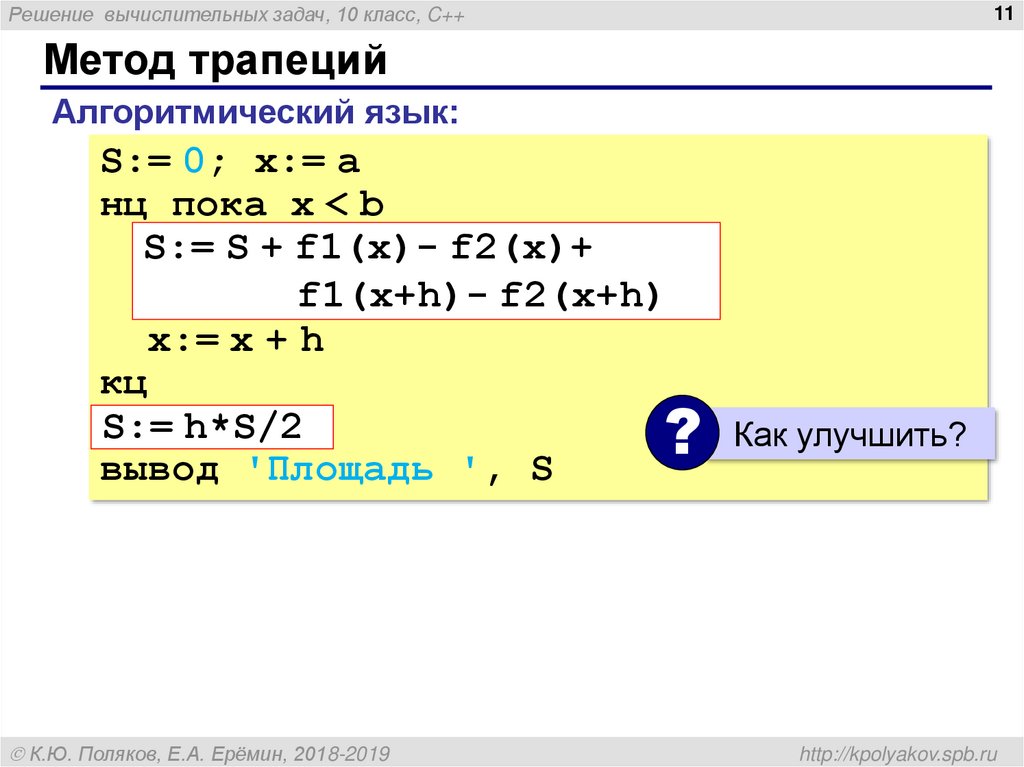
11. Метод трапеций

Решение вычислительных задач, 10 класс, C++
11
Метод трапеций
Алгоритмический язык:
S:= 0; x:= a
нц пока x < b
S:= S + f1(x)- f2(x)+
f1(x+h)- f2(x+h)
x:= x + h
кц
S:= h*S/2
Как улучшить?
?
вывод 'Площадь ', S
К.Ю. Поляков, Е.А. Ерёмин, 2018-2019
http://kpolyakov.spb.ru

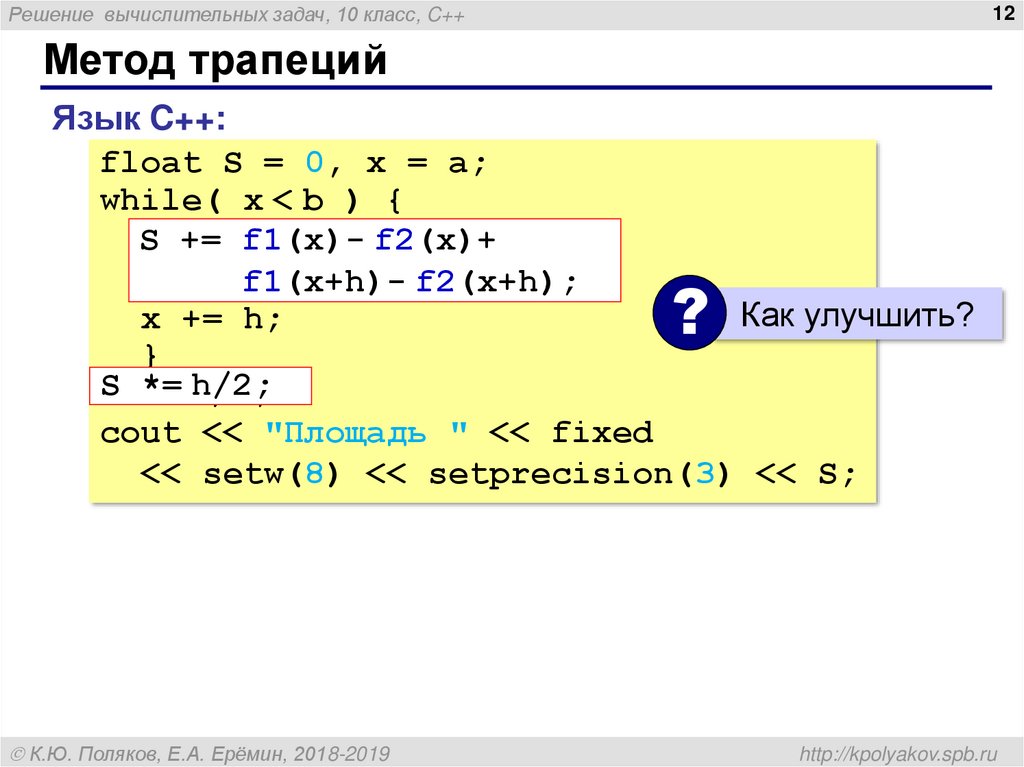
12. Метод трапеций

Решение вычислительных задач, 10 класс, C++
12
Метод трапеций
Язык C++:
float S = 0, x = a;
while( x < b ) {
f2(x) +
S += f1(x)- f2(x)+
f1(x+h)- f2(x+h);
Как улучшить?
x += h;
}
S *=
*= h/2;
h/2;
S
cout << "Площадь " << fixed
<< setw(8) << setprecision(3) << S;
?
К.Ю. Поляков, Е.А. Ерёмин, 2018-2019
http://kpolyakov.spb.ru