Решение вычислительных задач на компьютере

1. Решение вычислительных задач на компьютере

1
Решение
вычислительных
задач на компьютере
§ 69. Точность вычислений
§ 70. Решение уравнений
§ 71. Дискретизация
§ 72. Оптимизация
§ 73. Статистические расчёты
§ 74. Обработка результатов
эксперимента
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

2. Решение вычислительных задач на компьютере

2
Решение
вычислительных
задач на компьютере
§ 69. Точность вычислений
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

3. Погрешности измерений

Решение вычислительных задач, 10 класс
3
Погрешности измерений
«Недостатки математического образования с
наибольшей отчетливостью проявляются в
чрезмерной точности численных расчетов».
Карл Фридрих Гаусс.
Погрешность (ошибка) – отклонение измеренного или
вычисленного значения от истинного значения.
10
10
цена деления 0,1 см
9
9
8
8
7
7
6
6
5
5
4
3
2
1
К.Ю. Поляков, Е.А. Ерёмин, 2013
4
3
2
1
измерено
8,2 см
7,8 см
Толщина дна:
вычислено
0,4 см
фактически
8,1 ... 8,3 см
7,7 ... 7,9 см
фактически
0,2 ... 0,6 см
0,4 0,2 см
http://kpolyakov.spb.ru

4. Погрешности измерений

Решение вычислительных задач, 10 класс
4
Погрешности измерений
абсолютная
погрешность x
0,4 0,2
0,2 см
?
Можно ли оценить
точность измерений?
Относительная погрешность:
x
x *
x*
измеренное
истинное
значение
0,2
x
0,5 50%
0,4
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

5. Погрешности вычислений

Решение вычислительных задач, 10 класс
5
Погрешности вычислений
D 1,2 0,1 см
S
D2
S min
S ?
1,1309733552923255658465516179806...
4
1,12
0,950...
4
S 1,1 0,2 см
Smax
1,32
4
1,327...
0,2
x
100% 18%
1,1
Все практические расчеты выполняются неточно.
Погрешность результата вычислений определяется
погрешностью исходных данных.
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

6. Погрешности вычислений

Решение вычислительных задач, 10 класс
6
Погрешности вычислений
a 1000 0,001; b 0,002 0,001;
a c
x
c 1000 0,001; d 0,003 0,001.
b d
0,001
0,001
0,001
50% b
33%
a c
0,01% b
0,002
0,003
1000
1000 1000
неточные числа
x
166667
0,002 0,003
в знаменателе
1000 1000
xmax
750000
0,001 0,004
750000 166667
x
352%
1000 1000
166667
xmin
166667
0,003 0,002
Метод вычислительно неустойчив: малые погрешности
в исходных данных могут привести к большим
погрешностям в решении.
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

7. Источники погрешностей

Решение вычислительных задач, 10 класс
7
Источники погрешностей
• неточность исходных данных
• неточность записи вещественных чисел в двоичном
коде конечной длины
• погрешности приближенного вычисления некоторых
стандартных функций (sin, cos, …)
• накопление погрешностей при арифметических
действиях с неточными данными
• погрешность метода
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

8. Решение вычислительных задач на компьютере

8
Решение
вычислительных
задач на компьютере
§ 70. Решение уравнений
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

9. Методы решения уравнений

Решение вычислительных задач, 10 класс
9
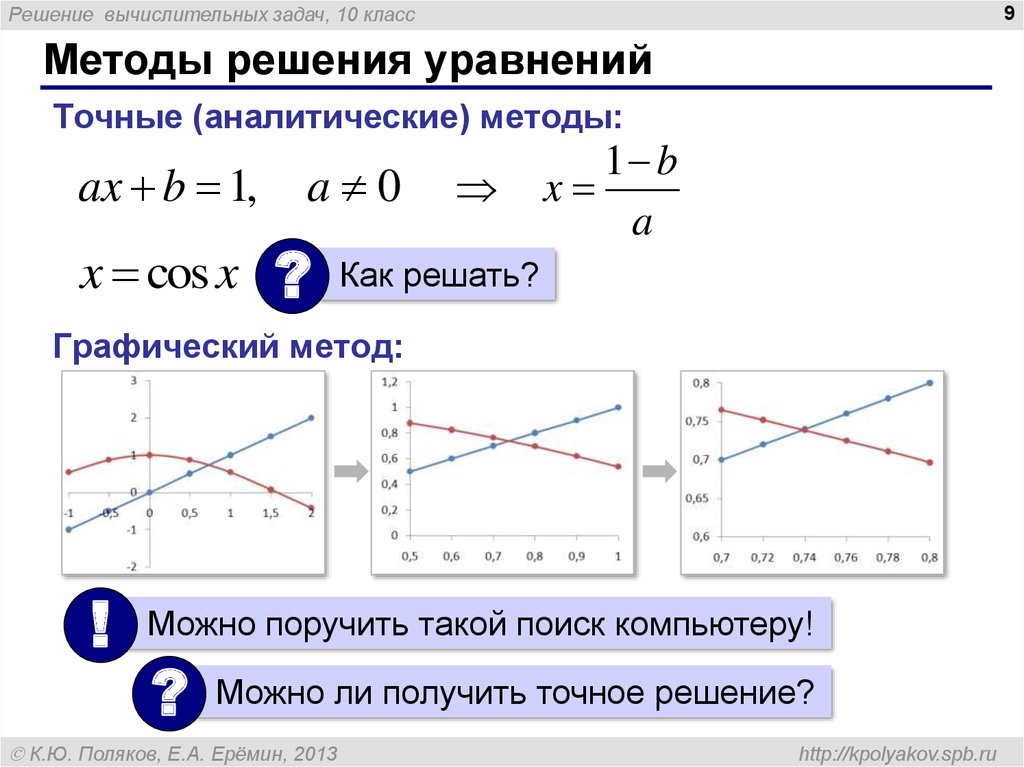
Методы решения уравнений
Точные (аналитические) методы:
ax b 1,
x cos x
a 0
?
1 b
x
a
Как решать?
Графический метод:
!
Можно поручить такой поиск компьютеру!
?
Можно ли получить точное решение?
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

10. Приближённые методы

Решение вычислительных задач, 10 класс
10
Приближённые методы
Сжатие отрезка:
1) выбрать начальный отрезок [a0, b0] (одно решение!)
2) уточнить решение с помощью некоторого
алгоритма: [a, b]
3) повторять шаг 2, пока длина отрезка [a, b] не станет
достаточно мала
a
?
x
a b
2
?
b
Как оценить ошибку?
Завершение работы:
К.Ю. Поляков, Е.А. Ерёмин, 2013
Что лучше выбрать в
качестве решения?
b a
x x
2
b a 2
*
допустимая
ошибка
http://kpolyakov.spb.ru

11. Приближенные методы

Решение вычислительных задач, 10 класс
11
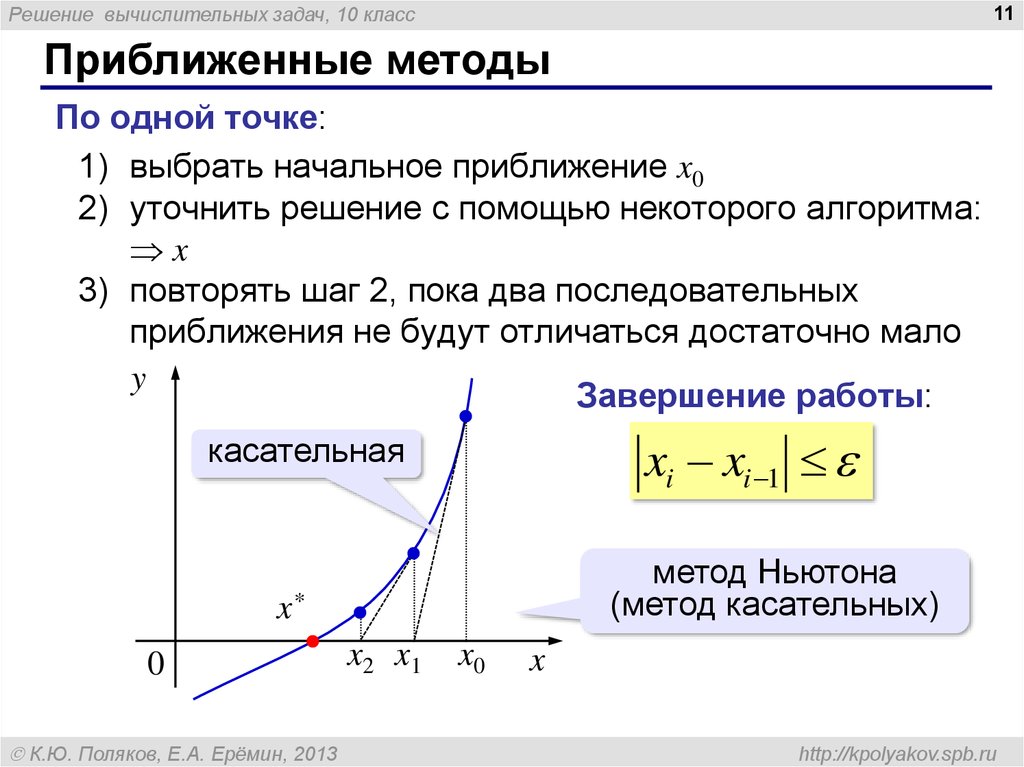
Приближенные методы
По одной точке:
1) выбрать начальное приближение x0
2) уточнить решение с помощью некоторого алгоритма:
x
3) повторять шаг 2, пока два последовательных
приближения не будут отличаться достаточно мало
y
Завершение работы:
xi xi 1
касательная
метод Ньютона
(метод касательных)
x*
0
К.Ю. Поляков, Е.А. Ерёмин, 2013
x2 x1
x0
x
http://kpolyakov.spb.ru

12. Приближенные методы

Решение вычислительных задач, 10 класс
12
Приближенные методы
Итерационные методы (лат. iteratio – повторение) –
основаны на многократном выполнении одинаковых
шагов, каждый из которых уточняет решение.
xk 1 f ( xk )
следующее
приближение
предыдущее
приближение
дают какое-то решение, если точное неизвестно
могут давать меньшие ошибки, чем вычисления по
точным формулам
решение приближенное: x
= 1,23345
ответ – число (зависимость от параметра?)
большой объем вычислений
не всегда просто оценить погрешность
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

13. Метод перебора

Решение вычислительных задач, 10 класс
13
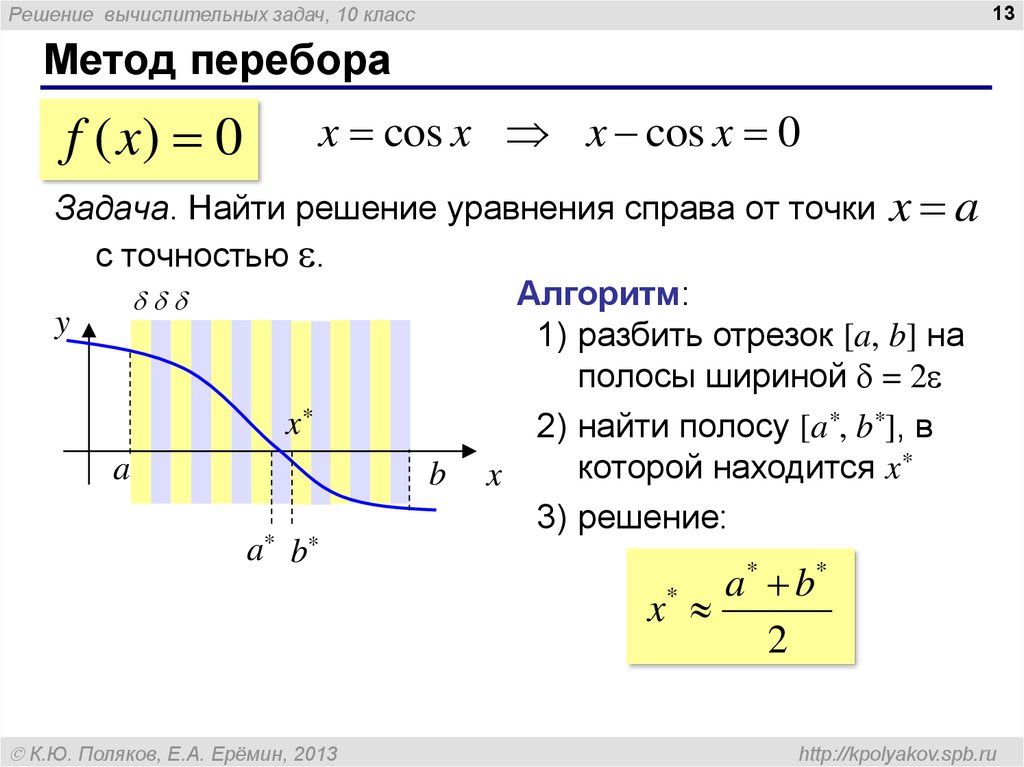
Метод перебора
f ( x) 0
x cos x x cos x 0
Задача. Найти решение уравнения справа от точки x a
с точностью .
Алгоритм:
y
1) разбить отрезок [a, b] на
полосы шириной = 2
x*
2) найти полосу [a*, b*], в
которой находится x*
a
b x
3) решение:
a* b*
*
*
a b
x
2
*
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

14. Есть ли решение на [x, x+ ]?

Решение вычислительных задач, 10 класс
14
Есть ли решение на [x, x+ ]?
нет решения
y
есть решение!
y
x*
0
x
x+
x
f ( x) 0
f (x ) 0
0
x*
x
нет решения
y
x+
x
x*
0
x
x
?
f ( x) 0
В чём отличие?
f (x ) 0
x+
f ( x) 0
f (x ) 0
f ( x) f ( x ) 0
!
Если непрерывная функция f (x) имеет разные знаки
на концах интервала [a, b], то в некоторой точке x*
внутри [a, b] она равна 0, то есть f (x* ) = 0!
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

15. Метод перебора (a = 0)

Решение вычислительных задач, 10 класс
15
Метод перебора (a = 0)
алг Перебор
нач
вещ eps, x, delta
eps:= 0.001
x:= 0 | x:= a
Когда остановится?
delta:= 2*eps
нц пока f(x)*f(x+delta) > 0
x:= x + delta
Зацикливание?
кц
вывод 'x = ', x+eps
кон
?
?
алг вещ f( вещ x )
нач
знач:= x - cos(x)
кон
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

16. Метод перебора (a = 0)

Решение вычислительных задач, 10 класс
16
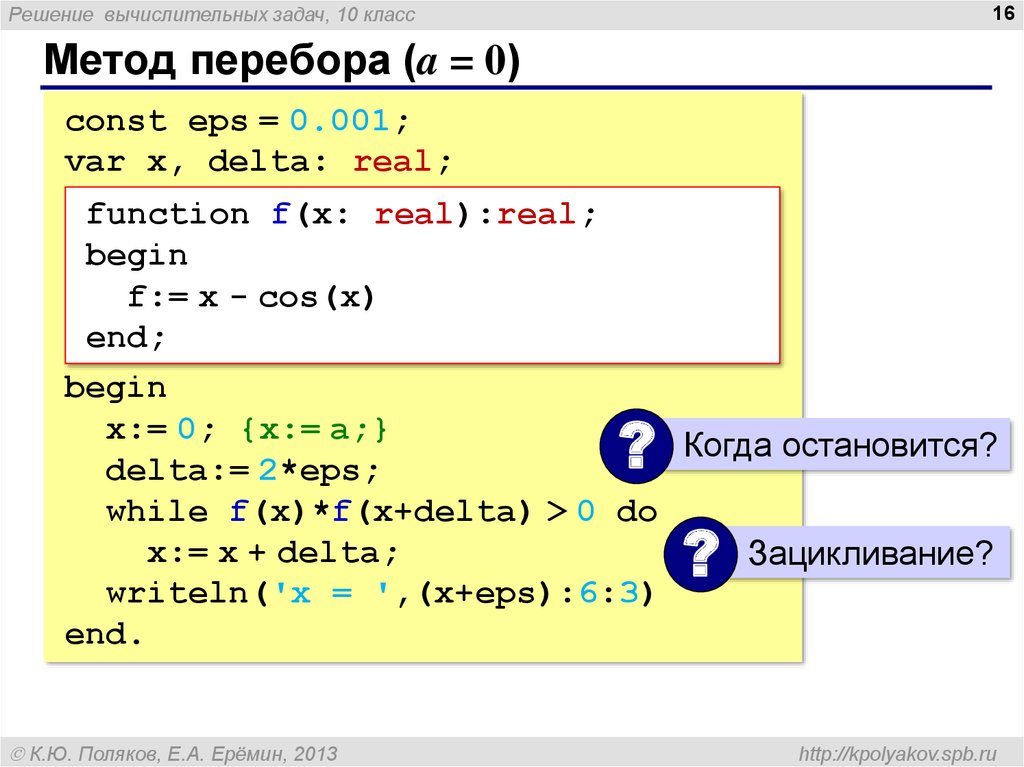
Метод перебора (a = 0)
const eps = 0.001;
var x, delta: real;
function f(x: real):real;
begin
f:= x - cos(x)
end;
begin
x:= 0; {x:= a;}
Когда остановится?
delta:= 2*eps;
while f(x)*f(x+delta) > 0 do
x:= x + delta;
Зацикливание?
writeln('x = ',(x+eps):6:3)
end.
?
?
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

17. Метод перебора

Решение вычислительных задач, 10 класс
17
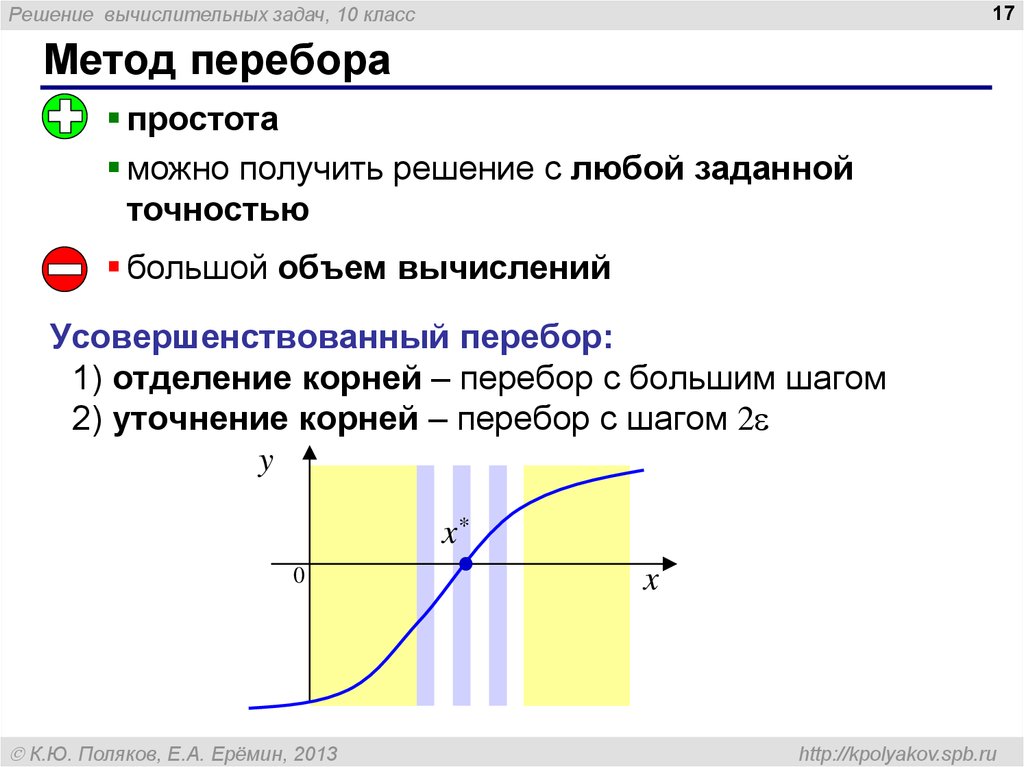
Метод перебора
простота
можно получить решение с любой заданной
точностью
большой объем вычислений
Усовершенствованный перебор:
1) отделение корней – перебор с большим шагом
2) уточнение корней – перебор с шагом 2
y
x*
0
К.Ю. Поляков, Е.А. Ерёмин, 2013
x
http://kpolyakov.spb.ru

18. Метод деления отрезка пополам

Решение вычислительных задач, 10 класс
18
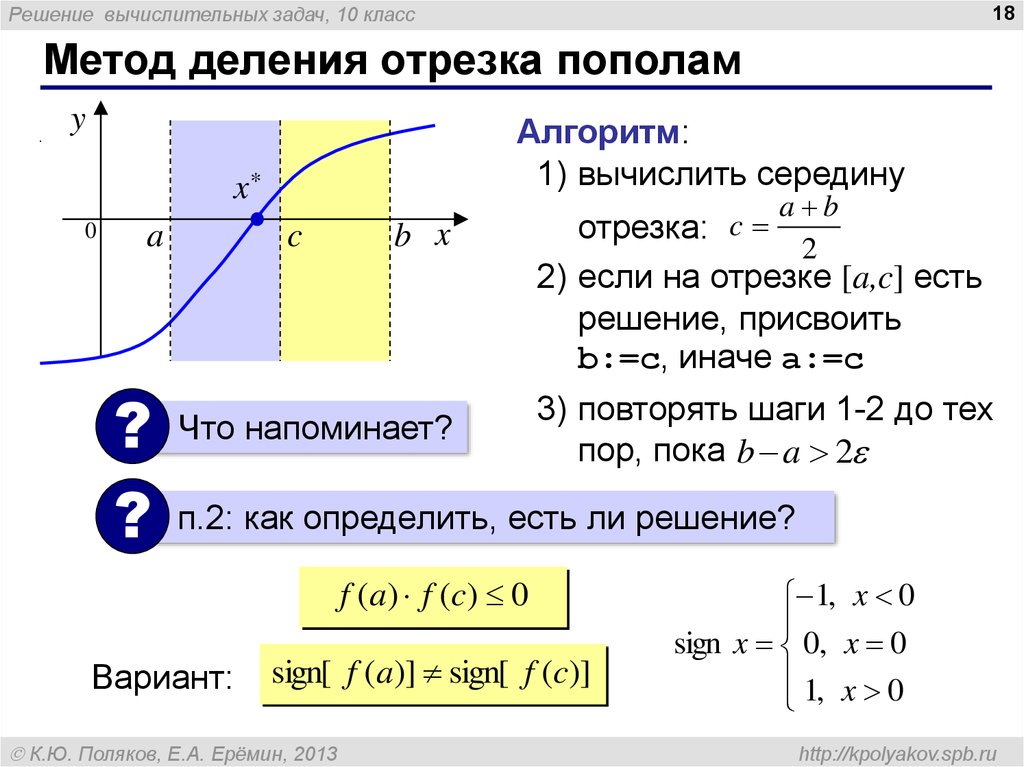
Метод деления отрезка пополам
.
y
Алгоритм:
1) вычислить середину
x*
0
c
a
b x
отрезка: c
a b
2
2) если на отрезке [a,c] есть
решение, присвоить
b:=c, иначе a:=c
?
?
Что напоминает?
3) повторять шаги 1-2 до тех
пор, пока b a 2
п.2: как определить, есть ли решение?
f ( a ) f (c ) 0
Вариант:
sign[ f (a)] sign[ f (c)]
К.Ю. Поляков, Е.А. Ерёмин, 2013
1, x 0
sign x 0, x 0
1, x 0
http://kpolyakov.spb.ru

19. Метод деления отрезка пополам

Решение вычислительных задач, 10 класс
19
Метод деления отрезка пополам
.
Алгоритмический язык:
delta:= 2*eps
нц пока b - a > delta
c:= (a + b) / 2
если f(a)*f(c) <= 0 то
b:= c
sign(f(a)) <> sign(f(c))
иначе
a:= c
все
кц
вывод 'x = ', (a+b)/2
?
Как меняется длина отрезка?
?
За сколько шагов уменьшится в 1000 раз?
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

20. Метод деления отрезка пополам

Решение вычислительных задач, 10 класс
20
Метод деления отрезка пополам
.
Паскаль:
delta:= 2*eps;
while b - a > delta do begin
c:= (a + b) / 2;
if f(a)*f(c) <= 0 then
b:= c
else a:= c;
end;
writeln('x = ', (a+b)/2:6:3);
?
Как меняется длина отрезка?
?
За сколько шагов уменьшится в 1000 раз?
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

21. Полёт мяча

Решение вычислительных задач, 10 класс
21
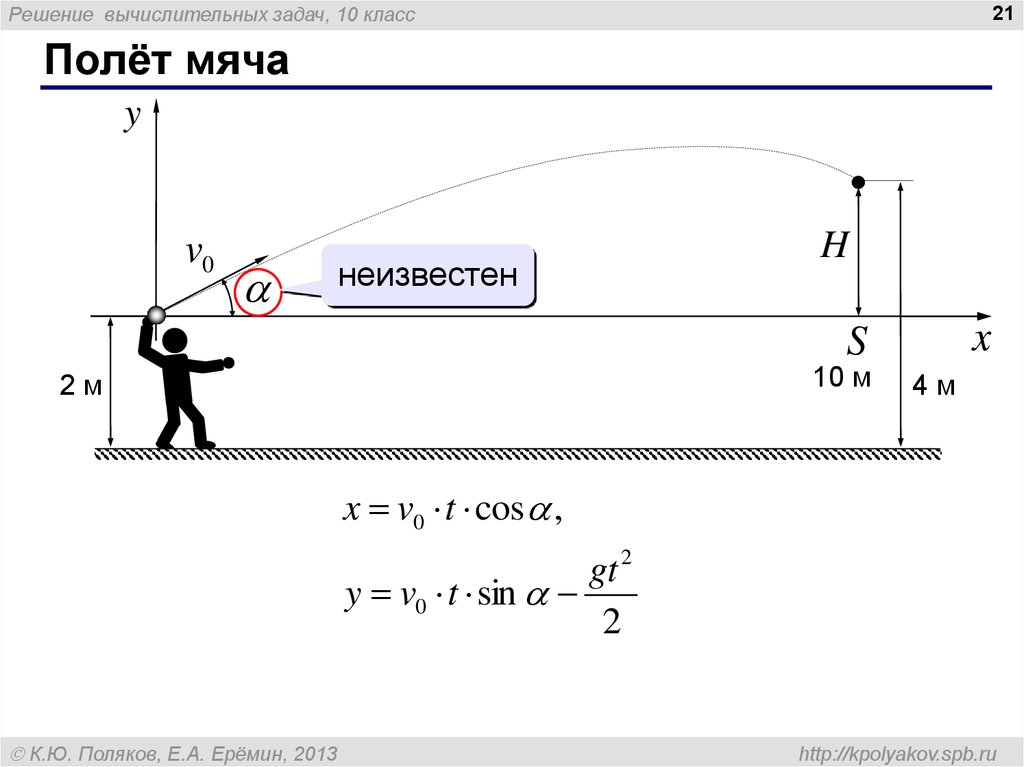
Полёт мяча
y
v0
неизвестен
H
x
S
10 м
2м
4м
x v0 t cos ,
gt 2
y v0 t sin
2
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

22. Полёт мяча

Решение вычислительных задач, 10 класс
22
Полёт мяча
Задача. Найти угол (и время t) при котором x = S и y = H:
gt 2
S v0 t cos , H v0 t sin
2
Решение:
S
t
v0 cos
v0 S sin
g S2
H
2
v0 cos
2v0 cos 2
g S2
f ( ) S tg 2
H 0
2
2v0 cos
Диапазон углов для поиска: [0 ...90 ] 0...
2
Как уточнить?
?
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

23. Уточнение диапазона углов

Решение вычислительных задач, 10 класс
23
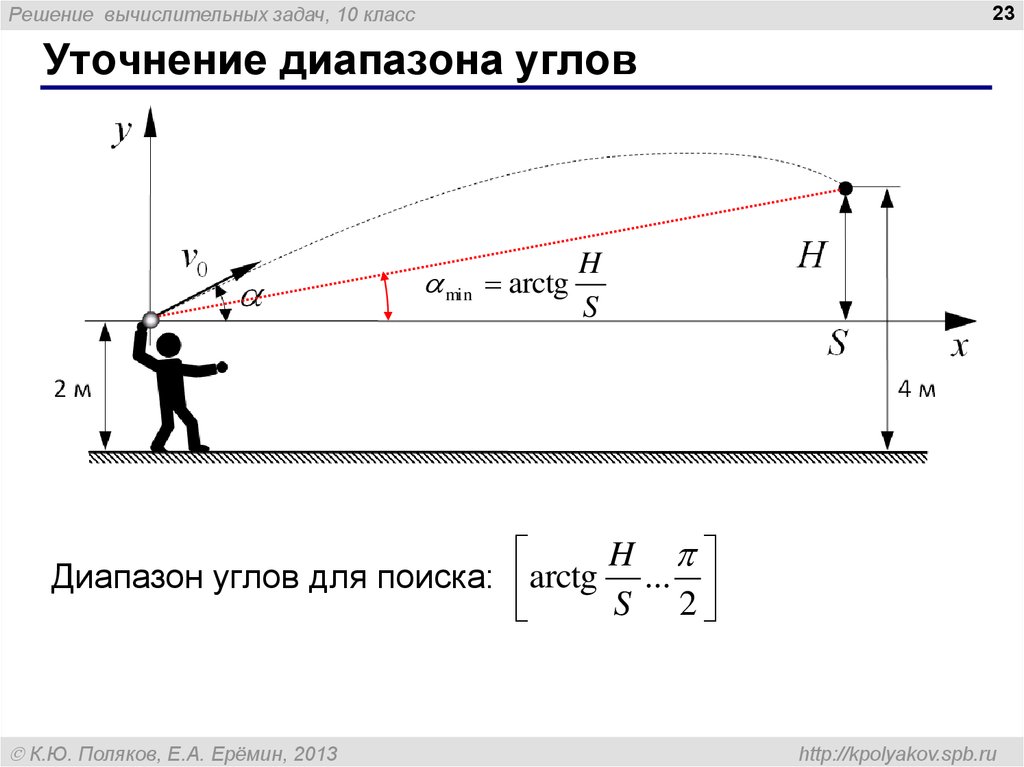
Уточнение диапазона углов
min arctg
H
S
H
Диапазон углов для поиска: arctg ...
S 2
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

24. Полёт мяча

Решение вычислительных задач, 10 класс
24
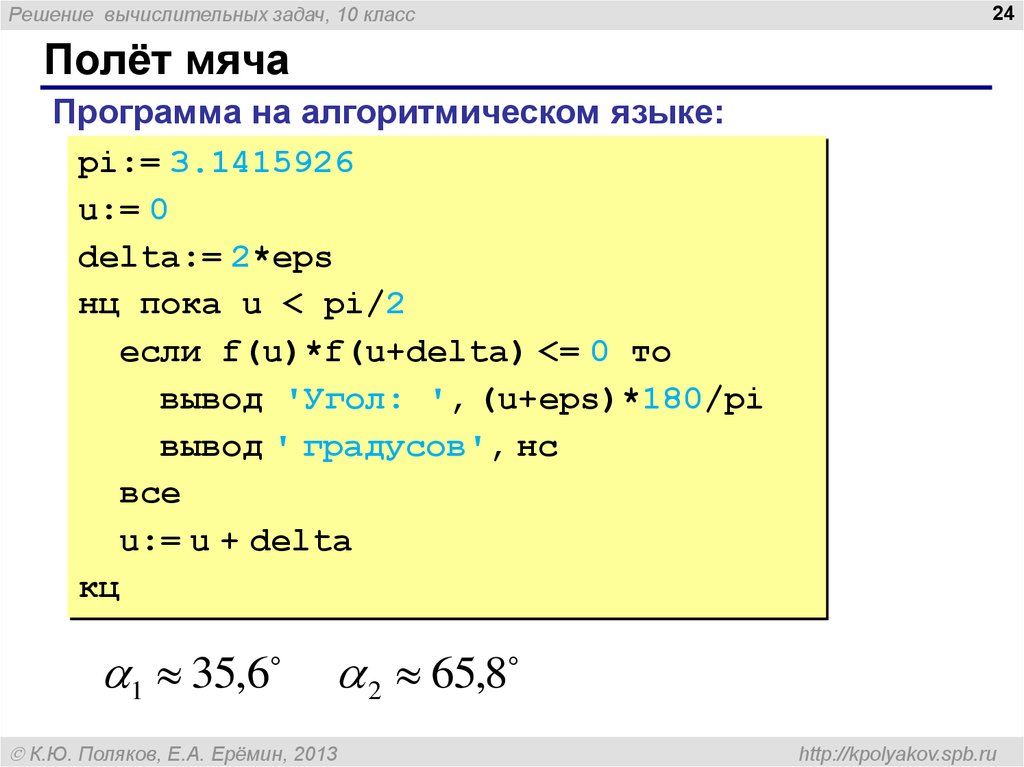
Полёт мяча
Программа на алгоритмическом языке:
pi:= 3.1415926
u:= 0
delta:= 2*eps
нц пока u < pi/2
если f(u)*f(u+delta) <= 0 то
вывод 'Угол: ', (u+eps)*180/pi
вывод ' градусов', нс
все
u:= u + delta
кц
1 35,6
2 65,8
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

25. Полёт мяча

Решение вычислительных задач, 10 класс
25
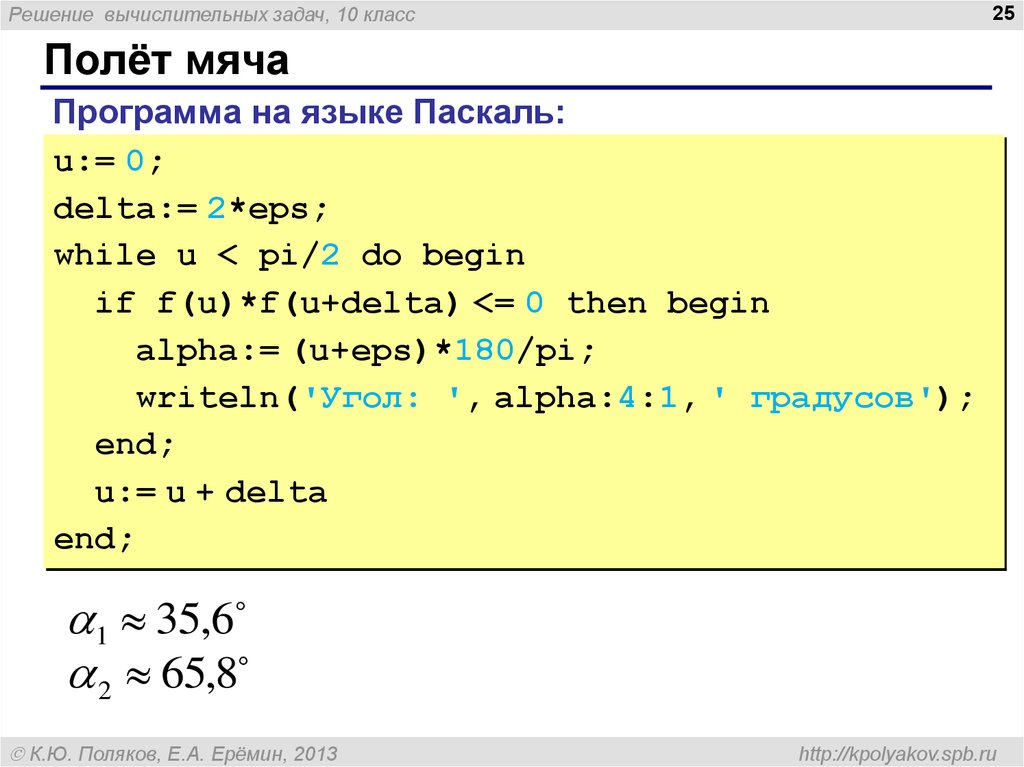
Полёт мяча
Программа на языке Паскаль:
u:= 0;
delta:= 2*eps;
while u < pi/2 do begin
if f(u)*f(u+delta) <= 0 then begin
alpha:= (u+eps)*180/pi;
writeln('Угол: ', alpha:4:1, ' градусов');
end;
u:= u + delta
end;
1 35,6
2 65,8
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

26. Полёт мяча

Решение вычислительных задач, 10 класс
26
Полёт мяча
Использование табличного процессора:
имя ячейки
или диапазона
Диапазон углов:
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

27. Полёт мяча

Решение вычислительных задач, 10 класс
27
Полёт мяча
S $B$1
Excel: РАДИАНЫ
Диаграмма XY:
Excel: Точечная
1 35
2 65
К.Ю. Поляков, Е.А. Ерёмин, 2013
3
2
1
0
-1
10
20
30
40
50
60
-2
-3
-4
-5
-6
http://kpolyakov.spb.ru

28. Полёт мяча

Решение вычислительных задач, 10 класс
28
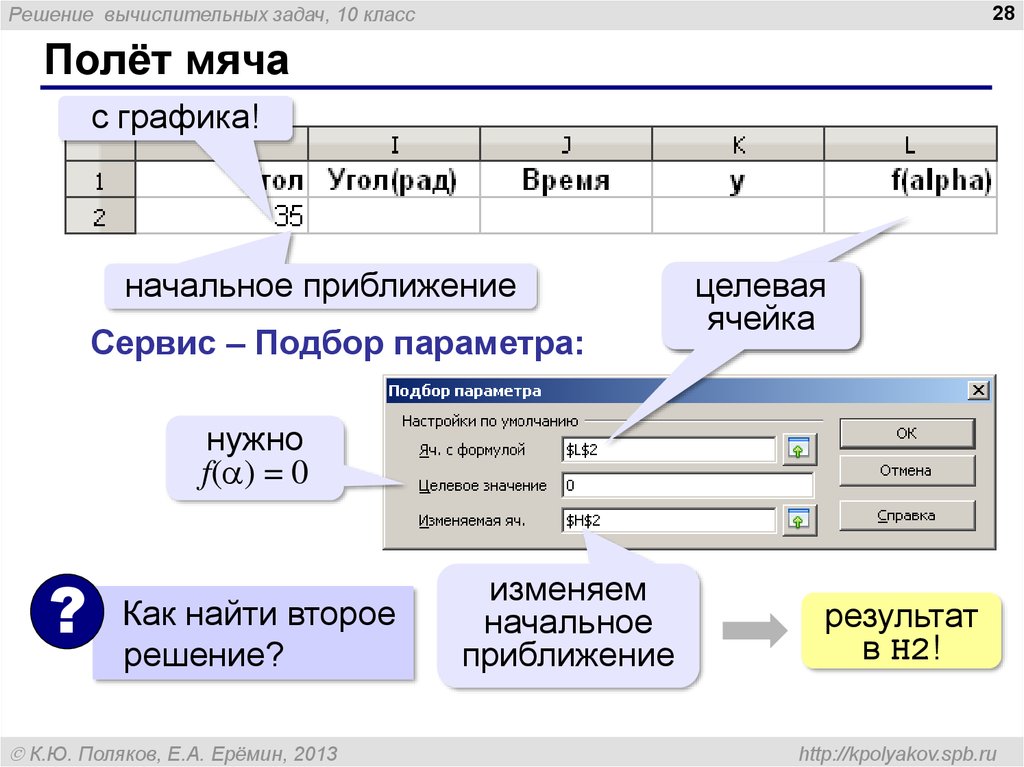
Полёт мяча
с графика!
начальное приближение
Сервис – Подбор параметра:
целевая
ячейка
нужно
f( ) = 0
?
Как найти второе
решение?
К.Ю. Поляков, Е.А. Ерёмин, 2013
изменяем
начальное
приближение
результат
в H2!
http://kpolyakov.spb.ru

29. Решение вычислительных задач на компьютере

29
Решение
вычислительных
задач на компьютере
§ 71. Дискретизация
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

30. Вычисление длины линии

Решение вычислительных задач, 10 класс
30
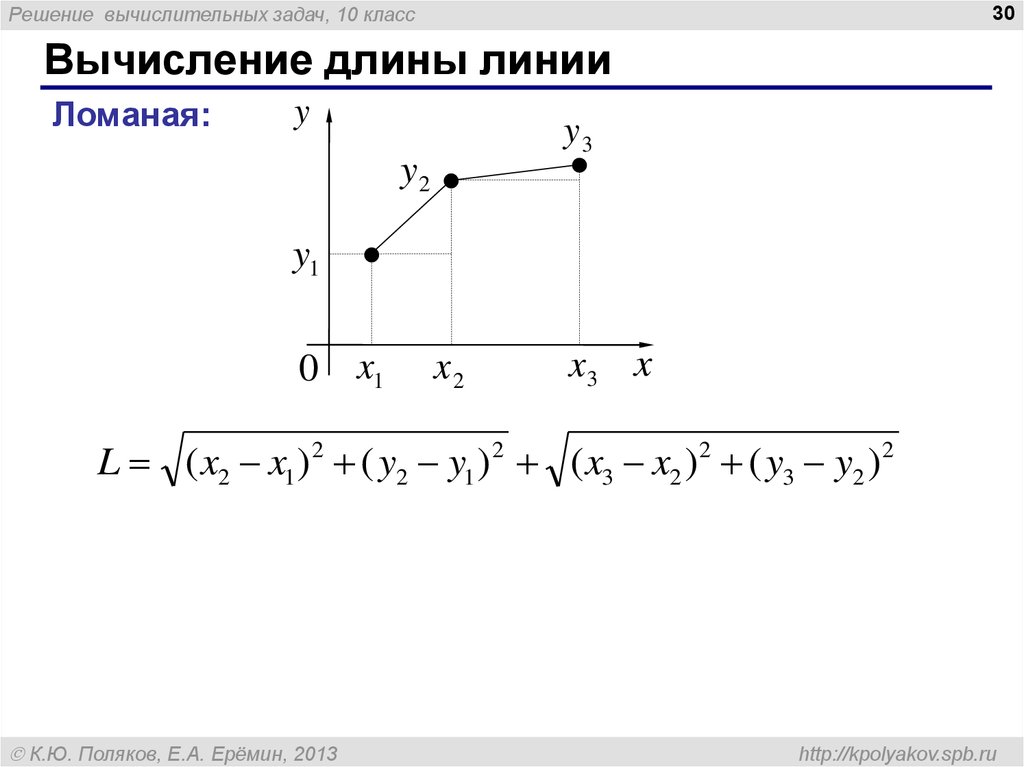
Вычисление длины линии
Ломаная:
y
y3
y2
y1
0 x1
x2
x3 x
L ( x2 x1 )2 ( y2 y1 )2 ( x3 x2 )2 ( y3 y2 )2
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

31. Вычисление длины линии

Решение вычислительных задач, 10 класс
31
Вычисление длины линии
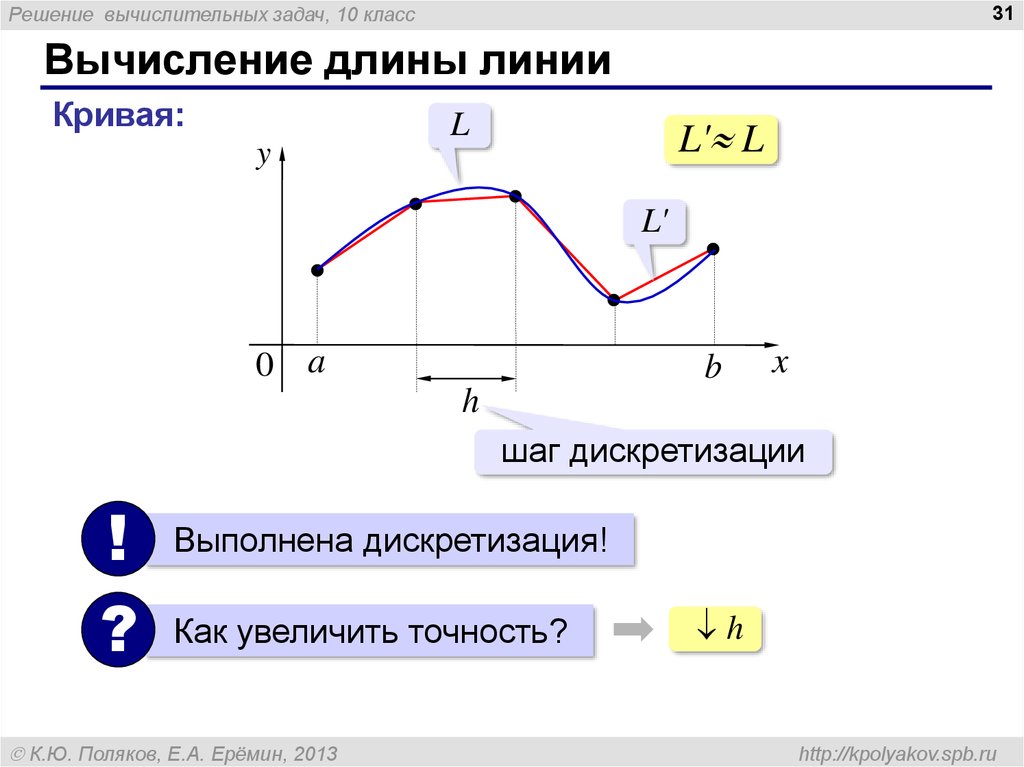
Кривая:
L' L
L
y
L'
0
a
b
x
h
шаг дискретизации
!
?
Выполнена дискретизация!
Как увеличить точность?
К.Ю. Поляков, Е.А. Ерёмин, 2013
h
http://kpolyakov.spb.ru

32. Дискретизация

Решение вычислительных задач, 10 класс
32
Дискретизация
• цель – представить задачу в виде, пригодном для
компьютерных расчётов
• есть потеря информации
• методы приближённые
• для уменьшения погрешности нужно уменьшать шаг
дискретизации
Что ухудшится?
?
• при малом шаге на результат могут сильно влиять
погрешности вычислений
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

33. Вычисление длины кривой

Решение вычислительных задач, 10 класс
33
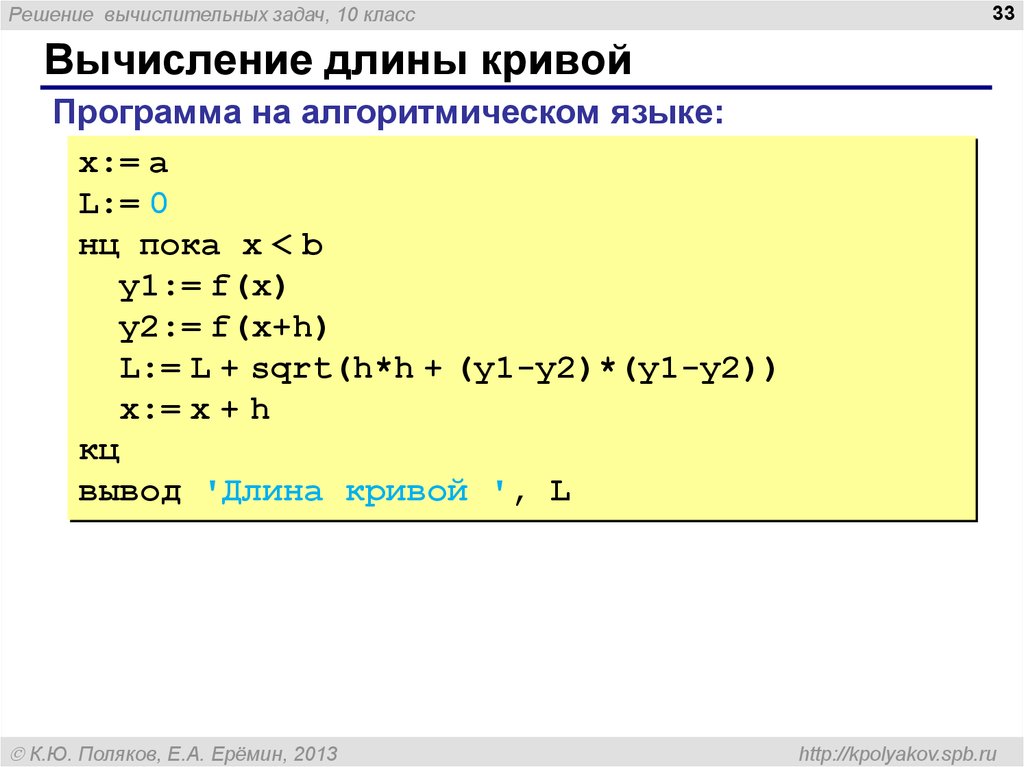
Вычисление длины кривой
Программа на алгоритмическом языке:
x:= a
L:= 0
нц пока x < b
y1:= f(x)
y2:= f(x+h)
L:= L + sqrt(h*h + (y1-y2)*(y1-y2))
x:= x + h
кц
вывод 'Длина кривой ', L
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

34. Вычисление длины кривой

Решение вычислительных задач, 10 класс
34
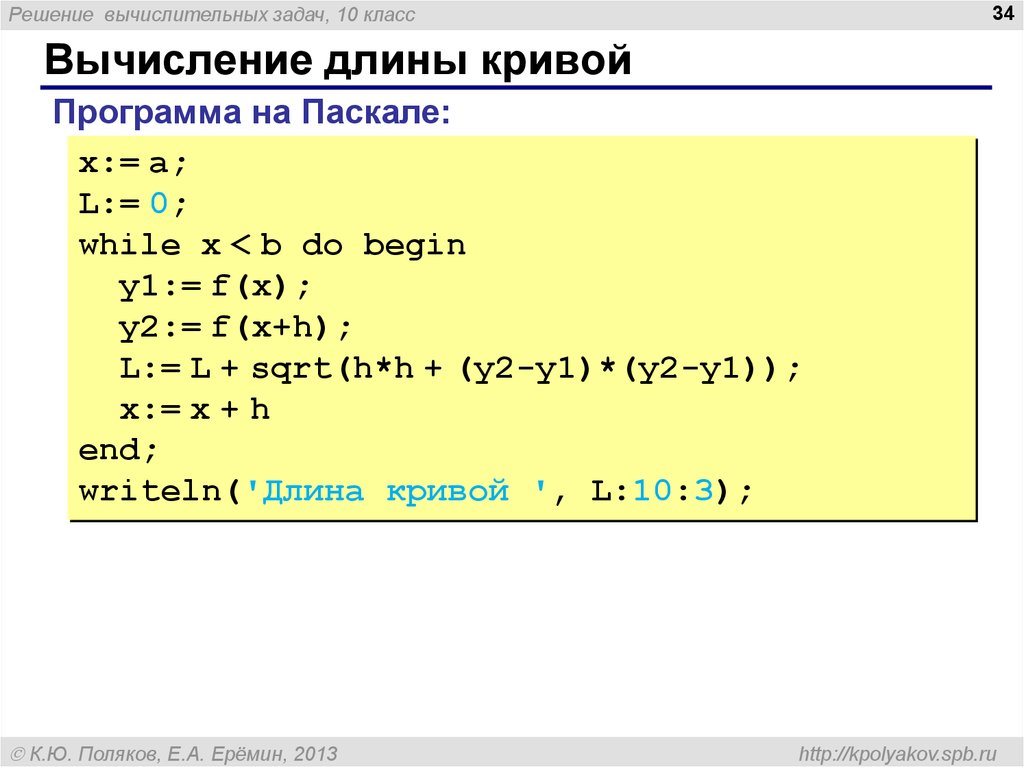
Вычисление длины кривой
Программа на Паскале:
x:= a;
L:= 0;
while x < b do begin
y1:= f(x);
y2:= f(x+h);
L:= L + sqrt(h*h + (y2-y1)*(y2-y1));
x:= x + h
end;
writeln('Длина кривой ', L:10:3);
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

35. Площадь фигуры

Решение вычислительных задач, 10 класс
35
Площадь фигуры
y
f1 ( x)
f 2 ( x)
a
!
b
x
Аналитически решается не всегда!
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

36. Дискретизация

Решение вычислительных задач, 10 класс
36
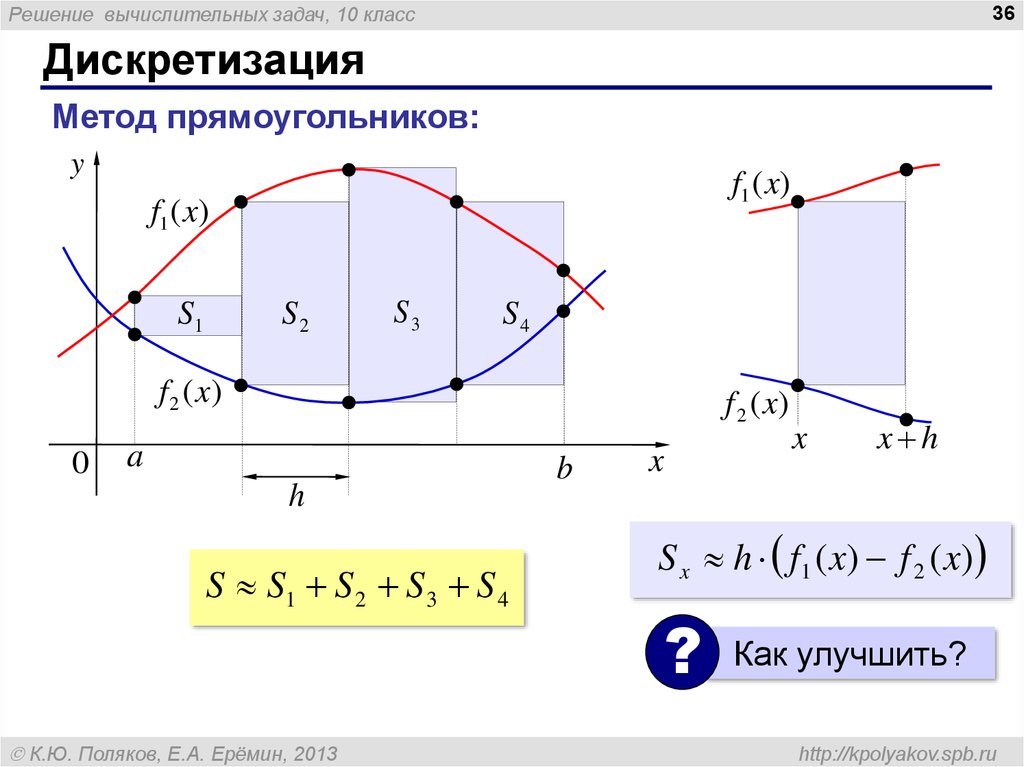
Дискретизация
Метод прямоугольников:
y
f1 ( x)
f1 ( x)
S2
S1
S3
S4
f 2 ( x)
0
f 2 ( x)
a
h
S S1 S 2 S 3 S 4
К.Ю. Поляков, Е.А. Ерёмин, 2013
b
x
x
x h
S x h f 1 ( x) f 2 ( x)
?
Как улучшить?
http://kpolyakov.spb.ru

37. Метод прямоугольников

Решение вычислительных задач, 10 класс
37
Метод прямоугольников
Алгоритмический язык:
S:= 0; x:= a
нц пока x < b
S:= S + f1(x+h/2) - f2(x+h/2)
x:= x + h
кц
в середине
S:= h*S
отрезка [x, x+h]
вывод 'Площадь ', S
Паскаль:
S:= 0; x:= a;
while x < b do begin
S:= S + f1(x+h/2)- f2(x+h/2);
x:= x + h
end;
S:= h*S;
writeln('Площадь ', S:8:3);
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

38. Метод трапеций

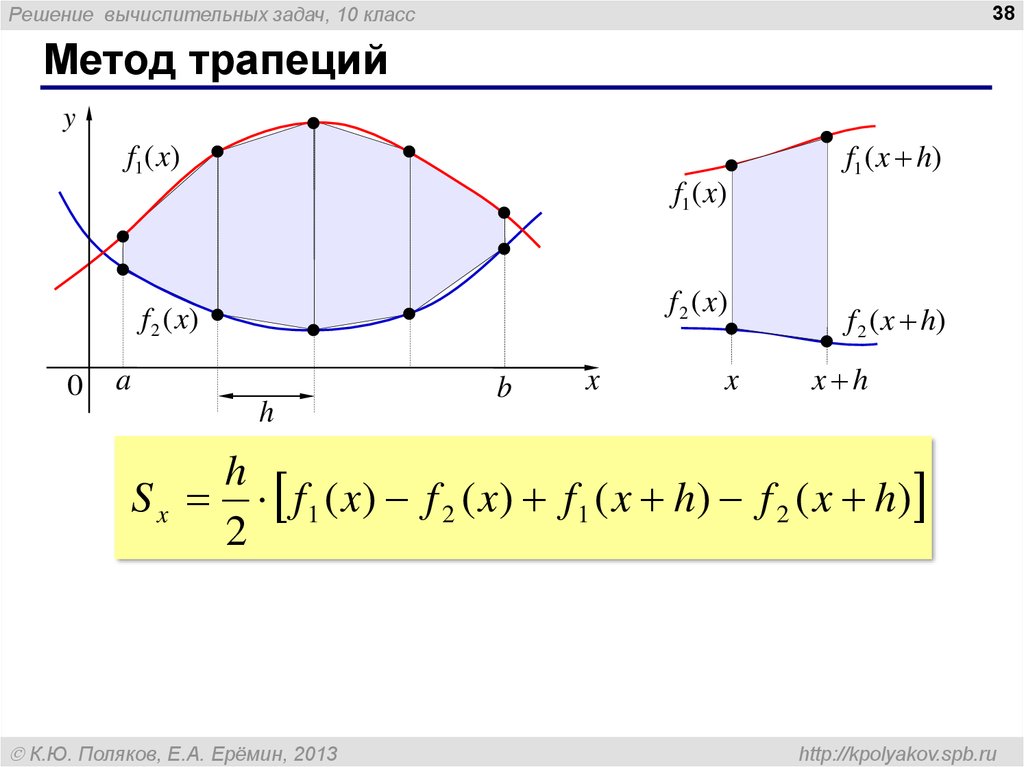
Решение вычислительных задач, 10 класс
38
Метод трапеций
y
f1 ( x h)
f1 ( x)
f1 ( x)
f 2 ( x)
f 2 ( x)
0
a
h
b
x
x
f 2 ( x h)
x h
h
S x f 1 ( x ) f 2 ( x ) f 1 ( x h) f 2 ( x h)
2
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

39. Метод трапеций

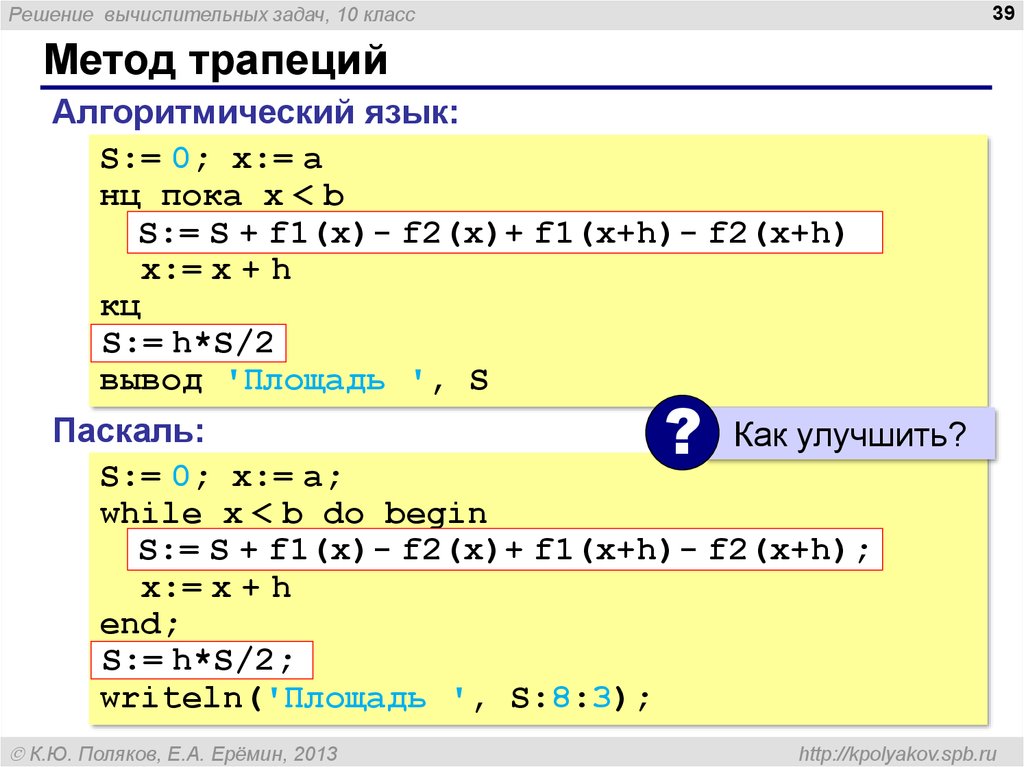
Решение вычислительных задач, 10 класс
39
Метод трапеций
Алгоритмический язык:
S:= 0; x:= a
нц пока x < b
S:= S + f1(x)- f2(x)+ f1(x+h)- f2(x+h)
x:= x + h
кц
S:= h*S/2
вывод 'Площадь ', S
?
Паскаль:
Как улучшить?
S:= 0; x:= a;
while x < b do begin
S:= S + f1(x)- f2(x)+ f1(x+h)- f2(x+h);
x:= x + h
end;
S:= h*S/2;
writeln('Площадь ', S:8:3);
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

40. Решение вычислительных задач на компьютере

40
Решение
вычислительных
задач на компьютере
§ 72. Оптимизация
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

41. Что такое оптимизация?

Решение вычислительных задач, 10 класс
41
Что такое оптимизация?
Оптимизация – это поиск наилучшего (оптимального)
решения задачи в заданных условиях.
1) Цель: выбрать неизвестный x, так чтобы
f ( x) min
или
целевая функция
f ( x) max
f ( x) min
2) Ограничения
задача
оптимизации
?
Почему неправильно «самый оптимальный»?
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

42. Что такое минимум?

Решение вычислительных задач, 10 класс
42
Что такое минимум?
f (x)
локальный
минимум
глобальный
минимум
x
• обычно нужно найти глобальный минимум
• большинство численных методов находят только
локальный минимум
!
Результат локальной оптимизации зависит от
начального приближения!
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

43. Метод дихотомии

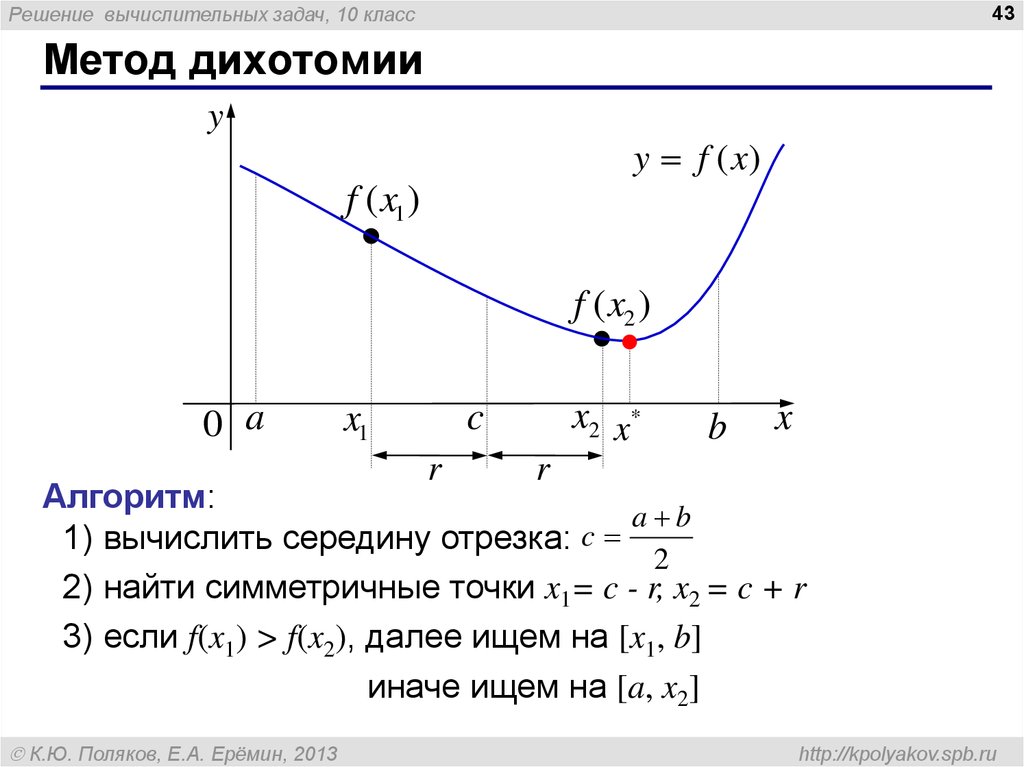
Решение вычислительных задач, 10 класс
43
Метод дихотомии
y
y f (x)
f ( x1 )
f ( x2 )
0 a
x2 x*
c
x1
r
b
x
r
Алгоритм:
a b
c
1) вычислить середину отрезка:
2
2) найти симметричные точки x1= c - r, x2 = c + r
3) если f(x1) > f(x2), далее ищем на [x1, b]
иначе ищем на [a, x2]
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

44. Метод дихотомии

Решение вычислительных задач, 10 класс
44
Метод дихотомии
a b
c
x1 c r , x 2 c r
2
?
Как выбрать r?
b a
0 r
r k (b a), 0 k 0,5
2
Уменьшение интервала:
стало
было
b a
k (b a) (0,5 k ) (b a )
2
!
Выгоднее выбирать k близко к нулю!
?
К.Ю. Поляков, Е.А. Ерёмин, 2013
Почему нельзя k = 0?
http://kpolyakov.spb.ru

45. Метод дихотомии

Решение вычислительных задач, 10 класс
45
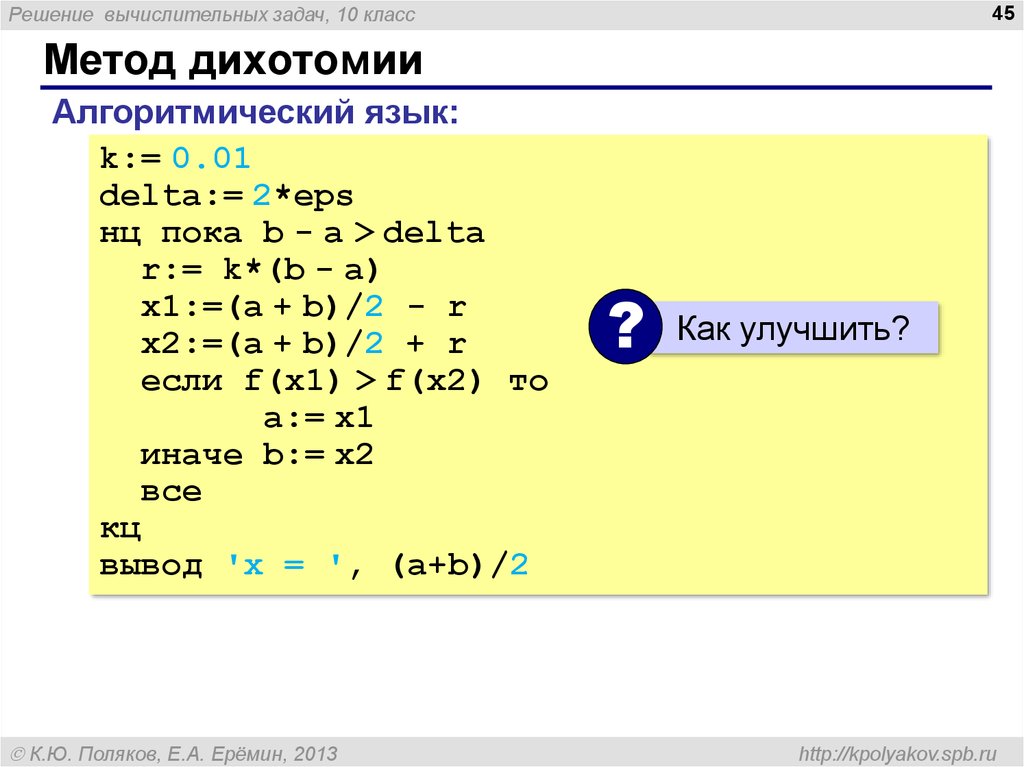
Метод дихотомии
Алгоритмический язык:
k:= 0.01
delta:= 2*eps
нц пока b - a > delta
r:= k*(b - a)
x1:=(a + b)/2 - r
x2:=(a + b)/2 + r
если f(x1) > f(x2) то
a:= x1
иначе b:= x2
все
кц
вывод 'x = ', (a+b)/2
К.Ю. Поляков, Е.А. Ерёмин, 2013
?
Как улучшить?
http://kpolyakov.spb.ru

46. Метод дихотомии

Решение вычислительных задач, 10 класс
46
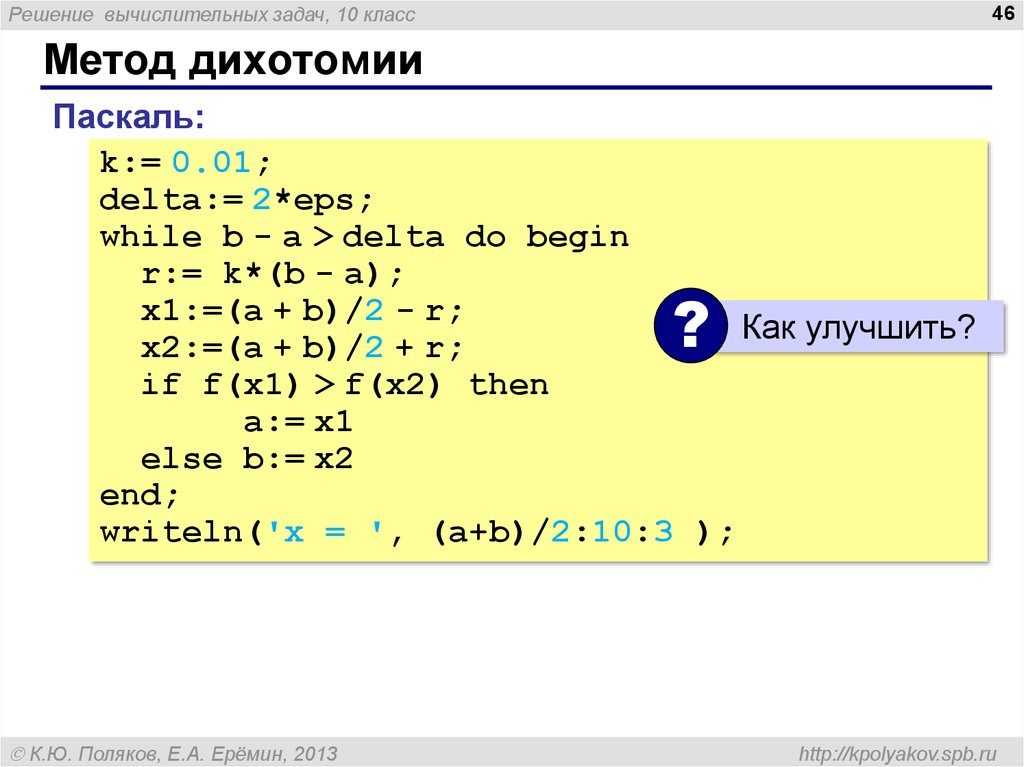
Метод дихотомии
Паскаль:
k:= 0.01;
delta:= 2*eps;
while b - a > delta do begin
r:= k*(b - a);
x1:=(a + b)/2 - r;
Как улучшить?
x2:=(a + b)/2 + r;
if f(x1) > f(x2) then
a:= x1
else b:= x2
end;
writeln('x = ', (a+b)/2:10:3 );
?
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

47. Метод золотого сечения

Решение вычислительных задач, 10 класс
47
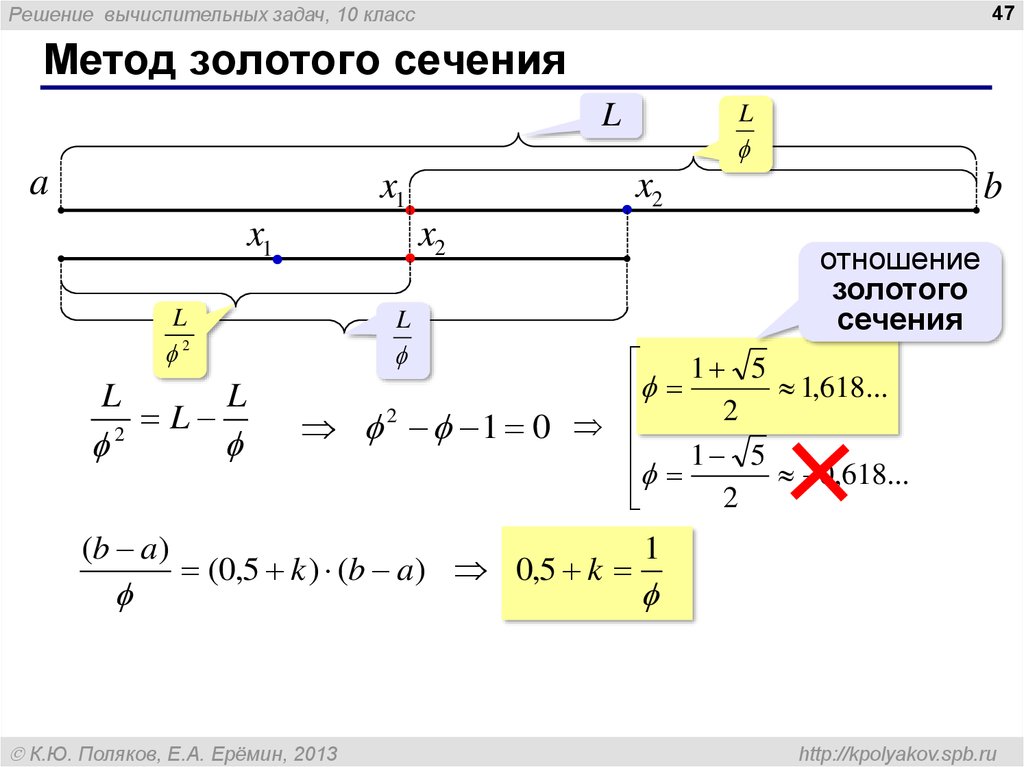
Метод золотого сечения
L
a
x2
x1
2
L
L
2
L
(b a)
L
x2
x1
L
L
2
отношение
золотого
сечения
1 5
1,618...
2
1 0
1 5
0,618...
2
(0,5 k ) (b a) 0,5 k
К.Ю. Поляков, Е.А. Ерёмин, 2013
b
1
http://kpolyakov.spb.ru

48. Оптимальный раскрой листа

Решение вычислительных задач, 10 класс
48
Оптимальный раскрой листа
1м
z
x
x
z
Цель:
V ( x) max
?
Ограничения:
?
V ( x) x (1 2 x) 2 max
Какие ограничения?
0 x 0,5
Какой результат ожидаете (по интуиции)?
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

49. Оптимальный раскрой листа

Решение вычислительных задач, 10 класс
49
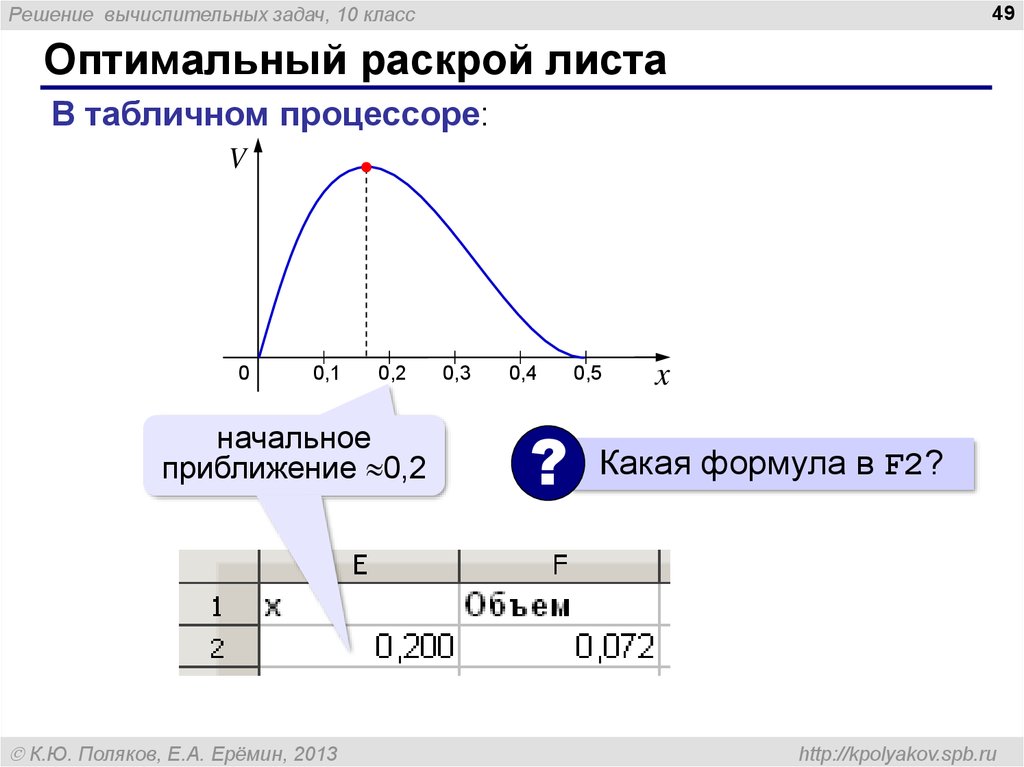
Оптимальный раскрой листа
В табличном процессоре:
V
0
0,1
0,2
начальное
приближение 0,2
К.Ю. Поляков, Е.А. Ерёмин, 2013
0,3
0,4
?
0,5
x
Какая формула в F2?
http://kpolyakov.spb.ru

50. Оптимизация в табличном процессоре

Решение вычислительных задач, 10 класс
50
Оптимизация в табличном процессоре
Задача оптимизации: найти максимум (или минимум)
целевой функции в ячейке …, изменяя значения ячеек
… при ограничениях ….
OpenOffice.org Calc:
модуль Solver for Nonlinear Programming
(входит в LibreOffice)
Excel:
надстройка Поиск решения
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

51. Оптимизация в табличном процессоре

Решение вычислительных задач, 10 класс
51
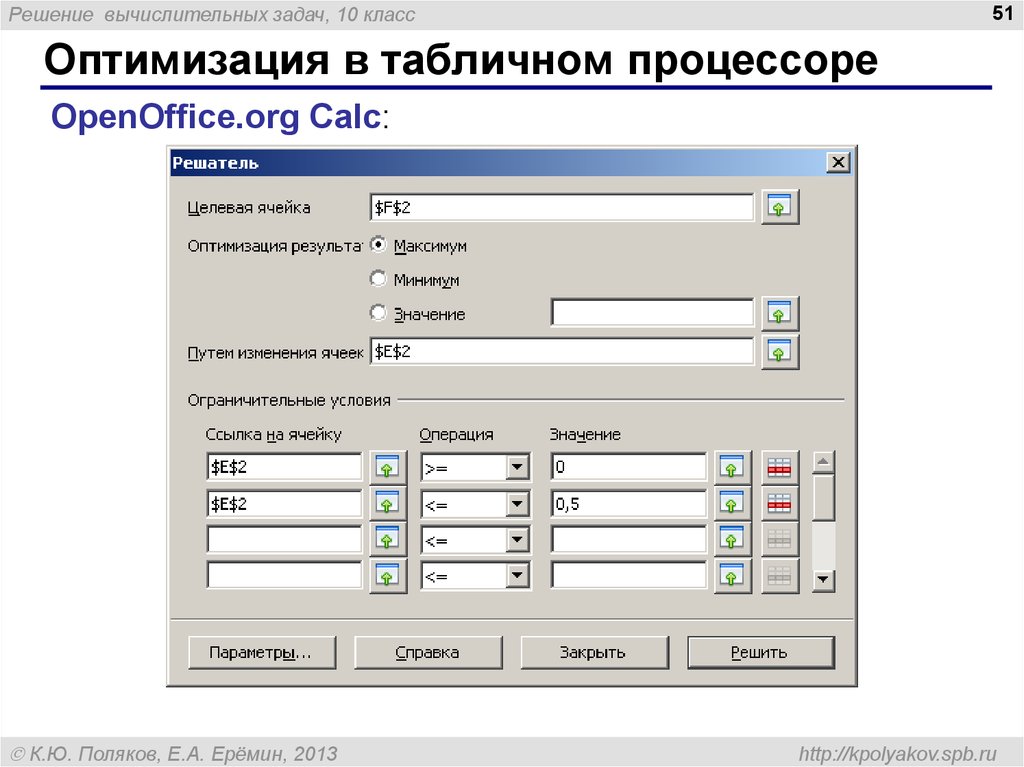
Оптимизация в табличном процессоре
OpenOffice.org Calc:
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

52. Оптимизация в табличном процессоре

Решение вычислительных задач, 10 класс
52
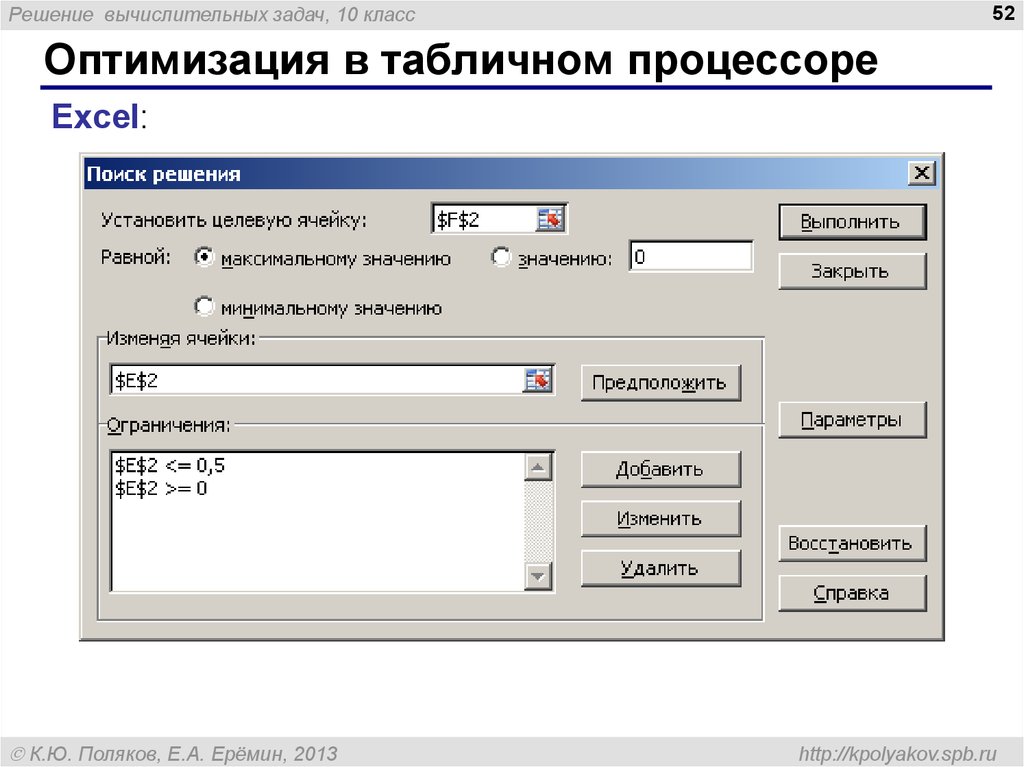
Оптимизация в табличном процессоре
Excel:
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

53. Решение вычислительных задач на компьютере

53
Решение
вычислительных
задач на компьютере
§ 73. Статистические
расчёты
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

54. Что такое статистика?

Решение вычислительных задач, 10 класс
54
Что такое статистика?
Статистика – это наука, которая изучает методы
обработки и анализа больших массивов данных.
Ряд данных:
x1 , x2 , ... xn
Свойства ряда данных:
сумма:
среднее:
минимальное:
максимальное:
количество чисел:
=SUM(A1:A20)
=AVERAGE(A1:A20)
=MIN(A1:A20)
=MAX(A1:A20)
=COUNT(A1:A20)
сколько ячеек удовлетворяет условию:
=COUNTIF(A1:A20;"=5")
=COUNTIF(A1:A20;">3")
К.Ю. Поляков, Е.А. Ерёмин, 2013
только числа!
=СУММ(A1:A20)
=СРЗНАЧ(A1:A20)
=МИН(A1:A20)
=МАКС(A1:20)
=СЧЁТ(A1:20)
СЧЁТЕСЛИ
http://kpolyakov.spb.ru

55. Дисперсия

Решение вычислительных задач, 10 класс
55
Дисперсия
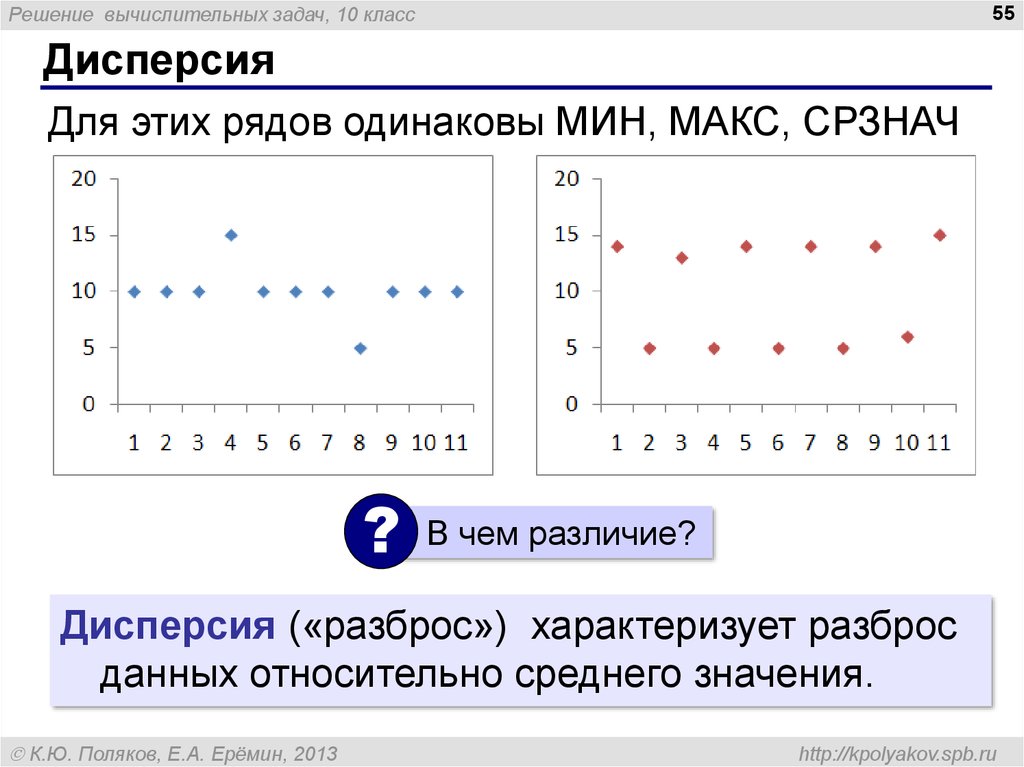
Для этих рядов одинаковы МИН, МАКС, СРЗНАЧ
?
В чем различие?
Дисперсия («разброс») характеризует разброс
данных относительно среднего значения.
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

56. Дисперсия

Решение вычислительных задач, 10 класс
56
Дисперсия
n
2
(
x
x
)
i
( x1 x ) 2 ( x2 x ) 2 ( xn x ) 2
Dx
i 1
n
n
x1 x2 xn
x
среднее арифметическое
n
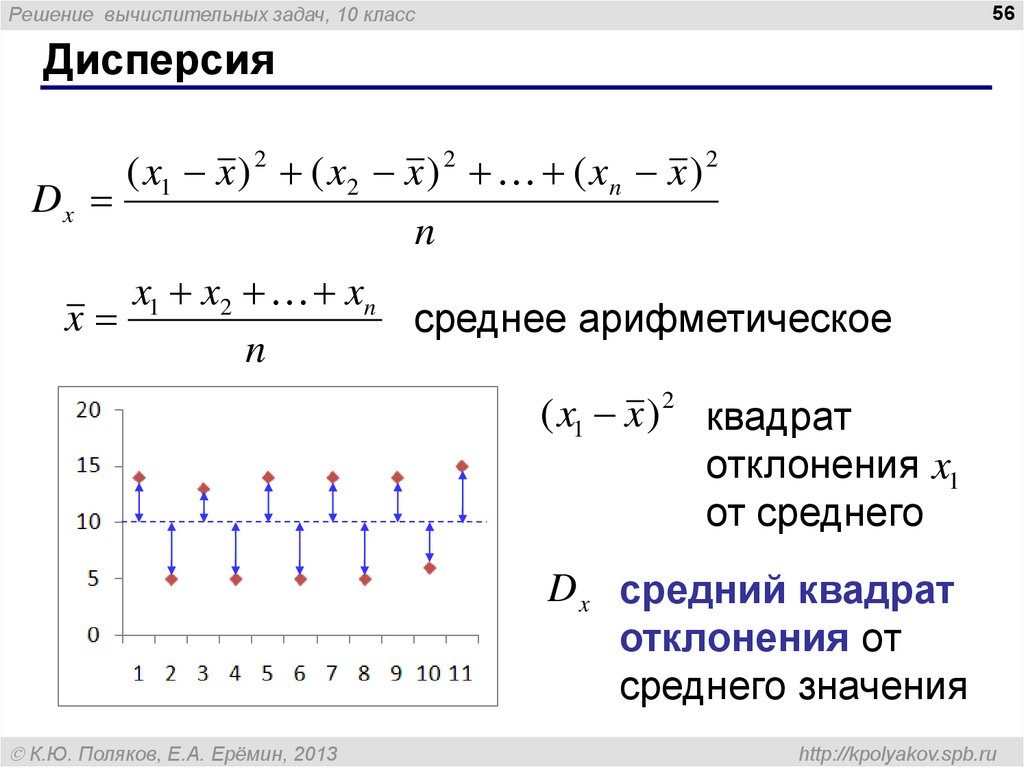
( x1 x )
2
квадрат
отклонения x1
от среднего
D x средний квадрат
отклонения от
среднего значения
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

57. Дисперсия и СКВО

Решение вычислительных задач, 10 класс
57
Дисперсия и СКВО
n
Dx
2
(
x
x
)
i
i 1
?
В каких единицах измеряется?
n
Что неудобно:
если x измеряется в метрах, то D x – в м2
СКВО = среднеквадратическое отклонение
x Dx
=STDEVP(A1:A20)
=СТАНДОТКЛОНП(A1:A20)
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

58. Условные вычисления

Решение вычислительных задач, 10 класс
58
Условные вычисления
Доставка:
• бесплатно при >500 руб.
• 20% для остальных
условие
если B2 > 500 то
C2:= 0
иначе
C2:= B2*0.2
все
К.Ю. Поляков, Е.А. Ерёмин, 2013
= IF(B2>500;0;B2*0,2)
=ЕСЛИ(B2>500;0;B2*0,2)
если «да»
если «нет»
http://kpolyakov.spb.ru

59. Сложные условия

Решение вычислительных задач, 10 класс
59
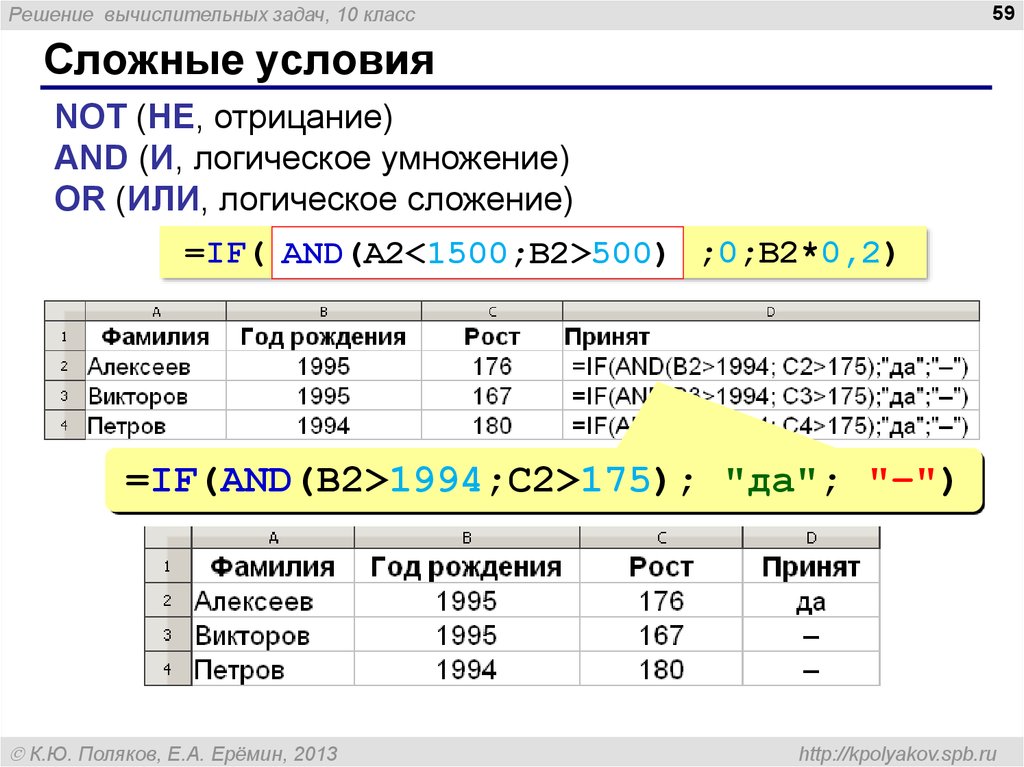
Сложные условия
NOT (НЕ, отрицание)
AND (И, логическое умножение)
OR (ИЛИ, логическое сложение)
=IF( AND(A2<1500;B2>500) ;0;B2*0,2)
=IF(AND(B2>1994;C2>175); "да"; "–")
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

60. Сложные условия

Решение вычислительных задач, 10 класс
60
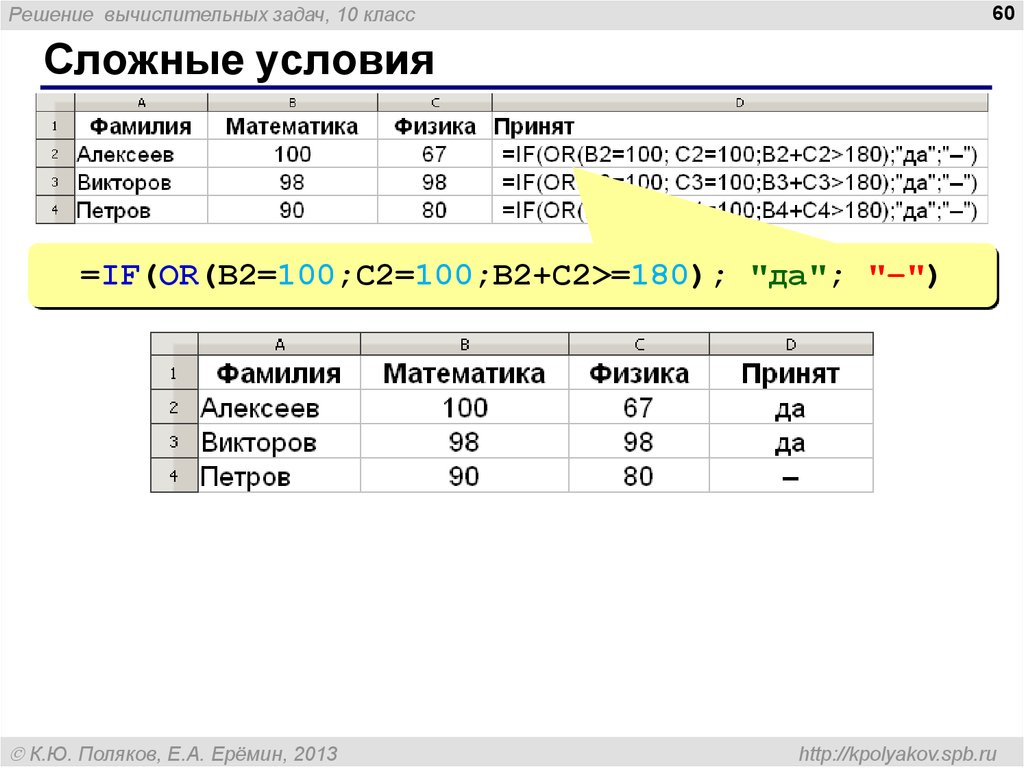
Сложные условия
=IF(OR(B2=100;C2=100;B2+C2>=180); "да"; "–")
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

61. Вложенные условия

Решение вычислительных задач, 10 класс
61
Вложенные условия
Доставка:
• бесплатно при >500 руб.
• 10% при >200 руб.
• 20% для остальных
если B2 > 500 то
C2:= 0
иначе
если B2 > 200 то
C2:= B2*0.1
иначе
C2:= B2*0.2
все
все
=IF(B2>500;0; IF(B2>200;B2*0,1;B2*0,2) )
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

62. Связь двух рядов данных

Решение вычислительных задач, 10 класс
62
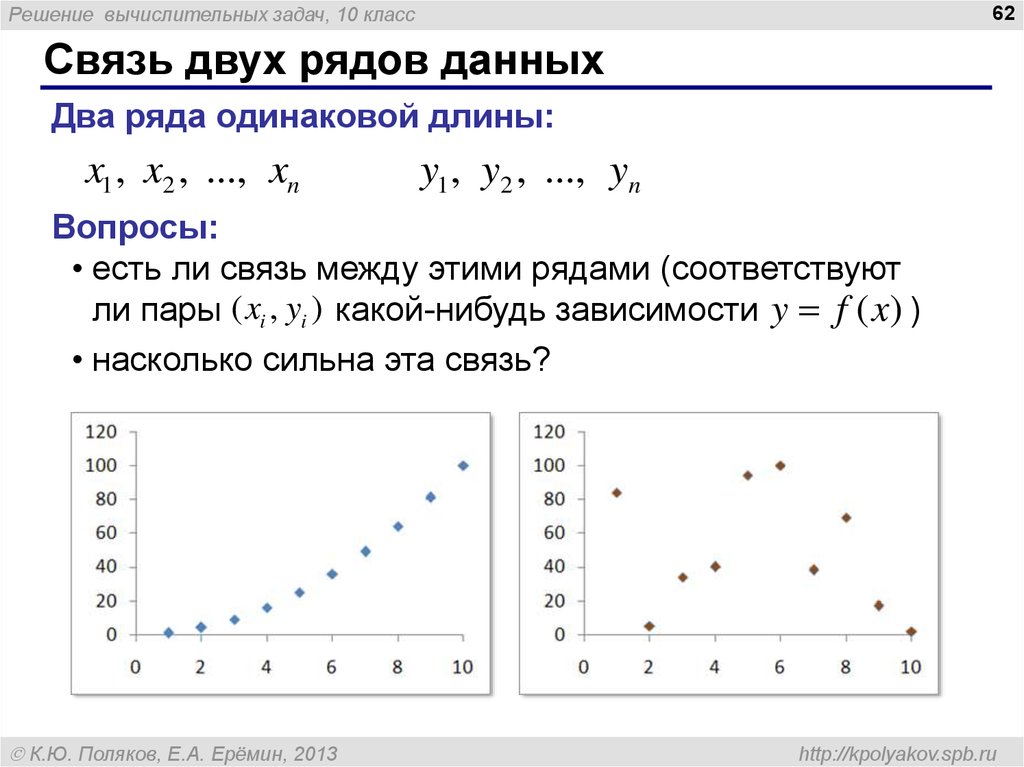
Связь двух рядов данных
Два ряда одинаковой длины:
x1 , x2 , ..., xn
y1 , y2 , ..., yn
Вопросы:
• есть ли связь между этими рядами (соответствуют
ли пары ( xi , yi ) какой-нибудь зависимости y f (x) )
• насколько сильна эта связь?
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

63. Коэффициент корреляции

Решение вычислительных задач, 10 класс
63
Коэффициент корреляции
средние рядов
n
1
( xi x )( yi y )
n i 1
xy
x y
СКВО рядов
?
?
В каких единицах
измеряется?
безразмерный!
Если x и y – один и
тот же ряд?
1 xy 1
=CORREL(A1:A20;B1:B20)
=КОРРЕЛ(A1:A20;B1:B20)
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

64. Коэффициент корреляции

Решение вычислительных задач, 10 класс
64
Коэффициент корреляции
Как понимать это число?
• если xy 0 : увеличение x приводит к увеличению y
• если xy 0 : увеличение x приводит к уменьшению y
• если xy 0 : связь обнаружить не удалось
Сильная связь: xy 0,5
xy 1 : линейная зависимость y kx b,
k 0
xy 1 : линейная зависимость y kx b, k 0
?
Если xy 0, то связи нет?
!
Метод для определения линейной зависимости!
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

65. Решение вычислительных задач на компьютере

65
Решение
вычислительных
задач на компьютере
§ 74. Обработка результатов
эксперимента
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

66. Закон Гука

Решение вычислительных задач, 10 класс
66
Закон Гука
F k
F
k
F
Fi
, (i 1,...n)
Несколько опытов: ki
i
?
К.Ю. Поляков, Е.А. Ерёмин, 2013
Что принять за k?
http://kpolyakov.spb.ru

67. Метод наименьших квадратов (МНК)

Решение вычислительных задач, 10 класс
67
Метод наименьших квадратов (МНК)
y k x
y2 Y3
y
y1
Y1
Y2
x1 x2
0
неизвестно!
y3
Yi k xi
x3 x
Ошибка определяется величиной:
n
2
2
2
E (k ) (Y1 y1 ) (Y2 y2 ) (Yn yn ) (Yi yi ) 2
i 1
Метод наименьших квадратов: E (k ) min
!
Это задача оптимизации!
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

68. Метод наименьших квадратов (МНК)

Решение вычислительных задач, 10 класс
68
Метод наименьших квадратов (МНК)
(Yi yi ) 2 (k xi yi ) 2 k 2 xi2 2kxi yi yi2
E (k ) A k B k C
2
n
A xi2
i 1
n
B 2 xi yi
i 1
n
C yi2
i 1
E
k*
k*
B
2A
k
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

69. Метод наименьших квадратов (МНК)

Решение вычислительных задач, 10 класс
69
Метод наименьших квадратов (МНК)
Алгоритмический язык:
A:= 0; B:= 0
нц для i от 1 до N
A:= A + x[i]*x[i]
B:= B + x[i]*y[i]
кц
k:= B / A
вещ A, B, k
вещ x[1:N], y[1..N]
N
k*
x y
i 1
N
i
i
Паскаль:
2
x
i
A:= 0; B:= 0;
i 1
for i:=1 to N do begin
A:= A + x[i]*x[i];
B:= B + x[i]*y[i]
end;
var A, B, k: real;
k:= B / A;
x,y: array[1..N] of real;
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

70. Метод наименьших квадратов (МНК)

Решение вычислительных задач, 10 класс
70
Метод наименьших квадратов (МНК)
Табличный процессор:
начальное
приближение
СУММКВРАЗН
Поиск решения: выбрать B1 так, что B2 min
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

71. Восстановление зависимостей

Решение вычислительных задач, 10 класс
71
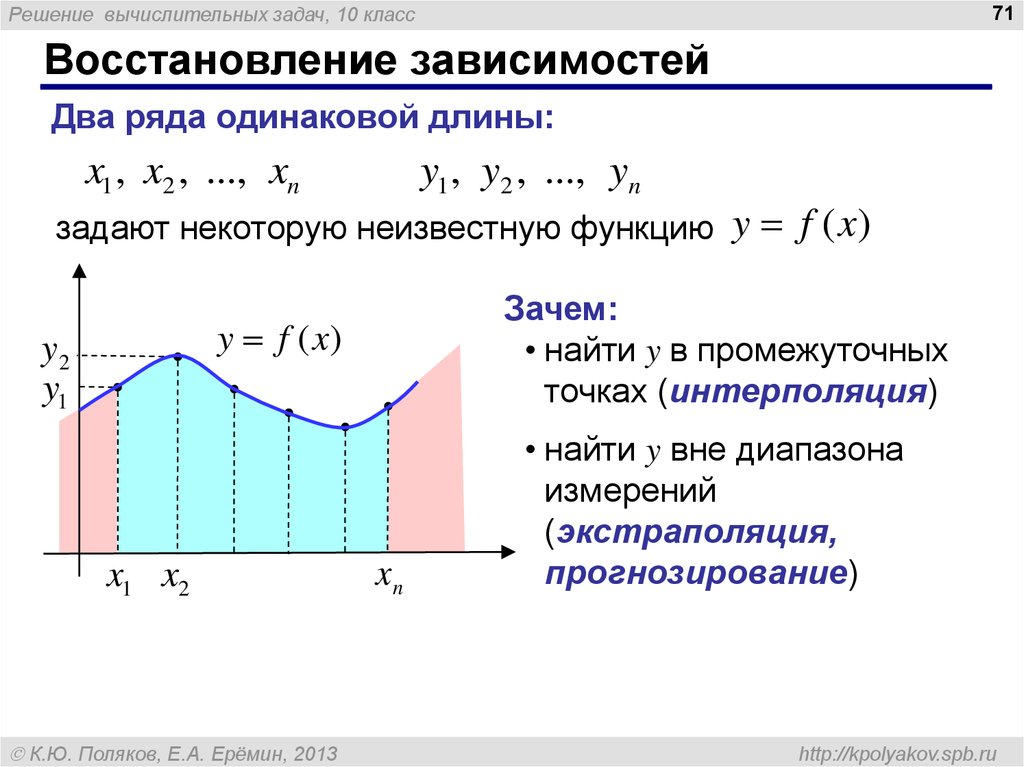
Восстановление зависимостей
Два ряда одинаковой длины:
y1 , y2 , ..., yn
x1 , x2 , ..., xn
задают некоторую неизвестную функцию y f (x)
Зачем:
• найти y в промежуточных
точках (интерполяция)
y f (x)
y2
y1
x1 x2
К.Ю. Поляков, Е.А. Ерёмин, 2013
xn
• найти y вне диапазона
измерений
(экстраполяция,
прогнозирование)
http://kpolyakov.spb.ru

72. Восстановление зависимостей

Решение вычислительных задач, 10 класс
72
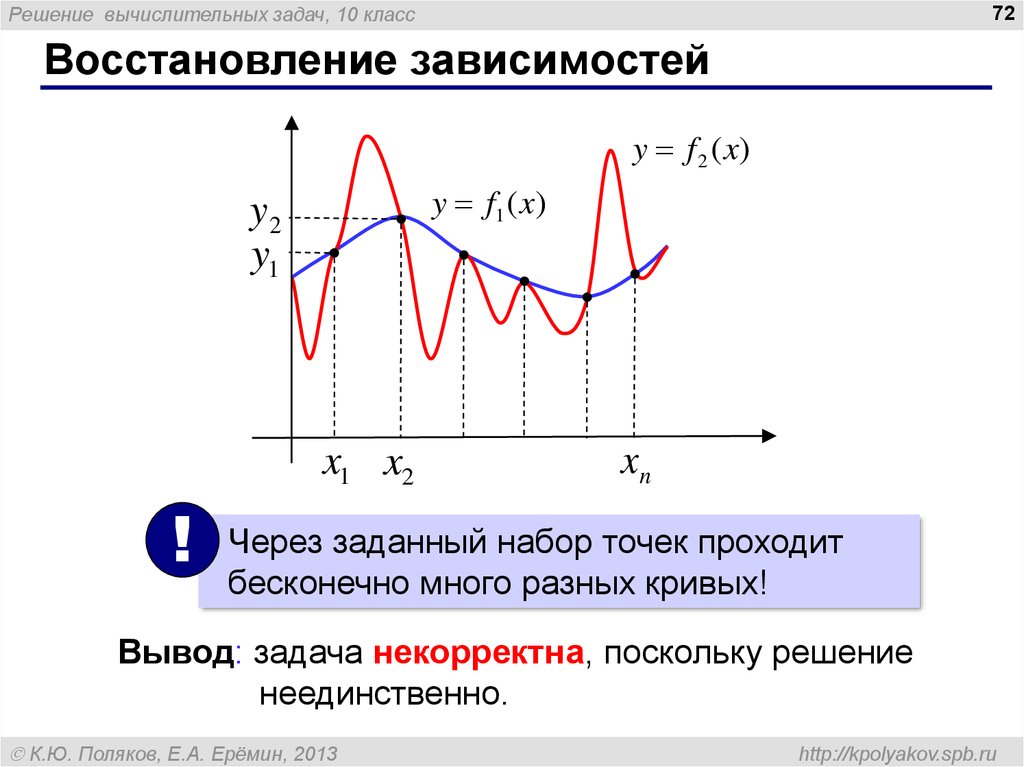
Восстановление зависимостей
y f 2 ( x)
y f1 ( x)
y2
y1
x1 x2
!
xn
Через заданный набор точек проходит
бесконечно много разных кривых!
Вывод: задача некорректна, поскольку решение
неединственно.
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

73. Восстановление зависимостей

Решение вычислительных задач, 10 класс
73
Восстановление зависимостей
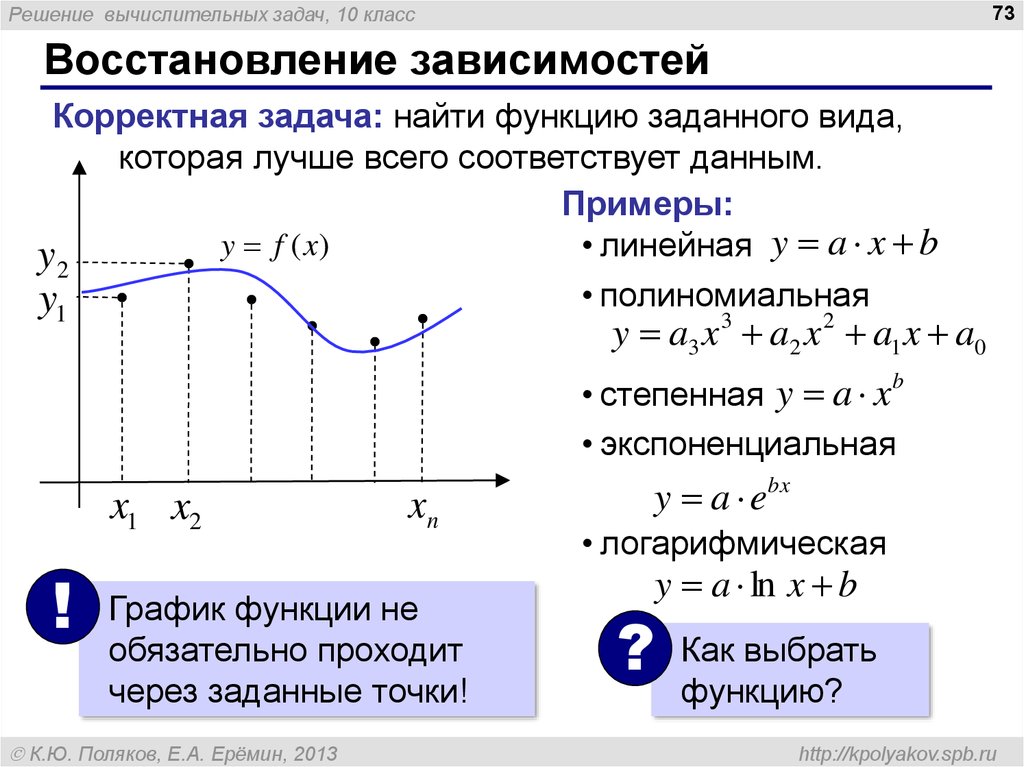
Корректная задача: найти функцию заданного вида,
которая лучше всего соответствует данным.
Примеры:
y f (x)
• линейная y a x b
y2
• полиномиальная
y1
y a3 x 3 a2 x 2 a1 x a0
• степенная y a x
• экспоненциальная
b
x1 x2
!
xn
График функции не
обязательно проходит
через заданные точки!
К.Ю. Поляков, Е.А. Ерёмин, 2013
y a ebx
• логарифмическая
y a ln x b
?
Как выбрать
функцию?
http://kpolyakov.spb.ru

74. Что значит «лучше всего соответствует»?

Решение вычислительных задач, 10 класс
74
Что значит «лучше всего соответствует»?
n
R2 1
(y Y )
i 1
n
i
(y
i 1
i
2
i
y)
2
( xi , yi ) заданные пары
значений
Yi f ( xi )
y – среднее значение yi
коэффициент
детерминации
Крайние случаи:
2
• если график проходит через точки: R 1
2
• если считаем, что y не меняется и Yi y : R 0
R 2 max когда
!
n
2
(
y
Y
)
i i min
i 1
Фактически – метод наименьших квадратов!
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

75. Восстановление зависимостей

Решение вычислительных задач, 10 класс
75
Восстановление зависимостей
Табличный процессор:
1) Диаграмма XY (Excel: Точечная)
2) ПКМ – Вставить линию тренда
тип функции
показать уравнение
коэффициент
детерминации
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

76. Прогнозирование

Решение вычислительных задач, 10 класс
76
Прогнозирование
12
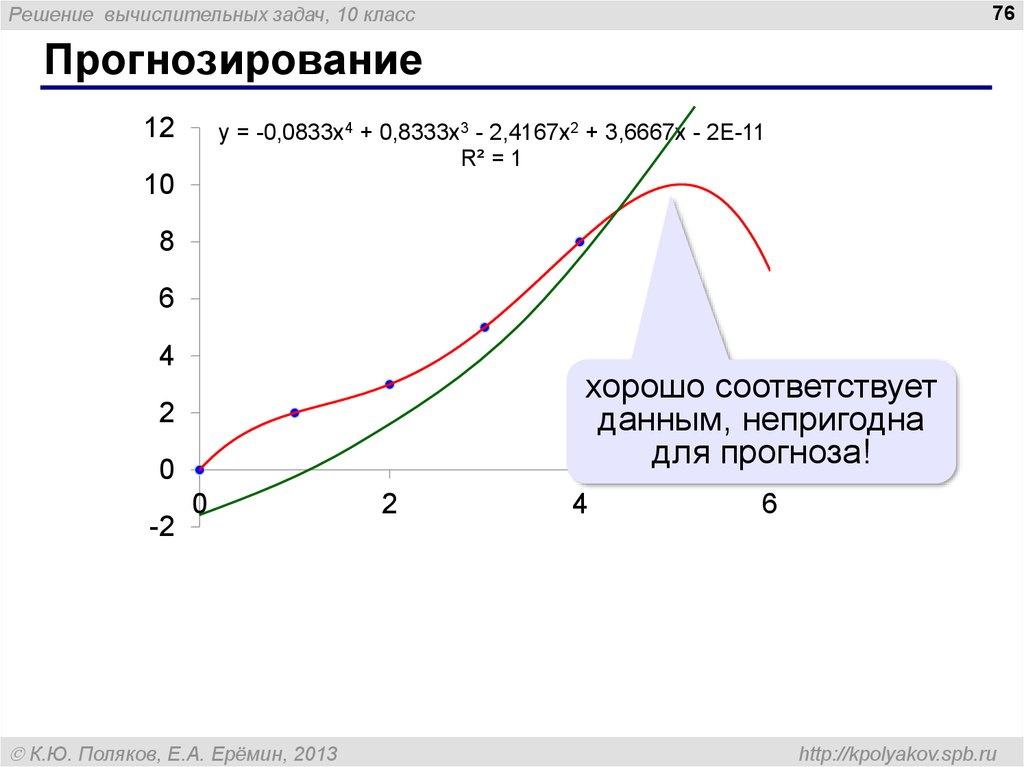
y = -0,0833x4 + 0,8333x3 - 2,4167x2 + 3,6667x - 2E-11
R² = 1
10
8
6
4
хорошо соответствует
данным, непригодна
для прогноза!
2
0
-2
0
К.Ю. Поляков, Е.А. Ерёмин, 2013
2
4
6
http://kpolyakov.spb.ru

77. Конец фильма

Решение вычислительных задач, 10 класс
77
Конец фильма
ПОЛЯКОВ Константин Юрьевич
д.т.н., учитель информатики
ГБОУ СОШ № 163, г. Санкт-Петербург
[email protected]
ЕРЕМИН Евгений Александрович
к.ф.-м.н., доцент кафедры мультимедийной
дидактики и ИТО ПГГПУ, г. Пермь
[email protected]
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

78. Источники иллюстраций

Решение вычислительных задач, 10 класс
78
Источники иллюстраций
1.
2.
3.
4.
vispo.ru
www.ars-sport.ru
иллюстрации художников издательства «Бином»
авторские материалы
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru