Плоские электромагнитные волны в диспергирующих средах. (Лекция 4)

1.

Лекция 4. Плоские электромагнитные волны
в диспергирующих средах
1. Поперечные электромагнитные волны в газе осцилляторов
- Дисперсионное уравнение
- Поглощение волн
2. Электромагнитные волны в изотропной плазме:
- Поперечные электромагнитные волны
- Продольные волны
3. Плоские волны в анизотропных средах
- Дисперсионное уравнение для волн в анизотропных средах
- Двойное лучепреломление
- Волны в плазме в магнитном поле
- Вращение плоскости поляризации

2.

k D( , k ) 0 ,
div D 0,
1 2D
rot rot E 2
.
2
c t
2
k [k E( , k )] 2 D( , k ) .
c
l ( , k ) 0
l ( , k )(k E l ) 0 ,
2 tr
k 2 ( , k ) 0
c
2 2 tr
tr 2 l
k 2 ( , k ) E 2 ( , k )E l .
c
c
2
02
2
0
k 2 1 2
c s2 i
2
1, 2
1 2
1
( s k 2 c 2 02 ) ( s2 k 2 c 2 02 ) 2 4 s2 k 2 c 2
2
2 10
( k c )
2
0
2
s
2
s
2 2 2
02
1
1 kc
kc,
2
2 2
2 s k c
02
2 s 2
s .
2 2
s k c
8
6
4
2
2
4
6
8
10

3.

02
02 k 2 c 2
1
1 kc
kc i 2
2 s2 k 2 c 2
( s k 2 c 2 ) 2
kc | k c |
2
s
2 2
02
1
2 s 2
i
s
2 2
s k c
2
s
10
8
02
k ( )
1 2
c
s2 i
6
4
3 .0
2
0 .0 2
2 .5
2
4
6
8
10
2
4
6
8
10
2 .0
1 .5
1 .0
0 .5
0 .0 4
2
4
6
0 .0 6
0 .0 8
0 .1 0
s
02
k ( s )
1 i
c
s
8
10

4.

2
Le
2
k 2 1
c ( i e )
Li Le :
1, 2
e Le :
2
2
e
Le
k c i
;
2 2
2
2 k c Le
2 2
k 2c 2
3 i e 2 2
2
k c Le
2
Le
5
1
2
3
4
5
4
0 .0 5
3
0 .1 0
2
1
0 .1 5
1
2
3
4
5
2
Le
k
1
c
( i e )
2
2
2
2 Le
: exp[ ( c) Le 1 z ], z 0
2 .5
2 .0
1 .5
1 .0
| | e : k
i 1 Le
2 (0)
(i 1)
c2
2 c e
0 .5
0 .5
1 .0
1 .5
2 .0
2 .5
3 .0

5.

2
Li2
Le
1
2 2
( i i ) k V i ( i e ) k 2V e2
| | Le : 1, 2
e2
k V
i e e2 Le2 k 2V 2e : 1 i e 1 (k 2V e2 Le2 ), 2 i e
4
2
2
Le
2
2
e
2
Le
Li2
kV e | | kV i : 1 2 2
0
k V e ( i i )
i2
1, 2 (k )
i i
4
2
kV e
is (k ) Li
2
Le
k 2V 2e
2
is
1 2
i2 is2 (k ) : 1 i i is (k ), 2 i i
0:
2
Li2 Le
2
2
k 1 rD 0, rD 2 2
V
i V e
1 2

6.

ki ij ( , k ) E j ( , k ) 0,
2
2
k
k
k
(
,
k
)
i j
ij
ij
E j ( , k ) 0.
2
c
2
2
det k ij ki k j 2 ij ( , k )
c
2 2
2
2
k z 2 xx E x 2 xy E y 2 xz E z ,
c
c
c
k {0,0, k z }
ij ji , ij 0
2 2
2
2
k z 2 yy E y 2 yx E x 2 yz E z ,
c
c
c
zz E z zx E x zy E y .
Dx xx E x , D y yy E y , Dz zz E z
2
2
2
2
2
2
2
2
2
k z k y 2 xx k z k x 2 yy k x k y 2 zz
c
c
c
2
2
2
2
2 2 2
2
k k k z k y 2 xx k z k x k z k x 2 yy
c
c
2
z
2
y
2
2
2
k k k x k y 2 zz 2k x2 k y2 k z2 0 .
c
2
x
2
y

7.

2
2
2
2
2
2
k z k x 2 yy zz k z xx k x 2 xx zz 0 .
c
c
ky 0
2
2
k z1
k
,
yy
x
2
c
2
2 xx
kz2
k
xx
x
c2
zz
tan k x c
A1 exp( i t ik 1 r ) A2 exp( i t ik 2 r )
2 k x2 c 2
tan 1, 2 k x k z1, 2
k {0,0, k z }
xx yy
2
Le
1 2
( ) ,
e2
xy yx
2
Le
e
i
ig ( ) ,
( 2 e2 )
2
Le
zz 1 2 || ( ).
ij ji
2 2
2
k z 2 ( ) E x i 2 g ( ) E y 0 ,
c
c
2 2
2
k z 2 ( ) E y i 2 g ( ) E x 0 ,
c
c
|| ( ) E z 0 .
2
2
2
k 2 ( ) 2 g ( ) ( 2 k z2 c 2 )( e ) Le
c
c
2
z
E x E y i E x (t , z ) A sin( t k z z ), E y (t , z ) A cos( t k z z )

8.

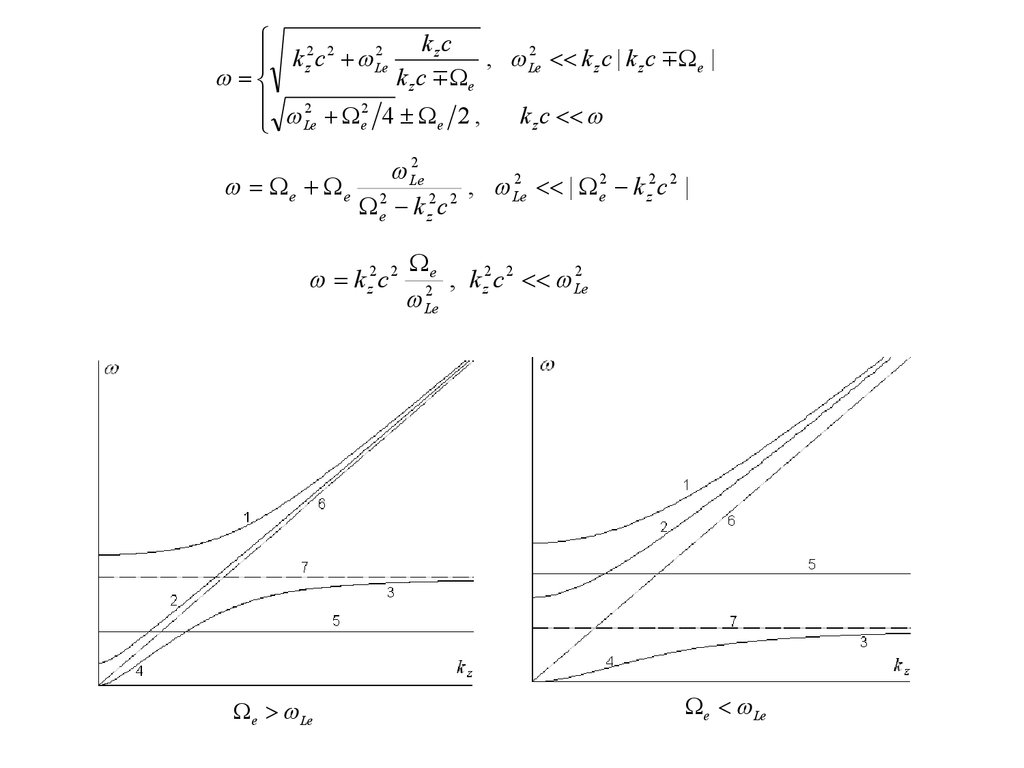
kzc
2 2
2
2
k
c
, Le
k z c | k z c e |
z
Le
k
c
z
e
2 2 4 2 ,
k z c
e
e
Le
2
Le
2
e e 2
, Le
| e2 k z2 c 2 |
2 2
e k z c
k z2 c 2
e Le
e
2
, k z2 c 2 Le
2
Le
e Le

9.

k {k x ,0,0}
( ) E x ig ( ) E y 0 ,
2 2
2
k 2 ( ) E y i 2 g ( ) E x ,
c
c
2 2
k 2 || ( ) E z 0 .
c
2
k x2 c 2 Le
2 2 ( ) g 2 ( )
2 2
k 2
0 ( 2 Le
) 2 e2 k x2 c 2 ( 2 2g )
c
( )
2
x

10.

ig
ij ig
0
0
0
0
||
k z2
g ,
c
k z 2 ( )
g.
c
k z1 ( )
( g ) 0
2
c
Ex E y i
2
E x (t , z ) A sin( t k z z )
E y (t , z ) A cos( t k z z )
E x1 (t , z ) A1 sin( t k z1 z 1 ),
E y1 (t , z ) A1 cos( t k z1 z 1 ),
E x 2 (t , z ) A2 sin( t k z 2 z 2 ),
E y 2 (t , z ) A2 cos( t k z 2 z 2 ).
E x1 (t ,0) E x1 (t ,0) 0,
E y1 (t ,0) E y1 (t ,0) A0 cos t ,
k k z 2 k z1 k z 2
E x (t , z ) E x1 (t , z ) E x 2 (t , z ) A0 cos t z1
z sin
z ,
2
2
k k z 2 k z1 k z 2
E y (t , z ) E y1 (t , z ) E y 2 (t , z ) A0 cos t z1
z cos
z .
2
2

11.

1
( k z1 k z 2 ) z g g g
2
с
1
z
1
2
e
Le
Le2
z
1
1
2
2
c e
( e )
( e )
2
Le
1
gz
2 с
2
1 e Le
z
2 c 2