Similar presentations:
Молекулярная физика (полный курс)
1.
Кафедра общей физикиГрГУ им. Янки Купалы
Мультимедийный курс лекций
«Молекулярная физика»
для студентов специальностей:
1-31 04 01-02 Физика (производственная деятельность);
1-31 04 01-03 Физика (научно-педагогическая деятельность).
Разработчик: Д.В. Гузатов, к.ф.-м.н.
Версия: 2.1
Гродно – 2012
2.
Содержание• Введение
• Основные представления молекулярно
-кинетической теории идеального газа
• Сведения из теории вероятностей
• Элементы статистической физики
• Распределение молекул идеального газа по
скоростям
• Кинематические характеристики молекулярного
движения
• Процессы переноса
сл. 5
сл. 16
сл. 34
сл. 45
сл. 56
сл. 76
сл. 86
2
3.
• Распределение молекул идеального газа воднородном поле сил
• Броуновское движение
• Теплоемкость идеального газа
• Первое начало термодинамики
• Второе начало термодинамики
• Энтропия
• Температура
• Термодинамические функции
• Реальный газ
• Состояния двухфазной системы
сл. 104
сл. 115
сл. 116
сл. 144
сл. 166
сл. 197
сл. 213
сл. 223
сл. 236
сл. 266
3
4.
Жидкость
Растворы и смеси
Фазовые переходы
Кристаллические твердые тела
сл. 278
сл. 322
сл. 356
сл. 375
4
5.
Молекулярная физикаТема 1:
Введение
5
6.
Содержание• Учебная литература по дисциплине
• Что изучает молекулярная физика?
• Модель материального тела. Агрегатные
состояния вещества.
• Методы описания макроскопических
систем.
6
7.
Учебная литература• А.Н. Матвеев / Молекулярная физика // Москва: Высшая школа, 1981.
– 400 с.
• Д.В. Сивухин / Общий курс физики, том 2. Термодинамика и
молекулярная физика // Москва: Наука, 1979. – 552 с.
• С.Э. Фриш, А.В. Тиморева / Курс общей физики, том 1. Физические
основы механики. Молекулярная физика. Колебания и волны //
Москва: Физматлит, 1962. – 468 с.
• Р.В. Телеснин / Молекулярная физика // Москва: Высшая школа, 1973.
– 360 с.
• А.К. Кикоин, И.К. Кикоин / Общий курс физики. Молекулярная
физика // Москва: Наука, 1976. – 480 с.
• М.С. Цэдрык / Курс агульнай фiзiкi. Цеплыня i малекулярная фiзiка //
Мiнск: Вышэйшая школа, 1994. – 232 с.
• И.Е. Иродов / Задачи по общей физике // Москва: Физматлит, 1979. –
368 с.
• В.Ф. Аскирка [и др.] / Механика. Молекулярная физика и
термодинамика // Гродно: изд-во ГрГУ им Я. Купалы. – 2005. – 184 с.
• Сборник задач по общему курсу физики. Термодинамика и
молекулярная физика / под ред. Д.В. Сивухина // Москва: Наука, 1976.
– 208 с.
7
8.
Молекулярная физикаМолекулярной физикой называют раздел физики,
занимающийся изучением зависимости физических
свойств и агрегатных состояний тел от их
внутреннего строения, сил взаимодействия между
частицами, образующими тела, и характера их
движения.
Все материальные тела состоят из мельчайших
частиц, называемых молекулами.
В зависимости от взаимодействия молекул друг с
другом материальные тела подразделяются на три
агрегатных состояния: газ, жидкость, твердое тело.
8
9.
Агрегатные состоянияВ газах молекулы настолько отдалены друг от
друга, что практически не взаимодействуют
между собой. Молекулы газа движутся от
столкновения до столкновения со стенками
сосуда или между собой равномерно и
прямолинейно. Это движение хаотично, т.е. в
среднем, в каждом направлении в любой
момент времени движется одинаковое число
молекул. Давление, оказываемое газом на
стенки сосуда, является следствием передачи
импульса от движущихся молекул, при их
соударении со стенками.
9
10.
Агрегатные состоянияВ твердых кристаллических телах силы
взаимодействия между молекулами очень
велики и поэтому молекулы не могут удалится
друг от друга на большие расстояния. В
результате совместного действия сил
притяжения и отталкивания молекулы
совершают колебания около некоторых
средних положений, называемых узлами
кристаллической решетки. Положению
молекул в узлах кристаллической решетки
соответствует минимальная энергия всего
твердого тела. Любое изменение расстояния
между молекулами в твердом теле требует
приложения внешней силы.
10
11.
Агрегатные состоянияМолекулярное движение в жидкостях
наиболее сложно. В нем наблюдаются черты,
присущие тепловому движению частиц как в
газах, так и твердых телах. Каждая молекула в
течение некоторого промежутка времени
колеблется около определенного положения
равновесия, которое само время от времени
смещается на расстояние, соизмеримое с
размерами молекул. В результате молекулы
внутри жидкости колеблются и медленно
перемещаются. Некоторое время они
находятся около определенных мест, как бы в
оседлом состоянии.
11
12.
Макроскопическая системаВ классической физике предполагают, что молекулы
движутся в соответствии с законами ньютоновской
механики. Однако число молекул в любом теле
очень велико: при обычных давлениях и
температурах в каждом кубическом метре газа
содержится порядка 1025 молекул, а в жидких и
твердых телах - порядка 1028 молекул. Поэтому
практически невозможно решить систему
уравнений для описания движения молекул и найти
вид траектории, а также закономерность движения
по ней для каждой отдельной молекулы. Именно
потому и говорят, что местоположение и скорость
каждой молекулы изменяются во времени
случайным образом.
12
13.
Методы описаниямакроскопических систем
Для изучения физических свойств
макроскопических систем, состоящих из
очень большого числа молекул, используют
два взаимно дополняющих друг друга
метода: статистический и
термодинамический.
13
14.
Статистический методСтатистический метод основан на законах
теории вероятностей и математической
статистики.
В совокупном движении огромного числа
молекул, координаты и скорости которых в
любой момент времени случайны,
проявляются статистические (вероятностные)
закономерности.
Раздел теоретической физики, в котором
изучают физические свойства
макроскопических систем с помощью
статистического метода, называется
статистической физикой.
14
15.
Термодинамический методТермодинамический метод состоит в изучении
физических свойств макроскопических систем путем
анализа условий и количественных соотношений для
процессов превращения энергии в рассматриваемых
системах.
Соответствующий раздел теоретической физики
называют термодинамикой.
Рассматриваемую макроскопическую систему в
термодинамике называют термодинамической
системой.
Физические величины, служащие для характеристики
состояния термодинамической системы, называют
термодинамическими параметрами (параметрами
состояния) системы. В качестве параметров состояния
в термодинамике используют объем, давление,
температуру и другие величины.
15
16.
Молекулярная физикаТема 2:
Основные представления
молекулярно-кинетической теории
идеального газа
16
17.
Содержание• Модель идеального газа. Законы идеального
газа.
• Понятие температуры. Идеально-газовая
шкала температур.
• Основное уравнение молекулярнокинетической теории газов.
17
18.
Идеальный газИдеальным газом называется газ, в котором
взаимодействие между молекулами
происходит только путем их упругих
столкновений между собой. Другие виды
взаимодействия в таком газе отсутствуют. В
реальном газе молекулы взаимодействуют
друг с другом (притягиваются и
отталкиваются). Любой реальный газ можно
считать идеальным, если он достаточно
разрежен.
Рассмотрим равновесный газ, т.е. газ
внутренние параметры которого зависят
только от его внешних параметров и
температуры.
18
19.
Идеальный газРавновесное состояние идеального газа (или любой
простой системы) полностью определяется
значениями всего лишь двух параметров —
температуры Т и объема V (химический состав газа
предполагается заданным). Соответственно,
давление в такой системе
P f V , T .
Это соотношение называют термическим
уравнением состояния, или уравнением состояния,
идеального газа. В термодинамике уравнение
состояния исследуемой системы предполагается
известным из опыта.
19
20.
Законы идеальных газовЗакон Бойля-Мариотта:
если T, m = const, то
Закон Гей-Люссака:
если P, m = const, то
Закон Шарля: если
V, m = const, то
PV const.
V
const.
T
P
const.
T
20
21.
Законы идеальных газовЗакон Дальтона: давление смеси газов
равно сумме парциальных давлений
каждого из газов, составляющих смесь.
Закон Авогадро: один моль газа при
нормальных условиях занимает объем
равный 22,41 л.
21
22.
Идеальный газМолем вещества называют такое его
количество, в котором находится NA = 6,02∙1023
молекул; NA - число Авогадро.
Нормальные условия соответствуют
температуре 273,15 градусов Кельвина (273,15
К) и давлению (1,013)·105 Па (паскалей).
Молярная масса = массе 1-го моля вещества.
Обозначается M (не путать с m – массой газа).
Количество молей ν = m/M = N/NA; N – число
молекул в веществе.
22
23.
Уравнение состоянияидеального газа
Законы идеального газа можно свести к
одному уравнению (уравнению
Менделеева-Клапейрона)
PV
R,
T
где R = 8,31 Дж/(моль·К) – универсальная
газовая постоянная.
23
24.
Уравнение состоянияидеального газа
Уравнение Менделеева-Клапейрона
допускает несколько различных форм
записи:
m
PV
RT , P nkT ,
M
где n – концентрация молекул;
k = R/NA = 1,38·10-23 Дж/К – постоянная
Больцмана.
24
25.
ТемператураТемпература в молекулярной физике – мера
хаотического движения молекул: чем больше
температура, тем быстрее движутся молекулы.
В термодинамике работают с абсолютной или
термодинамической температурой,
измеряемой по шкале Кельвина (K): T =
273,15 + t, где t – температура в градусах
Цельсия. Например, 10 градусов Цельсия
соответствует температура 283,15 К, а нулю
градусов Цельсия – температура 273,15 К.
25
26.
Идеально-газовая шкалаБыло замечено, что при постоянном объеме и
массе идеального (т.е. реального
разреженного) газа его давление зависит от
температуры по закону
P P0 1 t ,
где P0 – давление при начальной температуре.
С помощью закона Шарля получим
P P0 1 t P0
,
T
T
T0
или
T T0 T0 t.
Экспериментально измеренное α = 1/273,15 К-1.
26
27.
Основное уравнение молекулярнокинетической теории идеального газаРассмотрим сферический сосуд радиусом R
Молекула ударяет в
стенку в точке A,
передает стенке импульс.
Затем ударяется в точке
B, снова передает
импульс, и т.д. Давление
газа обусловлено
многократными
соударениями молекул со
стенками сосуда.
27
28.
Основное уравнение молекулярнокинетической теории идеального газаОбозначим ϑ – скорость молекулы идеального
газа. В соответствии с моделью идеального газа
молекулы испытывают только упругие
столкновения. Следовательно, изменение
импульса молекулы при ее ударе о стенку
p 2m0 cos ,
где m0 – масса молекулы. Среднее число ударов
молекулы о стенку в единицу времени будет равно
ср
AB
2 R cos
.
28
29.
Основное уравнение молекулярнокинетической теории идеального газаУмножая число ударов на передаваемый стенке
сосуда импульс, получим силу, которая действует
на стенку при ударах о нее одной молекулы
m0 2
F0 p ср
2m0 cos
.
2 R cos
R
Чтобы получить полную силу – необходимо
просуммировать по всем молекулам. Для
простоты будем считать, что все молекулы имеют
одинаковую массу. Тогда можно записать
N
m0
F F0,i
R
i 1
N
2
i.
i 1
29
30.
Основное уравнение молекулярнокинетической теории идеального газаВведем среднюю квадратичную скорость
молекул по формуле
кв
2 ,
2
1 N 2
i ,
N i 1
где N – число молекул в сосуде. Поскольку сила F и
давление на стенки сосуда связаны соотношением
F PS ,
где S – площадь поверхности сосуда, получим
1
2
PS P 4 R F m0 N кв2 ,
R
30
31.
Основное уравнение молекулярнокинетической теории идеального газаили
4 3 1
2
P
R Nm0 кв .
3
3
Следовательно, основное уравнение МКТ
можно записать в следующем виде:
1
2
PV Nm0 кв ,
3
где N – число молекул в объеме сосуда V; m0 –
масса одной молекулы; P – давление газа на
стенки сосуда.
31
32.
Основное уравнение молекулярнокинетической теории идеального газаОсновное уравнение МКТ можно
преобразовать, если учесть, что N= NAν, имеем
1
PV N A m0 кв2 ,
3
или
2
кв
PV
1
N A m0
.
T
T
3
Пользуясь уравнением МенделееваКлапейрона найдем
кв
3RT
3kT где k – постоянная
,
Больцмана.
N A m0
m0
32
33.
Основное уравнение молекулярнокинетической теории идеального газаС учетом того, что
m
E0
2
получим
2
0 кв
- средняя кинетическая энергия
движения молекулы,
3
i
E0 kT kT ,
2
2
где i – число степеней свободы молекулы газа (для
поступательного движения молекулы i=3). Из этого
выражения следует, что на одну степень свободы
приходится (1/2)kT энергии (теорема Больцмана).
Таким образом, температура – мера средней
кинетической энергии движения молекул газа.
33
34.
Молекулярная физикаТема 3:
Сведения из теории
вероятностей
34
35.
Содержание• Случайные величины. Определение
вероятности. Нормировка вероятности.
Эргодическая гипотеза. Плотность
вероятности.
• Теорема сложения вероятностей.
• Теорема умножения вероятностей.
• Среднее значение дискретной и
непрерывной случайных величин.
35
36.
Случайная величинаВ системе некоторых событий и некоторого
(большого) числа факторов, определяющих
реализацию событий, каждое событие имеет
смысл случайного, если мы не можем точно
определить факторы, приводящие к
реализации данного события. Мерой
реализации события служит его вероятность,
т.е. то сколь часто событие реализуется.
Например, если бросается игральная кость,
имеющая 6 граней, то вероятность выпадения
каждой из граней равна 1/6. Сумма всех
вероятностей равна 1.
36
37.
ВероятностьВероятностью i-го состояния wi или вероятностью
значения величины Li называется предел отношения
числа измерений Ni, дающих значение Li, к полному
числу измерений N, когда последнее неограниченно
возрастает, т.е.
Ni
wi lim
N
N
.
Вероятность i-го состояния wi определяется также как
предел ti, в течении которого система находится в этом
состоянии, к полному времени наблюдения T при
неограниченном возрастании последнего:
ti
wi lim .
T T
Условием нормировки вероятности является
очевидное соотношение
w 1.
i
i
37
38.
ВероятностьВместо того, чтобы рассматривать изменение
состояния системы во времени, можно мысленно
представить себе совокупность n систем,
тождественных с данной, но в некоторый момент
времени хаотически распределенных по всем
возможным состояниям ni. Такую систему называют
статистическим ансамблем. Вероятность того, что
при случайном измерении будет обнаружена
система, находящаяся в i-м состоянии, равна
ni
wi lim .
n n
Вероятность по ансамблю должна быть равна
вероятности состояния. Это предположение
называется эргодической гипотезой.
38
39.
ВероятностьЕсли состояния системы меняются не
дискретным, а непрерывным образом, то
определение рассмотренное ранее теряет
смысл. Вместо него следует использовать
dwL L dL,
где dwL – вероятность того, что величина L
лежит в интервале между L и L+dL, ρ(L) –
плотность вероятности.
Условием нормировки вероятности является
соотношение
dw L dL 1.
L
39
40.
Теорема сложения вероятностейПусть одновременные нахождения системы в
состояниях i и k являются взаимно
исключающими друг друга событиями.
Тогда время пребывания системы в одном из
этих состояний, – безразлично в каком именно
(т.е. либо в i-м либо в k-м), - будет равна сумме
времен пребывания в i-м и в k-м состояниях:
ti tk
ti
tk
wi k lim
lim lim wi wk
T
T T
T T
T
- это соотношение называется законом
сложения вероятностей.
40
41.
Теорема умножения вероятностейПусть имеются две совершенно независимые друг
от друга системы. Обозначим wL и wM вероятности
i
k
того, что первая система находится в состоянии Li и
вторая система находится в состоянии Mk.
Вероятности wL и wM являются независимыми, если
i
k
вероятность того, что первая система находится в
состоянии i, не зависит от того, что вторая система
находится в состоянии k. Тогда вероятность того, что
одновременно первая система находятся в состоянии
i, а вторая в состоянии k, равна
wLi M k wLi wM k
- это соотношение называется законом умножения
вероятностей.
41
42.
Теорема умножения вероятностейВ самом деле, пусть мы следим за обеими
системами одновременно. Первая система
проводит время tL =TwL в состоянии L=Li, а
i
i
вторая система из этого времени проводит
время tM =tL wM =TwL wM в состоянии M=Mk.
k
i
k
i
k
Искомая вероятность одновременного
нахождения первой системы в состоянии Li,
а второй в состоянии Mk равна
lim
T
TwLi wM k
wLi wM k ,
T
что и поясняет закон умножения вероятностей.
42
43.
Дискретная величинаL wi Li
i
L w L
2
2
i i
i
w 1
i
- среднее значение;
- квадрат среднего
квадратичного значения;
- условие нормировки.
i
Полезные соотношения
L L wi Li L wi Li L
i
L L
2
i
wi Li L
i
2
w
i
L L 0,
i
wi L2i 2 Li L L
i
2
L 2 L L L L L .
2
2
2
2
43
44.
Непрерывная величинаL L dL
- среднее значение;
L L dL
- квадрат среднего
квадратичного значения;
2
2
- условие нормировки.
dL 1
Полезные соотношения
L L L L dL L dL L
L L
2
L L
2
dL
dL L 2 L L L
2
L L 0,
2
dL
L 2 L L L L L .
2
2
2
2
44
45.
Молекулярная физикаТема 4:
Элементы статистической
физики
45
46.
Содержание• Микроскопическое состояние.
Макроскопическое состояние.
• Формулы элементарной комбинаторики.
Формула Стирлинга.
• Биноминальное распределение.
Распределения Пуассона и Гаусса.
• Вероятность макросостояния идеального
газа, реализуемая посредством различных
микросостояний.
46
47.
Микро- и макросостоянияМикроскопическое состояние идеального
газа характеризуется заданием всех координат
молекул и всех их скоростей, т.е. в общем
случае 6N величинами.
Макроскопическое состояние идеального
газа характеризуется заданием
термодинамических параметров: давления,
температуры, объема и массы.
Поскольку молекулы газа постоянно
хаотически движутся, то заданному
макросостоянию соответствует большое
число микросостояний.
47
48.
Формулы комбинаторикиФакториал целого и положительного числа
n определяется формулой
n! 1 2 3 ... n
0! 1
В случае больших n>>1 имеет место
формула Стирлинга
n
n!
e
n
2 n , e 2, 7183
Число сочетаний из n по m<n определяется
формулой
n!
m
Cn
m ! n m !
48
49.
Биноминальное распределениеБином Ньютона выражается формулой
n
m m n m
p
q
C
np q
n
m 0
Если p+q=1 и p, q>0, то бином Ньютона
превращается в биноминальное распределение
wm Cnm p m 1 p
n m
n
,
w
m 0
m
1
Биноминальное распределение соответствует
распределению вероятности того, что при n
испытаниях рассматриваемое событие
(имеющее вероятность p) реализуется m раз.
49
50.
Биноминальное распределениеПример: Распределение вероятностей при бросании
2-х игральных костей
Вероятность w при бросании 2-х игральных костей как
функция выпавших очков N
50
51.
Биноминальное распределениеВ случае больших n и m воспользуемся
формулой Стирлинга, получим
m
nep
n
wm
1 p .
mq
Дифференцируя это выражение по m и
приравнивая к нулю, получим
mmax np / q np m0
где m0 – соответствует максимуму
биноминального распределения.
51
52.
Распределение ПуассонаВ случае n>>m и np=m0=const можно
воспользоваться формулой Стирлинга
n!
n!
n m
n
m
m
wm
p 1 p
p 1 p
m ! n m !
m ! n m !
1 n n m
m! e e
n
n m
p m 1 p
n
m0
m
n
m0
1
,
m!
n
В пределе получим
m
m m
n
m0 m0 m0 e
w lim
1
0
m
n
m!
n
m!
- распределение Пуассона.
52
53.
Распределение ГауссаРассмотрим случай n>>m, но n, m>>1 и |m--m0|<<m, m0.
Прологарифмируем распределение Пуассона, получим
ln wm m ln m0 m0 ln m!
пользуясь формулой Стирлинга, получим
ln wm m ln m0 m ln m m m0
Разложим последнее выражение в ряд Тейлора вблизи
точки m=m0, ограничиваясь квадратичным членом.
Формула Тейлора разложения функции f(x) в окрестности
точки x0 (где |x--x0|<<x, x0) имеет вид
1
f x f x0 f x0 x x0
1!
1
1
2
3
f x0 x x0 f x0 x x0 ...
2!
3!
53
54.
Распределение ГауссаПредставим
ln wm f m m ln m0 m ln m m m0 ,
тогда
f m0 0,
f m0 0,
1
f m0 ,
m0
следовательно, можно записать
ln wm
или
m m0
2m0
m m0 2
wm C exp
,
2m0
2
...
w
m
1
m
- называется распределением Гаусса.
54
55.
Вероятность макросостоянияидеального газа
Вероятность макросостояния идеального
газа можно определить формулой
n!
n m
m
wm
p 1 p
m! n m !
где n – полное число молекул, находящееся в
полном объеме газа V, m – некоторое число
молекул (из общего их числа n), находящихся в
выбранном объеме V1, p=V1/V – вероятность
нахождения молекулы в объеме V1.
Наиболее вероятной концентрацией молекул в
объеме V1 является такая, которая соответствует
равномерному распределению молекул по объему.
55
56.
Молекулярная физикаТема 5:
Распределение молекул
идеального газа по скоростям
56
57.
Содержание• Границы применимости распределения Максвелла.
Принцип детального равновесия. Распределение
Максвелла по компонентам скорости.
Распределение Максвелла по абсолютному
значению скорости. Распределение Максвелла по
кинетической энергии.
• Характерные скорости. Число молекул в различных
участках распределения Максвелла. Приведенное
распределение Максвелла.
• Экспериментальная проверка распределения
Максвелла.
57
58.
Распределение МаксвеллаСкорости молекул в идеальном газе принимают
произвольные значения. Скорость молекулы зависит от
температуры. А сколько молекул из общего их числа
имеют ту или иную скорость при заданной
температуре? Ответ на этот вопрос дал Дж.К.Максвелл
в 1859 г. Распределение молекул по скоростям было
получено при следующих условиях: все молекулы
имеют одинаковую температуру (газ равновесный); при
соударениях молекул соблюдается условие детального
равновесия, т.е. при соударении пары молекул, когда
эти молекулы поменяли свои скорости, в газе всегда
найдутся две другие молекулы, которые приобрели те
же самые скорости, которые имелись в первой паре до
соударения, иначе, число молекул, имеющих заданную
скорость не меняется со временем; все молекулы
одинаковые (имеют одинаковую массу и размер).
58
59.
Распределение МаксвеллаМаксвелл предположил, что число молекул
газа, имеющих скорости в диапазоне от ϑx до
ϑx+dϑx, от ϑy до ϑy+dϑy и от ϑz до ϑz+dϑz равно
dN N0 A exp x2 y2 z2 d x d y d z ,
z
exp
z
e
.
где
Для нахождения нормировочного
коэффициента учтем, что
dN N0 , exp u du .
2
59
60.
Распределение МаксвеллаВ результате получим (хотя бесконечных скоростей
нет, оставляем бесконечные пределы при
интегрировании, т.к. интегралы быстро сходятся)
dN N0
N 0 A exp x2 y2 z2 d x d y d z
2
2
2
N 0 A exp x d x exp y d y exp z d z
N0 A .
3/2
Следовательно
A .
3/2
60
61.
Распределение МаксвеллаТаким образом
dN N0 exp x2 y2 z2 d x d y d z .
3/2
Для нахождения α вычислим квадрат средней
квадратичной скорости по формуле
кв2 2
1
2
dN
N0
3/2
2
2
d x d y d z ,
exp
где
2 x2 y2 z2 .
61
62.
Распределение МаксвеллаПреобразуем выражение
2
2
d x d y d z
exp
2
2
d x d y d z
exp
x
2
2
d x d y d z
exp
y
2
2
d x d y d z
exp
z
3 u 2 exp u 2 du.
62
63.
Распределение МаксвеллаДля вычисления последнего интеграла
поступим следующим образом. Обозначим
I
2
exp
u
du
.
Вычисляя производную
dI
1
u 2 exp u 2 du
,
3
d
2
находим
2
2
du
u
exp
u
1
.
3
2
Аналогичным образом получим
4
2
du
u
exp
u
3
.
5
4
63
64.
Распределение МаксвеллаТаким образом, получаем
3
2
2
exp d x d y d z 2 .
3/2
Данный интеграл можно вычислить иначе. Для
этой цели перейдем в «сферическое
пространство». Получим
0
2
2
2
2
2
exp
d
d
d
exp
4
d
x y z
4 exp 2 d 2
4
0
3
2
u exp u du 2
3/2
4
- тот же самый результат.
64
65.
Распределение МаксвеллаТаким образом, можно записать
2
1
dN
N0
3/2
3
2
3/2
3
.
2
С другой стороны, из основного уравнения МКТ
известно, что
2
кв
2
3kT
,
m0
значит
2
m0
3 3kT
,
.
2
m0
2kT
65
66.
Распределение МаксвеллаТаким образом, распределение Максвелла по
компонентам скорости имеет вид
1
dN
m0
w
N0 d x d y d z
2
kT
3/2
m0 2
exp
,
2kT
и распределение Максвелла по
абсолютному значению скорости имеет вид
1 dN
m0
w 4
N0 d
2
kT
3/2
m0 2 2
exp
.
2kT
66
67.
Давление газа на стенку сосудаДавление газа на стенку сосуда это импульс, передаваемый
молекулами стенке в единицу времени на единицу площади. При
этом мы должны учитывать только молекулы, движущиеся в
направлении стенки и перпендикулярно к ней. Пусть стенка
расположена где-то на положительной части декартовой оси x.
Тогда одна молекула передает стенке импульс 2m0ϑx, а за единицу
времени молекула пройдет расстояние ϑx. Следовательно,
изменение давления будет равно dPx=2m0(ϑx)2dNx+/V, где dNx+ –
учитывает, что молекула движется к стенке вдоль оси x, V – объем
сосуда. В результате для давления запишем
2N m m
Px 0 0 0
V 2 kT
2 N 0 m0 m0
V 2 kT
3/2
m0 2 2
0 exp 2kT x d x d y d z
m0 y2
m0 z2
m0 x2 2
exp 2kT d y exp 2kT d z 0 exp 2kT x d x
3/2
2
2kT
2 N 0 m0 m0 2 kT 1
N0
kT n0 kT .
V 2 kT m0 4
V
m0
3/2
3
67
68.
Кинетическая энергияПоскольку кинетическая энергия молекулы
m0 2
E
,
2
то можно записать
dN N0
2
kT
3
E
exp
EdE
kT
- распределение молекул по кинетической энергии.
Для средней энергии найдем
E
2
1
2
E
EdN
E
exp
EdE
3
N0
kT
kT 0
kT x
0
3/2
3
exp x dx
kT y exp y dy kT .
2
0
4
4
2
68
69.
Средняя арифметическая скоростьМы знаем среднюю квадратичную скорость. Вычислим
среднюю арифметическую скорость по формуле
1
m0
ср
dN 4
N0
2
kT
m0
2
2 kT
3/2
m0
2
2
kT
3/2
3/2
m0 2 2
0 exp 2kT d
m0 2 2 2
0 exp 2kT d
2kT
m
0
2
8kT
0 x exp x dx m0 .
Нарисуем распределение Максвелла
69
70.
Распределение Максвеллагде T3>T2>T1.
70
71.
Наивероятнейшая скоростьВидно, что распределение Максвелла имеет максимум.
Найдем соответствующую этому максимуму скорость,
которая называется наивероятнейшей скоростью.
Используем условие обращения в нуль производной в
соответствующей точке. Имеем
d 1 dN
0,
d N 0 d
нв
или
m0 2 2
d
exp
d
2kT
0.
нв
Вычисляя найдем
2kT
m0 2
2
0, нв
.
m0
kT
нв
71
72.
Приведенное распределениеВведем переменную
,
нв
Тогда распределение Максвелла примет т.н.
приведенный вид
dN
4
2
2
exp d .
N0
72
73.
Число молекул, имеющих скорости взаданном интервале
Для нахождения числа молекул ΔN, имеющих
скорости в диапазоне ϑ1<ϑ<ϑ2, следует найти
интеграл
3/2 2
2
m0 2
m0
N 4 N0
d .
exp
2 kT 1
2kT
К сожалению, такой интеграл можно
вычислить только численным способом. В
случае скоростей из диапазона от ϑ до ϑ+Δϑ, где
Δϑ<<ϑ, приближенно найдем
m0
N 4 N0
2
kT
Численное вычисление дает
3/2
m0 2 2
exp
.
2kT
N нв 0,5724 N0 , N нв 0, 4276 N0 .
73
74.
Экспериментальная проверкаЭксперимент Штерна
74
75.
Экспериментальная проверкаЭксперимент Элдриджа
75
76.
Молекулярная физикаТема 6:
Кинематические характеристики
молекулярного движения
76
77.
Содержание• Частота ударов о стенку.
• Поперечное сечение столкновений. Частота
столкновений.
• Средняя длина свободного пробега
молекул.
• Экспериментальное определение длины
свободного пробега молекул.
77
78.
Частота ударов о стенкуДля нахождения частоты ударов молекул о стенку
сосуда ν необходимо вычислить интеграл
3/2
m0 2
0 x exp 2kT d x d y d z
3/2
m0 y2
m0 x2
m0
ns
d y
d x exp
x exp
2 kT 0
2kT
2kT
1/2
m0 z2
m0 x2
m0
exp
d
ns
exp
d
z
x
x
2 kT 0
2kT
2kT
ns
m0
dN
ns
x
N0
2 kT
1/2
1
1 8kT
8kT 1
ns
exp
x
dx
ns
ns ср ,
4 m0 0
m0 4
4
где n – концентрация молекул, s – площадь стенки.
При вычислении было учтено, что вклад вносят только
молекулы, движущиеся в направлении стенки
(находящейся на положительной части оси x) и
имеющих направление скорости нормальное, по
78
отношению к стенке.
79.
Поперечное сечениеА насколько часты столкновения молекул газа между
собой? Пусть одна молекула движется со скоростью
ϑ, а остальные покоятся, тогда молекула испытает
столько столкновений, сколько молекул будет у нее на
пути. Столкновением можно считать такое событие,
когда центр молекулы-мишени будет отстоять от
траектории центра летящей молекулы не далее чем на
d=2r, где r – эффективный радиус молекулы, d –
эффективный диаметр молекулы.
79
80.
Частота столкновенийТ.е. в единицу времени произойдут столкновения
только с теми молекулами, которые попадают внутрь
цилиндра с сечением σ=πd2. где величина σ –
называется поперечным сечением столкновения.
Объем цилиндра (в единицу времени) σϑ, концентрация
частиц в объеме n, значит частота столкновений
n d n .
2
Если учесть, что все молекулы в газе движутся, то
предыдущую формулу необходимо изменить. Во-первых,
необходимо заменить ϑ→ϑср; и, во-вторых, учесть
относительность движения молекул по отношению друг к
другу. В результате для средней частоты столкновений
можно получить
ср 2n ср 2 d n ср .
2
80
81.
Длина свободного пробегаСредняя длина свободного пробега молекулы –
среднее расстояние, которое проходит молекула от
одного столкновения до другого. Учитывая, что
молекулы движется со средней скоростью ϑср, а
среднее время между столкновениями τст=1/νср,
получим для средней длины свободного пробега
lср ср ст
ср
1
kT
,
2
2
ср
2 d n
2 d P
где было учтено, что
P nkT .
81
82.
Длина свободного пробегаДля длины свободного пробега можно
получить другое выражение, исходя из общих
соображений. Действительно, по определению
lср xdw,
0
где dw – вероятность пролететь без соударений
путь x, а затем испытать столкновение в
интервале от x до x+dx. Эта вероятность
определяется отношением числа молекул,
испытавших первое столкновение в интервале
dx, к полному числу молекул N0.
82
83.
Длина свободного пробегаЧисло молекул dN, не испытавших столкновений в
интервале от 0 до x, пропорционально числу
молекул, которые долетели до точки x, и длине
интервала dx, где они испытали столкновение:
dN N x dx,
где знак минус указывает на то, что число молекул
уменьшается; α – некоторый коэффициент
пропорциональности. После интегрирования,
получим
N x N0 exp x .
83
84.
Длина свободного пробегаТаким образом, вероятность пролететь без
столкновений путь от 0 до x, а затем испытать
столкновение в интервале от x до x+dx, равна
N x
dN
dw
dx exp x dx.
N0
N0
Следовательно, длина свободного пробега равна
lср xdw x exp x dx
0
0
1
.
Наконец, число молекул, пролетевших без столкновений
путь от 0 до x, равно
x
N x N 0 exp
lср
.
84
85.
Экспериментальное определениедлины свободного пробега
Эксперимент Борна и Бормана
85
86.
Молекулярная физикаТема 7:
Процессы переноса
86
87.
Содержание• Процессы переноса в газах. Теплопередача,
трение, диффузия. Взаимодиффузия в газе
из различных молекул.
• Физические явления в разреженных газах.
• Основные особенности явлений переноса в
твердых телах и жидкостях.
87
88.
Процессы переносаСталкиваясь друг с другом молекулы
обмениваются импульсом и кинетической
энергией. Благодаря этому газ, например,
является проводником тепла. При этом, хотя в
общем газ не находится в равновесном
состоянии, можно говорить о локальном
равновесии, т.е. о локальной температуре газа.
Время восстановления локального
равновесия характеризуется средним
временем между столкновениями τст.
88
89.
Перенос тепла (теплопроводность)Процесс переноса тепла в положительном
направлении оси x описывается уравнением
Фурье
dT
dQ
sdt ,
dx
где dQ – элементарное приращение теплоты; χ
– коэффициент теплопроводности; dT/dx –
температурный градиент (знак минус
указывает на то, что поток тепла идет в
направлении уменьшения градиента
температуры); s – элемент площади
(нормальной к направлению переноса), через
которую идет поток; dt – элементарное
приращение времени.
89
90.
Перенос тепла (теплопроводность)В случае идеального газа коэффициент
теплопроводности может быть найден в следующем
виде
i
i
1 CV
knlср ср
R lср ср
lср ср ,
6
6M
3M
где i – число степеней свободы молекулы; n –
концентрация газа; lср – средняя длина свободного
пробега молекулы; ϑср – средняя арифметическая
скорость молекулы; M – молярная масса газа; ρ –
плотность газа; CV – молярная теплоемкость газа
при постоянном объеме.
Поскольку lсрρ=const для заданного газа, то
коэффициент теплопроводности идеального газа не
зависит от его плотности (правило Максвелла).
90
91.
Перенос трения (вязкость)Сила внутреннего трения (вязкость)
описывается формулой Ньютона
du
dF
s,
dx
где dF – элементарное приращение силы трения; η –
коэффициент внутреннего трения (динамический
коэффициент вязкости); u – скорость течения вещества
как целого в направлении перпендикулярном к
направлению действия силы (которая направлена в
положительную сторону оси x); du/dx – градиент
скорости течения вещества (знак минус указывает на то,
что сила действует в направлении уменьшения
градиента); s – элемент площади (нормальной к
направлению действия силы), на которую оказывается
воздействие.
91
92.
Перенос трения (вязкость)В случае идеального газа коэффициент
внутреннего трения может быть найден в
следующем виде
1
lср ср .
3
Поскольку lсрρ=const для заданного газа, то
коэффициент трения идеального газа не
зависит от его плотности (правило
Максвелла).
92
93.
Перенос массы (диффузия)Процесс переноса массы в положительном
направлении оси x описывается уравнением
Фика
d
dm D
sdt ,
dx
где dm – элементарное приращение массы; D –
коэффициент диффузии (самодиффузии);
dρ/dx – градиент плотности (знак минус
указывает на то, что диффузионный поток идет
в направлении уменьшения градиента
плотности); s – элемент площади (нормальной
к направлению переноса), через которую идет
поток; dt – элементарное приращение времени.
93
94.
Перенос массы (диффузия)В случае идеального газа коэффициент
диффузии может быть найден в следующем
виде
1
D lср ср .
3
Данный коэффициент диффузии описывает перенос
массы в идеальном газе из одинаковых молекул
(самодиффузия), когда в каком то его области возникает
отличный от нуля градиент плотности.
В том случае, если смешиваются два газа из различных
молекул, возникает явление называемое взаимной
диффузией, когда каждый из газов проникает в другой.
94
95.
Взаимная диффузияПроцесс взаимной диффузии двух газов
описывается системой уравнений
dm1
d 1
dm2
d 2
1 s D12
s,
2 s D21
s,
dt
dx
dt
dx
D2 n1 D1n2
1
1
D12 D21
, D1 lср ,1 ср ,1 , D2 lср ,2 ср ,2 ,
n1 n2
3
3
где индексы «1» и «2» различают первый и
второй газы; ϑ – гидродинамическая скорость
потока газа как целого; D12 =D21 –
коэффициент взаимной диффузии. При
записи данных выражений предполагалось, что
n1+n2=const.
95
96.
Ультраразреженный газЕсли длина свободного пробега молекул
превышает линейные размеры сосуда, в
котором заключен газ, то такой газ
называют ультраразреженным. В таком
газе молекулы не сталкиваются друг с
другом, поэтому все явления переноса
протекают иначе, чем в обычном идеальном
газе. Молекулы сталкиваются только со
стенками сосуда.
96
97.
Теплоперенос в ультраразреженном газеПусть в газе имеются две пластинки с
температурами T1 и T2. Тогда, для элементарно
приращения тепла можно получить
CV
1
dQ ср
T2 T1 Sdt T2 T1 Sdt ,
6
M
где S – площадь пластинки, а величина
CV
1
ср
6
M
- называется коэффициентом
теплопроводности ультраразреженного газа.
Видно, что эта величина пропорциональна
плотности газа: с уменьшением плотности
теплопроводность газа стремится к нулю.
97
98.
ЭффузияЕсли разделить ультраразреженный газ в сосуде на
две половины перегородкой с отверстием, то, если
размер отверстия будет меньше длины свободного
пробега, молекулы будут проходить через отверстие
по одиночке. Не сталкиваясь друг с другом. Такой
процесс истечения газа называется эффузией.
В случае тепловой эффузии, когда стенки обеих
частей сосуда находятся при различных
температурах T1 и T2, условием равновесия будет
равенство числа молекул проходящих в единицу
времени из одной части сосуда в другую.
Следовательно, можно записать
n1 ср ,1 n2 ср,2 ,
или
P1
T2
.
P2
T1
98
99.
ЭффузияЕсли имеется смесь двух
ультраразреженных газов при одной и той
же температуре, то через малое отверстие в
первую очередь будут проходить более
подвижные, т.е. более легкие молекулы.
Такое явление называется изотермической
эффузией. Изотермическая эффузия
используется, например, при разделении
изотопов (легких и тяжелых) молекул одного
и того же газа.
99
100.
Диффузия в твердом телеДиффузия (самодиффузия)в твердых
кристаллических телах осуществляется главным
образом следующими тремя путями.
1. Если в соседнем узле кристаллической решетки
имеется вакансия, то один из соседних атомов может
перескочить в вакантный узел.
2. Если атом покинул свой узел, а рядом нет вакансии, то
он располагается между узлами.
3. Может произойти обмен атомами в соседних узлах
решетки.
Коэффициент диффузии при этом имеет вид
W
D D0 exp ,
kT
где D0 – постоянная определяемая свойствами
вещества; W – энергия активации диффузии.
100
101.
Теплопроводность твердого телаКоэффициент теплопроводности
кристаллического твердого тела можно
представить в виде
CV
1
зв lф
,
3
M
где ϑзв – скорость звука в твердом теле; lф –
средняя длина свободного пробега фонона в
твердом теле (фонон – квазичастица,
являющаяся квантом (элементарной величиной)
коллективных колебаний атомов в кристалле).
101
102.
Процессы переноса в жидкостиКоэффициент диффузии (самодиффузии) в жидкости
имеет такой же вид как и для твердого тела. При этом
молекула жидкости находится не в узле
кристаллической решетки, а в некотором «месте
оседлой жизни». Перескочить молекуле из одного
места в другое проще (требуется меньше энергии),
чем для атома в узле кристаллической решетки.
Явление теплопроводности в жидкости сложно, и
каких-либо общих аналитических выражений пока не
получено. Можно лишь сказать, что теплопроводность
жидкостей лежит где то в середине между
теплопроводности газа и теплопроводности твердого
тела.
102
103.
Вязкость жидкостиКоэффициент вязкости жидкости при постоянной
температуре хорошо описывается формулой
Бачинского
A
,
V0 b
где A и b – постоянные, определяемые свойствами
жидкости (b – постоянная Ван-дер-Ваальса); V0 –
молярный объем жидкости.
Зависимость вязкости от температуры дается формулой
Френкеля
u
0 exp ,
kT
где η0 – постоянная определяемая свойствами
жидкости; u – глубина «потенциальной ямы», в
которой находится каждая молекула жидкости».
103
104.
Молекулярная физикаТема 8:
Распределение молекул идеального
газа в однородном поле сил
104
105.
Содержание• Барометрическая формула. Распределение
Больцмана.
• Распределение Максвелла - Больцмана.
Распределение Гиббса.
• Экспериментальное подтверждение
распределения Больцмана.
• Модель атмосферы Земли. Рассеяние
атмосферы планет.
105
106.
Барометрическая формулаДля вывода барометрической формулы рассмотрим
цилиндрический сосуд с площадью основания s, который
находится в поле тяготения Земли. На некоторой высоте h*
выбираем слой газа толщиной dh и массой dm.
Рассматривая силы,
действующие на слой,
получим уравнение
P h dh s gdm P h s.
106
107.
Барометрическая формулаУчтем, что
dm h * sdh,
m0
M
h *
P h *
P h * ,
RT
kT
где m0 – масса молекулы; ρ(h*) – плотность газа на
высоте h* (температуру считаем не зависящей от
высоты). В результате получим
P h dh P h
m0 g
P h * .
dh
kT
107
108.
Барометрическая формулаПри стремлении dh→0 получим (h*→h)
dP h
m0 g
P h .
dh
kT
Решением этого уравнения является
m0 gh
P h P0 exp
, P0 P 0 ,
kT
- зависимость изменения давления с высотой, при
постоянной температуре, называемая барометрической
формулой.
С учетом того, что P nkT ,
получим
m0 gh
n h n0 exp
, n0 n 0 .
kT
108
109.
Распределение БольцманаБарометрическая формула является частным случаем
общего распределения, называемого распределением
Больцмана. В самом деле, учитывая, что
потенциальная энергия молекулы на высоте h
U m0 gh,
и n~N, получим
N
U
w exp
N0
kT
- распределение Больцмана. Данное
распределение справедливо не только для
гравитационного поля, но и для любого другого
однородного (и не только) поля сил.
109
110.
Распределение МаксвеллаБольцманаЕсли на идеальный газ действует
потенциальное поле (например, сила тяжести),
то распределение Максвелла должно быть
изменено с учетом распределения Больцмана.
Подставляя распределение Больцмана в
распределение Максвелла, получим
1
dN
m0
w
N0 d x d y d z
2 kT
3/2
m0 2
1
exp
U
kT
2
- распределение Максвелла-Больцмана.
110
111.
Распределение ГиббсаРаспределение Максвелла-Больцмана является
частным случаем общего распределения,
называемого распределением Гиббса
(полученного в 1901 г.):
Ei
gi exp
kT
,
wi
Ej
j g j exp kT
где gi – статистический вес (кратность вырождения
(повторения)) рассматриваемого состояния i системы,
имеющей энергию Ei. Распределение Гиббса широко
применяется для исследования как классических, так и
квантовых систем.
111
112.
Экспериментальное подтверждениеРаспределение Больцмана может быть применено не
только к молекулам, но и к любым другим малым
частицам. В частности, если взвесить малые частицы
в жидкости (чтобы они очень медленно там
двигались), и налить такую жидкость в высокий
сосуд, а затем подсчитать число частиц на различных
высотах в сосуде, то их число, как функция
расстояния от дна сосуда, должно удовлетворять
распределению Больцмана. Такой эксперимент был
выполнен Перреном. Он не только доказал
справедливость распределения Больцмана, но и
сумел вычислить постоянную Больцмана, значение
которой оказалось достаточно близким к
современному.
112
113.
Атмосфера ЗемлиСтруктура,
температура и давление
Состав
113
114.
Рассеяние атмосферыРаспределение Больцмана позволяет объяснить,
почему газ преимущественно собирается вблизи
поверхности планеты. Это объясняет
устойчивую атмосферу планеты. Тем не менее,
поскольку гравитационная сила притяжения не
очень велика, всегда находятся молекулы,
которые улетают все дальше от поверхности
планеты. В результате, атмосфера планеты
постепенно рассеивается, т.е. становится все
менее плотной. Тем не менее, это очень
медленный процесс и жизни на Земле он пока
не угрожает.
114
115.
Молекулярная физикаТема 9:
Броуновское движение
115
116.
СодержаниеБроуновское движение. Флуктуации.
Опыт Перрена.
Вращательное броуновское движение.
Опыт Капплера.
116
117.
Броуновское движениеАнглийский ученый Броун увидел в микроскоп, что
малые частицы пыльцы, взвешенные в воде, хаотически
движутся. Впоследствии было выяснено, что причина
такого хаотического движения – удары молекул о
поверхность малых частиц. Это послужило одним из
доказательств молекулярной структуры вещества.
117
118.
Броуновское движениеТеория броуновского движения была развита в работах
Эйнштейна и Смолуховского. Принцип расчета
характеристик броуновского движения связан с одной
стороны с явлением диффузии, а с другой стороны, с
понятием флуктуаций, т.е. с вероятностными
(статистическими) свойствами движения броуновских
частиц.
Движение броуновских частиц удовлетворяет уравнению
диффузии с коэффициентом
D bkT ,
где b – подвижность частицы. В случае сферических
частиц с радиусом a, можно получить
kT
D
,
6 a
где η – динамический коэффициент вязкости
118
жидкости, в которую помещены частицы.
119.
Броуновское движениеПусть σr – среднее квадратичное смещение
(флуктуация смещения) броуновских частиц за
некоторое малое время t. Тогда для коэффициента
диффузии (с помощью статистического подхода)
можно получить следующее выражение
D
r2
.
6t
Сравнивая оба выражения для коэффицента
диффузии получим
kT
r
t,
a
т.е. флуктуация смещения броуновской частицы
увеличивается при увеличении температуры и
времени как корень квадратный из этих величин.
119
120.
Опыт ПерренаЭкспериментальную проверку правильности
теории движения броуновских частиц осуществил
Перрен. Он изучил движение малых сферических
частиц в жидкости с известной вязкостью, при
заданной температуре, измеряя среднее
квадратичное смещение частиц за заданное
время. В результате своих опытов Перрену
удалось вычислить постоянную Больцмана,
значение которой хорошо совпало с его
результатами по изучению распределения
Больцмана. Тем самым была экспериментально
подтверждена теория броуновского движения, и,
как следствие, молекулярная структура
вещества.
120
121.
Вращательное броуновское движениеВращательное броуновское движение также можно
наблюдать экспериментально. Если на тонкой нити
подвесить легкое зеркальце, то оно будет совершать
хаотические вращательные колебания. По величине
угла отклонения зеркального блика (от некоторой
средней точки) можно судить о величине флуктуации
вращательных колебаний. Причиной этих флуктуаций
являются удары молекул о поверхность зеркала. Для
среднего квадратичного угла вращательных
колебаний зеркальца σφ можно получить
kT
,
G
где G – модуль кручения нити. Как видно из
формулы, флуктуация угла поворота зеркальца
нарастает при увеличении температуры.
121
122.
Опыт КапплераЭксперимент с зеркальцем на нити
осуществил Капплер. С помощью своих
опытов Капплеру удалось вычислить
постоянную Больцмана, значение которой
оказалось в хорошем согласии с результатами
Перрена. Тем самым в еще одном
эксперименте была подтверждена
молекулярная структура вещества.
122
123.
Молекулярная физикаТема 10:
Теплоемкость идеального газа
123
124.
Содержание• Внутренняя энергия идеального газа.
• Степени свободы молекул. Теорема о
равнораспределении энергии по степеням
свободы.
• Теплоемкость изотропных и однородных тел.
Теплоемкость идеального газа.
• Расхождение теории теплоемкостей
идеального газа с экспериментом.
• Элементы квантовой теории теплоемкости.
124
125.
Внутренняя энергияВсякая термодинамическая система в любом
состоянии обладает некоторой энергией,
называемой полной энергией системы.
Полная энергия включает в себя
кинетическую энергию механического
движения системы как целого или ее
макроскопических частей, потенциальную
энергию, зависящую от положения системы во
внешнем силовом поле (гравитационном,
электрическом или магнитном), а также
внутреннюю энергию, зависящую только от
внутреннего состояния системы.
125
126.
Внутренняя энергияВ состав внутренней энергии входит энергия
всевозможных видов движения и взаимодействия
друг с другом всех частиц (молекул, атомов, ионов и
т. п.), образующих рассматриваемую систему.
Например, во внутреннюю энергию газообразного
тела входят:
– а) кинетическая энергия хаотического (теплового)
поступательного и вращательного движения молекул;
– б) кинетическая и потенциальная энергия колебаний
атомов в молекулах;
– в) потенциальная энергия, обусловленная силами
межмолекулярного взаимодействия;
– г) энергия электронных оболочек атомов и ионов;
– д) энергия движения и взаимодействия частиц
(нуклонов) в ядрах атомов.
126
127.
Внутренняя энергияВнутренняя энергия является однозначной
функцией термодинамического состояния системы.
Ее значение в каком-либо произвольно выбранном
состоянии не зависит от того, каким образом
система пришла в это состояние.
Внутренняя энергия U в системе, находящейся в
состоянии термодинамического равновесия, зависит
только от температуры и внешних параметров
системы. Для простой системы
U f V , T .
Это соотношение называется калорическим
уравнением состояния простой системы
(химический состав системы предполагается
заданным).
127
128.
Внутренняя энергия идеального газаВ случае идеального газа, кинетическая
энергия беспорядочного движения всех его
молекул определяет его внутреннюю энергию.
Таким образом, для идеального газа
i
i
U N E N kT RT ,
2
2
где N – число молекул в газе; i – число
степеней свободы молекулы газа.
128
129.
Число степеней свободыТаким образом, для вычисления внутренней энергии
идеального газа необходимо знать число степеней
свободы молекул, составляющих газ. Числом степеней
свободы материального тела (в том числе и молекулы)
называется минимальное число независимых
переменных, с помощью которых можно задать
положение тела в пространстве. Например, у
материальной точки – 3 степени свободы, а у абсолютно
твердого тела несимметричной формы – 6 степеней
свободы. В общем случае у J-атомной молекулы 3J
степеней свободы. При этом, 3 степени свободы –
соответствуют поступательным движениям молекулы;
2 (для линейной (вытянутой в линию) молекулы) или 3
(для нелинейной молекулы) степени свободы
соответствуют вращательным движениям молекулы.
Оставшиеся степени свободы являются степенями
свободы колебательных движений атомов в молекуле.
129
130.
Число степеней свободыДля линейной J-атомной молекулы можно записать
iпост 3,
iвращ 2,
iколеб 3 J 5.
Для нелинейной J-атомной молекулы можно записать
iпост 3,
iвращ 3,
iколеб 3 J 6.
130
131.
Внутренняя энергия идеального газаВ соответствии с теоремой Больцмана, следует
считать, что на каждую степень свободы
приходится (1/2)kT кинетической энергии. При этом
необходимо учесть, что на каждое колебательное
движение затрачивается в 2 раза больше энергии,
что вызвано одновременным присутствием как
кинетической, так и потенциальной энергетических
составляющих колебательного движения.
Следовательно для внутренней энергии идеального
газа можно записать
i
U
пост
iвращ 2iколеб
2
i
RT RT .
2
В случае жестких молекул iколеб=0.
131
132.
ТеплоемкостьМолярной теплоемкостью называется
количество тепла, которое надо сообщить
одному молю рассматриваемого вещества,
чтобы поднять его температуру на 1 градус.
C
Q
dT
.
1
Удельной теплоемкостью называется
отношение молярной теплоемкости к
молярной массе вещества.
C
c .
M
132
133.
Теплоемкость идеального газаРассмотрим один моль идеального газа при
постоянном объеме. В этом случае газ не
будет совершать работу при сообщении ему
теплоты (объем газа не меняется и для
стороннего наблюдателя газ не совершает
никакой работы). А вся сообщенная теплота
будет затрачена на увеличение внутренней
энергии. Поэтому, молярная теплоемкость
идеального газа при постоянном объеме
имеет вид
dU
i
CV
R.
dT 1 2
133
134.
Внутренняя энергия идеального газаВнутренняя энергия идеального газа, с учетом
последнего соотношения, принимает вид
U CV T .
Полученное выражение будет справедливым
при любых процессах в идеальном газе (не
только в случае V=const).
Заметим также, что, вообще говоря,
внутренняя энергия верна с точностью до
произвольной аддитивной постоянной.
Однако, это обстоятельство не учитывалось,
поскольку эту константу всегда можно выбрать
равной нулю, если соответствующим образом
условится о точке отсчета внутренней энергии.
134
135.
Теплоемкость идеального газаРассмотрим один моль идеального газа при
постоянном давлении. В этом случае при
сообщении газу теплоты, помимо увеличения
своей внутренней энергии, газ будет
совершать работу A против внешних сил.
Для вычисления работы
представим себе газ,
заключенный в
цилиндрический сосуд с
площадью сечения s,
который закрыт невесомым
поршнем, на который
действует постоянная сила F.
135
136.
Теплоемкость идеального газаТогда, элементарное приращение работы
идеального газа, совершаемой против внешних сил,
при смещении поршня на величину dh, будет равно
F
A Fdh d hs PdV .
s
Следовательно, молярная теплоемкость идеального
газа при постоянном объеме примет вид
dU A
dV
CP
CV P
CV R,
dT 1
dT 1
где было использовано уравнение МенделееваКлапейрона. Полученное соотношение между
молярными теплоемкостями называется
соотношением Майера.
136
137.
Теплоемкость идеального газаЭкспериментальные исследования теплоемкости
газа выявили отклонения от классической теории
теплоемкости газов, которая была изложена выше с
тем, что наблюдается в эксперименте. Отклонения
связаны с зависимостью теплоемкости от
температуры, которой в классической теории не
существует.
Теплоемкость 2-х атомной молекулы
137
138.
Теплоемкость идеального газаТаким образом, газ ведет себя так, как если бы благодаря
изменению температуры происходит включение (или
выключение (замораживание)) различных степеней
свободы: при малой температуре включены лишь
поступательные степени свободы, затем при повышении
температуры включаются вращательные, а затем и
колебательные степени свободы.
Переход от одного режима движения к другому
происходит не скачком, а постепенно в некотором
интервале температур. Это объясняется тем, что при
определенной температуре возникает лишь возможность
для молекул переходить в другой режим движения, и эта
возможность реализуется не всеми молекулами сразу, а
лишь их частью. По мере повышения температуры все
большая доля молекул переходит в другой режим
движения и поэтому кривая теплоемкости изменяется
плавно в некотором интервале температур.
138
139.
Элементы квантовой теории теплоемкостиЗависимость теплоемкости от температуры можно
объяснить только в рамках квантовой теории. Поясним это
на примере вычислений Эйнштейна для молярной
теплоемкости кристалла при постоянном объеме (1900 г.)
.
В соответствии с классической теорией, если в одном моле
кристалла (который рассматривается как одна молекула)
возбуждены все степени свободы, то его кинетическая
(внутренняя) энергия равна
i
E kT 3N AkT 3RT ,
2
поскольку
i 3 3 2 3N A 6 6 N A 6 6 N A .
139
140.
Элементы квантовой теории теплоемкостиСледовательно
CV 3R.
Полученное соотношение называется законом
Дюлонга-Пти. Действительно, при высоких
температурах (когда возбуждены все степени
свободы) закон Дюлонга-Пти выполняется.
А вот при более
низких температурах
теплоемкость
принимает другие
значения, и стремится
к нулю при T→0.
140
141.
Элементы квантовой теории теплоемкостиЭйнштейн предположил, что каждый атом в
кристалле ведет себя как независимый
гармонический осциллятор с энергией
1
h
n n , n 0, 1, 2, ...
,
2
2
где h – постоянная Планка; ω – циклическая
частота колебаний осциллятора.
Тогда, в соответствии с распределением Гиббса,
средняя кинетическая энергия такого осциллятора
n
n exp
kT
n 0
.
2
n
exp
exp
1
kT
kT
n 0
141
142.
Элементы квантовой теории теплоемкостиДля внутренней энергии молярного кристалла
получим
U 3N A ,
а для теплоемкости найдем
Tc
exp
2
dU
T
Tc
CV
3R
, Tc
,
2
dT
k
T
Tc
exp T 1
где Tc – называется температурой Эйнштейна.
142
143.
Элементы квантовой теории теплоемкостиИз формулы Эйнштейна для молярной
теплоемкости кристалла следует
CV
3R,
T
CV
0.
T 0
Таким образом теория Эйнштейна объяснила
наблюдаемые экспериментально зависимости для
молярной теплоемкости кристалла. Тем не менее,
это объяснение качественное, а не количественное.
Правильное объяснение теплоемкости позднее дал
Дебай. Упущение Эйнштейна состояло в том, что он
рассматривал осцилляторы как независимые. На
самом же деле, колебания атомов в узлах решетки
влияют на колебания соседних атомов. Это и было
учтено Дебаем.
143
144.
Молекулярная физикаТема 11:
Первое начало термодинамики
144
145.
Содержание• Механический эквивалент теплоты. Первое
начало термодинамики.
• Изопроцессы в идеальном газе. Работа при
изопроцессах.
• Скорость звука в газах.
• Уравнение Бернулли. Скорость истечения
сжатого газа через малое отверстие из
баллона.
145
146.
Первое начало термодинамикиВозможны два различных способа изменения
энергии термодинамической системы при ее
взаимодействии с внешними телами: путем
совершения работы и путем теплообмена. В первом
случае обмен энергией между системой и
внешними телами осуществляется в форме работы
A, а во втором — в форме теплоты Q.
В отличие от внутренней энергии системы,
являющейся однозначной функцией состояния
системы, понятия теплоты и работы имеют смысл
только в связи с процессом изменения состояния
системы. Они являются энергетическими
характеристиками этого процесса.
146
147.
Механический эквивалент теплотыКалория определяется как количество теплоты, подвод
(или отвод) которого вызывает нагревание (или,
соответственно, охлаждение) одного грамма воды при
атмосферном давлении на один кельвин.
Эквивалентность теплоты и энергии была
продемонстрирована Д. Джоулем, показавшим серией
кропотливых опытов, что нагрев, вызываемый одной
калорией теплоты, — такой же, какой дает вполне
определенная и всегда одна и та же работа. Именно,
оказалось, что 1 кал = 4,187 Дж.
Число, показывающее отношение единицы механической
работы к единице теплоты, называют механическим
эквивалентом теплоты: I=4,187 Дж/кал.
Обратная ему величина называется тепловым
эквивалентом механической работы: I'=0,239 кал/Дж.
147
148.
Первое начало термодинамикиДля перевода системы из одного и того же
исходного состояния 1 в одно и то же конечное
состояние 2 нужно сообщить системе разные
количества теплоты и совершить над системой
разную работу в зависимости от вида
процесса 1-2, т. е. в зависимости от того, через
какие промежуточные состояния проходит
система. В то же время изменение внутренней
энергии системы не зависит от вида процесса
и полностью определяется конечным и
начальным состояниями.
148
149.
Первое начало термодинамикиМатематически первое начало термодинамики
формулируется следующим образом:
Q dU A,
где δQ – элементарное количество теплоты, переданное
системе; dU – элементарное приращение внутренней
энергии системы; δA – элементарное количество
работы, совершенной системой. Значок δ подчеркивают
тот факт, что работа и теплота зависят от вида процесса.
В то же время изменение внутренней энергии зависит
только от начального и конечного состояний системы,
что подчеркивается значком d.
Физически первое начало термодинамики
формулируется так: количество теплоты, переданное
системе, идет на увеличение внутренней энергии
системой и на совершение системой работы.
149
150.
РаботаРабота процесса на участке от состояния 1
до состояния 2 выражается формулой
2
A1 2 PdV .
1
Численно работа на
участке 1-2 равна
площади под кривой
рассматриваемого
процесса,
изображенного на
диаграмме P-V.
150
151.
ИзопроцессыСуществуют следующие изопроцессы.
1. Изохорный (изохорический): V=const.
2. Изобарный (изобарический): P=const.
3. Изотермический: T=const.
4. Адиабатный (адиабатический): Q=const.
5. Политропный (политропический):
C=const, где C - теплоемкость.
151
152.
Изохорный процессВ случае изохорного процесса: V=const,
следовательно δA=0. Это означает, что
Q dU CV dT , A 0,
Q1 2 U1 2 CV T2 T1 ,
A1 2 0, C CV .
152
153.
Изобарный процессВ случае изобарного процесса: P=const.
Следовательно
Q CP dT , A RdT , dU CV dT ,
Q1 2 CP T2 T1 ,
A1 2 R T2 T1 ,
U1 2 CV T2 T1 , C CP CV R.
153
154.
Изотермический процессВ случае изотермического процесса: T=const,
следовательно dU=0. Это означает, что
dV
Q A PdV RT1
, dU 0,
V
V2
Q1 2 A1 2 RT1 ln , U1 2 0, C .
V1
154
155.
Адиабатный процессВ случае адиабатного процесса: Q=const.
Следовательно
Q 0, dU A, dU CV dT ,
Q1 2 0, U1 2 CV T2 T1 ,
A1 2 CV T2 T1 , C 0.
Получим уравнение адиабатного процесса. Поскольку
RT
dU CV dT , A PdV
dV ,
V
можно записать
CP
dT
R dV
dV
1
,
.
T
CV V
V
CV
155
156.
Адиабатный процессИнтегрируя данное выражение, получим
TV
1
const ,
или, пользуясь уравнением МенделееваКлапейрона,
PV const , T P1 const.
Данные соотношения называются
уравнениями адиабатного процесса
(соотношениями Пуассона).
Постоянная γ>1 – называется показателем
адиабаты (показателем Пуассона).
156
157.
Адиабатный процессС учетом соотношений Пуассона, получим
T
A1 2 CV T1 T2 CV T1 1 2
T1
1
CV
T2
PV
T2
PV
V1
1 1
1 1
PV
1 .
1
1 1 1
R
T1 1 T1 1 V2
157
158.
Политропный процессВ случае политропного процесса: C=const.
Следовательно
Q CdT , dU CV dT ,
A Q dU C CV dT ,
Q1 2 C T2 T1 , U1 2 CV T2 T1 ,
A1 2 C CV T2 T1 .
Получим уравнение политропного процесса. Поскольку
Q CdT , dU CV dT , A
RT
V
dV ,
можно записать
CP C
dT
R dV
dV
n 1
, n
.
T
CV C V
V
CV C
158
159.
Политропный процессИнтегрируя данное выражение, получим
TV
n 1
const ,
или, пользуясь уравнением МенделееваКлапейрона,
1 n
PV const , T P
n
n
const.
Данные соотношения называются
уравнениями политропного процесса.
Постоянная n – называется показателем
политропы (не путать с концентрацией).
159
160.
Политропный процессС учетом уравнений политропы, получим
A1 2
T2
C CV T2 T1 T1 CV C 1
T1
n 1
CV C T2 PV
T
PV
V
1 1
2
1 1
1
PV
1
1
1
.
1 1
R
T1 n 1 T1 n 1 V2
Если известны показатели адиабаты и политропы,
то можно найти молярную теплоемкость
политропного процесса. Действительно
nCV CP n
CP C
n
, C
CV
CV C
n 1
n 1
n R
1
1
R.
n 1 1 1 n 1
160
161.
Скорость звука в газахСкорость звука в газах дается общим
выражением
dP
зв
.
d
Поскольку колебания плотности газа и
связанные с ними колебания температуры в
звуковой волне происходят очень быстро, а
теплопроводность газа мала, то для таких
процессов теплообмен не играет никакой роли.
Поэтому распространение звука можно
считать адиабатическим процессом.
161
162.
Скорость звука в газахВычислим производную dP/dρ. Поскольку
V~1/ρ и для адиабатного процесса
PV const ,
то
d P 0, dP P 1d 0,
следовательно
dP
P
,
d
P
RT
зв
.
M
Скорость звука в воздухе (при нормальных
условиях) равна 330 м/с.
162
163.
Уравнение БернуллиУравнение Бернулли относится к
ламинарному стационарному течению
идеальной жидкости. Оно имеет вид
P
2
u gh
const ,
2
где u – удельная (на единицу массы)
внутренняя энергия жидкости; P – давление
в жидкости; ρ – плотность жидкости; gh –
удельная потенциальная энергия жидкости;
ϑ2/2 – удельная кинетическая энергия
макроскопического течения жидкости.
163
164.
Скорость истечения газа из отверстияС помощью уравнения Бернулли вычислим
скорость истечения сжатого газа из баллона
через малое отверстие. Можно записать
u1
P1
1
gh1
2
1
2
u2
P2
2
gh2
2
2
2
,
где индекс «1» соответствует газу в баллоне, а
индекс «2» - газу вне баллона. Будем считать
скорость газа в баллоне значительно меньше
скорости газа вытекающего из баллона (ϑ1<<ϑ2).
Кроме того, пренебрежем изменением
потенциальной энергии (gh1≈gh2). Тогда, пользуясь
тем, что
P 1
1
1
u CV T RT CPT ,
M
M
M
164
165.
Скорость истечения газа из отверстияполучим
2
2
CP T1 T2 .
M
Воспользуемся тем, что быстрое истечение
газа из баллона – адиабатический процесс.
Имеем
1
1
1
T1 P
следовательно
1
2
T2 P
T2 P2
,
T1 P1
,
1
T2
P2
2
2
2
CPT1 1
CPT1 1 .
P1
M
M
T1
165
166.
Молекулярная физикаТема 12:
Второе начало термодинамики
166
167.
Содержание• Циклические процессы. КПД тепловой
машины.
• Прямой и обратный циклы Карно.
• Теоремы Карно. Необратимые циклы.
• Циклы Отто и Дизеля.
• Формулировки второго начала
термодинамики.
• Perpetuum mobile.
167
168.
Циклические процессыКруговым процессом (циклом) называется такой
процесс, в котором термодинамическая система,
претерпев ряд изменений, возвращается в исходное
состояние.
Круговой процесс может быть равновесным
(квазистатическим) или неравновесным. Всякий
равновесный процесс представляет собой
непрерывную последовательность равновесных
состояний термодинамической системы, то есть таких
состояний, в которых все параметры имеют
определенные значения и могли бы оставаться
таковыми сколь угодно долго при неизменных внешних
условиях. В равновесном процессе внешние условия
изменяются настолько медленно (в пределе —
бесконечно медленно), что в каждый момент времени
термодинамическая система успевает прийти в
равновесие с внешней средой.
168
169.
Циклические процессыВсякий равновесный процесс является
обратимым в следующем смысле:
термодинамическую систему можно вернуть
из конечного состояния в исходное, и при этом
во внешней среде не произойдет никаких
изменений. В обратном процессе система
побывает во всех тех состояниях, через
которые она проходила в прямом процессе. В
частности, при обратном переходе система
получит такое же количество теплоты, которое
она отдала во внешнюю среду, над системой
будет совершена такая же работа, которую
сама система совершила над внешними телами
в прямом процессе.
169
170.
Циклические процессыТепловой машиной называется любое
периодически действующее устройство,
которое производит работу за счет получаемой
извне теплоты.
Прямым круговым процессом (циклом
тепловой машины) называется цикл, в
котором полученная извне теплота
превращается в полезную работу.
Обратным круговым процессом (циклом
холодильной машины) называется цикл, в
котором работа затрачивается на перенос
теплоты от менее нагретых тел к более
нагретым телам.
170
171.
Циклические процессыНа диаграммах обратимый цикл
изображается в виде замкнутой кривой.
Прямой цикл
Обратный цикл
171
172.
Работа за циклПодсчитаем работу за цикл.
172
173.
Работа за циклРабота для процесса идущего по верхней
кривой
A PdV .
1 2
1a 2
Работа для процесса идущего по нижней
кривой
A2 1 PdV PdV .
2b1
1b 2
Полная работа за цикл
A
PdV PdV
1a 2
1b 2
- численно равна площади фигуры,
ограниченной кривой цикла.
173
174.
Теплота за циклПоскольку
U1 2 U 2 U1 , U 2 1 U1 U 2 U1 2 ,
то изменение внутренней энергии за цикл
U U1 2 U 2 1 0.
Тогда, в соответствии с первым началом
термодинамики, теплота за цикл будет равна
Q U A A,
т.е. общее количество сообщаемой системе
теплоты за цикл равно работе, совершаемой
системой за цикл.
174
175.
Теплота за циклВ прямом цикле A>0 и Q>0, т.е. подводится
тепло и система совершает работу.
В обратном цикле A<0 и Q<0, т.е. над
системой совершается работа и тепло
отводится.
175
176.
КПДЛюбая тепловая машина работает на основе
какого-либо цикла, а эффективность
тепловой машины определяется КПД.
Коэффициентом полезного действия
(КПД) тепловой машины называется
отношение произведенной машиной работы
за один цикл к суммарному количеству
теплоты, полученной машиной (от
термостатов).
176
177.
Прямой цикл КарноРассмотрим прямой цикл Карно (цикл паровой
машины) для идеального газа, состоящий из
двух изотерм и двух адиабат.
177
178.
Прямой цикл КарноНа участке 1-2 газ изотермически расширяют
при максимальной температуре Tмакс. Чтобы
температура не менялась к газу нужно
подводить тепло Q(+) (от нагревателя). На
участке 2-3 газ адиабатически охлаждают до
минимальной температуры T3=Tмин. На
участке 3-4 газ изотермически сжимается.
Чтобы температура не менялась, от газа
нужно отводить тепло Q(--) (к холодильнику).
На участке 4-1 газ адиабатически сжимают до
максимальной температуры T1=Tмакс.
178
179.
Прямой цикл КарноВычисляем
V2
Q1 2 RTмакс ln Q , Q2 3 0,
V1
V4
Q3 4 RTмин ln Q , Q4 1 0.
V3
1
Поскольку T2V2 1 T3V3 1 , T4V4 1 TV
,
1 1
и T1=T2=Tмакс, а T3=T4=Tмин, получим
V2
V4 V1
, следовательно Q RTмин ln 0.
V1
V3 V2
179
180.
Прямой цикл КарноРабота совершенная газом в прямом цикле Карно
V2
A Q1 2 Q2 3 Q3 4 Q4 1 R Tмакс Tмин ln 0.
V1
Значит прямой цикл Карно соответствует тепловой машине.
КПД прямого цикла Карно вычислим по формуле
Получим
A
Q Q
Q
1 .
Q
Q
Q
Tмин
1
.
Tмакс
Таким образом, КПД прямого цикла Карно
определяется отношением минимальной и
максимальной температур цикла. КПД становится
максимальным, если Tмин→0.
180
181.
Обратный цикл КарноРассмотрим обратный цикл Карно для
идеального газа, состоящий из двух изотерм и
двух адиабат.
181
182.
Обратный цикл КарноНа участке 1-2 газ изотермически расширяют
при минимальной температуре Tмин. Чтобы
температура не менялась к газу нужно
подводить тепло Q(+). На участке 2-3 газ
адиабатически сжимают до максимальной
температуры T3=Tмакс. На участке 3-4 газ
изотермически сжимают. Чтобы температура не
менялась, от газа нужно отводить тепло Q(--). На
участке 4-1 газ адиабатически охлаждают до
минимальной температуры T1=Tмин.
182
183.
Обратный цикл КарноВычисляем
V2
Q1 2 RTмин ln Q , Q2 3 0,
V1
V4
Q3 4 RTмакс ln Q , Q4 1 0.
V3
1
Поскольку T2V2 1 T3V3 1 , T4V4 1 TV
,
1 1
и T1=T2=Tмин, а T3=T4=Tмакс, получим
V2
V4 V1
, следовательно Q RTнагр ln 0.
V1
V3 V2
183
184.
Обратный цикл КарноРабота совершенная над газом в обратном цикле Карно
V2
A A Q1 2 Q2 3 Q3 4 Q4 1 R Tмакс Tмин ln 0.
V1
Значит обратный цикл Карно соответствует холодильной
машине.
Холодильный коэффициент обратного цикла Карно
вычислим по формуле
Tмин
Q
Q
1
,
A
Tмакс Tмин
Q Q
где η – КПД прямого цикла Карно с теми же
температурными параметрами, что и в обратном цикле.
Холодильный коэффициент становится максимальным,
если Tмин→Tмакс.
184
185.
Теоремы КарноПервая теорема Карно: все обратимые
машины, работающие по циклу Карно, имеют
одинаковый коэффициент полезного действия.
Или: КПД цикла Карно не зависит от рабочего
вещества и конструктивных деталей
осуществления цикла.
Вторая теорема Карно: КПД обратимого
цикла Карно больше КПД любого другого
обратимого цикла, в котором максимальные и
минимальные температуры равны
соответственно температуре нагревателя и
температуре холодильника цикла Карно.
185
186.
Необратимые циклыНеобратимые циклы – не равновесны,
поэтому их нельзя изобразить на
диаграммах.
Можно доказать, что КПД необратимой
машины, работающей по циклу Карно,
всегда меньше КПД обратимой машины,
работающей по тому же циклу и с тем же
нагревателем и холодильником:
Карно
Tмин
1
.
Tмакс
186
187.
Цикл ОттоРассмотрим прямой цикл Отто (цикл четырехтактного
бензинового двигателя внутреннего сгорания),
состоящий из двух изохор и двух адиабат.
187
188.
Цикл ОттоВ начальной стадии в цилиндр при постоянном давлении
засасывается смесь воздуха с парами бензина. Затем
всасывающий клапан закрывается, и при обратном ходе
поршня происходит адиабатическое сжатие смеси (участок 12). В конечной стадии сжатия в цилиндре проскакивает
электрическая искра, от которой взрываются нагретые при
адиабатическом сжатии пары бензина. В результате давление в
цилиндре повышается по изохоре 2-3. На этой стадии к
системе подводится теплота сгорания Q(+). Под возникшим в
цилиндре давлением поршень идет обратно, происходит
адиабатическое расширение газа (участок 3-4). По достижении
точки 4 открывается выпускной клапан, газы уносят теплоту
Q(--), давление газа падает. Охлаждение газа происходит по
изохоре 4-1. На четвертом ходе поршень выталкивает
продукты сгорания, и начинается новый цикл.
КПД цикла Отто
T4 T1
1
.
T3 T2
188
189.
Цикл ДизеляРассмотрим прямой цикл Дизеля (цикл
четырехтактного дизельного двигателя внутреннего
сгорания) , состоящий из изобары, изохоры и двух
адиабат.
189
190.
Цикл ДизеляВ начальной стадии в цилиндр засасывается воздух,
который при следующем ходе поршня сжимается
адиабатически (участок 1-2). В момент наибольшего
сжатия через форсунку в цилиндр вбрызгивается жидкое
топливо, которое при достаточно высокой температуре Т2
самовоспламеняется. Под действием возникшего
давления поршень идет обратно (участок 2-3-4). Однако
до тех пор, пока горит топливо (участок 2-3) давление не
падает. После сгорания топлива дальнейшее расширение
газа происходит адиабатически (участок 3-4). По
достижении точки 4 выпускной клапан открывается, и
происходит выхлоп (изохорическое падение давления,
участок 4-1), при котором уносится теплота Q(--). При
четвертом ходе поршень выбрасывает остатки продуктов
сгорания.
КПД цикла Дизеля 1 CV T4 T1 .
CP T3 T2
190
191.
Формулировки второго началатермодинамики
Карно: Наибольший коэффициент полезного действия
тепловой машины не зависит от рода посредствующего тела
и вполне определяется предельными температурами, между
которыми машина работает.
Клаузиус: Теплота не может переходить от холодного к
теплому телу сама собой, без компенсирующих процессов.
Томсон (Кельвин): Теплоту какого-либо тела невозможно
превратить в работу, не производя никакого другого
действия, кроме охлаждения этого тела.
Оствальд: Осуществление перпетуум мобиле второго рода
невозможно.
Планк: Невозможно построить периодически
действующую машину, которая не производит ничего
другого, кроме поднятия груза и охлаждения резервуара
теплоты.
191
192.
Perpetuum mobileВечный двигатель первого рода –
бесконечное совершение работы без затрат
топлива или других энергетических ресурсов
(нарушение закона сохранения энергии).
Вечный двигатель второго рода –
превращение в работу всего тепла,
извлекаемого из окружающих тел
(нарушение второго закона
термодинамики).
Постройка вечных двигателей
невозможна!
192
193.
Perpetuum mobile I193
194.
Perpetuum mobile I194
195.
Perpetuum mobile I195
196.
Perpetuum mobile II196
197.
Молекулярная физикаТема 13:
Энтропия
197
198.
Содержание• Теорема Клаузиуса. Энтропия.
• Энтропия идеального газа. Изменение
энтропии при необратимых процессах.
• Статистический характер второго начала
термодинамики.
• Третье начало термодинамики.
• Формулировки второго начала
термодинамики с помощью энтропии.
198
199.
Теорема КлаузиусаРассмотрим равновесный цикл 1a2b1. Разобьем этот
цикл на ряд бесконечно близких адиабат,
пересекающих линии прямого 1a2 и обратного 2b1
переходов. Эти линии разобьются на ряд бесконечно
малых отрезков. Через середину каждого отрезка
проведем изотермы.
199
200.
Теорема КлаузиусаТаким образом, мы получили сетку,
состоящую из прямых циклов Карно. Для
каждого i-го цикла можно вычислить КПД
b
b
Q
i
Ti
i 1 a 1
, i 1, 2, 3, ...
a
Ti
Qi
где δQi(a) – теплота, переданная i-м нагревателем;
δQi(b) – теплота, принятая i-м холодильником.
Пользуясь этим равенством, запишем
a
Qi
Ti
a
b
Qi
Ti
b
,
или
i
a
Qi
Ti
a
i
b
Qi
Ti
b
.
200
201.
Теорема КлаузиусаВеличина Q/T – называется приведенной
теплотой.
Таким образом, из последнего равенства
следует теорема Клаузиуса: сумма
приведенных теплот не зависит от пути
перехода.
Переписывая соотношение с учетом знака,
получим
i
a
Qi
Ti a
i
b
Qi
Ti b
0,
или
i
Qi
Ti
0
- равенство Клаузиуса (для обратимых циклов).
201
202.
Теорема КлаузиусаВ случае необратимых циклов можно
воспользоваться тем, что КПД такого цикла всегда
меньше КПД соответствующего ему цикла Карно. В
результате получим неравенство Клаузиуса (для
необратимых циклов)
Qi
i T 0.
i
Для произвольного циклического процесса можно
записать
Qi
i T 0.
i
А в случае непрерывного изменения
Q
T
0.
202
203.
ЭнтропияВ случае обратимых циклов последнее
соотношение имеет вид
Q
Q
Q
0,
или
0,
T
T 2b1 T
1a 2
иначе
1a 2
Q
T
2 b1
Q
T
1b 2
Q
T
,
т.е. интеграл с приведенной теплотой не
зависит от пути обратимого перехода. Значит
этот интеграл выражает изменение некоторой
функции состояния системы.
203
204.
ЭнтропияЭта функция состояния называется энтропией
и обозначается S. Изменение энтропии при
обратимом переходе 1-2 равно
2
S1 2 S2 S1
1
Q
T
.
В случае необратимого перехода 1-2 можно
получить
2
Q
S2 S1
.
T
1
204
205.
Энтропия идеального газаИзменение энтропии в обратимом процессе 12, происходящем в идеальном газе, можно
получить с помощью первого начала
термодинамики
T2
V2
dU
A
S1 2
CV ln R ln
T
T
T
T1
V1
1
1
1
P2
V2
CV ln CP ln .
P1
V1
2
Q
2
2
Для адиабатического процесса S1 2 0,
а для политропного
S1 2 C T2 T1 .
205
206.
ТеплообменТеплообмен между двумя телами, образующими
изолированную систему, является необратимым процессом.
Поскольку энтропия определяется только начальным и
конечным состояниями взаимодействующих тел, заменим
реальный процесс теплообмена между двумя телами (с
молярными теплоемкостями C1 и C2, количествами вещества ν1
и ν2, температурами T1 и T2) обратимым процессом
теплообмена, в котором каждое из тел обратимым образом
нагрелось до температуры T . Из уравнения теплового баланса
следует (T2>T1):
1C1T1 2C2T2
1C1 T T1 2C2 T2 T ,
T
или
1C1 2C2
,
Изменение энтропии в системе будет равно изменению
энтропии для каждого из тел в системе (i=1, 2)
S2 S1 S2 S1 S2 S1 , где S S C dT C ln T ,
i i
i i
T
Ti
T
следовательно
T
T
S2 S1 1C1 ln 2C2 ln 0, т.е. энтропия возросла.
206
T1
T2
1
1
2
2
i
2
i
1
T
i
207.
Расширение газа в пустотуПроцесс расширения газа в пустоту является
необратимым. Поскольку энтропия
определяется только начальным и конечным
состояниями газа, то реальный процесс
расширения газа от объема V1 до объема V2
можно заменить равновесным процессом
изотермического расширения 1-2.
Следовательно
2
S2 S1
1
V2
A1 2
R ln 0,
T
T
V1
Q
т.е. энтропия возросла.
207
208.
Смешивание газовПроцесс 1-2 смешивания двух различных газов
является необратимым. Представим изменение
энтропии в этом процессе как сумму изменений
энтропий для каждого из газов, необратимо
расширяющихся на полный объем. Считаем, что i-й
газ до смешивания занимает объем Vi и его
количество νi моль. В результате найдем
1
1
2
2
S2 S1 S2 S1 S2 S1
V1 V2
V1 V2
1 R ln
2 R ln
0,
V1
V2
т.е. энтропия возросла.
208
209.
Парадокс ГиббсаЕсли в предыдущем случае положить νi=ν и
Vi=V, тогда получим
S2 S1 2 R ln 2,
причем изменение энтропии не зависит от
сорта газа. Т.е., казалось бы, если смешать
одинаковые газы, то энтропия должна
возрасти. Но, на самом деле, ничего не
происходит. Данное противоречие называется
парадоксом Гиббса. Решение парадокса
Гиббса состоит в том, что полученная формула
не применима для одинаковых газов. В случае
одинаковых газов изменение энтропии равно
нулю.
209
210.
Статистический характер энтропииСвязь энтропии с термодинамической
вероятностью Ω была установлена Больцманом:
S k ln const ,
где k – постоянная Больцмана. Энтропия как
функция состояния верна с точностью до
произвольной аддитивной постоянной, которую
всегда можно положить равной нулю, если
соответствующим образом выбрать систему отсчета
энтропии.
Термодинамическая вероятность Ω>>1 и
максимальна в том случае, если молекулы газа
распределены равномерно, поскольку такое состояние
газа может быть осуществлено наибольшим числом
210
способов.
211.
Третье начало термодинамикиТретье начало термодинамики, еще называемое
теоремой Нернста, звучит следующим образом:
при стремление абсолютной температуры к нулю
энтропия любого тела также стремится к нулю, т.е.
lim S 0.
T 0
Это означает, что
T
S
0
Q
T
.
Из теоремы Нернста также следует, что
CV
0,
T 0
CP
0.
T 0
211
212.
Формулировка второго началатермодинамики с помощью энтропии
Клаузиус: Энтропия всякой изолированной
системы стремится к максимуму.
Больцман: Природа стремится к переходу
от состояний менее вероятных к
состояниям более вероятным.
212
213.
Молекулярная физикаТема 14:
Температура
213
214.
Содержание• Температура. Эмпирические шкалы
температур. Виды термометров.
• Международная практическая шкала
температур.
• Абсолютная термодинамическая шкала
температур.
• Отрицательные абсолютные температуры.
214
215.
ТемператураТемпература является количественной мерой
«нагретости» тела. Более нагретым является то,
«нагретость» которого уменьшается при
длительном контакте с другим телом, принимаемым
в этом случае, по определению, за менее нагретое.
Степень «нагретости» тела измеряется по
характеристикам материальных тел, зависящих от
«нагретости». Измерение «нагретости» сводится к
измерению некоторой величины тела, которая
изменяется с изменением «нагретости» тела.
Тело, выбираемое для измерения «нагретости»,
называется термометрическим, а величина,
посредством которой измеряется «нагретость»,
называется термометрической величиной.
215
216.
ТемператураНаиболее широко известными являются «нагретость»,
при которой кипит вода при атмосферном давлении, и
«нагретость», при которой она замерзает. Эти реперные
точки называются точкой кипения воды и точкой
замерзания.
Температурой называется числовое значение
величины, с помощью которой характеризуется
«нагретость» тела.
Температура выражается в градусах. Пусть точке
кипения присваивается температура t2, а точке
замерзания — температура t1, тогда градусом
температуры называется величина
1o l2 l1 / t2 t1 ,
где l2 и l1 - термометрические величины
термометрического тела в точках кипения и
замерзания воды, соответственно.
216
217.
Эмпирические шкалы температурТемпературой термометрического тела называется
число, которое определяется по формуле
lt l1
lt l1
t t1 o t1
t2 t1 ,
1
l2 l1
где lt - термометрическая величина при измеряемой
«нагретости».
Наиболее известными эмпирическими шкалами
температур являются Цельсия и Фаренгейта, которые
отличаются значениями температур, приписанных
реперным точкам. В шкале Цельсия t2=100 и t1=0, а в
шкале Фаренгейта t2=212 и t1=32. Следовательно, одна и
та же «нагретость» характеризуется в этих шкалах разными
температурами:
lt l1
lt l1
18
tC 100
, tF 32 180
32 tC .
10
l2 l1
l2 l1
217
218.
Виды термометровЗначение температуры для одной и той же шкалы
температур зависит от термометрического тела.
Поэтому, термометры, использующие различные
термометрические тела, показывают различную
температуру. Совпадение показаний термометров
может быть только в реперных точках, если они
одинаковы для данных термометров.
Термометры бывают различными: газовыми,
жидкостными, твердотельными. Во всех них
используется то, что термометрическое тело (газ,
жидкость, твердое тело) меняют свои физические
характеристики (объем, длину, проводимость, и
проч.) в зависимости от температуры.
218
219.
Международная практическая шкалаМеждународная практическая шкала температур
образована таким образом, чтобы с ее помощью можно
было просто калибровать научные и технические приборы
и в то же время воспроизводить с технически максимально
возможной точностью термодинамическую шкалу
температур. Единицами температуры являются кельвин
и градус Цельсия в зависимости от начала отсчета
температур. Шкала температур постоянно уточняется в
соответствии с результатами научных исследований и
достижениями измерительной техники.
Между реперными точками температурная шкала
устанавливается с помощью интерполяционных формул,
по которым температура вычисляется по показаниям
термометров, принятых за стандартные.
Международная практическая шкала температур
чрезвычайно точно согласуется с термодинамической
шкалой температур в реперных точках и достаточно точно
во всех остальных точках.
219
220.
Термодинамическая шкалаНа основании 2-й теоремы Карно можно установить
абсолютную термодинамическую шкалу температур,
не зависящую от термометрического тела.
Рассмотрим систему изотерм и адиабат. Фигуры 1, 2, 3,
заключенные между двумя соседними изотермами и
двумя адиабатами, являются циклами Карно.
220
221.
Термодинамическая шкалаИз выражения для КПД цикла Карно можно записать
последовательность соотношений
Q1 T1
Q2 T2
Q3 T3
,
,
, ...
Q2 T2
Q3 T3
Q4 T4
или
T1 : T2 : T3 :... Q1 : Q2 : Q3 ...
Т.е. если задать какую-нибудь реперную точку
(например, температуру тройной точки воды 273,16 К),
то проведя последовательность прямых обратимых
циклов Карно можно вычислить произвольную
температуру (в произвольном процессе), если измерить
соответствующее величины Q. Такое определение
температуры не зависит от термометрического тела.
Оно впервые было дано Кельвином. В честь которого
была названа единица абсолютной термодинамической
температуры.
221
222.
Отрицательные абсолютныетемпературы
Понятно, что отрицательная абсолютная
термодинамическая температура не имеет физического
смысла.
Тем не менее, в квантовых системах понятие
отрицательной абсолютной температуры имеет вполне
определенный смысл: это мера способа заполнения
квантовых уровней энергии частицами. Если частицы
заполняют сначала нижние энергетические уровни, так,
что на более высоком уровне частиц меньше, то
температура положительна и совпадает по значению с
термодинамической. Если же создается инверсность
населенностей, т.е. на более низко расположенном
уровне частиц меньше, чем на более высоком, то
температуре приписываются отрицательные значения.
Тем не менее, такие значения все же не имеют
физического смысла.
222
223.
Молекулярная физикаТема 15:
Термодинамические функции
223
224.
Содержание• Термодинамические функции.
• Критерии устойчивости
термодинамических систем.
224
225.
Термодинамические функцииК настоящему времени из предшествующего
изложения известны термодинамические
параметры (параметры состояния): P – давление, V
– объем, T – температура.
А также термодинамические функции (функции
состояния): U – внутренняя энергия, S – энтропия.
Помимо этого, в физике получили широкое
распространение следующие термодинамическими
функциями: W – свободная энергия (функция
Гельмгольца), H – энтальпия, G – функция Гиббса.
Любая функция от термодинамических функций
также является термодинамической функцией.
225
226.
Дифференциалытермодинамических функций
1. Энтропия. С учетом соотношения δQ=TdS,
первое начало термодинамики принимает вид
TdS dU PdV
- называется основным термодинамическим
тождеством.
2. Энтальпия. Для энтальпии H=U+PV
можно получить
dH dU PdV VdP TdS VdP.
226
227.
Дифференциалытермодинамических функций
3. Свободная энергия. Для свободной
энергии W=U-TS можно получить
dW SdT PdV .
4. Функция Гиббса. Для функции Гиббса
G=W+PV=H-TS можно получить
dG SdT VdP.
227
228.
СоотношенияСледующие соотношения могут быть получены с
помощью дифференциалов термодинамических
функций:
U
W
P
, P
,
V S
V T
H
G
V
,
V
,
P S
P T
U
H
T
,
T
,
S V
S P
W
G
S
, S
,
T V
T P
где индекс внизу у скобки означает, что при
дифференцировании соответствующая величина
считается константой.
228
229.
СоотношенияСледующие соотношения между производными,
называемые соотношениями Максвелла, могут
быть получены:
T
P
,
V S
S V
T V
,
P S S P
S P
,
V T T V
S
V
.
P T
T P
229
230.
Термодинамическая устойчивостьСостояние равновесия адиабатически
изолированной системы достигается при
максимальности энтропии. Это означает, что
все бесконечно близкие состояния, переход в
которые возможен без подвода и отвода
теплоты, имеют меньшую энтропию. Второе
начало термодинамики запрещает переход в
такие состояния. А это означает, что состояние
адиабатической изолированной системы
устойчиво при максимальной энтропии
системы.
230
231.
Термодинамическая устойчивостьОбщая теория термодинамической устойчивости
была разработана Д.Гиббсом (1878 г.). Он
сформулировал следующие необходимые и
достаточные условия устойчивости для
изолированной системы.
1. При всех возможных изменениях состояния
системы, не влияющих на ее энергию, вариация
энтропии исчезает или отрицательна.
2. При всех возможных изменениях состояния
системы, не влияющих на ее энтропию, вариация ее
энергии исчезает или положительна.
Под вариацией рассматриваемой физической
величины подразумевается ее малое изменение,
происходящее при малом изменении параметров, от
которых зависит рассматриваемая величина.
231
232.
Система с V=const и S=constНеравенство Клаузиуса δQ<TdS и первое
начало термодинамики позволяют записать
dU PdV TdS 0.
Поскольку для рассматриваемой системы
V=const и S=const, значит
dU 0,
т.е. в системе могут самопроизвольно
происходить лишь процессы с уменьшением
внутренней энергии. Следовательно,
устойчивым является состояние при
минимуме внутренней энергии.
232
233.
Система с P=const и S=constНеравенство Клаузиуса δQ<TdS и первое
начало термодинамики позволяют записать
dU PdV TdS 0.
Поскольку для рассматриваемой системы
P=const и S=const, значит
dU PdV d U PV dH 0,
т.е. в системе могут самопроизвольно
происходить лишь процессы с уменьшением
энтальпии. Следовательно, устойчивым
является состояние при минимуме
энтальпии.
233
234.
Система с T=const и P=constНеравенство Клаузиуса δQ<TdS и первое
начало термодинамики позволяют записать
dU PdV TdS 0.
Поскольку для рассматриваемой системы
T=const и P=const, значит
dU PdV TdS d H TS dG 0,
т.е. в системе могут самопроизвольно
происходить лишь процессы с уменьшением
функции Гиббса. Следовательно,
устойчивым является состояние при
минимуме функции Гиббса.
234
235.
Принцип Ле Шателье – БраунаПринцип Ле Шателье — Брауна: если на
систему, находящуюся в устойчивом
термодинамическом равновесии,
воздействуют внешние факторы,
стремящиеся вывести ее из этого состояния,
то в системе возникают процессы,
стремящиеся уничтожить изменения,
вызываемые внешними воздействиями.
235
236.
Молекулярная физикаТема 16:
Реальный газ
236
237.
Содержание• Силы межмолекулярного взаимодействия. Потенциал
межмолекулярного взаимодействия.
• Уравнение Ван-дер-Ваальса. Вириальное уравнение
состояния.
• Изотермы газа Ван-дер-Ваальса. Метастабильные
состояния. Критическое состояние.
• Приведенное уравнение состояния. Закон
соответственных состояний.
• Экспериментальные изотермы. Сравнение уравнения
Ван-дер-Ваальса с экспериментальными данными.
• Внутренняя энергия газа Ван-дер-Ваальса.
• Эффект Джоуля-Томсона. Сжижение газов.
237
238.
Силы межмолекулярноговзаимодействия
Существует в основном два типа связей атомов в
молекуле.
1. Ионная связь. В некоторых случаях имеются
электрон или несколько электронов, которые очень
слабо связаны с атомом в целом. Эти электроны легко
теряются атомом, в результате чего образуется
положительно заряженный ион. В других случаях,
наоборот, не только все электроны очень крепко связаны
с атомом, но при благоприятных условиях атом охотно
захватывает электрон или даже два электрона и
превращается в отрицательно заряженный ион. Такие
атомы при образовании молекулы превращаются в ионы
с отрицательным знаком заряда. Между ионами
действуют кулоновские силы притяжения, которые
и обеспечивают образование молекулы. К числу
таких молекул относится, например, молекула
хлористого натрия NaCl.
238
239.
Силы межмолекулярноговзаимодействия
2. Ковалентная связь. Ионная связь не в состоянии
объяснить существование молекул, состоящих из
двух одинаковых атомов, таких, например, как Н2,
02, N2 и др., потому что два атома входят в молекулу
равноправно и нет оснований для одного из них
стать положительным ионом, а для другого —
отрицательным. Существующая в таких молекулах
связь между атомами называется ковалентной.
Механизм образования этой связи основан на
обобществлении электронов при сближении двух
атомов, т.е. оба атома притягиваются кулоновскими
силами к электронному сгустку, образованному их
электронами.
239
240.
Ван-дер-Ваальсова связьПри сравнительно больших расстояниях между
молекулами действуют силы притяжения, называемые
силами Ван-дер-Ваальса. Эти силы возникают
вследствие того, что при небольшом смещении
отрицательных и положительных зарядов в нейтральной
молекуле она перестает быть нейтральной в
электрическом отношении, превращаясь в электрический
диполь, т.е. совокупность разноименных, одинаковых по
абсолютному значению, расположенных на близком друг
от друга расстоянии зарядов. При сближении молекул
электрические поля составляющих их зарядов быстро
меняются во времени и лишь в среднем компенсируют
друг друга в различных точках пространства. Поэтому при
сближении молекулы поляризуют друг друга, причем
обращенные друг к другу стороны поляризованных
молекул обладают зарядами противоположного знака.
Такие взаимно поляризованные молекулы притягивают
240
друг друга.
241.
Потенциал межмолекулярноговзаимодействия
На малых расстояниях между молекулами действуют
силы отталкивания (кулоновские и др.). Это является
просто выражением того факта, что молекула занимает
некоторую область пространства и препятствует другим
молекулам проникать в эту область. Эти силы проявляются
в очень малой области, порядка размеров молекулы. На
больших расстояниях между молекулами действуют силы
притяжения (ван-дер-ваальсовы). Поэтому, поскольку
силы притяжения и отталкивания имеют разные знаки,
должно существовать такое расстояние между молекулами
r0, где силы компенсируют друг друга. Приближенный вид
потенциала межмолекулярного взаимодействия
(потенциала Леннарда-Джонса), как функции
расстояния между молекулами r, имеет вид
d 12 d 6 где u0 – постоянная; d – расстояние,
u u0 , на котором притяжение между
r r молекулами сменяется их
241
отталкиванием.
242.
Потенциал Леннарда-ДжонсаНа некотором расстоянии r0 между молекулами
образуется минимум энергии их взаимодействия,
т.е. устойчивое состояние двух молекул.
242
243.
Потенциал межмолекулярноговзаимодействия
Потенциал Леннарда-Джонса описывает случай двух
неподвижных молекул. В том случае, если одна из
молекул движется относительно другой, к потенциалу
Леннарда-Джонса следует добавить кинетическую
энергию налетающей молекулы. В этом случае
значение r0 не изменится, а изменится величина d. По
физическому смыслу d характеризует наименьшее
расстояние, на которое могут приблизиться
молекулы друг к другу. Значит, d – эффективный
диаметр молекулы, и связано с поперечным
сечением столкновений σ соотношением
d
.
243
244.
Газ Ван-дер-ВаальсаВ первом приближении молекулы реального
газа можно уподобить абсолютно твердым
шарикам с диаметром d, между которыми
действуют только силы взаимного притяжения.
Учет конечных размеров молекул позволяет
учесть действие сил взаимного притяжения
(молекула не может проникнуть в то же место
пространства, где уже находится другая
молекула). Такая модель газа впервые была
предложены Я. Ван-дер-Ваальсом в 1873 г. А
реальный газ, подчиняющийся уравнению Вандер-Ваальса был назван ван-дер-ваальсовским.
244
245.
Уравнение Ван-дер-Ваальса1. Поправка на недоступный объем. Рассмотрим один
моль ван-дер-ваальсового газа. Молекула газа может
находиться в любой его точке, за исключением тех мест,
где расположены остальные NA—1 молекул, т.е. молекуле
доступна лишь часть всего объема, равная V0—b (где V0 –
молярный объем). Для каждой пары взаимодействующих
молекул недоступной является та часть объема, в которой
расстояние между их центрами равно d, т.е. сфера с
объемом (4/3)πd3. Т.к. из NA молекул может быть
образовано
C2N =NA(NA-1)/2 пар, значит, полный
A
недоступный объем для
всех молекул равен C2N (4/3)πd3
≈NA2 (4/6)πd3 , и на каждую из них приходится A
N A2 4 / 6 d 3
1 3
b
4 N A d 4 N AVмол .
NA
6
Т.е. недоступный объем равен учетверенному объему
всех молекул газа.
245
246.
Уравнение Ван-дер-Ваальса2. Поправка на внутреннее давление. Сила давления газа на
стенку сосуда есть результат многочисленных столкновений
молекул с поверхностью стенки. Поэтому давление идеального
газа прямо пропорционально концентрации молекул n=NA/V0 в
слое, непосредственно прилегающем к стенке. Вследствие
притяжения ударяющих о стенку молекул всеми остальными
молекулами газа это давление уменьшается на некоторую
величину Pвнутр, называемую внутренним давлением.
Поскольку силы взаимодействия молекул очень быстро
убывают с расстоянием, то следует учитывать притяжение
прилежащего к стенке слоя лишь одним соседним с ним слоем.
Сила этого притяжения (рассчитанная на единицу площади)
пропорциональна концентрации молекул в обоих слоях, т.е.
Pвнутр n
2
N A2
V02
a
2,
V0
где множители α и a=αNA2 зависят от строения
взаимодействующих молекул, т.е. от вида газа.
246
247.
Уравнение Ван-дер-ВаальсаТаким образом, принимая во внимание поправку на
недоступный объем и уменьшение давления за счет
притяжения молекул, уравнение МенделееваКлапейрона для одного моля газа принимает вид
RT
a
P
2.
V0 b V0
Полученное уравнение называется уравнением Ван-дерВаальса для 1-го моля реального газа; постоянные a и b
называются постоянными Ван-дер-Ваальса. В случае,
если рассматривается ν молей, подстановкой V0=V/ν,
получим
2
RT a
P
2
V b V
- уравнение Ван-дер-Ваальса.
247
248.
Вириальное уравнение состоянияУравнение Ван-дер-Ваальса - не единственное
возможное уравнение, описывающее состояние
реального газа. Вид уравнения состояния зависит
от закона взаимодействия между молекулами.
Никакого точного уравнения для газов с
межмолекулярным взаимодействием не
существует. Наиболее общая форма уравнения
состояния реального газа, называемая
вириальным уравнением состояния, имеет вид
A1 T A2 T
PV0 RT
...
2
V0
V0
где Ai(T) – вириальные коэффициенты (i=1, 2, …).
248
249.
Уравнение ВдВ в вириальной формеЗапишем уравнение ВдВ для 1-го моля в виде
RT
a
b
PV0
,
1.
1 b / V0 V0 V0
Пользуясь формулой для геометрической
прогрессии
1
1 x x 2 x3 ..., x 1,
1 x
получим
RTb a RTb
RTb
PV0 RT
2 3 ...
V0
V0
V0
2
3
249
250.
Изотермы газа Ван-дер-ВаальсаФиксируя температуру T в уравнении для 1-го моля
газа Ван-дер-Ваальса можно получить следующие
зависимости.
T2>Tкр>T1
Tкр – критическая
температура,
соответствующая
критическому состоянию.
250
251.
Изотермы газа Ван-дер-ВаальсаВидно, что на изотермах газа Ван-дер-Ваальса (ВдВ) в
общем случае, при T<Tкр имеются «горбы».
Через эти «горбы» можно провести горизонтальную линию
так, что площади s1 и s2 будут равны (правило Максвелла).
Полученные таким образом точки A и E будут
соответствовать «началу» и «окончанию» (при сжатии газа
при постоянной температуре) двухфазного состояния в газе.
251
252.
Изотермы газа Ван-дер-ВаальсаПри сжатии газа ВдВ при постоянной
температуре T<Tкр наступает такой момент (V0
соответствует точке A), когда начинается
конденсация газа, т.е. наступает двухфазное
состояние (пар+жидкость). При дальнейшем
сжатии наступает такой момент, когда в
исследуемом объеме есть только жидкость (V0
соответствует точке E), т.е. двухфазное состояние
перестает существовать.
Однако, если сжимать газ при температуре T>Tкр,
то перехода в двухфазное состояние не
происходит. Газ сжимается как угодно, но
остается газом. Т.е. газ ВдВ в этом случае ведет
себя как идеальный.
252
253.
Изотермы газа Ван-дер-ВаальсаУчасток изотермы BCD характеризуется тем, что
на нем давление растет с увеличением объема
производная (dP/dV0>0). Ясно, что ни в одной из
точек этого участка система не может находится
в устойчивом состоянии - малейшие
флуктуации его разрушают. Т.е. на участке BCD
система не может устойчиво существовать.
В то же время на участках AB и DE давление с
увеличением объема падает (dP/dV0<0), т.е.
соответствующие состояния могут
существовать физически. Как же тогда система
переходит из A в E? Эксперимент показал, что
по линии ACE.
253
254.
Метастабильные состоянияЭксперименты также показывают, что участки изотермы
AB и DE могут быть реализованы. Данные участки
соответствуют метастабильным состояниям. Эти
состояния почти не устойчивы. Участок AB
соответствует состоянию переохлажденного пара, а
участок DE – состоянию перегретой жидкости.
Состояние переохлажденного пара можно получить с
помощью быстрого адиабатического охлаждения пара до
температур меньших температуры парообразования, а
состояние перегретой жидкости – с помощью
медленного нагрева чистой жидкости до температур
больших температуры кипения. Однако, малейшая
соринка, попавшая в емкость с веществом в
метастабильном состоянии, приводит к быстрой
конденсации переохлажденного пара или бурному
вскипанию перегретой жидкости.
254
255.
Критическое состояниеКритическое состояние характеризуется тем, что на
соответствующей ему изотерме отсутствуют «горбы», т.е.
имеется горизонтальный участок. Это означает
вырождение свойств уравнения ВдВ.
Если преобразовать уравнение ВдВ, то можно получить
PV Pb RT V aV0 ab 0
3
0
2
0
- кубическое уравнение, имеющее в общем случае 3 корня
(два горба на изотерме). В критическом состоянии (при Tкр,
Pкр и V0,кр) все 3 корня вырождаются в один, т.е. имеет место
V
3
2
2
3
V
0,
или
V
3
V
V
3
V
V
V
0
0, кр
0
0, кр 0
0, кр 0
0, кр 0.
3
Сравнивая последнее уравнение с записанным выше (при
критических значениях давления и температуры), найдем
a
8a
3
Pкр
,
T
,
V
3
b
,
и
PкрV0,кр RTкр .
кр
0, кр
2
27b
27 Rb
8
255
256.
Приведенное уравнение ВдВДелая замену в уравнении Ван-дер-Ваальса:
P PPкр , V VVкр , T TTкр ,
Получим приведенное уравнение Ван-дер-Ваальса
8T
3
P
2.
3V 1 V
Видно, что при выборе в качестве единиц критических
параметров вещества уравнение ВдВ принимает вид,
одинаковый для всех веществ. Отсюда можно заключить,
что и поведение различных веществ (в приведенных
величинах) одинаково. Это утверждение называется
законом соответственных состояний. Формулируется он
так: если два приведенных параметра вещества одинаковы,
то и третий параметр одинаков. Однако надо заметить, что
закон соответственных состояний все же не соблюдается
для реальных газов и жидкостей.
256
257.
Экспериментальные изотермыПервые эксперименты по проверке уравнения
Ван-дер-Ваальса провел Эндрюс, исследуя CO2.
T=const
257
258.
Экспериментальные изотермыТипичная экспериментальная изотерма
выглядит следующим образом.
Pн.п. – давление, соответствующее
горизонтальному участку экспериментальной
изотермы, называется давлением насыщенного
пара.
258
259.
Отличие результатовК сожалению, простая теория, связанная с использованием
уравнения ВдВ не всегда адекватно описывает реальную
ситуацию. Основные отличия следующие.
1. Для данного вещества постоянные а и b в уравнении
Ван-дер-Ваальса должны быть независимыми от
температуры. В действительности же они зависят от
температуры.
2. Из соотношения критических параметров следует, что
величина
PкрV0,кр
RTкр
3
0,375
8
должна быть универсальной постоянной для всех
веществ. В действительности же она изменяется.
Например, для воды она равна 0,23, а для гелия 0,31.
259
260.
Отличие результатов3. Соотношение V0,кр=3b не соблюдается. Более
точным соотношением является V0,кр≈2b.
4. В области двухфазных состояний уравнение
Ван-дер-Ваальса не обосновано теоретически и
дает расхождения с экспериментом.
260
261.
Внутренняя энергия газа ВдВВзаимодействие между молекулами газа ВдВ
обусловливает их взаимную потенциальную
энергию. Поэтому, наряду с величиной νCVdT, в
элементарное изменение внутренней энергии
газа dU должна входить работа против
внутренних сил притяжения dA’= Pвнутр dV.
Следовательно, для газа Ван-дер-Ваальса
dV
dU CV dT Pвнутр dV CV dT a 2 ,
V
2
или
U CV T
2a
V
.
261
262.
Эффект Джоуля-ТомсонаПропуская реальный газ по теплоизолированной трубке с
пористой перегородкой, Джоуль и Томсон обнаружили, что при
расширении, которым сопровождается прохождение газа через
перегородку, температура его несколько изменяется. В
зависимости от начальных давления и температуры изменение
приращения температуры ΔT имеет различные знаки («плюс»
или «минус»). Это явление получило название эффекта
Джоуля-Томсона. Если температура газа понижается (ΔT
<0), эффект называется положительным; если газ
нагревается (ΔT >0), эффект называется отрицательным.
Пусть индексом «1» выделены, параметры, описывающие
начальное состояния газа, а индексом «2» обозначим
параметры, соответствующие его конечному состоянию
(после расширения).
Можно доказать, что в эксперименте Джоуля и Томсона
сохраняется энтальпия, т.е. выполняется условие
H1 H 2 , или U1 PV
1 1 U 2 PV
2 2.
262
263.
Эффект Джоуля-ТомсонаПоскольку, после расширения газ имеет большой
объем, то, для простоты, его можно считать
идеальным.
Выражения для энтальпии имеют вид
2
2
2 a RTV
a
1 1
H1 CV T1 PV
1 1 CV T1
V1
V1 V1 b V1
2
2
2
RTV
RT
b
2
a
2
a
1 1
1
CV T1
CV R T1
,
V1 b
V1
V1 b
V1
и
H 2 CV T2 PV
2 2 CV R T2 .
Пользуясь условием равенства энтальпий, получим
RT1b 2a
T T2 T1
.
CV R V1 b V1
263
264.
Эффект Джоуля-ТомсонаТаким образом, знак эффекта Джоуля-Томсона
определяется знаком выражения, стоящего в квадратных
скобках.
RT1b 2a
В случае
0
V1 b
V1
- эффект получается нулевым.
Следует заметить, что эффект Джоуля-Томсона всецело
обусловлен отклонениями газа от идеальности. Для
идеального газа энтальпия H1 имеет вид
H1 CV R T1 ,
а условие равенства энтальпий принимает вид
CV R T1 CV R T2 , или T T2 T1 0.
Т.е. эффект является нулевым.
264
265.
Сжижение газовЭффект Джоуля-Томсона используется для
сжижения газов, путем их охлаждения. Широко
известен промышленный метод Линде.
265
266.
Молекулярная физикаТема 17:
Состояния двухфазной системы
266
267.
Содержание• Насыщенный пар. Правило рычага.
Зависимость давления насыщенного пара от
температуры.
• Поведение двухфазной системы при
изменении температуры при постоянном
объеме.
• Уравнение Клапейрона-Клаузиуса. Фазовая
диаграмма жидкость-пар.
• Влажность.
267
268.
Насыщенный парВ двухфазной системе жидкость и пар находятся в
динамическом равновесии и при данной температуре
имеют вполне определенные плотности и давления. Пар
называется насыщенным потому, что его нельзя
«уплотнить» при той же температуре. При попытке
«уплотнения» часть насыщенного пара превращается в
жидкость.
268
269.
Правило рычагаТипичная экспериментальная изотерма
выглядит следующим образом.
Pн.п. – давление насыщенного пара.
269
270.
Правило рычагаПусть нам известны объемы чистых жидкой
(V0ж) и газообразной (V0п) фаз, и мы хотим
найти сколько пара и сколько жидкости будет
находится в некотором промежуточном
состоянии (V0’). Можно показать, что
выполняется
mж V0п V0 y
.
ж
mп V0 V0
x
Данное правило называется правилом
рычага.
270
271.
Давление насыщенного параДавление насыщенного пара Pн.п. соответствует тому
давлению, которое образуется в равновесном двухфазном
состоянии. Это давление не зависит от объема, при его
изменении в V0ж <V0< V0п. Давление насыщенного пара
зависит от температуры.
Tтр – температура,
соответствующая тройной
точке (когда все три фазы
(жидкая, твердая и
газообразная) находятся в
равновесии).
271
272.
Поведение двухфазной системыВ двухфазной системе одновременно присутствуют две
фазы. Если при заданном объеме мы будем повышать
температуру, то в зависимости от начального
соотношения жидкой и газообразной фаз весь сосуд
постепенно заполнится либо жидкостью, либо паром.
272
273.
Фазовый переход жидкость-парФазовый переход жидкость-пар является
фазовым переходом первого рода.
Характерной особенностью таких
переходов является то, что они происходят
при постоянной температуре, называемой
температурой фазового перехода. Для
поддержания температуры перехода
постоянной в веществе выделяется или
поглощается скрытая теплота фазового
перехода (теплота парообразования,
конденсации). Эта теплота затрачивается на
изменение фазового состояния вещества.
273
274.
Уравнение Клапейрона-КлаузиусаРассматривая малый обратимый цикл Карно в
системе, находящейся в двухфазном состоянии,
можно получить уравнение КлапейронаКлаузиуса
dP
q
,
dT T Vп Vж
где q – удельная (на единицу массы) скрытая теплота
фазового перехода; V’п и V’ж – удельные объемы
газообразной и жидкой фаз.
Уравнение Клапейрона-Клаузиуса связывает давление,
при котором находится в равновесии двухфазная
система, с температурой.
Если известны удельная скрытая теплота перехода и
объемы жидкой и газообразной фаз, то решение
уравнения позволяет найти давление как функцию
температуры.
274
275.
Фазовая диаграмма жидкость-парПоскольку V’п > V’ж , то dP/dT>0 и давление
равновесного состояния фаз увеличивается с
ростом температуры.
275
276.
Влажность воздухаКак известно, в атмосфере воздуха всегда присутствует
некоторое количество водяного пара, которое называется
влажностью воздуха или просто влажностью.
Влажность бывает абсолютная и относительная.
Абсолютная влажность D – масса водяного пара,
которое помещается в 1 м3:
m
D ,
V
где m – масса водяного пара в объеме V. Максимальное
количество водяного пара, которое может находится в 1 м3
воздуха при определенной температуре, называется
максимальной абсолютной влажностью:
mmax
Dmax
.
V
где mmax – максимальная масса водяного пара в объеме
V.
276
277.
Влажность воздухаОтносительная влажность ψ – это отношение абсолютной
влажности воздуха к максимально возможной абсолютной
влажности:
D
P
,
Dmax Pн.п.
где P – парциальное давление водяного пара; Pн.п. –
давление насыщенного водяного пара.
Абсолютная и относительная влажности зависят от
температуры.
Точка росы – это та температура, до которой необходимо
охладить данный объем воздуха, чтобы весь водяной пар,
который в нем находится, перешел в жидкую фазу. При
понижении температуры до точки росы относительная
влажность воздуха достигает 100% и начинается
конденсация водяного пара.
277
278.
Молекулярная физикаТема 18:
Жидкость
278
279.
Содержание• Свойства и структура жидкостей. Жидкие
кристаллы. Теплоемкость жидкостей.
• Поверхностное натяжение. Условия равновесия на
границе двух жидкостей и на границе жидкость –
твердое тело.
• Давление под искривленной поверхностью
жидкости. Капиллярные явления. Поверхностноактивные вещества. Флотация.
• Испарение. Динамическое равновесие на границе
жидкость – пар. Кипение. Давление насыщенных
паров вблизи искривленной поверхности жидкости.
• Перегретая жидкость. Переохлажденный пар.
Пузырьковая камера. Камера Вильсона.
279
280.
Свойства и структура жидкостейВ твердом теле каждая частица (атом) колеблется около
своего положения равновесия, причем в идеальной
решетке кристалла все возможные «места» для частиц
заняты. Жидкость обладает более «рыхлой» структурой,
чем твердое тело, в ней имеются свободные места «дырки», благодаря чему молекулы могут перемещаться,
покидая свое место и занимая одну из соседних
свободных «дырок». Тепловое движение в жидкостях
носит следующий характер: каждая молекула в течение
некоторого промежутка времени колеблется около
определенного места равновесия. Молекула меняет место
равновесия, перемещаясь на отрезок порядка размеров
самих молекул. Таким образом, молекулы медленно
перемещаются внутри жидкости, пребывая часть времени
около определенных мест, находясь в «оседлом»
280
состоянии (теория Я.И. Френкеля).
281.
Свойства и структура жидкостейВ газе средняя кинетическая энергия теплового
движения молекул достаточна, чтобы преодолеть
силы притяжения между молекулами. Это ведет
к тому, что молекулы в газе разлетаются во все
стороны, и газ распространяется на весь
предоставленный ему объем. В жидкостях,
наоборот, средней кинетической энергии
теплового движения не хватает, чтобы
преодолеть силы сцепления. Благодаря этому
жидкость представляет собой тело
определенного объема. Из жидкости
вырываются лишь наиболее быстрые молекулы,
что ведет к процессу испарения жидкости.
281
282.
Свойства и структура жидкостейВзаимная потенциальная энергия двух молекул
газа имеет при некотором расстоянии r0 между
молекулами минимум. Однако глубина
образующейся потенциальной ямы u невелика и
меньше средней кинетической энергии (1/2)kT,
приходящейся на одну степень свободы.
Поэтому молекулы в газе не удерживаются друг
около друга, но, сблизившись, снова
разлетаются. Для молекул жидкости средняя
кинетическая энергия теплового движения
недостаточна, чтобы преодолеть силы взаимного
притяжения молекул друг к другу. В результате
молекулы располагаются достаточно близко друг
к другу, и каждая молекула окружена другими.
282
283.
Свойства и структура жидкостейКаждая молекула пребывает в потенциальной
яме около своего положения равновесия.
Однако для жидкости средняя энергия (1/2)kT
не на много меньше глубины ямы u, в
результате чего кинетическая энергия
отдельной молекулы, благодаря наличию
флуктуации, иногда оказывается достаточной,
чтобы молекула выскочила из потенциальной
ямы и заняла новое место между другой парой
молекул.
Указанный характер движения молекул в
жидкостях объясняет как медленность
диффузии в жидкостях, так и большую, по
сравнению с газами, вязкость жидкостей.
283
284.
Парная функция распределенияКоличественной характеристикой упорядоченности
структуры может служить парная функция распределения
g(r), которая определяется следующим образом. Пусть
некоторый наблюдатель находится в месте положения
некоторой молекулы и наблюдает среднюю плотность других
молекул в различных малых областях пространства,
характеризуемых радиус-вектором r. Распределение этой
плотности характеризуется функцией g(r).
В случае кристаллической
решетки твердого тела
плотность отлична от нуля
лишь вблизи узлов
кристаллической решетки.
В твердых
кристаллических телах
наблюдается дальний
порядок.
284
285.
Парная функция распределенияУ идеального газа распределение молекул одинаково по
всем направлениям и на всех расстояниях от начальной
точки, т.е. для газа g(r)=const.
У жидкости парная функция распределения изотропна,
но зависит от расстояния. Плотность g(r) колеблется
вокруг средней плотности и на достаточно больших
расстояниях становится равной средней плотности.
Жидкость
упорядочена в
ближнем порядке.
285
286.
Жидкие кристаллыЖидкие кристаллы проявляют упорядоченность, которая
является промежуточной между упорядоченностью жидкости и
твердых тел, приводящей к соответствующей анизотропии их
свойств. В соответствии с этим жидкие кристаллы делятся на две
группы.
Первая группа жидких кристаллов, называемых смектиками,
характеризуется одномерной пространственной
упорядоченностью. Жидкость представляется состоящей из
параллельных жидких слоев, регулярно следующих друг за
другом и отличающихся друг от друга упорядоченностью
структуры.
Вторая группа жидких кристаллов, называемых нематиками, не
имеет пространственной упорядоченности, а характеризуется
ориентационной упорядоченностью их молекул. Их молекулы
сильно вытянуты, и ориентационная упорядоченность возникает
из-за преимущественной ориентации этих длинных молекул. У
смектиков молекулы также сильно вытянуты. Поэтому можно
сказать, что особенностью жидких кристаллов с молекулярной
точки зрения является вытянутая структура их молекул,
приводящая к анизотропии свойств.
286
287.
Жидкие кристаллыСмектики
287
288.
Жидкие кристаллыНематики
Холестерики
288
289.
Теплоемкость жидкостейВнутренняя энергия жидкостей определяется не только
кинетической энергией тепловых движений молекул, но и
их потенциальной энергией взаимодействия. Опыт
показывает, что теплоемкость жидкостей зависит от
температуры, причем вид зависимости у разных жидкостей
различный. У большинства из них теплоемкость с
повышением температуры увеличивается, но есть и такие, у
которых, наоборот, - уменьшается.
У воды удельная
теплоемкость с
повышением температуры
сначала падает, а затем,
пройдя через минимум,
начинает расти.
289
290.
Поверхностное натяжениеПотенциальная энергия молекулы внутри
жидкости меньше потенциальной энергии
молекулы вне жидкости. Поверхностный слой
жидкости находится в иных условиях, чем весь
объем жидкости. Для перевода молекулы из
жидкости наружу необходимо преодолеть
определенный потенциальный барьер, т.е.
совершить определенную работу. Средняя
энергия теплового движения молекул
недостаточная, чтобы совершить эту работу, в
результате чего жидкость сохраняет объем.
290
291.
Поверхностное натяжениеРезультирующая сила, действующая на молекулу
внутри жидкости со стороны других молекул, в
среднем равна нулю. Иначе обстоит дело с
молекулами, находящимися у поверхности жидкости.
На молекулу в поверхностном слое действует с
разных сторон неодинаковое число молекул. Силы, с
которыми они действуют на молекулу вблизи
поверхности, в среднем не будут скомпенсированы,
возникнет результирующая сила, направленная
внутрь жидкости. Таким образом, на каждую
молекулу в поверхностном слое со стороны других
молекул действует сила, направленная внутрь
жидкости. На весь слой, лежащий у поверхности
жидкости, действуют силы, направленные нормально
к поверхности внутрь жидкости. Поверхностный
слой оказывает на всю жидкость некоторое давление.
291
292.
Поверхностное натяжениеЕсли на жидкость не действуют никакие другие силы, то
равновесным окажется такое положение поверхности, при
котором эти силы нормальны к поверхности. Жидкость, на
которую не действуют внешние силы, должна под влиянием
сил молекулярного давления принять сферическую форму.
Малые капли жидкости, для которых роль силы тяжести
относительно мала, действительно принимают вид
правильных сфер.
Из всех геометрических тел сфера имеет при данном объеме
наименьшую поверхность. Поэтому переход данной массы
жидкости от какой-либо несферической формы к сферической
связан с уменьшением ее поверхности. Следовательно,
действие сил молекулярного давления, под влиянием которых
жидкость принимает сферическую форму, аналогично
действию, которое возникло бы, если поверхность жидкости
представляла бы собою растянутую пленку, стремящуюся
сжаться.
292
293.
Поверхностное натяжениеДля того чтобы растянутую пленку удержать в равновесии,
нормально к линии ее границы, надо приложить силу F,
касательную к поверхности жидкости, называемую
силой поверхностного натяжения. Эта сила тем больше,
чем больше длина границы пленки l:
F l,
Коэффициент α, зависящий от
природы жидкости, называется
коэффициентом поверхностного
натяжения. Для данной жидкости
коэффициент поверхностного
натяжения α зависит от
температуры: с повышением
температуры он убывает. При
приближении температуры жидкости
к критической температуре Ткр
коэффициент поверхностного
натяжения α стремится к нулю. 293
294.
Поверхностное натяжениеОпределим элементарное приращение работы dA, которую
надо затратить, чтобы увеличить площадь поверхностной
пленки жидкости на малую величину ds. Для этого с
помощью силы F передвинем границу пленки на отрезок
dh параллельно самой себе. Тогда совершенная работа dA
равна
dA Fdh ldh ds.
Эта работа идет на увеличение
энергии пленки, которая представляет
собой ту часть внутренней энергии,
которая может быть превращена в
работу при изотермическом
процессе, т.е. на увеличение
свободной энергией W.
294
295.
Растяжение пленкиРассмотрим какое количество теплоты поглощает
(мыльная) пленка при ее растяжении. Пользуясь
определением свободной энергии, для энтропии
пленки получим
W s
S
s
.
T
T
T
Количество теплоты, поглощаемое пленкой при
равновесном изотермическом процессе 1-2, когда
ее площадь увеличивается от s1 до s2, имеет вид
Q1 2
T S2 S1 s2 s1 T
0.
T
295
296.
Условия равновесия на границе двухжидкостей
Если на поверхность одной жидкости поместить
каплю другой, более легкой жидкости, то возможны
два результата в зависимости от соотношения
поверхностных натяжений.
1. Величина α13<α23+α12. В этом случае получим
dl – элемент длины,
направленный вдоль
линии соприкосновения
трех сред 1, 2 и 3; α13, α23
и α12 – коэффициенты
поверхностного
натяжения между
соответствующими
средами.
296
297.
Условия равновесия на границе двухжидкостей
Условием равновесия является обращение в
нуль равнодействующих всех сил,
действующих на элемент dl
13 23 cos 1 12 cos 2 , 23 sin 1 12 sin 2 .
2. Если α13>α23+α12,
то капля растечется
по поверхности
жидкости.
297
298.
Условия равновесия на границежидкость-твердое тело
Если на поверхность твердого тела поместить каплю
жидкости, то возможны три результата.
1. Величина α13<α23+α12. В этом случае, при условии
того, что жидкость смачивает твердое тело, получим
Условием равновесия является
13 23 cos 12 .
298
299.
Условия равновесия на границежидкость-твердое тело
2. Величина α13<α23+α12. В этом случае, при условии
того, что жидкость не смачивает твердое тело,
получим
Условием равновесия является
13 23 cos 12 .
299
300.
Условия равновесия на границежидкость-твердое тело
3. Величина α13>α23+α12. В этом случае, капля
растечется по поверхности твердого тела, т.е.
жидкость полностью смачивает твердое тело.
300
301.
Давление под искривленнойповерхностью жидкости
Всякая изогнутая поверхность жидкости (или пленки)
оказывает на нее добавочное давление по сравнению с
тем, которое испытывает жидкость с плоской
поверхностью. В случае выпуклой поверхности это
добавочное давление положительно, а в случае вогнутой
– отрицательно.
301
302.
Давление под искривленнойповерхностью жидкости
Для добавочного давления можно получить
явное выражение, называемое формулой
Лапласа:
1 1
P ,
R1 R2
где R1 и R2 – главные радиусы кривизны
рассматриваемой поверхности жидкости.
В случае мыльной пленки, за счет того что
у нее две поверхности, добавочное
давление удваивается.
302
303.
Капиллярные явленияПри попадании жидкости в капилляр, между молекулами
жидкости и вещества, из которого изготовлен капилляр,
возникает взаимодействие (притяжение). Если это
взаимодействие сильнее, чем притяжение между молекулами
жидкости, то жидкость смачивает стенку капилляра. Иначе,
если взаимодействие слабее, - жидкость не смачивает стенку
капилляра. Из-за этого в трубке капилляра образуется
вогнутый или выпуклый мениск. За счет изогнутости мениска
на жидкость действует добавочное давление, что заставляет
жидкость смещаться вдоль капилляра.
303
304.
Капиллярные явленияВысота h, на которую поднимается вверх жидкость в
смачивающем ее цилиндрическом капилляре радиусом r, после
его соприкосновения с жидкостью, найдем из соотношений
2
r
P
gh, R
,
R
cos
т.е.
2 cos
h
,
r g
где φ – краевой угол
(угол смачивания); ρ –
плотность жидкости; g –
ускорение свободного
падения.
Аналогичная формула
получиться и для не
смачивающего
жидкость капилляра, но
в этом случае жидкость
304
опустится вниз.
305.
Поверхностно-активные веществаРастворение в жидкости различных добавок
вызывает изменение поверхностного натяжения.
Это особенно заметно в тех случаях, когда силы
взаимодействия между молекулами растворенного
вещества и растворителя сильно отличаются от
сил взаимодействия между молекулами
растворителя. Если последние больше первых, то
молекулы растворенного вещества, слабо
взаимодействующие с молекулами растворителя,
«выталкиваются» последними в поверхностный
слой. Концентрация молекул растворенного
вещества в поверхностном слое будет больше
концентрации их в объеме жидкости.
305
306.
Поверхностно-активные веществаВещества, собирающиеся в поверхностном слое
при растворении их в жидкости, называют
поверхностно-активными веществами, а
явление повышенной концентрации молекул этих
веществ в поверхностном слое растворителя
называют адсорбцией. Адсорбция молекул газа
или жидкости может происходить также и на
поверхности твердого тела, контактирующего с
газом или жидкостью (например, на поверхности
активированного угля). Поверхностно-активными
веществами по отношению к воде являются
многие органические вещества: жирные кислоты,
их соли, спирты, эфиры и др. Поверхностноактивные вещества вызывают уменьшение
поверхностного натяжения.
306
307.
Поверхностно-активные веществаЕсли силы взаимодействия между
молекулами растворенного вещества и
растворителя больше сил взаимодействия
между молекулами растворителя (например,
в случае раствора сахара в воде), то
наблюдается обратное явление —
концентрация молекул растворенного
вещества в поверхностном слое оказывается
меньшей, чем в остальном объеме раствора.
Такое явление называют отрицательной
адсорбцией.
307
308.
ФлотацияОсобенно важное значение для техники имеет
использование поверхностных явлений в
процессе обогащения руд, называемом
флотацией. Как правило, кусочки руды плохо
смачиваются водой, но хорошо смачиваются
жирными органическими веществами. В то же
время, пустая порода, всегда встречающаяся
вместе с рудой, хорошо смачивается водой и
плохо маслами. Если поместить раздробленную
руду вместе с породой в воду, в которой в виде
мельчайших капелек находятся специальные
масла, то кусочки породы окажутся смоченными
водой, а кусочки руды — маслом.
308
309.
ФлотацияИнтенсивно вспенивая образовавшуюся массу и
отделяя часть, уходящую вместе с пеной от той,
которая падает на дно сосуда, можно
значительно обогатить руду содержащимися в
ней ценными минералами. Обогащение
достигается в результате того, что
присутствующие в пене пузырьки воздуха
прилипают к маслянистому слою,
обволакивающему кусочки руды, и уносят их
вместе с пеной на поверхность. К смоченным
водой кусочкам пустой породы, удельный вес
которой обычно меньше удельного веса руды,
воздушные пузырьки не прилипают, и пустая
порода падает на дно.
309
310.
ИспарениеЕсли жидкость находится в открытом
сосуде, она постепенно испаряется, т.е.
переходит в газообразное состояние.
Испарение происходит при всякой
температуре, но для каждой данной
жидкости с повышением температуры
скорость испарения увеличивается.
310
311.
ИспарениеЯвление испарения объясняется тем, что в жидкостях,
как и в газах, молекулы обладают различными энергиями
как большими, так и меньшими средней энергии,
значение которой определяется температурой Т. Поэтому
при каждой температуре Т в жидкости находятся
настолько быстрые молекулы, что они, подходя к
поверхности жидкости, могут преодолеть притяжение
соседних молекул и, прорвавшись сквозь поверхностный
слой, вылететь за пределы жидкости. Чем выше
температура жидкости, тем больше число быстрых
молекул и тем, следовательно, быстрее идет испарение.
Во время испарения из жидкости вылетают более
быстрые молекулы, при этом они тратят часть своей
энергии на совершение работы против удерживающих их
внутри жидкости сил молекулярного притяжения. Отсюда
получается, что средняя энергия молекул, остающихся в
жидкости, убывает, т.е. жидкость охлаждается.
311
312.
Насыщенный парЕсли покинувшие жидкость молекулы удаляются из
пространства вблизи поверхности жидкости, то в конце
концов вся жидкость испарится. Если же молекулы,
покинувшие жидкость, не удаляются, а удерживаются
в замкнутом объеме около поверхности жидкости, то
дальнейший процесс развивается по-другому.
Покинувшие жидкость молекулы образуют пар.
Молекулы пара, попавшие в область вблизи
поверхности жидкости, силами притяжения
втягиваются в жидкость. Таким образом, скорость
испарения уменьшается. При дальнейшем увеличении
плотности пара достигается такая ситуация, когда число
молекул, покидающих жидкость за некоторое время,
равно числу молекул, возвращающихся в жидкость за то
же время. Наступает состояние динамического
равновесия. Пар в состоянии динамического
равновесия с жидкостью называется насыщенным.312
313.
Насыщенный парС увеличением плотности насыщенных паров поверхностное
натяжение жидкости уменьшается, поскольку силы,
направленные внутрь жидкости, уменьшаются ввиду роста
противоположно направленных сил со стороны насыщенного
пара. Отсюда же следует, что скрытая теплота
парообразования с повышением температуры уменьшается.
При критической температуре плотность насыщенных паров
становится равной плотности жидкости и различие между
ними исчезает. Это означает, что и поверхность исчезает, и,
следовательно, поверхностное натяжение и скрытая теплота
парообразования при критической температуре обращаются в
нуль.
При конденсации пара в жидкость его молекулы взаимно
притягиваются, в результате чего их скорости, а следовательно,
и их кинетическая энергия возрастают. Это ведет к
нагреванию образующейся жидкости: теплота, затраченная
при испарении, отдается обратно при конденсации пара.
313
314.
КипениеКогда при нагревании жидкости достигается температура, при
которой давление насыщенных паров равно внешнему
давлению, устанавливается равновесие между жидкостью и ее
насыщенным паром. При сообщении жидкости
дополнительного количества теплоты происходит немедленное
превращение соответствующей массы жидкости в пар.
Интенсивное превращение жидкости в пар происходит по
всему объему жидкости. Этот процесс называется кипением.
Температурой кипения является та температура, при которой
давление насыщенных паров становится равным внешнему
давлению. При увеличении давления температура кипения
увеличивается, а при уменьшении давления — уменьшается.
Воду в герметически закрытом сосуде можно нагреть до
температуры, значительно большей 100 оС, без того, чтобы она
закипела. С другой стороны, понизив достаточно давление над
поверхностью воды, например путем откачки воздуха из такого
сосуда, в котором находится жидкость, можно вызвать кипение
жидкости при комнатной температуре.
314
315.
Давление насыщенного параИскривление поверхности жидкости влияет на
давление насыщенного пара над ней. В случае
вогнутой поверхности давление уменьшается, а
в случае выпуклой – возрастает.
Можно получить следующее выражение для
изменения давления (формула Томсона)
2 п
P
,
R ж п
где ρж и ρп – плотности жидкости и
насыщенного пара; R – радиус сферической
поверхности жидкости.
315
316.
Перегретая жидкостьЕсли жидкость лишена примесей и не содержит
пузырьков пара, то при достижении температуры
кипения в ней стремятся образоваться пузырьки пара.
Но как только такой пузырек образуется внутри
жидкости, пар в нем, будучи насыщенным
относительно плоской поверхности жидкости,
является перенасыщенным относительно вогнутой
поверхности жидкости, которой ограничен
рассматриваемый пузырек. Поэтому пар пузырька
немедленно конденсируется в жидкость и пузырек
исчезает. Этому также способствует увеличение
давления на пузырек пара со стороны вогнутой
поверхности жидкости, ограничивающей пузырек.
Это давление также стремится раздавить
образовавшийся пузырек пара. Таким образом,
нагревая чистую жидкость выше температуры
кипения можно получить перегретую жидкость.
316
317.
Перегретая жидкостьКипение начнется, если в жидкость ввести нечто
такое, что обеспечит возможность образования
пузырьков пара, имеющих с самого начала
достаточно большой радиус для того, чтобы пар
в пузырьке не был слишком сильно пересыщен и
давление со стороны стенок пузырька не было
слишком велико. Таким веществом может быть,
например, порошок мела. Отдельные частицы
порошка являются теми «зародышами», вокруг
которых образуются пузырьки пара. Поэтому
при бросании щепотки мела в перегретую воду
возникает бурное кипение, напоминающее
взрыв.
317
318.
Переохлажденный парНасыщенный при некоторой температуре пар
является пресыщенным относительно более
низкой температуры. Поэтому при понижении
температуры насыщенного пара часть его
превращается в жидкость. В обычных условиях
пары воды конденсируются во всем объеме пара
в виде мельчайших капелек — тумана. Однако
если воздух, в котором находится насыщенный
пар, достаточно хорошо очищен от примесей, то
при охлаждении пара не происходит
превращения пара в жидкость и возникает
метастабильное состояние переохлажденного
пара.
318
319.
Переохлажденный парПри охлаждении насыщенного пара образуются
маленькие капельки жидкости. Однако они не могут
долго существовать, потому что насыщенный пар, в
котором они образуются, является ненасыщенным для
выпуклой поверхности капелек. Поэтому жидкость
капелек немедленно испаряется и капельки исчезают.
Для начала процесса конденсации надо обеспечить
существование такой ситуации, чтобы с самого начала
могли образовываться капельки жидкости достаточно
большого радиуса, для которых пар не явился бы
сильно ненасыщенным. Для этого необходимо наличие
зародышей конденсации. Такими зародышами могут
быть, например, ионы, пылинки.
319
320.
Пузырьковая камераЕсли через перегретую жидкость пролетает
заряженная частица, то она на своем пути
ионизирует атомы жидкости.
Ионизированные атомы становятся
«зародышами», вокруг которых образуются
пузырьки насыщенного пара. Другими
словами, перегретая жидкость вскипает
вдоль траектории движения заряженной
частицы, благодаря чему траектория хорошо
видна и может быть сфотографирована.
Такого рода приборы для исследования
траекторий заряженных частиц называются
пузырьковыми камерами. Они играют
очень большую роль в исследованиях
элементарных частиц.
320
321.
Камера ВильсонаЗаряженная частица на своем пути в
переохлажденном паре ионизует молекулы
пара. Ионы становятся центрами
конденсации, вокруг которых образуются
капельки жидкости. Благодаря этому вдоль
траектории частицы образуется туман и
траектория становится видимой. Это
позволяет исследовать заряженные частицы,
их взаимодействие и т.д. Такие приборы
называются камерами Вильсона. Они
сыграли большую роль в научных
исследованиях элементарных частиц.
321
322.
Молекулярная физикаТема 19:
Растворы и смеси
322
323.
Содержание• Жидкие растворы. Растворимость. Теплота
растворения. Идеальные растворы.
• Закон Рауля. Закон Генри.
• Зависимость растворимости от температуры.
• Диаграмма состояния раствора.
• Кипение жидких растворов. Диаграмма
состояния бинарных смесей.
• Осмос.
• Сплавы и твердые растворы.
323
324.
Жидкие растворыЖидкими растворами называется
молекулярная смесь двух или нескольких
веществ, находящихся в жидком
состоянии. Если одно из веществ
присутствует в растворе в значительно
большем количестве, чем другие, то оно
называется растворителем, а другие —
растворенными веществами. Растворы,
состоящие из двух веществ, называются
бинарными.
324
325.
РастворимостьРаствор может быть образован как в результате
растворения в жидкости твердых веществ, так и
смешением жидкостей. При этом возможны
различные случаи.
Бывают ситуации, когда в растворе может
присутствовать любое количество компонент. В
некоторых ситуациях существует предел
концентрации одного из веществ. При дальнейшем
добавлении этого вещества в раствор оно уже не
растворяется. Например, нельзя растворить в данном
количестве воды сколь угодно большое количество
сахара. В этом случае максимальная равновесная
концентрация называется растворимостью. Она
зависит от давления и температуры. Твердые вещества
всегда имеют предел концентрации при растворении в
жидкости. Жидкости в большинстве случаев
(например, спирт и вода) смешиваются в любых
пропорциях.
325
326.
Теплота растворенияМеханизм растворения сводится к разрыву
связей между молекулами каждого из исходных
веществ и образованию новых связей между
молекулами веществ, находящихся в растворе.
Во многих случаях при растворении молекулы
вещества распадаются на свои составные части
— ионы (у солей, щелочей и т. д.).
На разъединение молекул при растворении
вещества затрачивается определенная энергия.
Благодаря этому при растворении происходит
охлаждение. Энергия, затраченная на
растворение, называется теплотой
растворения.
326
327.
Теплота растворенияПосле разъединения молекул растворяемого
вещества силы притяжения между молекулами
растворенного вещества и растворителя могут быть
очень значительными, что приводят к образованию
комплексов молекул. При этом за счет работы сил
притяжения внутренняя энергия увеличивается и
происходит нагревание. Если это нагревание больше,
чем охлаждение при разъединении молекул
растворяемого вещества, то итог процесса
растворения сводится к нагреванию при растворении.
Выделяющаяся при этом теплота также называется
теплотой растворения. К таким случаям относится,
например, растворение кислот в воде.
Взаимодействие между молекулами в газах очень
слабое. Поэтому растворение газов в большинстве
случаев сопровождается выделением теплоты.
327
328.
Идеальные растворыЭто такие растворы, у которых теплота
растворения равна нулю. Ясно, что в этих
растворах характер взаимодействия между
молекулами растворенного вещества и
растворителя такой же, как и между
молекулами растворителя. Это означает,
что взаимодействие между молекулами в
растворе не меняется, если заменить
некоторое число молекул растворенного
вещества на такое же число молекул
растворителя, и наоборот.
328
329.
Закон РауляДавление насыщенных паров растворителя должно быть
меньше их давления над чистым растворителем во столько же
раз, во сколько плотность молекул растворителя меньше, чем
когда он является чистым, без растворенного в нем вещества.
Иначе говоря, давление насыщенных паров уменьшается во
столько раз, во сколько уменьшается концентрация
растворителя (закон Рауля):
1 P1 0
P1
,
1 2
где P1 – давление насыщенных паров растворителя над
раствором; P1(0) – давление насыщенных паров над
чистым растворителем; ν1 – количество молей
растворителя; ν2 – количество молей растворенного
вещества.
329
330.
Закон РауляАналогично для давления насыщенных паров
растворенного вещества получим
2 P2 0
P2
,
1 2
где P2 – давление насыщенных паров
растворенного вещества над раствором; P2(0) –
давление насыщенных паров над чистым
растворенным веществом.
Закон Рауля справедлив для идеальных
растворов. Однако он достаточно хорошо
выполняется также для всех слабых растворов
(не обязательно идеальных), если речь идет о
насыщенных парах растворителя.
330
331.
Закон ГенриЗакон Рауля можно прочитать справа налево. Тогда
он характеризует относительную концентрацию
вещества в растворе, если над раствором
поддерживается давление P2 насыщенных паров
этого вещества (закон Генри):
2
P2 ,
1 2
1
0 .
P2
Из закона Генри следует, что для увеличения
относительной концентрации растворенного
вещества в растворе необходимо увеличить
давление насыщенных паров растворенного
вещества над растворителем; а для уменьшения
концентрации – уменьшить давление.
331
332.
Зависимость растворимости оттемпературы
Если при растворении вещества происходит
нагревание, то при достижении насыщения попытка
дальнейшего нагревания путем добавления
растворяемого вещества приводит к его выпадению в
виде осадка (раствор уже насыщен!). Отсюда следует,
что при повышении температуры растворимость
веществ с положительной теплотой растворения
убывает.
Если при растворении вещества происходит
охлаждение, то при достижении насыщения попытка
дальнейшего охлаждения при добавлении
растворяемого вещества приводит к его выпадению в
виде осадка. Отсюда следует, что при понижении
температуры растворимость веществ с отрицательной
теплотой растворения убывает, а с повышением
температуры возрастает.
332
333.
Диаграммы состояния раствораРассмотрим диаграммы состояния жидких
бинарных смесей при постоянном (атмосферном)
давлении.
Данная диаграмма
соответствует жидкостям,
смешивающимся в
произвольном количестве
лишь при достаточно
высокой температуре.
Линия MNK характеризует
насыщенный раствор
жидкости A в жидкости B,
а линия RPK –
соответствует
насыщенному раствору
жидкости B в жидкости A.
333
334.
Диаграммы состояния раствораПри температуре T>Tк (критической
температуры смешивания) жидкости A и B
смешиваются в любых пропорциях.
Область ниже кривой MNKPR – соответствует
состоянию двухфазной системы с насыщенными
растворами жидкости A в жидкости B, и жидкости
B в жидкости A.
Область, расположенная левее линии MNK,
соответствует ненасыщенному раствору жидкости
A в жидкости B.
Область, расположенная правее линии RPK,
соответствует ненасыщенному раствору жидкости
B в жидкости A.
334
335.
Диаграммы состояния раствораДля характеристики состояния двухфазной
системы действует правило рычага.
Например, в состоянии характеризуемом
точкой O, массы насыщенного раствора
жидкости A в жидкости B (mAB) и раствора
жидкости B в жидкости A (mBA) обратно
пропорциональны длинам отрезков OP и
ON:
mAB OP
.
mBA ON
335
336.
Диаграммы состояния раствораСуществуют и другие диаграммы бинарных
жидких смесей.
Данная диаграмма
соответствует жидкостям,
смешивающимся в
произвольном количестве
лишь при достаточно
низкой температуре.
Линия MNK характеризует
насыщенный раствор
жидкости A в жидкости B,
а линия RPK –
соответствует
насыщенному раствору
жидкости B в жидкости A.
336
337.
Диаграммы состояния раствораПри температуре T<Tк жидкости A и B
смешиваются в любых пропорциях.
Область выше кривой MNKPR –
соответствует состоянию двухфазной
системы с насыщенными растворами
жидкости A в жидкости B, и жидкости B в
жидкости A.
Область, расположенная левее линии MNK,
соответствует ненасыщенному раствору
жидкости A в жидкости B.
Область, расположенная правее линии RPK,
соответствует ненасыщенному раствору
жидкости B в жидкости A.
337
338.
Диаграммы состояния раствораСуществуют диаграммы с двумя критическими
температурами смешивания.
Данная диаграмма
соответствует жидкостям,
смешивающимся в
произвольном количестве
лишь при достаточно
высоких (T>Tк1) и
достаточно низких
(T<Tк2) температурах.
Область ограниченная
линией соответствует
области двухфазных
состояний, а сама линия
соответствует
насыщенным растворам.
338
339.
Кипение жидких растворовДавление насыщенных паров компонент над раствором
зависит от концентрации. При заданном давлении при
достижении определенной температуры давление
насыщенных паров одной из компонент может стать
равным внешнему давлению, которое, однако, для этой
компоненты не равно давлению насыщенных паров при
этой температуре. Для первой компоненты при данной
температуре достигается кипение, а для второй — нет.
Поэтому первая компонента начнет энергично
превращаться в пар, а вторая будет превращаться в пар в
режиме испарения, т.е. значительно менее энергично.
Это приводит к тому, что концентрация компонент в паре
отличается от их концентрации в кипящей жидкости.
Благодаря этому относительная концентрация
компоненты кипящей жидкости изменяется, изменяется
температура ее кипения.
339
340.
Диаграммы состояния смесиРассмотрим диаграммы состояния системы паржидкий раствор при постоянном (атмосферном)
давлении.
Данная диаграмма
соответствует бинарной
смеси, компоненты
которой смешиваются в
любых пропорциях.
Область, ограниченная
замкнутой кривой
MNDRPM, соответствует
двухфазным состояниям,
когда в объеме имеются
одновременно и
насыщенный пар и
раствор.
340
341.
Диаграммы состояния смесиНиже кривой MPR находится однофазное
состояние, когда имеется только раствор.
Область выше кривой MNDR соответствует
однофазным состояниям системы в виде пара.
В состоянии, которое соответствует точке P,
имеется чистый раствор при температуре T,
концентрация которого задается абсциссой этой
точки (проекцией на горизонтальную ось). Точка
M характеризует парообразное состояние при
температуре T.
Точка O определяет двухфазную систему. При
этом, полная концентрация компонент в системе
дается абсциссой этой точки, а массы жидкой и
газообразной фаз относятся друг к другу обратно
пропорционально длинам отрезков OP и ON.
341
342.
Диаграммы состояния смесиПусть в замкнутом сосуде имеется раствор, концентрация
которого дается абсциссой точки P при температуре ниже T.
При повышении температуры система продолжает пребывать
в однофазном состоянии вплоть до температуры Т, когда
достигается состояние, в котором начинается кипение раствора
(точка P). Выкипающий пар имеет концентрацию,
характеризуемую точкой N. Следовательно, состав раствора в
результате кипения изменяется, причем концентрация
компоненты А в растворе увеличивается. Благодаря этому
увеличивается и температура кипения раствора. Если этот
процесс кипения происходит в замкнутом сосуде, объем
которого изменяется в процессе кипения так, что давление
остается постоянным (с помощью передвижения поршня), то
в процессе кипения соотношение между суммарными по
обеим фазам концентрациями компонент в системе не
меняется. Следовательно, изменение состояния системы при
кипении описывается дальнейшим движением вверх вдоль
прямой PD. При достижении точки D весь объем заполнен
паром, причем соотношение между массами компонент А и B
342
такое же, как и в жидкости в точке P, когда началось кипение.
343.
Разделение компонент раствораЕсли система не находится в замкнутом сосуде и
выкипающие пары удаляются от поверхности кипящего
раствора, то, аналогично описанному выше, будет
изменяться концентрация раствора и повышаться
температура его кипения. Однако при температуре
кипения система в этом случае будет все время
однофазной. Следовательно, изображающая состояние
системы точка движется вдоль кривой PR. При
достижении точки R компонента B полностью выкипит и
останется чистая жидкость А. На этом явлении основан
один из наиболее распространенных способов разделения
жидкого раствора по его компонентам. Пар является
обогащенным преимущественно веществом B, но в
некотором количестве в нем присутствует также и
вещество А. Поэтому этот пар может быть сконденсирован
и процесс повторен. В образующемся при этом паре
концентрация вещества B еще более увеличивается.
Повторяя этот процесс, можно с любой степенью чистоты
343
разделить компоненты А и B.
344.
Диаграммы состояния смесиСуществуют и более сложные диаграммы
состояния системы пар-жидкий раствор
при постоянном (атмосферном) давлении.
Точка O характерна
тем, что в ней состав
жидкости и
насыщенного пара
одинаков. Кроме того,
она соответствует
состоянию, к которому
придет кипящий
раствор, если пары над
ним удаляются.
344
345.
ОсмосПусть раствор некоторого вещества и чистый
растворитель разделены полупроницаемой
перегородкой, которая пропускает молекулы
растворителя, но не пропускает молекул
растворенного вещества. Тогда через достаточно
большой промежуток времени устанавливается
равновесие, при котором молекулы растворителя
свободно взаимодействуют между собой через
полупроницаемую перегородку. Давление на
перегородку за счет ударов по ней молекул
растворителя с обеих сторон будет в состоянии
равновесия одинаковым. Давление же растворенного
вещества не передается растворителю с другой стороны
перегородки. Таким образом, общее давление с одной
стороны перегородки, равное сумме давлений
растворенного вещества и растворителя, больше, чем
давление с другой стороны перегородки, равное
давлению растворителя.
345
346.
ОсмосВ результате уровень чистого растворителя
установится ниже уровня раствора. Если
первоначально уровни чистого растворителя и
раствора были одинаковы, то происходит
проникновение чистого растворителя через
полупроницаемую перегородку в область,
занятую раствором, в результате чего в этой
области повышаются давление и уровень
раствора. Это явление проникновения
растворителя через полупроницаемую
перегородку называется осмосом. Разность
давлений, которая возникает между областями,
занятыми чистым растворителем и раствором,
разделенными полупроницаемой перегородкой,
называется осмотическим давлением.
346
347.
ОсмосДля достаточно разбавленных растворов молекулы
растворенного вещества ведут себя, как в разреженном
газе. Осмотическое давление равно давлению
разреженного газа этих молекул, т.е. может быть
рассчитано по формуле для идеальных газов:
P
RT
V
,
где ν – число молей молекул растворенного вещества в
объеме V. Данное выражение называется законом ВантГоффа.
Явление осмоса играет огромную роль в животном и
растительном мире. Большинство перегородок в живых и
растительных организмах являются полупроницаемыми.
Например, осмотическое давление в растительных клетках
достигает нескольких атмосфер, благодаря чему жидкость
из почвы может подниматься по стволу деревьев на
большую высоту.
347
348.
Сплавы и твердые растворыПереход из жидкого состояния в твердое
происходит при определенных температуре и
давлении. Этот процесс называется
кристаллизацией. Обратный процесс
называется плавлением.
При понижении температуры жидкого
раствора при некоторой температуре
начинается кристаллизация и свойства
образующейся твердой фазы зависят от
компонент раствора и сильно отличаются друг
от друга. Рассмотрим вещества, состоящие из
двух компонент.
348
349.
Сплавы и твердые растворыМожет случиться, что в результате
кристаллизации образуется твердая фаза,
состоящая из смеси кристалликов различных
компонент вещества. Такая твердая фаза
называется сплавом.
Иногда в результате кристаллизации
образуется твердая фаза, состоящая из
кристаллов, построенных из атомов обеих
компонент вещества. Такая твердая фаза
называется твердым раствором.
349
350.
СплавыВ случае сплава ход кристаллизации зависит
от процентного соотношения компонент в
жидком растворе. При некоторой температуре
начинается кристаллизация одной из
компонент. Лишь при одном вполне
определенном соотношении между
компонентами начинается одновременная
кристаллизация обеих компонент. Такой
состав жидкого раствора называется
эвтектическим, а получающийся в результате
кристаллизации сплав называется
эвтектическим сплавом или эвтектикой.
350
351.
СплавыРассмотрим диаграмму состояния сплава.
Эвтектический состав
характеризуется абсциссой
точки Э. Если жидкий раствор
такого состава охлаждать, то
при температуре Тэ из раствора
начинают выпадать
одновременно кристаллы
обеих компонент и весь
процесс кристаллизации
завершается при постоянной
температуре. Получаемый в
результате этого эвтектический
сплав является смесью
кристалликов обеих
компонент. При плавлении
такого сплава все процессы
идут в обратном направлении.
351
352.
СплавыЕсли состав жидкого раствора отличается от
эвтектического, то процесс кристаллизации происходит
по-другому. Например, если жидкий раствор обогащен
компонентой В по сравнению с эвтектическим составом
и его состав характеризуется точкой N, то
кристаллизация начинается при температуре Т, однако
при этом из раствора выпадают кристаллы вещества В. В
результате этого жидкий раствор изменяет свой состав,
обогащаясь веществом А. Это означает, что его состав
изменяется ближе к эвтектическому и температура
кристаллизации уменьшается. В результате этого в
процессе кристаллизации происходит изменение условий
кристаллизации по линии NЭ. При достижении точки Э
кристаллизация происходит при постоянной
температуре Тэ, как и кристаллизация эвтектического
жидкого раствора. Получающаяся в результате
кристаллизации твердая фаза состоит из больших
кристалликов компоненты B. Кристаллики компоненты A
представляются в сплаве более мелкими, вкрапленными
352
между крупными кристалликами компоненты B.
353.
СплавыЛоманая линия MNЭPR разделяет жидкое
состояние, лежащее сверху, от двухфазного
состояния, когда присутствуют одновременно
жидкая и твердая фазы.
Ниже линии MNЭ лежит область двухфазных
состояний (жидкий раствор и твердая фаза) в
том случае, когда имеется преобладание
компоненты В по сравнению с эвтектическим
составом, а ниже линии ЭPR лежат
двухфазные состояния при преобладании
компоненты А в системе.
Горизонтальная линия Tэ отделяет
двухфазные состояния от твердых состояний,
которые располагаются ниже этой линии.
353
354.
Твердые растворыТвердые растворы делятся на твердые растворы
замещения, внедрения и вычитания.
В твердых растворах замещения часть атомов в
кристаллической решетке одной из компонент
замещается атомами другой компоненты.
В твердых растворах внедрения атомы одной из
компонент внедряются между узлами
кристаллической решетки второй компоненты.
В твердых растворах вычитания происходит не
только внедрение или замещение атомов одной
компоненты атомами другой, но и сохраняется
решетка другой компоненты, однако с пустыми
местами в части узлов.
354
355.
Твердые растворыДиаграмма состояния
твердых растворов
аналогична диаграмме
состояния жидких
растворов. Т.е. все выводы
для жидких растворов
будут справедливы и для
твердых. Отличие состоит
лишь в том, что вместо
газообразной фазы
следует рассматривать
жидкую фазу, а вместо
жидкой фазы – твердую
фазу.
355
356.
Молекулярная физикаТема 20:
Фазовые переходы
356
357.
Содержание• Особенности фазовых переходов. Фазовый
переход первого рода.
• Фазовые диаграммы.
• Жидкий гелий.
• Полиморфизм.
• Фазовые переходы первого и второго рода.
357
358.
Фазовые переходыПри достаточно низком давлении при
понижении температуры все вещества, за
исключением гелия, переходят в твердое
состояние, т.е. кристаллизуются. Жидкий
Не-II при давлении меньше 3 МПа
остается жидким вплоть до температуры
О К. Лишь при давлении свыше 3 МПа он
при достаточно низкой температуре
переходит в твердое состояние. Такое
поведение жидкого гелия обусловливается
квантовыми эффектами.
358
359.
Фазовые переходыПри высоком давлении с понижением температуры
большинство веществ также переходит в твердое
состояние. Исключением из этого правила является
ряд аномальных веществ, которые остаются
жидкими при очень большом давлении вплоть до
температуры О К. К аномальным относятся
вещества, плотность которых уменьшается при
переходе из жидкого в твердое состояние при
условии, что эта особенность сохраняется вплоть до
очень большого давления и малых температур. У
этих веществ температура плавления при
увеличении давления уменьшается. Например, вода
при температуре около 0 оС и давлении вблизи
атмосферного является аномальным веществом,
поскольку плотность льда меньше плотности воды.359
360.
Фазовый переход первого родаПереход из жидкого состояния в твердое
происходит при определенных температуре и
давлении. Этот процесс называется
кристаллизацией. Обратный процесс
называется плавлением. При плавлении
необходимо затрачивать теплоту для перевода
вещества из твердого состояния в жидкое без
изменения температуры. Эта теплота
называется скрытой теплотой плавления. При
кристаллизации выделяется теплота
кристаллизации. Кристаллизация и плавление,
также как кипение и конденсация, являются
фазовыми переходами первого рода.
360
361.
Фазовый переход первого родаПри достаточно малых давлениях переход в
твердое состояние осуществляется сразу из
газообразного состояния, минуя жидкую фазу,
и, наоборот, при нагревании твердого тела при
соответствующем давлении оно не плавится,
переходя в жидкое состояние, а сразу
переходит в газообразное состояние, как
говорят, возгоняется (сублимируется).
Кристаллизация из газообразного состояния и
возгонка также происходят при определенных
температуре и давлении и сопровождаются
поглощением или выделением скрытой
теплоты. Поэтому они также являются
фазовыми переходами первого рода.
361
362.
Фазовый переход первого родаСоотношение между давлением и температурой при
фазовом переходе первого рода дается уравнением
Клапейрона-Клаузиуса
dP
q
,
dT T V1 V2
В случае переходов жидкость-твердое тело и газтвердое тело q является скрытой удельной теплотой
кристаллизации (из жидкого или газообразного
состояния), V’2 - удельным объемом вещества в
твердом состоянии, V’1 - удельным объемом
вещества в жидком состоянии при переходе
жидкость-твердое тело или в газообразном
состоянии при переходе газ-твердое тело.
362
363.
Фазовая диаграммаРассмотрим фазовую диаграмму состояний газжидкость-твердое тело для нормального вещества.
363
364.
Фазовая диаграммаТочка А является тройной: в ней находятся
в равновесии одновременно газ, жидкость
и твердое тело. Давление и температура
тройной точки обозначены Pтр и Tтр.
0A является кривой сублимации: при
соответствующих давлении и температуре
происходит переход газ-твердое тело,
минуя жидкое состояние. Выше давления
тройной точки Pтр, но ниже критического
давления Pкр, переход из газообразного в
твердое состояние может быть осуществлен
только через жидкую фазу.
364
365.
Фазовая диаграммаАК является кривой перехода жидкость-газ. Она
начинается в тройной точке А и заканчивается в
точке К, обозначающей критическое состояние.
При температуре выше критической теряется
различие между жидкостью и газом.
АВ является кривой перехода жидкость-твердое
тело. Она не имеет конца, а продолжается
безгранично вверх (стрелка на верхнем конце
кривой). Это обусловлено тем, что жидкое
состояние отличается от кристаллического по
структуре и ни при каких обстоятельствах
кристаллическая структура не может стать
бесструктурной по самому определению.
365
366.
Фазовая диаграммаРассмотрим фазовую диаграмму состояний газжидкость-твердое тело для аномального вещества.
366
367.
Фазовая диаграммаУ аномальных веществ кривая АВ перехода
жидкость-твердое тело направлена не так, как
у нормальных веществ. Температура
плавления при повышении давления у таких
веществ понижается и, следовательно, они
могут при достаточно высоком давлении
оставаться жидкими до очень низкой
температуры.
367
368.
Жидкий гелийОсобое положение среди веществ занимает
гелий, который при давлении ниже 3 МПа
остается в жидком состоянии при температуре,
сколь угодно близкой к 0 К.
368
369.
Жидкий гелийТемпература тройной точки А лежит вблизи 2
К, а давление очень мало. При температуре
ниже тройной точки не происходит перехода
Не-I в твердое состояние, как это следовало
бы ожидать, а происходит фазовый переход,
известный как λ-переход (ламбда-переход).
Этот λ-переход осуществляется на линии АВ.
При нем жидкость остается жидкостью и
отсутствует скрытая теплота. Следовательно,
это не фазовый переход первого рода.
369
370.
Жидкий гелийСвое название λ-переход получил из-за поведения
теплоемкости, поскольку кривая, изображающая
теплоемкость вблизи температуры λ-перехода,
напоминает греческую букву λ. При температуре λперехода теплоемкость обращается в бесконечность.
370
371.
Жидкий гелийНе-II является бесцветной прозрачной жидкостью и не
отличается по внешнему виду от Не-I. Плотность
жидкостей одинаковы и по свойствам они резко
отличаются.
Наиболее важным свойством Не-II является его
сверхтекучесть, т.е. способность без трения протекать
через узкие отверстия. Свойство сверхтекучести
проявляется в Не-II лишь при достаточно малых
скоростях течения. Всегда существует некоторая
критическая скорость течения, выше которой явление
сверхтекучести исчезает.
He-II является смачивающей жидкостью для всех других
материалов. Это обусловлено тем, что силы
взаимодействия между атомами гелия слабее, чем силы
взаимодействия между атомами гелия с любыми другими
атомами. Поэтому у стенок сосуда уровень гелия
поднимается и гелий вытекает из сосуда.
371
372.
ПолиморфизмТвердые вещества могут находиться в различных
кристаллических модификациях, отличающихся между
собой структурой кристаллической решетки. Например,
углерод может существовать в виде графита и в виде алмаза,
имеется много модификаций льда, и т.д. Это явление
называется полиморфизмом. Переход твердого тела из одной
кристаллической модификации в другую называется
полиморфным превращением. При этом происходит
перестройка кристаллической решетки. Одновременное
существование двух модификаций возможно лишь при
определенном соотношении между температурой и давлением,
т.е. на диаграмме PT эти модификации будут разделены между
собой линией. Три модификации могут находиться в
равновесии лишь при одном значении P, Т, т.е. в тройной
точке.
Полиморфное превращение является фазовым переходом.
Оно сопровождается выделением или поглощением скрытой
теплоты перехода, которая связана с перестройкой
кристаллической решетки.
372
373.
Фазовый переход первого родаОтличительной особенностью фазовых
переходов первого рода является
скачкообразное изменение удельной внутренней
энергии и связанных с ней величин в точке
перехода и, следовательно, наличие скрытой
теплоты перехода. Переход совершается при
определенных температуре и давлении, и в
процессе перехода обе фазы одновременно
существуют в объеме и пространственно
разграничены. Переход жидкости в пар,
конденсация, кристаллизация и плавление
являются примерами фазовых переходов
первого рода.
373
374.
Фазовый переход второго родаФазовые переходы второго рода происходят сразу во
всем объеме и обязательно связаны с изменением
симметрии системы. Температура, при которой
происходит фазовый переход, называется точкой
Кюри. Поскольку переход происходит сразу во всем
объеме, не существует пространственного разделения
фаз и их нахождения в равновесии друг с другом.
Фазовый переход второго рода не сопровождается
выделением или поглощением теплоты фазового
превращения. Объем при переходе не меняется, но
теплоемкость в связи с изменением симметрии
системы меняется. Переход металла в сверхпроводящее
состояние и переход Не-I в Не-II являются примерами
фазовых переходов второго рода.
374
375.
Молекулярная физикаТема 21:
Кристаллические твердые тела
375
376.
Содержание• Симметрия твердых тел.
• Кристаллические решетки. Элементарная
ячейка. Кристаллические системы. Обозначения
атомных плоскостей и направлений.
• Решетки химических элементов и их
соединений.
• Теплоемкость кристаллических твердых тел.
• Дефекты в кристаллах. Дислокации.
• Физические процессы в кристаллах при
деформациях.
376
377.
Симметрия твердых телСимметрия тела выражает свойства его
совмещаться с самим собой при определенных
перемещениях, называемых преобразованиями или
операциями симметрии. Эти перемещения не
должны сопровождаться растяжениями, сжатиями,
сдвигами и другими деформациями, при которых
изменяются расстояния между точками тела.
К преобразованиям симметрии относятся:
1) параллельный перенос всех точек тела на
определенное расстояние (трансляция);
2) поворот тела вокруг некоторой оси на
определенный угол;
3) отражение в плоскости;
4) инверсия или отражение в точке,
а также все комбинации таких преобразований.
377
378.
Симметрия твердых телОпределенные геометрические точки, прямые и
плоскости, симметрично расположенные относительно
тела, называются его элементами симметрии. К ним
относятся ось симметрии, плоскость симметрии,
зеркально-поворотная ось, центр симметрии и пр.
Совокупность всех элементов симметрии тела
называется его группой симметрии.
Группы симметрии, содержащие только операции
отражения, поворота и инверсии, но не содержащие
трансляций, называются точечными группами. Такие
группы оставляют на месте по крайней мере одну точку
тела и описывают симметрию конечных фигур: атомов,
молекул, многогранников и пр.
Группы симметрии, содержащие, наряду с
перечисленными операциями, также трансляции,
описывают симметрию бесконечных систем с
периодической структурой. Они называются
пространственными группами.
378
379.
Симметрия твердых телЕсли тело переходит само в себя при повороте на угол 2π/n
(где n=1, 2, 3, ...) вокруг некоторой оси, то эта ось
называется поворотной осью или осью симметрии n-го
порядка (n=2, 3, 4 и 6).
Если тело переходит само в себя в результате зеркального
отражения в некоторой плоскости, то эту плоскость
называют плоскостью симметрии.
Операция поворота тела вокруг неподвижной оси на угол
2π/n с одновременным отражением его в плоскости,
перпендикулярной к той же оси, называется зеркальноповоротным преобразованием. Если в результате такого
преобразования тело переходит само в себя, то
соответствующую ось называют зеркально-поворотной
осью n-го порядка (n=2, 3, 4 и 6).
Если при инверсии относительно некоторой точки O тело
переходит само в себя, то точка О называется центром
симметрии тела. Если в теле есть зеркально-поворотная
ось второго порядка (n=2), то в нем есть и центр симметрии.
379
380.
Кристаллические решеткиОсновной особенностью кристаллов, отличающих
их от жидкостей и аморфных твердых тел, является
периодичность пространственного расположения
атомов, молекул и ионов, из которых состоит
кристалл. Такая периодичность называется
дальним порядком.
Совокупность таких периодически расположенных
атомов образует периодическую структуру,
называемую кристаллической решеткой. Точки, в
которых расположены сами атомы, называются
узлами (пространственной) кристаллической
решетки. Представление о пространственной
решетке в кристаллографии было введено О. Браве.
380
381.
ТрансляцияБудем предполагать, что кристаллическая решетка
неограниченная. Периодичность решетки
проявляется в так называемой трансляционной
симметрии. Трансляционная симметрия означает,
что существуют три некомпланарных вектора a1, а2 и
а3, характеризующиеся тем, что при смещении
решетки на вектор
T n1a1 n2 a2 n3a3 ,
где n1, n2 и n3 – целые числа (в том числе и
нули), она переходит сама в себя. Такие
смещения называются трансляциями, а
вектор T – вектором трансляции.
381
382.
Элементарная ячейкаЕсли при неизменных направлениях векторов a1, а2, а3
выбрать их длины минимальными, чтобы трансляциями
вдоль этих направлений можно было получить всю
кристаллическую решетку, то векторы a1, а2, а3
называются базисными векторами, а их совокупность –
базисом решетки. Параллелепипед с ребрами a1, а2, а3
называют базисным параллелепипедом. Вместе с
находящимися в нем атомами он образует элементарную
ячейку кристаллической решетки. Длины ребер такого
параллелепипеда называются основными периодами
решетки. Если элементарная ячейка содержит 8 атомов
в вершинах основного параллелепипеда, но не содержит
ни одного атома внутри объема или на гранях этого
параллелепипеда, то она называется примитивной. Все
другие ячейки называются сложными. Примитивная
пространственная решетка называется решеткой Браве.
382
383.
Кристаллические системыБраве показал, что существует 14 типов
примитивных решеток (решеток Браве),
разделяющихся на 7 кристаллических
систем.
383
384.
Кристаллические системы1. Кубическая система разделяется на:
простую (P), объемноцентрированную (I)
и гранецентрированную (F).
384
385.
Кристаллические системы2. Тетрагональная система разделяется на:
простую (P) и объемноцентрированную
(I).
385
386.
Кристаллические системы3. Гексагональная система (H).
386
387.
Кристаллические системы4. Робмоэдрическая система (R).
387
388.
Кристаллические системы5. Ромбическая система разделяется на:
простую (P), объемноцентрированную (I),
гранецентрированную (F) и
базоцентрированную (C).
388
389.
Кристаллические системы6. Моноклинная система разделяется на:
простую (P) и базоцентрированную (C).
389
390.
Кристаллические системы7. Триклинная система бывает только
простой (P).
390
391.
Положения атомовДля определения положения атомов в
кристаллической решетке пользуются
специальными прямолинейными
системами координат, называемыми
кристаллографическими. За начало
координат принимается один из узлов
решетки, а за координатные оси - ребра
соответствующего параллелепипеда Браве.
391
392.
НаправленияКристаллической плоскостью называется
всякая плоскость, в которой находится
бесконечное множество атомов решетки.
Практическое значение имеют только
плоскости, усеянные атомами достаточно
густо. Именно они служат естественными
гранями кристалла. Узловой линией
называется прямая, на которой расположено
бесконечное множество атомов решетки.
Основное значение имеют узловые линии,
на которых атомы расположены достаточно
густо.
392
393.
НаправленияДля определения направления кристаллических
плоскостей мы ограничимся примитивными
решетками. В таких решетках координаты всех
узлов целочисленны. Каждую кристаллическую
плоскость можно представить уравнением
x y z
1,
A B C
где A, B и C – длины отрезков (в единицах длин
базисных векторов), отсекаемые этой плоскостью на
координатных осях. Эти длины всегда выражаются
рациональными числами (положительными и
отрицательными).
393
394.
НаправленияТаким образом, уравнение плоскости всегда можно
записать в виде
hx ky lz D,
где h, k и l – целые числа. Можно считать, что они
не имеют общего множителя, т.к. на него всегда
можно сократить. Полученные целые числа
определяют направление кристаллической
плоскости. Эти числа называют индексами
Миллера. Для обозначения направления плоскости
индексы Миллера заключают в круглые скобки
(hkl). Если какой-либо из индексов отрицателен, то
знак « – » пишут над этим индексом.
394
395.
НаправленияДля указания направления какой-либо
узловой линии кристаллической решетки
достаточно указать разности координат двух
соседних идентичных узлов (в единицах
длин базисных векторов), лежащих на этой
линии. Полученные таким образом целые
числа называют индексами направлений и
заключают в квадратные скобки.
Например, индексами направлений
пространственной диагонали куба будут
[111].
395
396.
Реальные решеткиКубическая гранецентрированная решетка
NaCl .
396
397.
Реальные решеткиГексагональная решетка графита.
397
398.
Реальные решеткиСложная решетка алмаза состоит из двух
кубических гранецентрированных решеток.
398
399.
Теплоемкость кристалловКак уже отмечалось, при вычислении
теплоемкости кристаллов (см. Тему 10)
Эйнштейн не правильно предположил, что в
кристалле могут быть возбуждены все частоты
колебаний атомов, расположенных в узлах
кристаллической решетки. На самом деле атомы
влияют друг на друга и, поэтому, не все частоты
являются разрешенными. В частности,
существует некоторая предельная частота ωmax,
выше которой колебаний с такой частотой нет.
Правильное выражение для теплоемкости было
получено П. Дебаем в 1912 г.
399
400.
Теплоемкость кристалловВ соответствии с теорией Дебая внутренняя энергия
молярного кристалла может быть вычислена по формуле
U 3N A ,
где (см. Тему 10)
g d ,
2
0
exp
1
kT
а функция распределения частот g(ω) имеет вид
9N A 2
3 , max ,
g max
0,
max .
max
400
401.
Теплоемкость кристалловПосле преобразований можно получить
max
TD
U U 0 3RT D , TD
,
k
T
где U0 – нулевая энергия кристалла
1
U0
2
max
g d ;
0
TD – температура Дебая; и функция Дебая
имеет вид
y
3
x3dx
D y 3
.
y 0 exp x 1
401
402.
Теплоемкость кристалловВ случае высоких температур (T→∞)
можно получить
TD
D 1, и U U 0 3RT ,
T
и, следовательно, молярная теплоемкость
кристалла имеет вид
U
CV
T
3 R,
TD const
что согласуется с законом Дюлонга-Пти.
402
403.
Теплоемкость кристалловВ случае низких температур (T→0) можно
получить
TD
D
T 5
4
3 RT
TD
,
, и U U0
3
5TD
T
3
4
4
и, следовательно, молярная теплоемкость
кристалла имеет вид
U
CV
T
12 R 3
3
T
~
T
.
3
5TD
4
TD const
Эксперименты подтвердили зависимость
CV~T3 в области низких температур.
403
404.
Дефекты в кристаллахДефектами кристаллической решетки
называются отклонения от строгой
периодичности, которой определяется решетка.
Дефекты бывают макроскопическими и
микроскопическими. К первым относятся
трещины, макроскопические пустоты и
инородные макроскопические включения в
кристаллическую решетку. Вторые
обусловлены микроскопическими
отклонениями от периодичности. Они бывают
точечными и линейными, или
дислокациями.
404
405.
Точечные дефекты в кристаллахВакансия
Замещение
Внедрение
405
406.
Линейные дефекты в кристаллахКраевая
дислокация
Винтовая
дислокация
406
407.
Деформации твердых телВсе деформации твердых тел могут быть сведены к
двум элементарным деформациям – однородному
растяжению (сжатию) и сдвигу.
Нормальное напряжение (нормальная проекция
силы, деленная на площадь ее приложения) σ при
деформации растяжения (сжатия) связана с
относительным удлинением ε формулой
E ,
где E – модуль Юнга.
Касательное напряжение (тангенциальная проекция
силы, деленная на площадь ее приложения) τ при
деформации сдвига связана с относительным
сдвигом γ формулой
/ G,
где 1/G – коэффициент сдвига.
407
408.
Пластическая деформацияДеформации называются упругими, если после устранения
деформирующих напряжений размеры и форма тела
полностью восстанавливаются. Такой деформации
соответствует линейный участок зависимости σ от ε
(участок 0A). Максимальное напряжение σупр при котором
деформации сохраняют упругий характер, называется
пределом упругости.
408
409.
Пластическая деформацияПри дальнейшем увеличении напряжения
деформация растет более быстро, чем
напряжение (участок АВ). После устранения
напряжения тело не восстанавливает прежнюю
форму и размеры, у него наблюдается
остаточная деформация (участок 0D). Такая
необратимая деформация называется
пластической.
На границе участка пластической деформации
(точка В) может наступить такая ситуация, что
деформация растет при постоянном
напряжении (участок ВС). Эта область
называется областью текучести, а напряжение
σтек, при котором материал «течет», – пределом
текучести.
409
410.
Пластическая деформацияЗа областью текучести (после точки С)
поведение кривой σ = f(ε) может быть самым
разнообразным. Однако, во всех случаях при
определенном напряжении наступает предел,
после которого материал разрушается.
Напряжение, при котором наступает
разрушение, называется пределом прочности.
Вещества, у которых пределы упругости и
прочности близки друг к другу и область
текучести практически отсутствует, называются
хрупкими. У них разрушение наступает
практически сразу же после предела упругости
(например, у чугуна и закаленной стали).
410

















































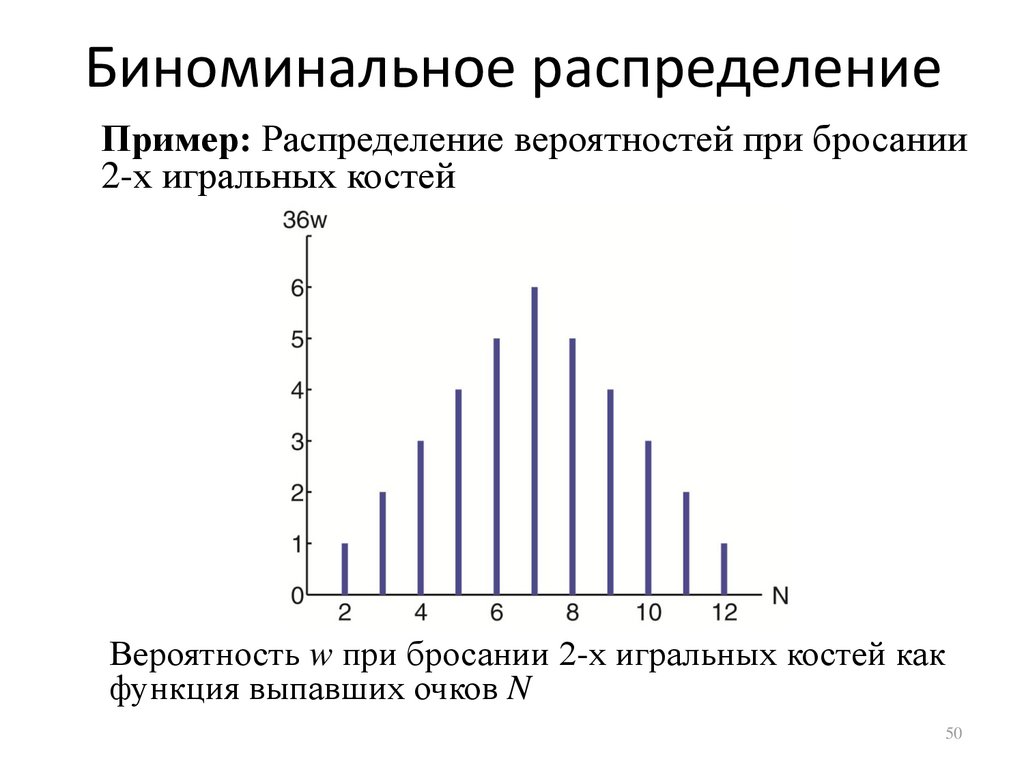



















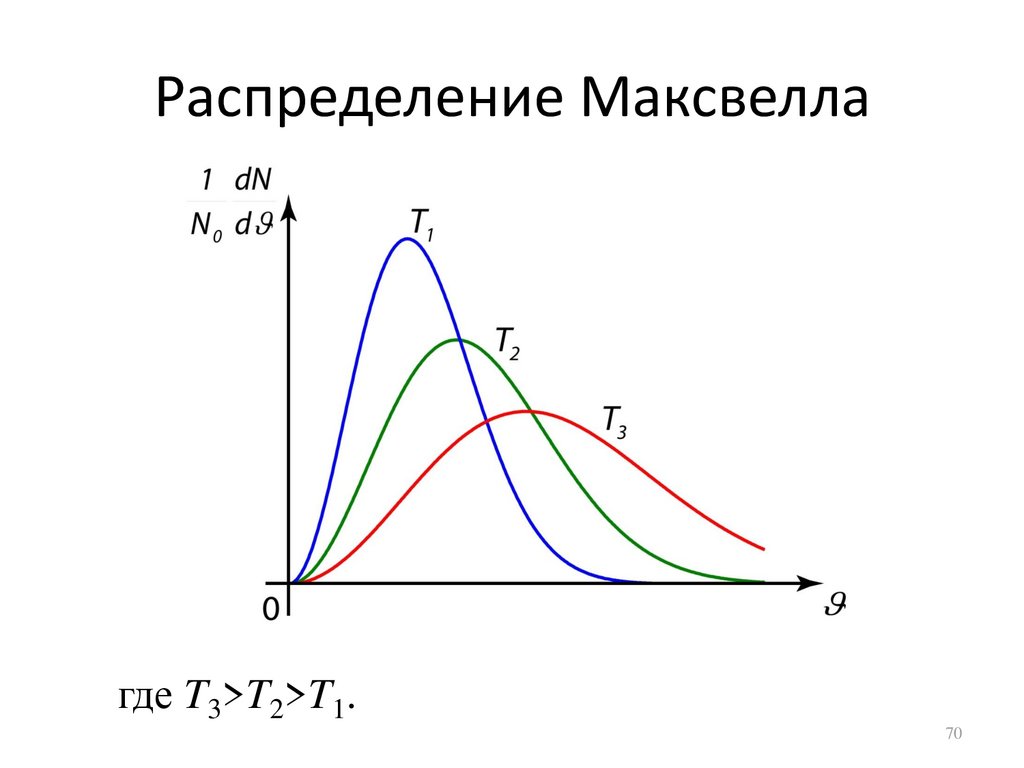













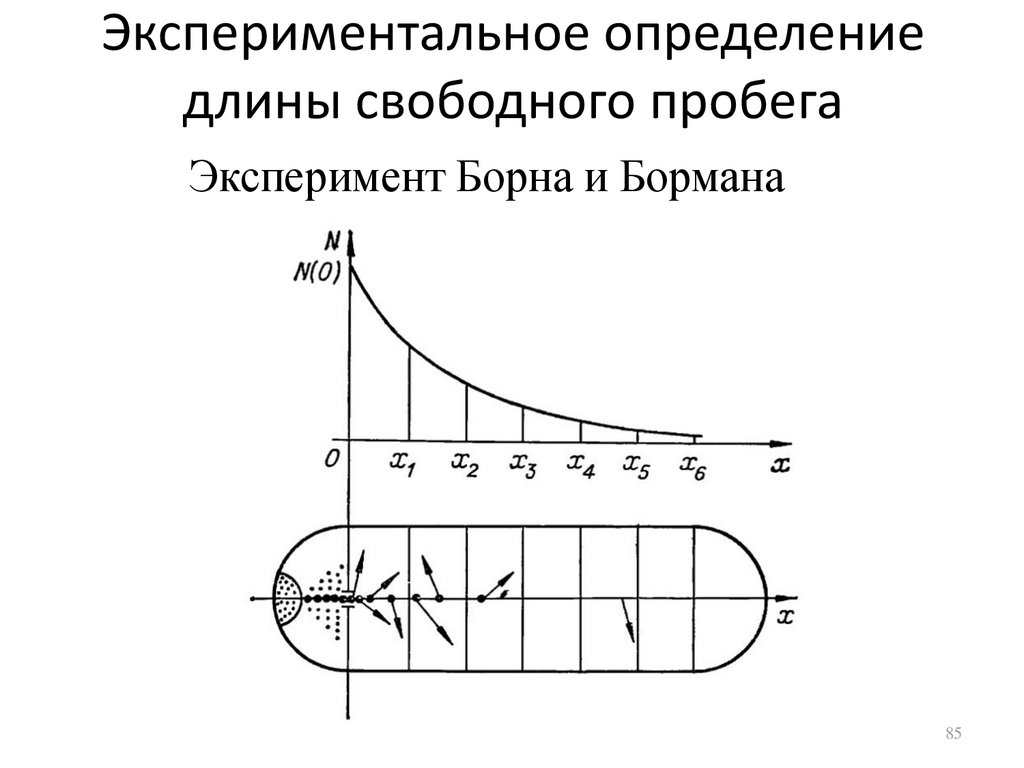































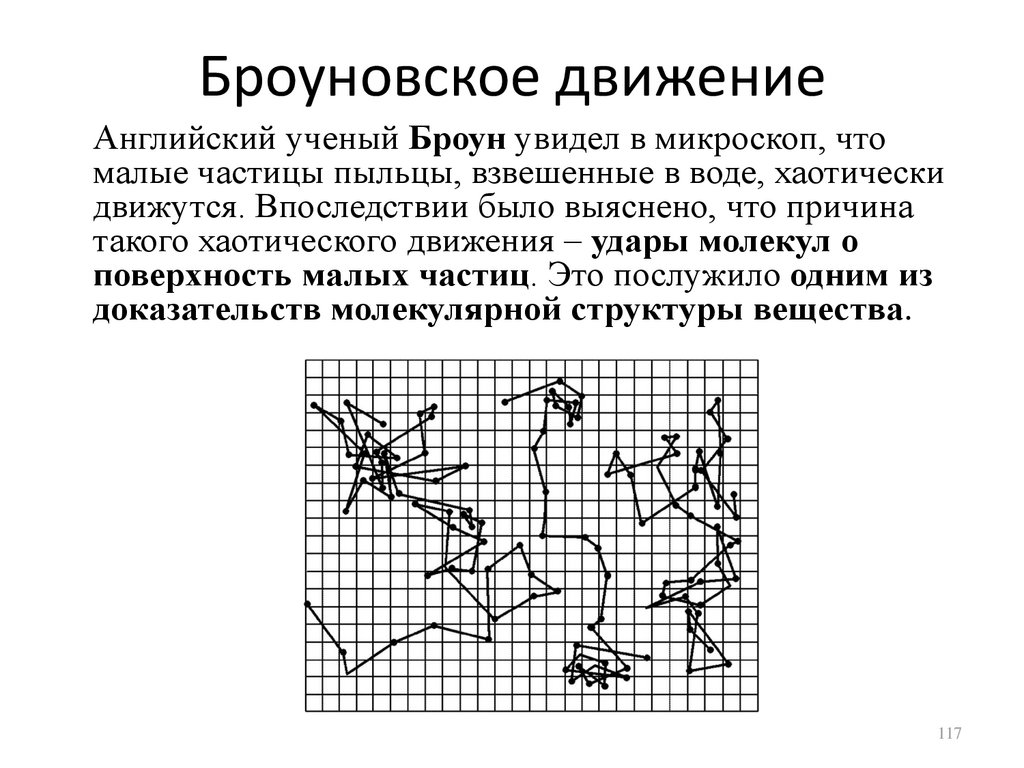

















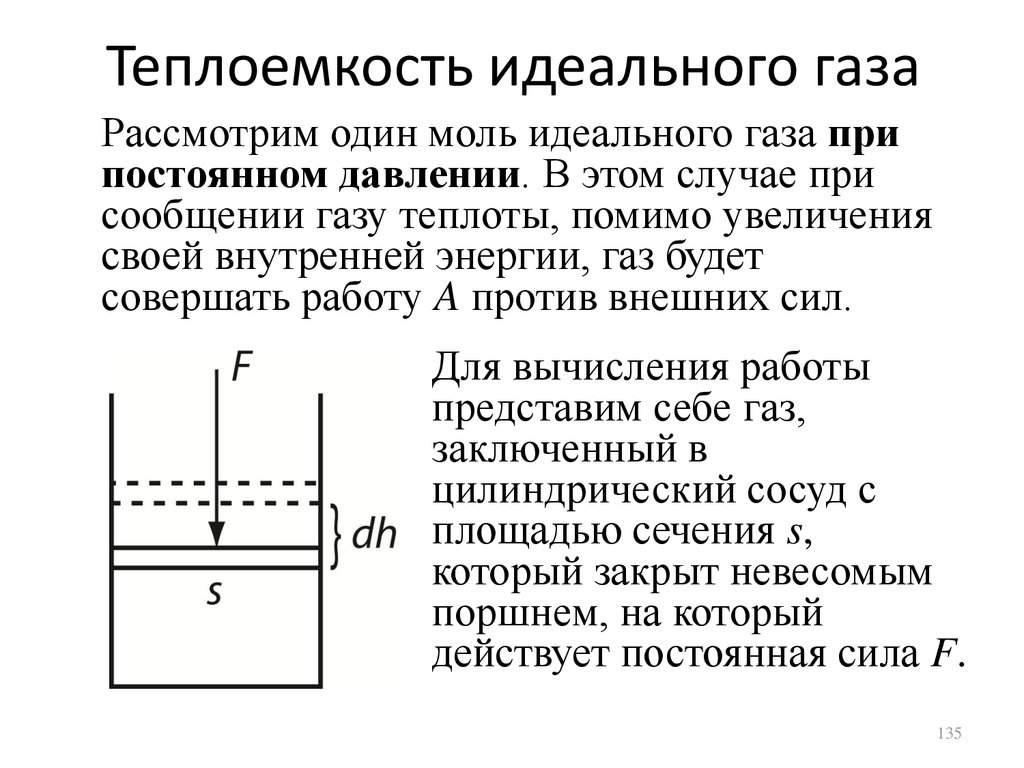




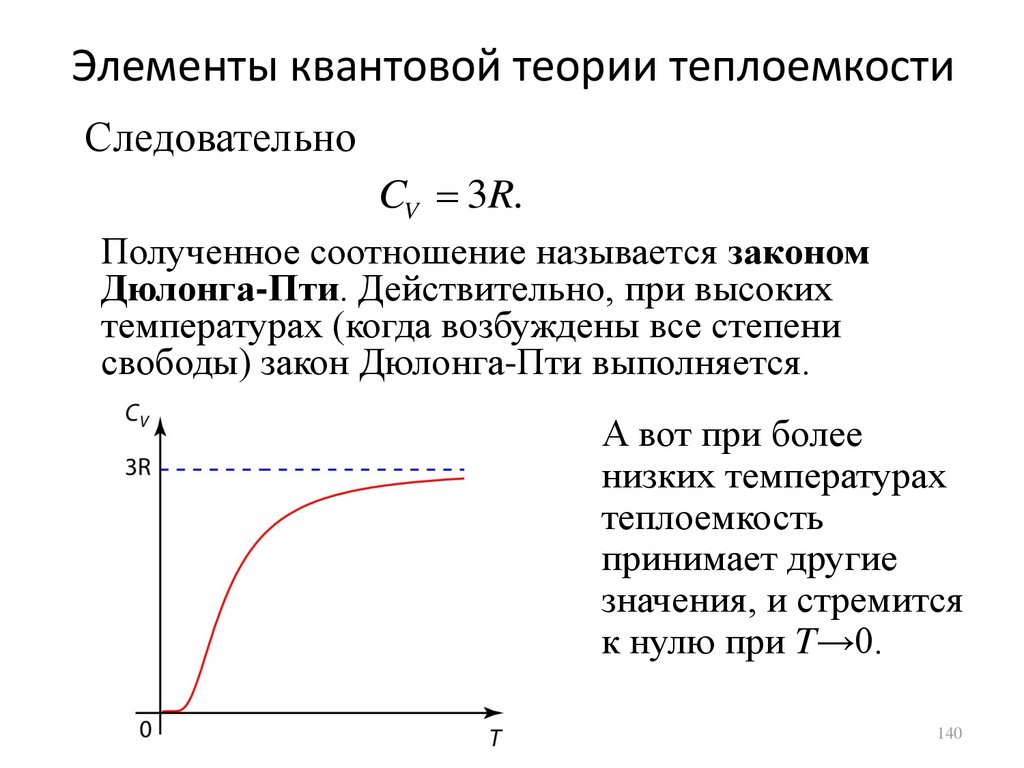









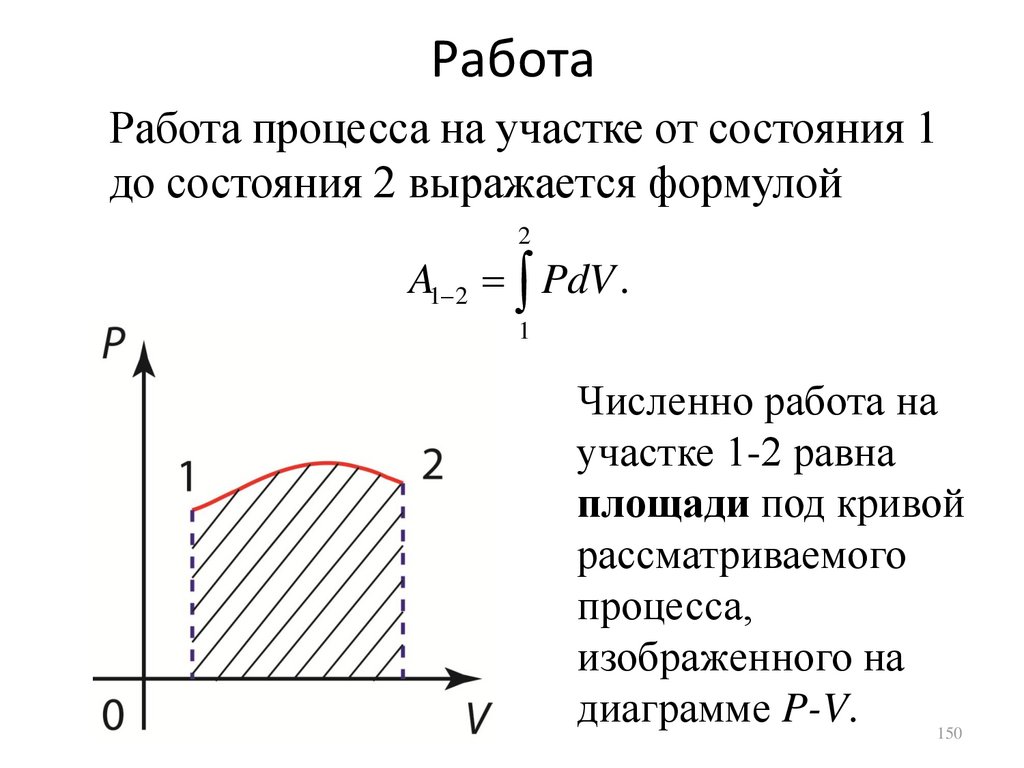

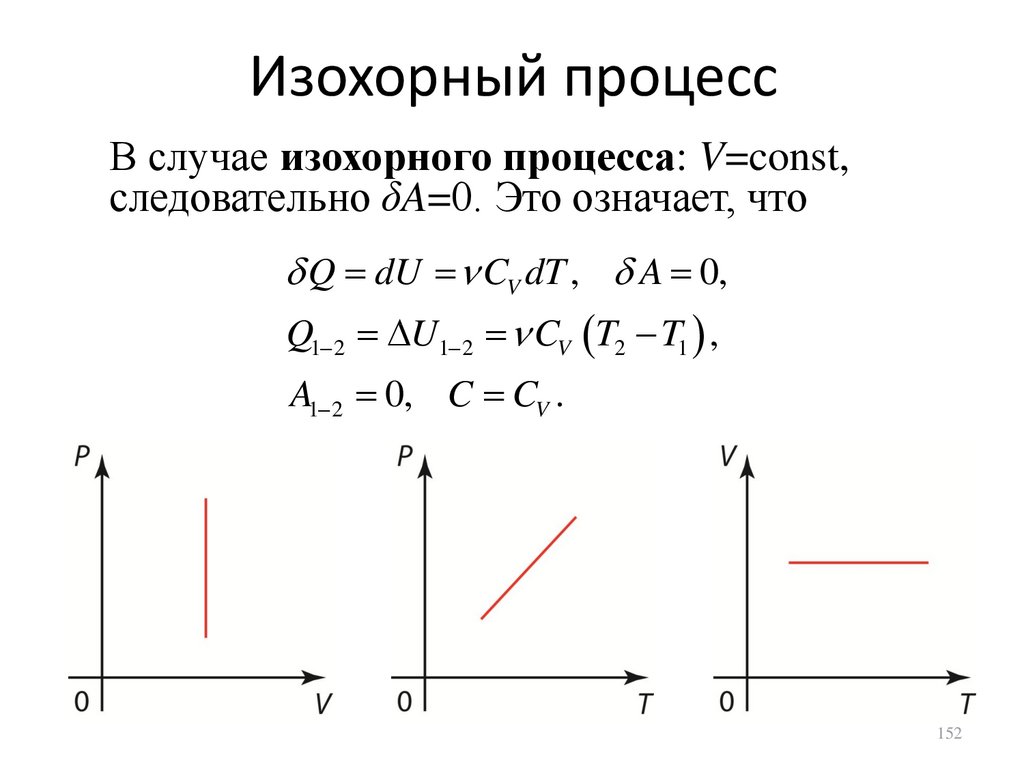




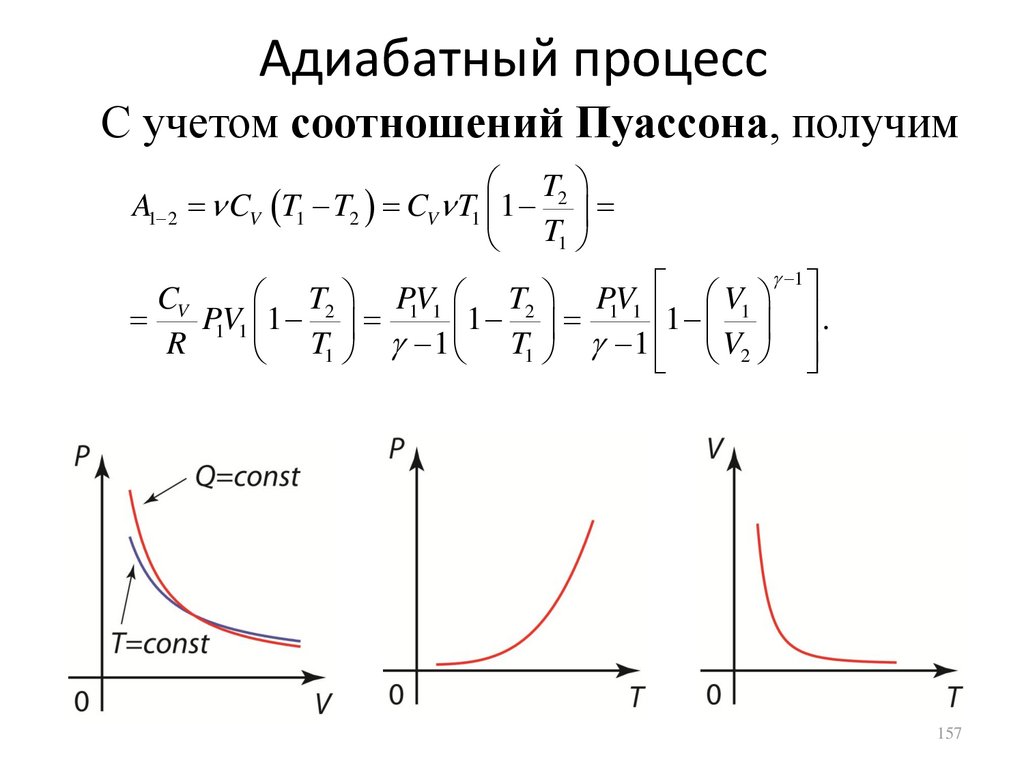













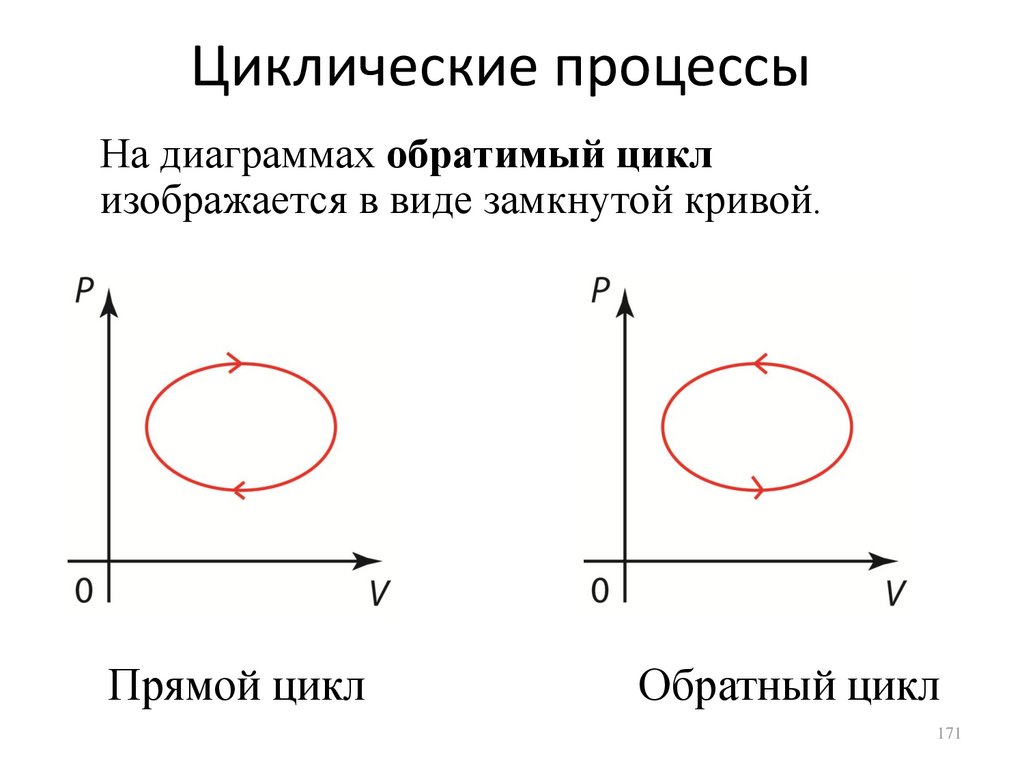
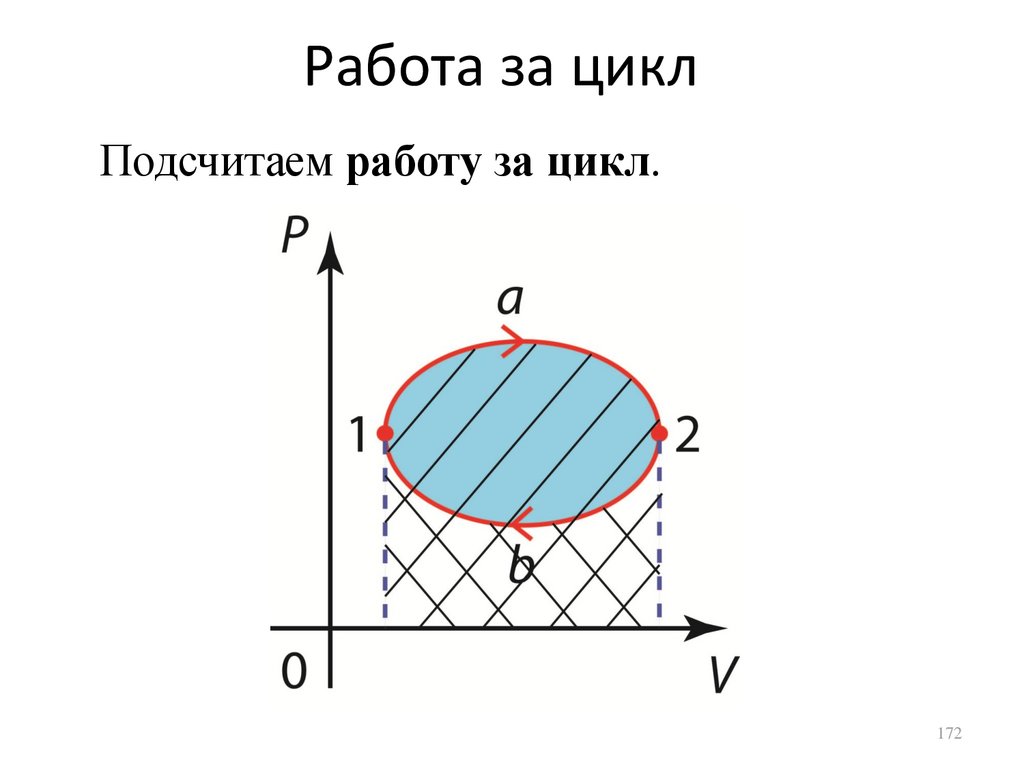














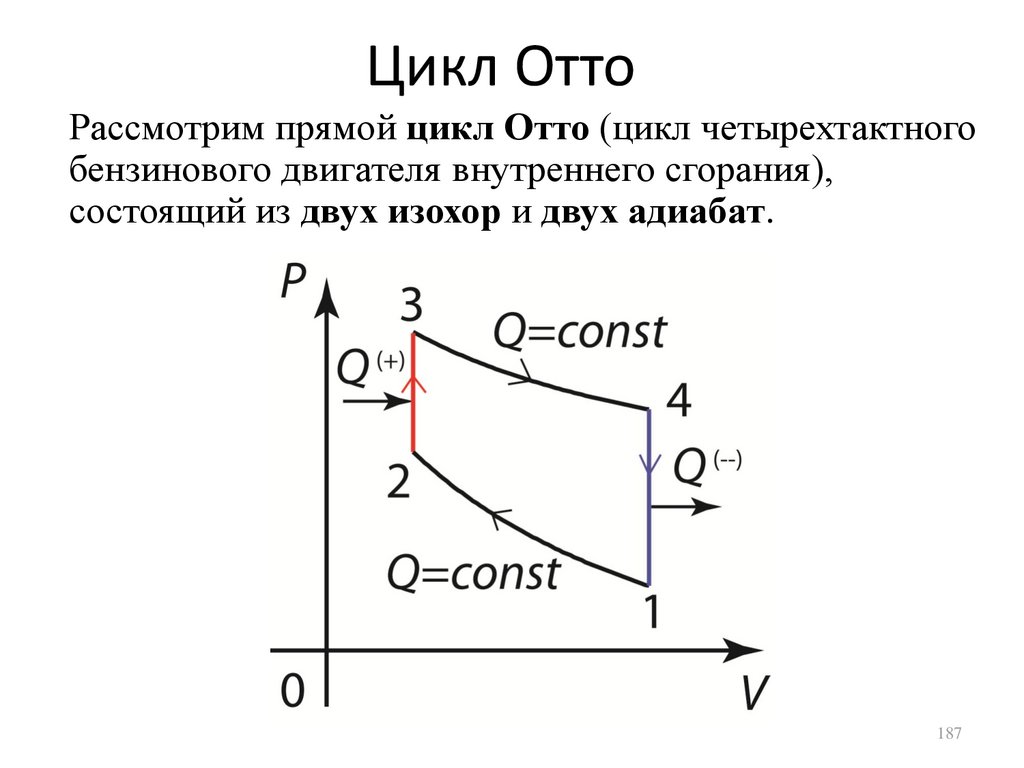

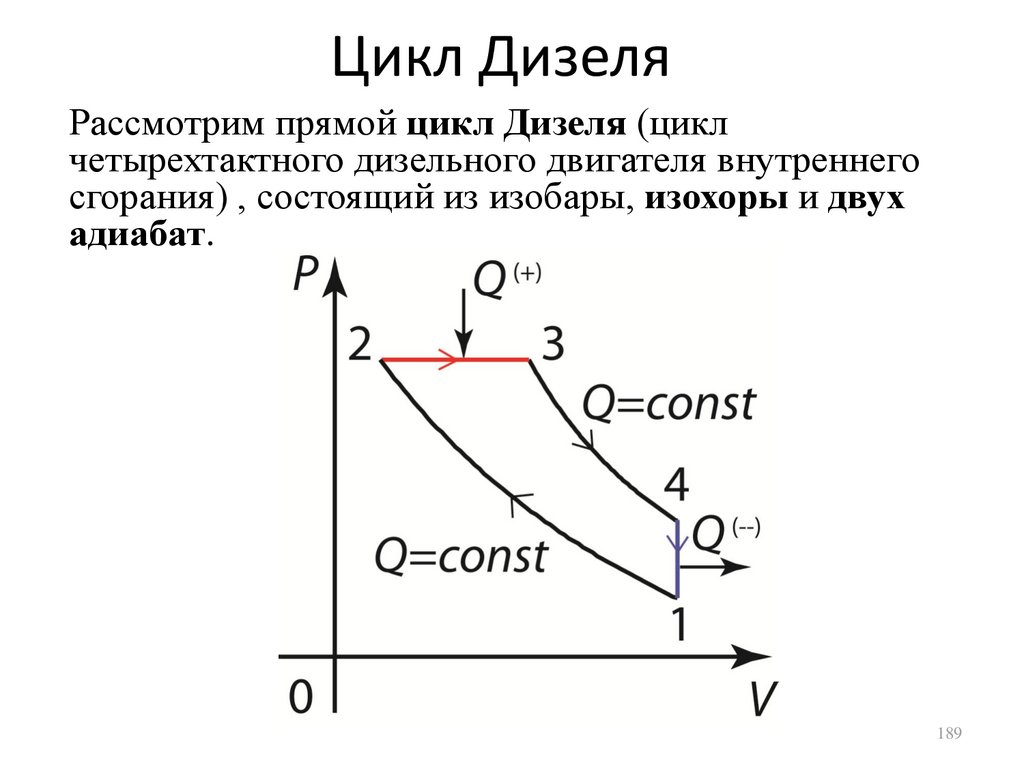







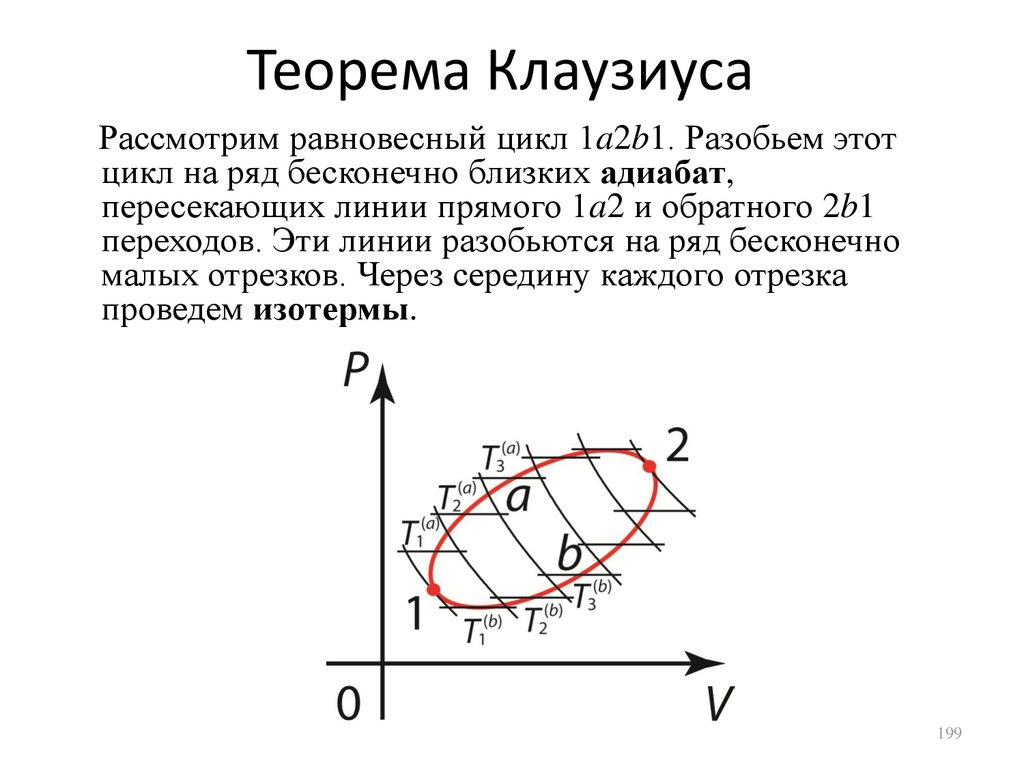




















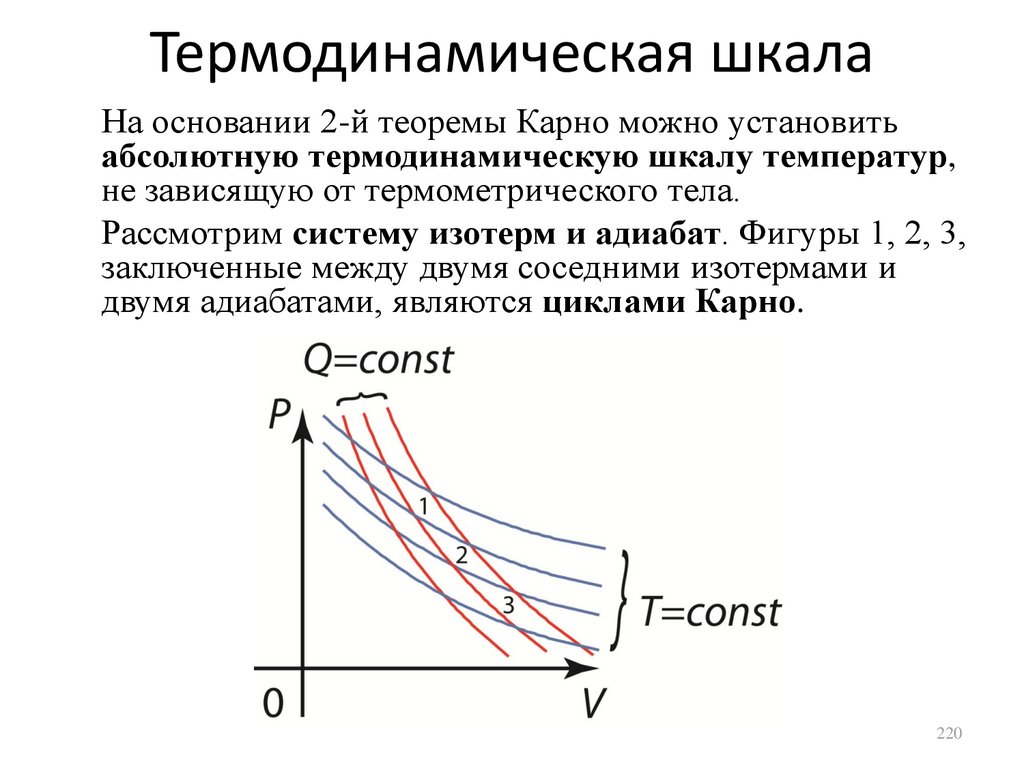





























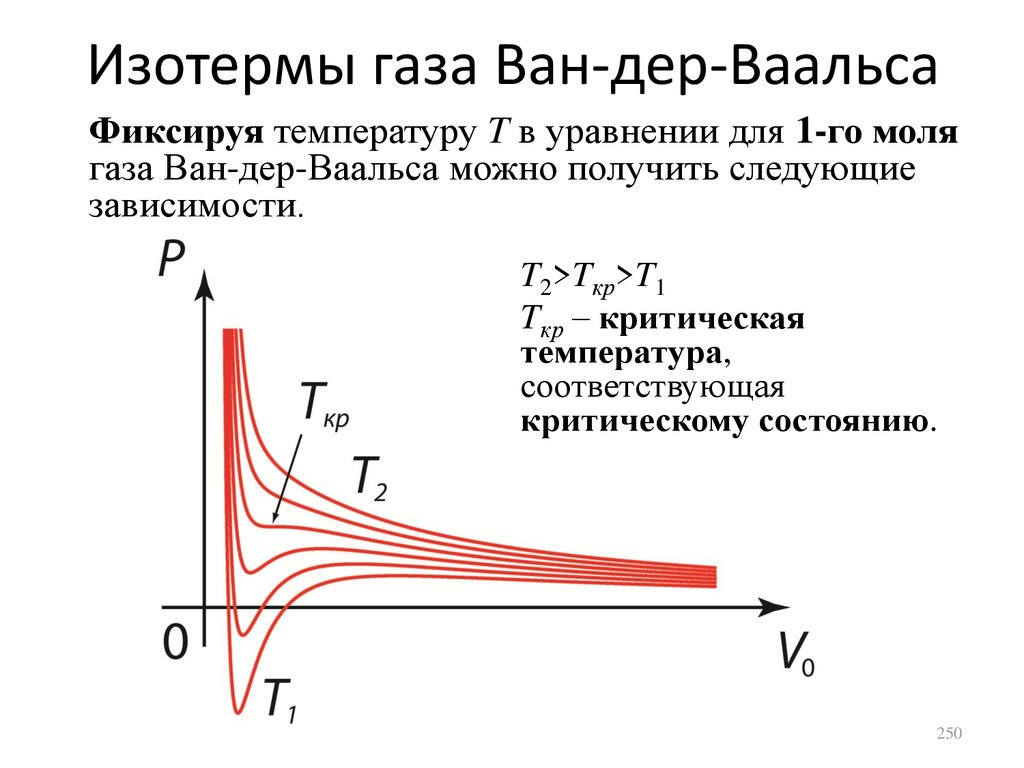
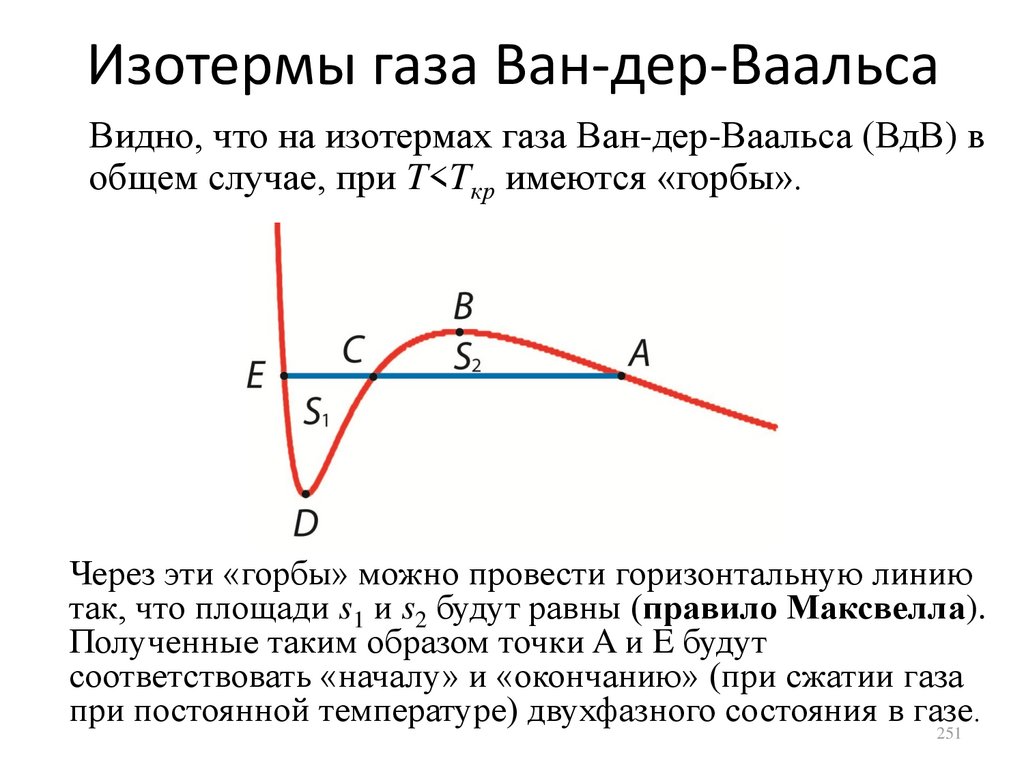






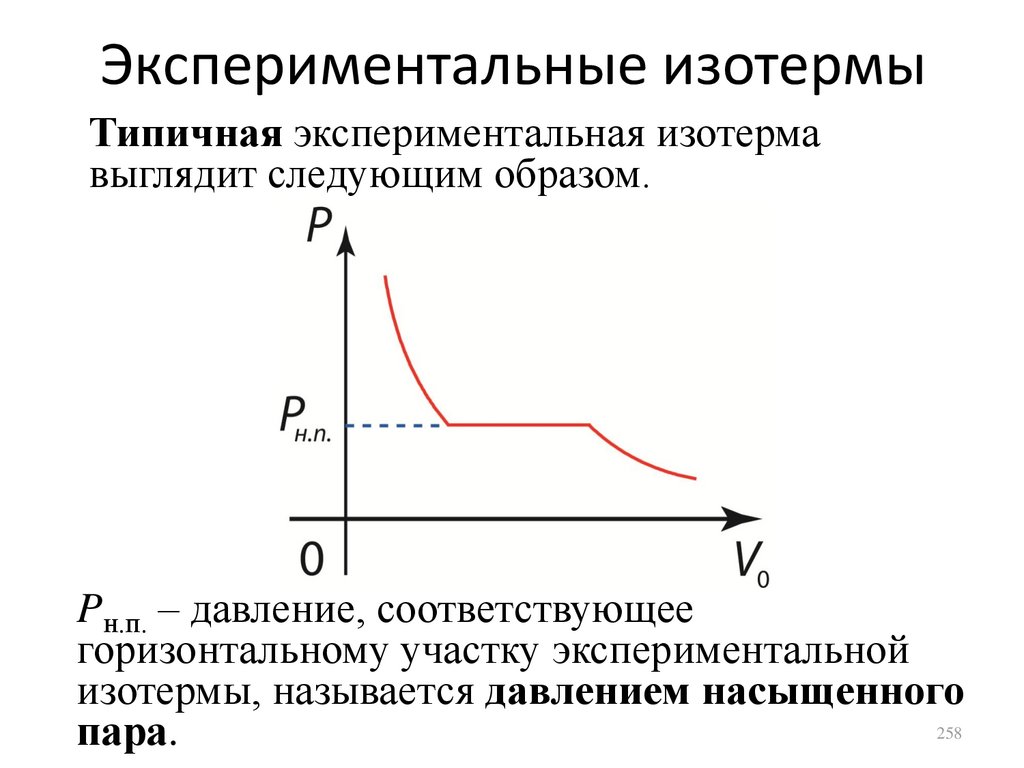






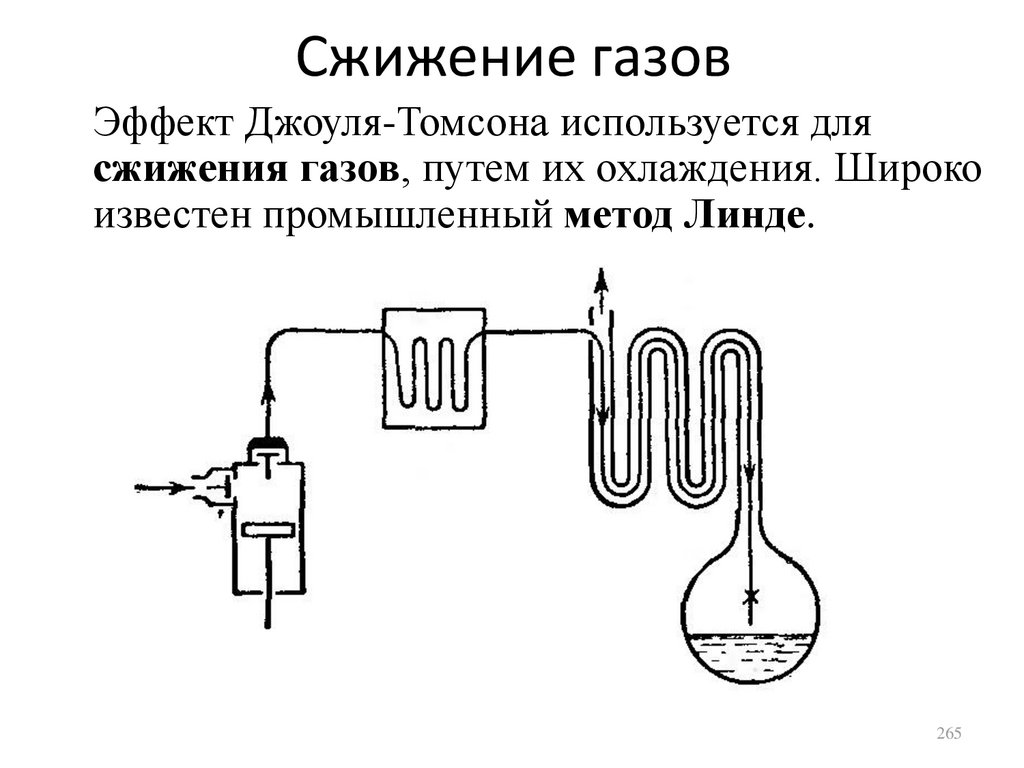



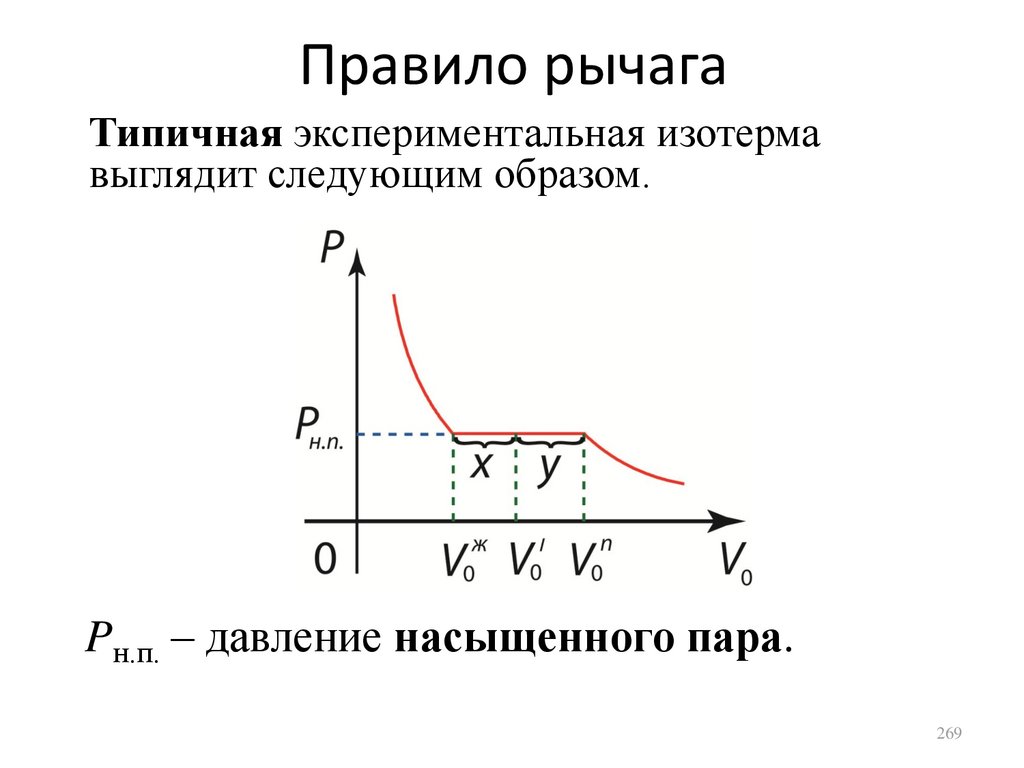

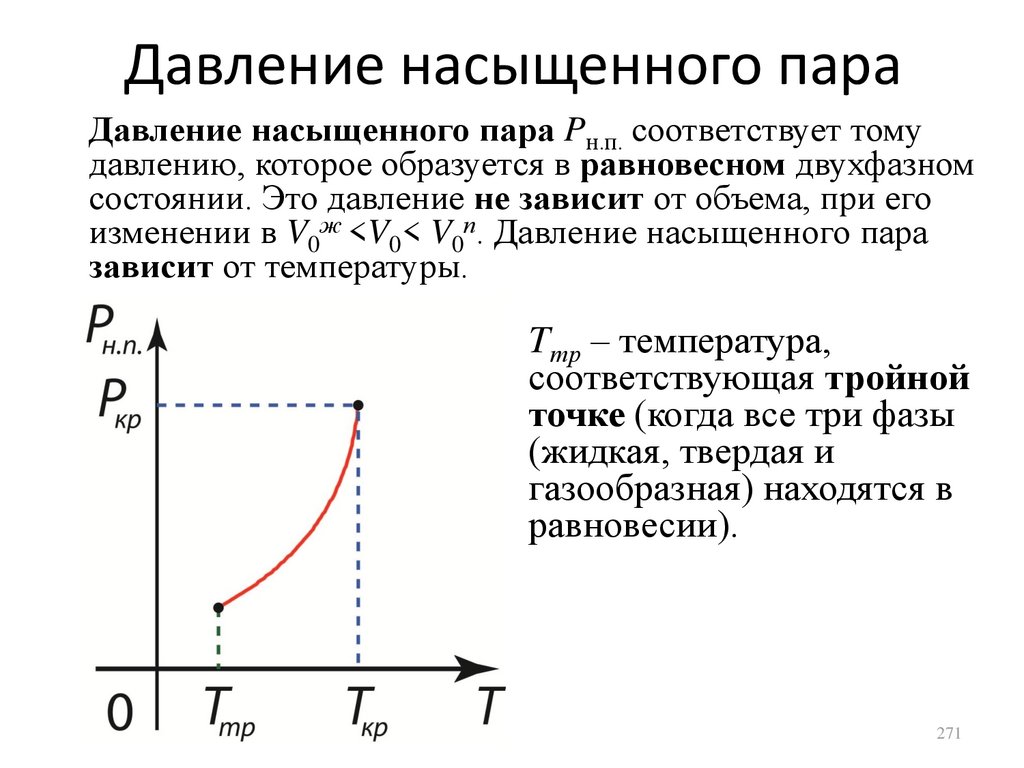
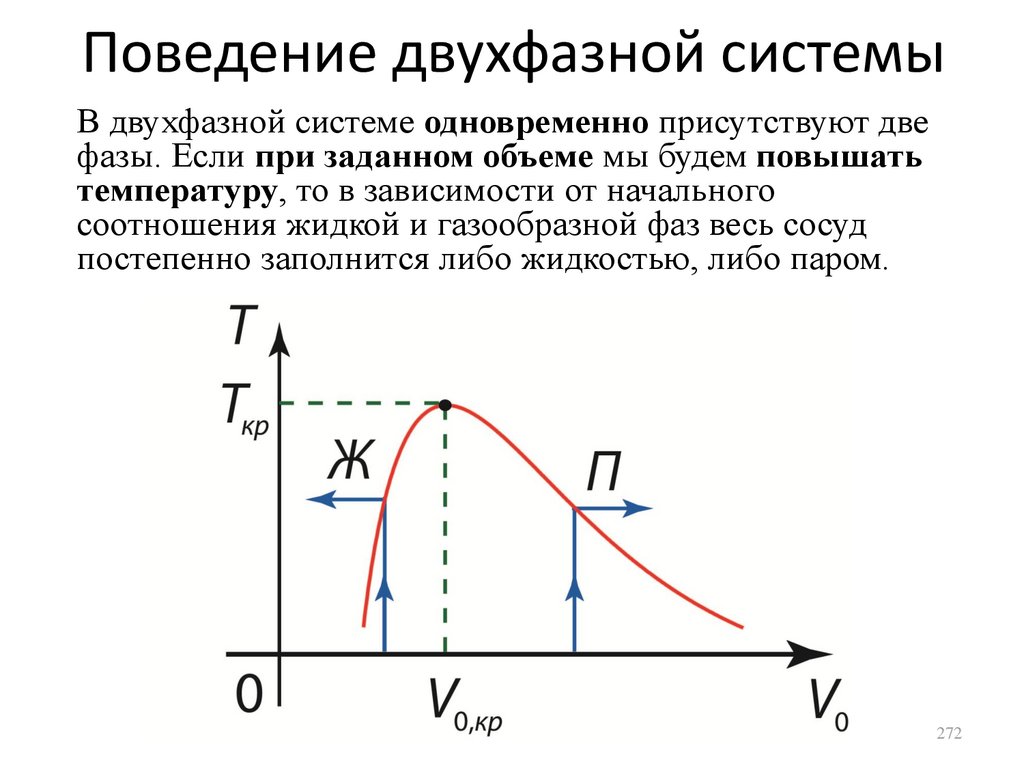















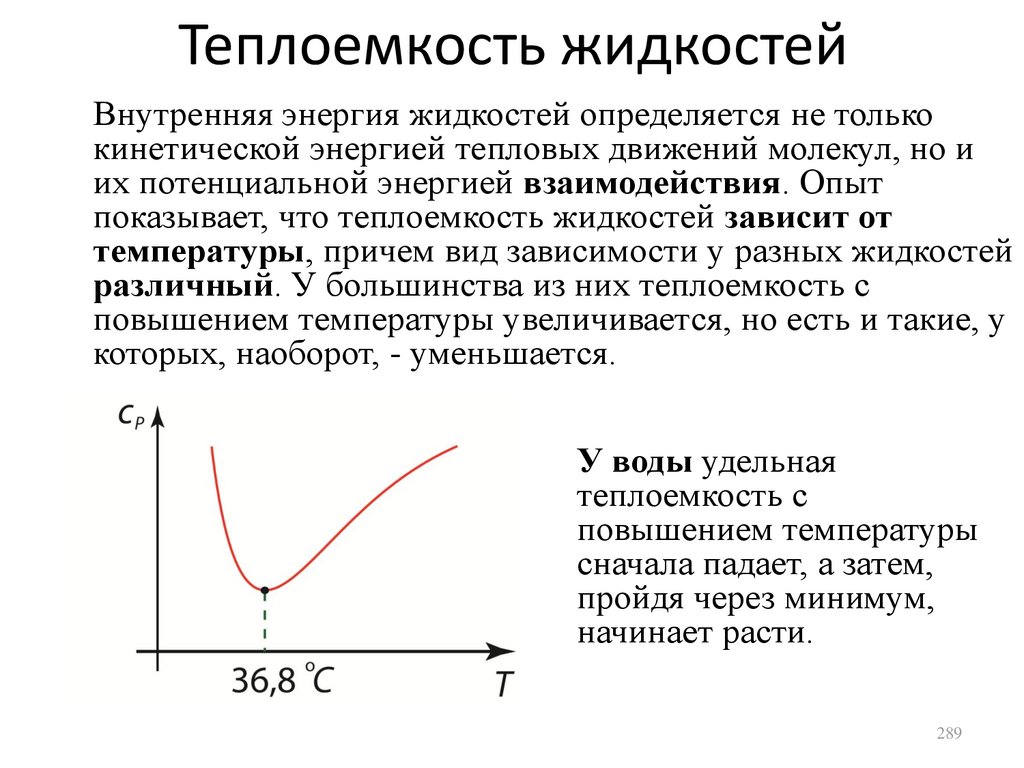



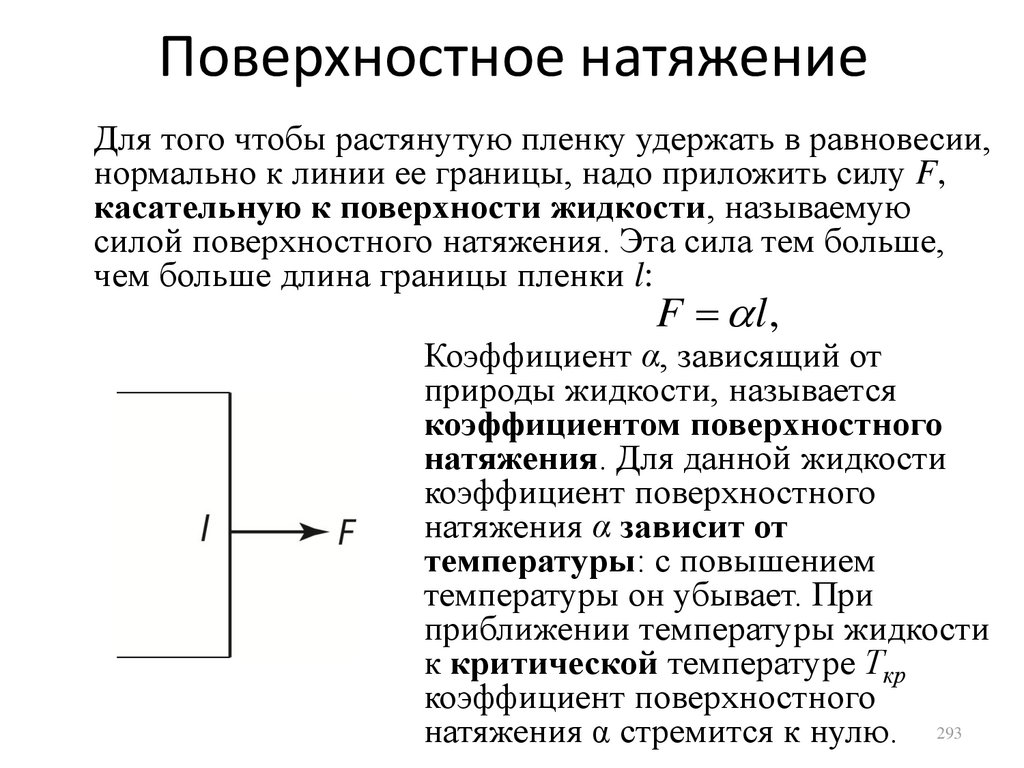
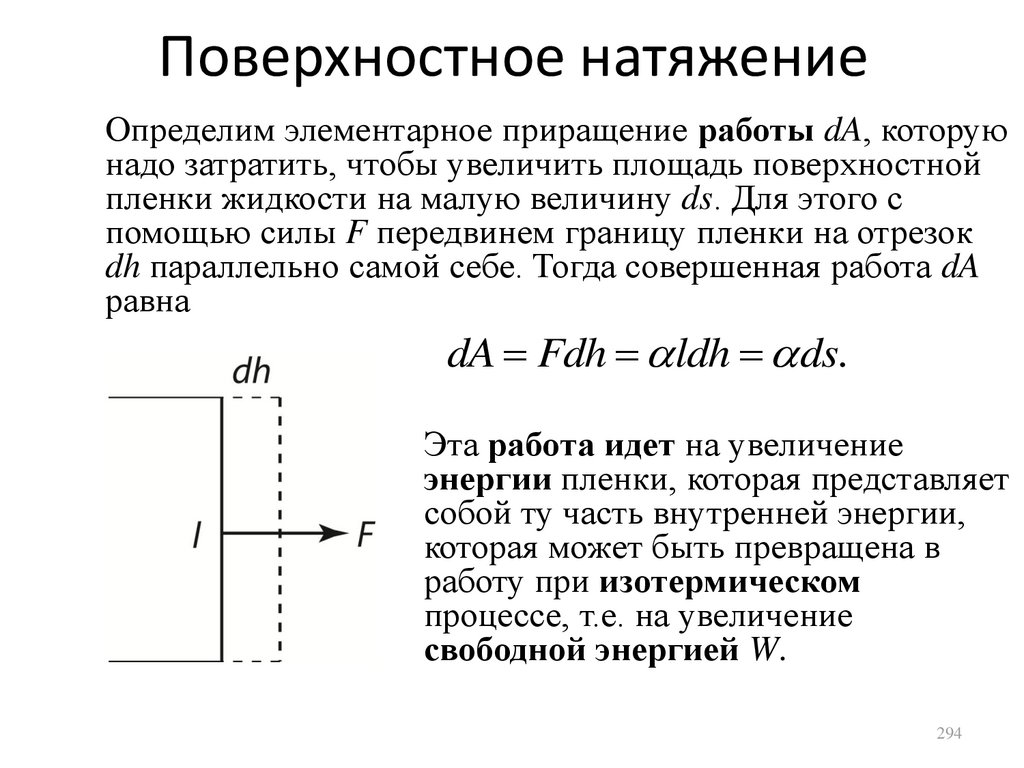

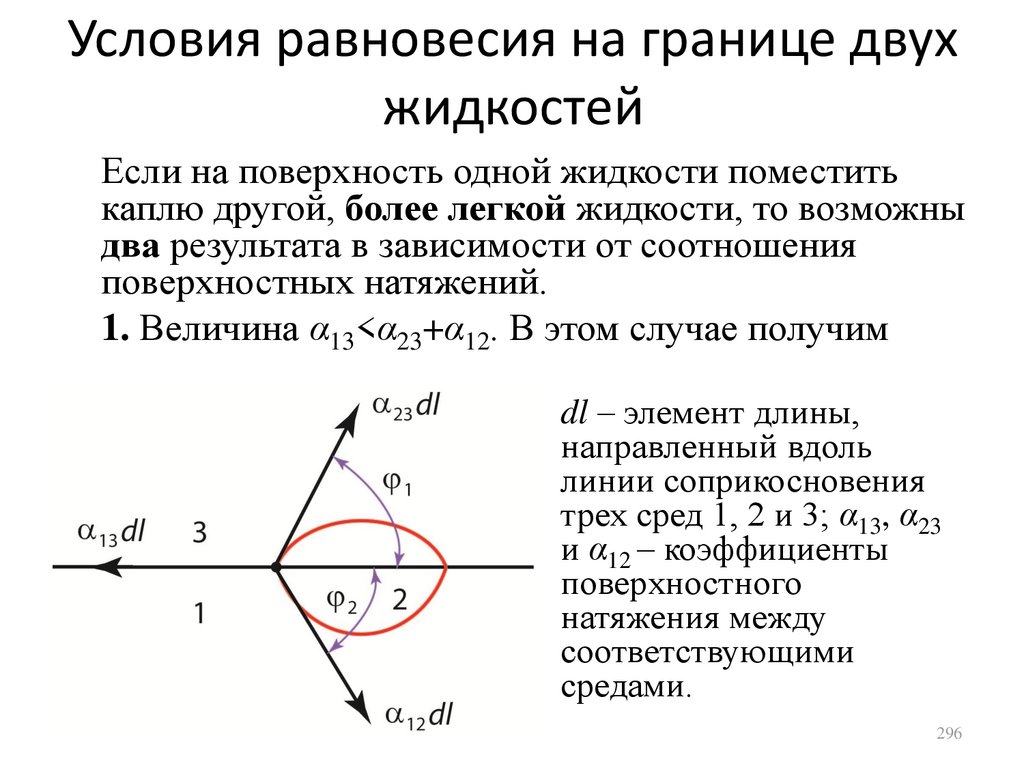




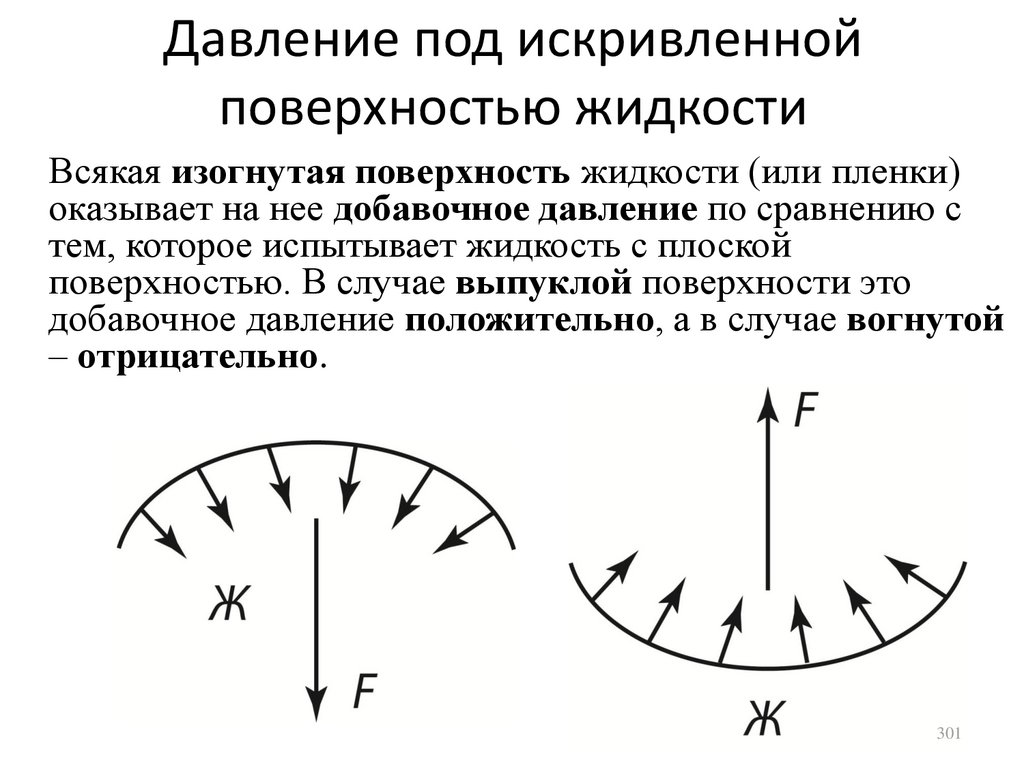

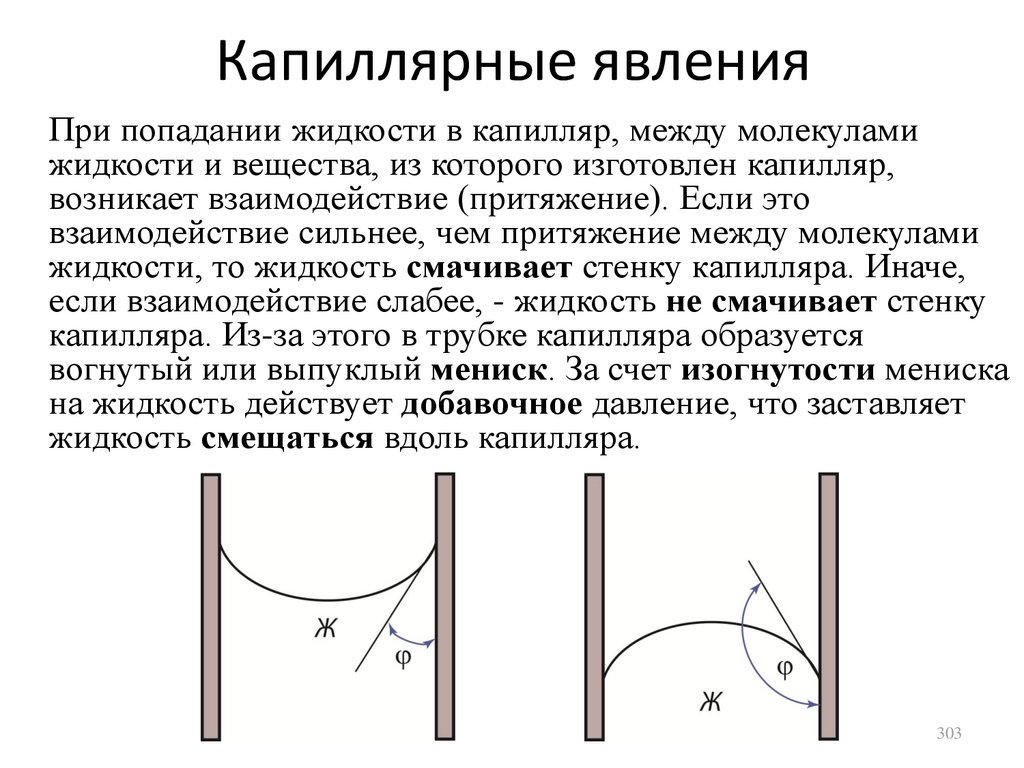
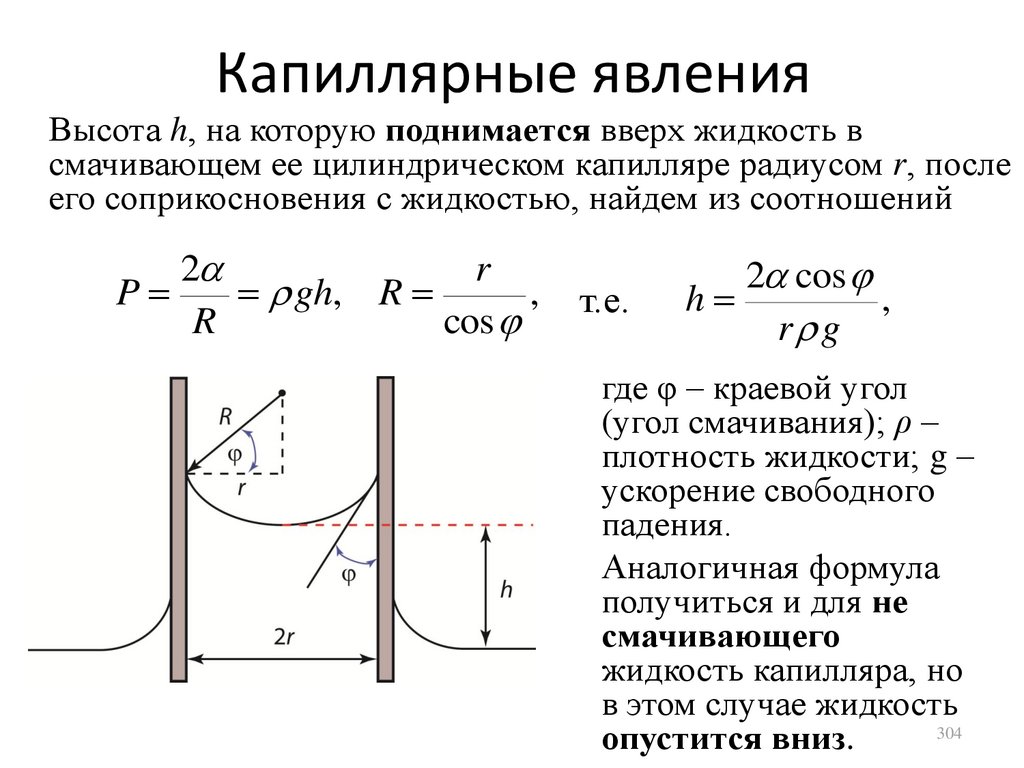




























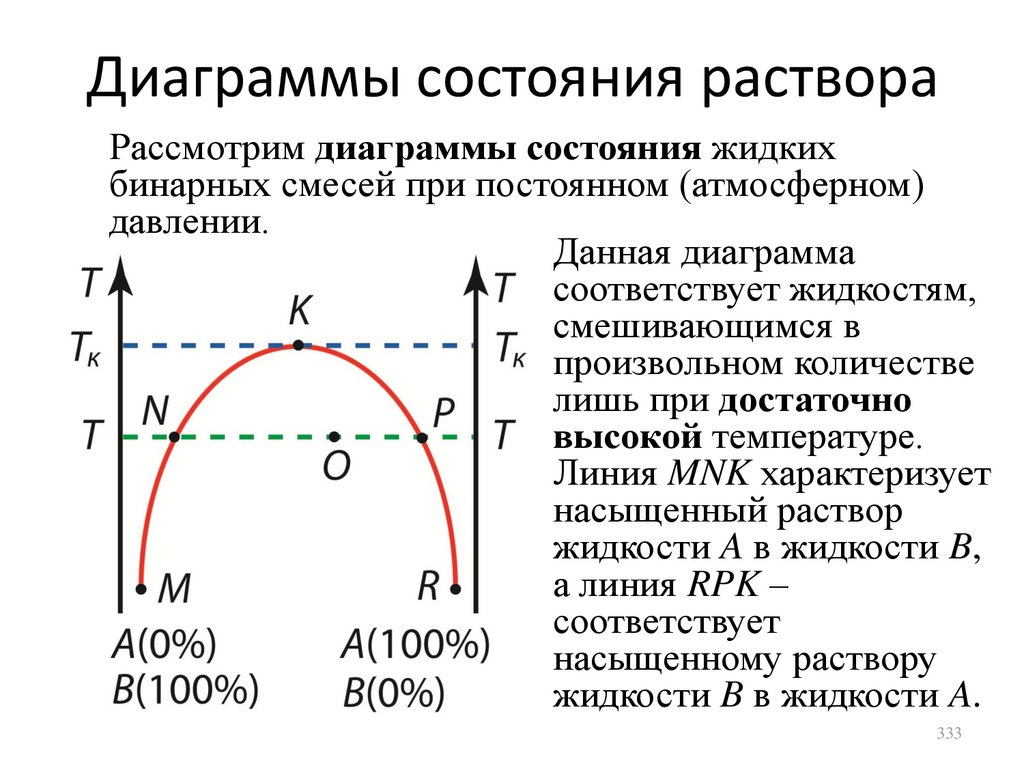


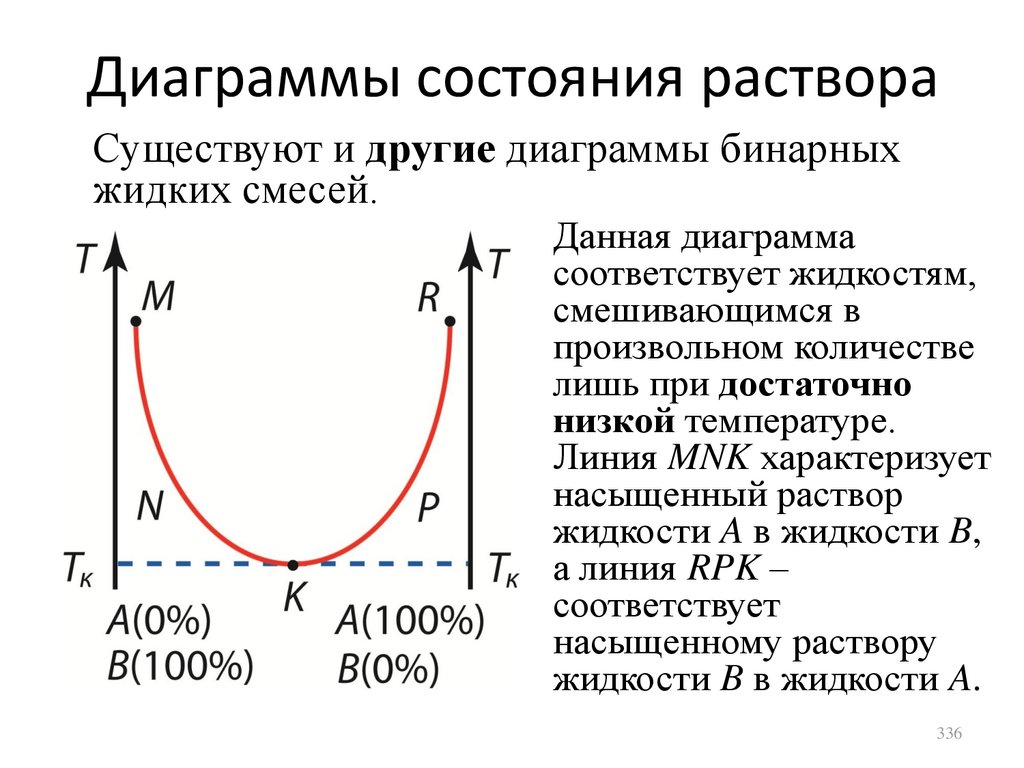



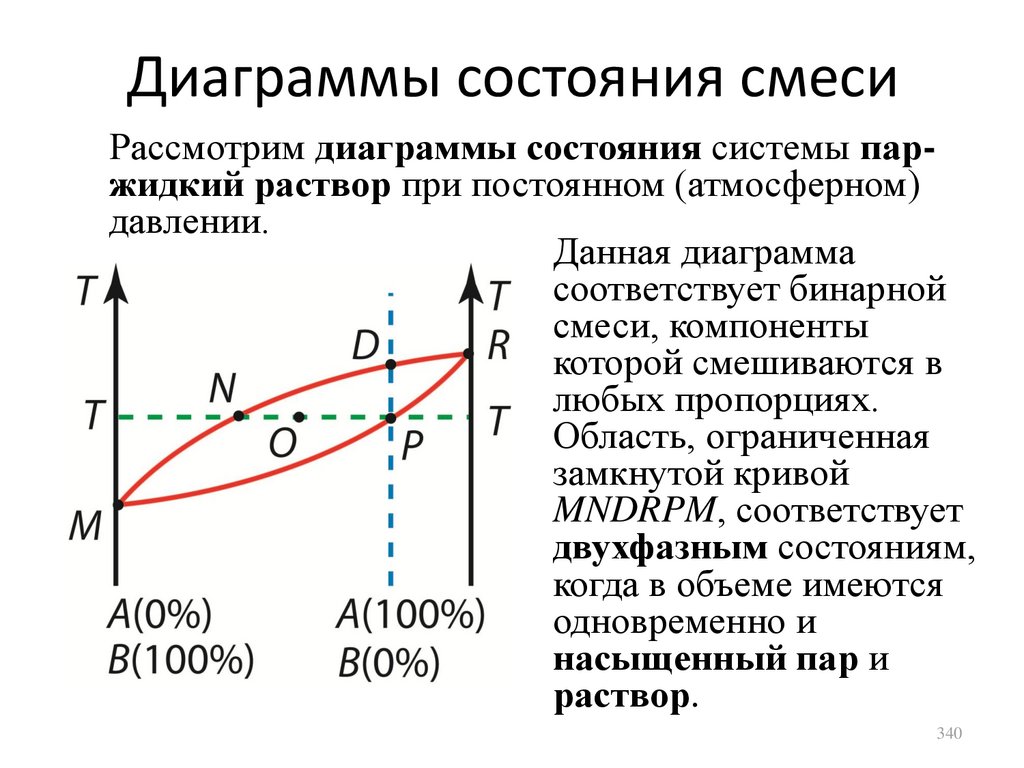



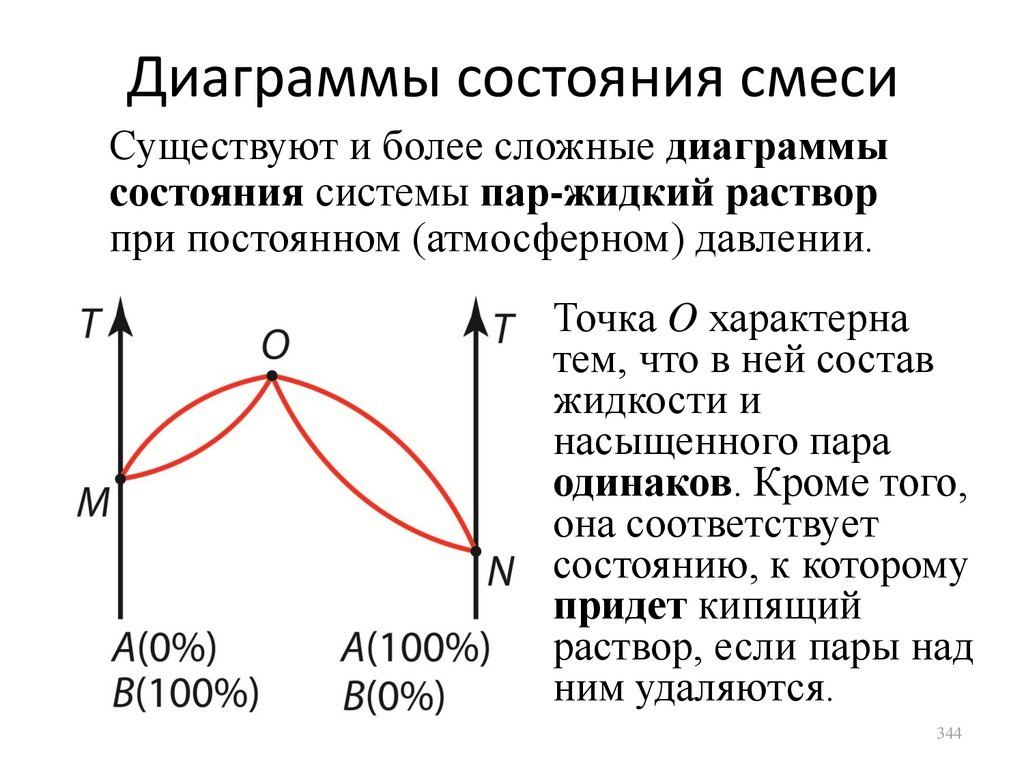






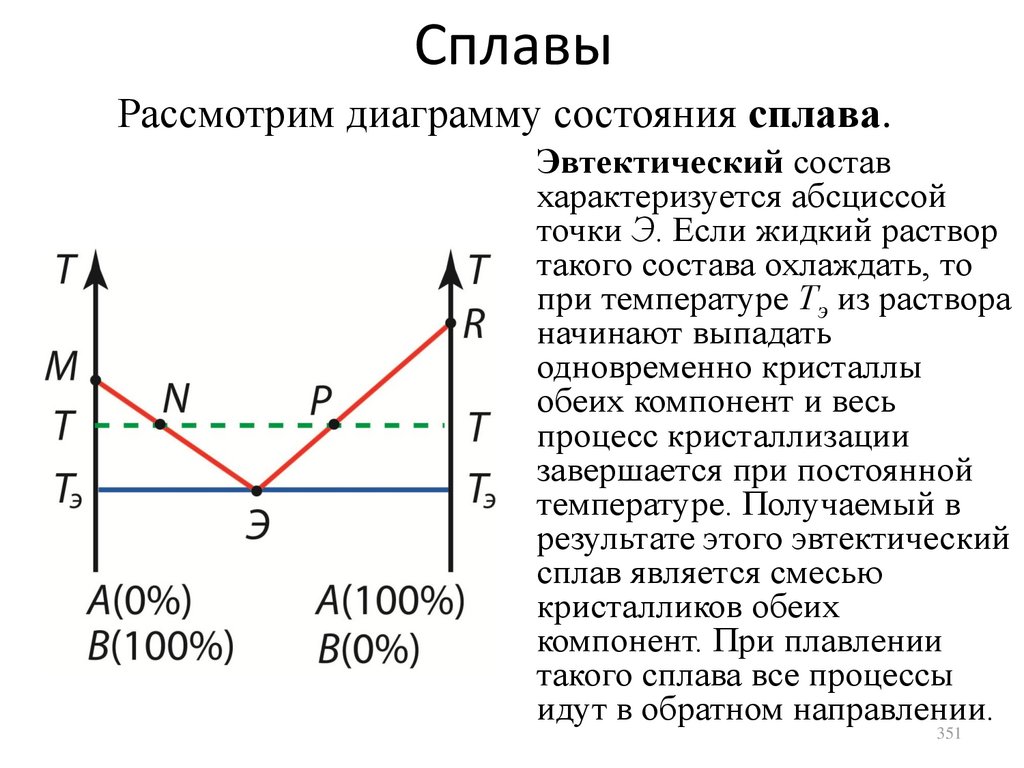



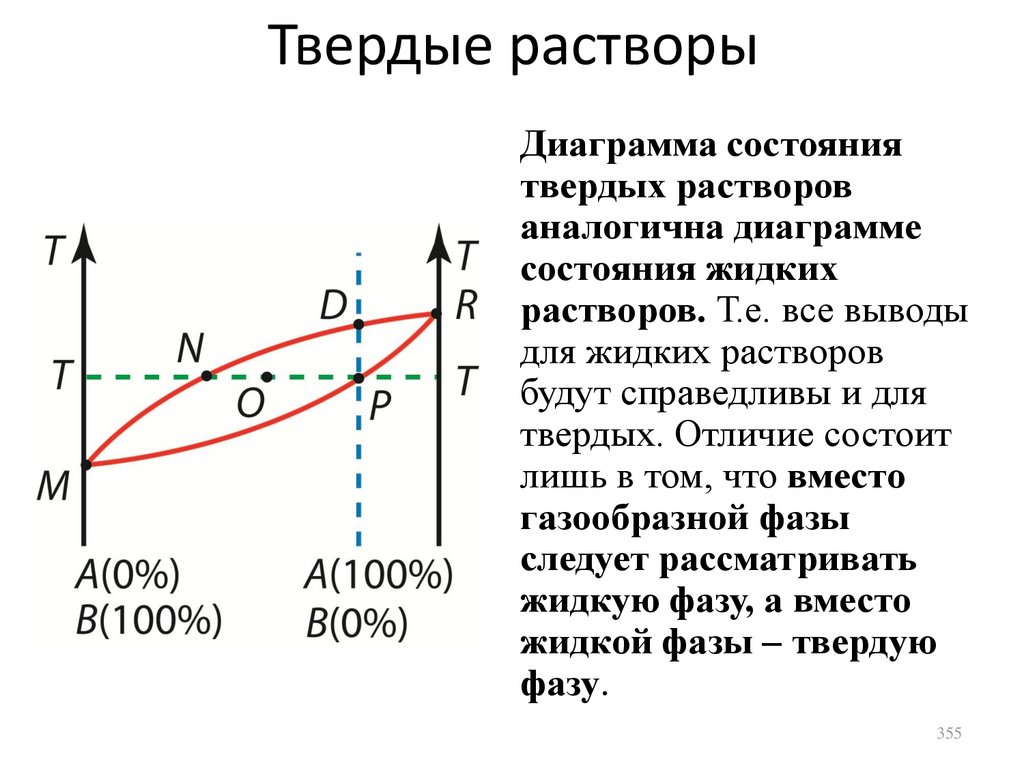







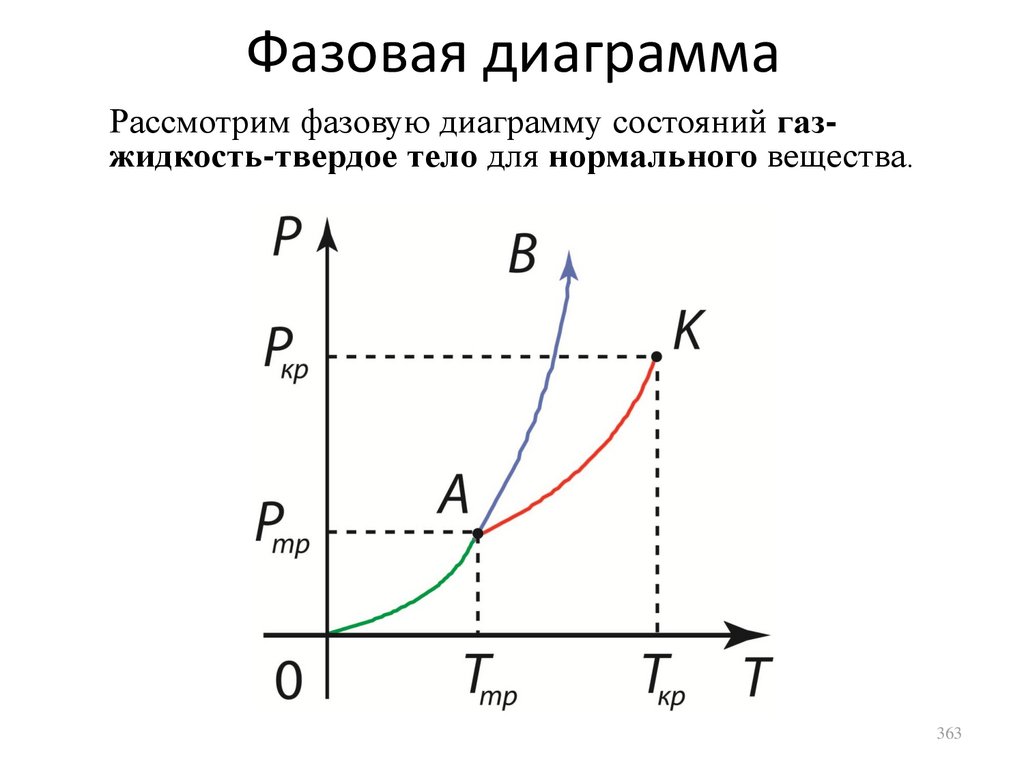




















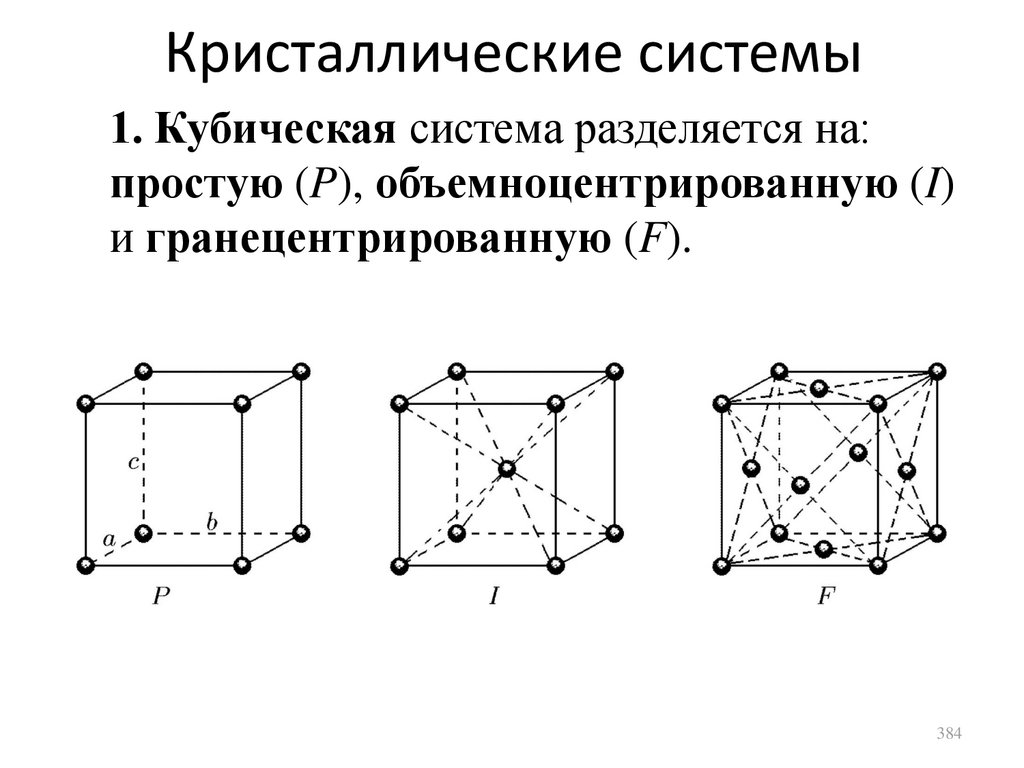
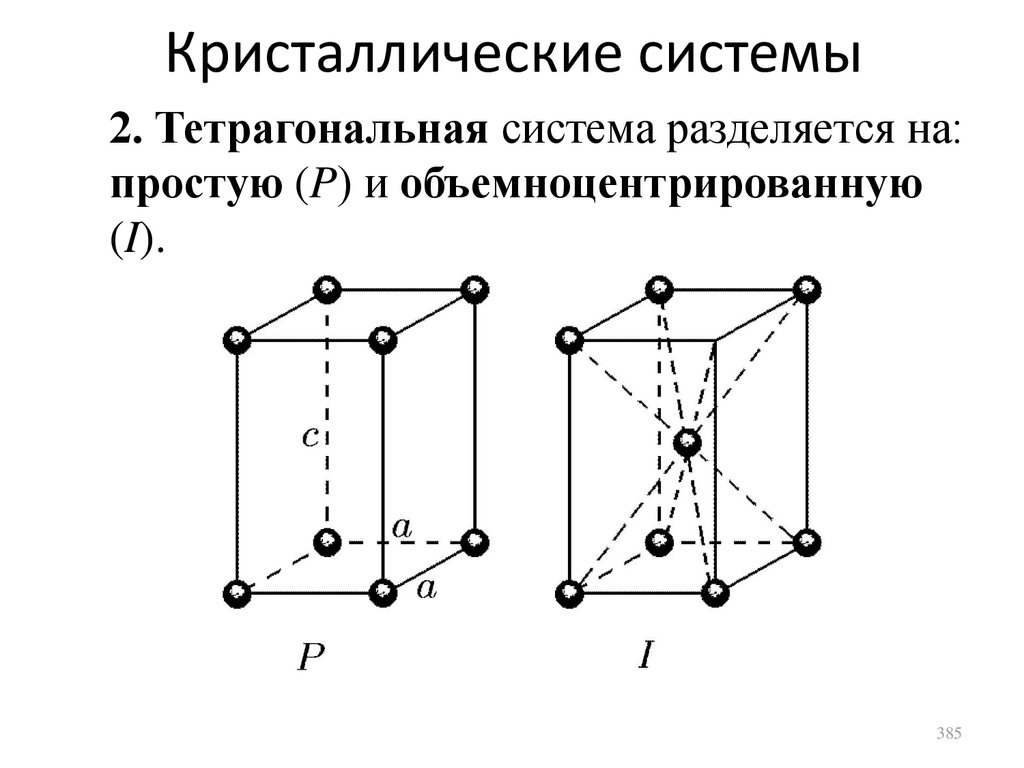

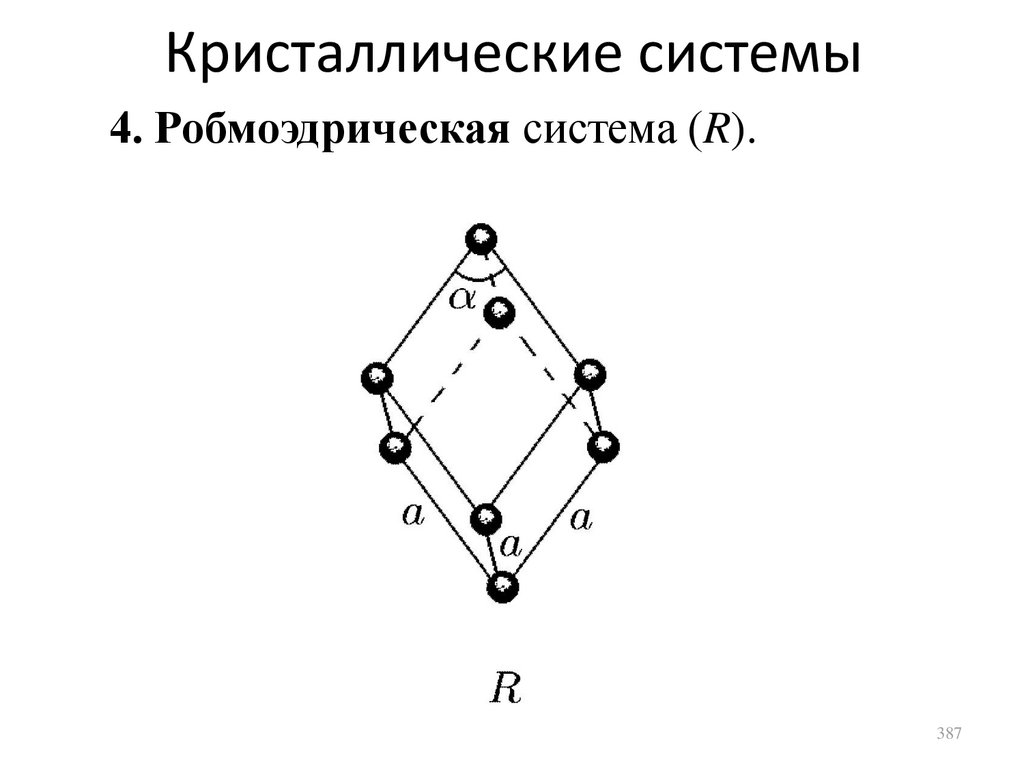
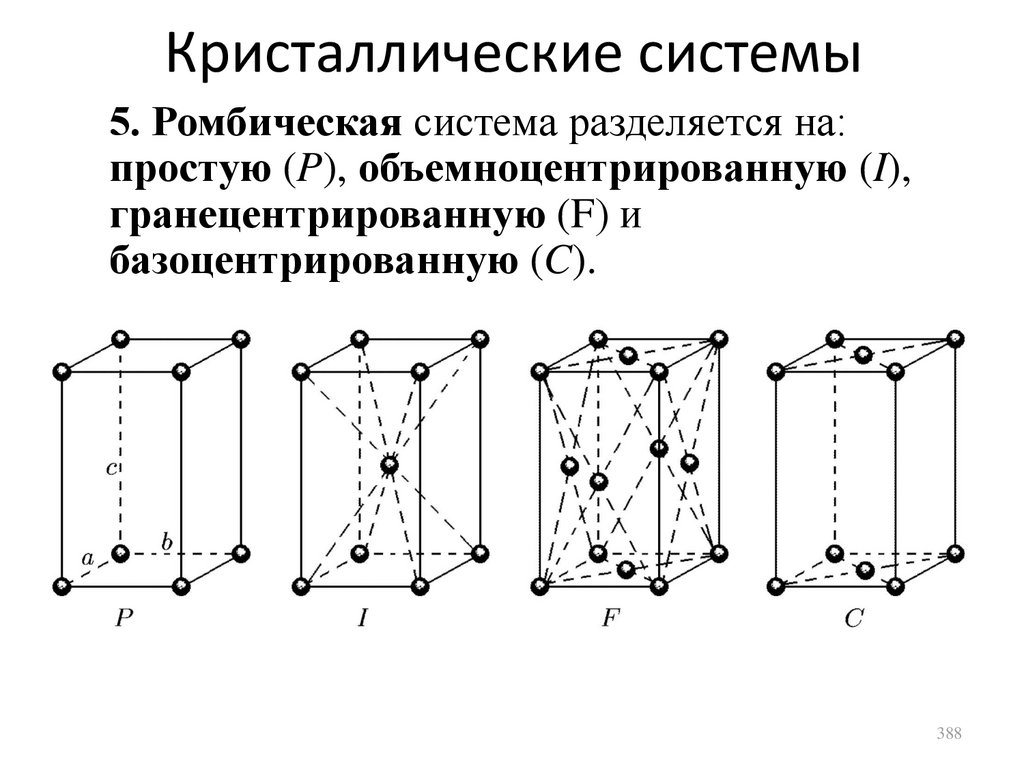
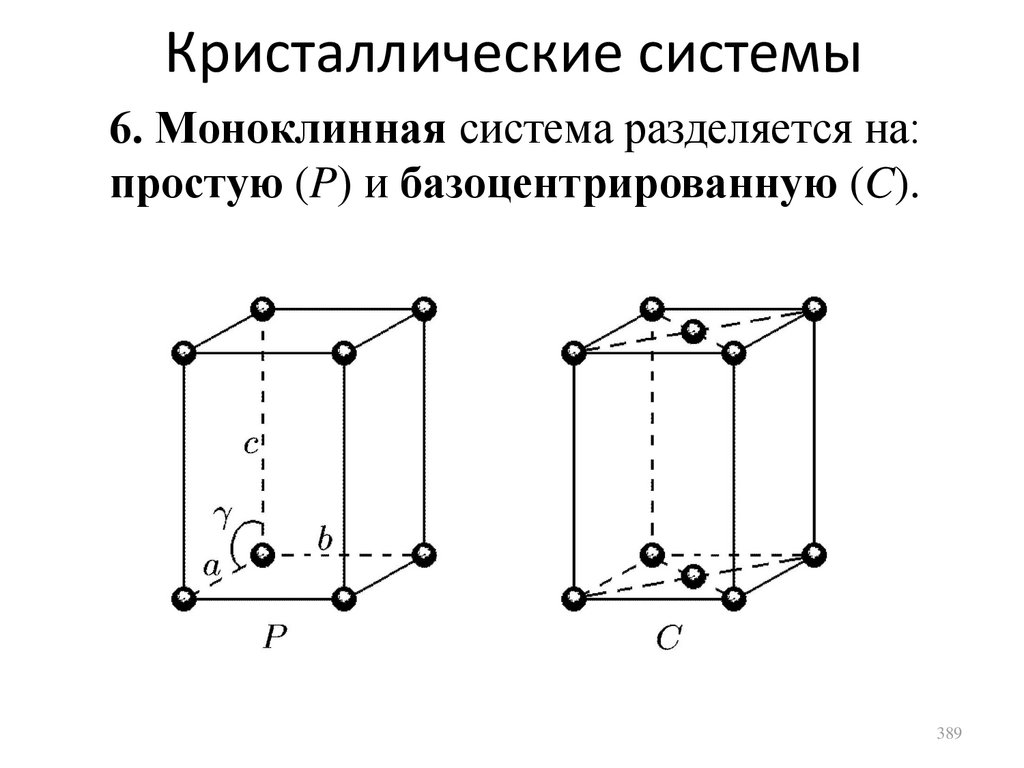
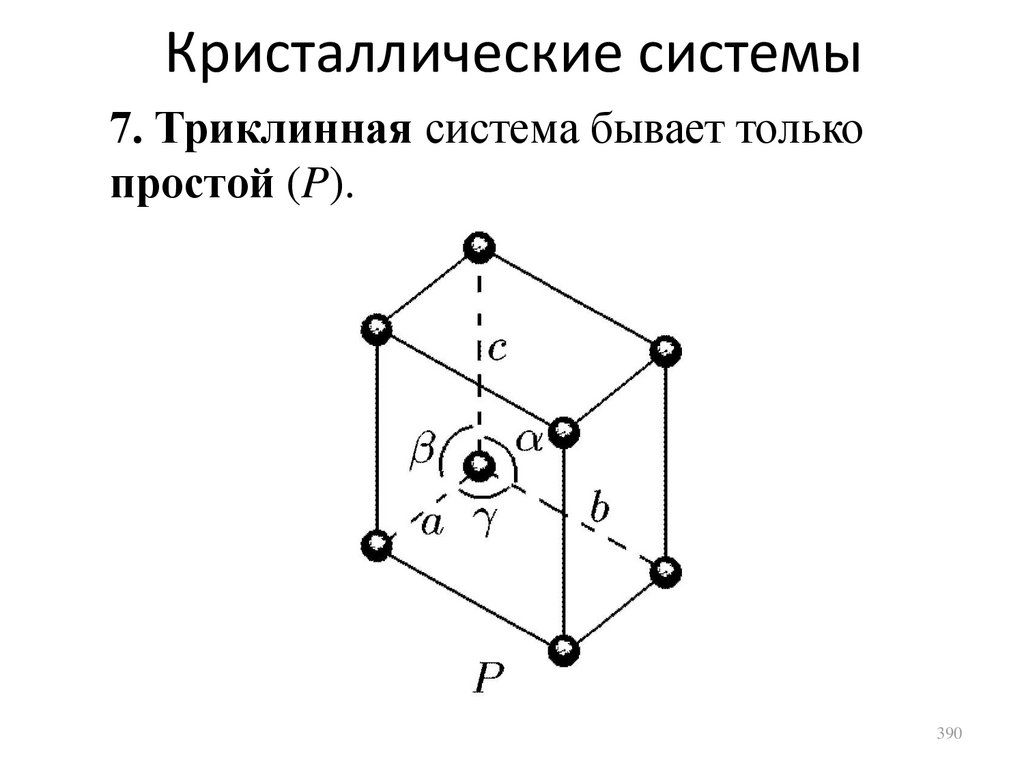







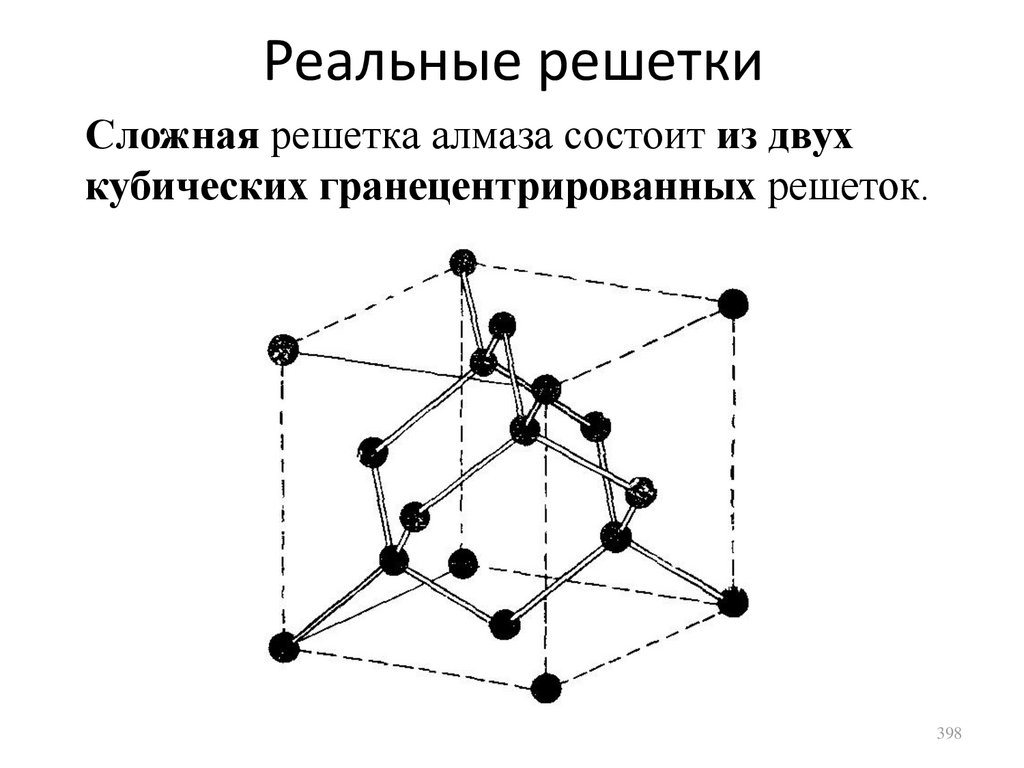






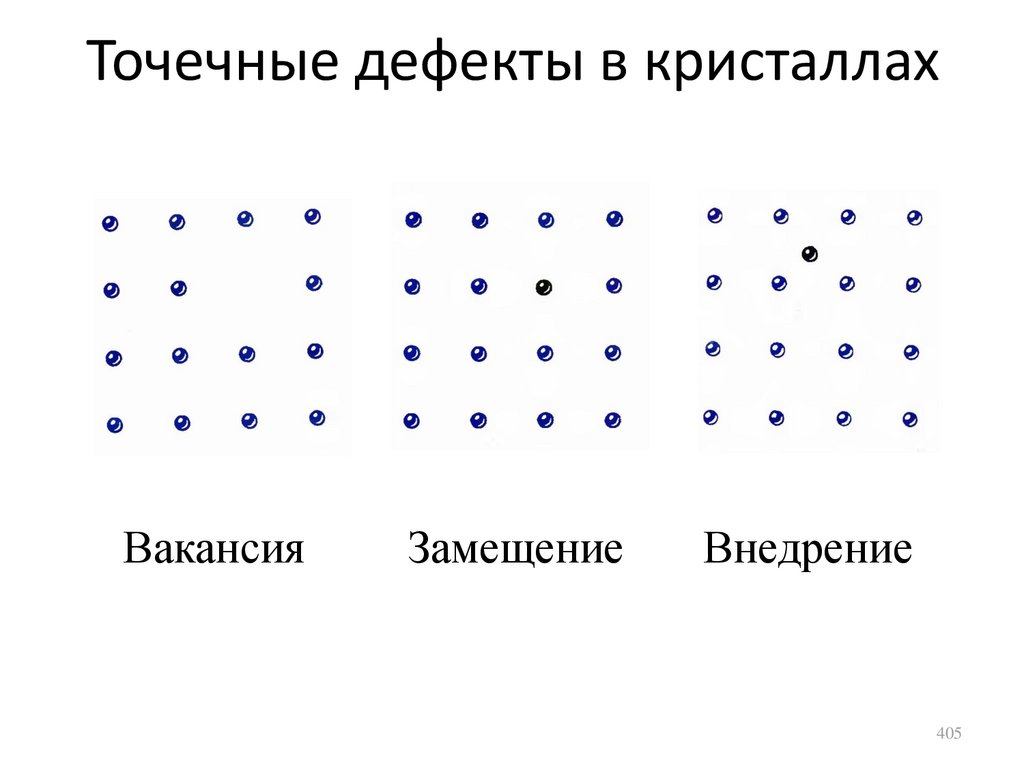


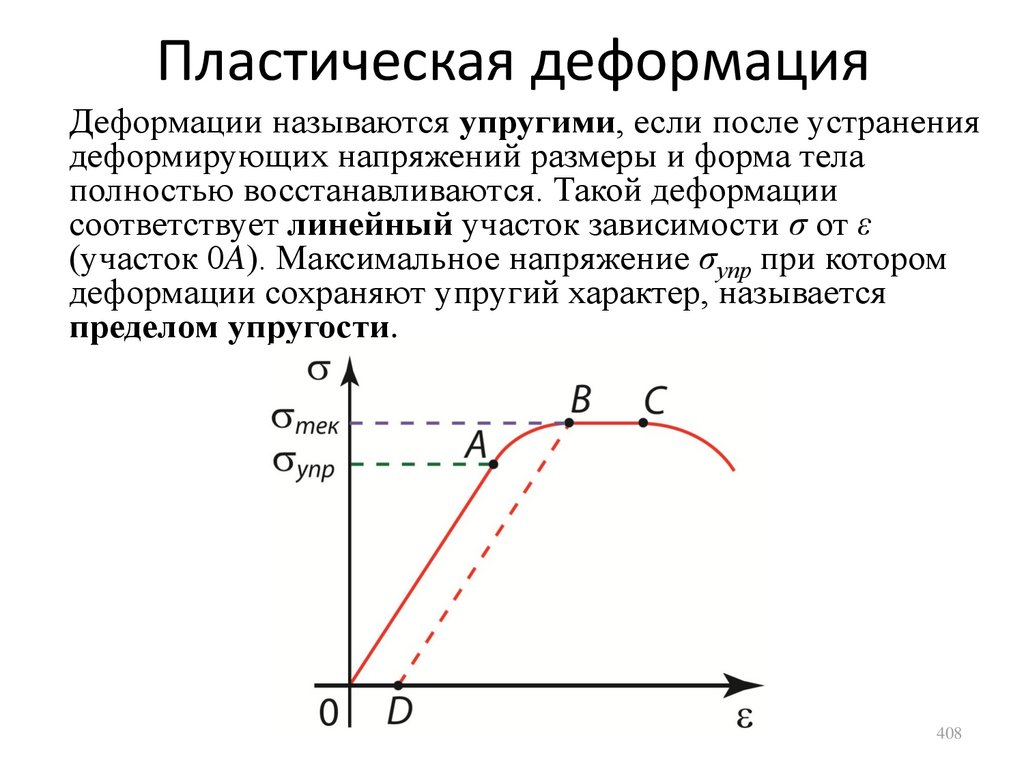


 physics
physics








