Similar presentations:
Иррациональные уравнения
1. ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ
2. Меню
1.2.
3.
4.
5.
6.
7.
Определение
Первый вид
Второй вид
Третий вид
Четвертый вид
Примеры для самостоятельного решения
Ответы
3. Иррациональными называются уравнения вида: и уравнения, сводящиеся к этому виду
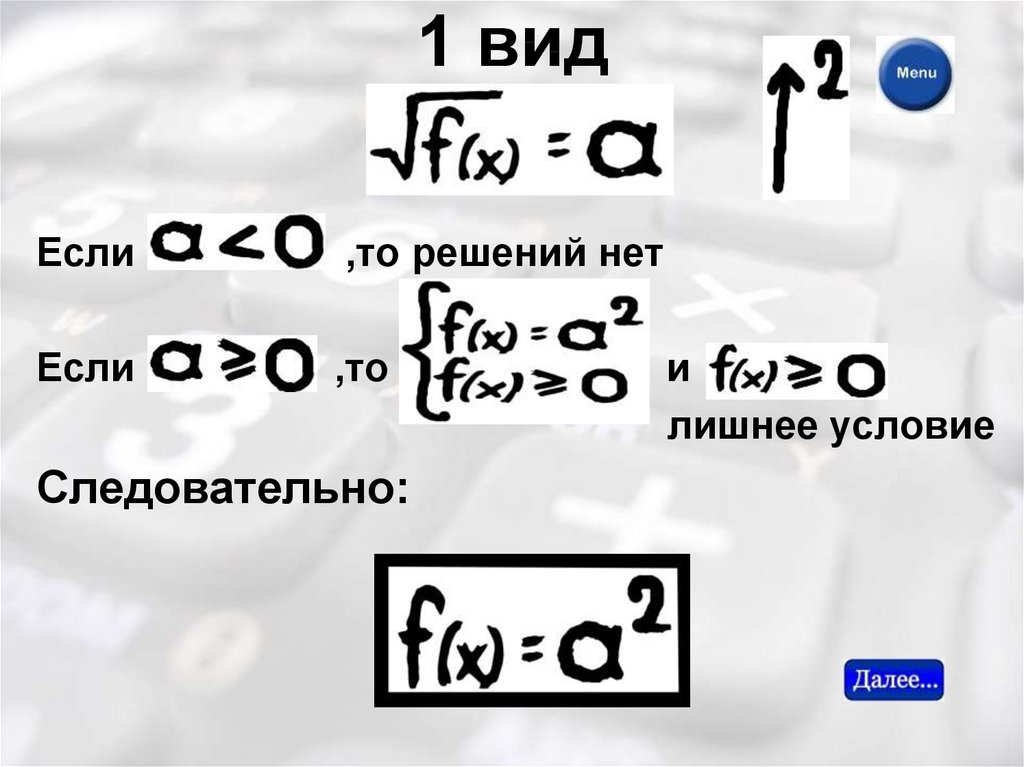
4. 1 вид
Если,то решений нет
Если
,то
Следовательно:
и
лишнее условие
5. Пример
Решить уравнениеРешение.
Возведем обе части уравнения в квадрат.
Перенесем -3 из левой части уравнения в правую и
выполним приведение подобных слагаемых.
Полученное неполное квадратное уравнение имеет
два корня -2 и 2.
Ответ: х = 2 и -2
6. 2 вид
Еслии
,то
лишнее условие
Следовательно:
7. Пример
Решить уравнениеРешение.
Возведем обе части уравнения в квадрат.
Запишем условие
Раскроем скобки, перенесем 1 - х из правой части
уравнения в левую и выполним приведение
подобных слагаемых.
Получим следующие значения х
Ответ: х = 0
8. 3 вид
Еслии
,то
одно из этих условий
лишнее
Следовательно:
9. Пример
Решить уравнениеРешение.
Возведем обе части уравнения в квадрат.
Запишем условие
Раскроем скобки, перенесем 5х - 2 из правой части
уравнения в левую и выполним приведение
подобных слагаемых.
Решив квадратное уравнение,
получим следующие значения х
Ответ: х = 1
10. 4 вид
Учитывая чтоимеет смысл при
Находим ОДЗ и решаем систему неравенств
Записываем условие равносильности и
решаем уравнение
11. Пример первый
Решить уравнениеРешение.
Запишем ОДЗ
Возведем обе части уравнения в квадрат.
Записываем условие равносильности и решаем
уравнение
12.
Составляем систему из ОДЗ и условия равносильностии решаем ее
Ответ: х = 1
13. Пример второй
Решить уравнениеРешение способом замены переменной
Тогда
Подставляем замены в исходное уравнение
14. Возведем в квадрат
Ответ : Х=315. Примеры для самостоятельного решения.
1)2)
3)
4)
5)
16. № 1
№1Решение:
Возведем в квадрат
Ответ:
17. № 2
№2Ответ:
18. № 3
№3Возводим в квадрат
Решаем квадратное уравнение
Ответ:
19. № 4
№4Решение:
Находим корни квадратного уравнения
Ответ :
20. № 5
№5Ответ: нет решений




















 mathematics
mathematics








