Similar presentations:
شرح كامل رياضيات الصف الاول بوربوينت
1. جمهورية مصر العربية
جمهورية مصر العربيةمحافظة بنى سويف
ادارة الفشن
التعليمية
مدرسة بسفا
العدادية
2. مـــــــــــــــــــادة
مـــــــــــــــــــادةالرياضيات
الصف الول
العدادى
3. اعداد
اعدادالستاذ /احمد محمد
جابر
موبيل/
0117564042
4. تحت اشراف موجه المادة
اشرافتحت
تحت اشراف
المادة
موجه المادة
موجه
محمد
الفاضل/محمد
الستاذالفاضل/
))11الستاذ
مصطفى
مصطفى
5.
الجبرالجبر
الهندسة
الهندسة
الحصاء
الحصاء
6.
الوحدةالولى
الوحدة
الوحدة
الثانية
الثانية
7. مجموعة الاعداد النسبية
الوحدة الولى العداد مجموعة العدـاد النسـبية
• مقارنة وترتيب العداد النسبيية
•
اـلنـسـبيـة
اـلـعـداـدـ
الـعـملـياـتـ علـىـ
النسبية
العدادالنسبية
جمعالعداد
)1)1جمع
وخواصها
وخواصها
ضرب العداد النسبية
)2
)2ضرب العداد النسبية
وخواصها
وخواصها
العداد
وقسمة
طرح
)
3
)3طرح وقسمة العداد
النسبية
الـعـقلـى
بـ
الـحـساـ
)4
النسبية
)4
الـحـساـبـ
القائمة
القائمة
الرئيسية
الـعـقلـى
خروج
خروج
8. الوحدة الثانية الجبر
الوحدة الثانية الجبر
الحدود والمقادير الجبرية
الحدود المتشابهة
ضرب الحدود الجبرية وقسمتها
جمع المقادير الجبرية وطرحها
ضرب حد جبرى فى مقدار جبرى
ضرب مقدار جبرى مكون من حدين فى
مقدار جبرى اخر
قسمة مقدار جبرى على حد جبرى
التحليل بإخراج العامل المشترك
القائمة
القائمة
الرئيسية
خروج
خروج
9. الوحدة الرابعة الأحصاء
الوحدة الرابعة الحصاء
قرأءة البيانات وتفسيرها
تمثيل البيانات
القائمة
القائمة
الرئيسية
خروج
خروج
10. الوحدة الثالثة الهندسة
الوحدة الثالثة الهندسة
مفاهيم هندسية
إنشاءات هندسية
التطابق
تطابق مثلثين
التوازى
نظرية فيثاغورث
القائمة
القائمة
الرئيسية
خروج
خروج
11.
جالزاوية :
هى اتحاد شعاعين لهما نفس نقطة البداية
تسمى نقطة البداية رأس الزاوية
ويسمى الشعاعين ضلعى الزاوية
ب
أ
لحظ أن :
•
تقاس الزاوية بالدرجات والدقائق والثوانى
•
60 = 1دقيقة
•
60 = 1ثانية
•
الزاوية تجزىء المستوى إلى ثلثة مجموعات من النقاط
على الزاوية
خارج الزاوية
داخل الزاوية
القائمة
القائمة
الرئيسية
السابق
السابق
التالى
التالى
القائمة
القائمة
الفرعية
خروج
خروج
12. مفاهيم هندسية
مـفاهيمـهندسيةالقطعة المستقيمة:
هى مجموعة مكونة من نقطتين أ ,ب وجميع النقط الواقعة بينهما
ب
يمكن قياس طولها بالمسطرة.
أ
الشعاع :
عبارة عن قطعة مستقيمة ممتدة من احد طرفيها بل حدود
له نقطة بداية ول تتحدد له نقطة نهاية ول يمكن أقياسه
ب
الخط المستقيم :
هو مجموعة غير منتهية من النقط يتعين بإى نقطتين علية
أ
ليس له بداية وليس له نهاية ول يمكن قياس طوله
لحظ ان :
ب
• أب أب أب
• أب ≠ ب أ
• يتساوى الشعاعين اذا كان لهما نفس البداية ونفس
التجاه
الساب
القائمة
القائمة
الساب
القائمة
القائمة
خروج
التالى
الفرعية
خروج
التالى
ق
الرئيسية
13.
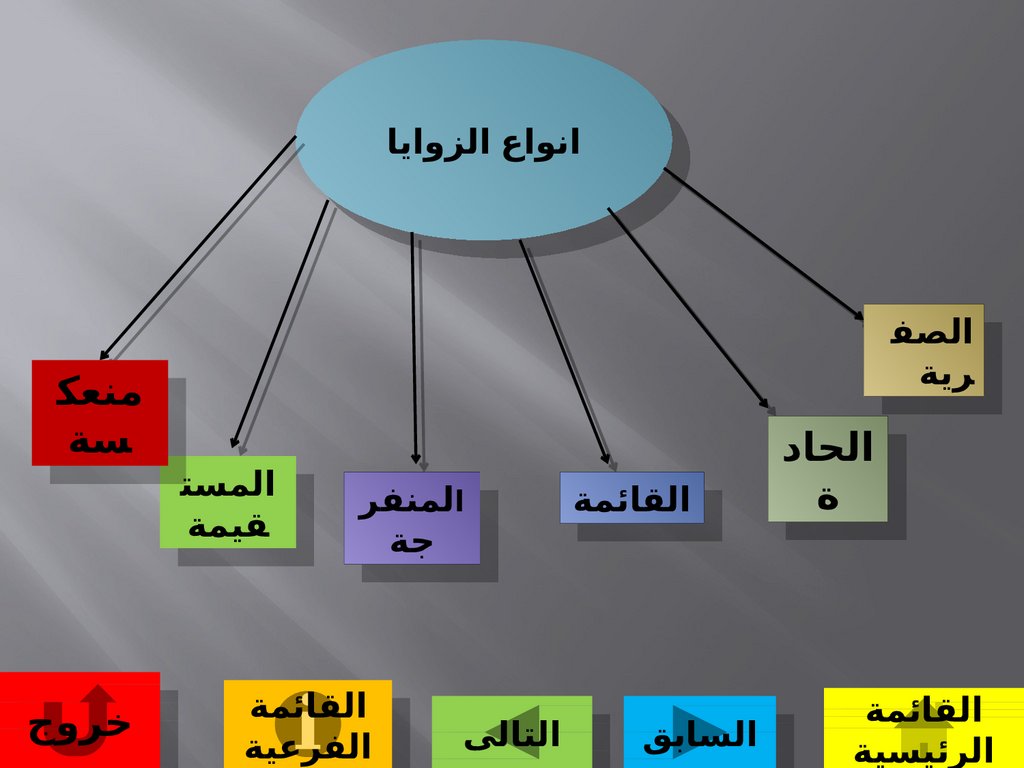
انواع الزواياانواع الزوايا
الصف
الصف
رية
رية
الحاد
الحاد
ةة
القائمة
القائمة
الرئيسية
القائمة
القائمة
السابق
السابق
المنفر
المنفر
جة
جة
التالى
التالى
المست
المست
قيمة
قيمة
القائمة
القائمة
الفرعية
منعك
منعك
سة
سة
خروج
خروج
14.
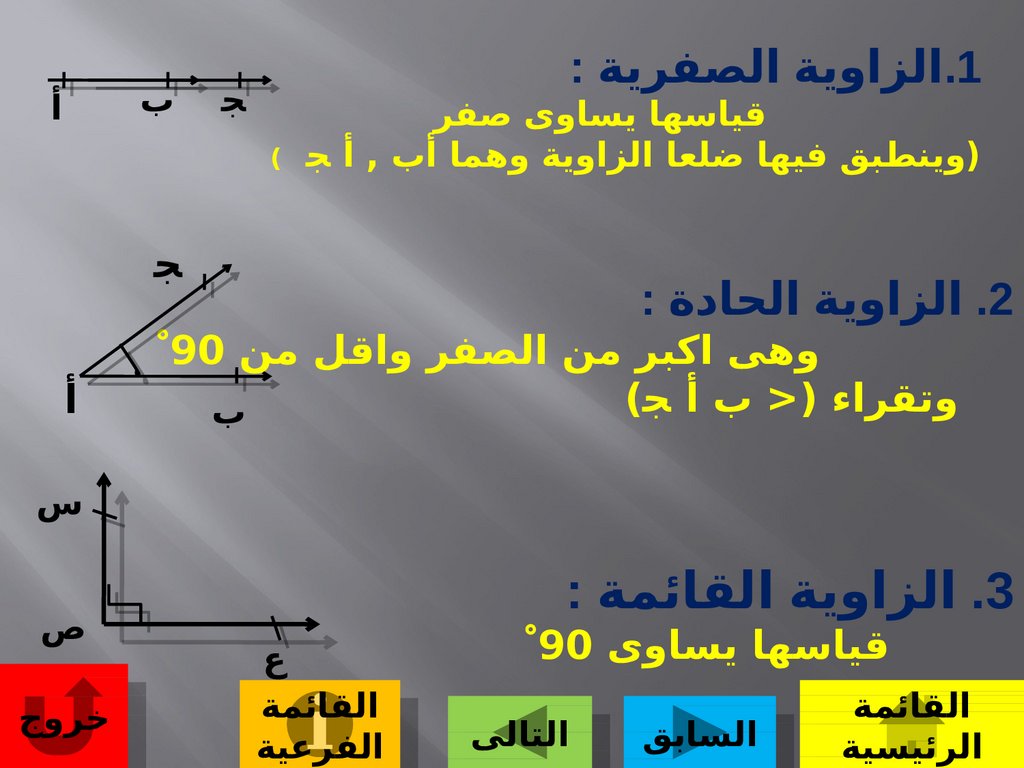
.1الزاوية الصفرية :قياسها يساوى صفر
(وينطبق فيها ضلعا الزاوية وهما أب ,أ ج
ج
ب
أ
)
ج
.2الزاوية الحادة :
وهى اكبر من الصفر واقل من 90
وتقراء (< ب أ ج)
ب
أ
س
.3الزاوية القائمة :
قياسها يساوى 90
القائمة
القائمة
الرئيسية
السابق
السابق
التالى
التالى
ع
القائمة
القائمة
الفرعية
ص
خروج
خروج
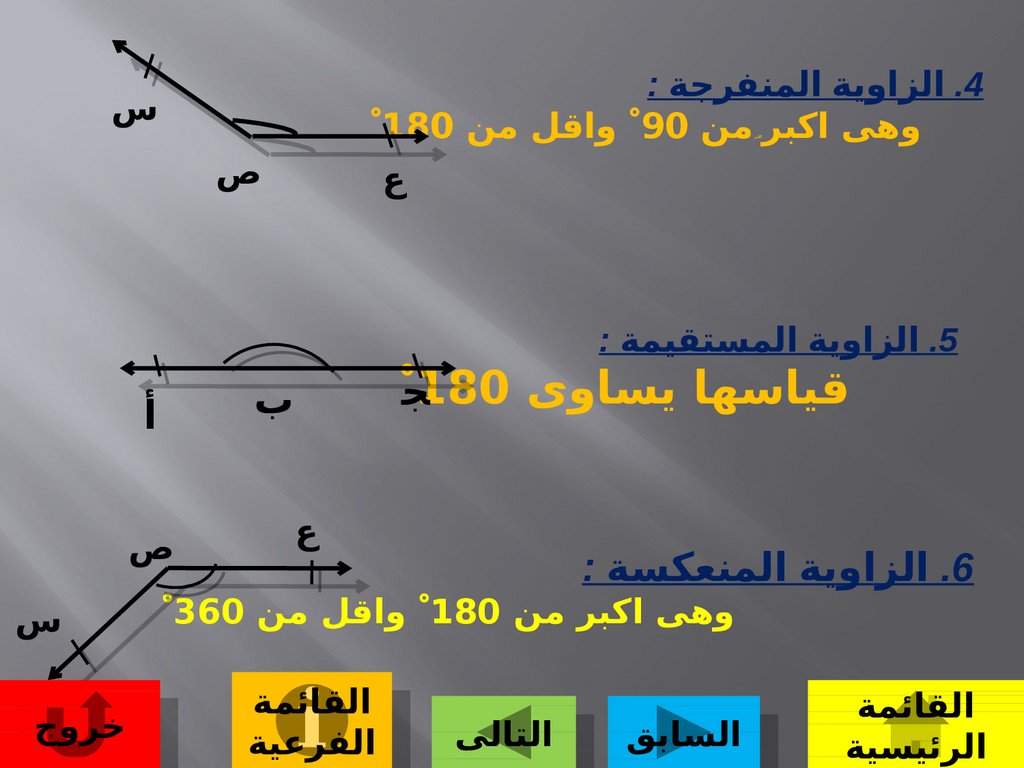
15. 4. الزاوية المنفرجة : وهى اكبراكبر من 90 ْ واقل من 180 ْ
.4الزاوية المنفرجة :وهى اكبر من 90واقل من 180
س
اكبر
ص
ع
.5الزاوية المستقيمة :
قياسها يساوى 180ج
ب
ع
.6الزاوية المنعكسة :
أ
ص
وهى اكبر من 180واقل من 360
القائمة
القائمة
الرئيسية
السابق
السابق
التالى
التالى
القائمة
القائمة
الفرعية
س
خروج
خروج
16.
العلقات بين الزواياالعلقات بين الزوايا
المتجاورتان ::
الزاويتان المتجاورتان
)1الزاويتان
)1
فى
الخران فى
والضلعان الخران
وضلع والضـلعان
رأس وضلع
فى رأس
يشتركان فى
زاويتان يشتركان
هما زاويتان
هما
المشترك.
الضلع المشترك.
من الضلع
مختلفتين من
جهتين مختلفتين
جهتين
مشترك
شعاع مشترك
ب شعاع
ب ,,ب
الرأس ب
فى الرأس
مشتركتان فى
ج) مشتركتان
ب ج)
(< ب
) <( ,,
ب )
(< أأ ب
(<
المشترك
والض
الضلع المشترك
من الضلع
مختلفتين من
جهتين مختلفتين
فى جهتين
ب جج فى
ب أأ ,,ب
ـلعان ب
والضلعان
ج
أ
المتتامتان::
الزاويتان المتتامتان
))22الزاويتان
ل
90
قياسهما 90
مجموع قياسهما
زاويتان مجموع
هما زاويتان
هما
90
ع)=90
ص ع)=
لص
+ق(< ل
ل )) +ق(<
صل
ق(<ع ص
ق(<ع
السابق
السابق
التالى
التالى
س
ص
ع
المتكاملتان ::
الزاويتان المتكاملتان
))33الزاويتان
180
قياسهما 180
مجموع قياسهما
زاويتان مجموع
هما زاويتان
هما
180
أ)= 180
ب أ)=
ق(< وو ب
+ق(<
و) +
ب و)
ق(< جج ب
ق(<
ج
القائمة
القائمة
الرئيسية
ب
القائمة
القائمة
الفرعية
و
ب
أ
خروج
خروج
17.
انلحظان
لحظ
القياس
فى القياس
متساوية فى
الواحدة متساوية
الزوايا الواحدة
متممات الزوايا
)1متممات
)1
القياس
فى القياس
متساوية فى
الواحدة متساوية
الزوايا الواحدة
مكملت الزوايا
)2مكملت
)2
ضلعيها
فإن ضلعيها
متكاملتان فإن
المتجاورتان متكاملتان
الزاويتان المتجاورتان
كانت الزاويتان
اذا كانت
)3اذا
)3
واحدة
استقامة واحدة
على استقامة
المتطرفان على
المتطرفان
ضلعيها
فإن ضلعيها
متتامتان فإن
المتجاورتان متتامتان
الزاويتان المتجاورتان
كانت الزاويتان
اذا كانت
)4اذا
)4
متعامدان
المتطرفان متعامدان
المتطرفان
مستقيم
تقاطع مستقيم
من تقاطع
الحادثتان من
المتجاورتان الحادثتان
الزاويتان المتجاورتان
)5الزاويتان
)5
متكاملتان
المستقيم متكاملتان
هذا المستقيم
على هذا
بداية على
نقطة بداية
وشعاع نقطة
وشعاع
منصف الزاوية:
هو الشعاع الذى يقسم الزاوية الى زاويتان لهما
نفس القياس
••
القائمة
القائمة
الرئيسية
السابق
السابق
التالى
التالى
القائمة
القائمة
الفرعية
خروج
خروج
18.
بالرأس::المتقابلتان بالرأس
الزاويتان المتقابلتان
))44الزاويتان
من
وكل من
واحدة وكل
رأس واحدة
فى رأس
مشتركتان فى
زاويتان مشتركتان
هما زاويتان
هما
أ
إحداهما
ص
ضلعى إحداهما
ضلعى
الخرى
ضلعى الخرى
من ضلعى
ضلع من
مع ضلع
واحدة مع
استقامة واحدة
على استقامة
على
م
س
ب
نتيجة
نتيجة
با
كل زاـ
متقابلتان با
ويتان متقابلتان
زاويتان
فإن كل
مستقيمين فإن
تقاطع مستقيمين
اذا تقاطع
اذا
القياس
فى القياس
متساويتان فى
لرأس متساويتان
لرأس
نقطة
حول نقطة
المتجمعة حول
الزوايا المتجمعة
قياسات الزوايا
مجموع قياسات
))55مجموع
360
== 360
القائمة
القائمة
الرئيسية
السابق
السابق
التالى
التالى
القائمة
القائمة
الفرعية
خروج
خروج
19.
هندسيةإنشاءات
إنشاءات هندسية
اول :إنشاء منصف لزاوية معلومة
المعطيات :أ ب ج زاوية معلومة كما بالشكل
المسطرة ب
المطلوب :رسم منصف للزاوية أ ب ج باستخدام أ
والفرجار
ج
خطوات العمل:
ص
ج
)1نركز سن الفرجار عند راس الزاوية وبفتحة مناسبة
نرسم قوس يقطع ب أ ,ب ج فى النقطتين س ,صـ
)2نركز سن الفرجار عند كل من س ,ص
وبنفس الفتحة نرسم قوسين يتقاطعين فى نقطة
)3نرسم ب فيكون الشعاع المنصف للزاوية أ بأ ج
جأ
س
ب
ب
مثال :باستخدام الدوات الهندسيةارسم ▲أ ب ج المتساوى
الضلع وطول ضلعة 5سم ,نصف كل من زاويتى (< أ ب ج ) < ( ,أ ج
ب) بحيث يتقاطع المنصفان فى نقطة م
القائمة
القائمة
الرئيسية
الساب
الساب
التالى
التالى
القائمة
القائمة
الفرعية
خروج
خروج
20.
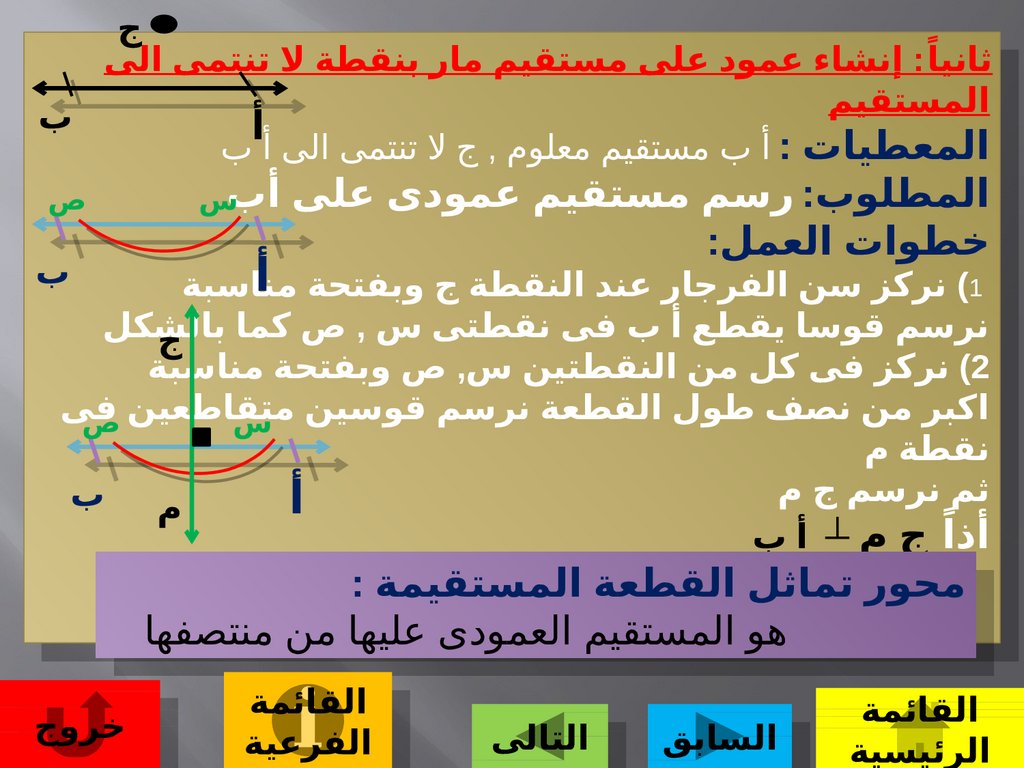
جثانيا ً :إنشاء عمود على مستقيم مار بنقطة ل تنتمى الى
ثانيا ً :إنشاء عمود على مستقيم مار بنقطة ل تنتمى الى
المستقيم
ب
المستقيم
أ
المعطيات :أ ب مستقيم معلوم ,ج ل تنتمى الى أ ب
المعطيات :أ ب مستقيم معلوم ,ج ل تنتمى الى أ ب
أبس
علىأب
عمودىعلى
مستقيمعمودى
رسممستقيم
المطلوب:رسم
المطلوب:
العمل:
خطوات
:
العمل
خطوات
أ
ص
ب
)1نركز سن الفرجار عند النقطة ج وبفتحة مناسبة
)1نركز سن الفرجار عند النقطة ج وبفتحة مناسبة
بالشكل
نرسم قوسا يقطع أ ب فى نقطتى س ,ص كما
ج
بالشكل
نرسم قوسا يقطع أ ب فى نقطتى س ,ص كما
)2نركز فى كل من النقطتين س ,ص وبفتحة مناسبة
)2نركز فى كل من النقطتين س ,ص وبفتحة مناسبة
فى
اكبر من نصف طول القطعة نرسم
متقاطعين ص
قوسين س
فى
متقاطعين
اكبر من نصف طول القطعة نرسم قوسين
نقطة م
نقطة م
ثم نرسم ج م
ب
أ
م
ثم نرسم ج م
أذا ً ج م ┴ أ ب
أذا ً ج م ┴ أ ب
المستقيمة: :
القطعة
تماثل
محور
محور تماثل القطعة المستقيمة
منتصفها
منمنتصفها
عليهامن
العمودىعليها
المستقيمالعمودى
هوالمستقيم
هو
القائمة
القائمة
الرئيسية
السابق
السابق
التالى
التالى
القائمة
القائمة
الفرعية
خروج
خروج
21.
جمعلومة:
لزاوية
مطابقة
زاوية
إنشاء
:
ثالثا
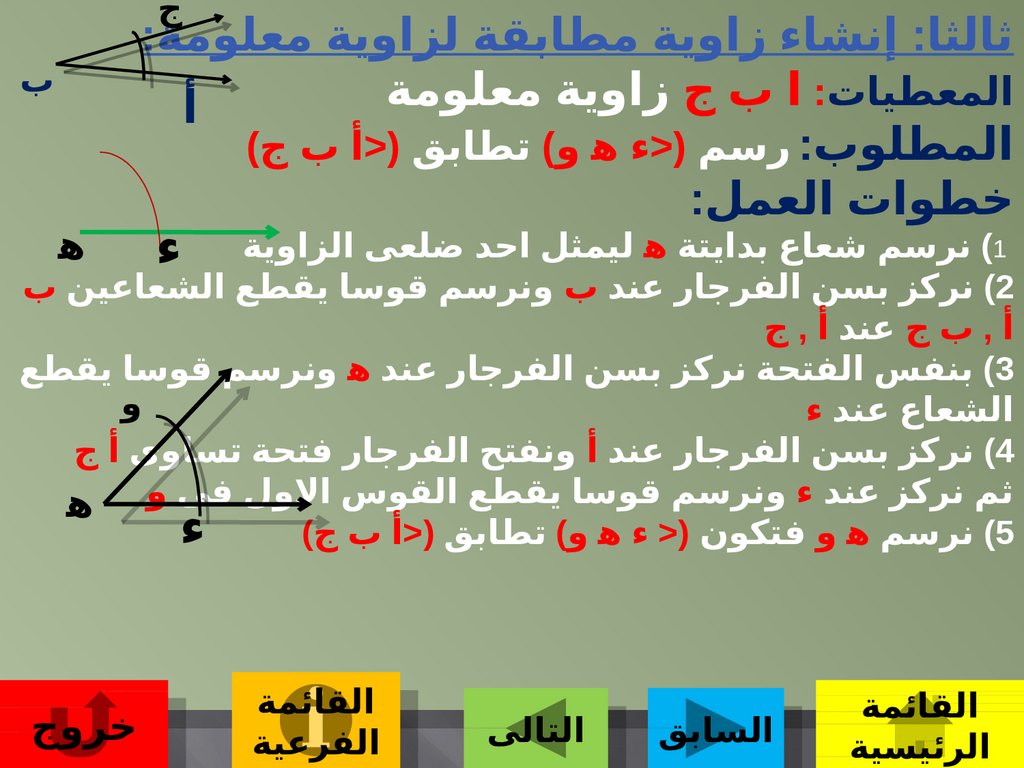
ثالثا :إنشاء زاوية مطابقة لزاوية معلومة:
معلومة
أ
زاويةمعلومة
بججزاوية
المعطيات:ا اب
المعطيات:
ج)
بج)
(<أب
تطابق(<أ
و)تطابق
رسم(<(< ههو)
المطلوب:رسم
المطلوب:
العمل:
خطواتالعمل:
خطوات
ب
ه
)1نرسم شعاع بدايتة ه ليمثل احد ضلعى الزاوية
)1نرسم شعاع بدايتة ه ليمثل احد ضلعى الزاوية
)2نركز بسن الفرجار عند ب ونرسم قوسا يقطع الشعاعين ب
)2نركز بسن الفرجار عند ب ونرسم قوسا يقطع الشعاعين ب
أ ,ب ج عند أ ,ج
أ ,ب ج عند أ ,ج
)3بنفس الفتحة نركز بسن الفرجار عند ه ونرسم قوسا يقطع
)3بنفس الفتحة نركز بسن الفرجار عند ه ونرسم قوساويقطع
الشعاع عند
الشعاع عند
)4نركز بسن الفرجار عند أ ونفتح الفرجار فتحة تساوى أ ج
)4نركز بسن الفرجار عند أ ونفتح الفرجار فتحة تساوى أ ج
ثم نركز عند ونرسم قوسا يقطع القوس الول
فىوو ه
ثم نركز عند ونرسم قوسا يقطع القوس الول فى
)5نرسم ه و فتكون (< ه و) تطابق (<أ ب ج)
)5نرسم ه و فتكون (< ه و) تطابق (<أ ب ج)
القائمة
القائمة
الرئيسية
السابق
السابق
التالى
التالى
القائمة
القائمة
الفرعية
خروج
خروج
22.
التطابقالتطابق
فى
متساويتان فى
كانت متساويتان
إذا كانت
المستقيمتان إذا
القطعتان المستقيمتان
تتطابق القطعتان
)1تتطابق
)1
صحيح
والعكس صحيح
الطول والعكس
الطول
سم
ص == 44سم
سص
سم ,,س
ب == 44سم
أأ ب
صحيح))
ص
والعكس صحيح
((والعكس
سص
ب≡≡ س
أذن أأ ب
أذن
والعكس
القياس والعكس
فى القياس
متساويتان فى
كانت متساويتان
إذا كانت
الزاويتان إذا
تتطابق الزاويتان
))22تتطابق
صحيح
صحيح
50
ص عع)) == 50
سص
(< س
ق (<
ب جج)) == ق
(< أأ ب
ق(<
ق
صحيح ))
ص عع))
والعكس صحيح
(( والعكس
سص
(< س
ب جج)) ≡≡ (<
(<أأ ب
أذن (<
أذن
المضلعين
رؤوس المضلعين
بين رؤوس
تطابق بين
وجد تطابق
إذا وجد
المضلعان إذا
يتطابق المضلعان
))33يتطابق
فى
نظيره فى
المضلع نظيره
فى المضلع
رأس فى
وكل رأس
ضلع وكل
كل ضلع
يطابق كل
بحيث يطابق
بحيث
الخر
المضلع الخر
المضلع
كان
إذا كان
مضلع إذا
أى مضلع
يتطابق أى
يتطابق
الطول
فى الطول
متساوية فى
المتناظرة متساوية
أضلعها المتناظرة
أضلعها
القياس
فى
متساوية
المتناظرة
زواياهما
القياس
فى
متساوية
المتناظرة
زواياهما
القائمة
القائمة
الساب
القائمة
القائمة
خروج
الساب
التالى
خروج
الفرعية
الرئيسية
التالى
23.
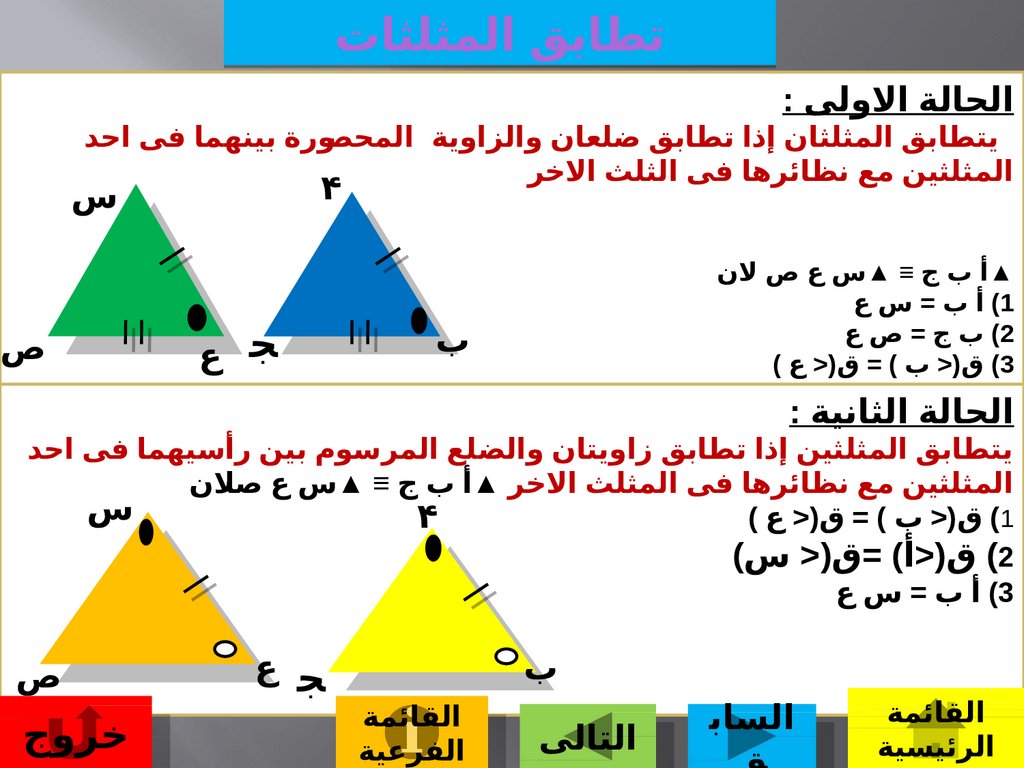
تطابق المثلثاتالحالة الولى :
يتطابق المثلثان إذا تطابق ضلعان والزاوية المحصـورة بينهما فى احد
المثلثين مع نظائرها فى الثلث الخر
۴
▲أ ب ج ≡ ▲س ع ص لن
)1أ ب = س ع
)2ب ج = ص ع
)3ق(< ب ) = ق(< ع )
ب
س
ج ع
ص
الحالة الثانية :
يتطابق المثلثين إذا تطابق زاويتان والضلع المرسوم بين رأسيهما فى احد
المثلثين مع نظائرها فى المثلث الخر ▲أ ب ج ≡ ▲س ع صلن
س
)1ق(< ب ) = ق(< ع )
۴
)2ق(<أ) =ق(< س)
)3أ ب = س ع
ب
القائمة
القائمة
الرئيسية
الساب
الساب
التالى
التالى
القائمة
القائمة
الفرعية
ج ع
ص
خروج
خروج
24.
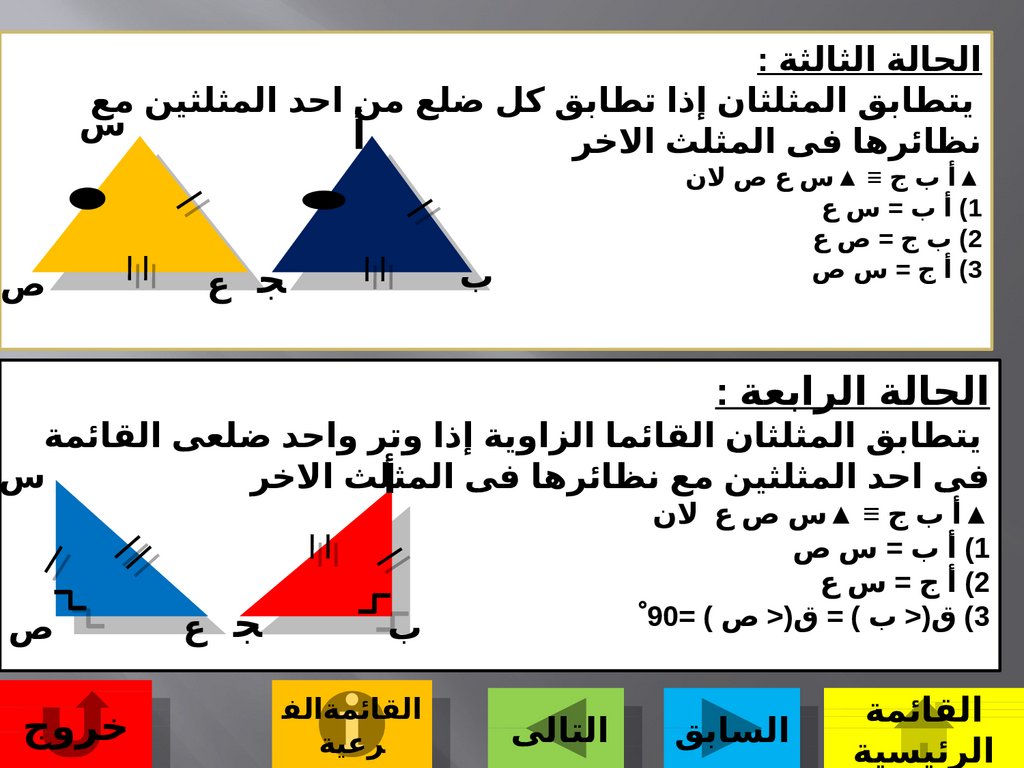
الحالة الثالثة :يتطابق المثلثان إذا تطابق كل ضلع من احد المثلثين مع
س
أ
نظائرها فى المثلث الخر
▲أ ب ج ≡ ▲س ع ص لن
)1أ ب = س ع
)2ب ج = ص ع
)3أ ج = س ص
ب
ج ع
ص
الحالة الرابعة :
يتطابق المثلثان القائما الزاوية إذا وتر واحد ضلعى القائمة
س
المثلث الخر
فى احد المثلثين مع نظائرها فى
أ
▲أ ب ج ≡ ▲س ص ع لن
)1أ ب = س ص
)2أ ج = س ع
)3ق(< ب ) = ق(< ص ) =90
القائمة
القائمة
الرئيسية
السابق
السابق
ب
التالى
التالى
القائمةالف
القائمةالف
رعية
ج ع
ص
خروج
خروج
25.
التوازىالتوازى
مستقيم
قطع مستقيم
من قطع
الناتجة من
الزوايا الناتجة
ازواج الزوايا
بين ازواج
العلقة بين
العلقة
متوازيين::
لمستقيمين متوازيين
لمستقيمين
2 1
متوازيين
مستقيمين
متوازيين
مستقيم مستقيمين
قطع مستقيم
إذا قطع
إذا
3 4
ل
فإن.
فإن.
القياس
متساويتين 5
فى6القياس
فى
متبادلتين متساويتين
زاويتين متبادلتين
كل زاويتين
)1كل
)1
بالتبادل م
(<7 8 ))66
بالتبادل
ق(<
)=ق
(<=)44
ق(<
بالتبادل ,,ق
(< ))55بالتبادل
ق(<
)=ق
(<=)33
ق(<
مثل ::ق
مثل
فى
متساويتين فى
متناظرتين متساويتين
زاويتين متناظرتين
كل زاويتين
))22كل
القياس
القياس
(<))66
ق(<
)= ق
(<=)22
ق(<
(< ,, ))88ق
ق(<
)= ق
(<=)44
ق(<
(< ,, ))55ق
ق(<
)=ق
(<=)11
ق(<
مثل ::ق
مثل
بالتناظر
(< ))77بالتناظر
ق(<
)= ق
(<=)33
ق(<
,,ق
القاطع
من
كل
القائمةالفالقاطع
واحدة من
جهة واحدة
وفى جهة
داخلتين وفى
زاويتين داخلتين
القائمةزاـويتين
))33كل
القائمةالف
خروج
القائمة
متكاملتان
التالى
السابق
رعية
متكاملتان
خروج
التالى
الرئيسية السابق
رعية
26.
ملحظات هامةملحظات هامة
)1اذا كان ل ∩ م= Ǿفان ل //م
)2المستقيمان المتوازيان البعد بينهما ثابت
)3المستقيم العمودى على احد مستقيمين
متوازيين فى المستوى يكون عمودى على
الخر
)4المستقيمان العموديان على ثالث متوازيان
)5المستقيمان المزازيان لثالث متوازيان
)6اذا قطع مستقيم احد مستقيمين متوازيين
فإنة يقطع الخر
القائمة
القائمة
الرئيسية
السابق
السابق
التالى
التالى
القائمةالف
القائمةالف
رعية
خروج
خروج
27.
مستقيمينتوازىمستقيمين
شروطتوازى
شروط
يتوازى المستقيمان إذا قطعهما مستقيم ثالث وحدث
إحدى الحالت التية:
)1زاويتان متبادلتان متساويتان فى القياس
)2زاويتان متناظرتان متساويتان فى
القياس
نتيجة
نتيجة
)3زاويتان داخلتان وفى جهة واحدة من
القاطع متكاملتان
القائمةال
القائمة
الساب
التالى القائمةال
القائمة
الساب
خروج
فرعية
الرئيسية
مستقيمات متوازية
عدة
إذا قطع
التالى
وكانت اجزاءخروج
مستقم ق
فرعية
الرئيسية
28.
نظرية فيثاغورثنظرية فيثاغورث
فى المثلث القائم الزاوية مساحة المربع
المنشأ على الوتر يساوى مجموع مساحتى
المربعين المنشأين على ضلعى القائمة .أ
▲۴ب ج قائم الزاوية فى ب
وت
ضل
اذن ( ۴ج)( =2أ ب) ( + 2ب ج)2
ر
ع
ومنها نستنتج أن :
ج ضلع ب
( )1ب ج) ۴( =2ج) 2ــــ (أ ب)2
۴( = 2ج) 2ــــ ( ب ج)2
( )2أ ب)
مثال
مثال
اوجد مساحة المضلع الظلل؟
القائمة
القائمة
الرئيسية
الساب
الساب
التالى
التالى
9
9
سم2
سم2
16
16
سم2
سم2
القائمةال
القائمةال
فرعية
خروج
خروج
29.
فيثاغورثنظريةفيثاغورث
عكسنظرية
عكس
إذا كان مجموع مساحتى المربعين
المنشأين على ضلعين فى مثلث يساوى
مساحة المربع المنشأ على الضلع
الثالث كانت الزاوية المقابلة لهذا
الضلع قائمة.
أ
اذا كان:
(أ ب) ( + 2ب ) ۴( =2 )2
فان
ق(<أ ب ج ) = 90
القائمة
القائمة
الرئيسية
السابق
السابق
التالى
التالى
ج
القائمةالف
القائمةالف
رعية
رعية
ب
خروج
خروج
30.
الحدود والمقادير الجبريةالحدود والمقادير الجبرية
عامل
عددى
هو ما تكون من حاصل ضرب عاملين او اكثر فمثل ً 3 :س حد جبرى يتكون
هو 3
الحد الجبرى:
من عاملين
عامل رمزى
او جبرى هو
س
درجة الحد الجبرى :هى مجموع اسس الرموز الجبرية المكونة للحد
5 )1س حد جبرى من الدرجة الولى ,معامله , 5وعدد عوامله 2هما , 5
صف
س
ر
9 - )2س صـ 2حد جبرى من الدرجة الثالثة ,معامله – 9
لحظ ان:
2 - )3حد جبرى من الدرجة الصفرية ,حيث يمكن كتابة على صورة – 2س
الدرجة 2الصفرية
من
عدد يعتبر حد جبرى
أى
مثال
س 3-س 5س
مثال
ص3
3
س
الحد
الجبرى
معامل الحد
درجة الحد
عدد عوامل
الحد
القائمة الرئيسية
القائمة الرئيسية
السابق
السابق
التالى
التالى
القائمةالفرع
القائمةالفرع
ية
ية
خروج
خروج
31.
المقدار الجبرى :هو ما تكون من حدين جبريين اواكثر
درجة المقدار الجبرى :هى اعلى درجة للحدود
المكونة له
مثال:
المقدار الجبرى 3 :س – 7ص 5 +مكون من ثلثة
حدود وهو من الدلرجة الولى
يسمى الحد المطلق لنة ل يحتوى
العدد 5
(
ياتى :
اكمل ما
س: 1
رمزحد جبرى عدد
اى ص
علىس
5 )1
عوامله ...........ومعامله .............ودرجتة )2 ...ص حد
جبرى عدد عوامله ...........ومعامله .............
ودرجتة ............
2-)3س ص حد جبرى عدد
عوامله ...........ومعامله .............ودرجتة ......
)4المقدار الجبرى 3س 3ص 2 – 3س 2ص 1 +من
الدرجة ..............وعدد حدوده .......
القائمةالفرع
القائمة
خروج
القائمةالفرع
التالى
السابق
.............ودرجة
معامله
الرئيسيةحد جبرى
القائمة6
- )5
........................خروج
ية
التالى
السابق
الرئيسية
ية
32.
الحدود الجبريةالحدود الجبرية
المتشابهة
المتشابهة
الحدود الجبرية المتشابهة :
هى التى تتكون من نفس الرموز الجبرية
وبنفس السس
مثل :
• 3سص4,صس,سص
• 2س 2ص ,س 2ص 5 ,ص س2
الحدود الجبرية الغير متشابهة :
مثل :
• 2س 2 ,س 2 , 2س3
• س 2ص 5 ,س ص2
اختصار المقدار الجبرى :
هو وضع المقدار الجبرى فى ابسط صورة وذلك عن
طريق جمع الحدود الجبرية المتشابهة باستخدام خاصيتى
البدال والدمج
القائمة
القائمة
الرئيسية
الرئيسية
السابق
السابق
التالى
التالى
القائمةالفرعية
القائمةالفرعية
خروج
خروج
33.
اول ً :جمع وطرح الحدود الجبرية المتشابهة:ل يمكن إجراء عمليتى الجمع او الطرح إل على
الحدود المتشابهة فقط
مثال : 1اجمع :
لحل
ا
2س5,س,س4-,س
الناتج= 2س 5 +س +س 4 -( +س)
= [ ] )4 -( +1 + 5 + 2س = 4س
مثال : 2اختصر لبسط صورة :
3أ 4 +ب 5 +أ +ب – 9أ – 3ب
الناتج = ( 3أ 5 +أ – 9أ) 4 +ب +ب – 3ب)
والدمج
= -أ 2 +ب
مثال : 3اطرح :
5س 2ص من 3ص س2
لحل
ا
خاصيتى البدال
الحل
ناتج الطرح= ( 3ص س 5 ( – ) 2س 2ص)
= 3س 2ص – 5س 2ص = 2 -س 2ص
مثال:4للتفكير
زيادة 7- :س 2ص ع عن – 2س 2ص ع القائمةالفرعي
القائمة
ما
القائمةالفرعي
التالى
السابق
القائمة
ة
الرئيسية
التالى
السابق
ة
الرئيسية
خروج
خروج
34.
ثانيا :ضرب وقسمة الحدود الجبرية ضرب حد جبرى × حد جبرى
.1نضر ب المعاملت العددية ( مع مراعاة قاعدة الشارات)
.2نضرب الرموز المتشابهة وعند الضرب نجمع السس
اياتى :
كمل ما
ثال : 1ا
ا
م
تذكر أن :قاعدة
4 س 3 × 2س= .............
تذكر أن :قاعدة
الشارات
5 س × 2س 4- × 3س ص......................= 2
الشارات
• • ()+( = )+( × )+
3 - ( س 2ص...........................= 2) 3
• ()+( = )+( × )+
• ()+(= )-( × )-
قسمة حد جبرى على حد جبرى ≠صفر • ()+(= )-( × )-
• ()-(= )-( ×)+
()-(= )-
.1عند قسمة الساسات المتشابهة • (×)+
السس
نطرح
×()-(= )+
• ()-
.2القسمة على صفر ليس لها معنى()-(= )+(× )-
مثال :2اوجد خارج قسمة:
12 س 3ص 3 = 6س ص3
4س 2ص3
30 - س 4ص 15 - = 6ص4
2س 4ص2
القائمة
القائمة
الرئيسية
الرئيسية
السابق
السابق
التالى
التالى
القائمةالفرع
القائمةالفرع
ية
ية
خروج
خروج
35.
جمع وطرح المقاديرجمع وطرح المقادير
الجبرية
اول ً :جمع الجبرية
المقادير الجبرية
الطريقة الرأسية
الطريقة الفقية
نرتب المقادير تصاعدى او
.1نستخدم البدال والدمج
تنازليا حسب السس
نضع الحدود المتشابهة تحت
.2نستخدم خاصية التوزيع
بعضها
ج:
ا
د نات
ا
اوج
ااال: 1
ااااا
مثااا
3س 2 +ص 4 +ع 2 ,س +ص – 7ع
الحل
ناتج الجمع= 3س 2 +ص 4 +ع 2 +س +ص – 7ع
= ( 3س 2 +س) 2(+ص +ص) 4(+ع – 7ع)
= 5س 3 +ص – 3ع
اال: 2
اااااا
ااااا
مثا
ير
ا
للتفك
اوجد ناتج جمع 3 :س5 – 2س ص – 4ص 2 , 2س ص – ص2
5 +س 2
القائمة
القائمة
الرئيسية
الرئيسية
السابق
السابق
التالى
التالى
القائمةالفر
القائمةالفر
عية
عية
خروج
خروج
36.
المقاديرطرحالمقادير
ثانيا: :طرح
ثانيا
الجبرية
الجبرية
توجد طريقتان اطرح المقادير الجبرية
(أ ) الطريقة الفقية
الرأسية
(ب) الطريقة
ااال :1اطرح:
ااااا
ثاااا
ا
م
المقدار 7أ +ب 5 -ج من 8أ 3 +ج – 5ب
الحل
المطروح -منه8 -أ – 5ب 3 +ج
+
المطروح 7 +أ +ب – 5ج
باقى الطرح أ 6 -ب 8 +ج
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
:
ا
امثلة
)1اجمع 2 :أ 3-ب 5 +ج ,أ 8 +ب – 3ج
3 )2س4 – 2س - , 6 +س4 – 2س 7+
)3ما زيادة 3 :س7- 3س 1+عن س5 – 3س4 + 2س 3-
)4مانقص 5 :س3 + 2س – 4عن 3س7 – 2س 3-القائمةالفرع
القائمة
القائمة
الرئيسية
السابق
السابق
التالى
التالى
القائمةالفرع
ية
ية
خروج
خروج
37.
ضرب حد جبرى فىضرب حد جبرى فى
مقدار جبرى
مقدار جبرى
عند ضرب حد جبرى فى مقدار جبرى نضرب هذا الحد
فى جميع حدود المقدار
اال:1
ااااا
اااا
مثا
وجد
ا
تج:
نا
3 .1س × (2س3 -ص )
2- .2ب ×(3 – 7ب)
الحل
3 .3س× 2س – 3س × 3ص= 6س9- 2س ص
2- .4ب × 2-(– 7ب )× 3ب= 14-ب 6 +ب2
مثااااااااااال :2للتفكير
اختصر2 :س (س+ص) – س(3س – ص) ثم اوجد
القيمة العددية عندما س= , 2-ص =1-
القائمة
القائمة
الرئيسية
الرئيسية
السابق
السابق
التالى
التالى
القائمةالفرعي
القائمةالفرعي
ة
ة
خروج
خروج
38.
ضرب المقادير الجبريةضرب المقادير الجبرية
المكونة من حدين
المكونة من حدين
()1ضرب مقدار جبرى ذى حدين × مقدار اخر
ذى حدين
عند الضرب نتبع الطريقة الفقية او الرأسية
اال:1
ااااا
ثااااا
ا
م
اضرب
ا حاصل
اوجد
(2أ 3 +ب ) فى المقدار ( 3أ – 5ب)
2
2
ا
الحل
( 2أ 3+ب ) × (3أ – 5ب)
= 2أ(3أ – 5ب ) 3 +ب ( 3أ – 5ب)
= 6أ 10 -أ ب 9 +ب أ – 15ب 6 =2أ -أ ب 15 -
ب2
تدريب :اوجد ناتج :
(2أ +ب ) ( 3أ – ب)
القائمة
القائمة
الرئيسية
الرئيسية
السابق
السابق
التالى
التالى
القائمةالفرعي
القائمةالفرعي
ة
ة
خروج
خروج
39.
( )2الضرب بمجرد النظر :ا :اوجد
ااال
ااااا
مثااا
صل
حا
( 3س2( )4 +س )1+
:
ا
ضرب
ا
ل
الح
الول ×
الول6س2
2س=)1 +
الوسطين+
الطرفين
+
11س
الثانى×ال
ثانى 4 +
(3س( )4 +
تدريب :اكمل ماياتى:
4( .1س -ص) ( 3س 2-ص) = .........ــــ ...........
..............+
( .2س2 + 2ص2 ( ) 2س– 2
7ص..............................=) 2
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــ
( )3مجموع حدين × الفرق بينهما = مربع الحد الول ـــــ
مربع الحد الثانى
مثاااااااال :اوجد حاصل الضرب:
2 ( .3س2 ( )3 +س 4 = )3-س 2ـــــ 9
القائمةالفر
التالى
السابق
القائمة الرئيسية
القائمةالفر
عية
التالى
السابق
......................
الرئيسيةس 3 ( )1 +س= )1 -
القائمة3 ( .4
عية
خروج
خروج
40.
( )4مربع مقدار مكون من مجموع او فرق حدين =مربع الول × 2 ±الول×
الثانى +مربع الثانى
مثاااااااااال :اوجد ناتج:
2 ( .1س 4 = 2)3 +س 12 + 2س 9 +
5 ( .2س – 4ص ) 25 = 2س 40 – 2س ص 16 +ص2
3 ( .3أ – ................................= 2)7
3 ( .4س +ص)............................= 2
تدريب :اختصر لبسط صورة :
• ( 2أ – ب) ( 4 – 2أ +ب ) ( أ – ب)
القائمة
القائمة
الرئيسية
السابق
السابق
التالى
التالى
القائمةالفرعي
القائمةالفرعي
ة
ة
خروج
خروج
41.
قسمة مقدار جبرى على حدقسمة مقدار جبرى على حد
جبرى
جبرى
عند قسمة مقدار جبرى على حد جبرى نقسم كل حد من
حدود المقدار الجبرى على ذلك الحد:
مثااااااااال :اوجد خارج قسمة :
6 .1أ 12 +ب على 6
الحل
6أ 12 +ب = أ 2 +ب
6
6
24( .2س 3ص12 + 2س 2ص ) 3على 6س
ص.......................=3
30 .3س 2ص 15 – 3س 3ص 5 + 4س 2ص ) 2على 5س2
ص................=2
تدريب:
ص– 3
إذا كان 2س2ص هو احد عاملى المقدار 6س3
القائمةالفرعي
القائمةالفرعي
التالى
السابق
القائمة الرئيسية
ة
الخر؟
العامل
فما
2
ص
القائمة2س2
التالى
السابق
الرئيسية
ة
خروج
خروج
42.
التحليل باخراج العاملالتحليل باخراج العامل
المشترك
صورة حاصل ضرب
• تحليل العدد هو جعلة على
المشترك
عاملين او اكثر
• تحليل المقدار الجبرى هو ان نضعه على صورة
حاصل ضرب عاملين او اكثر
قاعدة :أ ب ±أج = أ ( ب ±ج) = ( ب ±ج) أ
ل :1حلل
ااااا
ااااا
مثااا
8 )1س 12 + 3س4
ى:
ا
مايات
الحل
العامل المشترك ( ع .م .أ) هو 4س3
= 4س3 + 2 ( 3س)
24 )2س 3ص – 16س 2ص................................= 4
2 )3أ ( س +ص)ـ 3 +ب ( س+ص)=.............................
ااوجد
تحليل
ا
ال
دام
ا
:2باستخ
ا
ااال
اااااا
ااااا
مثا
3700 = 100 × 37 = ) 81+ 19 (37 = 81 × 37 + 19 × 37 .1
....................................................= 54 × 46 + 2)46 ( .2
................................. = 28 × 49 – 28 × 9 + 2)28(× 5 .3
القائمة
القائمة
الرئيسية
السابق
السابق
التالى
التالى
القائمةالفرعي
القائمةالفرعي
ة
ة
اتج :
ا
ن
خروج
خروج
43.
الوحدة الرابعة :قراءةالوحدة الرابعة :قراءة
وتفسير البيانات
البيانات
اولً :العمدةوتفسير
البيانية :
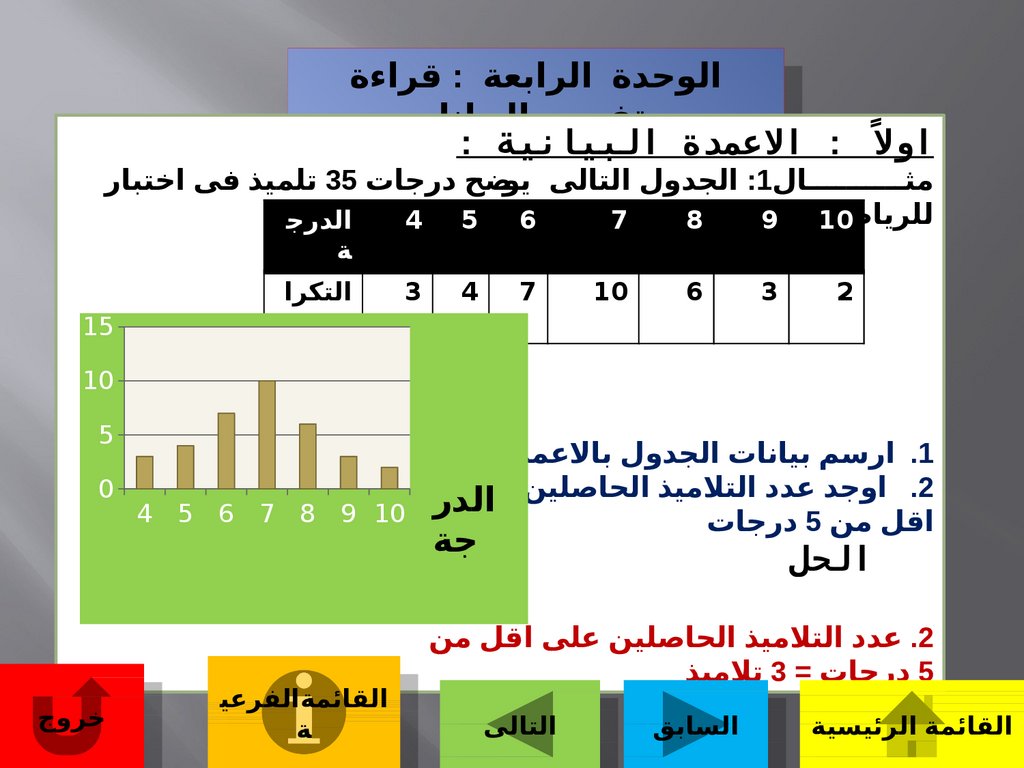
مثــــــــــال :1الجدول التالى يوـضح درجات 35تلميذ فى اختبار
درجات
الدرج
4 5
6
7
من 810
للرياضيات 9
10
ة
2
3
6
10
7
4
3
التكرا
ر
15
10
5
.1ارسم بيانات الجدول بالعمدة البيانية
.2اوجد عدد التلميذ الحاصلين على
0
الدر
4 5 6 7 8 9 10
اقل من 5درجات
جة
الحل
.2عدد التلميذ الحاصلين على اقل من
5درجات = 3تلميذ
القائمة الرئيسية
القائمة الرئيسية
السابق
السابق
التالى
التالى
القائمةالفرعي
القائمةالفرعي
ة
ة
خروج
خروج
44.
ثانيا :الخط البانىثانيا :الخط البانى
المنكسر
المنكسر
يبين درجات طالب فى امتحان
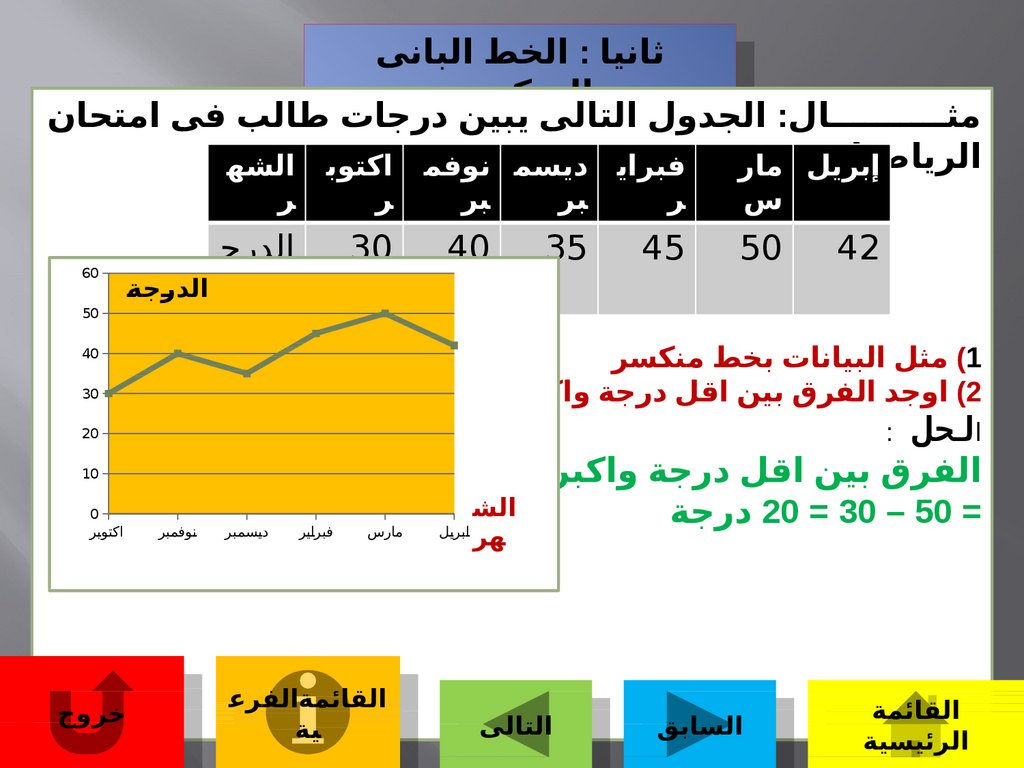
مثــــــــــال :الجدول التالى
شهور
إبريلفى
الرياضيات
ديسم نوفم اكتوب الشه
مارستةفبراي
42
س
ر
بر
بر
ر
ر
50
45
35
40
30
الدرج
ة
الدرـجةـ
50
)1مثل البيانات بخط منكسر
)2اوجد الفرق بين اقل درجة واكبر درجة
الحل
الفرق بين اقل درجة واكبر درجة
الش
= 20 = 30 – 50درجة
ابببريبل
40
30
:
هـر
القائمة
القائمة
الرئيسية
الرئيسية
السابق
السابق
التالى
التالى
60
20
10
مارس
فبرابيبر
ديبسمببر
القائمةالفرع
القائمةالفرع
ية
ية
نبوفمببر
0
اكتوببر
خروج
خروج
45.
ثالثا :القطاعات الدائريةثالثا :القطاعات الدائرية
تعتمد هذه الطريقة على ان الدئرة تنقسم الى 360
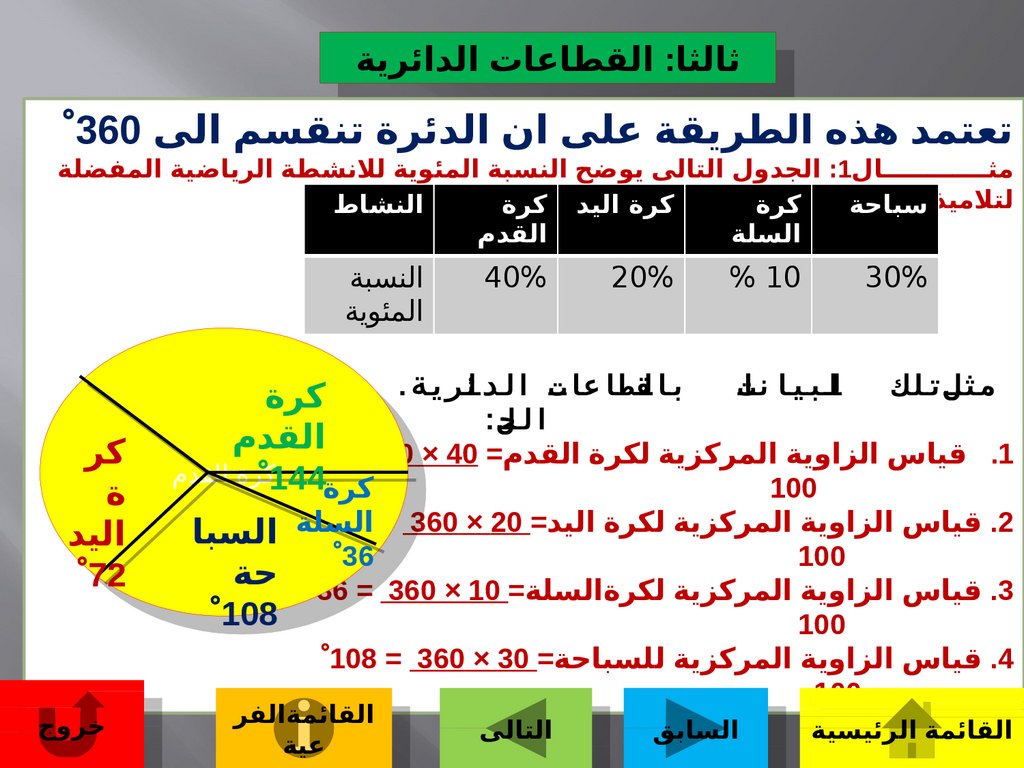
مثــــــــــــال :1الجدول التالى يوضح النسبة المئوية للنشطة الرياضية المفضلة
المدارس:
لتلميذ احدى
النشاط
كرة اليد كرة
كرة
سباحة
القدم
السلة
30%
% 10
20%
40%
النسبة
المئوية
ئرية.
ا الدا
قطاعات
ا
بال
لبيانا
ت
ا
اتلك
مثل
كرة
ل:
ا
الح
القدم
.1قياس الزاوية المركزية لكرة القدم= 144 = 360 × 40
144كرة القدم
100
كرة كرة القدم
.2قياس الزاوية المركزية لكرة اليد= 72 = 360 × 20
السلة السبا
100
36
.3قياس الزاوية المركزية لكرةالسلة= 36 = 360 × 10حة
108
100
كر
ة
اليد
72
.4قياس الزاوية المركزية للسباحة= 108 = 360 × 30
100
القائمة الرئيسية
القائمة الرئيسية
السابق
السابق
التالى
التالى
القائمةالفر
القائمةالفر
عية
خروج
خروج
46.
البياناتتمثيلالبيانات
تمثيل
اولً :المنوال :
هو القيمة الكثر تكرار وشيوعا فى المجموعة
مثاااال :1اوجد المنوال لمجموعة القيم التية:
الحل :المنوال هو 7
4 , 7 , 7 , 5 ,3 )1
6 , 4 , 5 , 6 , 7 , 5 , 6 )2الحل :المنوال هو 6
4 , 5 , 6 , 7 , 5 , 6 )3الحل :المنوال هو 6 , 5
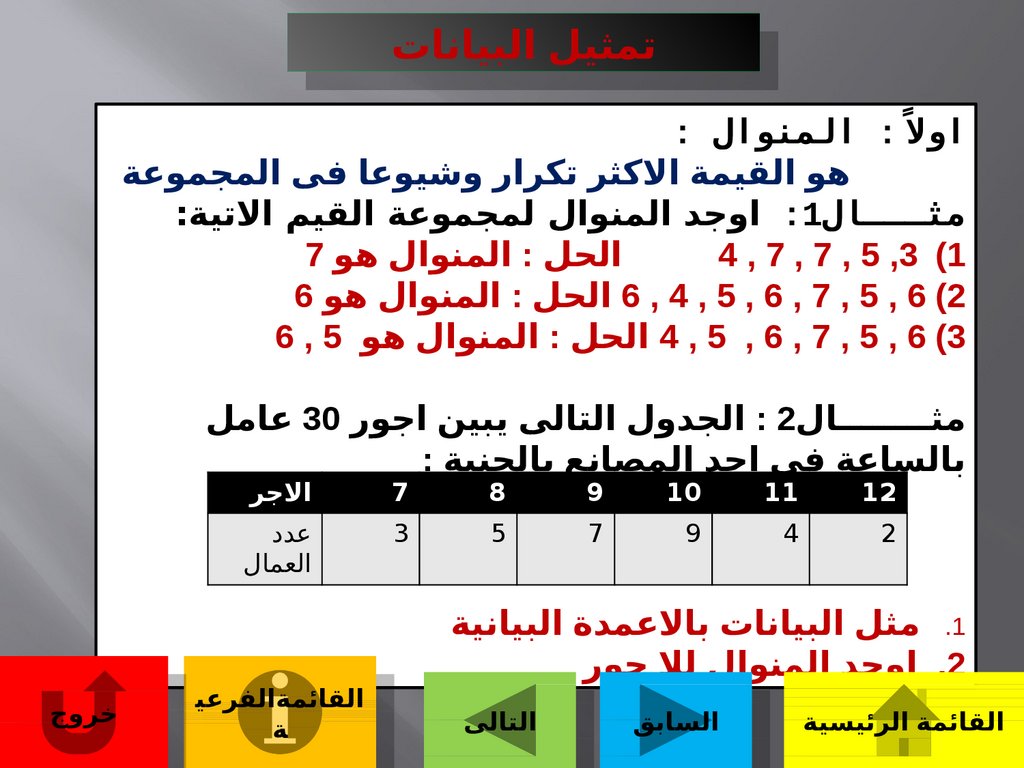
مثــــــــال : 2الجدول التالى يبين اجور 30عامل
بالساعة فى احد المصانع بالجنية :
12
11
10
9
8
7
الجر
2
4
9
7
5
3
عدد
العمال
.1مثل البيانات بالعمدة البيانية
.2اوجد المنوال لل جور
القائمة الرئيسية
القائمة الرئيسية
السابق
السابق
التالى
التالى
القائمةالفرعي
القائمةالفرعي
ة
ة
خروج
خروج
47.
ثانيا :الوسيط :هو القيمة التى تقسم المجموعة الى شطرين متساوين بعد
ترتيب المجموعة
رلمجموعة القيم :
مثــــــــــ1ــــــــــال :اوجد الوسيط
ان::
تذكران
تذكر
القيم
10 , 15 , 11 , 17 , 12
عددالقيم
كانعدد
اذاكان
اذا
فردى
فردى
الحل
ن11++
=
الوسيط
ترتيب
ترتيب الوسيط= ن
نرتب القيم ترتيب تصاعدى او تنازليا
22
القيم
17 , 15 , 12 , 11 , 10
عددالقيم
كانعدد
اذاكان
اذا
زوجى
زوجى
12
اذن الوسيط=
ترتيب الوسيط الثالث
ن ,,
الوسيط==ن
ترتيبالوسيط
ترتيب
ن22+
ن+
22
22
مثـــــــ2ــــــــال :اوجد الوسيط للقيم التية , 3 , 7 , 5 :
9,4,6
الحل
نرتب القيم 9, 7 , 6 , 5 , 4 , 3 :
الوسيط = 5.5 = 6 +5
عدد القيم زوجى
القائمةالفرع
التالى 2
خروج
القائمةالفرع
السابق
القائمة الرئيسية
القائمة الرئيسية
السابق
التالى
ية
ية
خروج
48.
ثالثا :الوسط الحسابى:هو القيمه التى تتمركز عندها جميع قيم التوزيع
الوسط الحسابى لمجموعه قيم= مجموعه القيم
عدد القيم
اااا1
ااااا
مثا
3 , 10 , 7
ال :اوجد الوسط الحسابى للقيم , 2 , 8
اااا
اااااا
ا
لحل
ا
الوسط الحسابى = مجموعه القيم = 30 = 3 + 10 +7 + 2 +8
=6
5
5
عدد القيم
تدريب :1اذا كان السط الحسابى لل عداد , 7 , 3س 6, 9,هو 7فان س
الدرجة
6
9
12
15 .......................
17
=
عدد
4
7
5
8
6
الطلب
امتحان
تدريب :2الجدول التى يبين توزيع درجات 30طالبا فى
الرياضيات
القائمة
الحسابى
اوجد :
القائمة )1السط السابق
الرئيسية
السابق
الرئيسية )2الوسيط
القائمةالفرعي
الدرجات
لهذة
القائمةالفرعي
التالى
ة
التالى
ة
خروج
خروج
49.
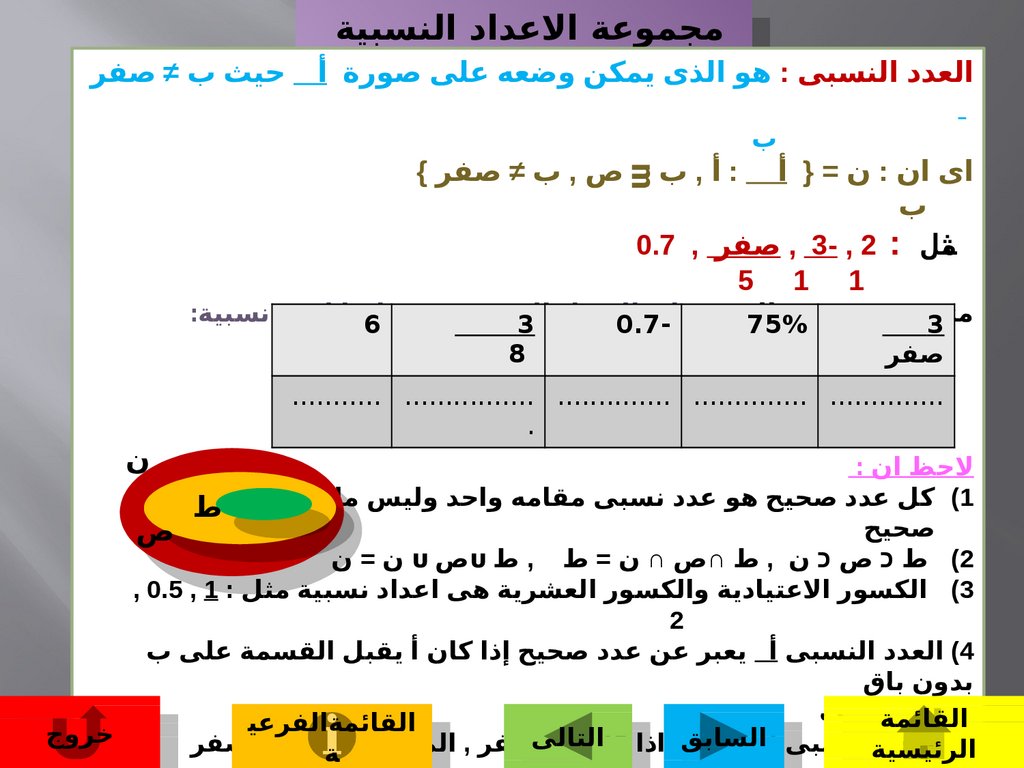
مجموعة العداد النسبيةمجموعة العداد النسبية
العدد النسبى :هو الذى يمكن ن
وضعه على صورة أ حيث ب ≠ صفر
ن
ب
:أ ,ب ᴟص ,ب ≠ صفر }
اى ان :ن = { أ
ب
ثل , 3- , 2 :صفر 0.7 ,
ا
م
5 1 1
وايها ليس نسبية:
اى
مثـــ1
التية نسبية 6
العداد 3
0.7
ـــــــــــــــال :بين -
75%
3
صفر
8
........... ................ .............. .............. ..............
.
ن
لحظ ان :
نسبى عدد
)1كل عدد صحيح هو عدد نسبى مقامه واحد وليس مل عدد
ط
صحيح
ص
)2ط ص ن ,ط ∩ص ∩ ن = ط ,ط ᴜص ᴜن = ن
)3الكسور العتيادية والكسور العشرية هى اعداد نسبية مثل , 0.5 , 1 :
2
)4العدد النسبى أ يعبر عن عدد صحيح إذا كان أ يقبل القسمة على ب
بدون باق
القائمة ب
القائمةالفرعي
خروج
القائمة
التالى
السابق
القائمةالفرعي
يساوى صفر
صفر اذا كان أ
الرئيسيةالنسبى أ =
العدد
)5
خروج
التالى= صفر ,المقام ل ة
السابق
50.
)6العدد النسبى أ يكون موجبا اذا كان أ × ب > صفرب
)7العدد النسبى أ يكون سالبا اذا كان أ × ب < صفر
ب
ثال :بين اى العداد التية نسبى موجب وايها نسبى سالب :
ا
م
2 , 3 , 2 , 7- , 11- , 3 , 2
6 4- 9- 4ب2
3
8
7
تمثيل العداد النسبية على خط العداد
مثاااااااااااال :مثل على خط العداد العدد النسبى
3
4
أ
حل
ا
ا ل
1 2 3
3عدد نسبى موجب يقع بين صفر 1 1 ,
4
4 4 4
نقسم المسافة بين العددين الى اربع اجزاء متساوية
اذن النقطة أ تمثل العدد 3
4
تدريب :مثل على خط العداد العدد النسبى 2-
3
القائمة
القائمة
الرئيسية
السابق
السابق
التالى
التالى
القائمةالفرعية
القائمةالفرعية
صف
ر
خروج
خروج
51.
الشكال المختلفة للعدد النسبىالشكال المختلفة للعدد النسبى
)1كتابة العدد النسبى كعدد عشرى منته :
نجعل مقام العدد النسبى 10او مضاعفتها
• مثــــال :اكتب كل من العداد النسبية التية على
صورة عدد عشرى منته :
9 , 3, 1
5
4 4
الحل
0.25 = 1 )1
4
0.75 = 25 ×3 = 3 )2
25 ×4 4
1.8 = 2 × 9 = 9 )3
2× 5 5
القائمة
القائمة
الرئيسية
الرئيسية
السابق
السابق
التالى
التالى
القائمةالفر
القائمةالفر
عية
عية
خروج
خروج
52.
)2كتابة العدد النسبى على صورة نسبة مئوية :وذلك جعل مقام العدد النسبى = 100
ل:1
اااا
ااااا
مثااا
اكتب كل من العداد النسبية التية على صورة
نسبة مئوية :
9, 3, 1
5
4
4
الحل
25% = 25 = 25 × 1 = 1 )1
100 25
4 4
.............................. = 3 )2
4
.................................= 9 )3
5
القائمة الرئيسية
القائمة الرئيسية
السابق
السابق
التالى
التالى
القائمةالفر
القائمةالفر
عية
عية
خروج
خروج
53.
)3كتابة العدد النسبى كعدد عشرى دائرى غيرمنته:
ر ان :
ا
تذك
وضع نقطة فوق الرقم الدائر الول والرقم الدائر الخير معناه ان
الرقمين وما بينهما دائر
ال :1اكتب العداد التية فى صورة عدد
اااااا
ااااا
مثا
عشرى دائرى :
2 , 2
11 3
الحل
0.6 = 0.66666000 = 2دائر
3
0.18 = 0.18181818 = 2دائر
11
مثــــــــــــــال : 2اكتب العدد النسبى 6بجميع صوره
القائمةالفرع
القائمة
خروج
القائمةالفرع
المختلفة
التالى
السابق
القائمة
ية
خروج
الرئيسية
الرئيسية
السابق
التالى
ية
54.
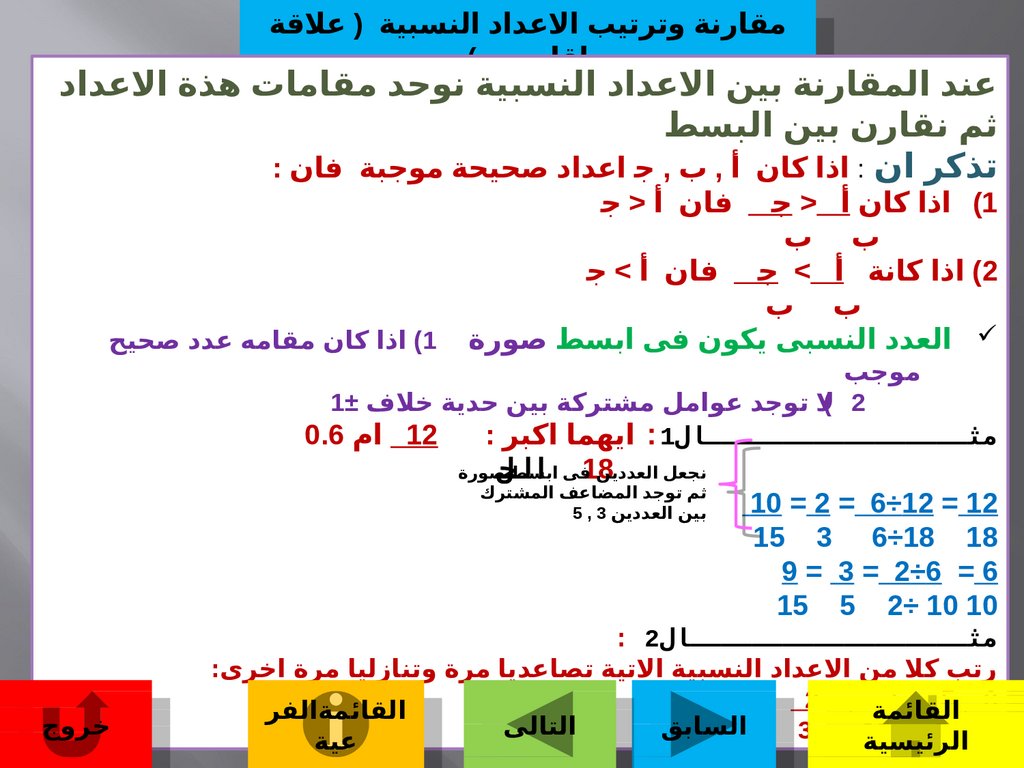
مقارنة وترتيب العداد النسبية ( علقةمقارنة وترتيب العداد النسبية ( علقة
اقل من )
المقارنة بين العداداقل من )
النسبية نوحد مقامات
عند
ثم نقارن بين البسط
تذكر ان :اذا كان أ ,ب ,ج اعداد صحيحة موجبة فان :
)1اذا كان أ < ج
ب ب
)2اذا كانة أ > ج فان أ > ج
ب ب
العدد النسبى يكون فى ابسط صورة
هذة العداد
فان أ < ج
)1اذا كان مقامه عدد صحيح
موجب
) 2ل توجد عوامل مشتركة بين حدية خلف 1±
12ام 0.6
مثاااااااااااااااااال :1ايهما اكبر :
18
10 = 2 = 6÷12 = 12
15 3 6÷18 18
9 = 3 = 2 ÷6 = 6
15 5 2÷ 10 10
ا
ل
الح
نجعل العددين فى ابسط صورة
ثم توجد المضاعف المشترك
بين العددين 5 , 3
مثااااااااااااااااااال: 2
رتب كل من العداد النسبية التية تصاعديا مرة وتنازليا مرة اخرى:
القائمة 2 ,
7, 5, 3
القائمةالفر
التالى
السابق
القائمةالفر
القائمة
3
12
6 4
عية
الرئيسية
التالى
السابق
عية
الرئيسية
خروج
خروج
55.
كثاقة العداد النسبيةكثاقة العداد النسبية
بين اى عددين نسبيين يوجد عدد ل نهائى من العداد
النسبية المحصورة بينها
ال :1اوجد عدد نسبى يقع بين 3 , 1
اااا
ثااااا
ا
م
4 2
الحل
4= 1× 1= 2× 1= 1
8 2 4
2 2 2
6= 2× 3= 3
8
2 4 4
اذن العدد النسبي المحصور بين 3 , 1هو 5
8
4 2
مثااااااااااااال : 2اوجد ثلثة اعداد نسبية بين 0.4 , 1 :
3
مثاااااااااااال :3اوجد اربعة اعداد نسبية تقع بين 3 , 3
بحيث يكون واحد منهما صحيحا
الرئيسية4
القائمة 2
الرئيسية
القائمة
السابق
السابق
التالى
التالى
القائمةالفر
القائمةالفر
عية
عية
خروج
خروج
56.
العمليات على العدادالعمليات على العداد
النسبية
اولً :عملية الجمع:
النسبية
• اذا كان المقامان متساويان نضع المقام كما هو ونجمع
البسطين
أ +ج=أ+ج
قاعدة
ب ب ب
نوحد المقامات اذا كانت المقامات مختلفة
أ +ج = أ ×ء +ج×ب
قاعدة
بء
ب ء
اال :اوجد ناتج جمع:
اااا 1ااااا
مثا
3 )1
5
3 )2
5
4 = 3+1 = 1 +
5
5
5
31 = 21+10 = 5×2 + 7×3 = 2 +
35
35
35
7
تدريب :احسب قيمة ماياتى:
)10.17-(+ 4.2 )1
9.67 +2.75
- )2
القائمة
القائمة
الرئيسية
السابق
السابق
التالى
التالى
القائمةالفر
القائمةالفر
عية
عية
خروج
خروج
57.
خواص عملية الجمع فى نخواص عملية الجمع فى ن
)1النغلق :اى ان حاصل جمع اى عددين نسبيين يساوى
عدد نسبى
7 = 3 +4
فمثل=3 +2 :
10
10
10 5
)2البدال :اى ان العدد النسبى :أ +ج = ج +أ
ب ب ب ب
)3الدمج :اى ان تبديل مكان القوس ل يغير قيمة الناتج
فمثل ً2- =1 + 3 - = 1 + ) 2 + 5- ( :
3 3
3 3
3
3
= 2- =3 + 5 - = ) 2 + 1 (+ 5-
3 3
3
3
3
3
)4المحايد الجمعى :الصفر هو المحايد اـلجمعى لعملية
الجمع
فمثل ً + 10 :صفر = صفر 10 = 10 +
3
3
3
)5المعكوس الجمعى :لكل عدد معكوس جمعى هو نفس العدد باشارة
القائمةالفرع
صفر
مخالفة ما عدا الصفر معكوسه الجمعى هو نفس العدد
القائمة
خروج
القائمةالفرع
التالى
السابق
القائمة
ية
خروج
الرئيسية
التالى
السابق
ية
58.
ثانيا :ضرب العداد النسبةثانيا :ضرب العداد النسبة
)1اذا كان أ ,ج عددين نسبيين فان أ × ج = أ × ج
ب ء ب×ء
ب ء
)2اذا كان أ ,ج عددين نسبيين فان أ × ج = أ × ج
ب ب ب2
ب ب
مثااااااااااال :
اوجد ناتج :
21 =3 ×7 )1
40 5 8
120- =15 ×8- )2
36
4 9
خوـاص عملية الضرب :
)2
)3
)4
)5
)6
)7
)8
النغلق
البدال
الدمج او التجميع
المحايد الضربى هو الواحد الصحيح
المعكوس الضربى واكن الصفر ليس له معكوس ضربى
حاصل ضرب اى عدد نسبى× معكوسه الضربى = 1
عملية الضرب تتوزع على عملية الجمع
القائمة الرئيسية
القائمة الرئيسية
السابق
السابق
التالى
التالى
القائمةالفر
القائمةالفر
عية
خروج
خروج
59.
ثالثا :عمليتى الطرحثالثا :عمليتى الطرح
والقسمة
والقسمةعددين نسبيين فان ( أ -
)3طرح العداد النسبية :اذا كان أ ,ج
ج )=أ
-( +ج )
ب
ء
ب
ء
ب
ء
ل :اوجد ناتج :
مثاا
4- = 7- + 3 = 7 - 3 )1
9
9 9 9
9
11 = )10-( + 21 = ) 2- ( + 3 = 2 - 3 )2
35
35
7
5 7
5
لحظ ان :
)1الطرح يحقق خاصية النغلق فقط
)2الطرح فى ن ليس ابدالى وليس ت دامجة
)3الطرح فى ن ل يوجد بة عنصر محايد ول معكوس
جمعى
تدريب :اوجد ناتج:
القائمة ) 1 - 4 ( - ) 3 +
2 ( )2
التالى
السابق
القائمة
الرئيسية 7السابق7
3التالى
القائمةالفر
القائمةالفر
عية
عية
خروج
خروج
60.
)4عملية القسمة :اذا كان أ ,ج عددين نسبيين فان أ ÷ ج = أ × ء
بج
ب ء ب ج
ب ء
مثــــــــــال :اوجد ناتج :
12 = 2× 6 = 3 ÷ 6 )1
15
3
5
2
5
................ = ) 4- ( ÷ 14- )2
7
................... = )7 -( ÷ 3 )3
8
خواص القسمة :
)2
)3
)4
)5
)6
= أء
القسمة تحقق النغلق ما عدا القسمة على الصفر
ليست ابدالية
ليست دامجة
ل يوجد عدد محيد
ل يوجد معكوس
تدريب :اختصر لبسط صورة
( ) 2 ÷ 4- ( ) 3 ÷ 2 2
3
4
5
القائمة
القائمة
الرئيسية
السابق
السابق
التالى
التالى
القائمةالفر
القائمةالفر
عية
خروج
خروج
61.
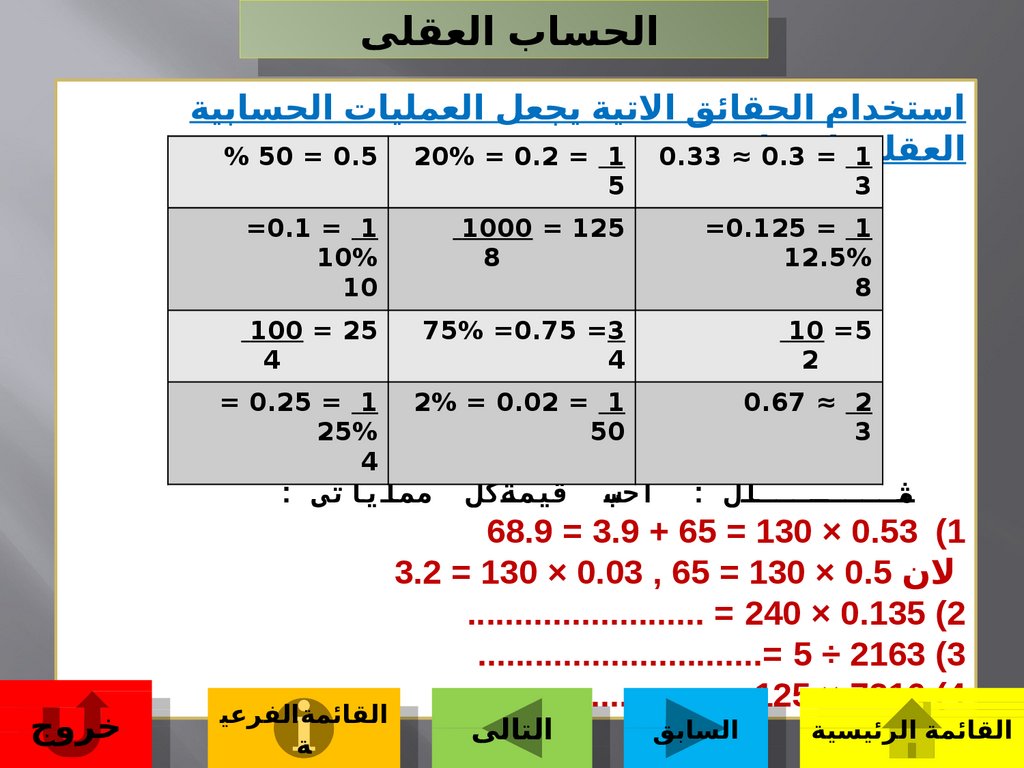
العقلىالحساب
الحساب العقلى
استخدام الحقائق التية يجعل العمليات الحسابية
اسهل≈% 50 = 0.5 20% = 0.2 = 1 0.33 :
العقلية = 0.3
1
3
5
=0.125 = 1
12.5%
8
1000 = 125
8
=0.1 = 1
10%
10
10 =5
2
75% =0.75 =3
4
100 = 25
4
0.67 ≈ 2
3
2% = 0.02 = 1
50
= 0.25 = 1
25%
4
ال :
ااااا
ثااااا
ا
م
ا
ب
احس
اكل
قيمة
اياتى :
مما
68.9 = 3.9 + 65 = 130 × 0.53 )1
لن 3.2 = 130 × 0.03 , 65 = 130 × 0.5
......................... = 240 × 0.135 )2
..............................= 5 ÷ 2163 )3
........................ = 125 × 7216 )4
القائمةالفرعي
القائمة الرئيسية
القائمة الرئيسية
السابق
السابق
التالى
التالى
القائمةالفرعي
ة
خروج
خروج














































 mathematics
mathematics

