Similar presentations:
مهارات التعامل مع اختبار القدرات
1.
مهارات التعامل مع اختبار القدراتإعداد
محمود بن معتوق النمري
المشرف على قادر
تقديم
د /احمد بن علي الزيلعي الشريف
أمين مصادر التعلم
2.
فنيات التعامل مع اسئلة الكمي2
3.
إرشادات سريعة للتعامل مع اسئلة الكمي التركيز مطلوب
استفد من كل معطى في السؤال
ً
اسال نفسك دوما ما المطلوب ؟
ال تفصل في الحل
من افضل الطرق الستثمار الوقت تجربة االختيارات إذا لم تتضح فكرة الحل
استبعد متى ما استطعت ذلك
االرقام في االختبار باللغة العربية .انتبه ال تحل اثناء
استعدادك وتدربك باالرقام االنجليزية .
3
4.
اختبار القدرات في الجزء الكمي يعتمد اعتماد كبير على اساسيات الرياضياتونصيحتي لك من اجل ان تحصل على درجة عالية في االختبار
تجود نفسك في هذه االساسيات
ان ِّ
من اك ثر االساسيات التي تتكرر في االختبار وتحتاج لها
/1جدول الضرب ( اسرار الضرب )
/2الكسور
/3الجذور
/4االسس
/5االعداد العشرية
/6النسبة المئوية
/7التناسب
/8المعدل (الوسط الحسابي)
/9قياس الزوايا
/10االشكال ( المثلث – الدائرة – المربع – المستطيل )
/11الرسوم البيانية
5.
افكار لحل اسئلة الجزء الكميالفكرة / 1المقدار الواحد
تنبيهات :
/1مفتاح الحل بهذه الطريقة هو ان يكون المعطى في السؤال عدة اشياء
/2اول خطوات الحل هو إجابة السؤال :ما قيمة المقدار الواحد ؟
ً
/3ثاني الخطوات نوجد قيمة المقدار الواحد دائما عن طريق القسمة
/4نوجد المطلوب في السؤال
6.
افكار لحل اسئلة الجزء الكميالفكرة / 1المقدار الواحد
تمرين (: )1
إذا كانت تكلفة 5صناديق تفاح 120لاير .فكم تكون تكلفة 7صناديق من التفاح ؟
د 175 .لاير
ج 168 .لاير
ب 72 .لاير
ا 24 .لاير
7.
افكار لحل اسئلة الجزء الكميالفكرة / 1المقدار الواحد
تمرين (: )2
في الشكل لدينا سبعة مربعات متطابقة فإذا كان مجموع مساحتها 112سم2
فإن محيط الشكل يساوي :
د64 .سم
ج32 .سم
ب4 .سم
ا16 .سم
8.
افكار لحل اسئلة الجزء الكميالفكرة / 2جزء من عدد
تنبيهات مهمة للحل:
/1مفتاح الحل بهذه الطريقة يوجد في السؤال وهو (من ) قبلها عدد وبعدها عدد معلوم او مجهول فيكون ما قبلها الجزء وما بعدها الكل
ً /2
دائما نعوض عن رمز %ب القسمة على ) 100 ÷ ( 100
مثال :إليجاد جزء من اي عدد :نضرب الجزء في العدد على النحو التالي :
نستبدل حرف ( من ) بعالمة الضرب (× ) ونضرب ما قبلها فيما بعدها
ً
مثال %5من 30
30× %5
15 5
5
= ( 1.5حذفنا األصفار التي في البسط مع األصفار التي في المقام )
×= 3 × = 30
=
10 10
100
/3إذا كنا نتعامل مع العدد 100ا ي ان العدد 100هو العدد الكلي الذي جاء بعد حرف ( من ) ففي هذه الحالة نوجد %10و %25و %60
مباشرة بحذف عالمة النسبة المئوية مع العدد ، 100مثال %5من 100نحذف ( %مع ) 100ويتبقى العدد ( ) 5هو الحل ،وهكذا .
/4مهم إذا اختلف العدد الكلي عن 100فنضرب النسبة المئوية في العدد الكلي عن طريق جزء من عدد كما في التنبيه رقم 1و 2السابقة مثال
20
×18 = 6 × 2 = 60
%20 :من = 60 × % 20 = 60
ً 100
/5العدد الذي ياتي بعد من دائما عدد مك تمل %100
9.
افكار لحل اسئلة الجزء الكميالفكرة / 2جزء من عدد
امثلة /
20
1
× = = 20
4
4
18
1
× 6 = = 18
3
3
( )1مقدار الربع من = 20
( )2قيمة ثلث من = 18
ُ
ْ
1
( )3خمس الخمسين =
أي خمس من خمسين = × = 50
5
80
( )4قيمة %80من = 60
48= 6 × 8 = 60
×
100
5
50
=
5
10
( حذفنا األصفار التي
في البسط مع األصفار
التي في المقام )
10.
افكار لحل اسئلة الجزء الكميالفكرة / 2جزء من عدد
تمرين (: )3
إذا كان سعر دراجة خفض بنسبة %25ثم خفض السعر الجديد بنسبة %20فإن
ً
التخفيضان معا يساويان :
ج%35 .
ب%40 .
ا%45 .
د%30 .
11.
افكار لحل اسئلة الجزء الكميالفكرة / 3تحويل العدد العشري لكسر والعكس
امثلة /
= 0,2
= 4,03
= %3
12.
افكار لحل اسئلة الجزء الكميالفكرة / 3تحويل العدد العشري لكسر والعكس
تمرين (: )4
ما قيمة %5من : 0,02
ب0.001 .
ا0.0001 .
ج0.01 .
د0.1 .
13.
افكار لحل اسئلة الجزء الكميالفكرة / 3تحويل العدد العشري لكسر والعكس
تمرين (: )5
: %
ا0,75 .
ب0,075 .
ج0,0075 .
د0,00075 .
14.
افكار لحل اسئلة الجزء الكميالفكرة / 4التدرج المنتظم
تنبيهات :
/1مفتاح الحل بهذه الطريقة ان يحتوي السؤال على عددين احدهما ك تب
آ
عدد صحيح واالخر ك تب %
/2العددين إما يمثلون شيء واحد او العددين يمثلون شيء مختلف
/3إذا كان العددين يمثلون شيء واحد نضع العددين امام بعض
كخطوة اولى ثم نكمل باقي الخطوات
/4إذا كان العددين مختلفين نضع العدد الصحيح وامامه
مكملة النسبة %ثم نكمل باقي الخطوات
15.
افكار لحل اسئلة الجزء الكميالفكرة / 4التدرج المنتظم
خطوات الحل :
/1نضع العدد الصحيح وامامه %او مكملة %
/2نقسم العددين على معامل ( %نحصل على المقدار الواحد )
/3نتاكد من المطلوب في السؤال ونوجده .
16.
افكار لحل اسئلة الجزء الكميالفكرة / 4التدرج المنتظم
تمرين (: )6
العدد 27يمثل %9من العدد :
ب240 .
ا210 .
300
ج270 .
د.
17.
افكار لحل اسئلة الجزء الكميالفكرة / 4التدرج المنتظم
تمرين (: )7
صرف فهد من راتبه %70وبقي 1500فكم راتبه :
ج4000 .
ب3500 .
ا1500 .
د5000 .
18.
افكار لحل اسئلة الجزء الكميالفكرة / 4التدرج المنتظم
تمرين (: )8
تبرع رجل بمبلغ مالي قدره %10من 8000فما مقدار التبرع :
د8000 .
ج800 .
ب90 .
ا80 .
19.
افكار لحل اسئلة الجزء الكميالفكرة / 5التناسب
20.
افكار لحل اسئلة الجزء الكميالفكرة / 5التناسب
تمرين (: )9
اخذ 6عمال لعمل سجادة يدوية 30يوم .فكم يلزم عدد من العمال لعمل نفس السجادة
في 20يوم
ا4 .
ب6 .
ج9 .
د11 .
21.
افكار لحل اسئلة الجزء الكميالفكرة / 5التناسب
تمرين (: )10
قرا خالد ك تاب من صفحة 116إلى صفحة 120في 10دقائق فكم ساعة يستغرقها إذا كان
الك تاب 600صفحة ؟
ا25 .
ب20 .
ج10 .
د15 .
22.
افكار لحل اسئلة الجزء الكميالفكرة / 6التناسب المركب ( الضرب التبادلي)
خطوات الحل :
آ
ً
ً
/1نرتب المتغيرات نضع اوال الفاعل واخرا الزمن وبينهما المفعول به
/2نوزع االرقام حسب معطيات السؤال
/3نهتم بالمجهول س وما يضرب في المجهول س نضعه في المقام
وباقي االعداد في البسط
23.
افكار لحل اسئلة الجزء الكميالفكرة / 6التناسب المركب
تمرين (: )11
إذا كانت ثالثة قطط تستغرق ثالث دقائق في قتل ثالث فئران ،فكم دقيقة تستغرق مئة
قطة في قتل مئة فار ؟
ا100 .
ب3 .
ج9 .
د27 .
24.
افكار لحل اسئلة الجزء الكميالفكرة / 6التناسب المركب
تمرين (: )12
ً
يقطع ثالثة عمال ثالثة الواح خشبية إلى الواح متساوية في ثالث دقائق .كم لوحا يقطعها
9عمال في اربع ساعات ؟
ا9 .
ب3 .
ج8 .
د720 .
25.
افكار لحل اسئلة الجزء الكميالفكرة / 7المتغيرات
تنبيهات :
/1نتنبه لشروط السؤال
/2نهتم بالمطلوب في السؤال
/3لو احتوى السؤال على متغير واحد فقط افضل حل هو التعويض باالختيارات
26.
افكار لحل اسئلة الجزء الكميالفكرة / 7المتغيرات
تمرين (: )13
آ
ً
ً
ً
ً
َ
إذا كان س عددا فرديا ،و ص عددا زوجيا فاي من االعداد االتية فردي :
ا 2 .س +ص
ب .س 2 +ص
ج .س ص
د .س2ص
27.
افكار لحل اسئلة الجزء الكميالفكرة / 7المتغيرات
تمرين (: )14
28.
افكار لحل اسئلة الجزء الكميالفكرة / 8تحويل الكسر ل %
تنبيهات :
ً
/1نركز على مقام الكسر االول ونجعله مساويا ل 100ليساوي %
/2الكسر الثاني مهم ان نتنبه هل مرتبط بالعدد االساسي
ام مرتبط بالمتبقي بعد الكسر االول
29.
افكار لحل اسئلة الجزء الكميالفكرة / 8تحويل الكسر ل %
تمرين (: )15
30.
افكار لحل اسئلة الجزء الكميالفكرة / 8تحويل الكسر ل %
تمرين (: )16
في إحدى المدارس الثانوية ملزم كل طالب باالشتراك في نشاط ال صفي واحد فقط،
فإذا كان ثالثة اخماس الطالب اخذوا النشاط الرياضي ،وربع الطالب المتبقين التحقوا
بالنشاط العلمي وبقية الطالب التحقوا بالنشاط الثقافي ؟ فكم نسبة الذين اختاروا
النشاط الثقافي ؟
ا%15 .
ب%20 .
ج%25 .
د%30 .
31.
افكار لحل اسئلة الجزء الكميالفكرة / 9مسائل العمر
32.
افكار لحل اسئلة الجزء الكميالفكرة / 9مسائل العمر
تمرين (: )17
عمر احمد اكبر من عمر اخيه محمود ب 5سنوات .فبكم سنة يكبر احمد اخاه محمود
بعد 10سنوات
د.
ج5 .
ب10 .
ا15 .
50
33.
افكار لحل اسئلة الجزء الكميالفكرة / 9مسائل العمر
تمرين (: )18
إذا كان عمر فهد بعد 8سنوات يساوي ثالثة اضعاف عمره منذ 4سنوات .فما عمره
آ
االن ؟
د8 .
ج6 .
ب10 .
ا4 .
34.
افكار لحل اسئلة الجزء الكميالفكرة / 9مسائل العمر
تمرين (: )19
إذا كان احمد 3اضعاف عمر ابنه .بعد عشر سنوات يصبح عمر االبن 20سنة .فما عمر
آ
احمد االن ؟
ا21 .
ب30 .
ج10 .
د40 .
35.
افكار لحل اسئلة الجزء الكميالفكرة / 9مسائل العمر
تمرين (: )20
احمد اكبر من ماجد ب 6سنوات .بعد سنتين يصبح عمر احمد ضعف عمر ماجد .فما
آ
عمر احمد االن ؟
ا 4 .سنوات
ب 10 .سنوات
ج12 .سنة
د14 .سنة
36.
افكار لحل اسئلة الجزء الكميالفكرة / 10االستفادة من االشكال
تنبيهات :
/1التركيز مطلوب الستخراج معطيات السؤال من الرسم
/2في حالة إيجاد مساحة الجزء المظلل نتبع الخطوات :
ا /نتعرف على االشكال في السؤال
ب /نحسب مساحات االشكال
ج /نطرح المساحات إليجاد المطلوب
37.
افكار لحل اسئلة الجزء الكميالفكرة / 10االستفادة من االشكال
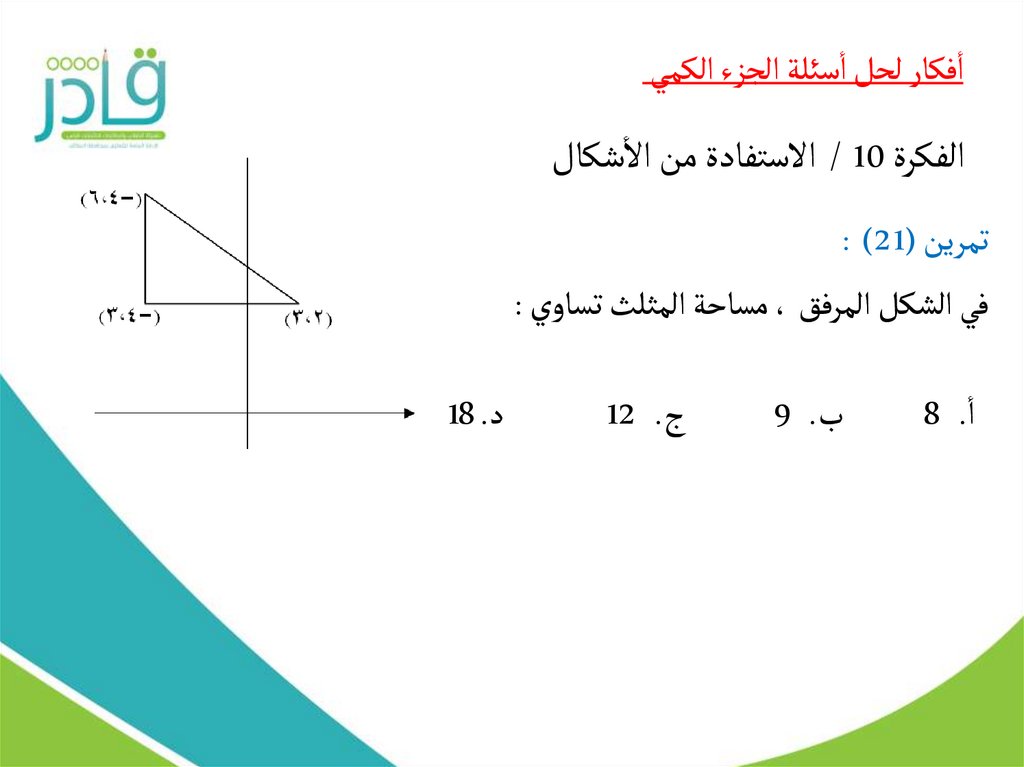
تمرين (: )21
في الشكل المرفق ،مساحة المثلث تساوي :
ا8 .
ب9 .
ج12 .
د18 .
38.
افكار لحل اسئلة الجزء الكميالفكرة / 10االستفادة من االشكال
تمرين (: )22
طول ضلع المربع ا ب ج د = 4
اوجد مساحة المنطقة المظللة في الشكل المرفق .
ً
َ
َ
َ
إذا علمت ان كال من ك و ل و م و ن هي مراكز الدوائر
ً
التي تمثل االقواس الموجودة في الشكل جزءا منها
ب 4 .ط
ا16 .
د4+16 .ط
ج4-16 .ط
39.
افكار لحل اسئلة الجزء الكميالفكرة / 10االستفادة من االشكال
تمرين (: )23
في الشكل المقابل :
ضلعا المربع مماسان للدائرة التي مساحتها 25ط
فإن مساحة المربع =
ا25 .
ب50 .
ج75 .
د100 .
40.
افكار لحل اسئلة الجزء الكميالفكرة / 11اسئلة المقارنة
تنبيهات :
ً
/1اقرا السؤال جيدا وافهم معطياته ،وتنبه لشروطه
/2إذا وجد متغيرات في السؤال ولم يحدد اي مجموعة تنتمي لها
هذه المتغيرات فغالب اإلجابة هي د
وحتى نتاكد نعوض مرة باعداد موجبة واخرى سالبة
حسب الوقت المتاح
/3إذا كانت القيمتين في السؤال ارقام نستبعد ( د )
41.
افكار لحل اسئلة الجزء الكميالفكرة / 11اسئلة المقارنة
في كل من التمارين التالية قيمتان :االولى في الجهة اليمنى ،
والثانية في الجهة اليسرى .قارن بين القيمتين ثم اختر
ا) إذا كانت القيمة االولى اكبر من القيمة الثانية
ب) إذا كانت القيمة الثانية اكبر من القيمة االولى
ج) إذا كانت القيمتان متساويتان
د) إذا كانت المعطيات غير كافية
42.
افكار لحل اسئلة الجزء الكميالفكرة / 10االستفادة من االشكال
تمرين (: )24
اذا كان ا < ب < ج < د
القيمة الولى
القيمة الثانية
اب
جد
43.
افكار لحل اسئلة الجزء الكميالفكرة / 10مسائل المقارنة
تمرين (: )25
44.
افكار لحل اسئلة الجزء الكميالفكرة / 10مسائل المقارنة
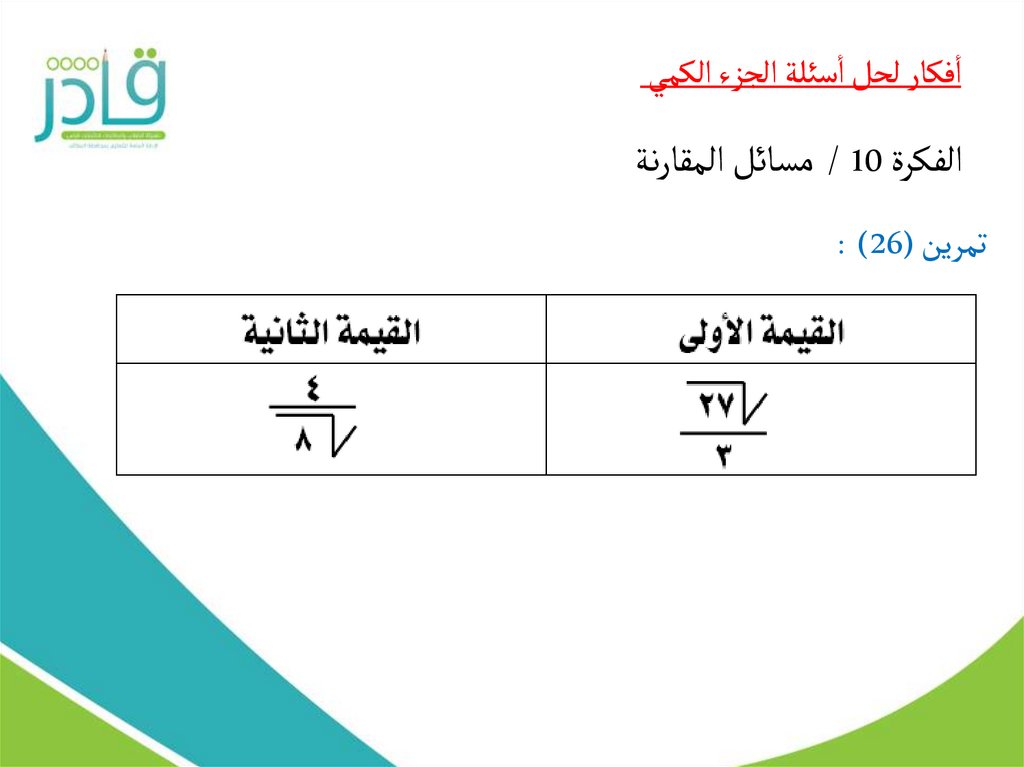
تمرين (: )26
45.
افكار لحل اسئلة الجزء الكميالفكرة / 10مسائل المقارنة
46.
افكار لحل اسئلة الجزء الكميالفكرة / 12الرسوم البيانية
تنبيهات :
/1ركز اثناء قراءتك للسؤال
/2اهتم فقط بالمطلوب في السؤال
47.
افكار لحل اسئلة الجزء الكميالفكرة / 12الرسوم البيانية
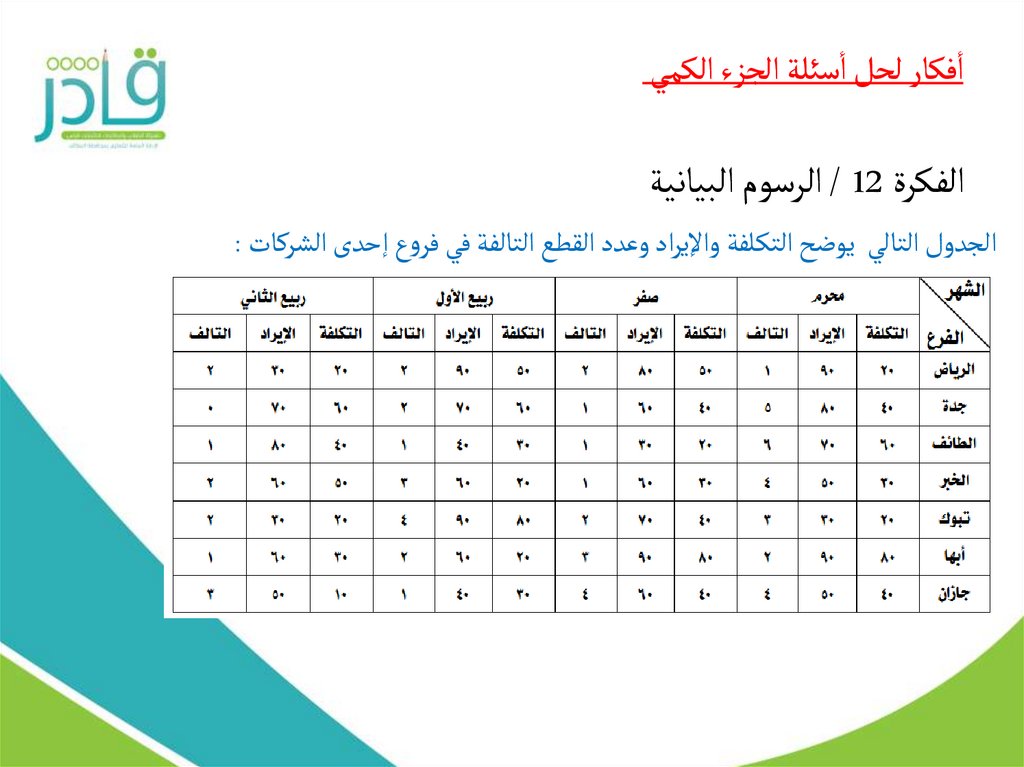
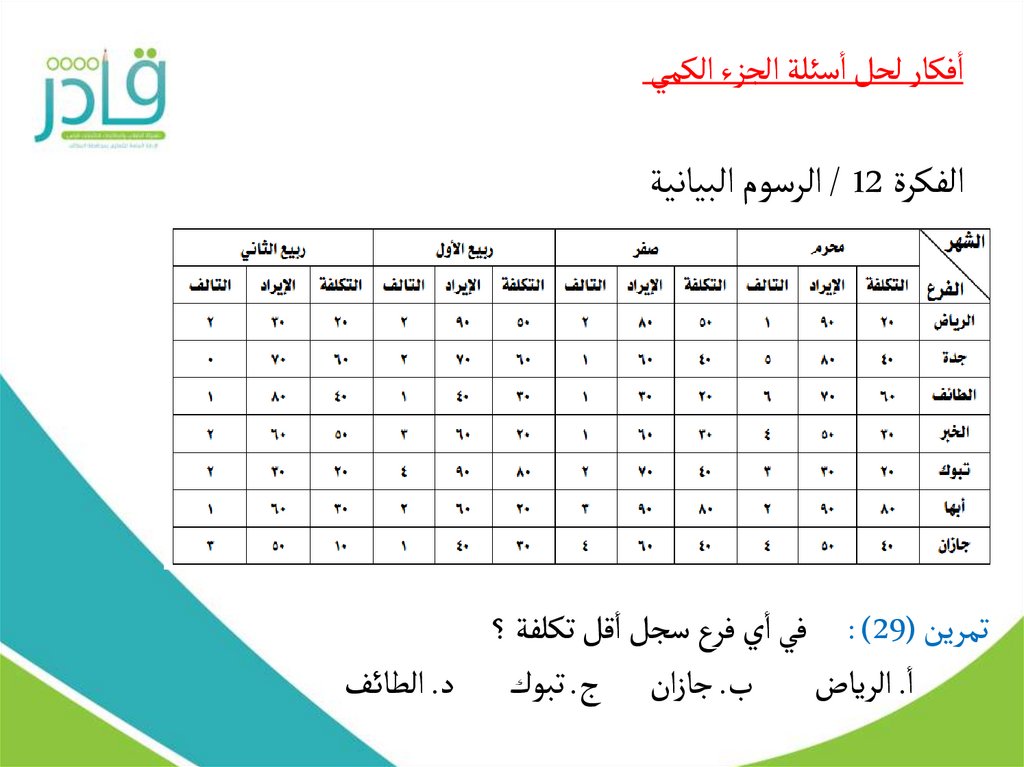
الجدول التالي يوضح التكلفة واإليراد وعدد القطع التالفة في فروع إحدى الشركات :
48.
افكار لحل اسئلة الجزء الكميالفكرة / 12الرسوم البيانية
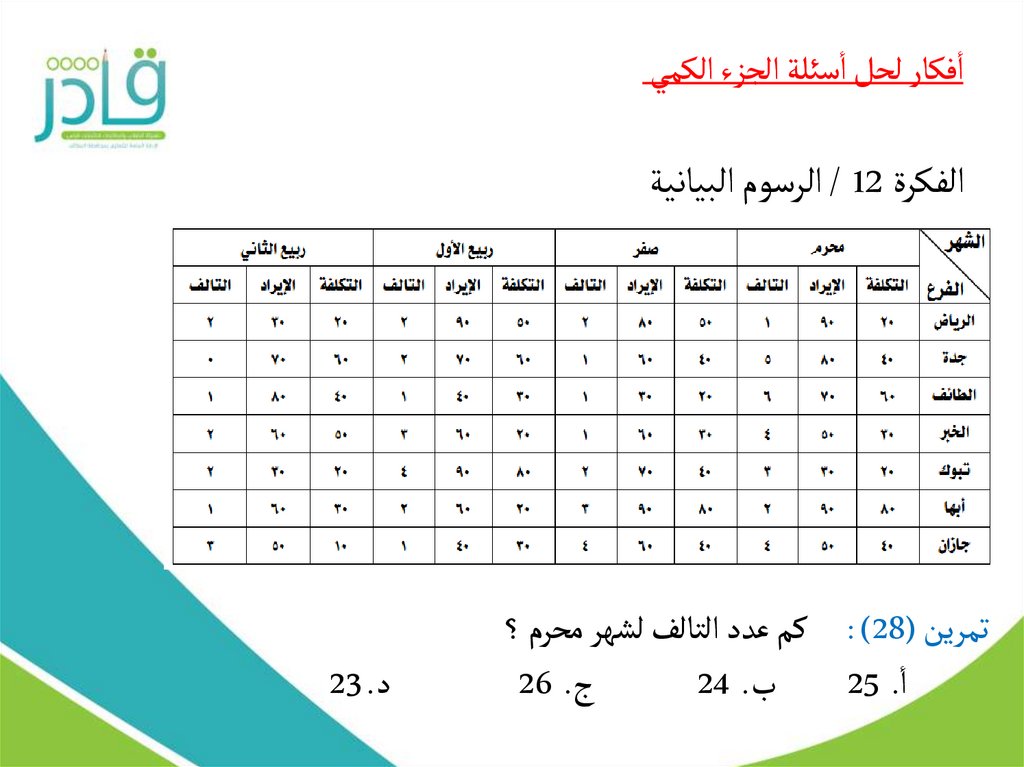
تمرين ( : )28كم عدد التالف لشهر محرم ؟
ج26 .
ب24 .
ا25 .
د23 .
49.
افكار لحل اسئلة الجزء الكميالفكرة / 12الرسوم البيانية
تمرين ( : )29في اي فرع سجل اقل تكلفة ؟
ا .الرياض ب .جازان ج .تبوك د .الطائ ف
50.
افكار لحل اسئلة الجزء الكميالفكرة / 12الرسوم البيانية
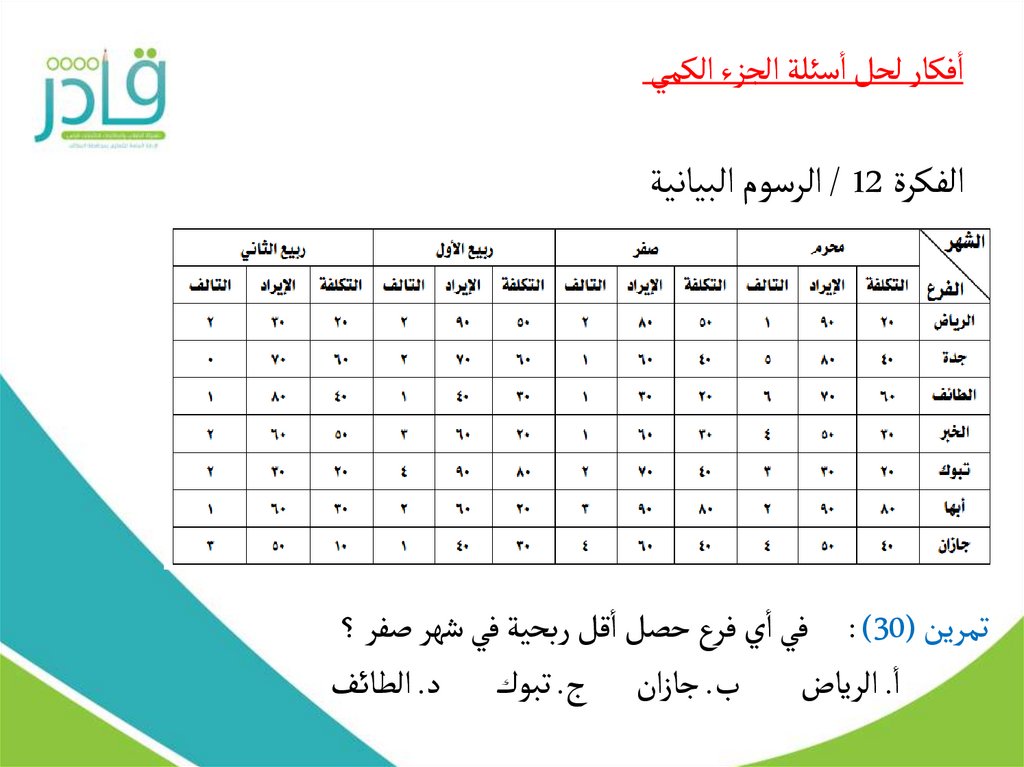
تمرين ( : )30في اي فرع حصل اقل ربحية في شهر صفر ؟
ا .الرياض ب .جازان ج .تبوك د .الطائ ف
51.
افكار لحل اسئلة الجزء الكميالفكرة / 12الرسوم البيانية
الرسم البياني المجاور يمثل نتائج طالب مدرسة عددهم 300طالب
52.
افكار لحل اسئلة الجزء الكميالفكرة / 12الرسوم البيانية
الرسم البياني المجاور يمثل نتائج طالب مدرسة عددهم 300طالب
تمرين ( : )31كم عدد الطالب الراسبين ؟
ج120 .
ب90 .
ا60 .
د150 .
53.
افكار لحل اسئلة الجزء الكميالفكرة / 12الرسوم البيانية
الرسم البياني المجاور يمثل نتائج طالب مدرسة عددهم 300طالب
















































 mathematics
mathematics
