Similar presentations:
Система нелинейных уравнений (СНУ)
1.
Система нелинейных уравнений (СНУ).В общем случаи систему нелинейных уравнений можно записать как:
f1 ( x1, x2 , x 3 ,....., xn ) 0
f 2 ( x1 , x2 , x 3 ,....., xn ) 0
. . . . . . . . .
f n ( x1 , x2 , x 3 ,....., xn ) 0
или
f (x) 0
Решением СНУ является такой вектор
[x,fun]=fsolve(@f,[x1 x2]);
*
x
при подстановке которого в систему последняя обращается в тождество.
Методы простых итераций
1. Прямой подход получения эквивалентной системы нелинейных уравнений
Преобразуем Систему нелинейных уравнений к эквивалентному виду:
x ( x )
(
0
)
x
Последующие приближения найдем
Выберем некоторое начальное приближение
(1) (0)
( 2) (1)
(3) ( 2)
по формулам
x ( x ); x ( x ); x ( x );
Произвольное приближение (итерационную формулу) запишем как:
( k ) ( k 1)
x
( x
)
1
2.
( k )x
На каждой итерации вычисляем вектор
( k )
x
( k 1)
x
( k )
и проверяем условие окончания итерационного процесса
|| x
||
где заданная точность
2x1 x 22 1 0
Решить СНУ с точностью =0.1
2
3
x
1 x2 2 0
при
( 0)
x
0.5
0.5
Преобразуем каждое уравнение
x 22 1
x1 1 ( x )
2
x 2 2 ( x ) 3x12 2
x1
x 2
(1)
(0) 0.52 1
(1)
(1)
0
.
63
0.13
( x )
1 ( 0)
; x
; || x || 1.7544
2
- 1.75
( x ) 3 0.52 2 1.25
2
2
3.
x1x 2
( 2)
x1
x 2
(3)
(1) 1.252 1
( 2) 0.65
( 2)
1.28
1 ( x )
; x
; || x || 0.7802
2
(
1
)
0.42
( x ) 3 0.632 2 0.83
2
( 2) ( 0.832 1
(3) - 0.44
(3)
0.84
1 ( x )
; x
; || x || 3.7784
2
(
2
)
3.75
( x ) 3 1.282 2 2.92
2
Итерационный процесс расходится.
x1 1 ( x )
Попробуем, по другому осуществить преобразование.
x2 2
3
x 2 2 ( x ) 2 x1 1
x1
x 2
(1)
(0) 0.5 2
(1) 0.413
(1)
0.913
1 ( x )
; x
; || x || 0.648
3
0.000
( 0)
0.500
( x ) 2 0.5 1
3
2
4.
x1x 2
( 2)
( 2)
0.816
; || x || 0.9138
0.909
x1
x 2
(3)
(3)
0.985
; || x || 0.202
0.796
x1
x 2
( 4)
0.965
; || x
0.985
x1
x 2
(5)
(5)
0.997
; || x || 0.038
0.965
( 4)
|| 0.189
Процесс сходится к решению.
2. Общий подход получения эквивалентной системы нелинейных уравнений
x ( x )
Если не удаётся преобразовать исходную СНУ к эквивалентному виду, который будет
сходится, то можно воспользоваться общим приемом.
f ( x ) 0 ; f ( x ) 0 ;
Итерационную формулу запишем
где матрицу
x x f ( x )
( k )
x
( k 1)
x
( k 1)
f ( x
)
можно представить диагональной, а подбором значений элементов, можно добиться 4
сходимость итерационного процесса.
5.
Метод Ньютона-Рафсона( k 1)
Пусть известно некоторое приближение
Запишем исходную систему в виде
x
( k 1)
f (x
к решению
( k )
x
*
x
) 0,
где
( k )
x
( k 1)
*
x x
Разложим функцию в ряд Тейлора и ограничимся линейными членами.
( k 1)
f (x
( k )
x
( k 1)
) f (x
( k 1)
)
f (x
)
( k 1)
( k )
x
0
x
( k 1)
f (x
( k 1)
)
( k )
x
( k 1)
f (x
)
x
( k )
Это система линейных уравнений относительно
x
5
6.
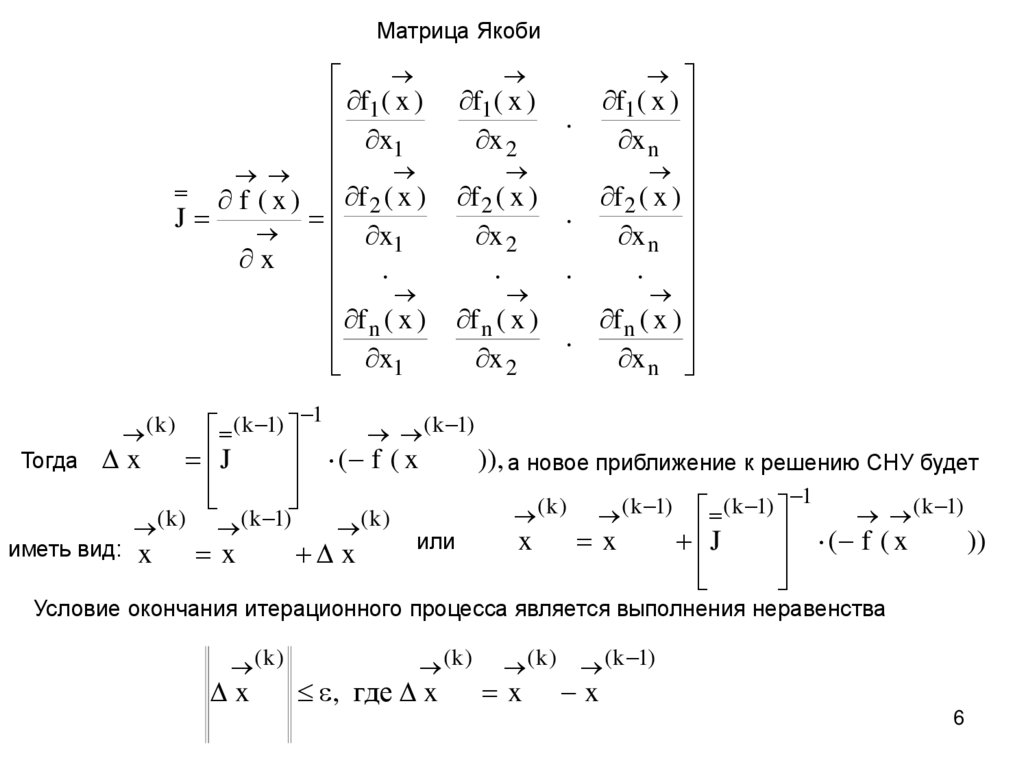
Матрица Якобиf1 ( x )
x1
f ( x ) f ( x )
2
J
x1
x
.
f n ( x )
x1
(k )
Тогда
x
иметь вид:
( k 1)
J
( k )
x
( k 1)
x
1
f1 ( x )
x 2
.
f 2 ( x )
.
x 2
.
.
f n ( x )
.
x 2
f1 ( x )
x n
f 2 ( x )
x n
.
f n ( x )
x n
( k 1)
( f ( x
( k )
x
)), а новое приближение к решению СНУ будет
( k )
или
x
( k 1)
x
( k 1)
J
1
( k 1)
( f ( x
))
Условие окончания итерационного процесса является выполнения неравенства
( k )
x
( k )
, где x
( k )
x
( k 1)
x
6
7.
Решить приведенный выше пример =0.1x1
x 2
(1)
x1
x 2
( 0)
2
6 x10
0 1
2 x2
1
( 0)
x
0.5
0.5
2 x2
2
J
1
6 x1
( 0)
1
0
.
5
2
1
0.25
f1 ( x )
(
0
)
f ( x ) 0.5 3 1 1.75
2
0.5 1 1 0.25 2
0.5 3 2 1.75 3.25
(1)
x
(1)
1.5
; || x || 3.132
2.75
x1
x 2
( 2)
( 2)
1.323
; || x || 1.53
1.878
x1
x 2
(3)
(3)
1.070
; || x || 0.684
1.243
x1
x 2
( 4)
( 4)
1.007
; || x || 0.223
1.029
x1
x 2
(5)
(5)
1.000
; || x || 0.029
1.001
7
8.
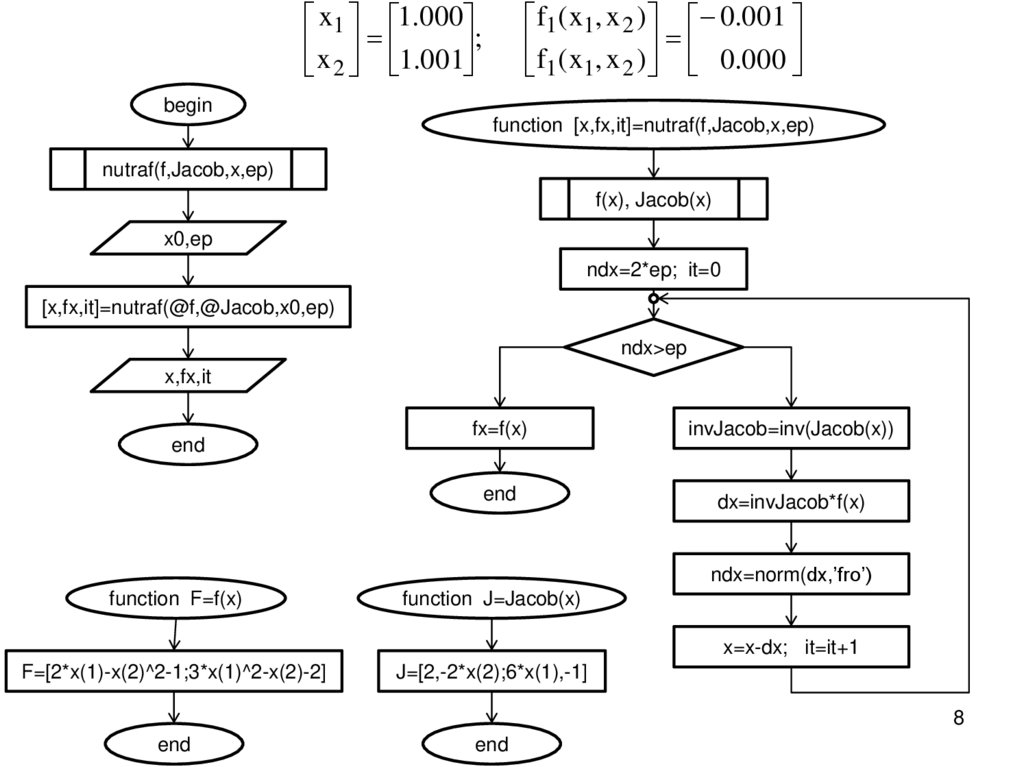
f1 ( x1, x 2 ) 0.001f ( x , x ) 0.000
1 1 2
x1 1.000
x 1.001 ;
2
begin
function [x,fx,it]=nutraf(f,Jacob,x,ep)
nutraf(f,Jacob,x,ep)
f(x), Jacob(x)
x0,ep
ndx=2*ep; it=0
[x,fx,it]=nutraf(@f,@Jacob,x0,ep)
ndx>ep
x,fx,it
end
fx=f(x)
invJacob=inv(Jacob(x))
end
dx=invJacob*f(x)
ndx=norm(dx,’fro’)
function F=f(x)
function J=Jacob(x)
x=x-dx; it=it+1
F=[2*x(1)-x(2)^2-1;3*x(1)^2-x(2)-2]
J=[2,-2*x(2);6*x(1),-1]
8
end
end






 mathematics
mathematics








