Similar presentations:
Решение нелинейного уравнения. Тема 6
1. Тема 6 §1 Решение нелинейного уравнения
fx 0
Требуется найти все или некоторые корни уравнения
f x 0
Исследование характера корней: расположения,
количества, кратности корней;
Отделение корней: выделение областей, в каждой из
которых находится единственный корень;
Уточнение корней: вычисление интересующих корней с
наперед заданной точностью.
2. построение таблицы f(x)
x0x1
x2
x3
x4
+
-
+
+
+
... x
n 1
xn
-
-
3.
для многочленаf x a0 a1 x ... am x
m
если выполнены неравенства
m
f x0 0, f x0 0, f x0 0,..., f x0 0,
то положительные корни не превосходят
действительно:
x0
m
f x0
f x0
m
x x0 ...
x x0
f x f x0
1
m!
4.
f (x)x
5.
f x ( x) x(x)
x1
(x)
x2
x
6. 1. Дихотомия
Метод деления пополамМетод бисекции
x0 , x1 , x2 ,..., xт , x , xm xm 1
f x
g x
k
x x
7. 2. Метод простой итерации
x xxn 1 xn , n 0 ,1,2 ,...
x0 , x1 , x2 ,..., xт , x
x x
Исследуем условия сходимости:
xn 1 x xn x xn x
x q 1
xn 1 x q xn x
8.
x aa
a
a
x , x
xn 1
x
x
xn
Пример
2
метод не сходится вообще
x
a
x
2
1
1
a
1
a
1
a
x x , x x xn 1 xn
2
x
2
x
2
xn
метод сходится при любом начальном приближении
x
1
a
1 2 0
2
x
9. Условие окончания итерационного цикла
еслиx 0 приближения то слева, то справа от корня
xn 1 x xn x xn x
тогда
если
xn xn 1
x 0 приближения с одной стороны от корня
xn 1 xn q xn xn 1
xn 1 xn
q
xn xn 1
an 1
xn 1 xn xn xn 1
ak
1 q
2 xn xn 1 xn 1
k n 1
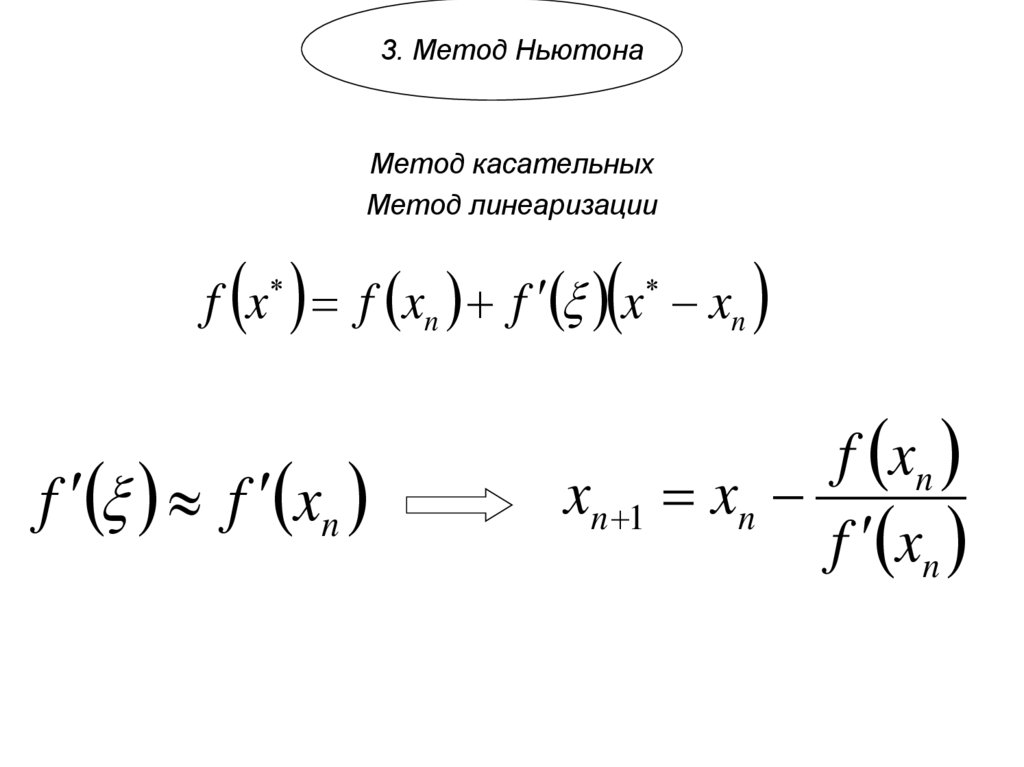
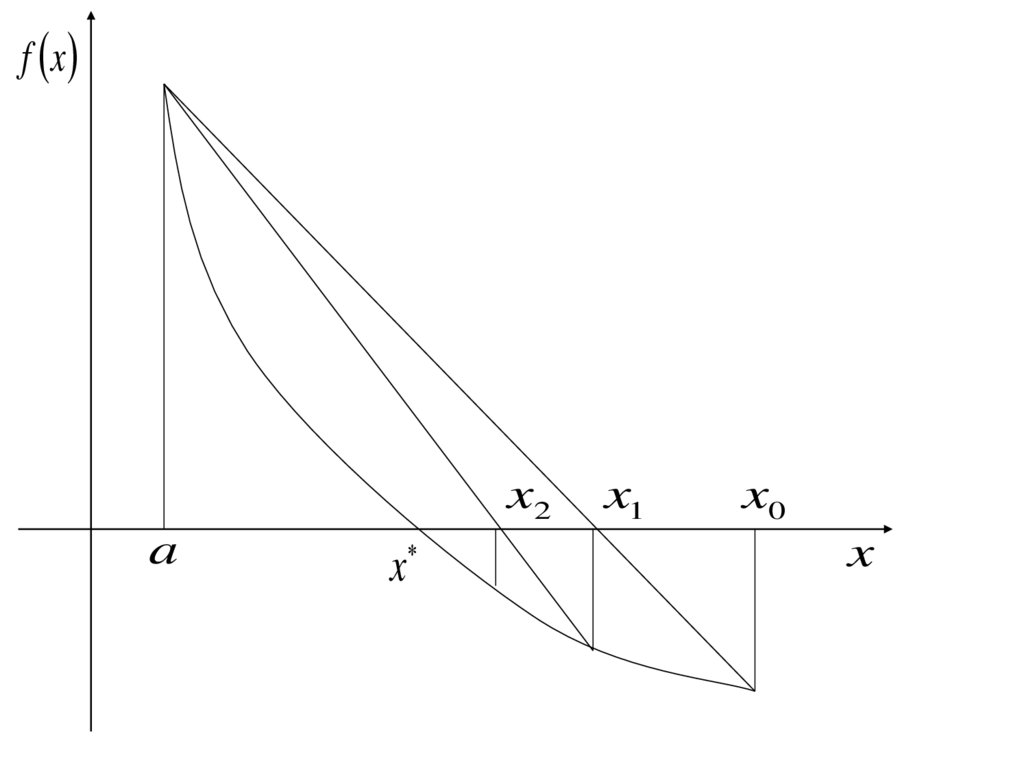
10. 3. Метод Ньютона
Метод касательныхМетод линеаризации
f x f xn f x xn
f f xn
f xn
xn 1 xn
f xn
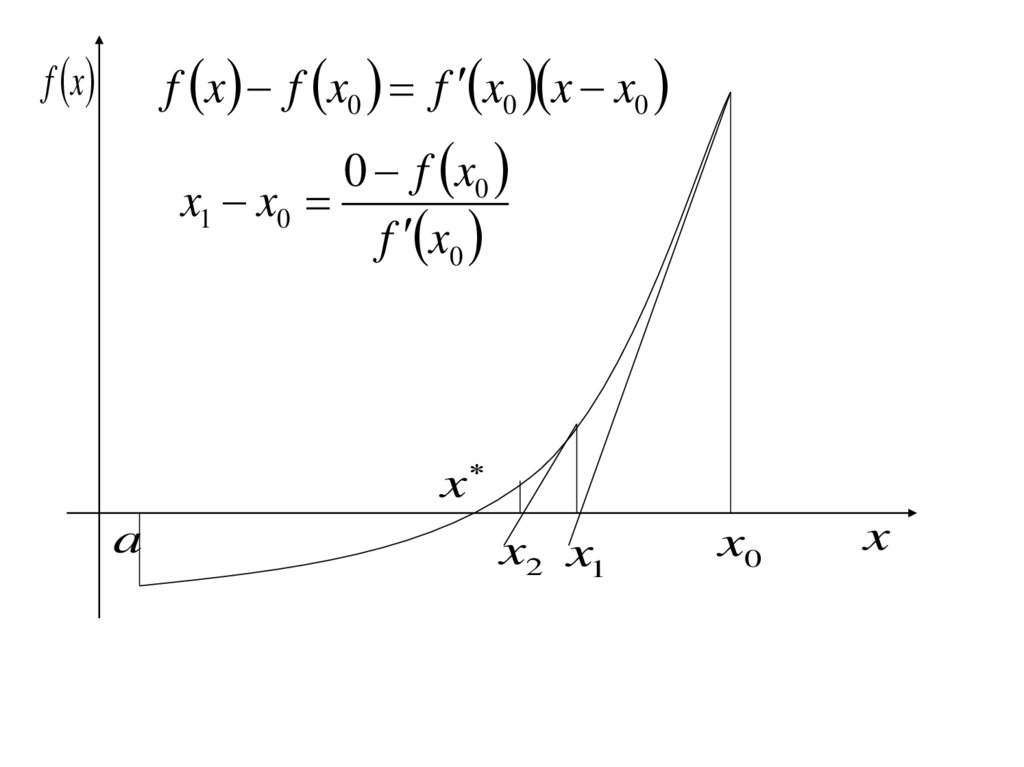
11.
f xf x f x0 f x0 x x0
0 f x0
x1 x0
f x0
x
a
x2 x1
x0
x
12. сходимость метода Ньютона
f xf x f x
x x
x 1 1
2
f x
f x
x 0
скорость сходимости метода Ньютона
xn 1 x xn x
x
2
x x xn x
xn x ... x
2
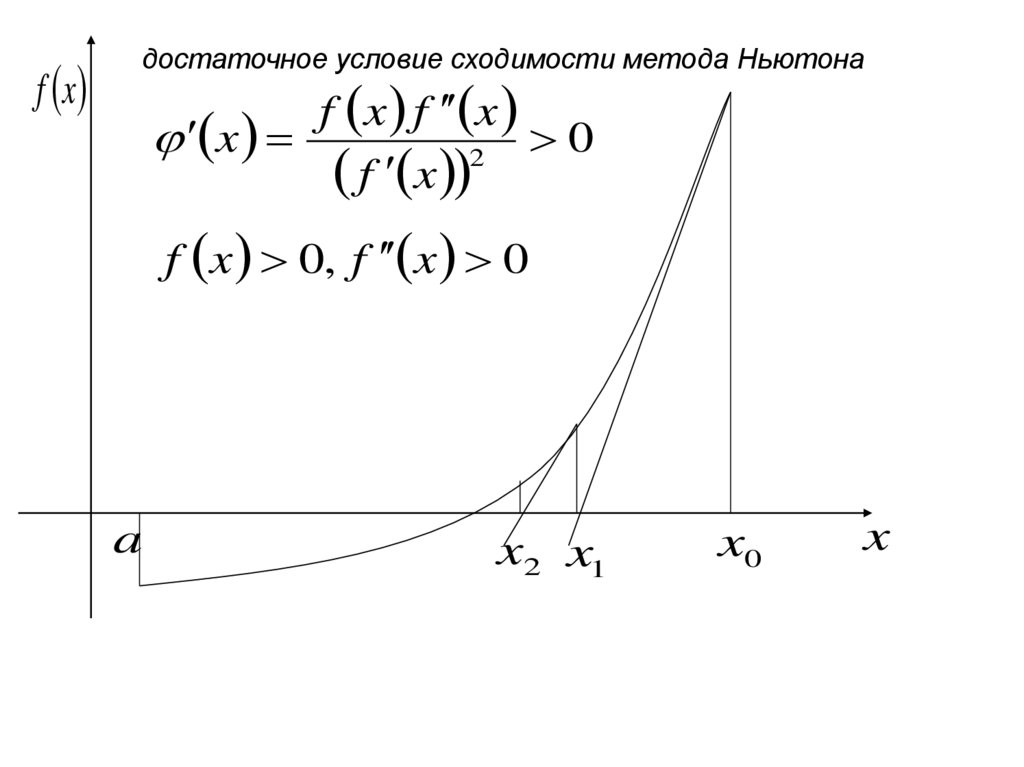
13.
f xдостаточное условие сходимости метода Ньютона
f x f x
x
0
2
f x
f x 0, f x 0
a
x2 x1
x0
x
14.
f xf x f x
x
f x 2
x0
f x 0, f x 0
x1 x2
b x
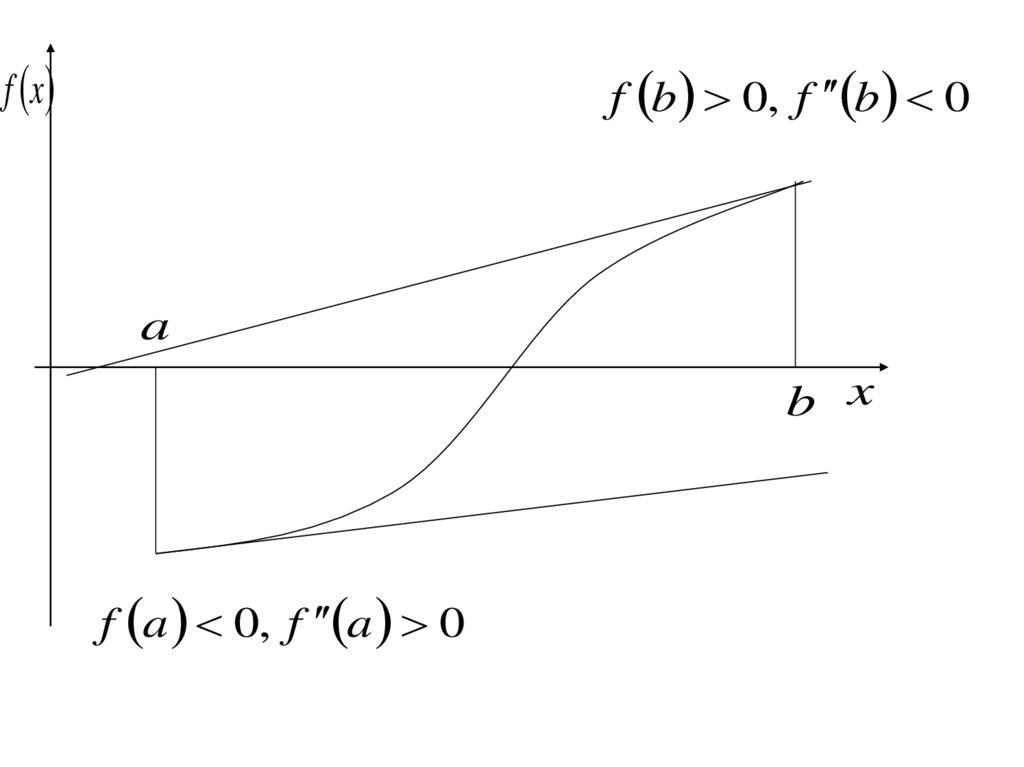
15.
f xf b 0, f b 0
a
b x
f a 0, f a 0
16. 4. Модифицированный метод Ньютона
f xnxn 1 xn
f xn
Если
f xn
xn 1 xn
, n 0,1,...
f x0
f f1 x , f 2 x ,..., f m x
T
тогда
xn 1 xn f xn f xn
1
для уменьшения количества арифметических операций
на одном шаге итерации используется модификация
xn 1 xn f x0 f xn
1
17. 5. Метод секущих
f x5. Метод секущих
x3
x2
x1
x0
x
18.
Уравнение прямойx x1
f x f x1
x0 x1 f x0 f x1
0 f x1
x2 x1 x0 x1
f x0 f x1
xn xn 1
xn 1 xn f xn
f xn 1 f xn
преимущества метода секущих: простота реализации
нет производных
недостатки метода секущих: неизбежные погрешности,
возникающие при вычитании близких чисел в знаменателе
сходимость не более, чем линейная
19.
x xn 1f xn 1 x f x xn 1
x x f x
f xn 1 f x
f xn 1 f x
xn 1 f f xn 1 f f xn 1 f xn 1 f f xn 1 x
x
2
f f xn 1
xn 1 ff f xn 1 f xn 1 f xn 1 f f xn 1 xn 1 ff f xn 1 xf
2
f f xn 1
2
f xn 1 f f x xn 1
f
x
f
x
x
x
n
1
n 1
x
2
f f xn 1
f xn 1
20.
f xn 1 f x x xn 1x
f xn 1
но с другой стороны, по формуле Тейлора
f
2
f xn 1 f x f x xn 1 x
xn 1 x
2
числитель равен
f
2
f xn 1 f x xn 1 x
xn 1 x
2
следовательно
f x xn 1
x
2 f xn 1
2
21. 6. Метод хорд
f x6. Метод хорд
x0
x1
x2
x
b
x
22.
x a f x f aУравнение хорды
b a f b f a
0 f a
x1 a b a
f b f a
если неподвижный правый конец отрезка: в
b xn
xn 1 xn f xn
f b f xn
x0 a, n 1,2,...
получаем ограниченную сверху монотонно возрастающую
последовательность приближений
a x0 x1 x2 ... x b
23.
f xx2
a
x
x1
x0
x
24.
если неподвижный левый конец отрезка: аxn a
xn 1 xn f xn
f xn f a
x0 b, n 1,2,...
получаем ограниченную снизу монотонно убывающую
последовательность приближений
a x ... x2 x1 x0 b
возможны варианты:
1.
f x 0, f x 0
2.
f x 0, f x 0
неподвижный конец отрезка
для метода хорд:
для которого знак функции
совпадает со знаком
ее второй производной
3.
f x 0, f x 0
f x f x 0
4.
f x 0, f x 0
25. Другие методы решения нелинейного уравнения
Метод Шредера:f xn f xn
xn 1 xn
2
f xn f xn f xn
Классификация методов решения
1.
Метод простой итерации, послед. приближений
2.
Метод секущих
k
3.
Метод Ньютона
k 2
4.
Метод Галлея
k 3
5.
Метод Чебышева
k n N
k 1
5 1
1.61....
2
Найти самостоятельно
26.
Метод Чебышёва построения итерационных процессов высшего порядкаПредположим, что существует функция g(u), обратная к f(u). При этом u=
g[f(u)], U = g(0).
Пусть, кроме того, f(u) непрерывна и имеет необходимое число непрерывных
производных,
Обратная функция имеет такое же количество непрерывных производных, как
и f(u).
Разложим функцию g(f[u]) = g(h) в ряд Тейлора в окрестности корня - точки w =
f(u)
Тогда, учитывая, что u = g[f(u)], w = f(u), h = f(v), получим
Можно показать, что итерационный метод
имеет порядок сходимости n + 1. Для вычисления производных обратной
функции u = g[f(u)] воспользуемся правилом дифференцирования сложной
функции:
27.
метод секущих – установление факта о сверхлинейнойсходимости метода
Вержбицкий В.М. Численные методы
(линейная алгебра и нелинейные
уравнения). – М.: ОНИКС 21 век, 2005.
метод Галлея , методы Чебышева, метод Шредера и другие
энциклопедия математических формул и
математических достижений в мире
автор Вольфрам (Wolfram)
Mathworld
CКМ «Математика»
28. Продолжение рассмотрения метода Ньютона
≈ 300 лет назад Токакадзу ║ с Ньютоном открыл методf xn
xn 1 xn
, n 0,1,...
f x0
1.
если х – число, f - функция
2.
если х – функция, f - оператор
3.
если х – последовательность, f - оператор
4.
если х – матрица, f - преобразование
29.
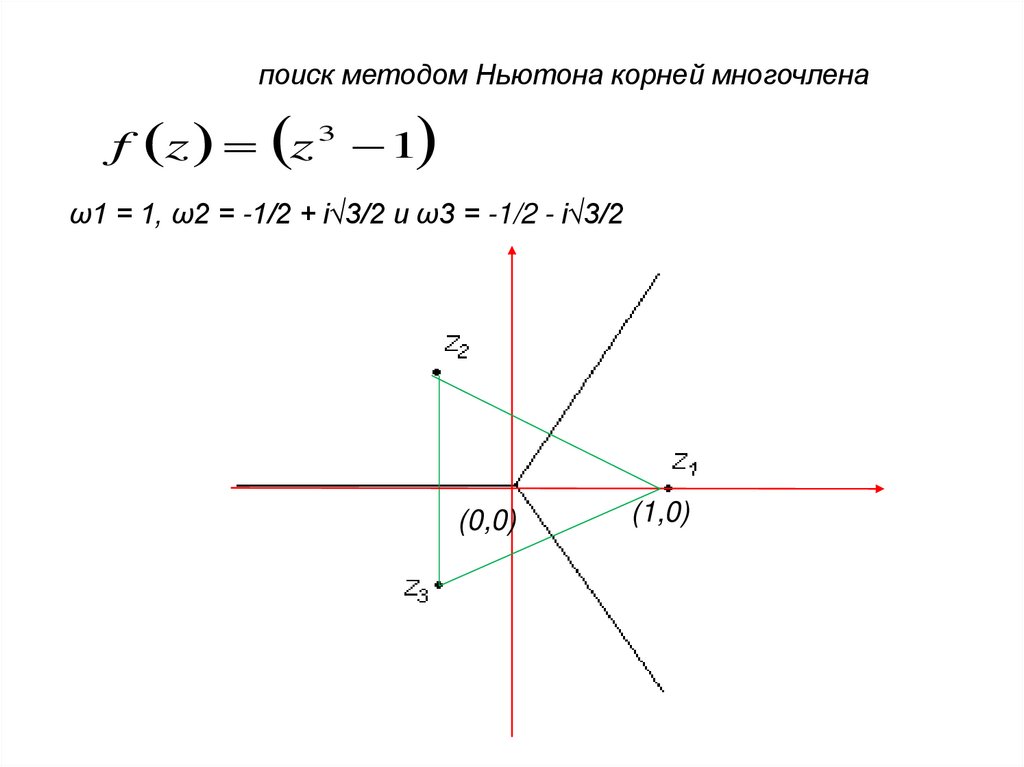
поиск методом Ньютона корней многочленаf z z 3 1
ω1 = 1, ω2 = -1/2 + i√3/2 и ω3 = -1/2 - i√3/2
(0,0)
(1,0)
30.
фрактал - бассейн Ньютона31.
32.
33.
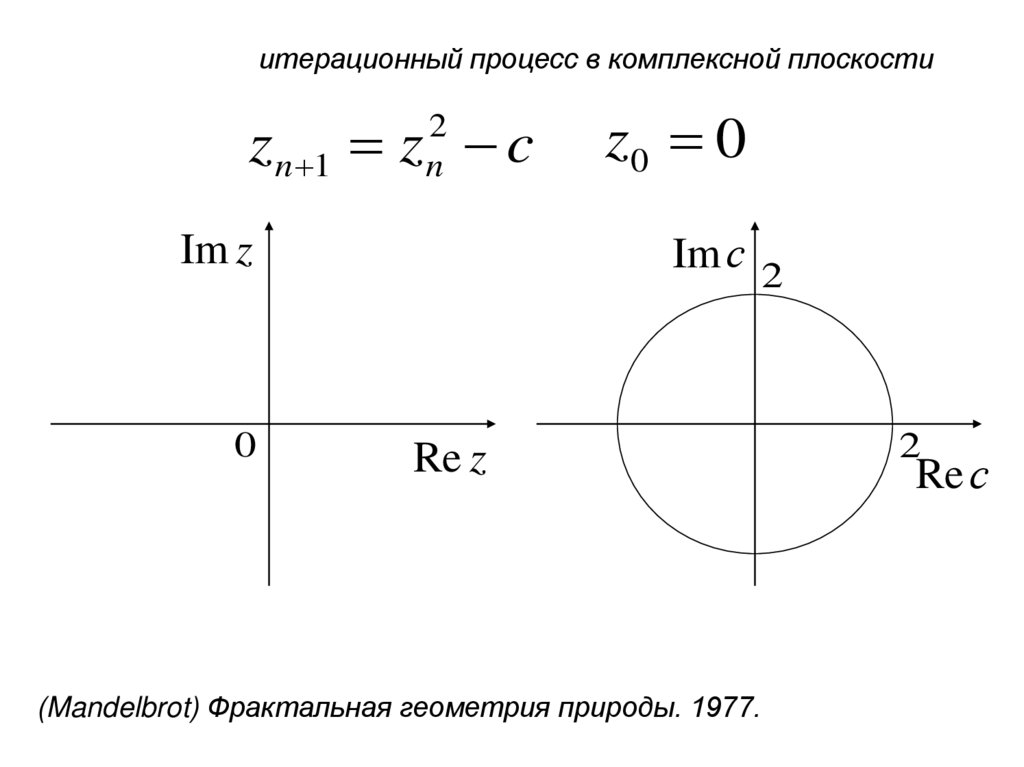
итерационный процесс в комплексной плоскостиz n 1 z c
2
n
Im с 2
Im z
0
z0 0
Re z
(Mandelbrot) Фрактальная геометрия природы. 1977.
2
Re с
34.
фрактал – множество Мандельброта – это геометрияитерационного процесса



























 mathematics
mathematics








