Similar presentations:
Последовательность. Понятие о пределе последовательности
1. Последовательность. Понятие о пределе последовательности
Раздел Начала математического анализа2. Цель:
разъяснение смысл понятий«последовательность», «n-ый член
последовательности», знакомство со
способами задания последовательности
Последовательность
Действия над последовательностями
Определение предела
последовательности
3.
Какие события в нашей жизни происходятпоследовательно? Приведите примеры
таких явлений и событий
числа
Времена
года
месяца
Дата/время
И.т.д.
алфавит
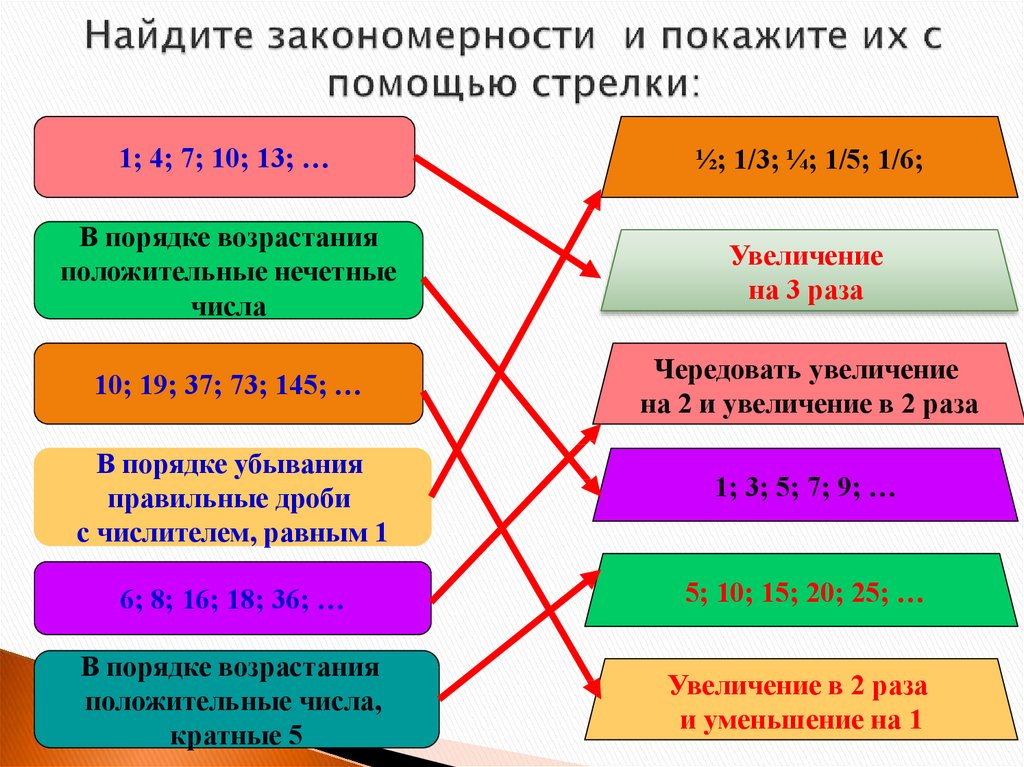
4. Найдите закономерности и покажите их с помощью стрелки:
1; 4; 7; 10; 13; …½; 1/3; ¼; 1/5; 1/6;
В порядке возрастания
положительные нечетные
числа
Увеличение
на 3 раза
10; 19; 37; 73; 145; …
Чередовать увеличение
на 2 и увеличение в 2 раза
В порядке убывания
правильные дроби
с числителем, равным 1
1; 3; 5; 7; 9; …
6; 8; 16; 18; 36; …
5; 10; 15; 20; 25; …
В порядке возрастания
положительные числа,
кратные 5
Увеличение в 2 раза
и уменьшение на 1
5. Числовая последовательность
Функцию y=f(x),x∈N называют функцией натуральногоаргумента или числовой последовательностью и
обозначают: y=f(n) или y1,y2,...,yn,... или y(n)
Последовательности можно задать:
1. Словесно(Представляет собой закономерность или правило
расположения членов последовательности, описанный словами)
2.
Аналитически (Последовательность задается формулой n-
3.
Рекуррентно (рекурсия-возврат. Вычисляя новый член
4.
Графически (Числовая последовательность задается
го члена, по которой можно найти любой член
последовательности)
последовательности, мы как бы возвращаемся назад, к уже
вычисленным, предыдущим членам)
графиком, который представляет собой изолированные точки)
6. Примеры
1.В последовательности, где общая
формула an=3*n, написать:
a) первые четыре члена
a1=3*1=3 a2=3*2=6 a3=….
a4=…
a) двадцатый член
a20=…
2.
Последовательность задана y1 = 3; yn = yn–1 + 4,
если n = 2, 3, 4,…(в формуле вместо n подставить числа)
7.
Последовательности заданы формулами:an=n4
an=2n-5
an=n+4
an=(-1)nn2
an=-n-2
an=3n-1
Выполните следующие задания:
1. Впишите пропущенные члены последовательности:
1; ___; 81; ___; 625; …
5; ___; ___; ___; 9; …
-1; 4; ___; ___; -25; …
___; ___; 3; 11; ___;
___; -4 ; ___; ___; -7; …
2; 8; ___; ___; ___; …
2. Укажите, какими числами являются члены этих последовательностей
Положительные и
отрицательные
Положительные
Отрицательные
8. Примером последовательности может являться треугольник Паскаля
11?
1
6?
1
1
4
1
3
1
2
6
1
3
1
4
1
1
5
10
10
5
Продолжи строчку!
15
?
1
?20 ?15 ? 6 ? 1
9. 2. Действия над последовательностями
Последовательностьназывается возрастающей, если для любого
n∈N выполняется неравенство an<an+1
Последовательность называется убывающей,
если для любого n∈N выполняется
неравенство an>an+1
Возрастающие и
убывающей последовательности
называются монотонными
10. 3. Определение предела последовательности
Число А называется пределом последовательности a1, a2, …,если, начиная с некоторого места, все члены этой
последовательности будут сколь угодно мало отличаться от А
Обозначение:
11. Свойства пределов последовательностей
1.2.
3.
4.
, где









 mathematics
mathematics








