Similar presentations:
Модуль геометрия №11. ГИА 2013
1. ГИА 2013 Модуль ГЕОМЕТРИЯ №11
Автор презентации:Гладунец Ирина Владимировна
учитель математики МБОУ гимназия №1
г.Лебедянь Липецкой области
1
2. Модуль «ГЕОМЕТРИЯ» №11
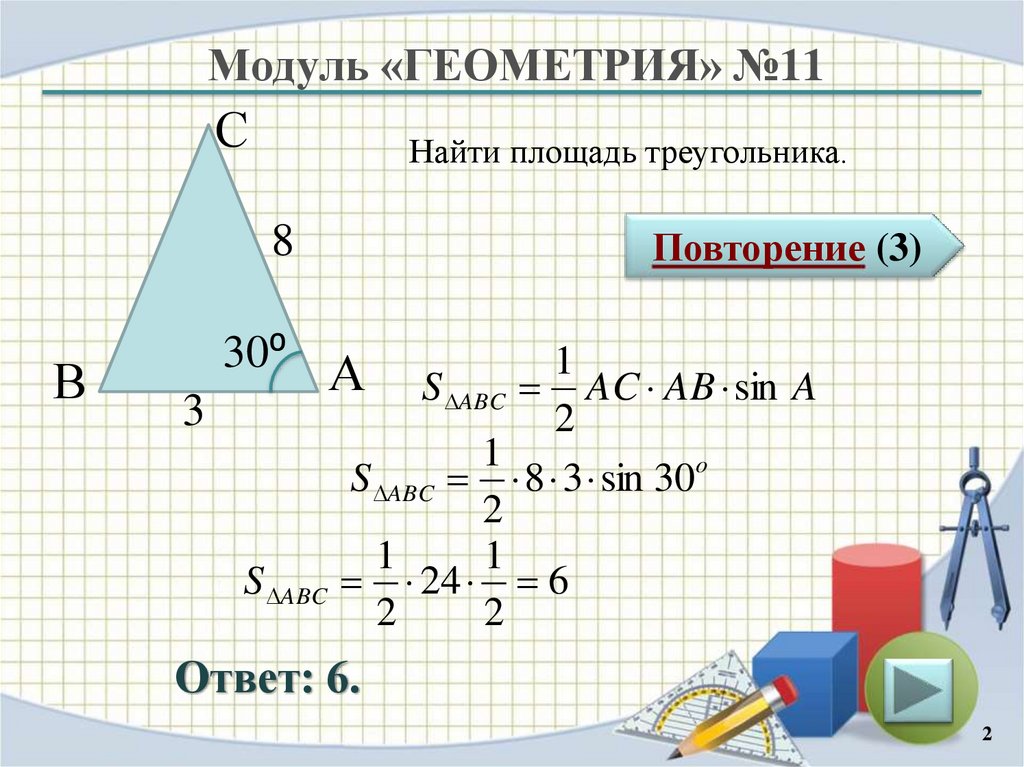
СНайти площадь треугольника.
8
В
30⁰
3
S ABC
Повторение (3)
А
1
S ABC AC AB sin A
2
1
S ABC 8 3 sin 30o
2
1
1
24 6
2
2
Ответ: 6.
2
3. Повторение
Площадь треугольника равна половинепроизведения двух сторон на синус угла между
ними
3
4. Модуль «ГЕОМЕТРИЯ» №11
В7
С
Катет АС на 2 больше катета ВС.
Найти площадь треугольника
А
Повторение (3)
АС=ВС+2=7+2=9
1
S ABC AC BC
2
1
S ABC 7 9 31,5
2
Ответ: 31,5.
4
5. Повторение
Площадь прямоугольного треугольника равнаполовине произведения катетов
5
6. Модуль «ГЕОМЕТРИЯ» №11
АВ
4
1
cos A
2
Найти площадь треугольника
Повторение (3)
С
sin 2 A cos 2 A 1
1 2
3
sin A 1 cos A 1 ( )
2
2
1
S ABC AC AB sin A
2
1
3
S ABC 4 4
4 3
2
2
2
Ответ: 4 3 .
6
7. Повторение
Площадь треугольника равна половинепроизведения двух сторон на синус угла между
ними
Сумма квадратов синуса и косинуса одного и
того же угла равна единице
7
8. Модуль «ГЕОМЕТРИЯ» №11
СВ H
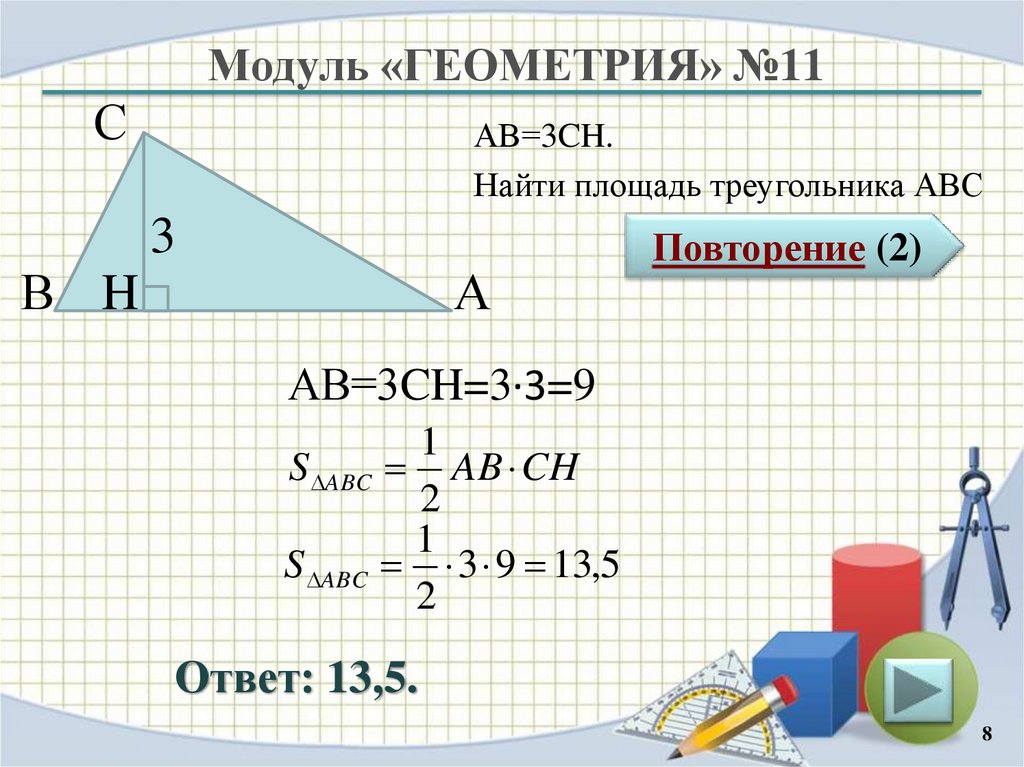
АВ=3CH.
Найти площадь треугольника АВС
3
А
Повторение (2)
АВ=3CH=3∙3=9
1
S ABC AB CH
2
1
S ABC 3 9 13,5
2
Ответ: 13,5.
8
9. Повторение
Высота треугольника – это отрезок,проведенный из вершины к противоположной
стороне под прямым углом
Площадь треугольника равна половине
произведения основания на высоту
9
10. Модуль «ГЕОМЕТРИЯ» №11
В1
r
2
Повторение (1)
O
С
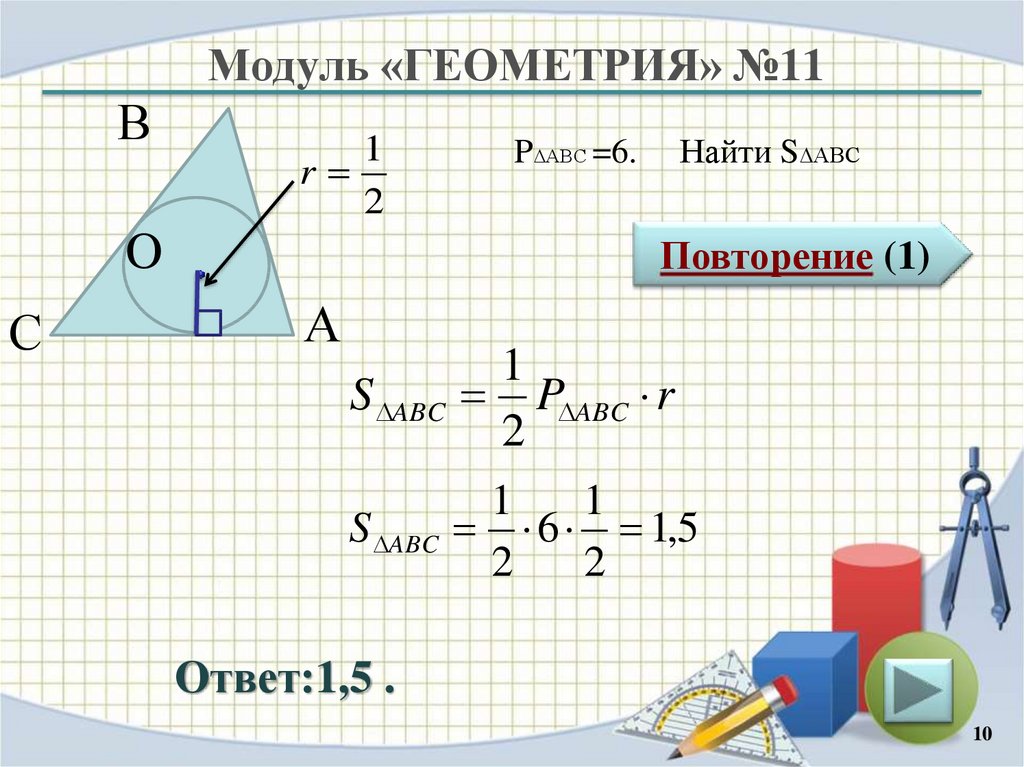
Найти S∆ABC
P∆ABC =6.
А
S ABC
1
P ABC r
2
S ABC
1
1
6 1,5
2
2
Ответ:1,5 .
10
11. Повторение
Вписанной в треугольник окружностьюназывается окружность, которая касается всех
сторон треугольника
Если в треугольник вписана окружность, то
площадь треугольника равна произведению
полупериметра треугольника на радиус
вписанной окружности
11
12. Модуль «ГЕОМЕТРИЯ» №11
СD
В
8
5
А
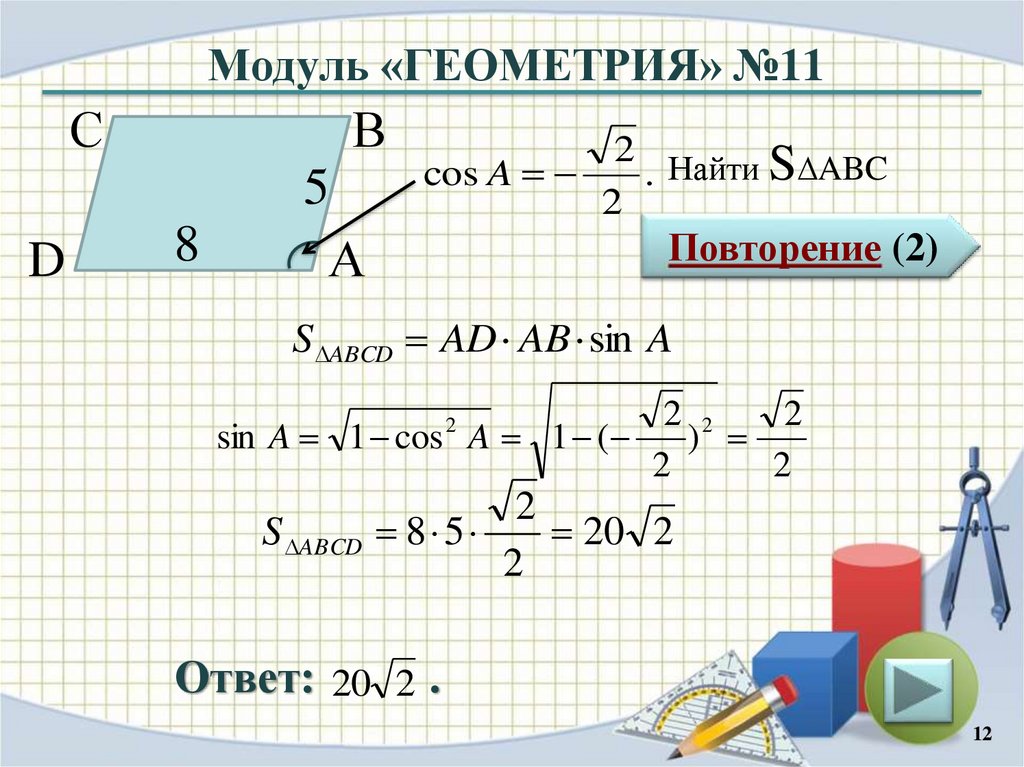
2 Найти S∆ABC
cos A
.
2
Повторение (2)
S ABCD AD AB sin A
2 2
2
sin A 1 cos A 1 (
)
2
2
2
S ABCD
2
8 5
20 2
2
Ответ: 20 2 .
12
13. Повторение
Площадь параллелограмма равнапроизведению двух сторон на синус угла между
ними
Сумма квадратов синуса и косинуса одного и
того же угла равна единице
13
14. Модуль «ГЕОМЕТРИЯ» №11
АВ
С
D
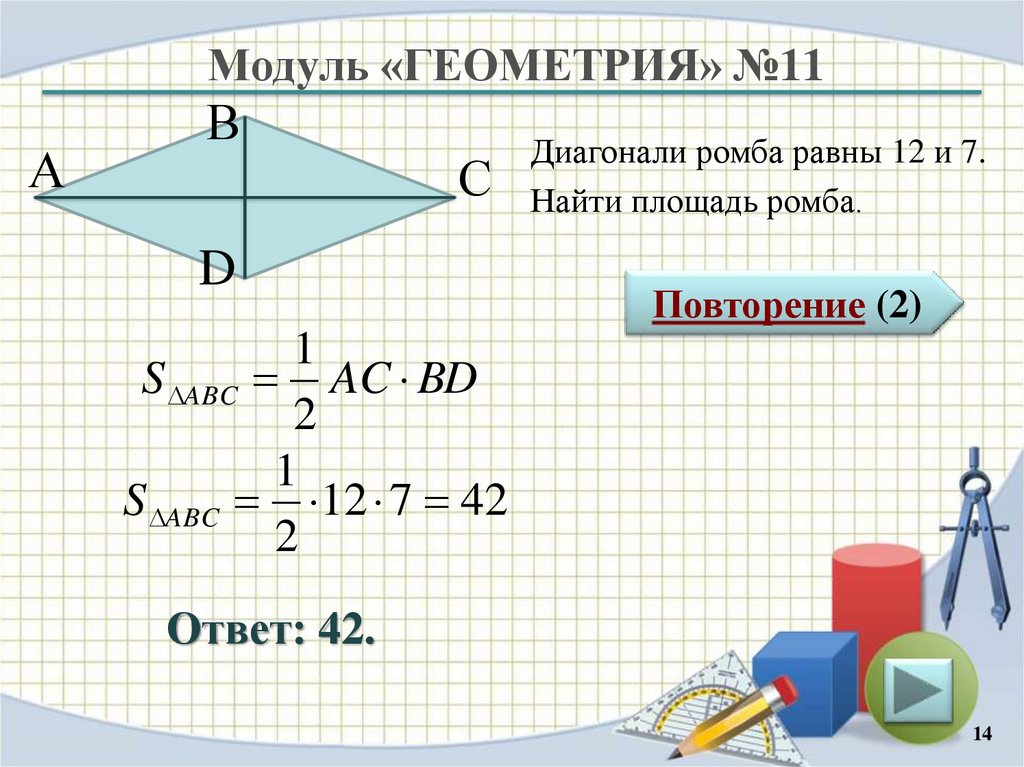
Диагонали ромба равны 12 и 7.
Найти площадь ромба.
Повторение (2)
1
S ABC AC BD
2
1
S ABC 12 7 42
2
Ответ: 42.
14
15. Повторение
Ромб – это параллелограмм с равнымисторонами
Площадь ромба равна половине произведения
его диагоналей
15
16. Модуль «ГЕОМЕТРИЯ» №11
ВАH
С
14
ABCD – трапеция. ВС в 2 раза меньше AD.
Найти площадь трапеции
Повторение (2)
D
S ABCD
AD BC
BH
2
ВС=14:2=7
BC=DH=7
S ABCD
14 7
7 73,5
2
Ответ: 73,5.
16
17. Повторение
Трапеция – это четырехугольник, две стороныкоторого параллельны
Площадь трапеции равна произведению
полусуммы оснований на высоту
17
18. Модуль «ГЕОМЕТРИЯ» №11
В60⁰
О
А
С
АС=10.
Найти площадь прямоугольника
D
Повторение (5)
АО=ВО=10:2=5
В ∆АОВ, где ∠ВАО= ∠АВО=(180⁰-60⁰):2=60⁰ ⇒
АВ=5
По теореме Пифагора в ∆АВD
ÀD ÂD2 AÂ2 102 52 5 3
S AB AD 5 5 3 25 3
Ответ: 25 3 .
18
19. Повторение
Диагонали прямоугольника равны и делятсяточкой пересечения пополам
В равнобедренном треугольнике углы при
основании равны
Если угол разбит на части, то его градусная
мера равна сумме его частей
В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов
Площадь прямоугольника равна произведению
соседних сторон
19
20. Модуль «ГЕОМЕТРИЯ» №11
ВА
М
С
135⁰
8
H
К
D
ABCD – равнобедренная трапеция
MK=8, боковая сторона равна 5.
Найти площадь трапеции.
AD BC
MK
8
2
∠АВH=90⁰=135⁰-90⁰=45⁰ ⇒
Повторение (4)
∠ВАH= ∠АВC=45⁰
По теореме Пифагора в ∆АВH, где AH=BH=х ⇒
1
1 2
5
2
BH
AÂ
5
2
2
2
5
AD BC
20 2
S ABCD
BH ⇒ S ABCD 8
2
2
Ответ: 20 2 .
20
21. Повторение
Площадь трапеции равна произведениюполусуммы оснований на высоту
Средняя линия трапеции равна полусумме
оснований
Если в прямоугольном треугольнике острый угол
равен 45⁰, то и другой острый угол равен 45⁰
В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов
21
22. Модуль «ГЕОМЕТРИЯ» №11
СP∆ABC =98.
Повторение (4)
25
А
H
Найти S∆ABC
В
АВ=P∆ABC –2ВС=98–2∙25=48
Т.к. ∆АВС равнобедренный, то АH=HB=48:2=24
По теореме Пифагора в ∆АСH
CH AC 2 AH 2 252 242 7
1
S ABC AB CH
2
1
S ABC 48 7 168
2
Ответ: 168.
22
23. Повторение
Периметр треугольника – это сумма длинсторон треугольника
Высота в равнобедренном треугольнике,
проведенная к основанию является медианой
В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов
Площадь треугольника равна половине
произведения основания на высоту
23
24. Модуль «ГЕОМЕТРИЯ» №11
СА
H
В
В прямоугольном треугольнике высота,
проведенная из вершины прямого угла,
равна медиане, проведенной из того же угла,
АВ=6. Найти S∆ABC
Повторение (4)
Если высота треугольника равна медиане, то ∆АВС –
равнобедренный с основанием АВ ⇒ ∠А=∠В=45⁰
∆HBC прямоугольный и равнобедренный, так как∠В=45⁰
⇒ CH=HВ=AB:2=3
1
S ABC AB CH
2
1
S ABC 6 3 9
2
Ответ: 9.
24
25. Повторение
Если высота треугольника является имедианой, то такой треугольник
равнобедренный
Если прямоугольный треугольник
равнобедренный, то его острые углы равны 45⁰
В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов
Площадь треугольника равна половине
произведения основания на высоту
25
26. Модуль «ГЕОМЕТРИЯ» №11
АМодуль «ГЕОМЕТРИЯ» №11
3
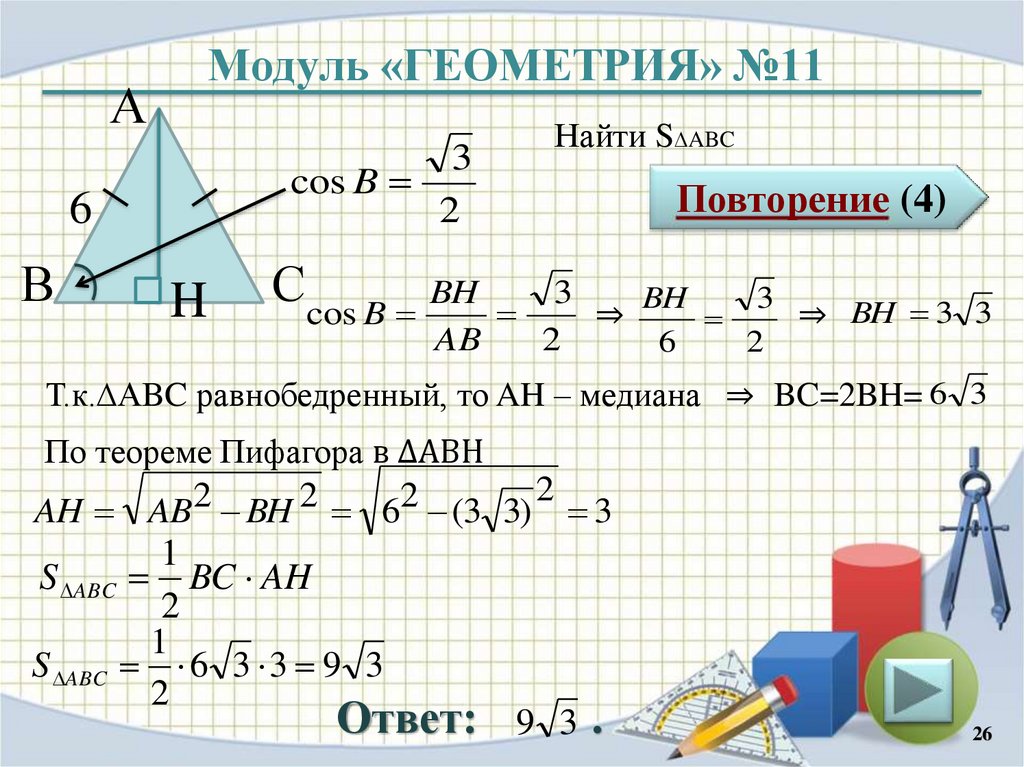
cos B
2
6
В
H
Найти S∆ABC
Повторение (4)
Сcos B BH
3
⇒ BH 3 ⇒ BH 3 3
AB
2
6
2
Т.к.∆АBC равнобедренный, то AH – медиана ⇒ BC=2BH= 6 3
По теореме Пифагора в ∆АВH
2
2
2
2
AH AB BH 6 (3 3) 3
1
S ABC BC AH
2
1
S ABC 6 3 3 9 3
2
Ответ: 9 3 .
26
27. Повторение
Косинус острого угла прямоугольноготреугольника равен отношению прилежащего
катета к гипотенузе
Высота прямоугольного треугольника,
проведенная к основанию, является медианой
В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов
Площадь треугольника равна половине
произведения основания на высоту
27
28. Модуль «ГЕОМЕТРИЯ» №11
АВ
5
D
15
С
Четырехугольник АВСD описан около
четырехугольника, радиуса 4,5.
Найти S∆ABCD.
Повторение (4)
Соединим центр окружности с вершинами четырехугольника
Получим треугольники, высоты которых равны радиусу окружности
AB+DC=AD+BC ⇒
S∆AОB +S∆BOC =S∆COD +S∆AOD
S
⇒
SABCD =2(S∆AОB +S∆BOC)
1
a h
2
S ABCD
1
1
1
2 ( 5 4,5 15 4,5) 2 ( (5 15) 4,5) 90
2
2
2
Ответ: 90.
28
29. Повторение
Если в четырехугольник можно вписатьокружность, то суммы противоположных
сторон четырехугольника равны
Если фигура разбита на части, то площадь
фигуры равна сумме площадей ее частей
Радиус, проведенный в точку касания
перпендикулярен касательной
Площадь треугольника равна половине
произведения основания на высоту
29
30. Модуль «ГЕОМЕТРИЯ» №11
А18
60⁰
В
O
С
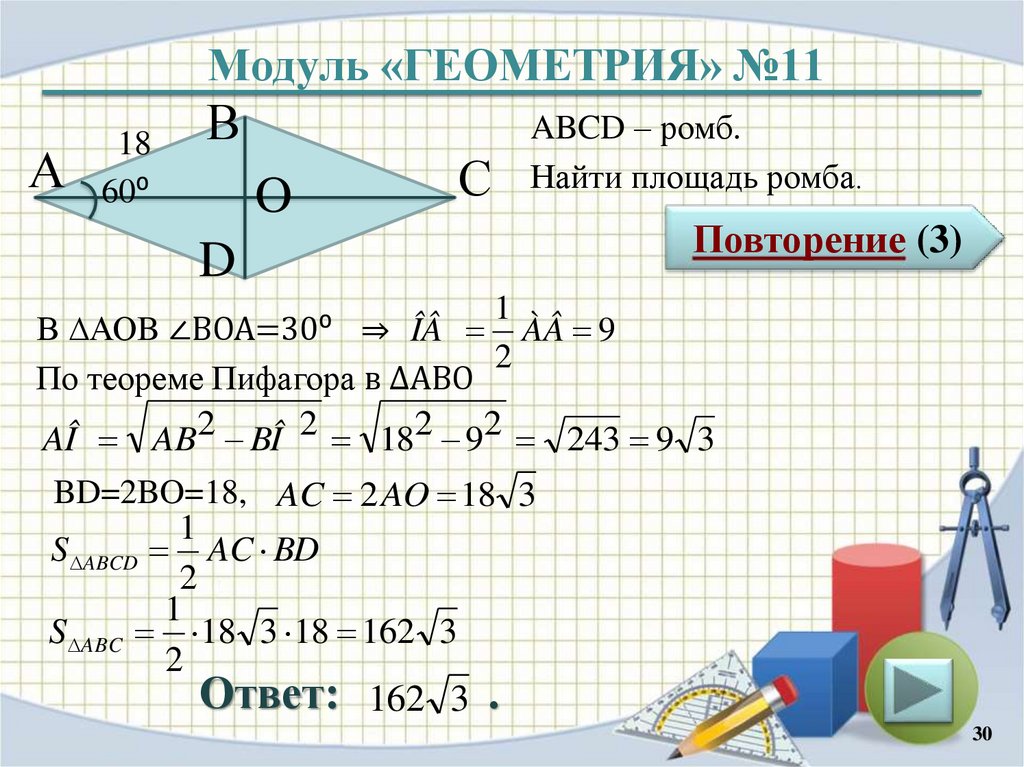
ABCD – ромб.
Найти площадь ромба.
D
Повторение (3)
1
В ∆АОB ∠ВОА=30⁰ ⇒ ÎÂ ÀÂ 9
2
По теореме Пифагора в ∆АВО
AÎ AB2 BÎ 2 182 92 243 9 3
BD=2BO=18, AC 2 AO 18 3
1
S ABCD AC BD
2
1
S ABC 18 3 18 162 3
2
Ответ: 162 3 .
30
31. Повторение
Диагонали ромба перпендикулярны и делятуглы ромба пополам
В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов
Площадь ромба равна половине произведения
его диагоналей
31
32. Модуль «ГЕОМЕТРИЯ» №11
С3
5
А
3
В
5
D
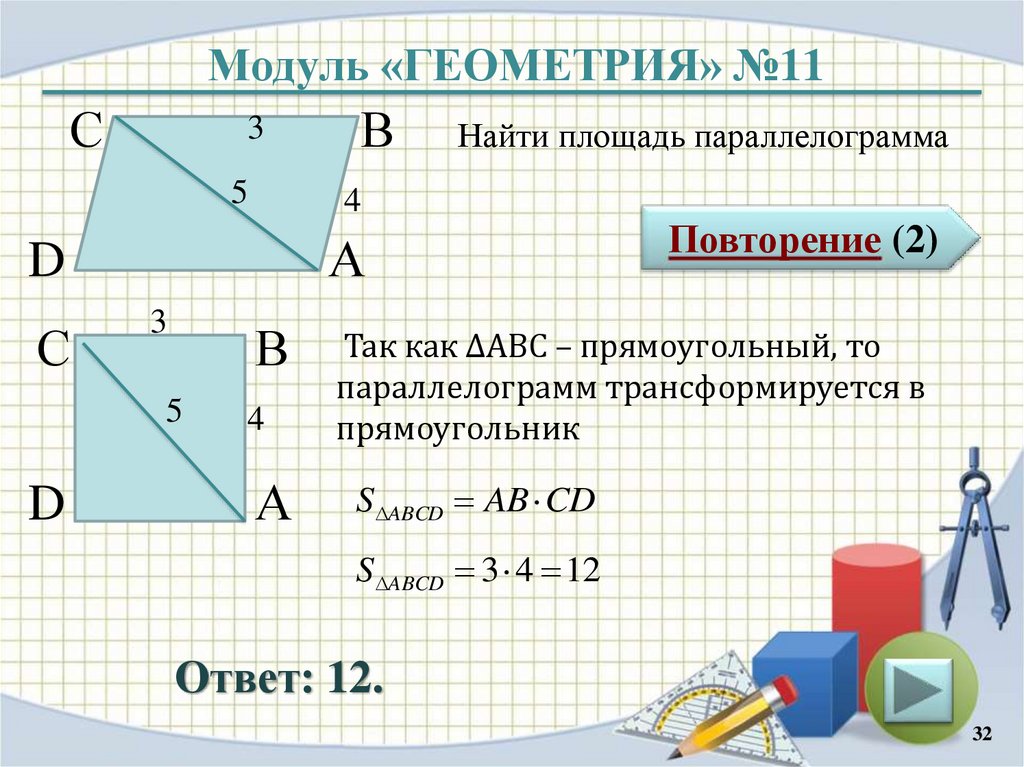
Найти площадь параллелограмма
4
D
С
В
4
А
Повторение (2)
Так как ∆АВС – прямоугольный, то
параллелограмм трансформируется в
прямоугольник
S ABCD AB CD
S ABCD 3 4 12
Ответ: 12.
32
33. Повторение
Треугольник, в котором стороны равны 3,4,5называется Пифагоровым (т.е. треугольник
является прямоугольным)
Площадь прямоугольника равна произведению
его измерений
33
34. Модуль «ГЕОМЕТРИЯ» №11
АO
30⁰
Дуга сектора равна 8π. Найти площадь
сектора.
Повторение (2)
В
Сокр.=360⁰:30⁰∙ 8π=96π
C
Сокр.=2πr ⇒ r
2
S ñåê.
S ñåê.
r
2
96
48
2
360
48 2
0
30
192
0
360
Ответ: 192π .
34
35. Повторение
Длина окружности равна удвоенномупроизведению числа π на радиус окружности
r
Площадь кругового сектора
S ñåê.
вычисляется по формуле
360
2
35
36. Модуль «ГЕОМЕТРИЯ» №11
Найти площадь кольца3
5
Повторение (2)
S r2
Sêîëüöà r12 r22 ⇒
Sêîëüöà 52 32 (25 9) 16
Ответ: 16 .
36
37. Повторение
Площадь круга равна произведению числа πна квадрат радиуса круга
Если фигура разделена на части, то его
площадь равна сумме площадей его частей
37
38. Модуль «ГЕОМЕТРИЯ» №11
СМодуль «ГЕОМЕТРИЯ» №11
6 3
А
В
Найти площадь круга, вписанного в
равносторонний треугольник
Повторение (3)
a3 6 3
6
a3 R 3 ⇒ R
3
3
1
1800
1
0
r Rñîs
R cos 60 R ⇒ r 6 3
2
n
2
S r2
S 3 9
2
Ответ: 9 .
38
39. Повторение
Сторона правильного треугольника, в которыйвписана окружность, равна a3 R 3
Радиусы вписанной и описанной окружности
около правильного многоугольника связаны
1800
формулой r Rñîs
n
Площадь круга равна произведению числа π
на квадрат радиуса круга
39
40. Модуль «ГЕОМЕТРИЯ» №11
Найти площадь круга, вписанного вквадрат со стороной 18.
18
Повторение (3)
a4
18
9 2
2
2
0
2
180
2
0
9 2 9
r Rñîs
R cos 45
R ⇒ r
2
n
2
a4 R 2
⇒ R
S r2
S 9 81
2
Ответ: 81 .
40
41. Повторение
Сторона правильного четырехугольника, вкоторый вписана окружность, равна a R 2
4
Радиусы вписанной и описанной окружности
около правильного многоугольника связаны
1800
формулой r Rñîs
n
Площадь круга равна произведению числа π
на квадрат радиуса круга
41

































 mathematics
mathematics








