Сфера и шар. Вывод уравнения сферы

1. Сфера и шар

2. Цель обучения:

• 10.4.10 знать уравнение сферы и применять
его при решении задач.

3.

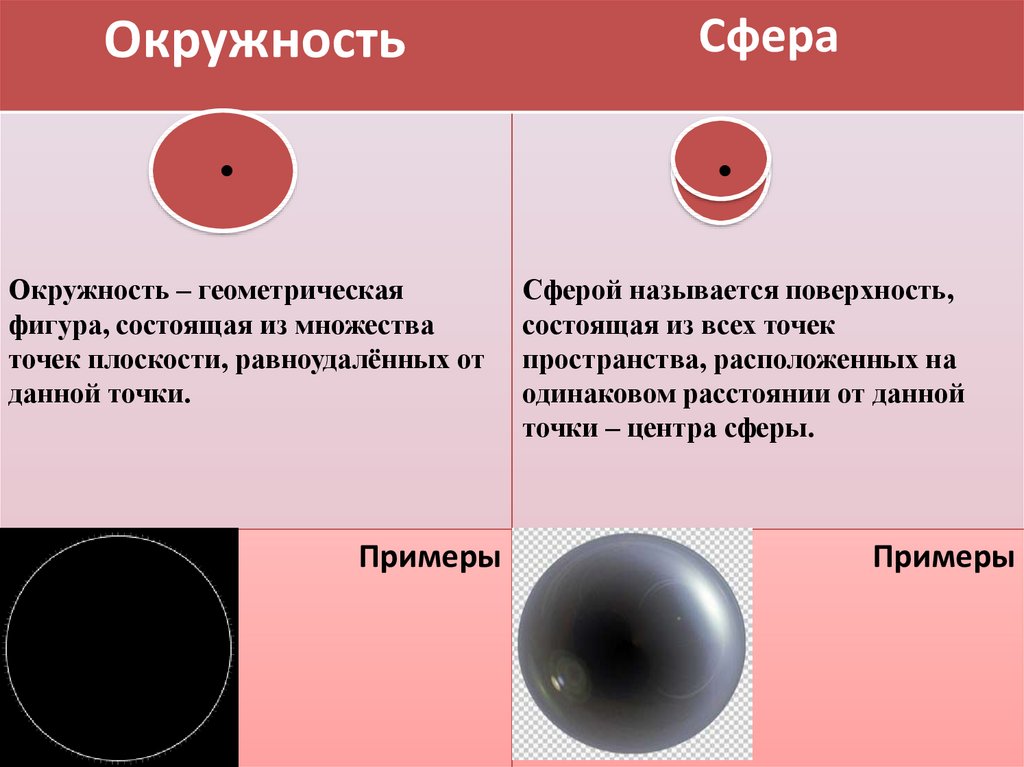
Окружность
Окружность – геометрическая
фигура, состоящая из множества
точек плоскости, равноудалённых от
данной точки.
Примеры
Сфера
Сферой называется поверхность,
состоящая из всех точек
пространства, расположенных на
одинаковом расстоянии от данной
точки – центра сферы.
Примеры

4.

R
О
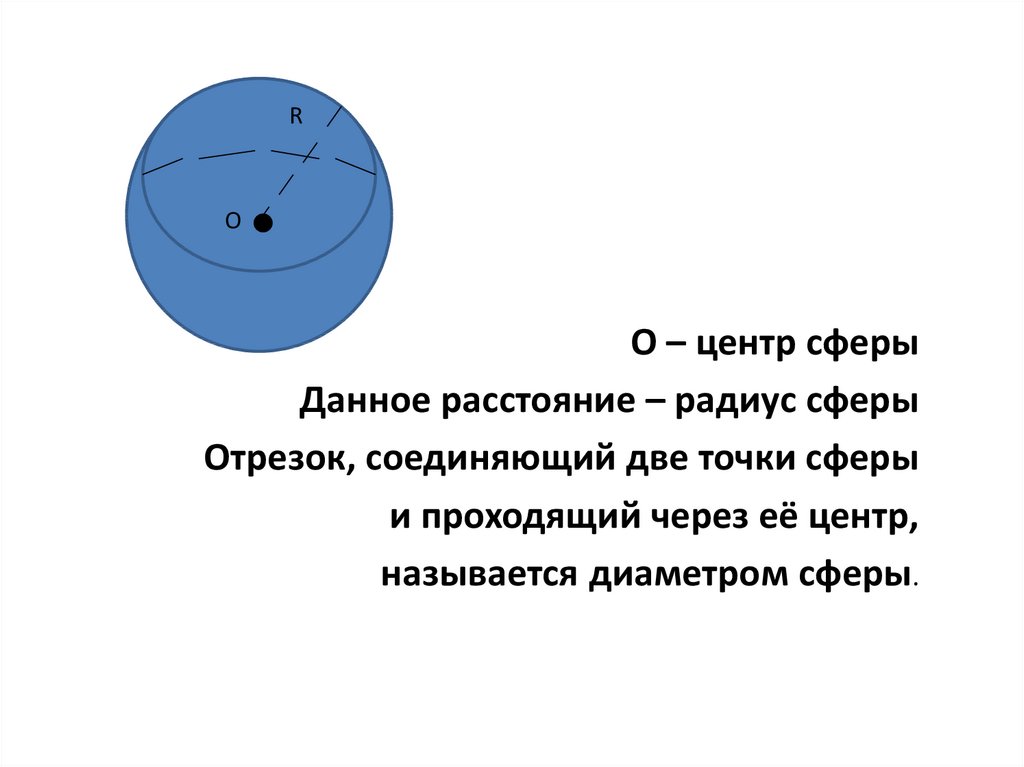
О – центр сферы
Данное расстояние – радиус сферы
Отрезок, соединяющий две точки сферы
и проходящий через её центр,
называется диаметром сферы.

5.

6.

Круг
Дайте определение
круга
Шар
Дайте определение шара
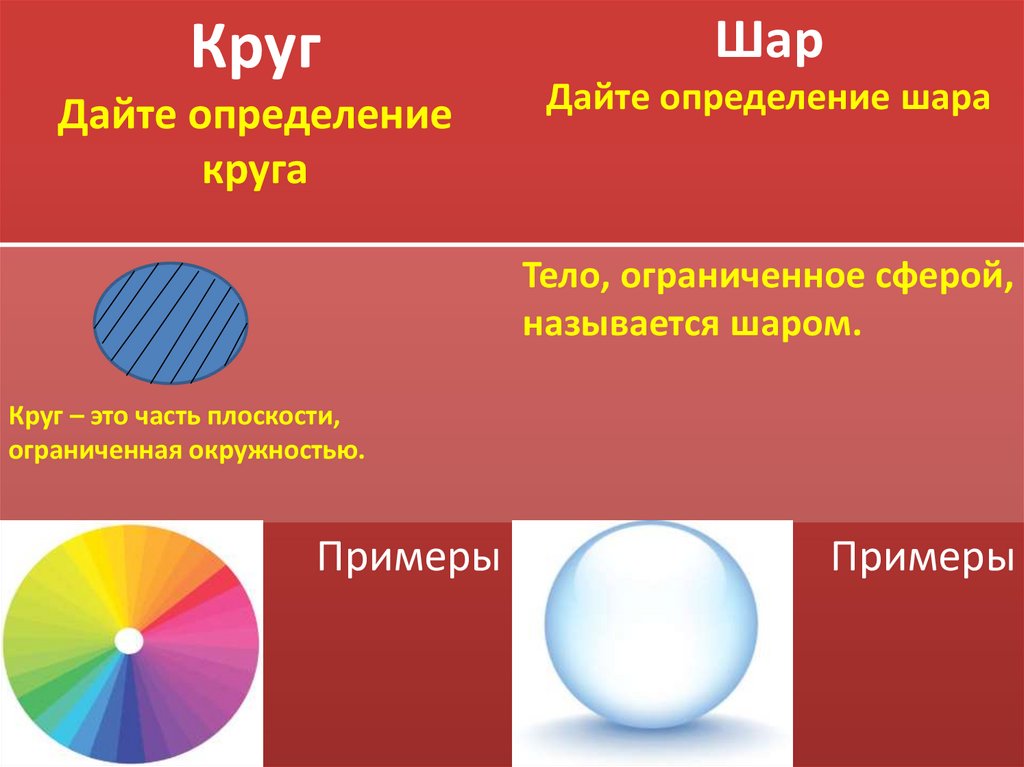
Тело, ограниченное сферой,
называется шаром.
Круг – это часть плоскости,
ограниченная окружностью.
Примеры
Примеры

7.

8. Сфера, как тело вращения

А
С
В
Вывод: Сфера может быть получена
вращением полуокружности вокруг её
диаметра.

9.

Сфера может быть
получена вращением
полуокружности
вокруг её диаметра, а
шар – вращением
полукруга вокруг его
диаметра.

10. Уравнение сферы

z
M (x; y; z)
Дано : сфера, R, С
М (x; y; z)
Доказать:
,
( x0 ; y0 ; z0 )
( x x0 ) 2 ( y y0 ) 2 ( z z0 ) 2 R 2
C (x 0 ; y0 ; z0 ) y
Доказательство:
1)Найти расстояние от точки М ( x; y; z ) до
x
MC ( x x0 ) 2 ( y y0 ) 2 ( z z0 ) 2
2) MC=R
3)
( x x0 ) 2 ( y y0 ) 2 ( z z0 ) 2 R
( x x0 ) 2 ( y y0 ) 2 ( z z0 ) 2 R 2
C ( x0 ; y0 ; z0 )

11. Уравнение сферы с центром в начале координат

x²+y²+z²=R²