Сфера и шар

1.

СФЕРА и ШАР

2. Вспомните, что такое

• Окружность
• Круг

3.

Определение сферы
• Сферой называется поверхность, состоящая из всех
точек пространства, расположенных на данном
расстоянии (R) от данной точки (центра т.О).
R
О
диаметр

4.

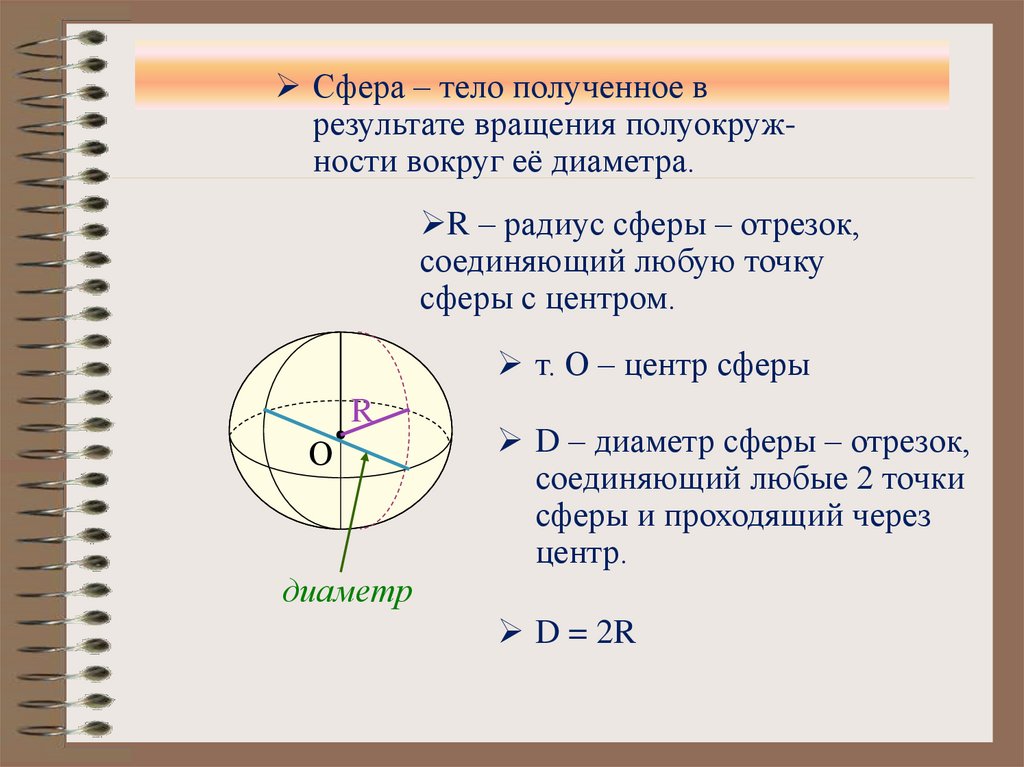
Сфера – тело полученное в
результате вращения полуокружности вокруг её диаметра.
R – радиус сферы – отрезок,
соединяющий любую точку
сферы с центром.
т. О – центр сферы
R
О
D – диаметр сферы – отрезок,
соединяющий любые 2 точки
сферы и проходящий через
центр.
диаметр
D = 2R

5. Шар

• Тело, ограниченное сферой,
называется шаром.
• Центр, радиус и диаметр
сферы являются также
центром, радиусом и
диаметром шара.
• Шар радиуса R и центром О
содержит все точки
пространства, которые
расположены от т. О на
расстоянии, не превышающем
R.

6. Исторические сведения о сфере и шаре

• Оба слова «шар» и «сфера» происходят от греческого слова
«сфайра» - мяч.
• В древности сфера и шар были в большом почёте.
Астрономические наблюдения над небесным сводом вызывали
образ сферы.
• Пифагорейцы в своих полумистических рассуждениях
утверждали, что сферические небесные тела располагаются
друг от друга на расстоянии пропорциональном интервалам
музыкальной гаммы. В этом усматривались элементы мировой
гармонии. Отсюда пошло выражение «музыка сферы».
• Аристотель считал, что шарообразная форма, как наиболее
совершенная, свойственна Солнцу, Земле, Луне и всем
мировым телам. Так же он полагал, что Земля окружена рядом
концентрических сфер.
• Сфера, шар всегда широко применялись в различных областях
науки и техники.

7. Проанализируйте определения сферы и шара

• Приведите примеры сферы в
окружающем нас мире
• Приведите примеры шара

8. Как изобразить сферу?

R
О
• Отметить центр сферы (т.О)
• Начертить окружность с
центром в т.О (это мы учились
делать на алгебре)
• Изобразить видимую горизонтальную дугу
• Изобразить невидимую
горизонтальную дугу
• Провести радиус сферы R

9. Вспомним уравнение окружности

• Зададим прямоугольную
систему координат Оxy
у
М(х;у) • Построим окружность c центром
в т. С и радиусом r
• Расстояние от произвольной. М
(х;у) до т.С вычисляется по
формуле:
С(х0;у0)
• МС =
О
х
(x – x0)2 + (y – y0)2
МС = r , или МС2 = r2
следовательно уравнение
окружности имеет вид:
(x – x0)2 + (y – y0)2 = r2

10. Уравнение сферы

• Зададим прямоугольную систему
координат Оxyz
• Построим сферу c центром в т. С
и радиусом R
z
М(х;у;z)
R
C(x0;y0;z0)
у
х
МС =
(x – x0)2 + (y – y0)2 + (z – z0)2
• МС = R , или МС2 = R2
следовательно уравнение
сферы имеет вид:
(x – x0)2 + (y – y0)2 + (z – z0)2 = R2

11.

• Задача 1.
Зная координаты центра С(2;-3;0) и
радиус сферы R=5, записать уравнение
сферы.

12. Взаимное расположение сферы и плоскости

• Найдите в учебнике информацию о возможных вариантах
взаимного расположения сферы и плоскости
• От чего зависит взаимное расположение сферы и
плоскости
• Что можно сказать о взаимном расположении сферы
радиуса 5ед. и плоскости, находящейся на расстоянии 3ед.
от сферы

13.

Задача 2.
Шар радиусом 41 дм пересечен плоскостью,
находящейся на расстоянии 9 дм от центра. Найти
радиус сечения

14. Площадь сферы

Площадь сферы радиуса R:
Sсф=4πR2

15.

Задача 3
Найти площадь поверхности сферы,
радиус которой = 6 см.