Еще одна формула корней квадратного уравнения

1.

Тема урока:
Цель урока:
«Еще одна формула корней квадратного
уравнения»
Вывести формулу (II) нахождения корней квадратного
уравнения с четным вторым коэффициентом; формировать
умения применять формулы I и II для решения квадратных
уравнений
Девиз урока:
«Думать - коллективно!
Решать - оперативно!
Отвечать - доказательно!
Бороться - старательно!
И открытия нас ждут обязательно! »

2.

.
Актуализация знаний
ax bx c 0
ax 2 bx 0 ax 2 0
2
ax c 0.
2
Не всегда уравненья
Разрешают сомненья
Но итогом сомненья
Может быть озаренье
3.Что
1.Что
такое
такое
корень
уравнение?
уравнения?
7.Как
5.Почему
получаются
коэффициент
неполные
а не
9.Какие
уравнения
называются
квадратные
может равняться
уравнения?
нулю?
неполными
квадратными
уравнениями?
10.Сколько
6.Какие
4.Какое
существуют
уравнение
корнейчисла
может
называется
квадратные
8.Как
называются
а,иметь
в, с?
2.Что значит решить уравнение?
уравнения?
уравнение
квадратным?
каждого вида?

3.

Разложение
левой части на множители;
Применение
теоремы
Виета
По сумме коэффициентов
квадратного уравнения
Способы
решения
квадратных
уравнений
Метод выделения
полного квадрата;
Графический.
Введение
новой переменной
Применение формул корней квадратного
уравнения;

4.

x 10 x 16 0
2
2
а b
a2 2ab b2
а b 2 a2 2ab b2
x 2 * 5 x 25 25 16 0,
2
x 5 9 0,
2
x 5 9,
2
x 5 3; x 5 3,
x1 2; x2 8
Ответ : x1 2; x2 8.

5.

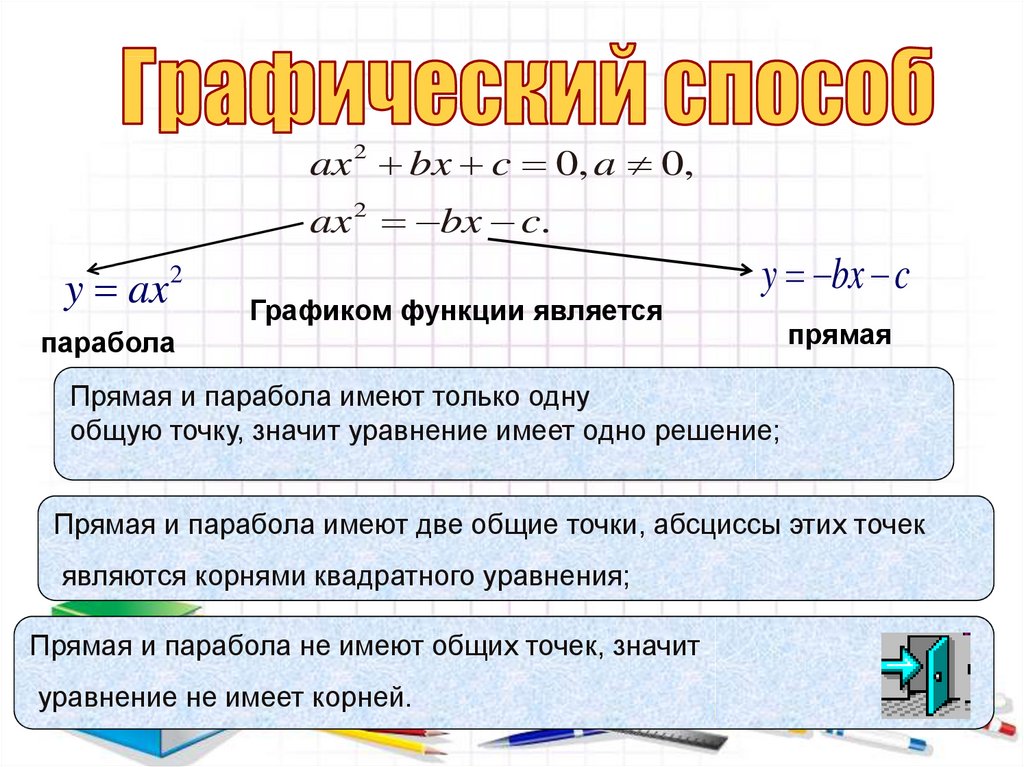
ax 2 bx c 0, a 0,
ax 2 bx c.
y ax
2
Графиком функции является
y bx c
парабола
прямая
Прямая и парабола имеют только одну
общую точку, значит уравнение имеет одно решение;
Прямая и парабола имеют две общие точки, абсциссы этих точек
являются корнями квадратного уравнения;
Прямая и парабола не имеют общих точек, значит
уравнение не имеет корней.

6.

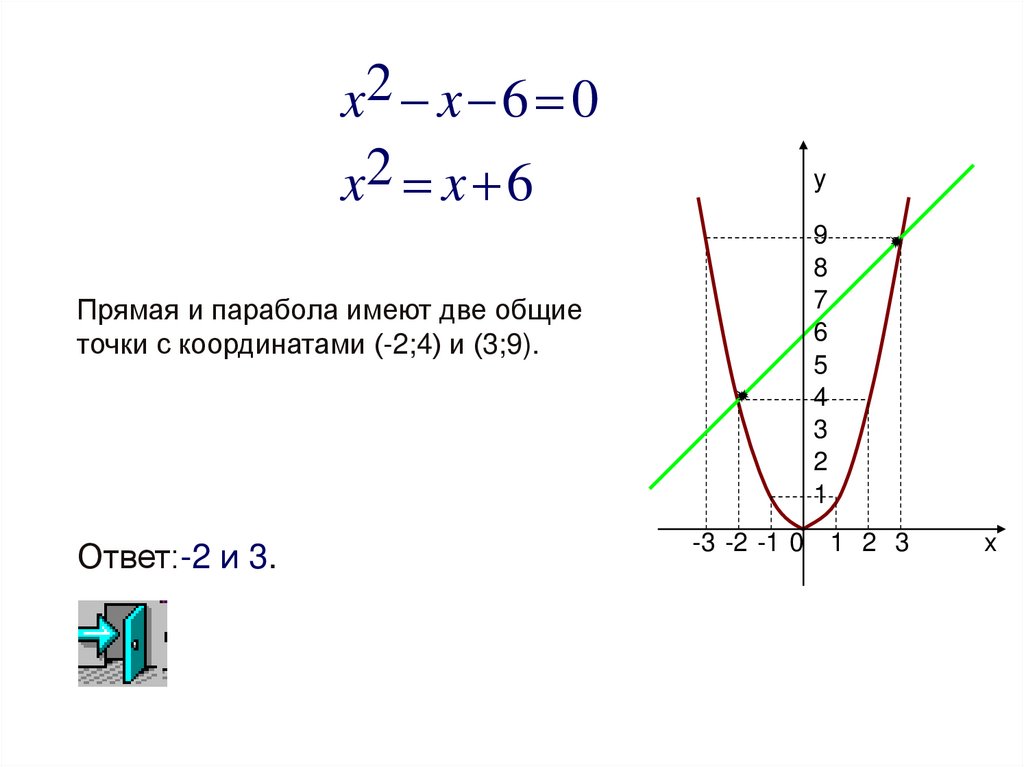
x2 x 6 0
x2 x 6
y
9
8
7
6
5
4
3
2
1
Прямая и парабола имеют две общие
точки с координатами (-2;4) и (3;9).
Ответ:-2 и 3.
-3 -2 -1 0
1 2 3
x

7.

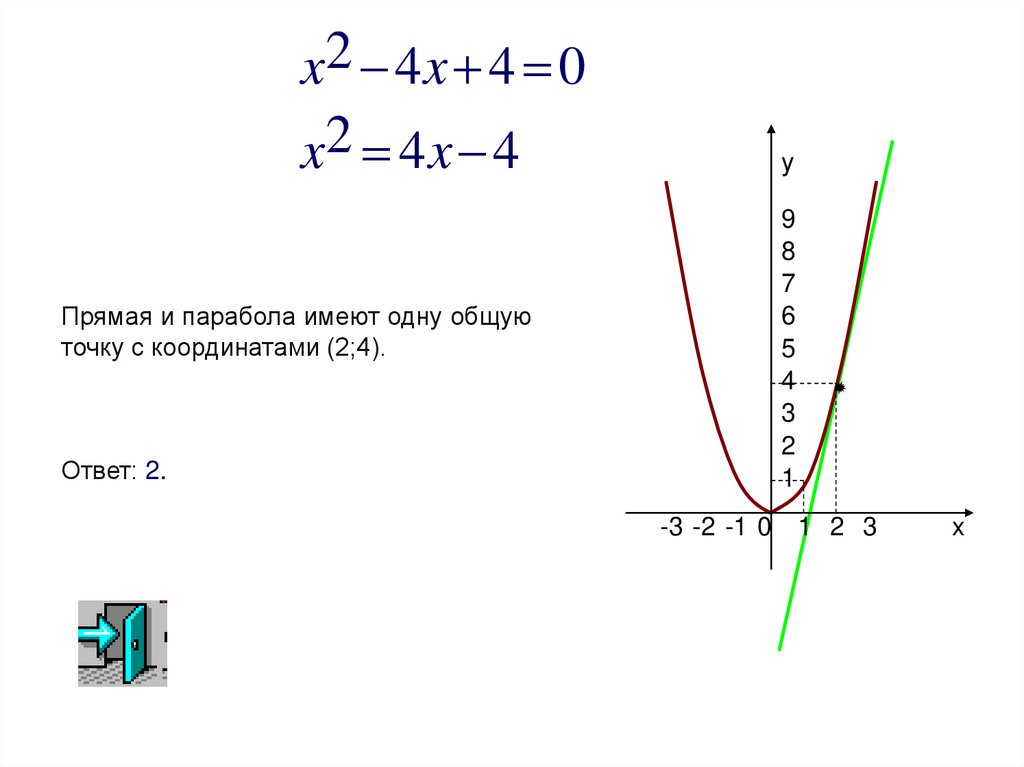
x2 4 x 4 0
x2 4 x 4
y
9
8
7
6
5
4
3
2
1
Прямая и парабола имеют одну общую
точку с координатами (2;4).
Ответ: 2.
-3 -2 -1 0
1 2 3
x

8.

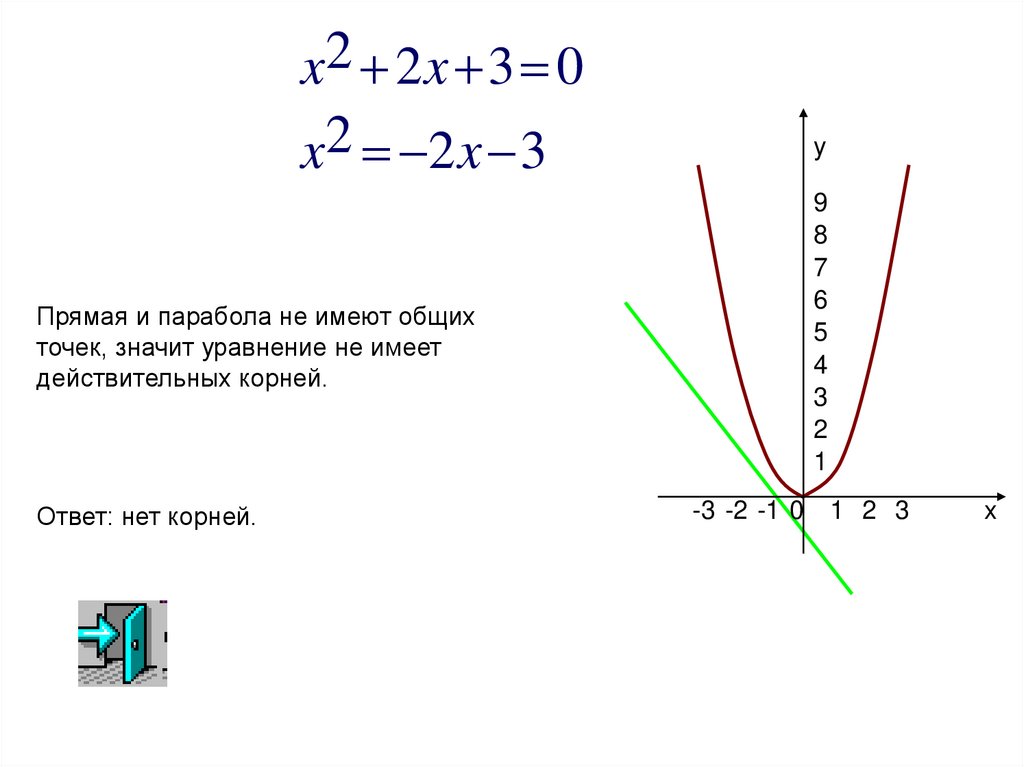
x2 2 x 3 0
x2 2 x 3
y
9
8
7
6
5
4
3
2
1
Прямая и парабола не имеют общих
точек, значит уравнение не имеет
действительных корней.
Ответ: нет корней.
-3 -2 -1 0
1 2 3
x

9.

D= b2- 4ас
1. Если b2-4ac >0, то квадратное уравнение
имеет два различных действительных корня
>
2. Если b2-4ac =0, то квадратное уравнение имеет
два совпадающих действительных корня.
=
3. Если b2-4ac <0, то квадратное уравнение
не имеет действительных корней.
<

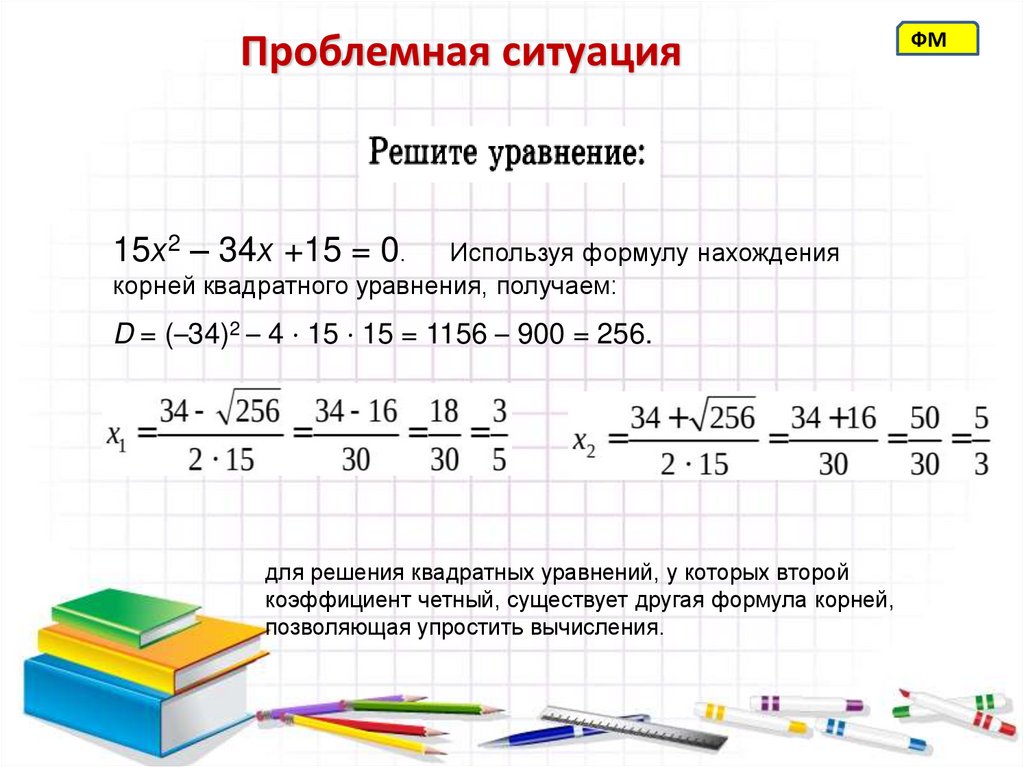
10. Проблемная ситуация

15х2 – 34х +15 = 0.
Используя формулу нахождения
корней квадратного уравнения, получаем:
D = (–34)2 – 4 · 15 · 15 = 1156 – 900 = 256.
для решения квадратных уравнений, у которых второй
коэффициент четный, существует другая формула корней,
позволяющая упростить вычисления.
ФМ

11.

ax 2 bx c 0
b b2 4ac
x1,2
.
2a
D b 4ac – неотрицательное число
2
b - четное число, b=2k
Оказывается, если b четное
число, то данную формулу можно
упростить
2k (2k ) 2 4ac 2k 4k 2 4ac 2k 4(k 2 ac)
x1,2
2a
2a
2a
2
2
2
k
k
ac
2k 2 k ac
k k 2 ac
.
2a
a
2a
k k 2 ac
x1,2
.
a
a 1: x1,2 k k 2 c .
x2 2kx c 0

12. Изучение нового материала

Мы получили, что корнями уравнения
является пара чисел:
Преимущества данной формулы, на первой взгляд, не так и заметны, но
на самом деле при вычислении используются числа поменьше, под знаком корня
квадратного нам не надо доумножать на 4, в знаменателе мы делим только на
коэффициент а.
Самым удобным использование полученной формулы, представляется
при равенстве старшего коэффициента единице.
Для уравнения
корнями будут служить пара чисел:

13.

Первичное закрепление изученного материала
После вывода формулы возвращаемся к решенному уравнению и
применяем новую формулу:
15х2 – 34х +15 = 0 ;
15х2 – 2*17х +15 = 0
D = (–17)2 – 15 · 15 = 289 – 225 = 64;
Решить уравнение двумя способами:

14. Проверка

Мы сравнили, формулы корней квадратного уравнения на конкретном
примере.
Пример 1. Решить уравнение:
Решение.
Способ 1. Решим данное уравнение формулой, которой использовали
раньше:
Способ 2. Решим с помощью формулы полученной на данном уроке:
Ребята, согласитесь, вторым способом найти решение оказалось гораздо
проще. У данного способа только один недостаток, в том что, в случае нечетного
коэффициента b, этот способ не применим.

15.

физминутка
Выполним задание,
Задержим дыхание.
Раз, два, три, четыре –
Снова дышим:
Глубже, шире…
глубоко вдохнули.
спину потянули,
руки вверх подняли
радугу нарисовали
повернулись на восток,
продолжаем наш урок

16.

Решите уравнения:
1.
2.
3.
4.
5.
3х2+17х-6=0;
5х2+38х-16=0;
24х2+58х-5=0;
6х2-27х+12=0
x2+8x+10=0