Similar presentations:
Метод координат. Нахождение углов
1. МеТОД КООРДИНАТ В ЗАДАЧАХ С2
МЕТОД КООРДИНАТ ВЗАДАЧАХ С2
Нахождение углов.
2.
В задаче C2 рассматриваются многогранники,на основе которых,
как правило, нужно найти одну из следующих
величин:
•Угол между скрещивающимися прямыми —
•это угол между двумя прямыми, которые
• пересекаются в одной точке и параллельны
данным прямым.
•Угол между прямой и плоскостью —
• это угол между самой прямой и
• ее проекцией на данную плоскость.
•Угол между двумя плоскостями —
•это угол между прямыми, которые лежат в данных
плоскостях
и перпендикулярны линии пересечения
этих плоскостей.
Прямые всегда задаются двумя точками
на поверхности или
внутри многогранника, а плоскости — тремя.
Сами многогранники всегда задаются длинами
своих граней.
3.
Для того, чтобы использовать метод координат,надо хорошо знать формулы. Их три:
•Главная формула — косинус угла φ между
•векторами a = (x1; y1; z1) и b = (x2; y2; z2):
•Уравнение плоскости в трехмерном пространстве: Ax + By + Cz + D = 0,
где A, B, C и D — действительные числа, причем, если плоскость проходит
через начало координат, D = 0. А
если не проходит, то D = 1.
•Вектор, перпендикулярный к плоскости Ax + By + Cz + D = 0,
имеет координаты: n = (A; B; C) и
называется вектором нормали к плоскости.
4.
Задача. Найти косинус угла между векторами a = (4; 3; 0) и b = (0; 12; 5).Решение.
Поскольку координаты векторов нам даны, подставляем их в первую
формулу:
Ответ: 36/65
5.
Задача.Составить уравнение плоскости, проходящей через точки
M = (2; 0; 1), N = (0; 1; 1) и K = (2; 1; 0),
если известно, что она не проходит через начало координат.
Решение.
Общее уравнение плоскости: Ax + By + Cz + D = 0, но,
поскольку искомая плоскость не проходит через начало координат — точку
(0; 0; 0)
то положим D = 1.
Поскольку эта плоскость проходит через точки M, N и K, то координаты этих
точек
должны обращать уравнение в верное числовое равенство.
Подставим вместо x, y и z координаты точки M = (2; 0; 1). Имеем:
A · 2 + B · 0 + C · 1 + 1 = 0 ⇒ 2A + C + 1 = 0;
Аналогично, для точек N = (0; 1; 1) и K = (2; 1; 0) получим уравнения:
A · 0 + B · 1 + C · 1 + 1 = 0 ⇒ B + C + 1 = 0;
A · 2 + B · 1 + C · 0 + 1 = 0 ⇒ 2A + B + 1 = 0;
6.
Итак, у нас есть три уравнения и три неизвестных.Составим и решим систему уравнений:
Получили, что уравнение плоскости имеет вид:
− 0,25x − 0,5y − 0,5z + 1 = 0.
Ответ: − 0,25x − 0,5y − 0,5z + 1 = 0
7.
Задача.Плоскость задана уравнением 7x − 2y + 4z + 1 =
0. Найти координаты вектора,
перпендикулярного данной плоскости.
Решение. Используя третью формулу, получаем
n = (7; − 2; 4)
Ответ: n = (7; − 2; 4)
8.
Вычисление координат векторовТеорема. Чтобы найти координаты вектора,
надо из координат его конца вычесть координаты начала.
Задача. В пространстве расположены три точки, заданные
своими координатами: A = (1; 6; 3), B = (3; − 1; 7) и C = (− 4; 3; − 2).
Найти координаты векторов AB, AC и BC.
Решение. Рассмотрим вектор AB: его начало находится в точке A,
а конец — в точке B. Следовательно, чтобы найти его координаты,
надо из координат точки B вычесть координаты точки A:
AB = (3 − 1; − 1 − 6; 7 − 3) = (2; − 7; 4).
Аналогично, начало вектора AC — все та же точка A,
зато конец — точка C. Поэтому имеем:
AC = (− 4 − 1; 3 − 6; − 2 − 3) = (− 5; − 3; − 5).
Наконец, чтобы найти координаты вектора BC,
надо из координат точки C вычесть координаты точки B:
BC = (− 4 − 3; 3 − (− 1); − 2 − 7) = (− 7; 4; − 9).
Ответ: AB = (2; − 7; 4); AC = (− 5; − 3; − 5); BC = (− 7; 4; − 9)
9.
Введение системы координатСамое замечательное свойство этого метода
заключается в том,
что не имеет никакого значения,
как именно вводить систему координат.
Если все вычисления будут правильными,
то и ответ будет правильным.
Некоторые рекомендации,
как лучше ввести систему координат
для самых часто встречающихся
в задаче C2 многогранников:
10.
11.
12.
13.
14.
15.
16.
Решение задач методом координат упрощает знание опорной задачи:17.
Угол между прямымиа
р
q
b
р
q
cos =
р
- направляющий вектор прямой а
q
- направляющий вектор прямой b
- угол между прямыми
p x1 ; y1 ; z1
q x2 ; y2 ; z2
| x1 x2 + y1 y2 + z1 z 2 |
x12 + y12 + z12 x22 + y22 + z 22
18.
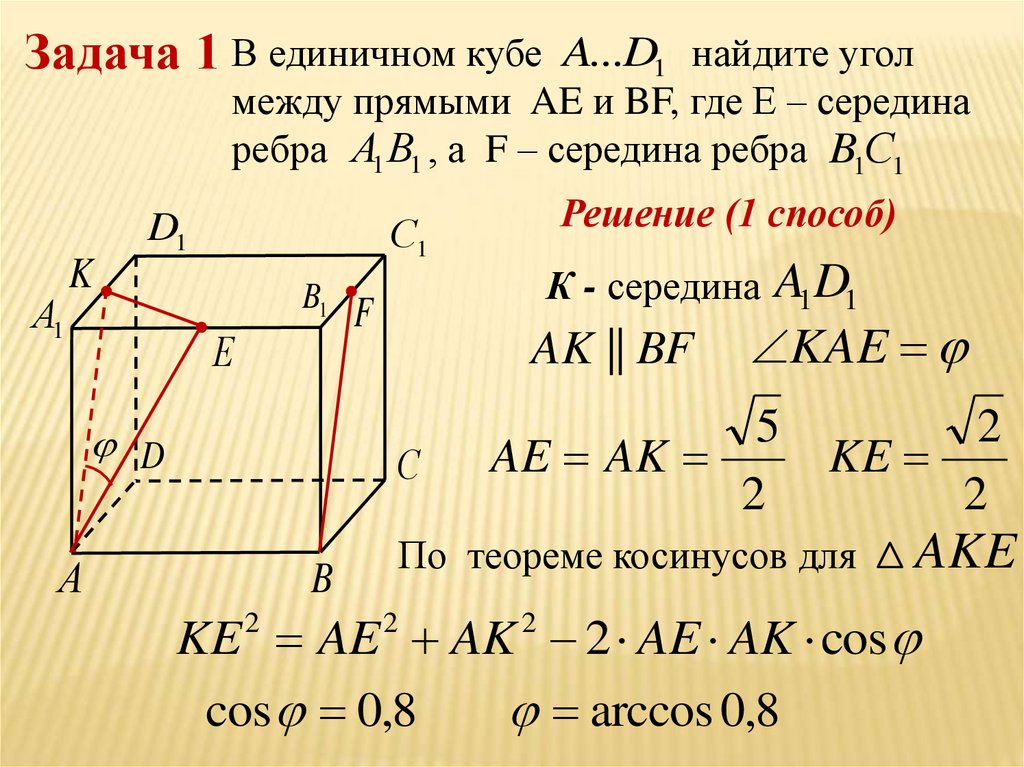
Задача 1 В единичном кубе A...D1найдите угол
между прямыми AE и BF, где Е – середина
ребра А1В1 , а F – середина ребра B1С1
А1
K
Е
A1D1
KAE
К - середина
B1 F
D
А
Решение (1 способ)
С1
D1
AK || BF
С
5
AE AK
2
2
KE
2
По теореме косинусов для
B
AKE
KE AE AK 2 AE AK cos
cos 0,8
arccos 0,8
2
2
2
19.
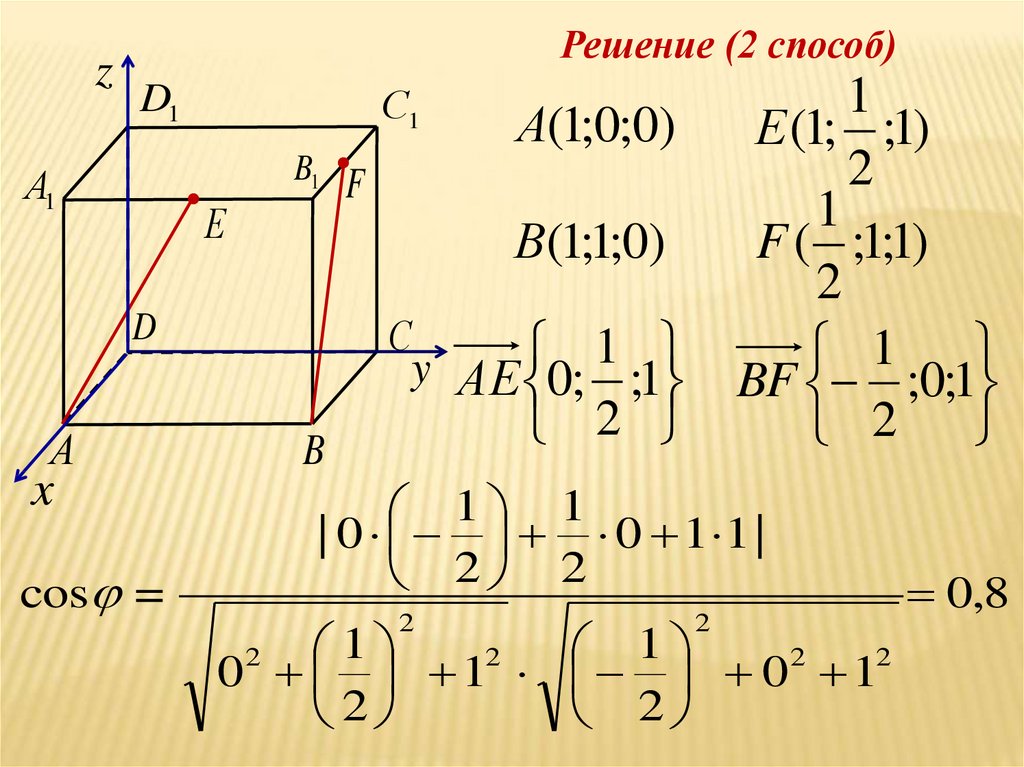
zРешение (2 способ)
1
А(1;0;0)
Е (1; ;1)
B1 F
2
1
В(1;1;0)
F ( ;1;1)
2
С
1
1
y АЕ 0; ;1
BF ;0;1
2
2
B
С1
D1
А1
Е
D
А
x
cos =
1 1
| 0 0 1 1 |
2 2
2
2
1
1
2
2
2
0 1 0 1
2
2
2
0,8
20.
Задача 2 В правильной треугольной призме ABCA1B1C1все ребра которой равны 1, найдите косинус угла между
прямыми AD и CE, где D и E - соответственно
середины ребер A1C1 и B1C1
z С
1
С
E
D
А1
А
1
3
2
B
1
y
B
x
y
1
2
B1
С
Решение.
А
x
21.
Координаты правильной треугольнойпризмы
z С (0;0;1)
1
1 3
B1 ( ; ;1)
2 2
А1 (1;0;1)
С (0;0;0)
y
x
А(1;0;0)
1 3
B( ; ;0)
2 2
22.
Решение.1
D( ;0;1)
2
z С1 (0;0;1)
1 3
Е ( ; ;1)
4 4
1 3
B1 ( ; ;1)
2 2
А1 (1;0;1)
С (0;0;0)
y
x
А(1;0;0)
1 3
B( ; ;0)
2 2
1
АD ;0;1
2
1 3
СЕ ;
;1
4 4
23.
1АD ;0;1
2
cos =
1 3
СЕ ;
;1
4 4
1 1
3
| 0
1 1 |
2 4
4
2
1
1 3
2
2
2
1
0 1
2
4 4
2
cos =
2
7
8
5
5
2
2
0,7
24.
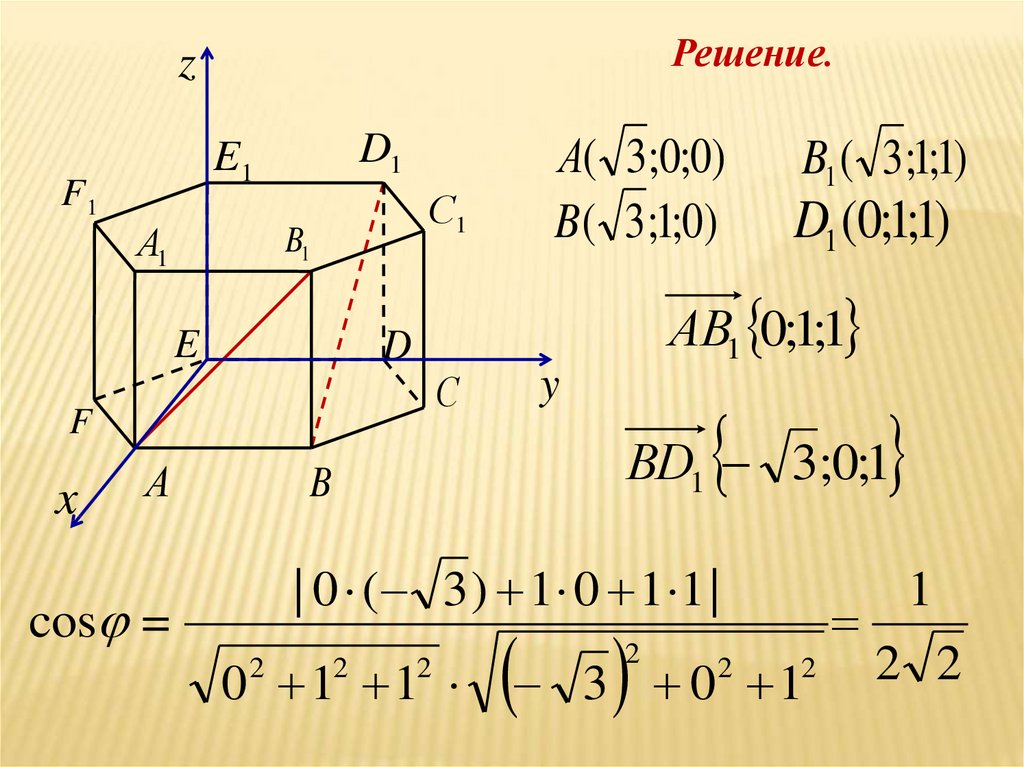
Задача 3 В правильной шестиугольной призме A...F1все ребра которой равны 1, найдите косинус угла между
прямыми AB1 и BD1
Решение.
z
F1
Е
D1
E1
А1
E
F
x
А
B
1
1
2
F
D
D
y
С1
B1
1
С
3
2
1
С
3
2
y
А
x
В
25.
Координаты правильной шестиугольнойпризмы
D
(
0
;
1
;
1
)
E
(
0
;
0
;
1
)
1
1
z
F1
E1
А1
D1
B1
Е
x
С1
D
y
F
А
В
С
А1 ( 3;0;1)
3 3
С1 ( ; ;1)
2 2
B1 ( 3;1;1)
E (0;0;0)
D(0;1;0)
3 1
F1 ( ; ;1)
2 2
3 3
3 1
F ( ; ;0) С ( ; ;0)
2 2
2 2
А( 3;0;0)
B ( 3;1;0)
26.
Решение.z
F1
D1
E1
А1
С1
B1
E
С
F
x
B1 ( 3;1;1)
D1 (0;1;1)
АВ1 0;1;1
D
А
А( 3;0;0)
B ( 3;1;0)
y
ВD1 3;0;1
B
| 0 ( 3 ) 1 0 1 1 |
cos =
0 1 1
2
2
2
3 0
2
2
1
2
1
2 2
27.
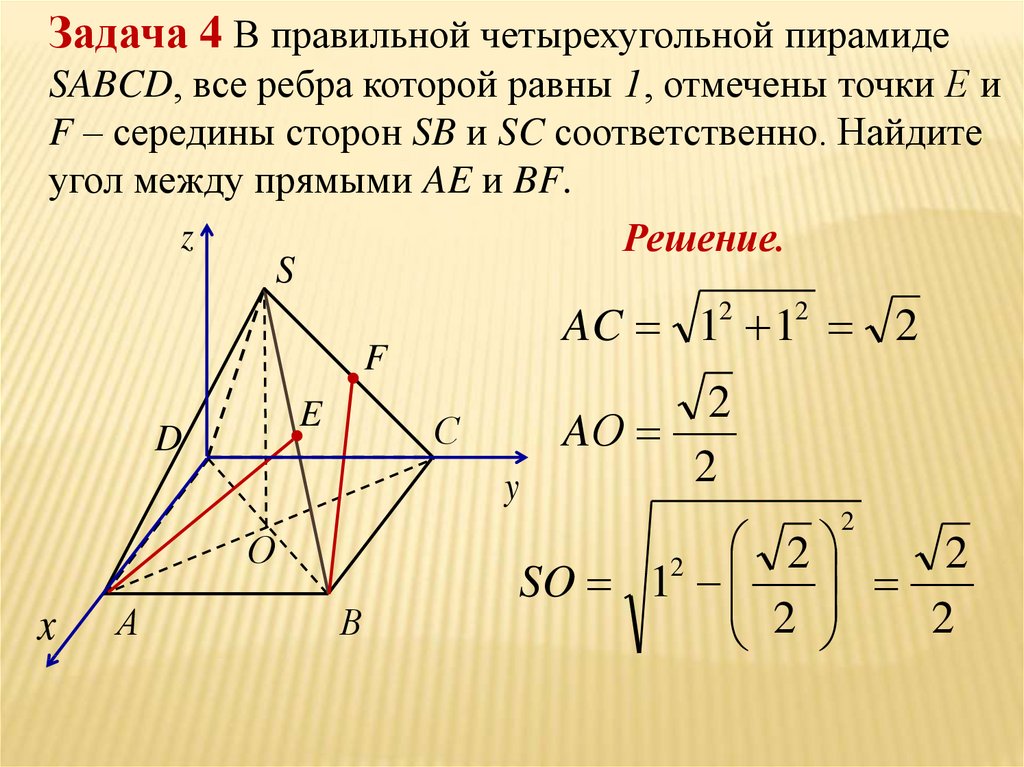
Задача 4 В правильной четырехугольной пирамидеSABCD, все ребра которой равны 1, отмечены точки Е и
F – середины сторон SB и SC соответственно. Найдите
угол между прямыми AE и BF.
z
Решение.
S
F
E
D
О
x
А
В
AC 12 12 2
2
С
AО
2
y
2
2
2
2
SO 1
2
2
28.
Координаты правильной четырехугольнойпирамиды
z
D(0;0;0)
1 1 2
S( ; ;
)
2 2 2
С (0;1;0)
y
x А(1;0;0)
В(1;1;0)
29.
zD
1 1 2
S( ; ;
)
2 2 2
F
E
С (0;1;0)
y
x
А(1;0;0)
В(1;1;0)
1 3 2
АE ; ;
4 4 4
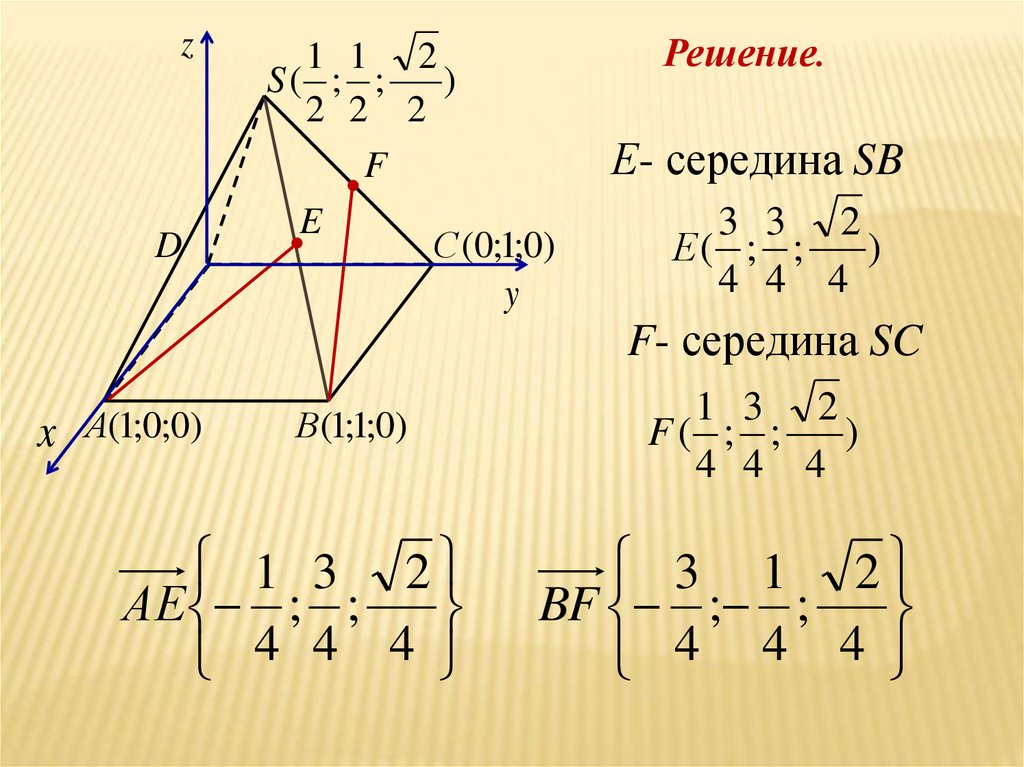
Решение.
Е- середина SB
3 3 2
Е( ; ;
)
4 4 4
F- середина SC
1 3 2
F( ; ;
)
4 4 4
3 1 2
BF ; ;
4 4 4
30.
1 3 2АE ; ;
4 4 4
cos =
3 1 2
BF ; ;
4 4 4
1 3 3 1
2 2
|
|
4 4 4 4 4 4
2
1 3 2
3 1 2
4 4 4
4 4 4
2
2
1
cos
6
2
2
1
arccos
6
2




















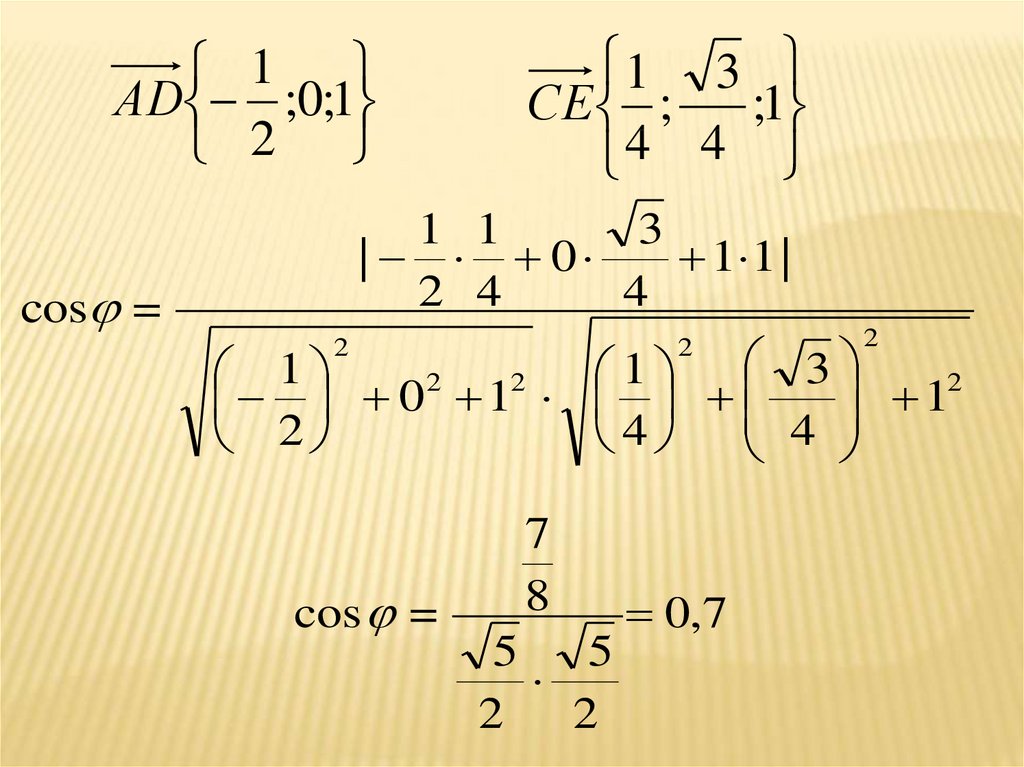



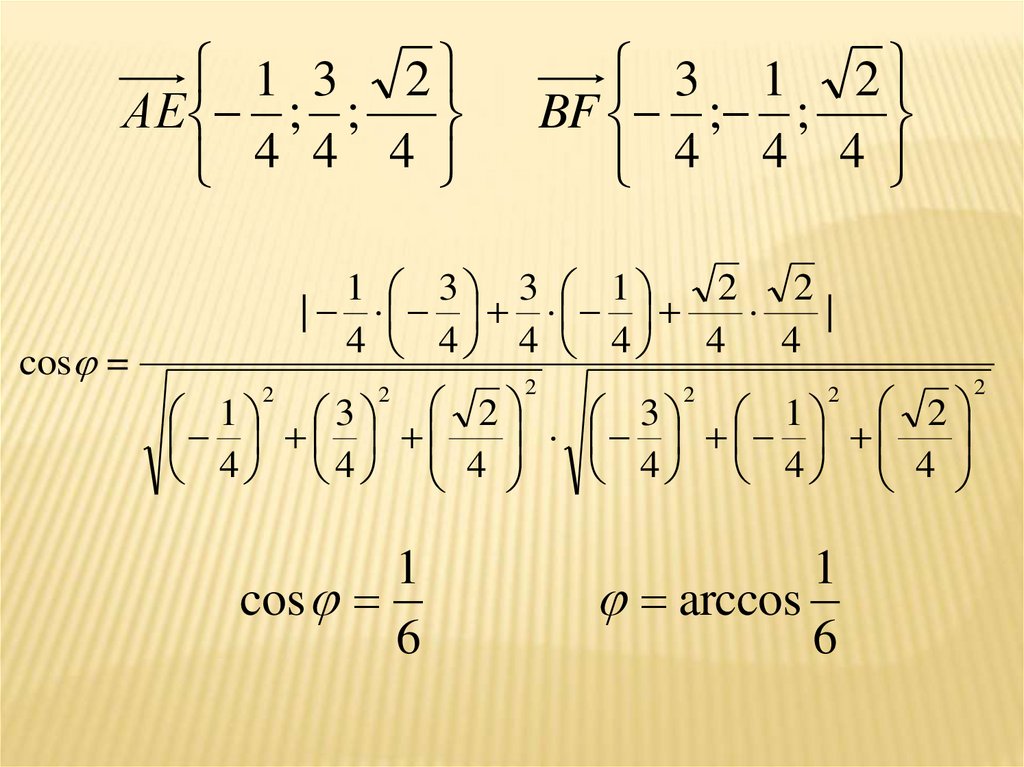
 mathematics
mathematics








