Способы нахождения расстояний и углов в пространстве с помощью метода координат

1.

1. Обобщить виды и способы нахождения
расстояний и углов в пространстве с помощью
метода координат, используя учебные конспекты
и справочные таблицы учебника.
2. Через решение на нахождение расстояний и углов
в
пространстве
двумя
способами
(геометрическим и методом координат) сделать
вывод о преимуществе второго для ряда задач
этого блока.
3. Расширить представление о применении метода
координат в решении стереометрических задач
на построение сечений.

2.

На ребрах BB, AD, CD куба взяты соответственно точки B2, P, Q – середины
ребер. На диагонали А1С1взята точка R1, такая что A1R1 : А1С1 = 3:4.
Считая ребро куба а, найти расстояние
а) B2R1
б) PF, где F середина R1Q.
B1
C
2. Найдем координаты
нужных точек:
O
А(а; 0; 0),RС(0; а; 0), B1(0; 0; а), C1(0; а; а),
B(0; 0; 0), D(а; а; 0), А1(а; 0; а)
1
1
1
А1
D1
B2
B
А
По
формулам
координат
середины отрезка или
1. Введем
систему
координат.
F
деления измерения
отрезка
в данном
За единицу
примемотношении
ребро куба а.
находим О1(а/2; а/2; а),
P(а; а/2; 0),
R1(а/4; 3а/4; а), B2(0; 0; а/2),
C
F(3а/8; 7а/8; а/2), Q(а/2; а; 0).
3. Находим длину отрезка как расстояние
Q
между двумя точками
по соответствующей
формуле. D
P
a 14
R1 B2
4
5а 2
PF
8

3.

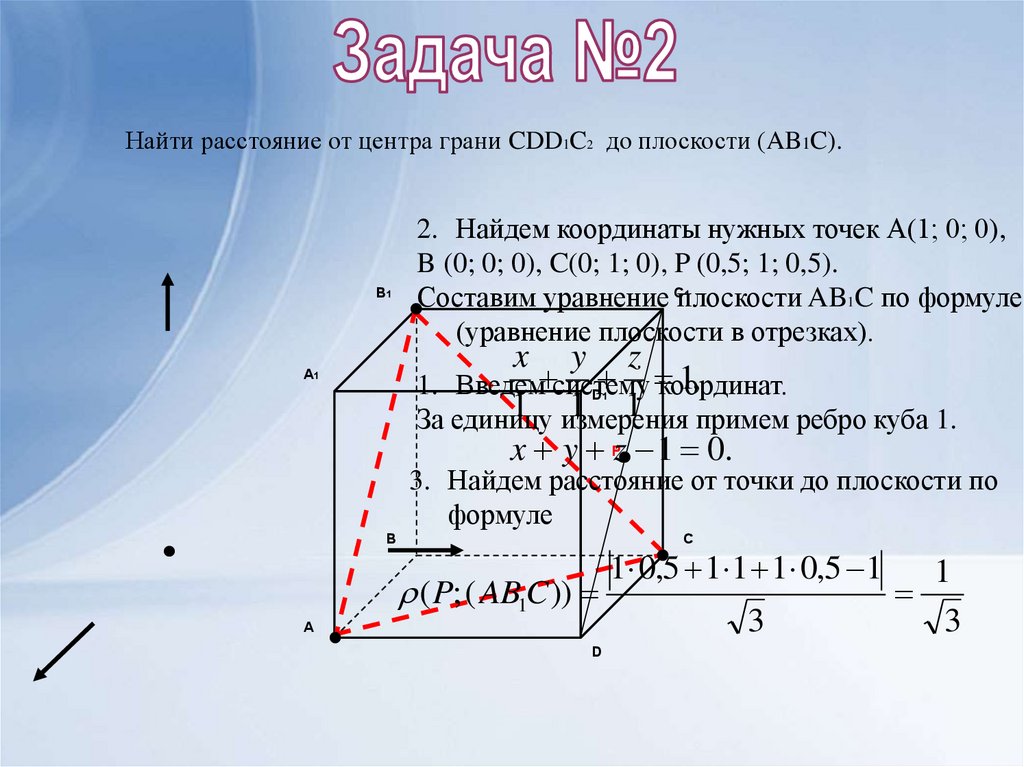
Найти расстояние от центра грани CDD1C2 до плоскости (AB1C).
B1
2. Найдем координаты нужных точек А(1; 0; 0),
B (0; 0; 0), C(0; 1; 0), P (0,5; 1; 0,5).
Составим уравнение Cплоскости AB1C по формуле
(уравнение плоскости в отрезках).
1
x y z
координат.
1,
1. Введем систему
D
1 измерения
1 1
За единицу
примем ребро куба 1.
x y Pz 1 0.
А1
1
3. Найдем расстояние от точки до плоскости по
формуле
B
C
( P; ( AB1C ))
А
D
1 0,5 1 1 1 0,5 1
3
1
3

4.

Расстояние между
двумя точками А и В
AB ( X B X A ) 2 (YB YA ) 2 ( Z B Z A ) 2
Расстояние от
точки А до плоскости α
( A; )
AX 0 AY0 AZ 0
A B C
2
2
2
, где n ( A, B, C ),
1. Задать МК а, где К основание
Расстояние от
точки M до прямой а
2. Найти
Расстояние
между параллельными
плоскостями α и
β
перпендику ляра
координаты К , используя условие : МК а 0.
3. МК ( М ; а ) ( Хм Хк ) 2 (Ум Ук ) 2 ( Zм Zк ) 2
1. Найти координаты
Расстояние между двумя
скрещивающимися
прямыми а и в
A( x0 ; y0 ; z 0 )
2. Определить
3. ( А; )
некоторой
плоскость
|| а,
Ах0 Ву 0 Сz0 D
А2 В 2 С 2
точки А а.
в .
.
: Ах Ву Сz D1 0
: Ах Ву Сz D2 0
( ; )
D2 D1
А2 В 2 С 2
,
где
n n n,
n( А; В; С )

5.

cos
Угол между прямыми а и в
a1b1 a 2 b2 a3 b3
a a a b b b
где a (a1 , a 2 , a 3 )
b (b1 , b2 , b3 )
2
1
2
2
2
3
2
1
2
2
2
3
,
1. Найти координаты направляющ его
вектора прямой a (a1 ; a2 ; a3 )
Угол между прямой а
и плоскостью α
2. Написать уравнение плоскости и определить
координаты n ( A, B, C )
3. sin
a1 A a2 B a3C
a12 a22 a32 A2 B 2 C 2
1.Написать уравнения плоскостей и .
Угол между
плоскостями
αиβ
2. Определить координаты n1 ( A1 , B1 , C1 ); n2 ( A2 , B2 , C2 )
3. cos
A1 A2 B1 B2 C1C2
A12 B12 C12 A22 B22 C22

6.

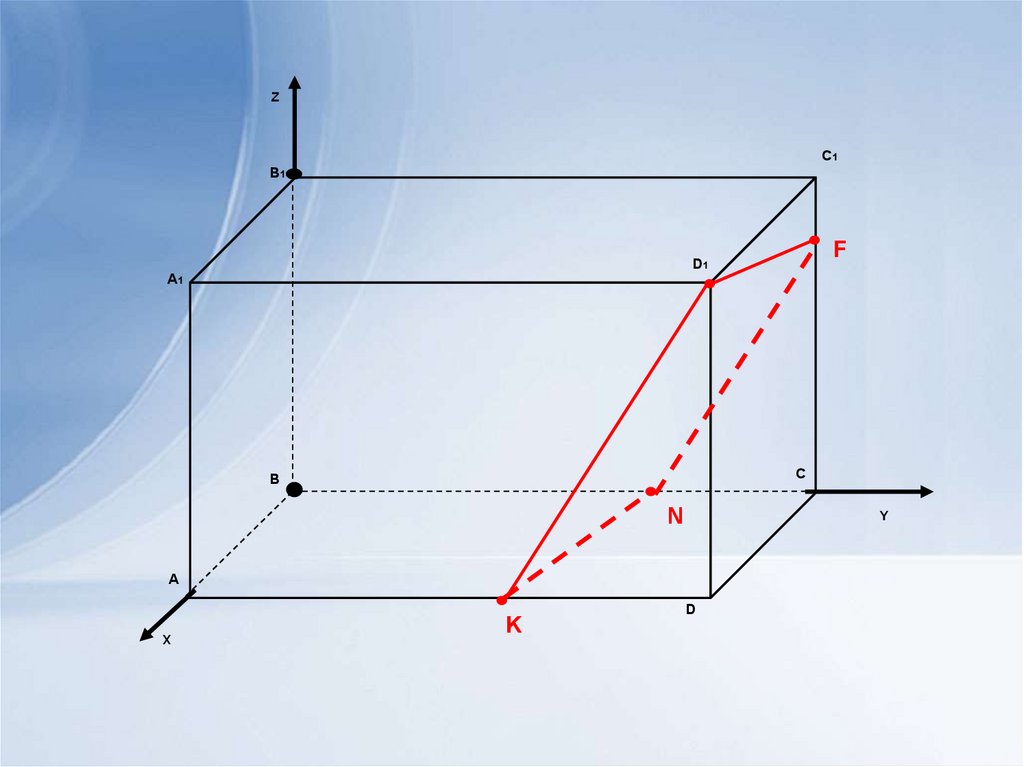
В прямоугольном параллелепипеде АВСDA1B1C1D1 AB, AB:AD:AA1=1:3:2
Построить сечения параллелепипеда плоскостью, проходящей через точку
D1 и перпендикулярно прямой B1D.
Z
B1
А1
2. Для построения сечения найдем координаты
Найдем координаты еще двух точек М и К,
для чего:
а) Напишем уравнение искомой плоскости
C
сечения
α построим
вектору
нормали
и точке D1.
По точкам
искомое
сечение
1. 3.
Введем
систему
координат.
KD1FN нужных точек.
Найдем координаты
n A(1;
B1D
D(1; 30;; 0),
2);C(0;3;0),
x D(1;3;0),
3 y 2 z 6 0.
0;, 0),BD1B(0;
A1(1;0;2), B2(0;0;2), C1(0;3;2), D1(1;3;0).
б) Найдем точки пересечения α с осями
координат и некоторыми
ребрами куба.
C
Y
α∩OY=N, N(0; YN; 0);
3YN-6=0, YN=2,
N(0;2;0)
D
α∩AD=K, K(1; YК; 0);
1+3YK-6=0, YK=5/3,
1
1
B
А
X
K(1;5/3;0)

7.

Z
C1
B1
А1
C
B
N
Y
А
X
F
D1
K
D