Similar presentations:
Арифметические устройства
1.
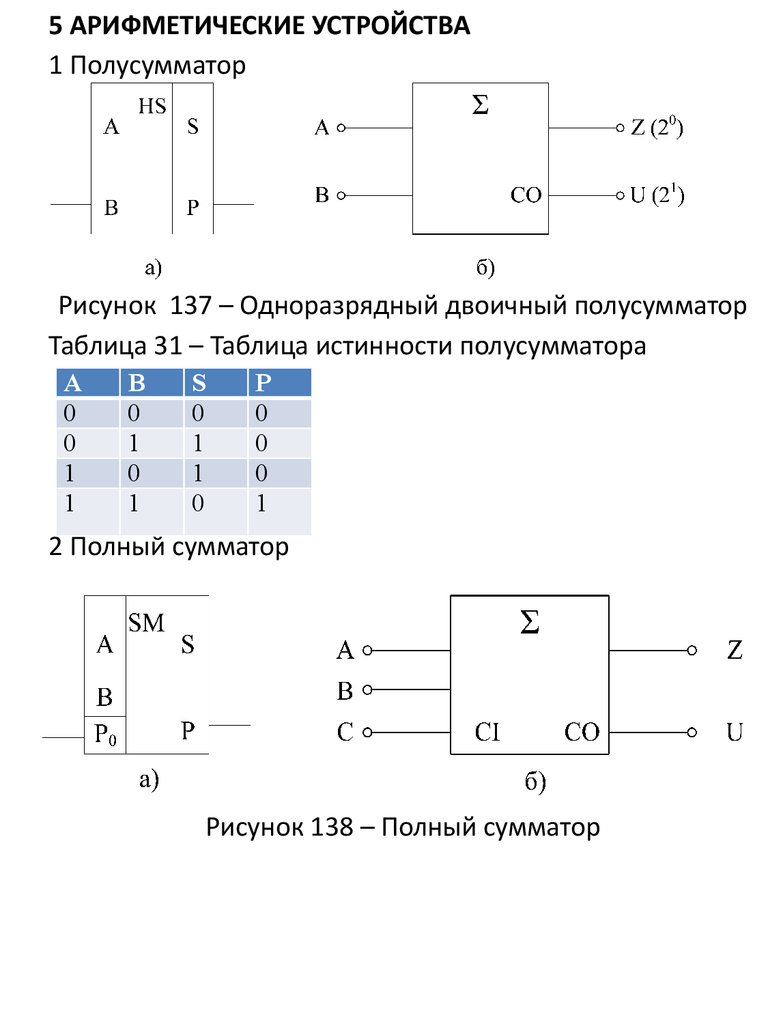
5 АРИФМЕТИЧЕСКИЕ УСТРОЙСТВА1 Полусумматор
Рисунок 137 – Одноразрядный двоичный полусумматор
Таблица 31 – Таблица истинности полусумматора
А
0
0
1
1
В
0
1
0
1
S
0
1
1
0
Р
0
0
0
1
2 Полный сумматор
Рисунок 138 – Полный сумматор
2.
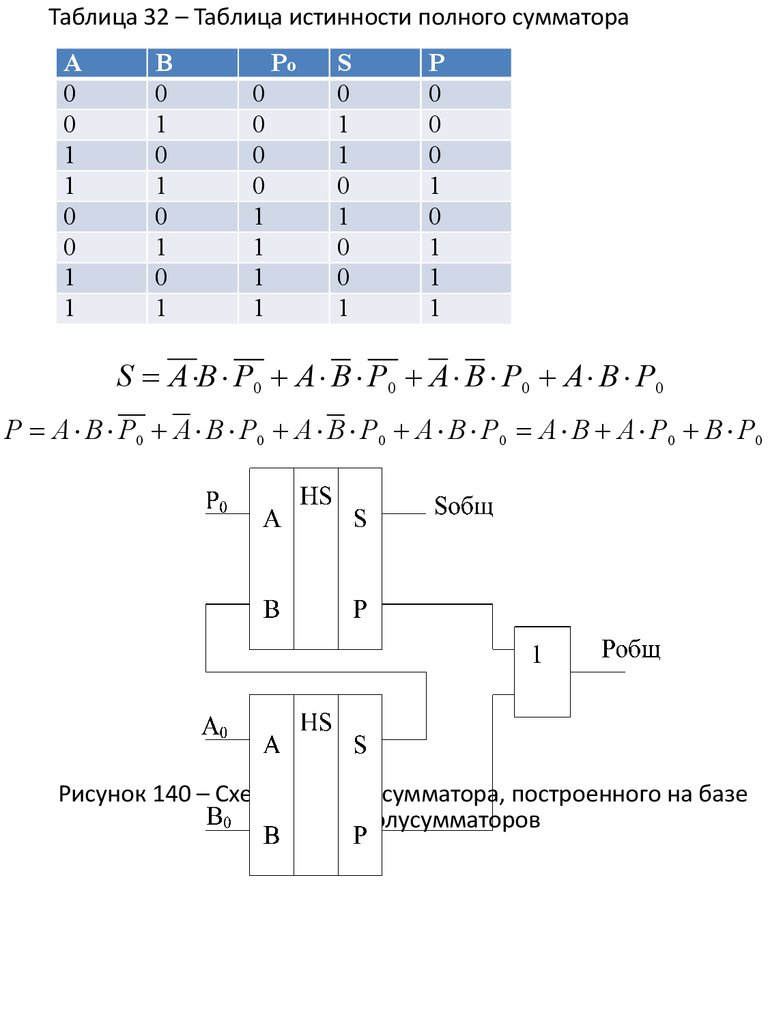
Таблица 32 – Таблица истинности полного сумматораА
0
0
1
1
0
0
1
1
В
0
1
0
1
0
1
0
1
Po
0
0
0
0
1
1
1
1
S
0
1
1
0
1
0
0
1
Р
0
0
0
1
0
1
1
1
S А В Р0 А В Р0 А В Р0 А В Р0
Р А В Р0 А В Р0 А В Р0 А В Р0 А В А Р0 В Р0
Рисунок 140 – Схема полного сумматора, построенного на базе
двух полусумматоров
3.
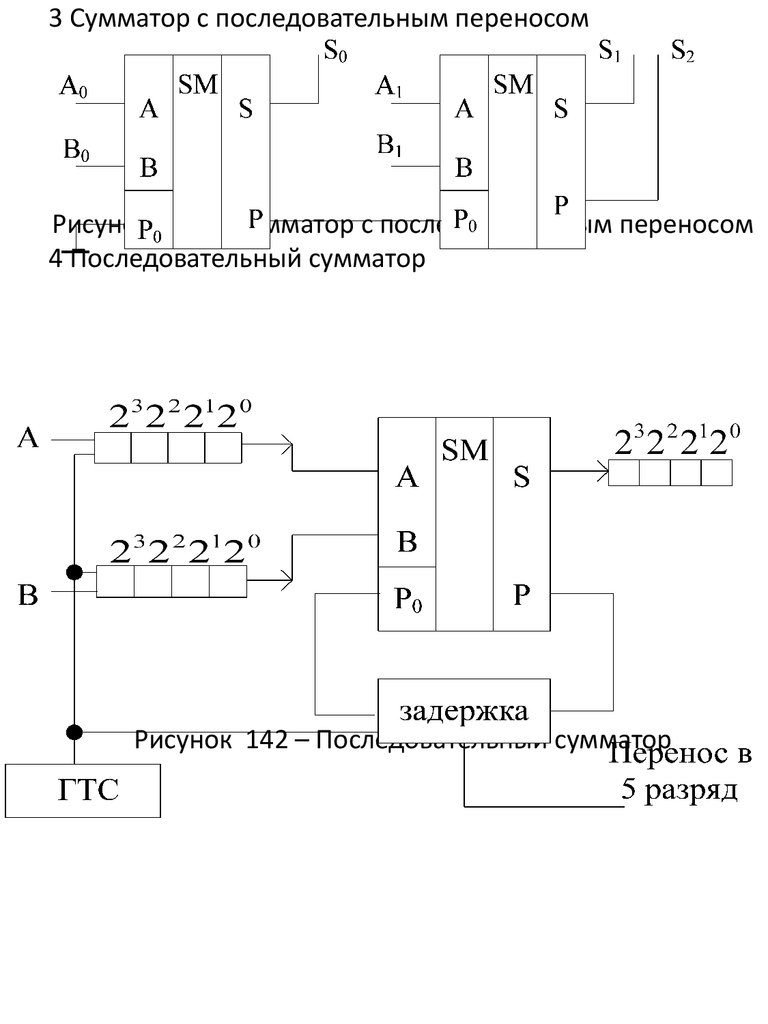
3 Сумматор с последовательным переносомРисунок 141 – Сумматор с последовательным переносом
4 Последовательный сумматор
Рисунок 142 – Последовательный сумматор
4.
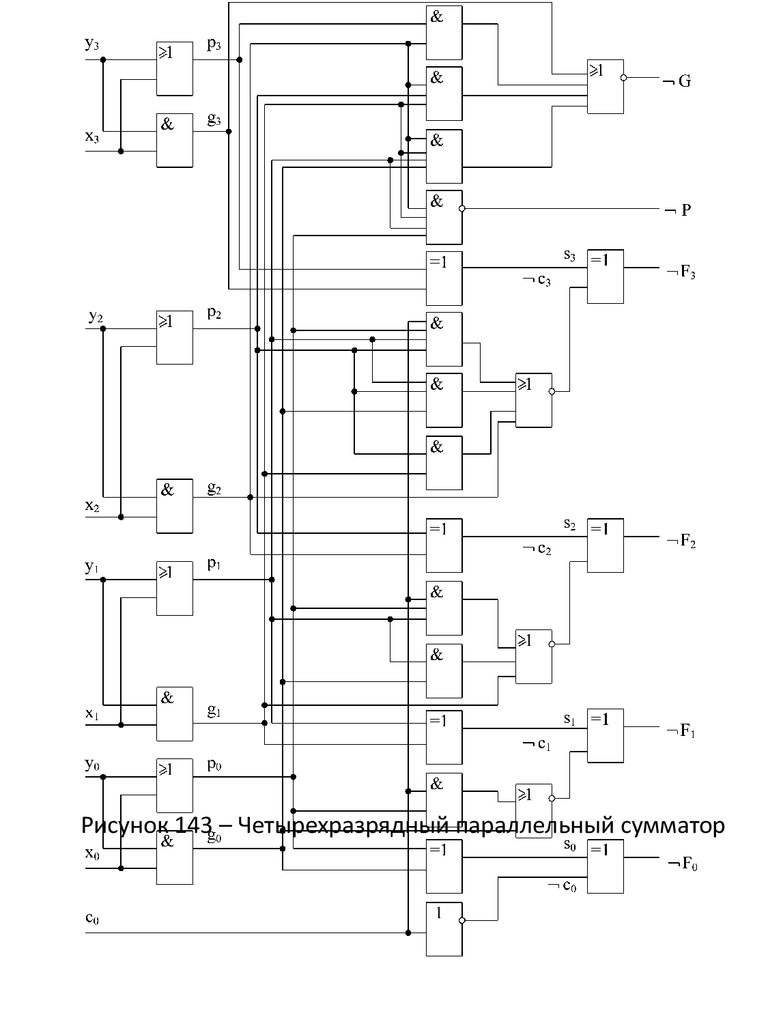
Рисунок 143 – Четырехразрядный параллельный сумматор5.
5 Цифровые компараторыТаблица 34 – Таблица истинности двухбитового
компаратора
у1
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
у0
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
х1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
х0
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
х=у
1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
х<у
0
0
0
0
1
0
0
0
1
1
0
0
1
1
1
0
х>у
0
1
1
1
0
0
1
1
0
0
0
1
0
0
0
0
DECy
0
0
0
0
1
1
1
1
2
2
2
2
3
3
3
3
DECx
0
1
2
3
0
1
2
3
0
1
2
3
0
1
2
3
( õ ó) ó1 ó0 õ1 õ0 ó1 ó0 õ1 õ0 ó1 ó0 õ1 õ0 ó1 ó0 õ1 õ0
6.
Условимся, чтох=у – это =;
х<у – это <;
х>у – это >.
Карта Карно будет иметь вид:
( х у) х1 у1 х0 у1 у 0 у 0 х1 х0
( х у) у1 х1 у 0 х1 х0 х0 у1 у 0
( х у) ( х y) ( х y) ( х у) ( х у)
7.
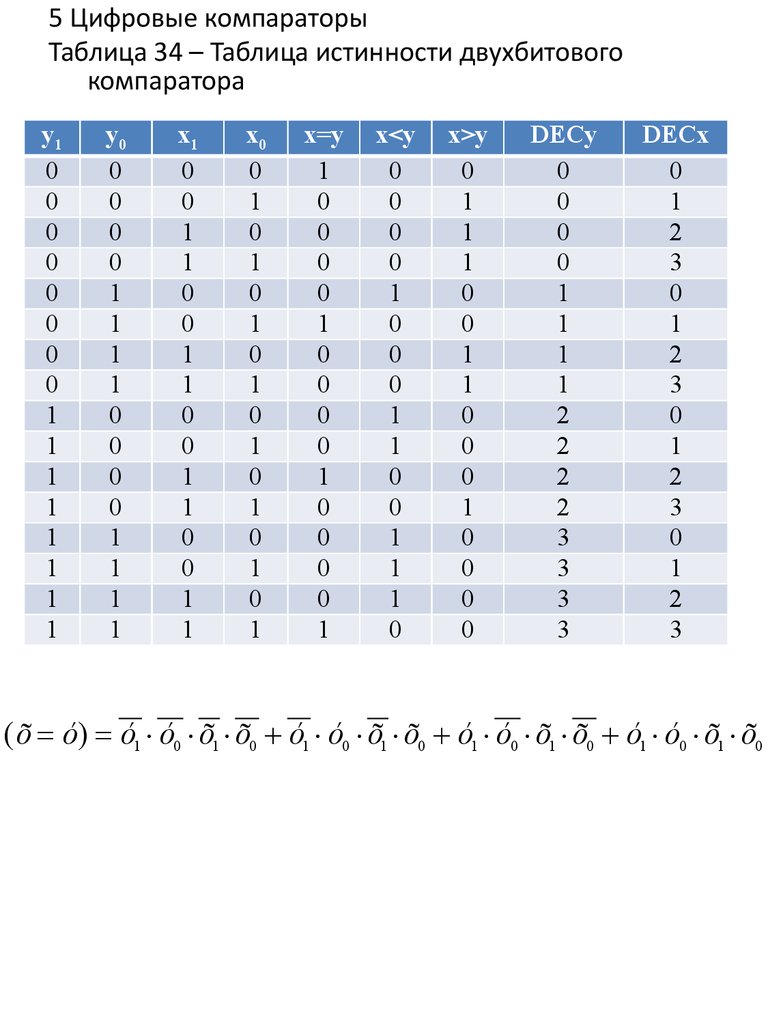
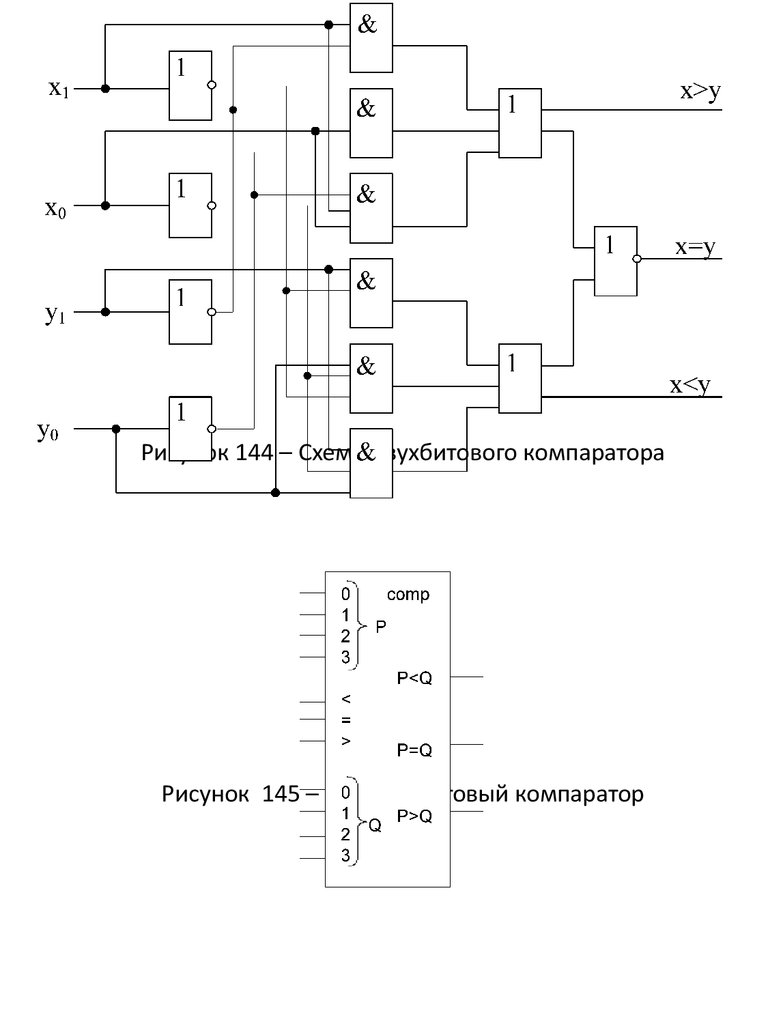
Рисунок 144 – Схема двухбитового компаратораРисунок 145 – Четырехбитовый компаратор
8.
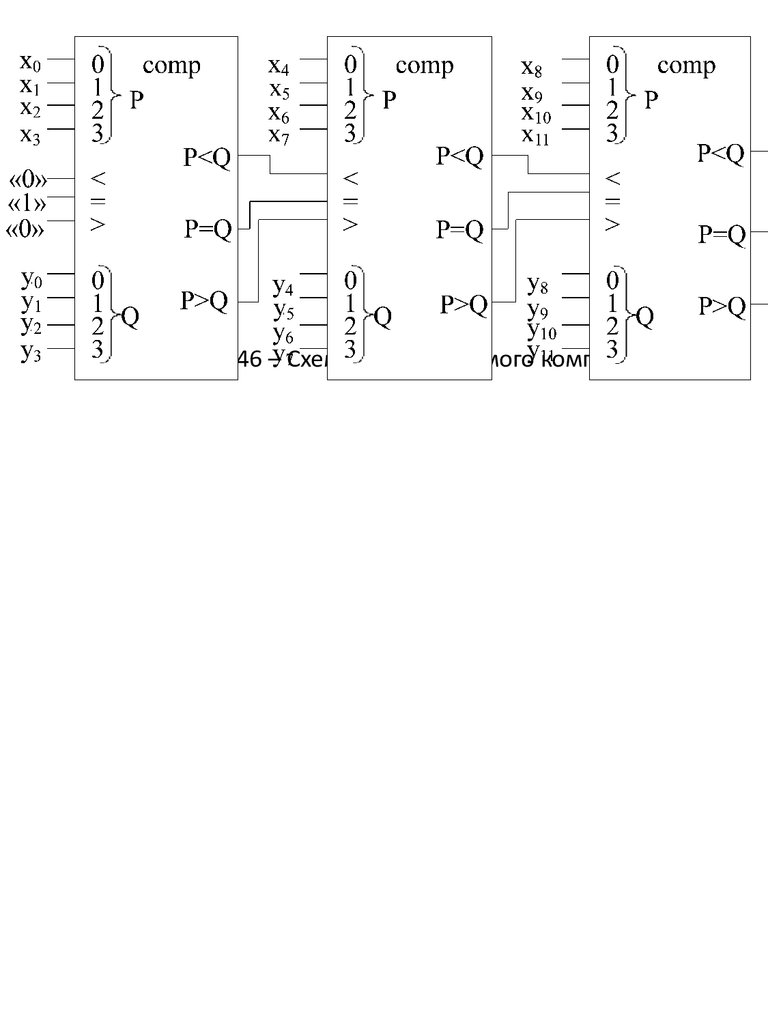
Рисунок 146 – Схема каскадируемого компаратора9.
1Схема контроля четности для трехразряднойпередающей шины.
Таблица 35 – Таблица истинности для схемы контроля
четности
х2
0
0
0
0
1
1
1
1
х1
0
0
1
1
0
0
1
1
х0
0
1
0
1
0
1
0
1
Четн.
1
0
0
1
0
1
1
0
Нечетн.
0
1
1
0
1
0
0
1
10.
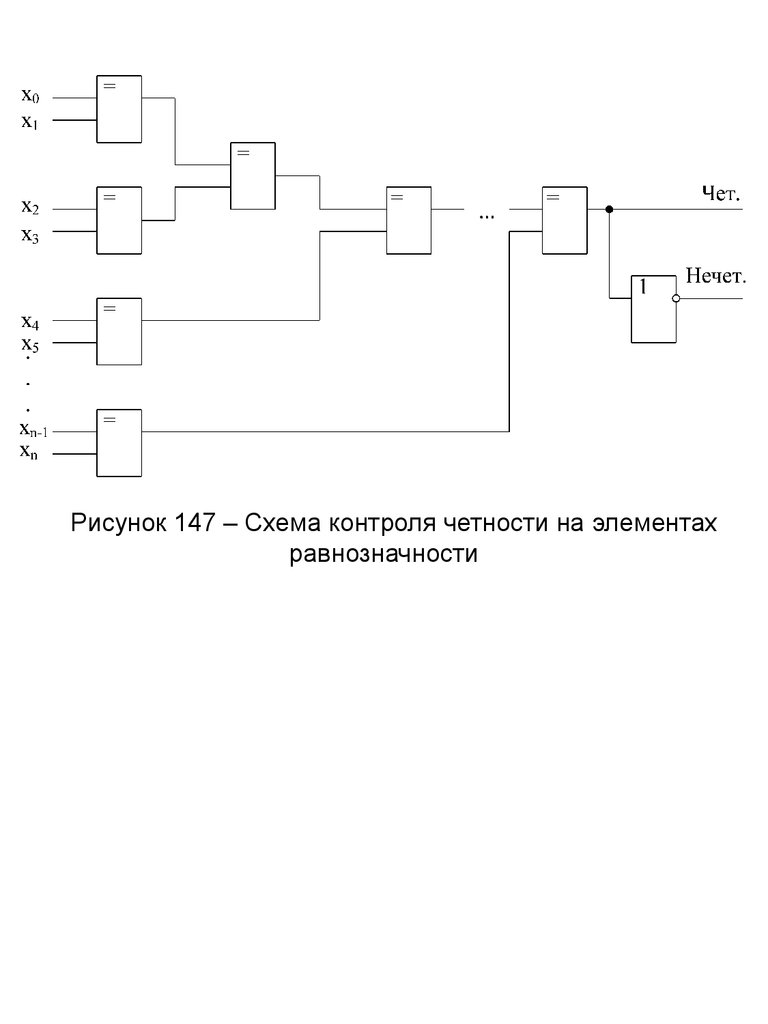
Рисунок 147 – Схема контроля четности на элементахравнозначности


 electronics
electronics








