Similar presentations:
Определение волнового процесса. Процесс распространения колебаний
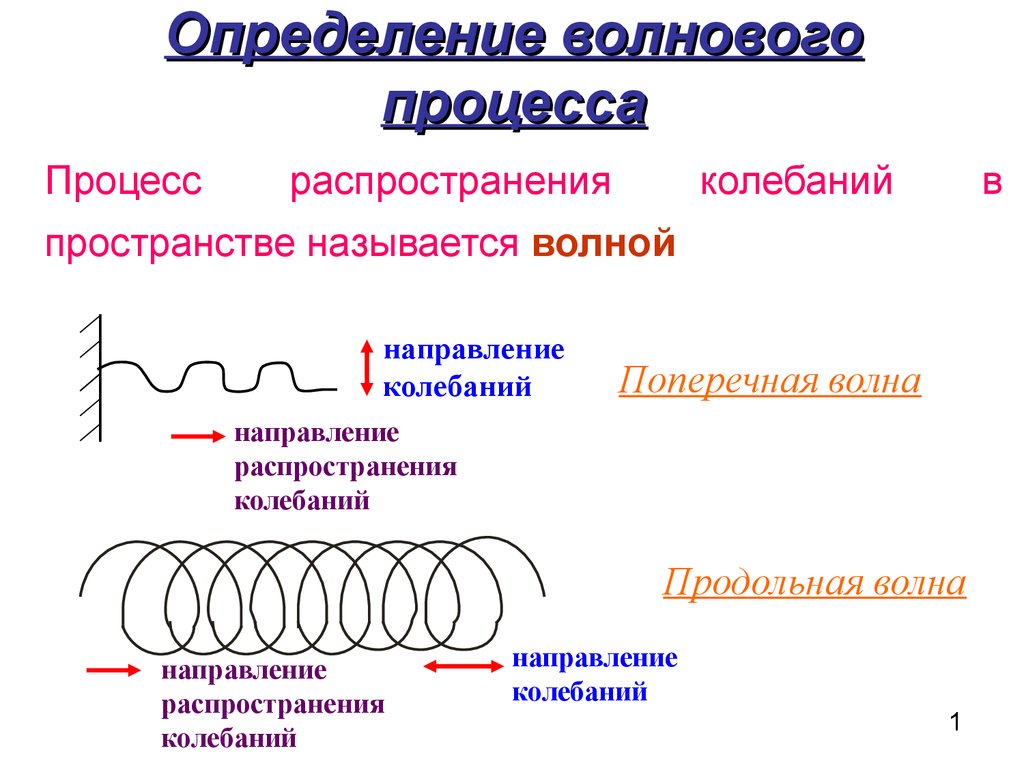
1. Определение волнового процесса
Процессраспространения
колебаний
в
пространстве называется волной
направление
колебаний
Поперечная волна
направление
распространения
колебаний
Продольная волна
направление
распространения
колебаний
направление
колебаний
1
2.
Областьпространства,
колеблются все частицы
волновым полем
внутри
которого
среды, называются
Фронт волны – граница, отделяющая частицы,
начавшие колебаться, от частиц, не начавших
колебаться
Волновая поверхность – поверхность, на которой
все частицы находятся в одинаковом положении
(т.е. в одной фазе)
2
3.
Фронт волны(Ф.В.)
плоский
плоские
волны
сферический
сферические
Ф.В.
Ф.В.
Фронт волны - плоскость
Фронт волны - сфера
3
4.
Уравнение плоской волныУравнением волны называется выражение, которое даёт
смещение колеблющейся точки с течением времени и
описывает положение всех точек волны в любой
фиксированный момент времени
В точке О – источник гармонических колебаний
Y0(t) = A cosωt
y
V
колебания в плоскости x = 0
Соседние точки начнут колебаться с запозданием. В точку М
M
(произвольную) колебания придут через время τ
= x/V
x V – скорость распространения волны
O
x
Плоская поперечная
волна
Для момента времени t:
yM(t) = y0(t´) = A cosωt;
A – амплитуда колебаний
ω – круговая частота
x
y M ( t ) A cos t
V
x
y (t ) A cos t
V
t t t
x
V
Уравнение плоской
поперечной волны
4
5.
2πT
ω
T – период колебаний
ω – круговая частота
Тогда уравнение волны запишется:
2
x
y (t ) A cos t
T V
2 t 2 x
y (t ) A cos
VT
T
2 x
y0
VT
- начальная фаза
Все точки волны колеблются с одинаковой амплитудой A, с
одним и тем же периодом T (с одной частотой), но с
различными начальными фазами 2πx / VT
5
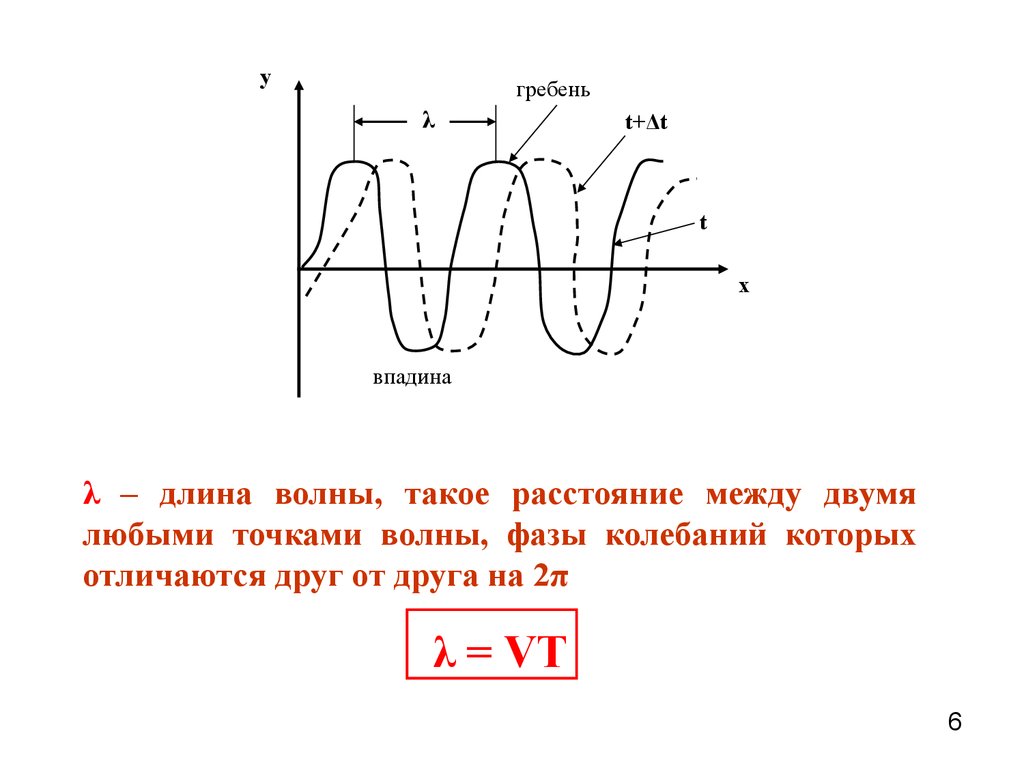
6.
yгребень
λ
t+Δt
t
x
впадина
λ – длина волны, такое расстояние между двумя
любыми точками волны, фазы колебаний которых
отличаются друг от друга на 2π
λ = VT
6
7.
Подставим λ в уравнение волны, получимt x
y (t ) A cos 2
T
Выведенное уравнение справедливо и для продольной
волны. Это относится и к определению λ
7
8. Интерференция механических волн
Интерференция механическихволн
Если в среде одновременно распространяется несколько волн, то
частица среды одновременно участвует в нескольких волновых движениях.
При малых амплитудах колебаний справедлив принцип суперпозиции
Колебание каждой точки среды является суммой независимых
колебаний, вызванных каждой из проходящих через данную точку волн в
отдельности
Независимые волны, которые в
процессе
своего
распространения
одновременно проходят через одну и ту
же точку среды, складываются, но не
искажают друг друга – принцип
суперпозиции
(Леонардо-да Винчи)
Пример: Волны на поверхности
воды от двух брошенных
камешков
8
9.
Когерентные волны:Если частоты колебаний одинаковы и разность фаз не
изменяется со временем, то такие волны называются
когерентными
Интерференция волн: в результате наложения
(суперпозиции) когерентных волн наблюдается явление,
носящее название интерференции волн. При этом
колебания в одних точках волнового поля усиливают
друг друга, в других – ослабляют
Пример:
Два стержня прикреплены к ножке
камертона и погружены в воду. Если
периодически ударять по камертону, то
стержни будут источниками колебаний,
которые создадут когерентные волны
9
10. Расчет интерференционной картины
О2х2
О1 и О2 – источники когерентных волн
О1
М – произвольная точка волнового поля,
в которой происходит суперпозиция волн
х1
М
x2 и x1 – расстояние от источников
колебаний до точки М
Колебания y1, вызванные первой волной в т.М
t x1
y 1 A 1cos2π
T λ
Колебания y2, вызванные второй волной в т.М
t x2
y 2 A 2cos2π
T λ
А1 и А2 – амплитуды волн. Пусть А1 = А2
10
11.
Результирующее колебание в т.М:t x1
t x2
y y 1 y 2 Acos2π A cos 2
T λ
T
x 2 x1
t x1 x 2
t x1 x 2
2A cos 2
B cos 2
cos 2
2
2
2
T
T
11
12.
x 2 x1t
y B cos 2
2
T
Результирующее колебание
x 2 x1
B 2 A cos 2
2
Амплитуда
результирующего
колебания
12
13.
Анализ результирующего колебанияt x 2 x1
y B cos 2
;
2
T
x 2 x1
B 2 A cos 2
2
1. Результирующее колебание (y) будет также
гармоническим колебанием с тем же периодом Т, что
и для источника
2. Амплитуда результирующего колебания зависит от
разности расстояний (х2-х1) точки М от источников
x2-х1 – разность хода волн
13
14.
Рассмотрим два предельных случая:1.
х2-х1=nλ;
n=0,
±1; ±2…
разность хода волн равна целому числу длин волн
B = ±2A
2.
Усиление колебаний в этих точках
пространства (max. интерференции)
х2-х1 = (2n+1) λ/2
разность хода равна нечетному числу полуволны
2n 1
B 2 A cos
2 A cos n sin n 0
2
2
B=0 В этих точках пространства волны гасят
друг друга (min. интерференции)
14
15.
При интерференции волн энергия Еколебаний точек волнового поля
перераспределяется в зависимости от
соотношения фаз в каждой точке
Е ~ (амплитуда)2
В некоторых
колебаний
точках
–
усиление
В других mочках – гашение колебаний
Общая
энергия
колебаний
изменяется,
происходит
перераспределение
не
ее
15
16. Принцип Гюйгенса. Дифракция механических волн.
Принцип Гюйгенса (конец XVII века)Каждая точка волнового поля, пришедшая в колебание, сама становится
источником вторичных волн. Результирующая волна, распространяющаяся
дальше, сама становится источником вторичных волн. Результирующая волна,
распространяющаяся дальше, является результатом наложения и интерференции
всех волн от этих вторичных элементарных источников
(1)
(2)
Источники вторичных волн точечные. Фронт волны
является источником когерентных волн
V – скорость распространения волны
→V
r = V· ∆t, волны от точечного источника – сферические
(r – радиус сферы фронта волны)
(1) Фронт волны в момент времени t
t
t + ∆t
(2) Фронт волны в момент времени t + ∆t
16
17.
Применяя принцип Гюйгенса, можно придти к выводу, что воднородной среде плоская волна остается плоской, а
сферическая – сферической.
Ф.в. (2)
Ф.в. (1)
Ф.в. (2)
Ф.в. (1)
Ф.в. – фронт волны
17
18.
Дифракция – явление огибания волнами препятствий, т.е.явление непрямолинейного распространения волн
Принцип Гюйгенса позволяет объяснить явление дифракции
Пример 1: плоская волна падает на поверхность экрана, в
котором имеется отверстие (d << λ)
d – диаметр отверстия, λ – длина волны
Отверстие
в
экране
можно
рассматривать как точечный источник
Волна
заходит
в
область
геометрической тени, т.е. наблюдается
явление дифракции
18
19.
Пример 2:Ф.в. за экраном
Даже в случае широкого фронта волны
(Ф.в.) наблюдается отклонение от
прямолинейного распространения
Пример 3:
За малой преградой благодаря явлению
дифракции тень не образуется
19

















 physics
physics








