Погрешности измерений при проведении школьного физического эксперимента

1. Погрешности измерений при проведении школьного физического эксперимента

Ляпцев Александр
Викторович
доктор физикоматематических наук,
профессор

2. Погрешность измерения — оценка отклонения измеренного значения величины от её истинного значения. Погрешность измерения

является
характеристикой (мерой) точности
измерения.
Абсолютная погрешность, запись в виде:
k=1,380 6488(13)×10−23 Дж/К, или k=1,380 6488×10−23±0,000 0013×10−23 Дж/К.
Здесь Δk=0,0000013 10-23 Дж/К = 1,3 10-29 Дж/К
Относительная погрешность:
Δk/k=10-6 = 10-4 %

3. Классификация по причинам возникновения

Инструментальные / приборные погрешности — погрешности, которые
определяются погрешностями применяемых средств измерений и
вызываются несовершенством принципа действия, неточностью
градуировки шкалы, ненаглядностью прибора
Простейшая оценка для приборов, имеющих шкалу – половина деления
шкалы. Для цифровых приборов – удвоенное значение последнего
(младшего) разряда индикатора.
Более строго с использованием класса прибора, указанного в инструкции,
например: http://l-micro.ru/index.php?id=1
В этом случае рекомендуется учитывать как класс прибора, данный
производителем, так и погрешность последних цифр. Например, если
указано, что в данном диапазоне погрешность измерений составляет 0,25%,
то, если прибор показывает значение x, абсолютную погрешность следует
взять равной Δx=0,0025 x +2D

4. Классификация по причинам возникновения

Методические погрешности — погрешности, обусловленные
несовершенством метода, а также упрощениями, положенными в основу
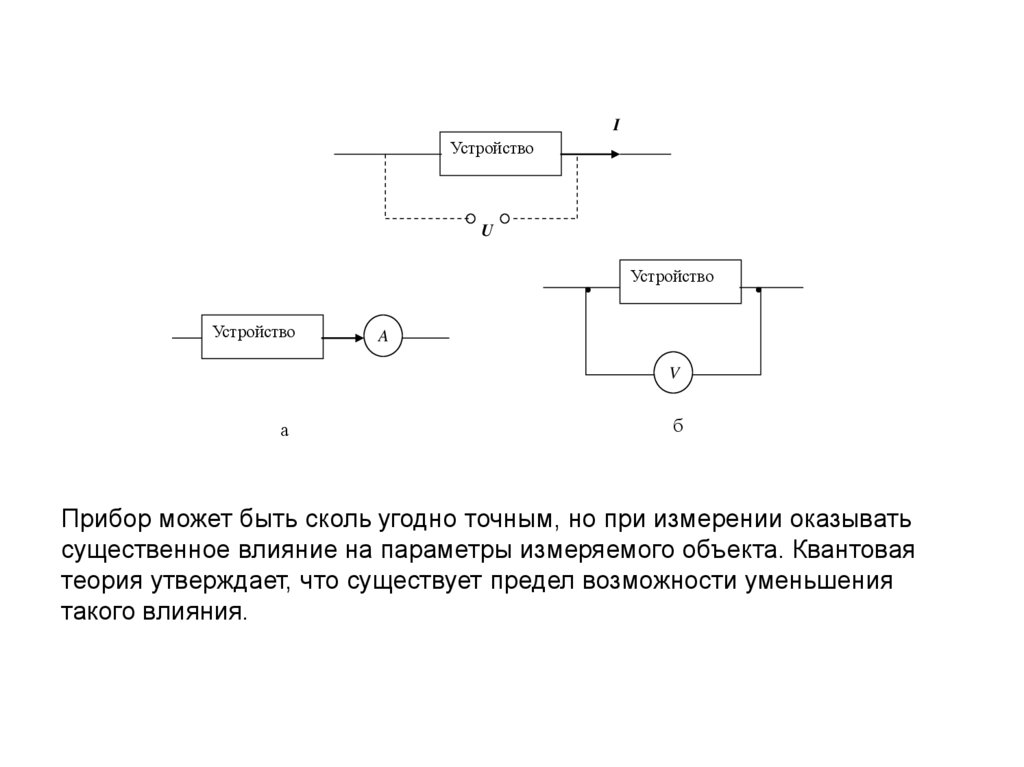
методики. В частности, погрешности, обусловленные влиянием прибора на
объект исследования. Примеры

5.

I
Устройство
U
Устройство
Устройство
A
V
а
б
Прибор может быть сколь угодно точным, но при измерении оказывать
существенное влияние на параметры измеряемого объекта. Квантовая
теория утверждает, что существует предел возможности уменьшения
такого влияния.

6. Классификация по причинам возникновения

Погрешности, обусловленные вероятностным характером явлений и
процессов в природе.
n
Среднее (среднее арифметическое) значение:
x
x
i 1
i
n
n
Среднее квадратичное отклонение:
S
2
(
x
x
)
i
i 1
Условно (!) берут в качестве оценки погрешности
n
x (3S )2 ( xdevice )2

7. Классификация по причинам возникновения

• Субъективные / операторные / личные
погрешности — погрешности,
обусловленные степенью внимательности,
сосредоточенности, подготовленности и
другими качествами оператора.

8. Погрешности величин, определяемых косвенным методом

Если искомая величина определяется из измеренных величин по формуле:
y y( x1 , x2 ,..., xn )
n
y
i 1
y
xi
xi
то абсолютная погрешность искомой
величины связана с абсолютными
погрешностями измеренных величин
формулой:
В частности для простейших формул:
n
n
y ai xi y ai xi
i 1
n
i 1
y xi
i 1
i
i
y
y
xi
y
xi
абсолютные погрешности
складываются
относительные погрешности
складываются

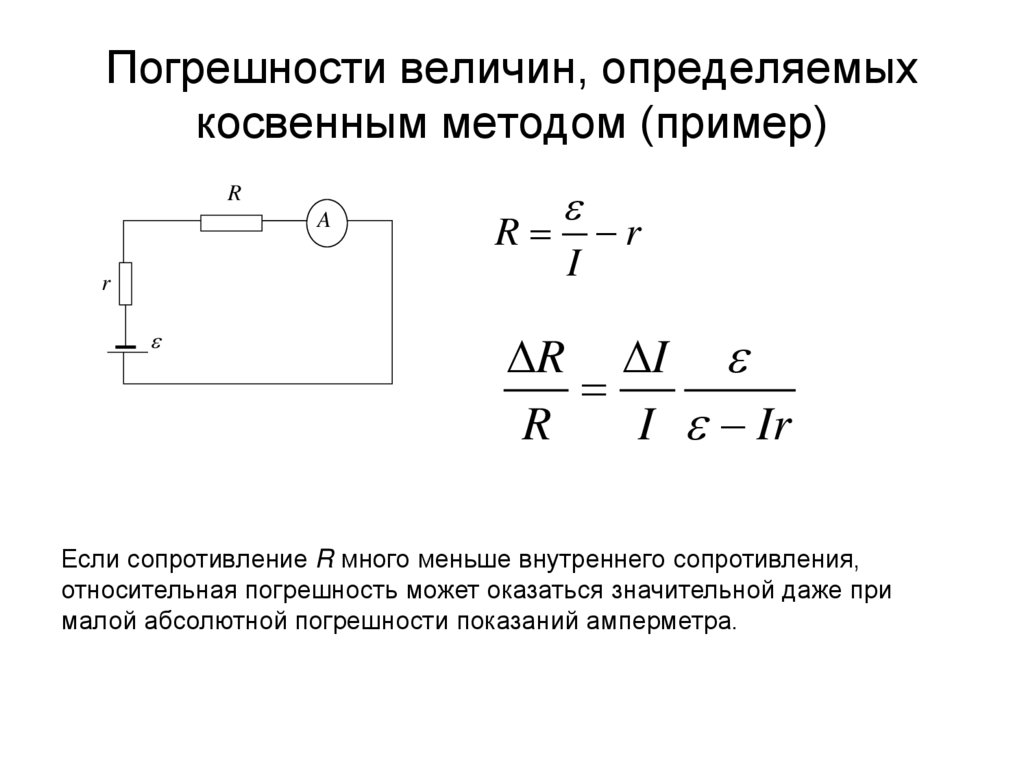
9. Погрешности величин, определяемых косвенным методом (пример)

R
A
r
R
I
r
R I
R
I Ir
Если сопротивление R много меньше внутреннего сопротивления,
относительная погрешность может оказаться значительной даже при
малой абсолютной погрешности показаний амперметра.

10. Погрешности величин, определяемых косвенным методом (пример)

Определение ускорения тела на наклонной плоскости по пройденному
пути и времени движения.
at 2
2S
S
a 2
2
t
t
S
a S
t
2
a
S
t

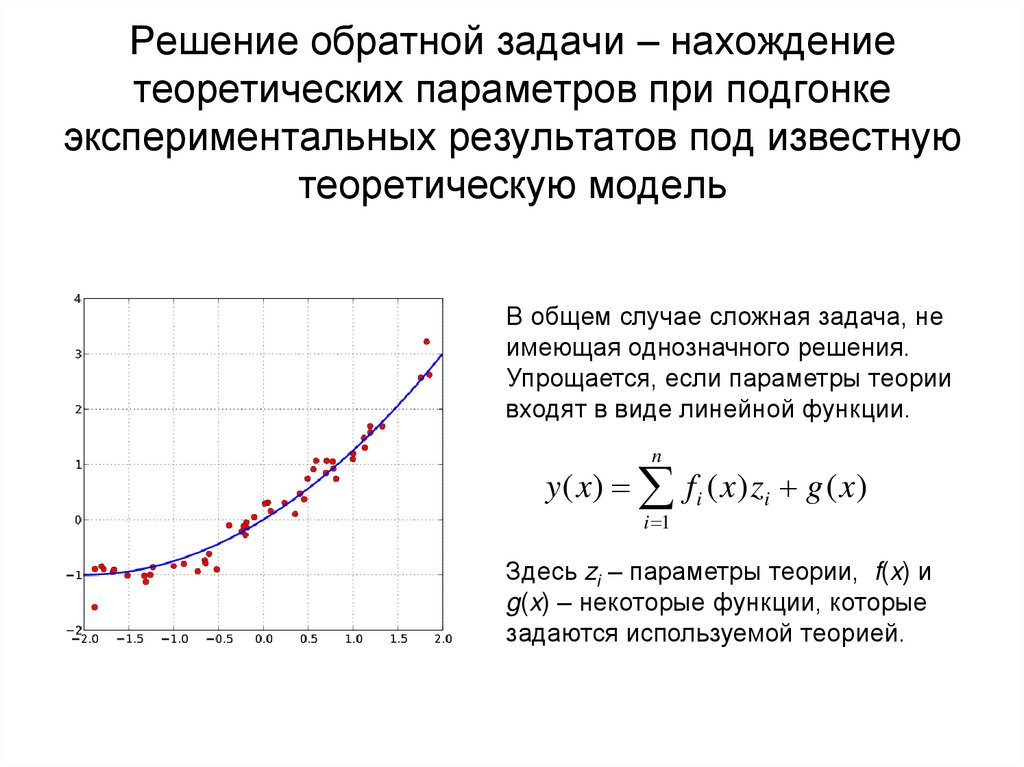
11. Решение обратной задачи – нахождение теоретических параметров при подгонке экспериментальных результатов под известную

теоретическую модель
В общем случае сложная задача, не
имеющая однозначного решения.
Упрощается, если параметры теории
входят в виде линейной функции.
n
y ( x ) f i ( x ) zi g ( x )
i 1
Здесь zi – параметры теории, f(x) и
g(x) – некоторые функции, которые
задаются используемой теорией.

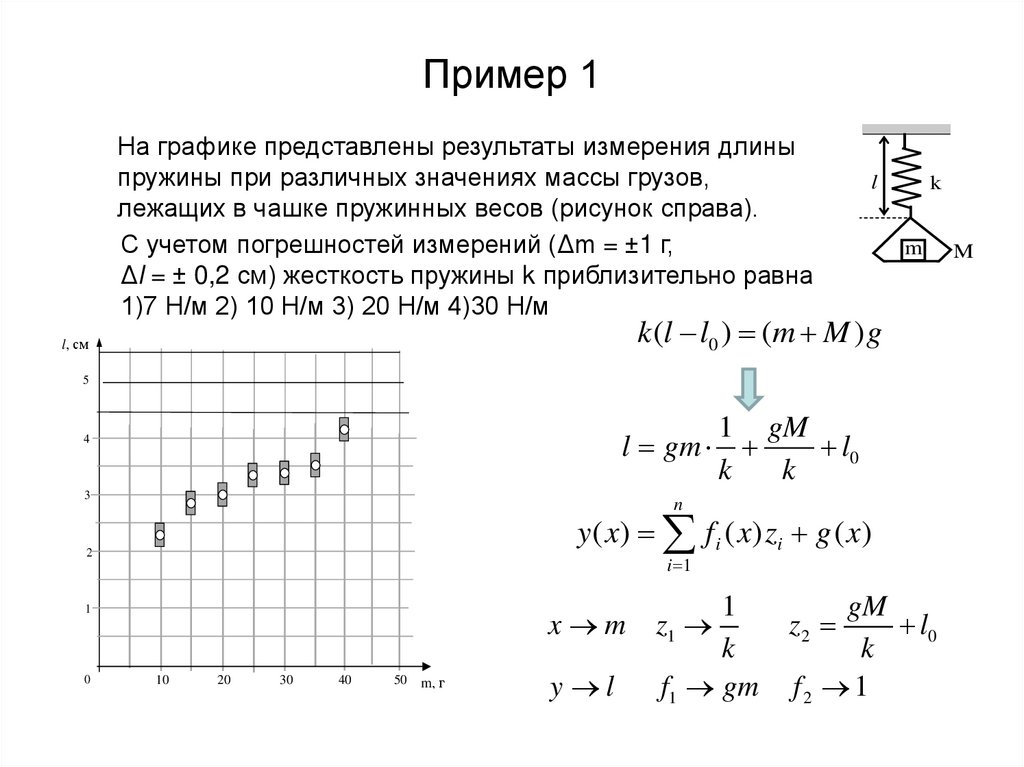
12. Пример 1

На графике представлены результаты измерения длины
пружины при различных значениях массы грузов,
лежащих в чашке пружинных весов (рисунок справа).
С учетом погрешностей измерений (Δm = ±1 г,
Δl = ± 0,2 см) жесткость пружины k приблизительно равна
1)7 Н/м 2) 10 Н/м 3) 20 Н/м 4)30 Н/м
l
k
m
k (l l0 ) (m M ) g
l, см
5
1 gM
l gm
l0
k
k
4
3
n
y ( x ) f i ( x ) zi g ( x )
2
i 1
1
0
x m
10
20
30
40
50
m, г
y l
1
k
f1 gm
z1
gM
l0
k
f2 1
z2
M

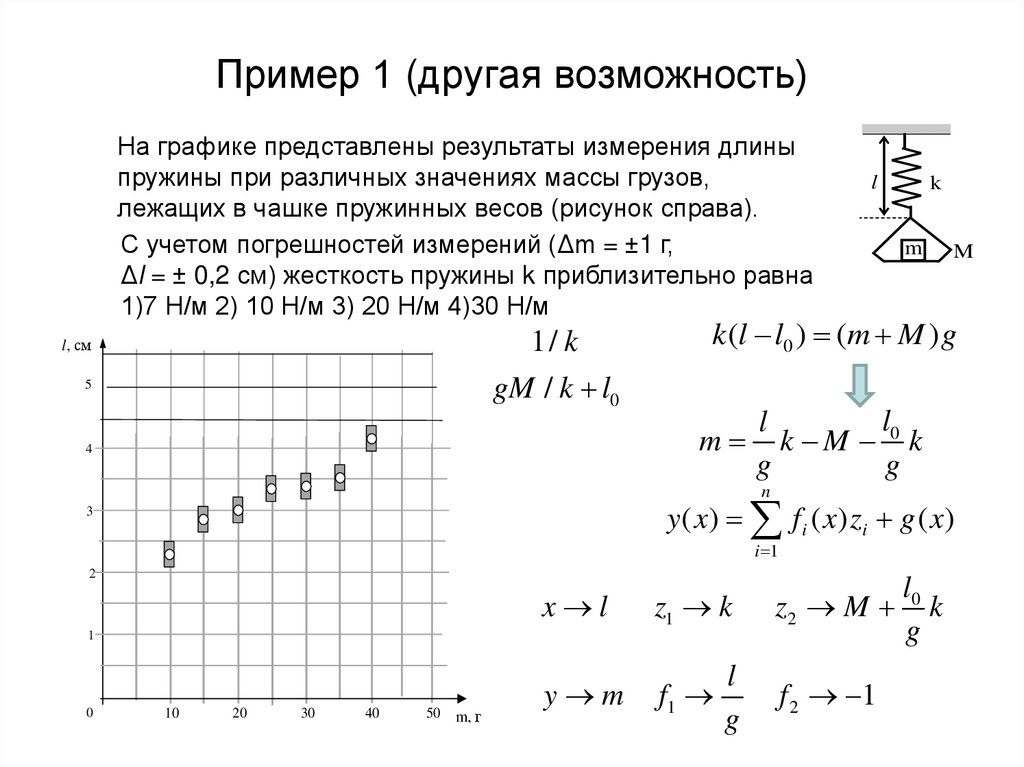
13. Пример 1 (другая возможность)

На графике представлены результаты измерения длины
пружины при различных значениях массы грузов,
лежащих в чашке пружинных весов (рисунок справа).
С учетом погрешностей измерений (Δm = ±1 г,
Δl = ± 0,2 см) жесткость пружины k приблизительно равна
1)7 Н/м 2) 10 Н/м 3) 20 Н/м 4)30 Н/м
1/ k
l, см
l
k
m
k (l l0 ) (m M ) g
gM / k l0
5
l0
l
m k M k
g
g
4
n
y ( x ) f i ( x ) zi g ( x )
3
i 1
2
x l
z1 k
y m
f1
1
0
M
10
20
30
40
50
m, г
l
g
l0
z2 M k
g
f 2 1

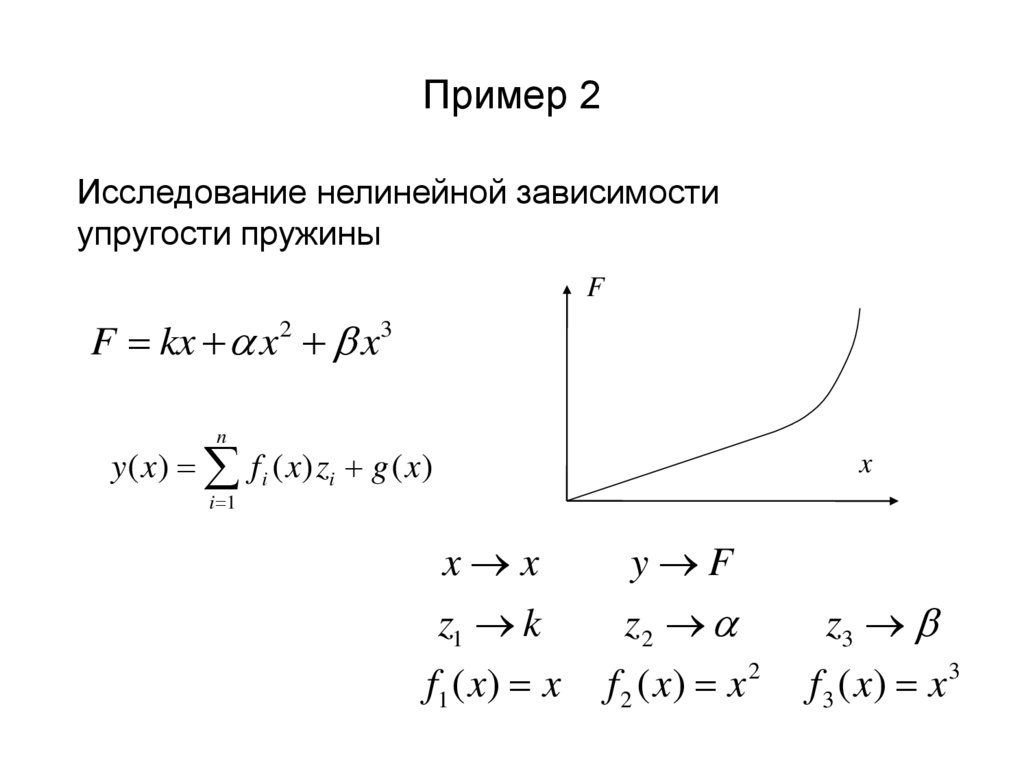
14. Пример 2

Исследование нелинейной зависимости
упругости пружины
F
F kx x2 x3
n
y ( x ) f i ( x ) zi g ( x )
x
i 1
x x
y F
z1 k
z2
z3
f1 ( x) x
f 2 ( x) x 2
f3 ( x) x 3

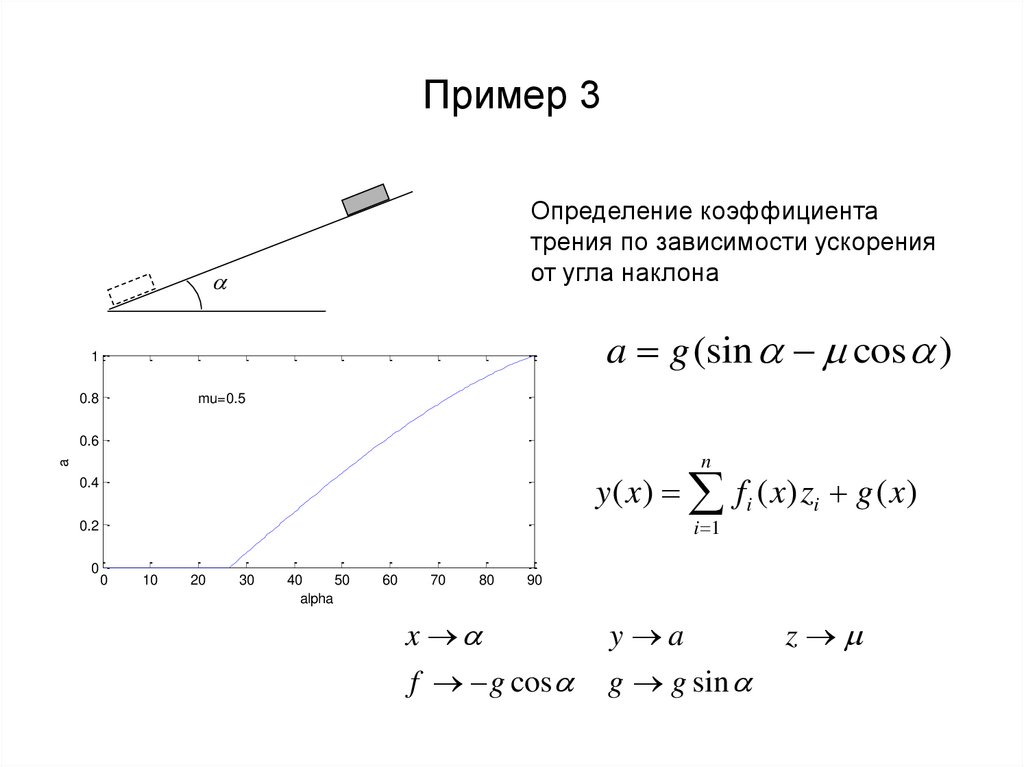
15. Пример 3

Определение коэффициента
трения по зависимости ускорения
от угла наклона
a g (sin cos )
1
0.8
mu=0.5
0.6
n
a
y ( x ) f i ( x ) zi g ( x )
0.4
i 1
0.2
0
0
10
20
30
40
50
alpha
60
70
80
90
x
y a
f g cos
g g sin
z

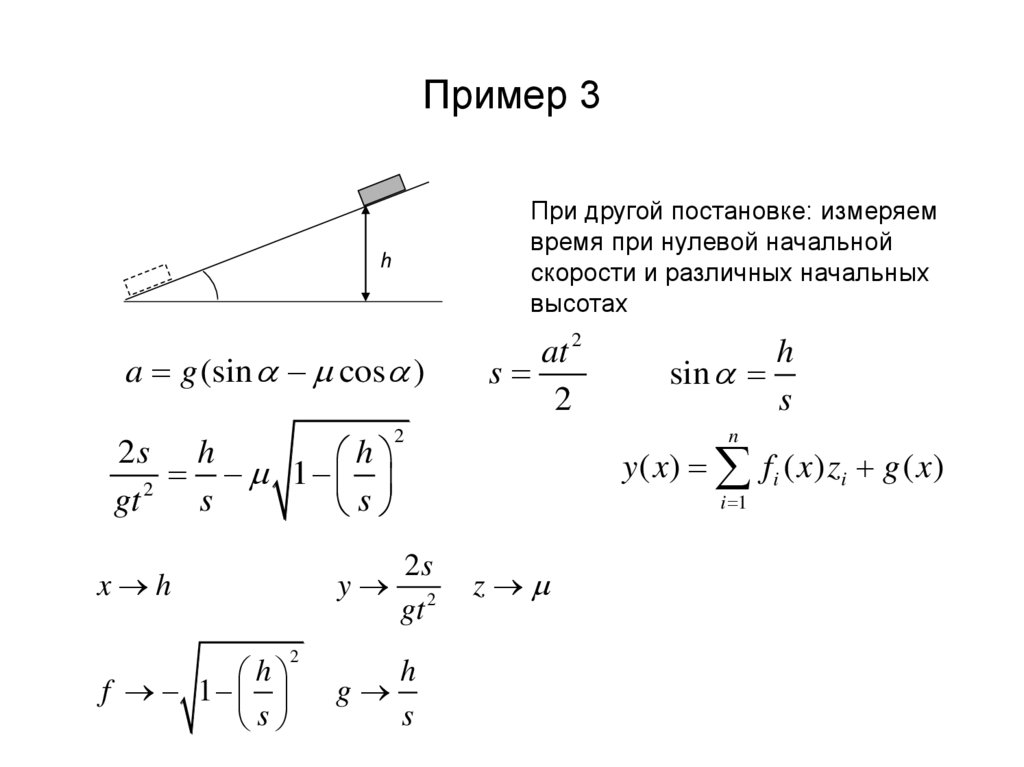
16. Пример 3

При другой постановке: измеряем
время при нулевой начальной
скорости и различных начальных
высотах
h
a g (sin cos )
2s h
h
1
2
gt
s
s
x h
h
f 1
s
y
2
at 2
s
2
2
h
sin
s
n
y ( x ) f i ( x ) zi g ( x )
i 1
2s
gt 2
h
g
s
z

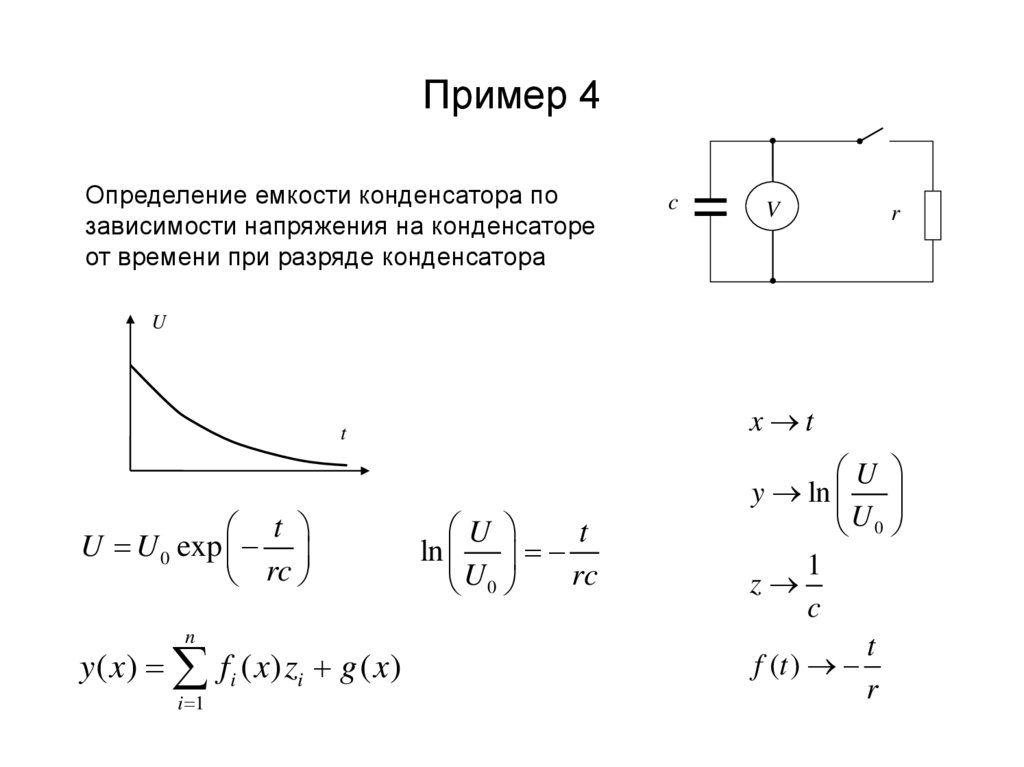
17. Пример 4

Определение емкости конденсатора по
зависимости напряжения на конденсаторе
от времени при разряде конденсатора
c
V
r
U
x t
t
t
U U 0 exp
rc
n
y ( x ) f i ( x ) zi g ( x )
i 1
U
t
ln
rc
U0
U
y ln
U
0
1
z
c
t
f (t )
r

18. Метод наименьших квадратов

n
y ( x ) f i ( x ) zi g ( x )
i 1
Параметры теории z подбираются так, чтобы минимизировать
функцию:
I y j g ( x j ) fi ( x j ) zi
j 1
i 1
m
n
2
Здесь n – число параметров, а
m – число точек
Это квадратичная положительная функция от параметров z,
следовательно при некотором наборе параметров она достигает
минимума. Параметры определяются из условия равенства частных
производных по этим параметрам нулю:
I
0, i 1, 2,..., n
zi
Это система линейных уравнений,
причем число уравнений равно числу
параметров

19. Метод наименьших квадратов

n
y ( x ) f i ( x ) zi g ( x )
i 1
I
0, i 1, 2,..., n
zi
n
A
k 1
I y j g ( x j ) fi ( x j ) zi
j 1
i 1
m
n
2
После проведения вычислений
получим систему уравнений:
z Bi , i 1, 2,..., n
где
ik k
Aik fi ( x j ) f k ( x j ) Bi y j g ( x j ) fi ( x j )
m
m
j 1
j 1
Несмотря на то, что система уравнений выглядит громоздкой, в случае
одного или двух параметров ее решение не вызывает сложности

20. Метод наименьших квадратов. Оценка «погрешности»

О погрешности можно говорить лишь условно, поскольку
экспериментальные данные могут совершенно не соответствовать какойлибо теоретической функции. Поэтому однозначной оценки не сделать. В
случае, когда число точек m превосходит число параметров n для оценки
погрешности параметра zn можно воспользоваться формулой:
I min A
jj
z j
m n
1
m
где
Aik fi ( x j ) f k ( x j )
j 1
Imin - минимальное значение функции I,
которое достигается при подстановки
полученных решений

21.

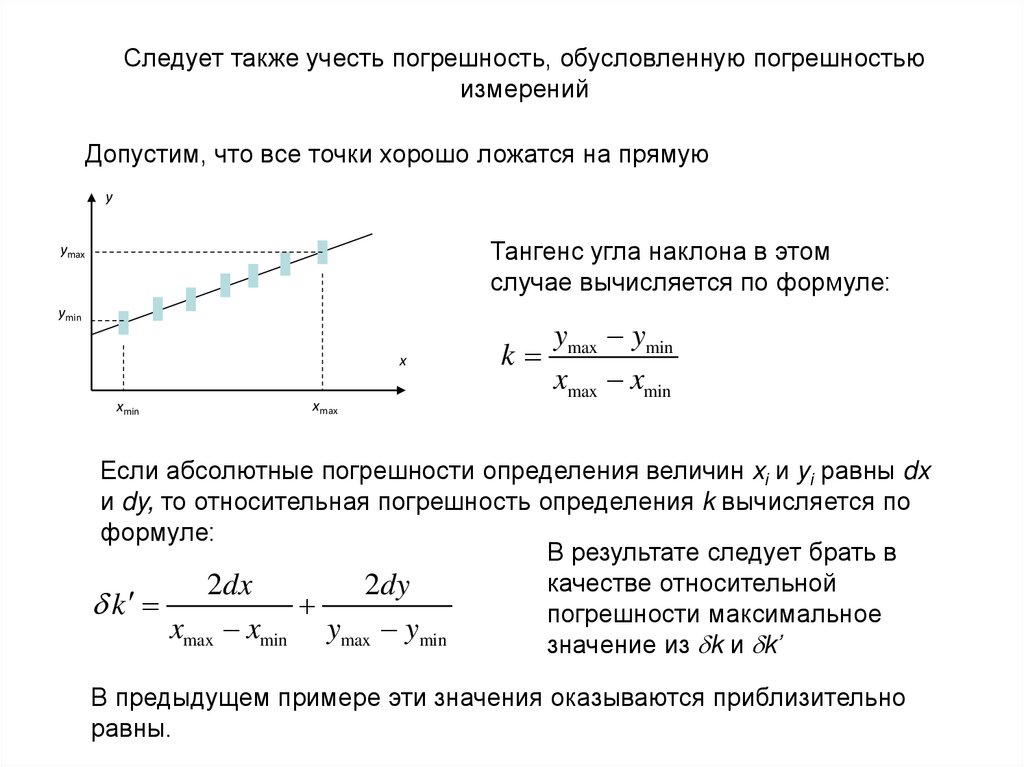
Следует также учесть погрешность, обусловленную погрешностью
измерений
Допустим, что все точки хорошо ложатся на прямую
y
Тангенс угла наклона в этом
случае вычисляется по формуле:
ymax
ymin
x
xmin
xmax
ymax ymin
k
xmax xmin
Если абсолютные погрешности определения величин xi и yi равны dx
и dy, то относительная погрешность определения k вычисляется по
формуле:
В результате следует брать в
качестве относительной
2dx
2dy
k
погрешности максимальное
xmax xmin ymax ymin
значение из k и k’
В предыдущем примере эти значения оказываются приблизительно
равны.

22. Погрешности при использовании метода наименьших квадратов при нелинейной зависимости от параметров

n
При линейной зависимости
I min A 1
jj
z j
m n
y ( x ) f i ( x ) zi g ( x )
i 1
При нелинейной
зависимости
m
Aik fi ( x j ) f k ( x j )
j 1
y( x) F ( x, z1 , z2 ,..., zn )
Допустим, что найдены оптимальные параметры
z0i
Тогда при варьировании параметров вблизи оптимальных
F ( x, z1 , z2 ,..., zn )
fi ( x)
zi
так, что после вычисления
параметров их значения следует
взять оптимальными

23. Погрешности при использовании метода наименьших квадратов при нелинейной зависимости от параметров

I y j g ( x j ) fi ( x j ) zi
j 1
i 1
m
n
2
I y j Fi ( x j , zi )
j 1
i 1
m
n
F ( x, z1 , z2 ,..., zn )
fi ( x)
zi
Далее при вычислении
погрешности можно
использовать предыдущие
формулы
m
Aik fi ( x j ) f k ( x j )
j 1
В частном случае одного
параметра
I min A 1
jj
z j
m n
I min m F ( x j , z )
z
m 1 j 1
z
2
1
2

24. Погрешности при использовании метода наименьших квадратов при нелинейной зависимости от параметров

Пример: вертикальное падение тела с учетом сопротивления воздуха.
Линейная зависимость силы сопротивления от скорости
y (t , ) F (t , ) g t 2 1 exp( t / )
где смысл параметра - время, за которое устанавливается
постоянная скорость падения.
F (t , )
g t 2 2 t exp( t / )
I min m F (t j , )
m 1 j 1 z
2
1

25. Погрешности при использовании метода наименьших квадратов при нелинейной зависимости от параметров

Пример: вертикальное падение тела с учетом сопротивления воздуха.
Квадратичная зависимость от силы сопротивления скорости
y(t, ) F (t, ) g ln ch(t / )
где смысл параметра - время, за которое устанавливается
постоянная скорость падения.
F (t , )
g ln ch(t / th(t / )
I min m F (t j , )
m 1 j 1 z
2
1