Similar presentations:
Пример использования проматриц в задачах управления электромеханическими системами
1. Пример использования проматриц в задачах управления
электромеханическими системами2.
Методы современной теории управления_ Асанов А.З. _
2
3.
34.
45.
56.
67.
78.
89.
Методы современной теории управленияАсанов А.З. _
_
9
10.
Рассматривается электромеханическая система с электродвигателем постоянного тока с независимымвозбуждением.
q
Mm
k m , kl , k у
J1 , J 2
d1 , d 2
Rя,Lя
Mc
uу
I
- угловая скорость (частота вращения) ротора электродвигателя,
- электромеханический момент,
- постоянные величины, определяемые конструктивными параметрами машины,
- моменты инерции ротора и присоединенных масс, приведенные к валу ротора,
- коэффициенты вязкого трения в осях машины,
- электрическое сопротивление и индуктивность якорной цепи электродвигателя,
- момент независимой внешней силы (нагрузка),
- управляющий входной сигнал,
- ток якорной цепи двигателя
Положим
10
11.
Введем в рассмотрение расширенный вектор состояния объектаТогда математическая модель объекта
C 1 0 0
или
C 0 1 0
или
1 0 0
C
0 1 0
11
12.
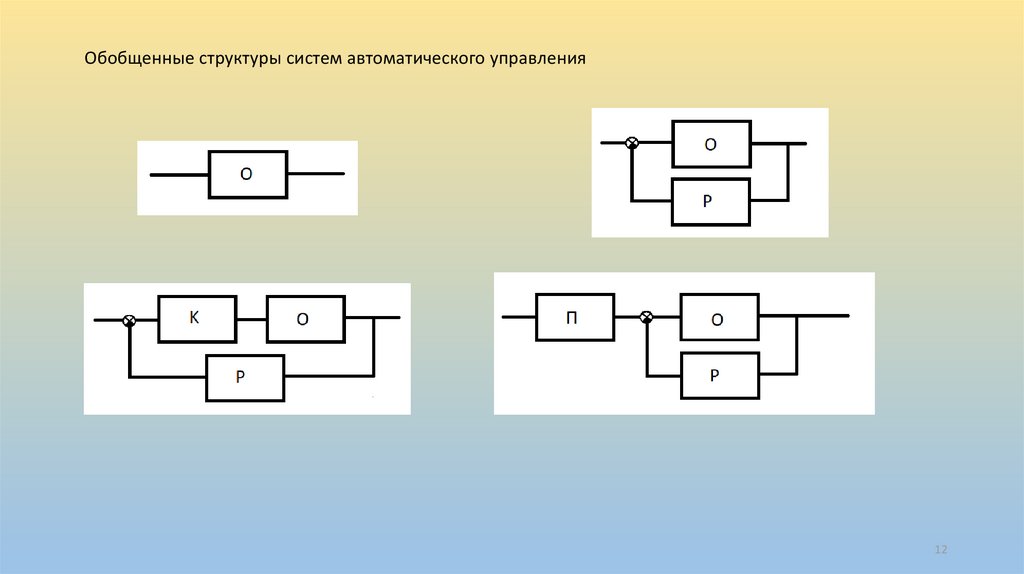
Обобщенные структуры систем автоматического управления12
13.
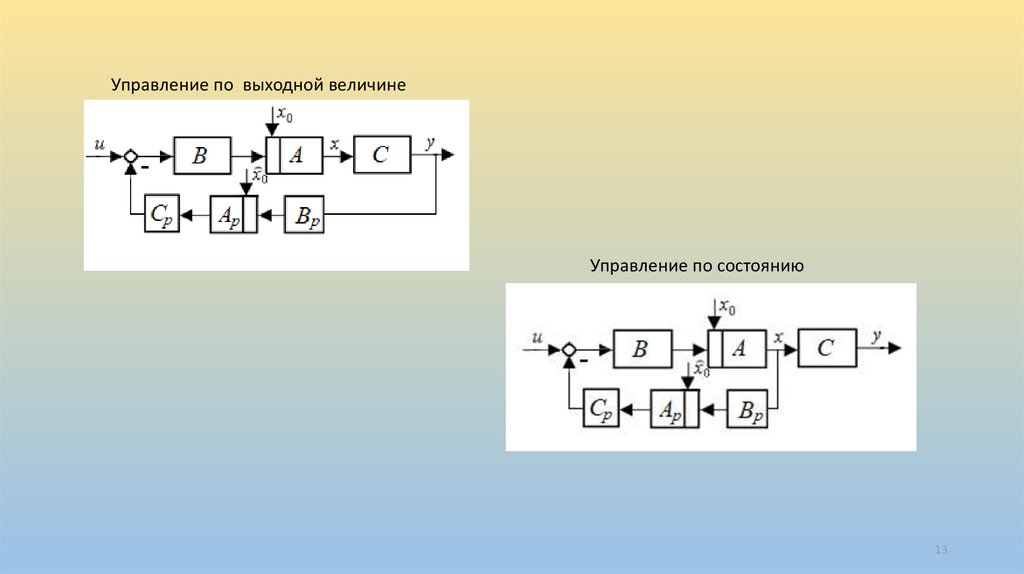
Управление по выходной величинеУправление по состоянию
13
14.
Структура наблюдателя состоянияСтруктура системы управления с наблюдателем состояния
14
15.
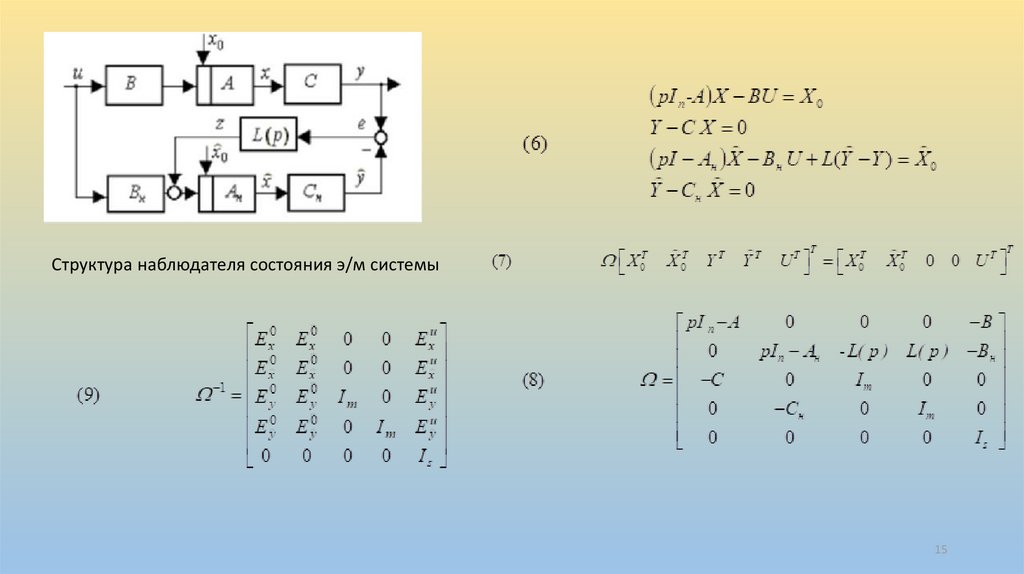
Структура наблюдателя состояния э/м системы15
16.
В качестве цели задачи синтеза, вводим понятие ошибки наблюдения16
17.
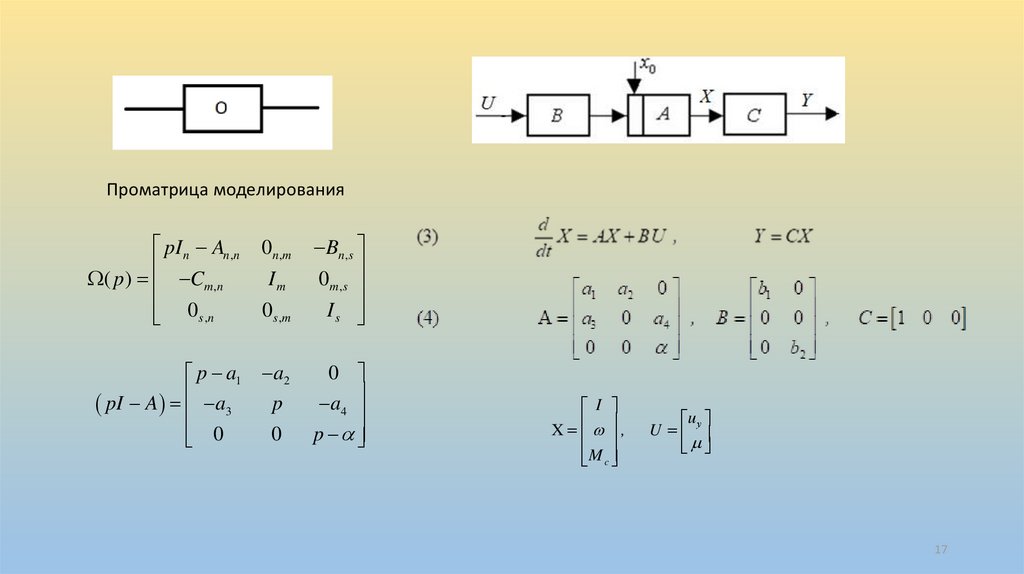
Проматрица моделированияpI n An,n
( p) Cm,n
0s ,n
0 s ,m
Bn,s
0 m ,s
I s
p a1 a2
p
pI A a3
0
0
0
a4
p
0 n ,m
Im
I
X ,
M c
u
U у
17
18.
p a1 a2a
p
3
0
0
0
1
0
0
0
0
x
x( p)
x0 Fx 0 ( p ) 0
y ( p ) 1 ( p ) 0 F x0 ( p ) I
m
y
u ( p )
u ( p ) 0
0
0
0 b1
a4
0
0
p
0
0
0
1
0
0
0
1
0
0
0
0
0
b2
0
0
1
Fxu ( p ) x0
u
Fy ( p ) 0
I S u ( p)
18
19.
Matlabпример
>> syms p
I=eye(3)
>> A=[-1 2 0;-3 0 -4;0 0 -5]
A=
-1
-3
0
I=
1
0
0
0
1
0
0
0
1
B=
2
0
0
>> F=p*I-A
0
0
3
F=
>> C=[1 0 0]
C=
1
2 0
0 -4
0 -5
0
[ p + 1, -2, 0]
[ 3, p, 4]
[ 0, 0, p + 5]
0
19
20.
>> H=inv(F)H=
[ p/(p^2 + p + 6),
[ -3/(p^2 + p + 6),
[
0,
2/(p^2 + p + 6),
(p + 1)/(p^2 + p + 6),
0,
-8/(p^3 + 6*p^2 + 11*p + 30)]
-(4*(p + 1))/(p^3 + 6*p^2 + 11*p + 30)]
1/(p + 5)]
>> Fox=H
Fox =
[ p/(p^2 + p + 6),
[ -3/(p^2 + p + 6),
[
0,
2/(p^2 + p + 6),
(p + 1)/(p^2 + p + 6),
0,
-8/(p^3 + 6*p^2 + 11*p + 30)]
-(4*(p + 1))/(p^3 + 6*p^2 + 11*p + 30)]
1/(p + 5)]
20
21.
>> Fux=H*BFux =
[ (2*p)/(p^2 + p + 6),
[ -6/(p^2 + p + 6),
[
0,
-24/(p^3 + 6*p^2 + 11*p + 30)]
-(12*(p + 1))/(p^3 + 6*p^2 + 11*p + 30)]
3/(p + 5)]
>> Foy=C*H
Foy =
[ p/(p^2 + p + 6),
2/(p^2 + p + 6),
-8/(p^3 + 6*p^2 + 11*p + 30)]
>> Fuy=C*H*B
Fuy =
[ (2*p)/(p^2 + p + 6), -24/(p^3 + 6*p^2 + 11*p + 30)
21
22.
Вопросы для самостоятельной проработки1. Изучение соответствующих разделов учебного пособия [3];
2. Применительно к индивидуальному объекту управления (ОУ):
• найти все передаточные функции (от каждого входа – к каждому выходу)
• оценить устойчивость (степень устойчивости) каждого канала управления;
• осуществить компьютерное моделировании и найти все переходные характеристики;
22

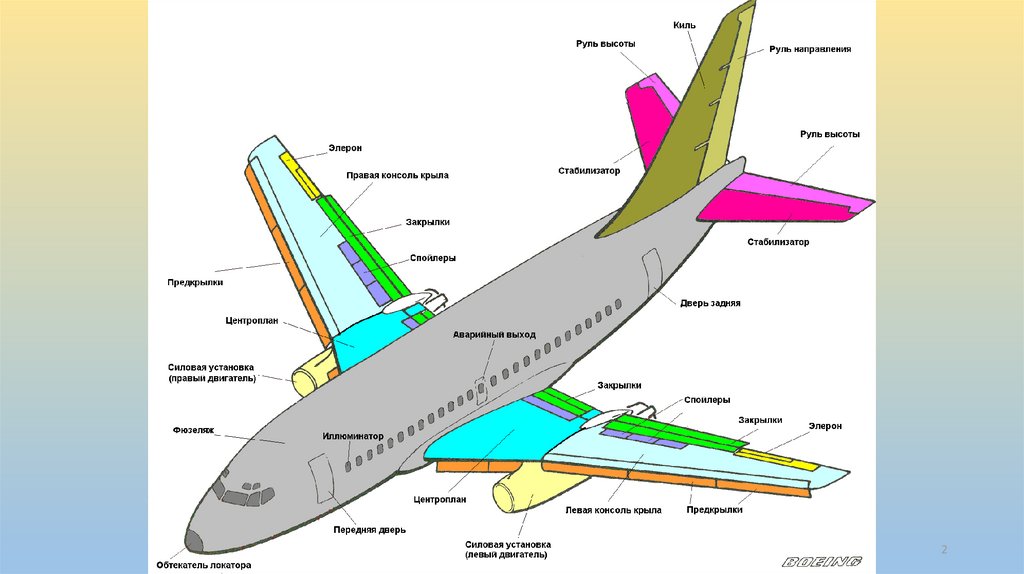
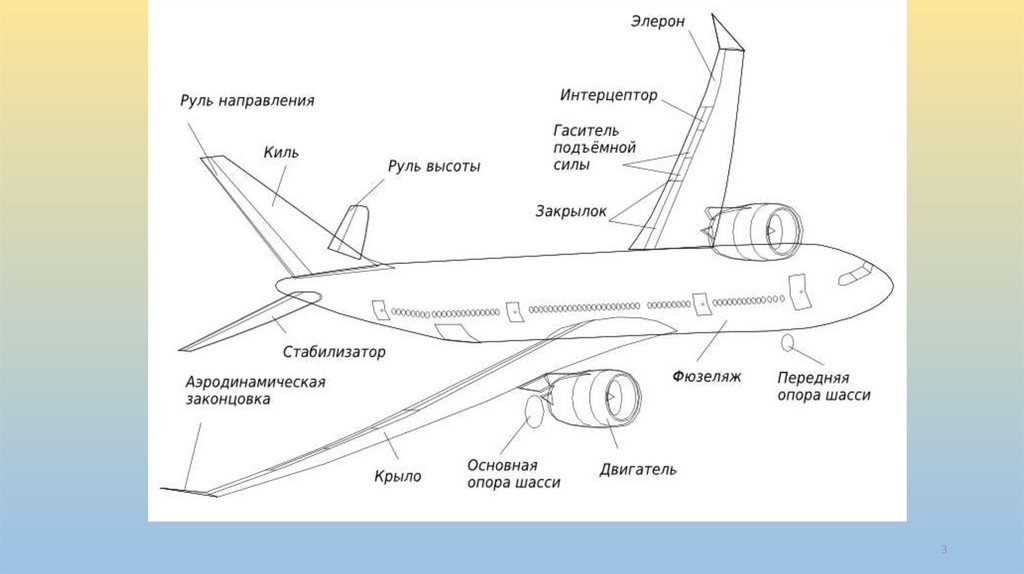
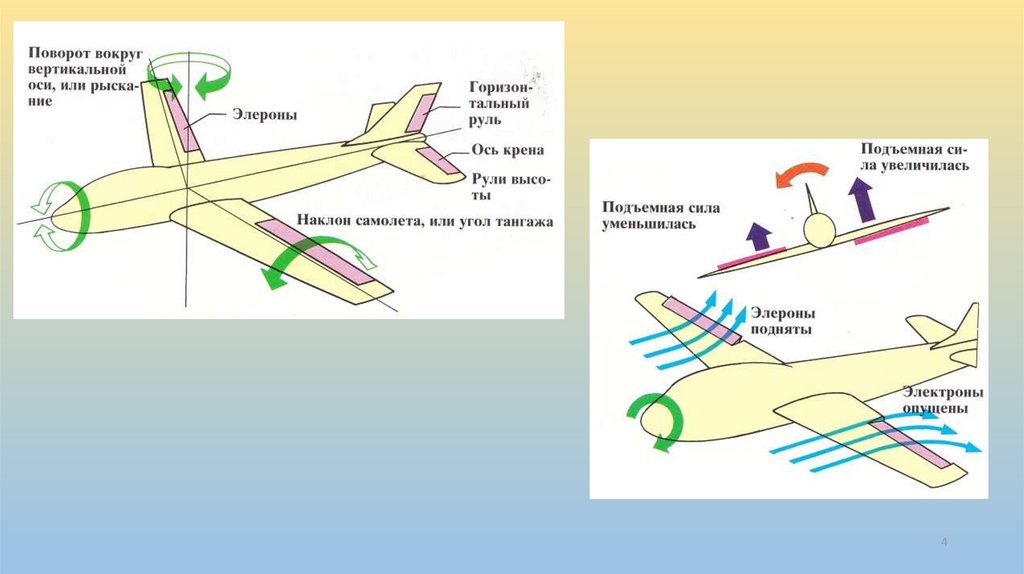
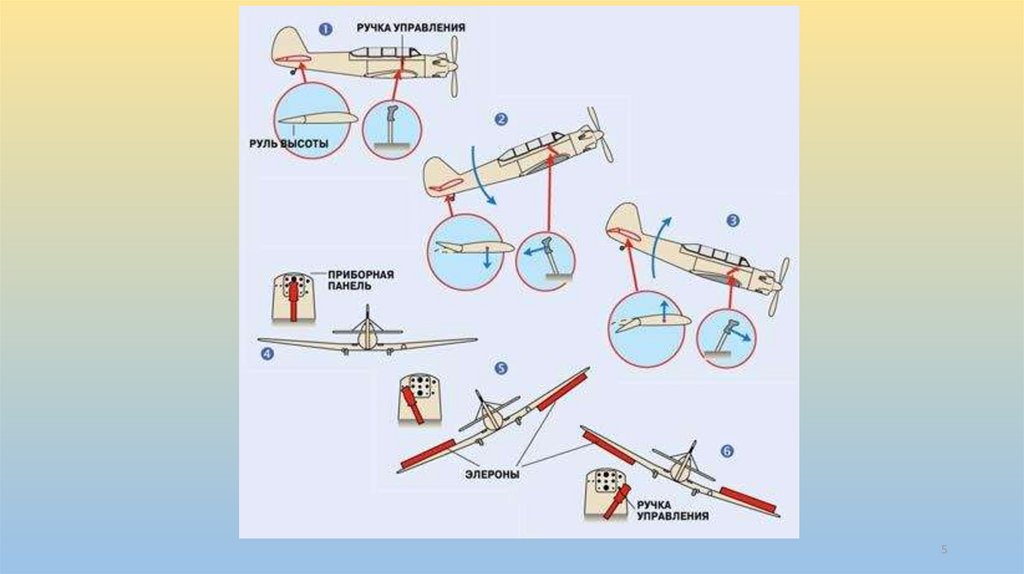








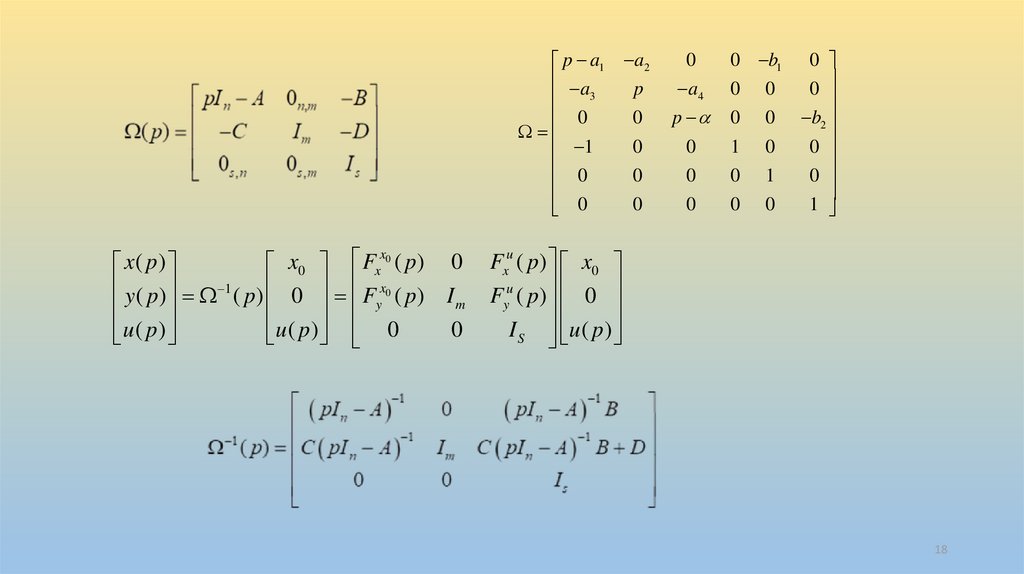
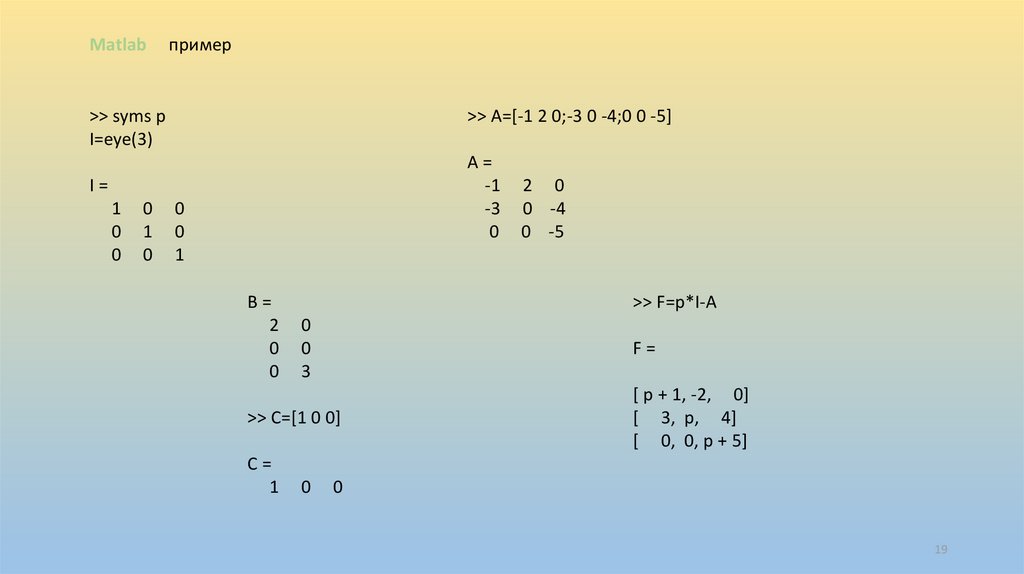
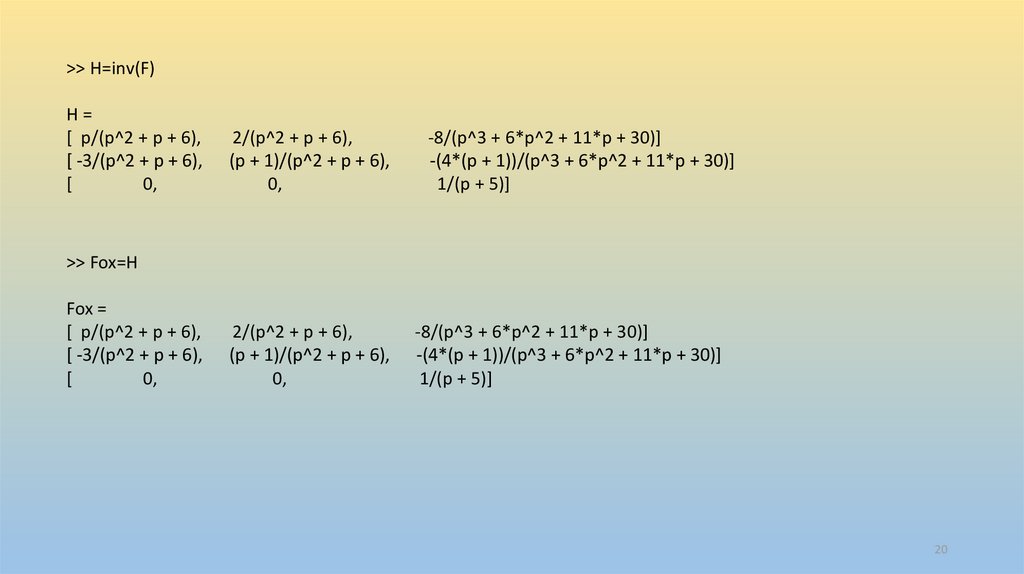
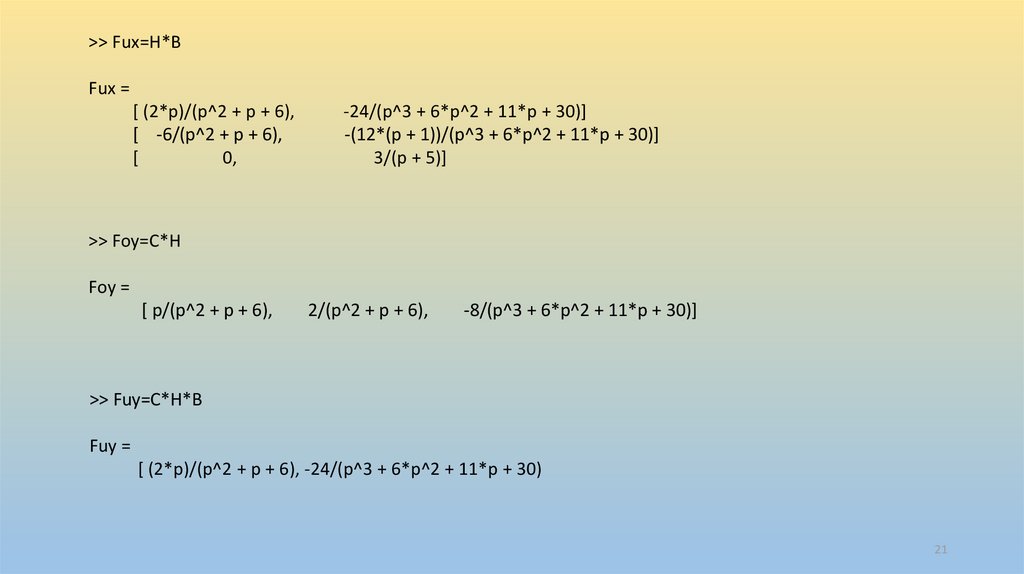

 mechanics
mechanics








