Similar presentations:
Теория и практика обработки результатов измерений в примерах
1. ВВОДНОЕ ЗАНЯТИЕ
Теория и практикаобработки результатов
измерений
1
2.
Бросая в водукамешки, смотри на
круги, ими
образуемые: иначе
такое бросание
будет пустою
забавой.
2
КОЗЬМА ПРУТКОВ
3.
Есть и другая точка зрения….I Д.Ю. Иванов, Т.Н. Князева, Ю.Н. Лазарева
Введение
в математическую
обработку результатов
эксперимента
(БГТУ, 2018)
II Д.Ю. Иванов, Ю.Н. Лазарева
Математическая обработка
результатов измерений
в примерах
(БГТУ, 2019)
3
Ну!
И зачем нам всё это…?
4. Проблема эфира
Для наукиПроблема эфира
Проблема эфира, который заполняет всё мироздание, волновала науку с давних пор. В 1887 г.
Майкельсон и Морли предприняли сложнейший для своего времени эксперимент по
определению влияния движения Земли по орбите на скорость света .
В результате, никакого влияния обнаружено не было. Но чтобы это доказать и, главное, чтобы
все в это поверили, скорость света следовало измерять с соответствующей точностью.
Попробуем её оценить. Скорость света: с=300000 км/с, а скорость движения Земли: v=30 км/с.
Из этих чисел видно, что абсолютная погрешность измерения скорости света не должна была
превышать (3÷4) км/с. Много это или мало?
На этот вопрос отвечает другой способ определения точности измерений – относительная
погрешность: ε=Δc/c. Из приведённых данных получаем ε=10-4, или одна сотая процента.
Значит, прежде, чем приступать к проведению столь сложного и дорогостоящего
эксперимента, его авторы должны были убедиться, что это им по силам.
Кстати, современная точность определения скорости света: ε=10-9
Прежде, чем мы перейдём к другому примеру, отметим, что только что мы познакомились с
двумя способами описания точности измерений: абсолютной и относительной
погрешностями.
подробнее см. I стр. 7
4
.
5.
Для практикиПроизводство винтовок и патронов к ним
Пусть, например, один из цехов завода производит стволы, а другой
– патроны. Понятно, что и те, и другие должны подходить друг
другу в любых комбинациях. Для этого их размеры должны быть
достаточно жёстко заданы и отклонения от регламента не могут
выходить за определённые пределы. Чтобы этого достичь, заводу
потребуется завести у себя целую науку – метрологию, частью
которой и является теория погрешностей.
И в обычной жизни мы сталкиваемся с измерениями на каждом
шагу, часто даже не замечая этого (примерка одежды, расстановка
мебели, определение веса и т.п.). При этом чаще всего в этих
случаях нас устраивают даже не слишком точные приборы и
измерения.
5
6. Существует ли истинный размер?
Тем не менее, всё же может возникнуть вопрос: а нельзя ли, если очень нужно,провести измерения абсолютно точно, определив тем самым истинную
величину?
Представим себе, что мы могли бы неограниченно увеличивать точность
измерения, скажем, линейных размеров предмета. К чему мы пришли бы в конце
концов? Мы стали бы чувствовать движение отдельных атомов. Отсюда видно,
что истинного значения измеряемой величины не существует в принципе.
Как же быть?
Опыт показывает, что если достаточно чувствительным прибором (это важно)
много раз измерять одну и ту же величину (длину, массу, силу тока и т.п.), то при
каждом измерении мы будем в силу случайных причин получать не одинаковые
результаты. Метрологи сказали бы, что результат каждого измерения отягощён
случайной погрешностью.
6
7. Прямые и косвенные измерения
Измерения, проведённые непосредственно с помощью тех или иных приборов,называются прямыми, а вычисление искомой величины по формулам, связывающим
эту величину с другими параметрами, определёнными в ходе прямых измерений,
носит название косвенных измерений.
Одну и ту же величину часто можно определить как с помощью прямых, так и
посредством косвенных измерений.
Например, массу тела можно узнать, взвесив его на весах, но её же можно рассчитать,
зная плотность материала, на основе прямого измерения объёма тела по формуле
m=Vρ.
Сопротивление проводника можно измерить непосредственно омметром, но можно и
рассчитать по закону Ома, использовав прямые измерения силы тока и напряжения:
R=U/I.
Погрешности прямых и косвенных измерений в силу их принципиально различной
природы находят поэтому и принципиально разными методами. В первом случае –
это теория вероятностей, а во втором – дифференциальное исчисление.
7
8.
Прямые измеренияВ основе подхода к оценке результата прямых измерений и его
случайной погрешности лежат достаточно простые и интуитивно
понятные идеи, но потребовался талант К.Ф. Гаусса (1777-1855),
которого ещё при жизни называли «королём математиков»,
чтобы эти идеи оформились в изящную законченную
математическую теорию.
Каковы же эти идеи?
наилучшим
8
значением измеряемой физической величины
является среднее арифметическое x
отклонения от среднего в сторону меньших и больших значений
равновероятны;
чем больше отклонение от среднего, тем меньше измерений
попадает в этот диапазон Δx. Иначе говоря, функция
распределения ρ(x) по обе стороны от x есть монотонно
убывающая функция;
функция распределения ρ(x) с увеличением абсолютной
величины x должна приближаться к нулю асимптотически, т.е.
очень большие отклонения от среднего, хотя и маловероятны, но
все же возможны.
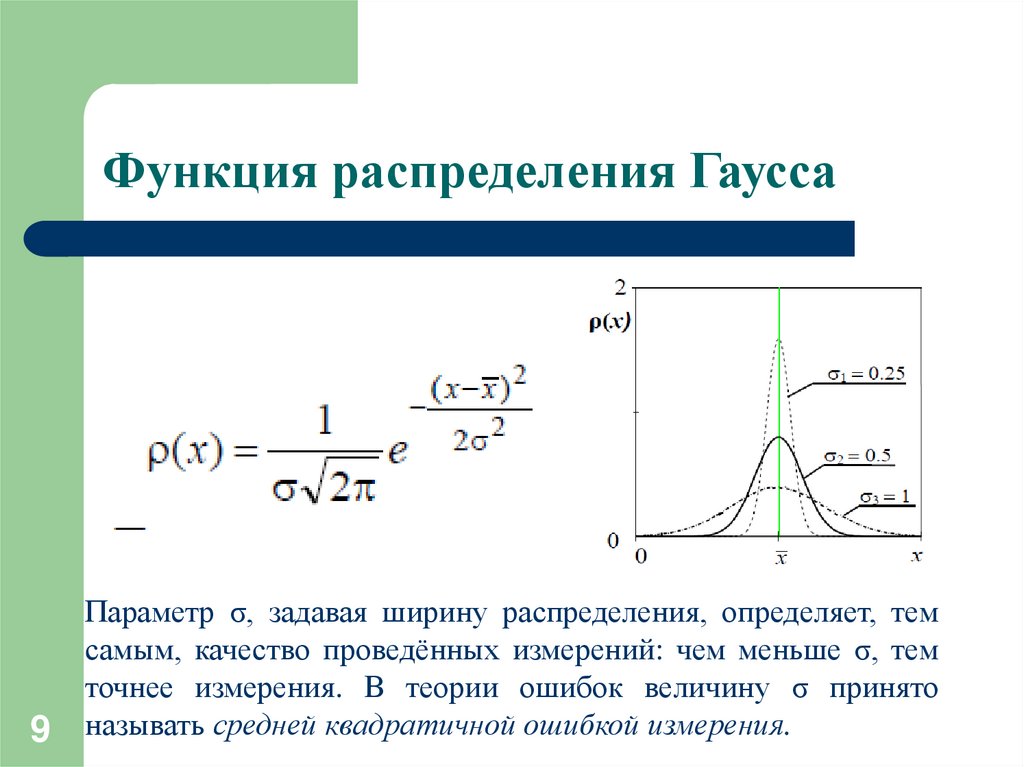
9. Функция распределения Гаусса
9Параметр σ, задавая ширину распределения, определяет, тем
самым, качество проведённых измерений: чем меньше σ, тем
точнее измерения. В теории ошибок величину σ принято
называть средней квадратичной ошибкой измерения.
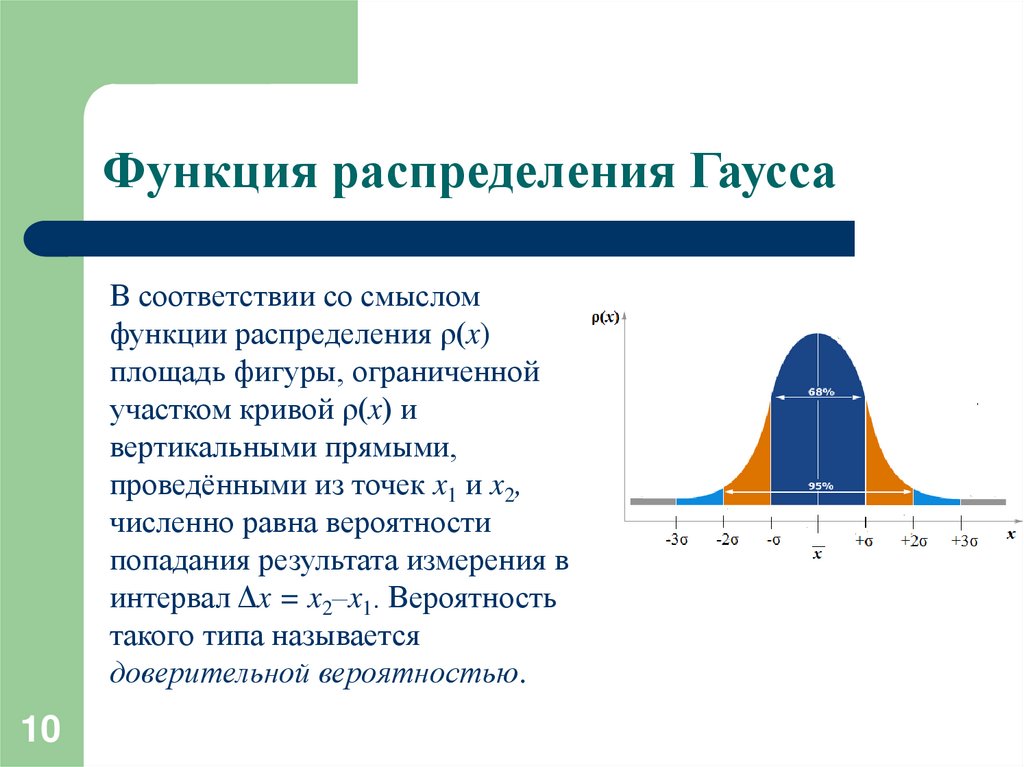
10. Функция распределения Гаусса
В соответствии со смысломфункции распределения ρ(x)
площадь фигуры, ограниченной
участком кривой ρ(x) и
вертикальными прямыми,
проведёнными из точек x1 и x2,
численно равна вероятности
попадания результата измерения в
интервал Δx = x2–x1. Вероятность
такого типа называется
доверительной вероятностью.
10
11. Доска Гальтона (видео)
Лучше всего влияние случайных причин на результат измерения можнопродемонстрировать с помощью устройства, изобретённого в 1873 г.
английским учёным Ф. Гальтоном (1822-1911). Доска Гальтона моделирует
основные свойства распределения Гаусса.
11
Она представляет собой ящик с прозрачной передней стенкой. В заднюю стенку
в шахматном порядке вбиты штырьки, образующие треугольник. Сверху в ящик
через воронку, выход из которой расположен ровно посередине между левой и
правой стенками, засыпают шарики. В идеальном случае, сталкиваясь со
штырьком, шарик каждый раз с одинаковой вероятностью может повернуть
либо направо, либо налево. Нижняя часть ящика разделена перегородками по
числу штырьков в нижнем ряду, в результате чего шарики, скатываясь на дно
ящика, образуют столбики, которые тем выше, чем ближе к середине доски.
При достаточно большом числе шариков внешний вид столбиков приближается
к кривой нормального распределения – кривой Гаусса.
12.
Предварительные итогиЕсли в неизменных условиях произвести
очень большое число измерений (в пределе
– бесконечно большое), то, построив кривую
Гаусса, можно будет :
найти среднее арифметическое всех
проведённых измерений (соответствует
максимуму кривой Гаусса). В теории
вероятностей оно называется
математическим ожиданием;
найти среднеквадратичную ошибку σ;
после чего записать окончательный
результат измерений в зависимости от
требуемой надёжности (доверительной
вероятности, α) следующим образом:
в науке (и в лаборатории) обычно считают
достаточными: α=0,95 и соответствующий
ей доверительный интервал в 2σ.
12
Подробнее см. I, стр. 8-12
13. Жизнь коротка, или распределение Стьюдента
13Основной недостаток теории Гаусса заключается в необходимости проведения
очень большого числа измерений, для чего ни у кого нет ни времени, ни
желания. Но что-то делать, ведь, было нужно. Это осознавали многие, но сделал,
как обычно, один человек.
Его звали Уильям Сили Госсет (1876 — 1937). Выпускник Оксфорда, Госсет, до
конца жизни работал в ирландской пивоваренной компании Гиннес, которая для
повышения качества и уменьшения себестоимости своей продукции, содержала
большой штат, состоящий из лучших учёных.
Проблема выбора наиболее подходящих сортов хмеля, стоявшая перед Гиннес, в
результате трансформировалась для Госсета во вполне академическую задачу:
насколько увеличится погрешность измерения в случае, когда имеется лишь
маленькая выборка из 2 или 10 образцов, по сравнению с выборкой в 1000
образцов?
И Госсет решил её. Но фирма, чтобы не открывать свои секреты другим
пивоварам, разрешила ему опубликовать свои результаты только под
псевдонимом. Он выбрал псевдоним Student. Сегодня его метод, известный как
«t-распределение Стьюдента» (Student’s t-distribution), являясь фундаментом
современной статистики, стал ещё и de facto стандартной частью
промышленных протоколов контроля качества.
14. Последовательность обработки прямых измерений
Определить среднее арифметическое по всей совокупности проведённых многократныхизмерений одной и той же физической величины по одной из формул:
или
• Сосчитать оценку среднеквадратичной ошибки среднего (применение распределения
Стьюдента начинается именно с этого момента). Поскольку число измерений n обычно
невелико, вычислить σ нельзя, но можно провести её оценку с помощью предложенной
Госсетом (Стьюдентом) формулы:
14
15. Последовательность обработки прямых измерений
И, наконец, определяемТо есть среднюю абсолютную погрешность Δx результата x определяем,
домножая полученную оценку на коэффициент Стьюдента tα(n), который для
заданной доверительной вероятности α зависит только от числа
произведённых измерений n
Подробнее см. I, стр. 13-18; II, 13-18 (рассмотрены примеры)
15
16. Обработка ряда виртуальных измерений
II, cтр. 13-18 (рассмотрены примеры)16
17. Полная погрешность прямых измерений
I, cтр. 15-18;II, стр. 10-13 (рассмотрены примеры)
17
18. Ошибка ошибки и корректная запись результата
I, стр. 28;II, стр. 7-9 (рассмотрены примеры).
18
19. Погрешности косвенных измерений
I, стр. 18-20 (обоснование);II, стр. 18-19, 22-23 (рассмотрены примеры)
19
20. Построение и анализ графиков
I, стр. 20-27;II, стр. 24-31
Оба пособия равноценно дополняют друг друга
20
21. Общие рекомендации по проведению физического эксперимента с написанием отчёта
II, стр. 3-7, 32-3521
22. Дополнение
Приложение I, стр. 29-42• Латинский и греческий алфавиты,
• некоторые приближённые математические формулы,
• основные физические постоянные,
• аналоговые и цифровые электроизмерительные приборы
Приложение II, стр. 36-40
• Простейшие механические измерительные приборы,
• таблица коэффициентов Стьюдента
22



















 mathematics
mathematics








