Основы теории ошибок измерений. Виды измерений и погрешностей

1. ОСНОВЫ ТЕОРИИ ОШИБОК ИЗМЕРЕНИЙ

Виды измерений и погрешностей
• Измерением какой-либо физической величины наз-ся
операция, в результате которой мы узнаем, во сколько
раз измеряемая величина больше (или меньше)
соответствующей величины, принятой за единицу
Виды измерений классифицируются:
– по способу получения результата (прямые и косвенные);
– по методу измерений (абсолютные, относительные и
пороговые);
– по условиям измерений (равноточные, неравноточные);
– по степени достаточности измерений (необходимые,
избыточные)

2.

При прямых измерениях измеряется непосредственно
исследуемая величина
При косвенных измерениях исследуемая величина
измеряется как функция по результатам измерения других
величин
Например, ускорение автомобиля при разгоне определяется
по результатам измерения расстояния и времени разгона;
вычисление плотности – по массе и объему
Абсолютные измерения – это прямые измерения в
единицах измеряемой величины
Относительные измерения представляют собой
отношения измеряемой величины к величине играющей роль
единицы или к величине, принимаемой за исходную
При пороговых измерениях фиксируется только факт
нахождения величины в одностороннем или двухстороннем
допуске (по принципу "да/нет")

3.

• Равноточные измерения проводятся в одинаковых
условиях одними и теми же измерительными приборами и
с одинаковой степенью тщательности. При этом в ряду
измерений нельзя отдать предпочтение какому-либо
одному или нескольким значениям
Неравноточные измерения не отвечают указанным выше
требованиям
Избыточные измерения имеют по сравнению с
необходимыми большее число измерений либо большую
точность, содержат среди измерений зависимые, т. е. дают
избыточную информацию
Надежность результатов исследования в значительной
степени зависит от точности измерений
Под точностью измерений понимают степень
соответствия результата измерения
действительному значению измеряемой величины

4.

Снять показания с прибора – не значит только измерить.
Необходимо еще оценить ошибки (погрешности) измерений
Погрешность измерения – это отклонение результата
измерения от истинного значения измеряемой величины
Под истинным значением измеряемой величины принято считать
– среднюю арифметическую величину ряда измерений;
– известное эталонное значение;
– величину, полученную в результате более точных (не менее
чем на порядок) измерений

5.

Основные источники ошибок
Первый источник заключен в датчике, который
неправильно реагирует на измеряемую величину.
Например, если тензосопротивление плохо наклеено на
упругий элемент, то деформация его решетки не будет
соответствовать деформации упругого элемента
Второй источник – измерительное устройство, в котором
возможны погрешности из-за неправильного
функционирования его механических или электрических
элементов
Третий источник – сам наблюдатель, который из-за
неопытности или усталости неправильно считывает
показания прибора
Ошибки могут возникнуть из-за влияния измерительного
устройства на объект измерения (например, при
разрушающем методе контроля), влияния окружающей
среды (температура, загазованность и т. п.), методических
погрешностей, допущенных экспериментатором

6.

Эти источники ошибок приводят к появлению трех типов
ошибок: случайных, систематических и грубых
Случайная погрешность – это погрешность, которая в
отдельных измерениях может принимать случайные, заранее
конкретно неизвестные значения.
Случайные погрешности обязаны своим происхождением ряду
как объективных, так и субъективных факторов, действие
которых неодинаково в каждом опыте и не может быть учтено.
Случайные погрешности различаются в отдельных измерениях,
сделанных в одинаковых условиях одними и теми же
измерительными приборами. Исключить случайные
погрешности нельзя. Можно только оценить их значение
Случайные погрешности определяются по законам теории
ошибок, основанной на теории вероятностей

7.

Систематическая погрешность – это погрешность,
вызванная факторами, действующими одинаковым образом
при многократном повторении одних и тех же измерений с
помощью одних и тех же измерительных приборов
В качестве примера систематической ошибки рассмотрим
случай взвешивания на чашечных весах с помощью
неточных гирь. Если взятая нами гиря имеет ошибку, скажем
0,1 г, то вес тела (пусть 1000 г) будет завышенным (или
заниженным) на эту величину, и чтобы получить верное
значение, необходимо учесть эту ошибку, прибавив к
полученному весу (или вычтя из него) 0,1 г, P=(1000±0,1) г
Грубая погрешность или промах вызывается просчетом
экспериментатора или неисправностью средств измерения,
или резко изменившимися внешними условиями
Грубые погрешности приводят к явному искажению рез-та,
поэтому их надо исключить из общего числа измерений

8.

По форме числового представления погрешности
делятся на абсолютные и относительные
Абсолютная погрешность – это разность между
результатом измерения и его истинным значением:
x x a
где x – результат измерения; a – истинное значение
Относительная погрешность – это погрешность,
приходящаяся на единицу измеренной величины;
она обычно выражается в процентах
x
100%.
a

9.

Случайные погрешности и их распределение
Чтобы выявить случайную погрешность измерений,
необходимо повторить измерение несколько раз
Если каждое измерение дает заметные от других
результаты, мы имеем дело с ситуацией, когда случайная
погрешность играет существенную роль
Наиболее вероятным значением измеряемой величины из
серии измерений является ее среднее значение
Разброс измеряемой величины относительно ее среднего
значения определяется величиной средней квадратической
погрешности отдельного измерения

10.

Пусть в эксперименте в результате независимых и
равноточных измерений постоянной величины а получены
значения х1, х2, …, хn
Абсолютные погрешности xi xi a рассматривают как
случайные величины
Независимость измерений понимается как взаимная
независимость случайных величин xi, а равноточность –
как подчинение величин xi одному и тому же закону
распределения (кроме того измерения сделаны одним и тем
же методом и с одинаковой степенью тщательности)
В качестве оценки неизвестной величины а по данным
измерений обычно берут среднее арифметическое x
результатов измерений
1 n
x
xi .
n
i 1
Дисперсия отдельных измерений 2
n
2
(
x
a
)
i
i 1
n 1
обычно неизвестна, и для ее оценки используется величина

11.

n
( xi x )2
Sn2 i 1
n 1
.
Среднюю квадратическую (стандартную) погрешность (СКО)
находятся по формуле 2 ,
2
для ее оценки вычисляется величина Sn Sn
lim Sn .
n
Величина
Sn
w
100 %
x
называется коэффициентом вариации
Обычно принимается, что погрешности подчиняются
нормальному закону распределения случайных величин

12.

При этом предполагается:
1) погрешности измерений могут принимать непрерывный
ряд значений;
2) при большом числе наблюдений погрешности равных
значений, но разных знаков встречаются одинаково часто;
3) частота появления погрешностей уменьшается с
увеличением величин погрешностей
Эти предположения приводят к закону распределения
погрешностей, описываемому формулой Гаусса:
y
1
2
e
( x ) 2
2 2
.

13.

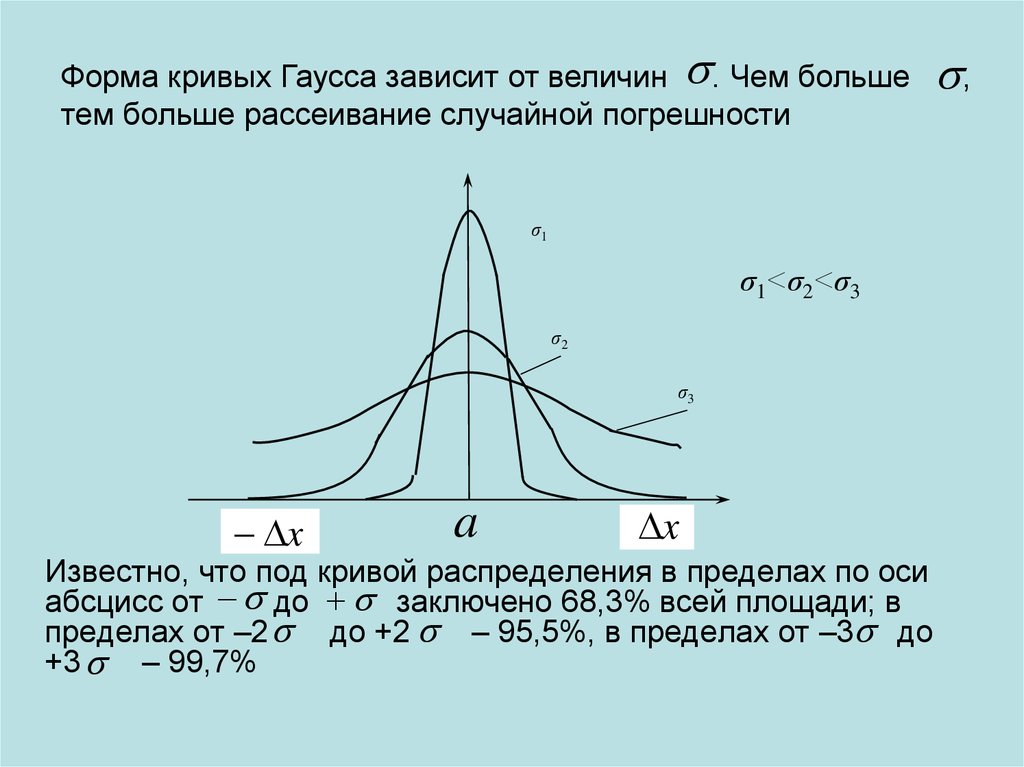
Форма кривых Гаусса зависит от величин . Чем больше
тем больше рассеивание случайной погрешности
σ1
σ1<σ2<σ3
σ2
σ3
x
a
x
Известно, что под кривой распределения в пределах по оси
абсцисс от до заключено 68,3% всей площади; в
пределах от –2 до +2 – 95,5%, в пределах от –3 до
+3 – 99,7%
,

14.

Замечание. В ряде случаев экспериментальные данные лучше
описываются другими законами распределения случайных
величин, например, законом Пуассона:
y
2 x 2
e
x!
.

15. Закон сложения случайных ошибок

Пусть измеряемая величина Z является суммой (или разностью)
двух величин X и Y, результаты измерений которых независимы.
2
2
2
Тогда, если S X , S Y , S Z – дисперсии величин X, Y и Z, то можно
доказать, что
S Z S X2 SY2
S Z2 S X2 S Y2
или
Если Z является суммой не двух, а большего числа
слагаемых, то закон сложения ошибок будет таким же, т. е.
средняя квадратичная ошибка суммы или разности двух (или
нескольких) независимых величин равна корню квадратному
из суммы дисперсий отдельных слагаемых
Для нахождения суммарной ошибки нужно складывать
не сами ошибки, а их квадраты

16.

Из закона сложения ошибок следуют два чрезвычайно важных
вывода
1: роль каждой из ошибок в общей ошибке результата.
Значение отдельных ошибок очень быстро падает по мере их
уменьшения
Пример: пусть X и Y – два слагаемых, определенных со
средними квадратичными ошибками S X и S Y , причем,
известно, что S Y В два раза меньше, чем S X . Тогда ошибка
суммы Z X Y будет
SZ2
S X2
SY2
S X2
S Z 1,1S X .
Sx 2 5 2
( ) SX .
2
4
В первую очередь надо уменьшать ошибку, имеющую
наибольшую величину

17.

Если нужная величина Z является разностью двух независимо
измеряемых величин X и Y, то из выражения для среднего
значения следует, что ее относительная погрешность
Sz
Z
S x2 S y2
X Y
будет тем больше, чем меньше X Y , и относительная
погрешность возрастает до бесконечности, если X Y
Невозможно добиться хорошей точности измерений какойлибо величины, строя измерения так, что она находится как
небольшая разность результатов независимых измерений
двух величин, существенно превышающих искомую. В
противоположность этому относительная погрешность суммы
Sz
Z
S x2 S y2
X Y
очевидно, не зависит от соотношения величин X и Y

18.

2: средняя квадратическая погрешность среднего
арифметического равна средней квадратической
погрешности отдельного результата, деленная на
Sn
корень квадратный из числа измерений
Sx
n
,
S n – средняя квадратичная погрешность отдельного измерения
Cреднеарифметическое ряда измерений
1 n
x1 x2
xn
x xi
n i 1
n n
n
согласно закону сложения случайных погрешностей
2
2
2
Sn2
Sn
Sn
2 Sn
Sx
,
n
n n
n
Это рассуждение относится лишь к измерениям, при которых
точность результата полностью определяется случайной
ошибкой

19.

При практической работе очень важно строго разграничивать
применение средней квадратичной ошибки отдельного
измерения S n и средней квадратичной среднего
арифметического S x
В тех случаях, когда требуется характеризовать точность
применяемого способа измерений, следует
характеризовать его ошибкой S n .
S x применяется всегда, когда нужно оценить погрешность
того числа, которое получили в результате всех
произведенных измерений

20.

Доверительный интервал и доверительная
вероятность
Обозначим истинное значение измеряемой величины через x,
погрешность измерения этой величины – x . Среднее
арифметическое значение, полученное в результате
измерений, будет x . Пусть означает вероятность того, что
результат измерений отличается от истинного значения на
величину, не большую, чем x .
или
P( x x x x)
P( x x x x x)
Вероятность называется доверительной вероятностью,
или коэффициентом надежности. Интервал значений от x x
до x x называется доверительным интервалом

21.

Для характеристики величины случайной ошибки
необходимо задать два числа, а именно: величину
самой ошибки (или доверительного интервала) и
величину доверительной вероятности
При обычных измерениях можно ограничиться
доверительной вероятностью 0,9 или 0,95
Для измерений, по условиям которых требуется
чрезвычайно высокая степень надежности, иногда задают
доверительную вероятность 0,997
Удобство применения стандартной ошибки в качестве
основного численного выражения погрешности наблюдений
заключается в том, что этой величине соответствует вполне
определенная доверительная вероятность, равная 0,68.
(Здесь и дальше полагаем, что ошибки распределены по
нормальному закону)

22.

Средней квадратичной ошибке
соответствует
доверительная вероятность 0,68, удвоенной средней
квадратичной ошибке (2
) – доверительная
вероятность 0,95, утроенной (3
) – 0,997
Определение доверительного интервала и доверительной
вероятности
При определении среднеквадратичной ошибки из малого
числа наблюдений находим последнюю с малой точностью
Заменяя S n на , мы уменьшаем надежность нашей оценки.
Чтобы учесть это обстоятельство, будем записывать
x n
вероятность через коэф. Стьюдента, найденные по t ,n
P( x t ,n
Sn
Sn
x x t ,n
) .
n
n
Sn

23.

Группы систематических погрешностей и методы их
компенсации
При измерениях необходимо учитывать и исключать
систематические ошибки, которые иногда могут быть так
велики, что совершенно исказят результаты измерений
Их можно разделить на четыре группы:
1. Погрешности, природа которых нам известна, и их
величина может быть достаточно точно определена
Такие ошибки могут быть устранены введением соотв-щих
поправок. Источники таких ошибок нужно тщательно
анализировать, величины поправок определять и учитывать в
окончательном результате
ПРАВИЛО: если поправка не превышает 0,005 от средней
квадратической ошибки результата измерений , то ею следует
пренебречь

24.

2. Погрешности известного происхождения, но неизвестной
величины
К числу таких погрешностей относится погрешность
измерительных приборов, которая определяется иногда
классом точности прибора. Если на приборе указан класс
точности 0,5, то это означает, что показания прибора
правильны с точностью до 0,5% от всей действующей шкалы
прибора
Электроизмерительные приборы характеризуются обычно
классом точности в пределах от 0,05 до 4. Менее точные
приборы обозначения класса не имеют
Максимальные погрешности, даваемые измерительными линейками,
микрометрами и некоторыми другими приборами, иногда наносят на самом
приборе, иногда указывают в прилагаемом к нему паспорте. Обычно дается
наибольшая абсолютная погрешность, которую вынуждены считать
постоянной по всей шкале прибора, если последний не сопровождается
специальной таблицей поправок для каждого деления шкалы. Последняя
прилагается только к наиболее точным измерительным приборам

25.

3. Ошибки, природа которых неизвестна, но которые могут
иметь существенное значение
Эта группа систематических ошибок самая опасная. Это
ошибки, о существовании которых мы не подозреваем, но
их величина может быть значительной. Они чаще всего
проявляются при сложных измерениях, и иногда бывает, что
какая-нибудь величина, которая считается определенной с
точностью, например, до 2 3%, в действительности
оказывается в 2 раза больше измеренного значения
Один из наиболее надежных способов убедиться в отсутствии
таких погрешностей – провести измерения интересующей
величины совсем другим методом и в других условиях.
Совпадение полученных результатов служит известной, хотя, к
сожалению, не абсолютной, гарантией их правильности. Бывает,
что и при измерении разными методами в результатах
присутствует ускользнувшая от наблюдателя систематическая
ошибка, и в этом случае оба совпавшие друг с другом результата
окажутся одинаково неверными

26.

4. Ошибки, обусловленные свойствами измеряемого объекта
Эта группа ошибок, хотя и не связана непосредственно с
измерительными операциями, может существенным
образом искажать результат измерений
Систематическая ошибка, связанная со свойствами
измеряемого объекта, часто может быть переведена в
случайную. Перевод систематических ошибок в случайные
часто оказывается полезным, так как позволяет улучшить
точность получаемых результатов
Можно перевести систематическую ошибку в случайную,
организовав измерения таким образом, что постоянный
фактор, влияющий на результат измерений, в каждом из них
действует разным образом, т.е. результат его действий носит
случайный характер. Этот прием называется рандомизацией.
Он позволяет практически исключить многие неизвестные
систематические ошибки

27.

Определение грубых погрешностей
Можно считать какое-то измерение промахом, если
вероятность случайного появления такого значения в данном
ряду измерений является достаточно малой
Если известно точное значение
, то вероятность
появления значения, уклоняющегося от среднего
арифметического x более чем на 3
, равна 0,003; и все
измерения, отличающиеся от на эту (или большую) величину,
могут быть отброшены как очень маловероятные
Алгоритм определения грубых погрешностей
Пусть известен ряд измерений случайных величин:
x1 , x 2 ,..., x r , x n .
Установим, есть ли среди этих значений измерения,
проведенные с грубыми погрешностями (промахами)

28.

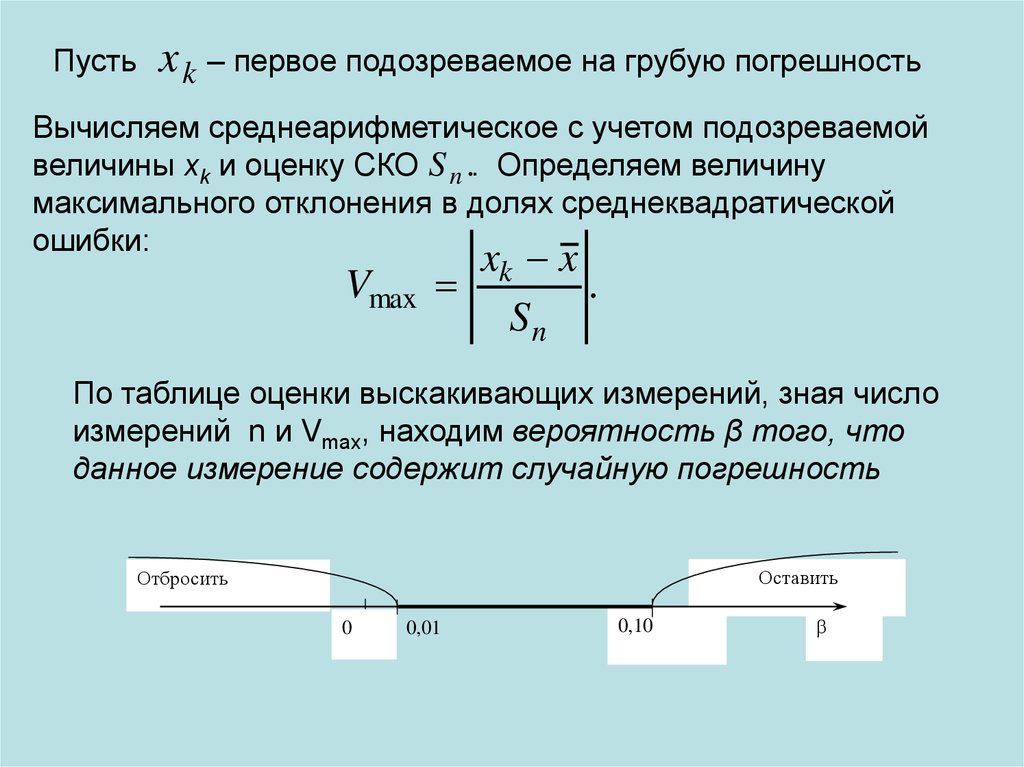
Пусть
x k – первое подозреваемое на грубую погрешность
Вычисляем среднеарифметическое с учетом подозреваемой
величины xk и оценку СКО S n .. Определяем величину
максимального отклонения в долях среднеквадратической
ошибки:
Vmax
xk x
.
Sn
По таблице оценки выскакивающих измерений, зная число
измерений n и Vmax, находим вероятность β того, что
данное измерение содержит случайную погрешность
Оставить
Отбросить
0
0,01
0,10
β

29.

Определение числа измерений
Допустим, что все систематические ошибки учтены, т.е.
поправки, которые следовало определить, вычислены, класс
точности прибора известен и есть уверенность, что
отсутствуют какие-либо существенные и неизвестные
источники систематических ошибок
Если случайная ошибка окажется меньше систематической,
то очевидно, что нет смысла пытаться еще уменьшить
величину случайной ошибки: все равно результаты
измерений не станут от этого заметно точнее, и, желая
получить большую точность, нужно искать пути к
уменьшению систематической ошибки. Наоборот, если
случайная ошибка больше систематической, то именно
случайную ошибку нужно уменьшать в первую очередь
Для уменьшения случайной ошибки следует произвести ряд измерений,
тем больший, чем меньшую величину случайной ошибки хотим получить.
Но нет смысла производить измерений больше, чем это необходимо,
чтобы систематическая ошибка существенно превышала случайную

30.

ПРАВИЛА
1. Если систематическая ошибка является определяющей,
т.е. ее величина существенно больше величины случайной
ошибки, присущей данному методу, то достаточно выполнить
измерение один раз
2. Если случайная ошибка является определяющей, то
измерения следует производить несколько раз. Число
измерений целесообразно выбирать таким, чтобы случайная
ошибка среднего арифметического была меньше
систематической ошибки с тем, чтобы последняя опять
определяла окончательную ошибку результата
Для уменьшения случайной ошибки результата могут быть
использованы два пути: улучшение точности измерений, т.е.
уменьшение величины σ, и увеличение числа измерений, т.е.
использование соотношения
.
x
n

31.

Считаем, что все возможности совершенствования техники
измерений уже использованы
Пусть систематическая ошибка измерений, определяемая
классом точности прибора или другими аналогичными
обстоятельствами, будет δ
Уменьшать случайную ошибку целесообразно только до тех
пор, пока общая погрешность измерений не будет полностью
определяться систематической ошибкой. Для этого
необходимо, чтобы доверительный интервал, определенный
с выбранной степенью надежности, был бы существенно
меньше величины систематической ошибки. Иначе говоря,
x .
Нет необходимости определять общую ошибку с точностью
большей 10%.
x / 10
x / 3
x / 2

32.

Надежность α с какой хотим установить доверительный
интервал, в большинстве случаев не должна превышать
0,95, хотя иногда требуются и более высокие значения α
Суммарная погрешность
Если систематическая и случайная погрешности измерений
близки друг к другу, они обе в одинаковой степени определяют
точность результата. Значение суммарных ошибок можно
оценить так: обозначим величину систематической ошибки δ,
дисперсию измерений – σ2, тогда в качестве верхней границы
суммарной ошибки можно принять 2 .
Вопрос о сложении систематических и случайных ошибок
актуален только тогда, когда одна из них не более чем в
несколько раз превышает другую. В противном случае в
качестве меры погрешности измерения следует указывать
только большую ошибку

33. Ошибки первого и второго рода

В тех случаях, когда измеряются какие-то свойства готовой
продукции (диаметр подшипника, состав металла, и т.п.),
задача измерений обычно состоит не в получении точного
значения измеряемой величины, а в необходимости
уложиться в определенные допуски, установленные для
данной продукции. Те изделия, которые не укладываются в
эти допуски, будем называть браком. Но следствием ошибок
измерений могут быть два обстоятельства: 1) хорошее
изделие бракуется и 2) брак пропускается
В той или иной мере ошибки Ι и ΙΙ рода всегда наблюдаются
Ввиду того, что ошибки Ι и ΙΙ рода всегда обусловлены
многочисленными факторами, их количественные
характеристики могут носить только статистический характер
и задаваться как вероятности РI и РII

34. ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА

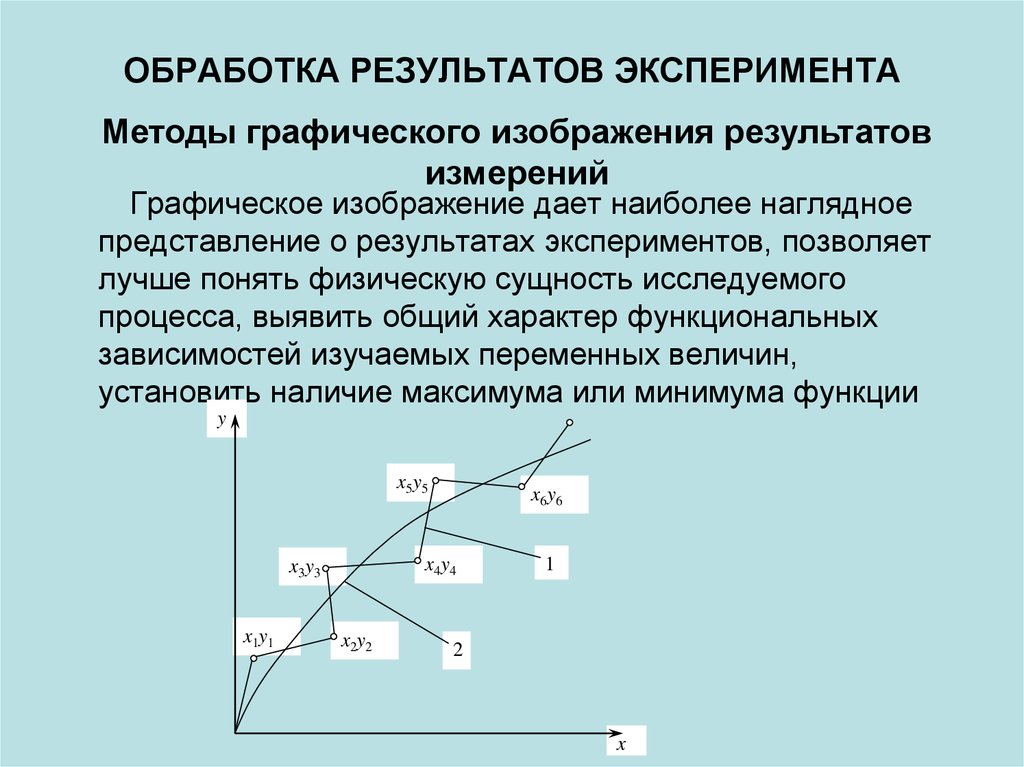
Методы графического изображения результатов
измерений
Графическое изображение дает наиболее наглядное
представление о результатах экспериментов, позволяет
лучше понять физическую сущность исследуемого
процесса, выявить общий характер функциональных
зависимостей изучаемых переменных величин,
установить наличие максимума или минимума функции
y
x5y5
x4y4
x3y3
x1y1
x6y6
x2y2
1
2
x

35.

При графическом изображении результатов экспериментов
большую роль играет выбор систем координат или
координатной сетки. Координатные сетки бывают
равномерными и неравномерными
Из неравномерных координатных сеток наиболее
распространены полулогарифмические, логарифмические,
вероятностные.
Назначение неравномерных сеток различное. В большинстве
случаев их применяют для более наглядного изображения
функций. Функция имеет различную форму на различных
сетках. Так, многие криволинейные функции спрямляют на
логарифмических сетках.
Правильно подобранный масштаб позволяет существенно
повысить точность результатов исследований.
Расчетные графики, имеющие максимум (минимум) функции
или какой-либо сложный вид, особо тщательно необходимо
вычерчивать в зонах изгиба. Количество точек на таких
участках должно быть значительно больше, чем на плавных

36. Методы подбора эмпирических формул

На основе экспериментальных данных можно подобрать
алгебраические выражения, которые называют
эмпирическими формулами. Такие формулы подбирают
лишь в пределах измерений значений аргумента x1,…,xn.
Эмпирические формулы имеют тем большую ценность, чем
больше они соответствуют результатам эксперимента
y f (x)
Эмпирические формулы часто незаменимы для анализа
измеренных величин. К эмпирическим формулам
предъявляют два основных требования:
по возможности они должны быть наиболее простыми и
точно соответствовать экспериментальным данным в
пределах изменения аргумента

37.

Эмпирические формулы являются приближенными
выражениями аналитических формул. Замену точных
аналитических выражений приближенными, более простыми
называют аппроксимацией, а функции –аппроксимирующими
Процесс подбора эмпирических формул состоит из двух этапов
•данные измерений наносят на сетку прямоугольных координат,
соединяют экспериментальные точки плавной кривой и
выбирают ориентировочно вид формулы
•вычисляют параметры формул, которые наилучшим образом
соответствовали бы принятой формуле
Метод выравнивания заключается в том, что кривую,
построенную по экспериментальным точкам, представляют
линейной функцией
Y a bX
Линеаризацию кривых можно легко осуществить на полу- или
логарифмических координатных сетках, которые применяют
при графическом методе подбора эмпирических формул

38.

Графический метод выравнивания может быть применен
в различных случаях, когда экспериментальная кривая на
сетке прямоугольных координат имеет вид плавной кривой
1.
y ax b
- степенная функция
Заменяя X = lgx и Y = lgy, имеем Y = lga + bX.
При этом экспериментальная кривая превращается в
прямую линию на логарифмической сетке
2.
y ae bx
Заменяя
- показательная функция
Y lg y
, имеем
Y lg a xb lg e
.