Similar presentations:
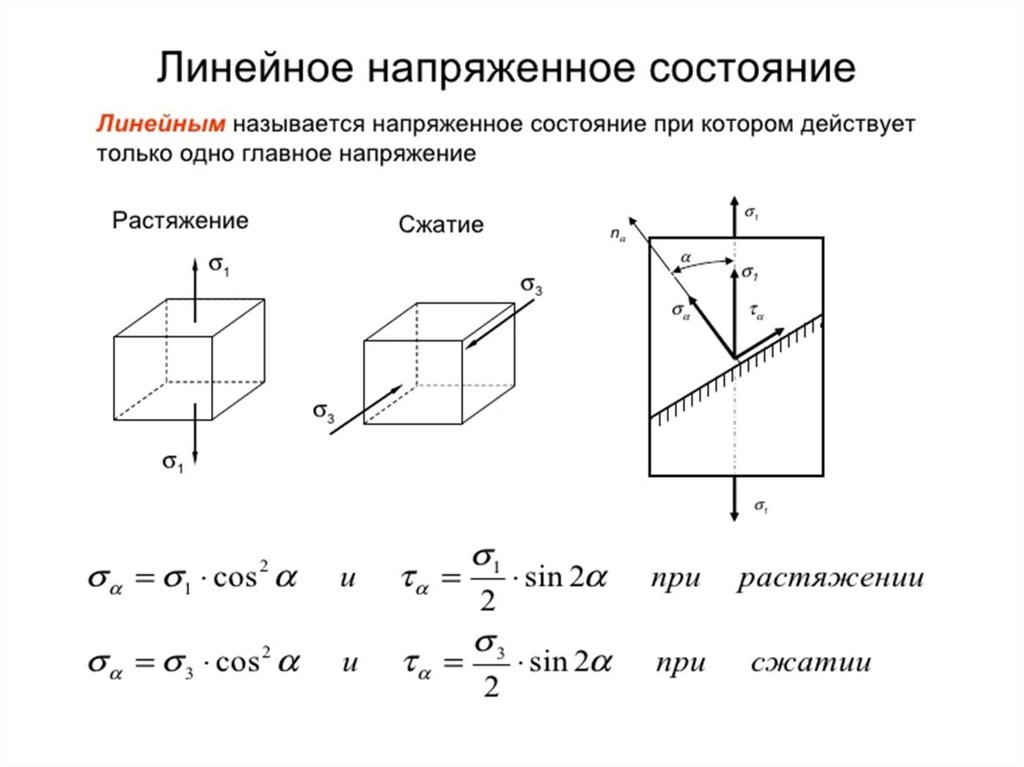
Сопротивление материалов. Напряженные и деформированные состояния
1.
2.
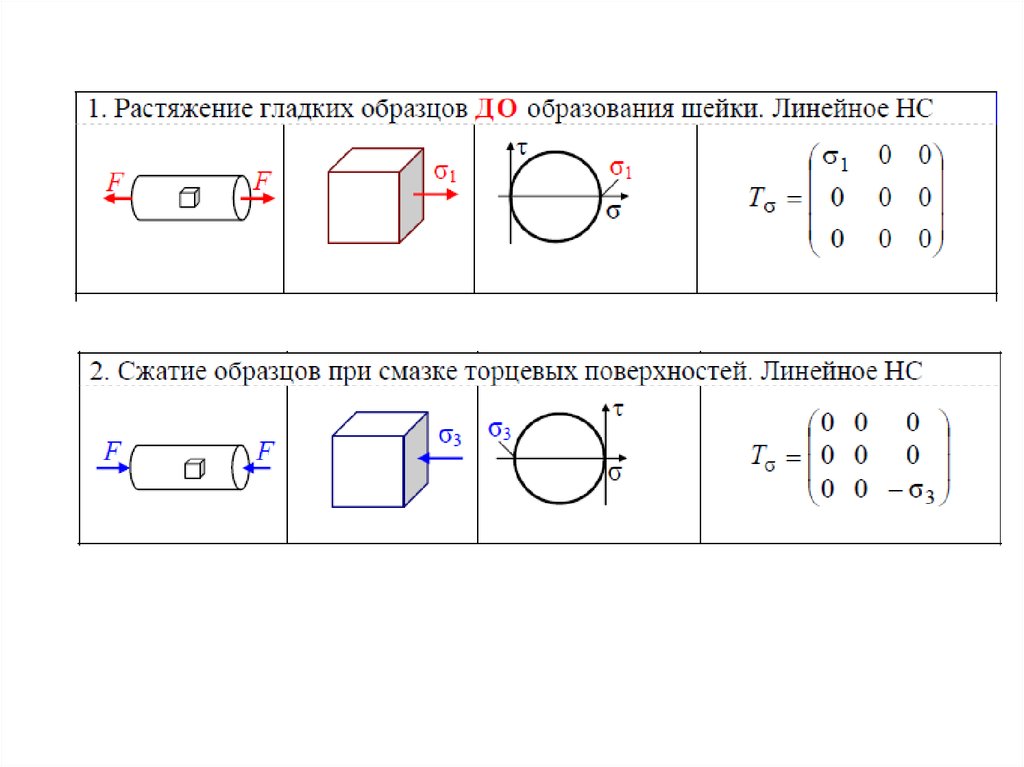
ПРИМЕРЫнапряженных и
деформированных состояний
(НДС)
3.
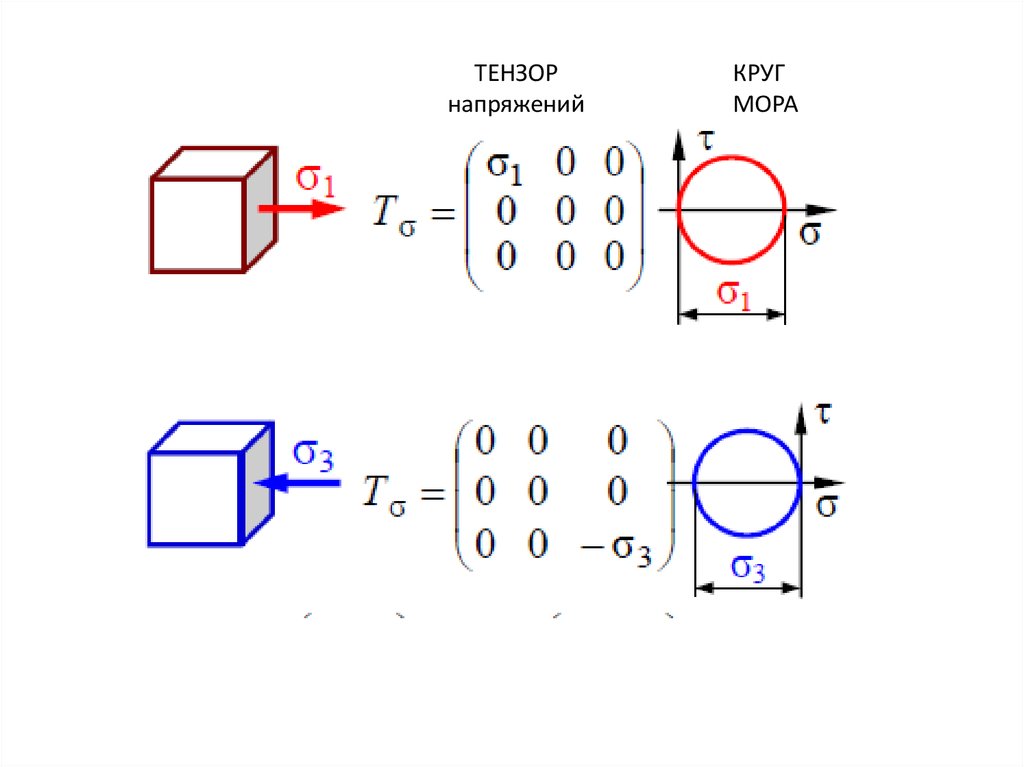
ТЕНЗОРнапряжений
КРУГ
МОРА
4.
5.
IF
II
F
II
I
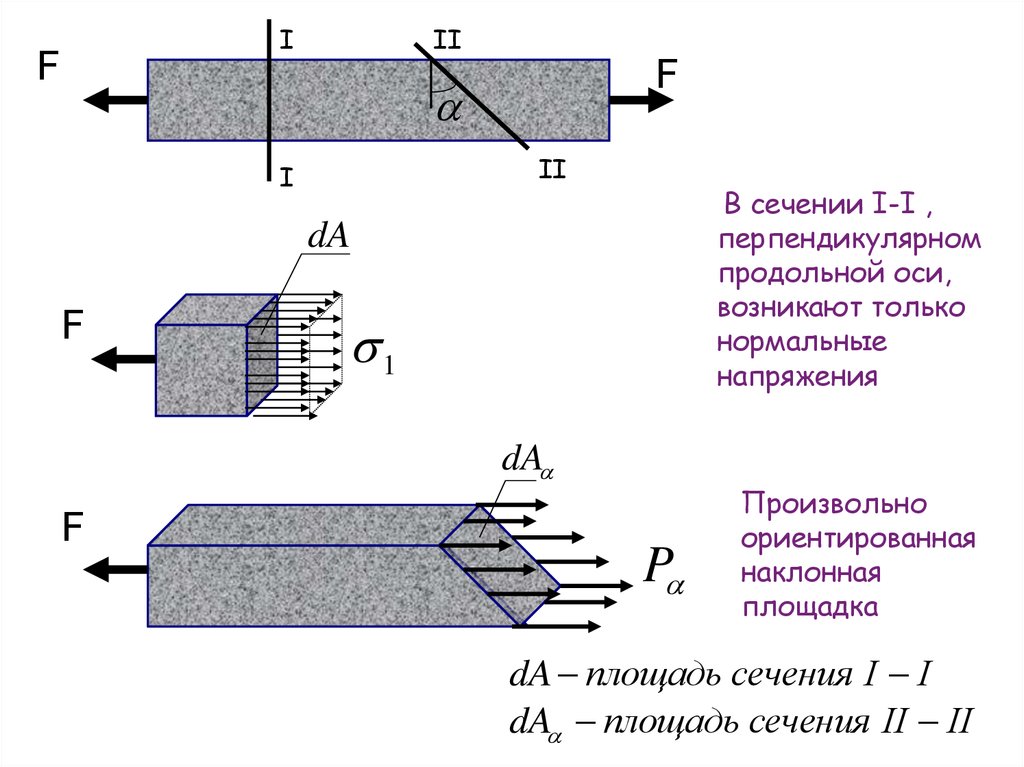
В сечении I-I ,
перпендикулярном
продольной оси,
возникают только
нормальные
напряжения
dA
F
1
dA
F
P
Произвольно
ориентированная
наклонная
площадка
dA площадь сечения I I
dA площадь сечения II II
6.
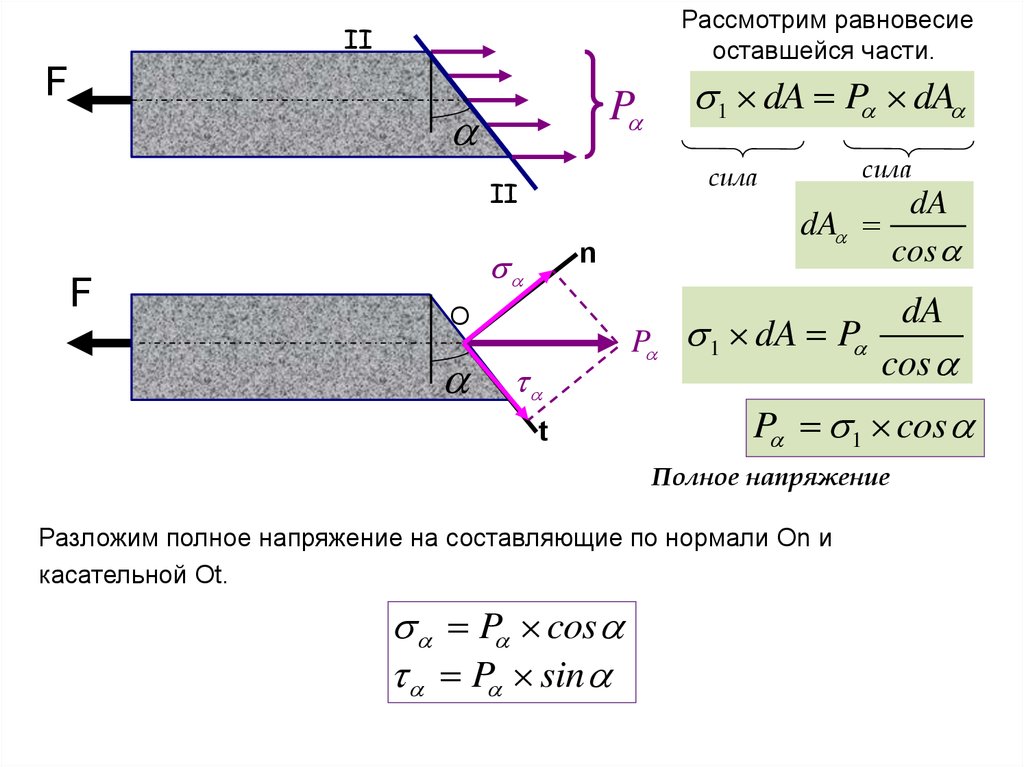
Рассмотрим равновесиеоставшейся части.
II
F
P
сила
II
F
n
O
1 dA P dA
t
сила
dA
dA
cos
dA
P 1 dA P
cos
P 1 cos
Полное напряжение
Разложим полное напряжение на составляющие по нормали On и
касательной Ot.
P cos
P sin
7.
P 1 cosподставим в
P cos
P sin
Получим
1 (cos )2 1
1 sin cos
1
2
sin 2
Если известны нормальные напряжения
можно определить
,
1
, то
в сечении стержня,
наклонённом к оси стержня под любым углом .
8.
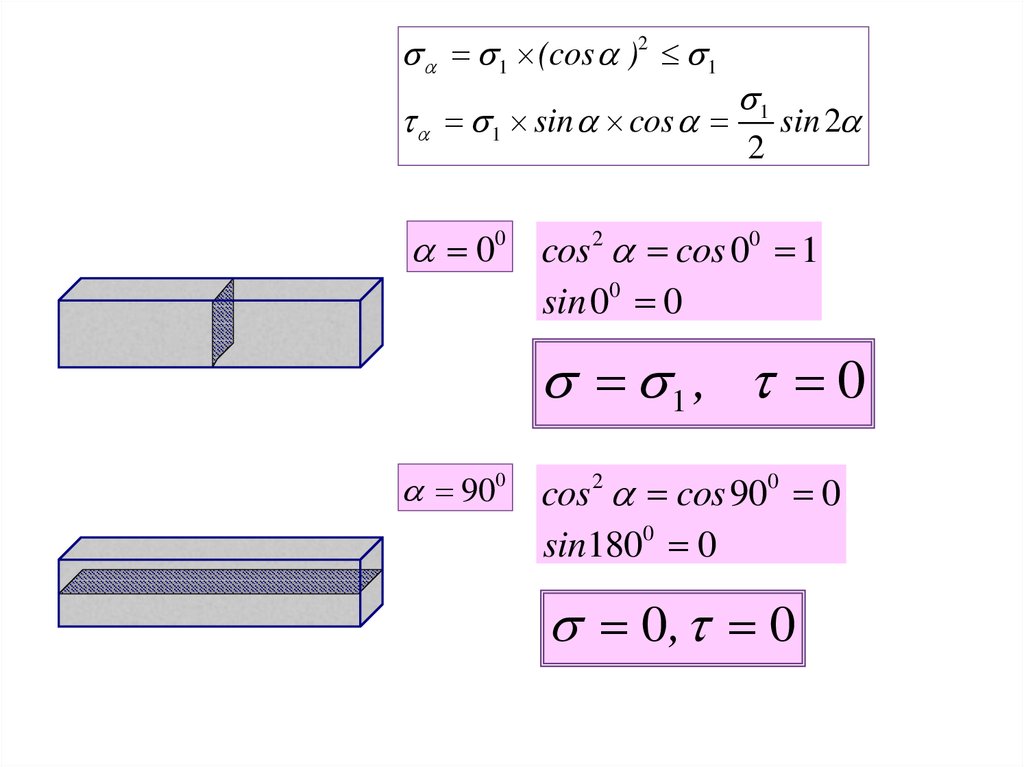
1 (cos )2 11 sin cos
1
2
sin 2
00 cos 2 cos 00 1
sin 00 0
1 , 0
900
cos 2 cos 900 0
sin1800 0
0, 0
9.
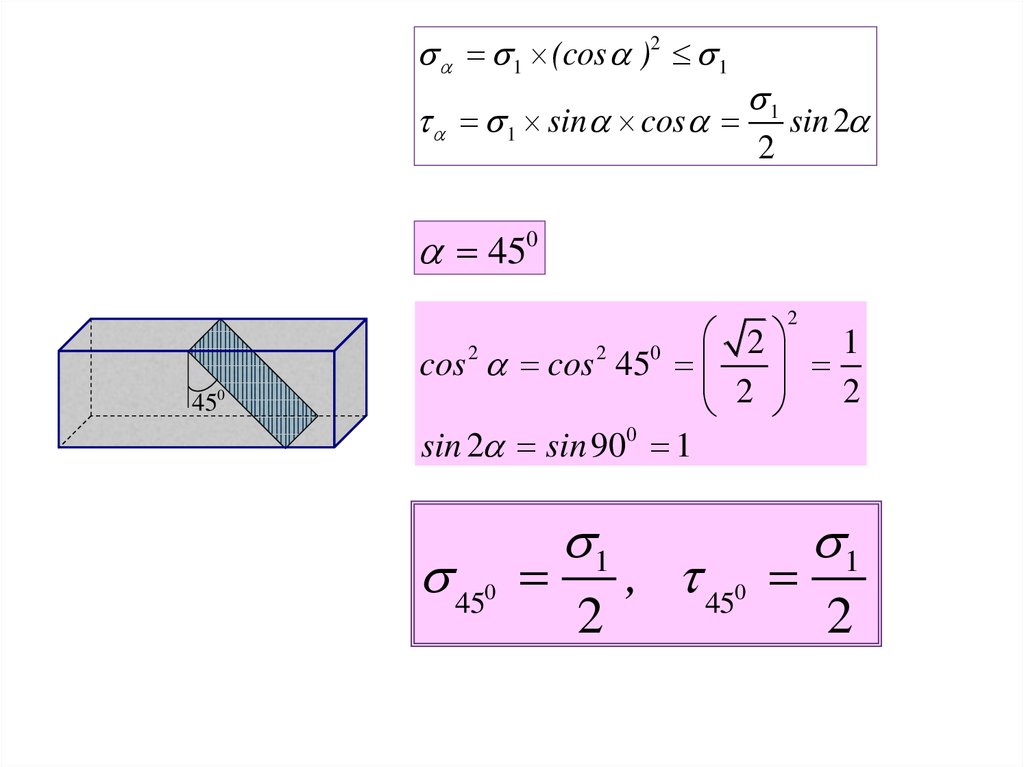
1 (cos )2 11
1 sin cos sin 2
2
450
2
2
1
cos cos 45
2
2
sin 2 sin 900 1
2
450
2
45
0
1
2
0
, 450
1
2
10.
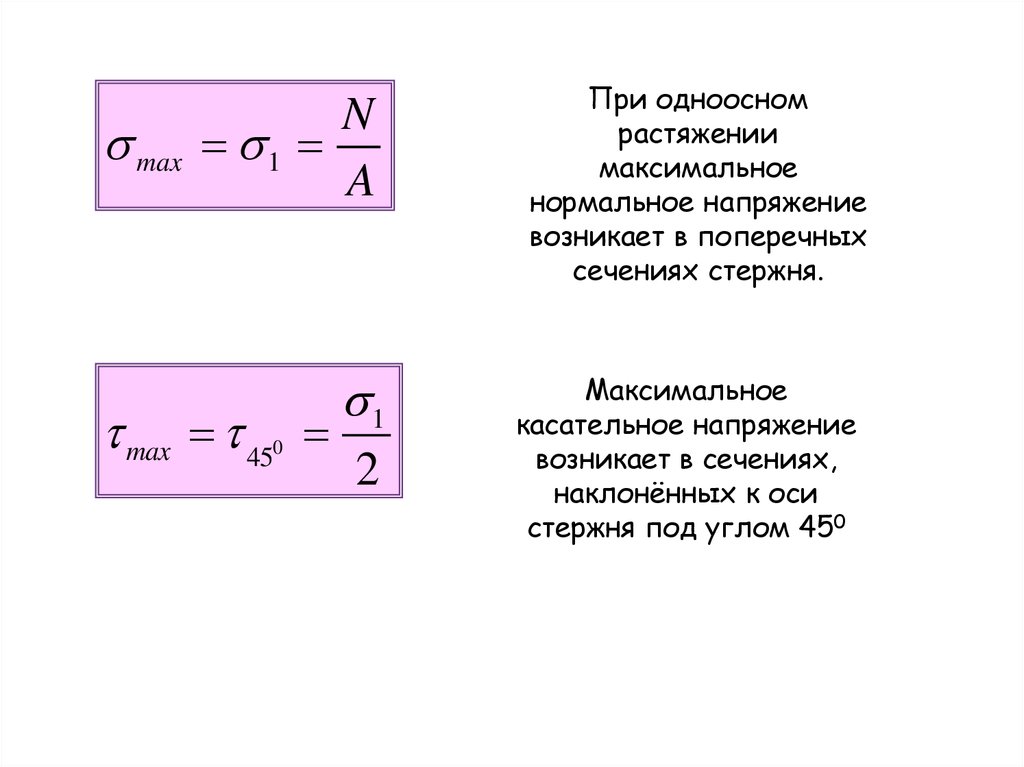
maxN
1
A
max 45
0
1
2
При одноосном
растяжении
максимальное
нормальное напряжение
возникает в поперечных
сечениях стержня.
Максимальное
касательное напряжение
возникает в сечениях,
наклонённых к оси
стержня под углом 450
11.
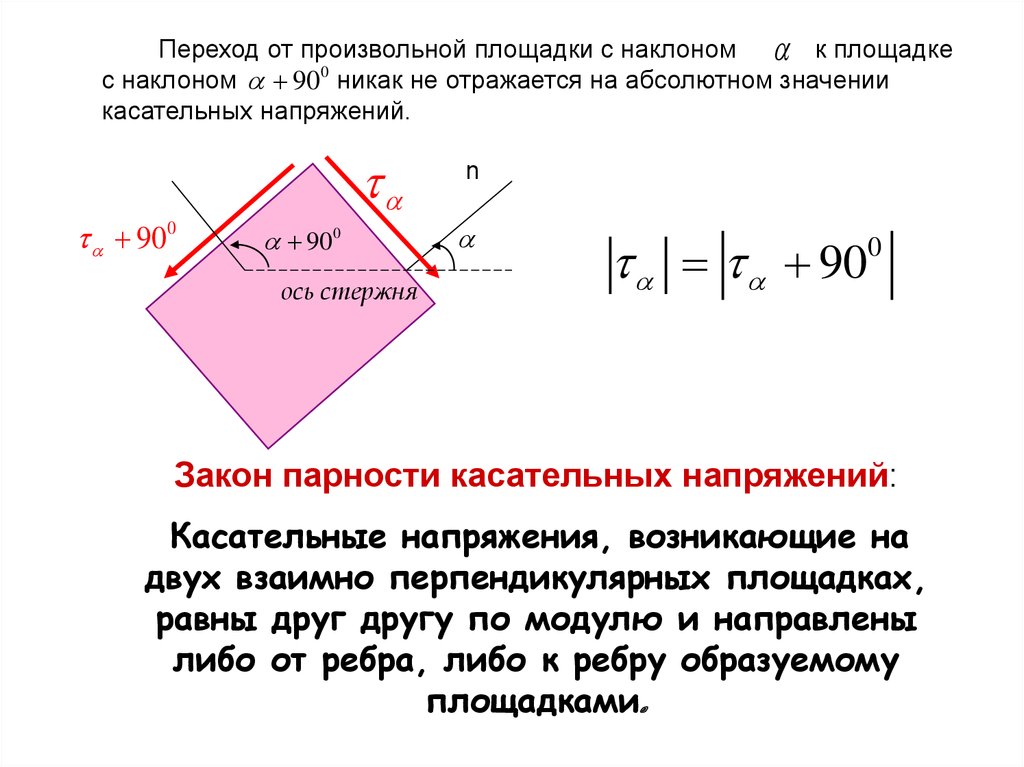
Переход от произвольной площадки с наклоном к площадкес наклоном 900 никак не отражается на абсолютном значении
касательных напряжений.
900
900
ось стержня
n
900
Закон парности касательных напряжений:
Касательные напряжения, возникающие на
двух взаимно перпендикулярных площадках,
равны друг другу по модулю и направлены
либо от ребра, либо к ребру образуемому
площадками.
12.
ЛИНЕЙНОЕ НДСТЕНЗОР
ДЕФОРМАЦИЙ
КРУГ МОРА
13.
14.
15.
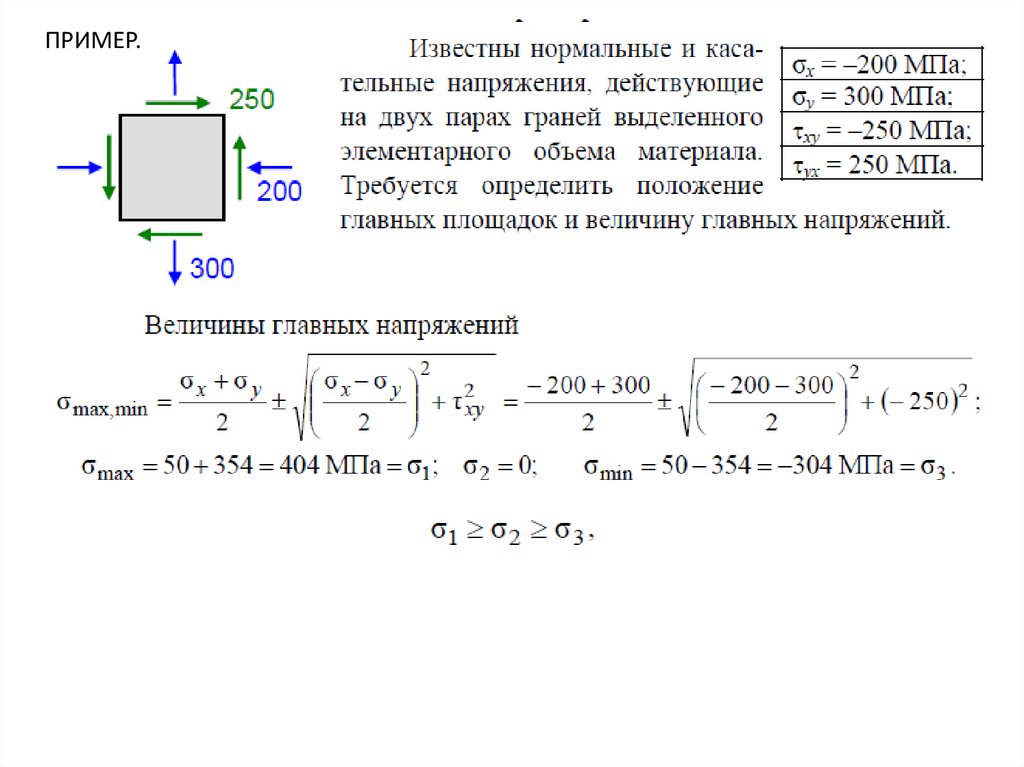
ПРИМЕР.16.
17.
18.
19.
20.
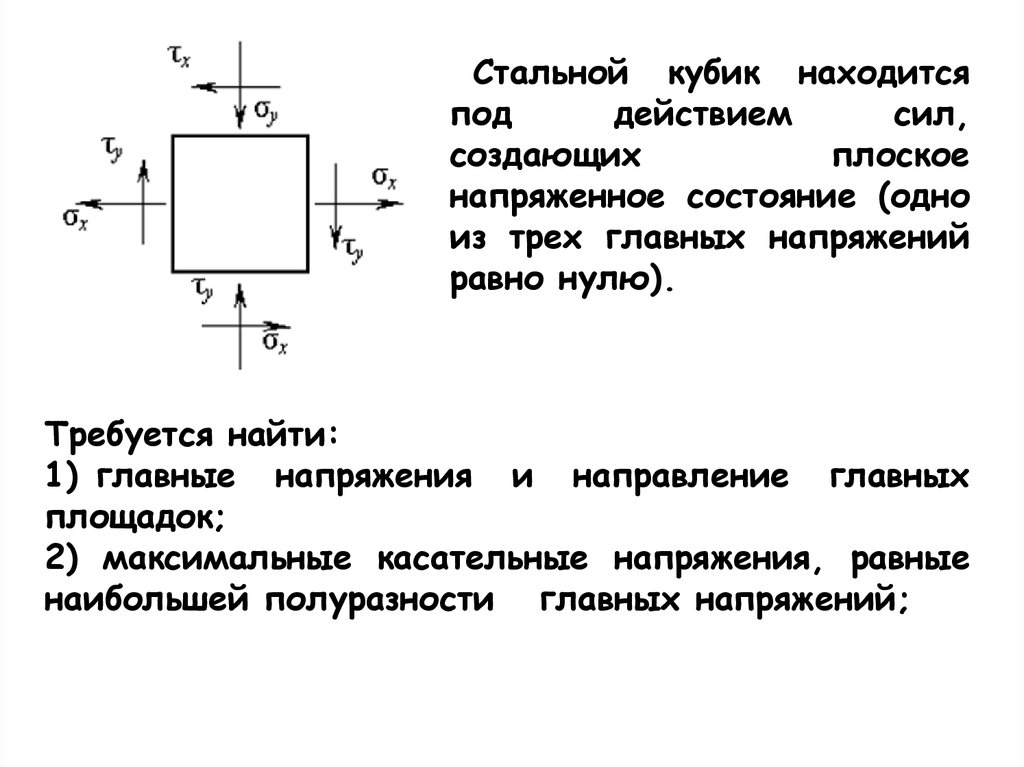
Стальной кубик находитсяпод
действием
сил,
создающих
плоское
напряженное состояние (одно
из трех главных напряжений
равно нулю).
Требуется найти:
1) главные напряжения и направление главных
площадок;
2) максимальные касательные напряжения, равные
наибольшей полуразности главных напряжений;
21.
3) главные деформации,
,
.
4) эквивалентное напряжение по четвертой
(энергетической) теории прочности;
5) относительное изменение объема;
6) удельную потенциальную энергию деформации.
22.
Правила знаков для нормальных и касательныхнапряжений:
1)растягивающее нормальное напряжение
положительно, а сжимающее - отрицательно.
2) Касательное напряжение по боковой грани призмы
положительно, если изображающий его вектор
стремится вращать призму по часовой стрелке
относительно любой точки, лежащей на внутренней
нормали этой грани.
23.
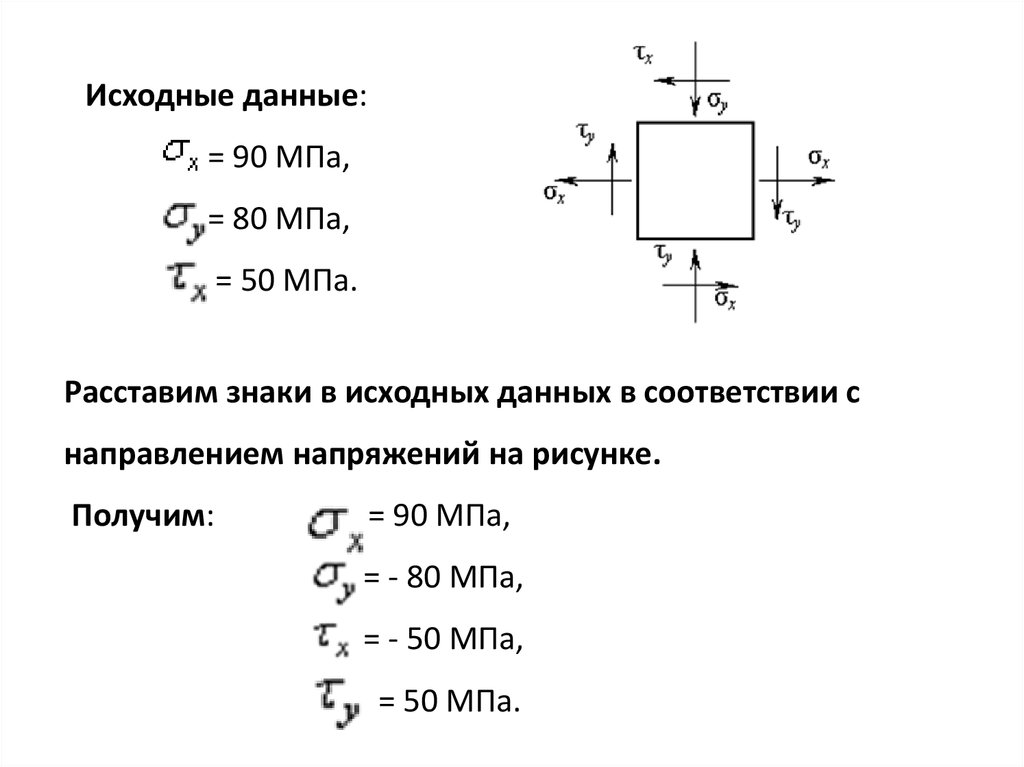
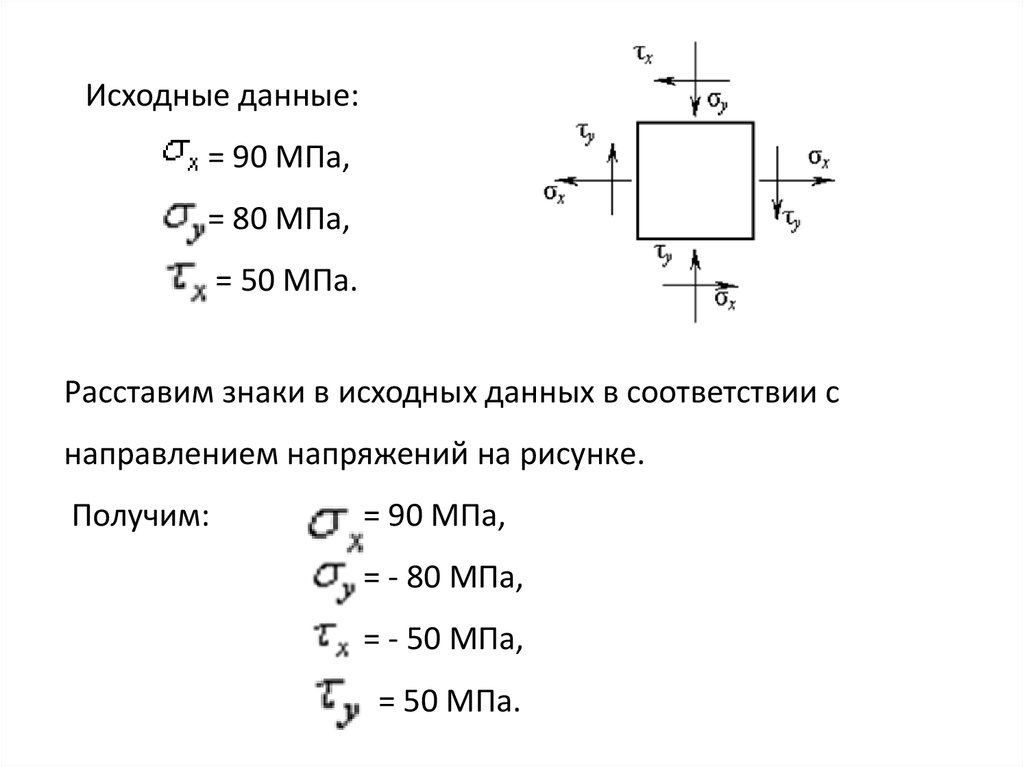
Исходные данные:= 90 МПа,
= 80 MПa,
= 50 МПа.
Расставим знаки в исходных данных в соответствии с
направлением напряжений на рисунке.
Получим:
= 90 МПа,
= - 80 MПa,
= - 50 МПа,
= 50 МПа.
24.
1. Найдем главные напряженияИндексы расставляют так, чтобы выполнялось неравенство
МПа
25.
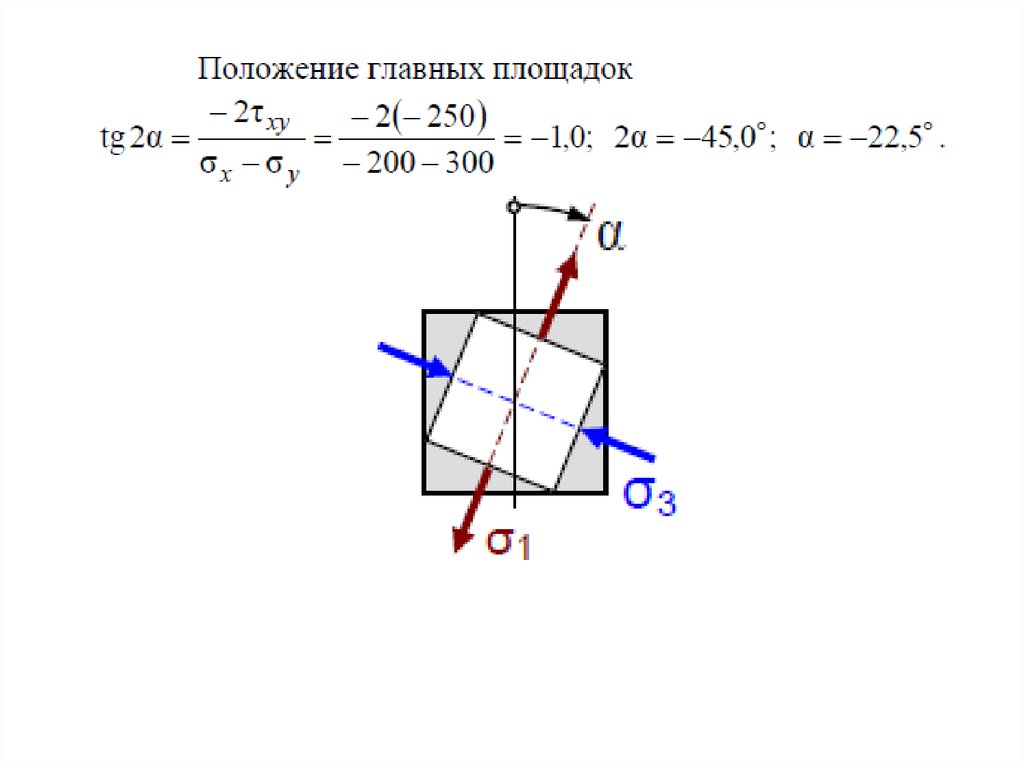
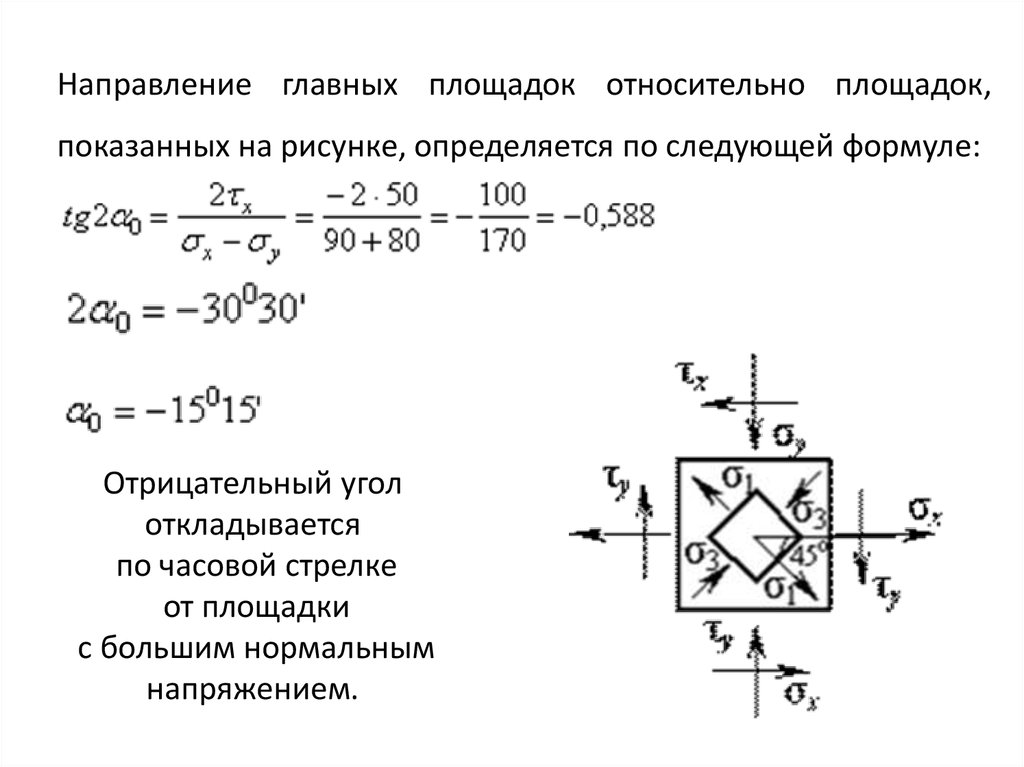
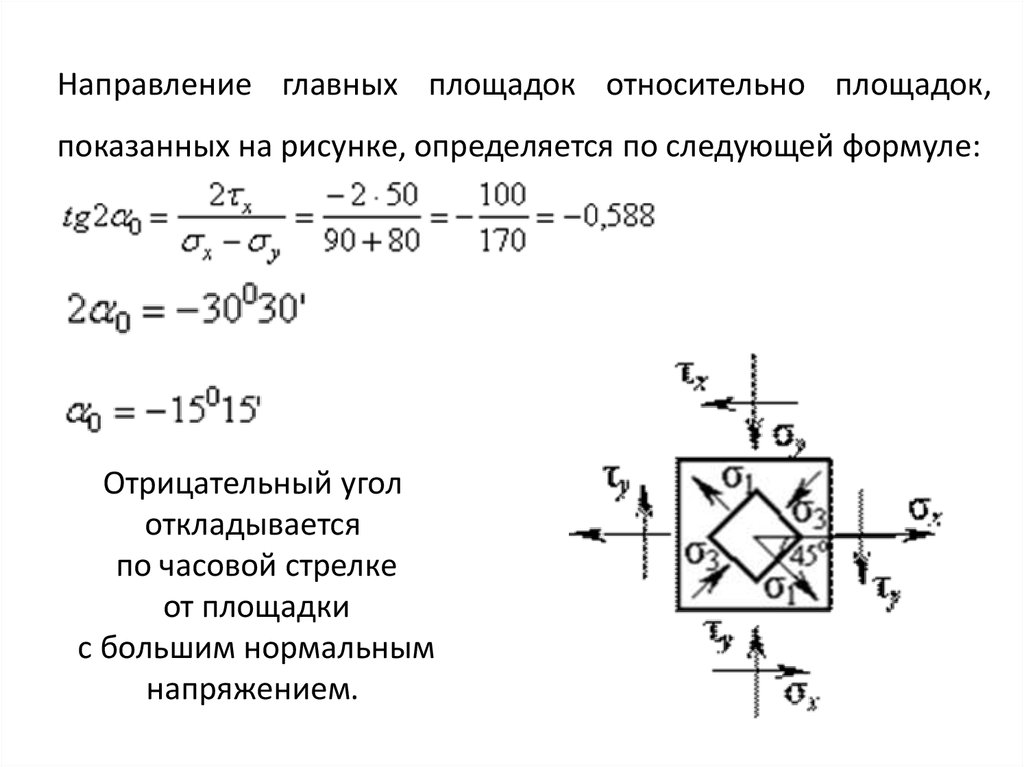
Направление главных площадок относительно площадок,показанных на рисунке, определяется по следующей формуле:
Отрицательный угол
откладывается
по часовой стрелке
от площадки
с большим нормальным
напряжением.
26.
2. Найдем максимальные касательные напряжения27.
Найдем главные деформации из обобщенного закона Гука:28.
4. Найдем эквивалентное напряжение3
29.
5. Найдем относительное изменение объема30.
Найдем удельную потенциальную энергию деформации31.
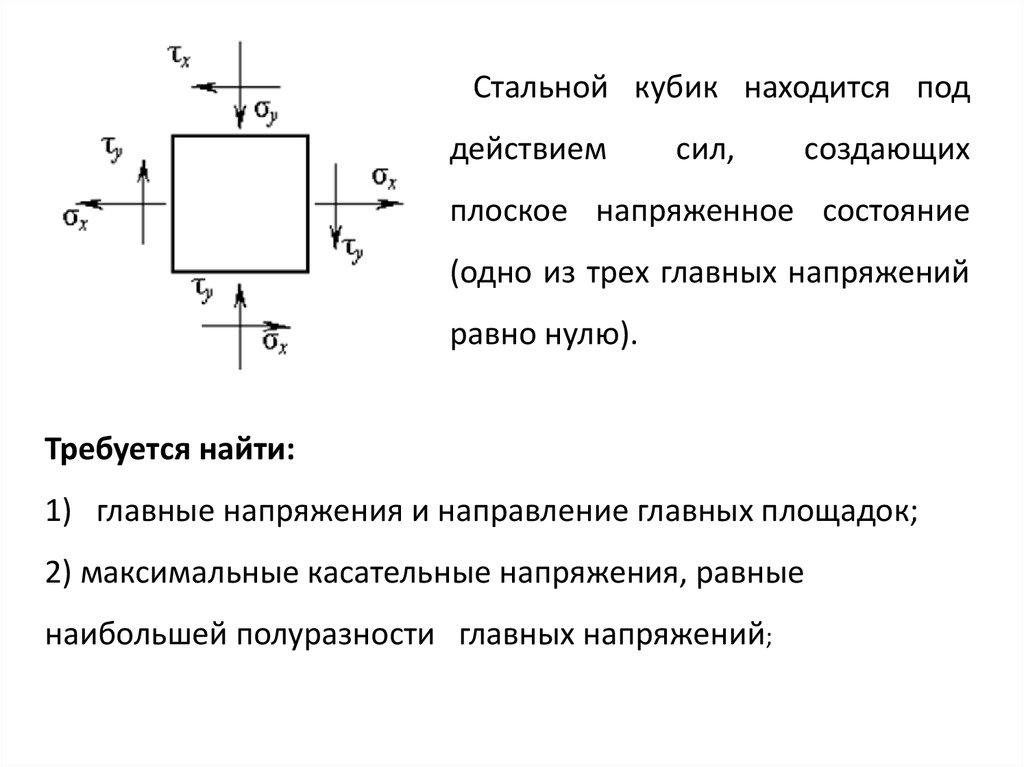
Стальной кубик находится поддействием
сил,
создающих
плоское напряженное состояние
(одно из трех главных напряжений
равно нулю).
Требуется найти:
1) главные напряжения и направление главных площадок;
2) максимальные касательные напряжения, равные
наибольшей полуразности главных напряжений;
32.
3) главные деформации,
,
.
4) эквивалентное напряжение по четвертой
(энергетической) теории прочности;
5) относительное изменение объема;
6) удельную потенциальную энергию деформации.
33.
Правила знаков для нормальных и касательных напряжений:1)растягивающее нормальное напряжение положительно,
а сжимающее - отрицательно.
2) Касательное напряжение по боковой грани призмы
положительно, если изображающий его вектор стремится
вращать призму по часовой стрелке относительно любой точки,
лежащей на внутренней нормали этой грани.
34.
Исходные данные:= 90 МПа,
= 80 MПa,
= 50 МПа.
Расставим знаки в исходных данных в соответствии с
направлением напряжений на рисунке.
Получим:
= 90 МПа,
= - 80 MПa,
= - 50 МПа,
= 50 МПа.
35.
1. Найдем главные напряженияИндексы расставляют так, чтобы выполнялось неравенство
МПа
36.
Направление главных площадок относительно площадок,показанных на рисунке, определяется по следующей формуле:
Отрицательный угол
откладывается
по часовой стрелке
от площадки
с большим нормальным
напряжением.
37.
2. Найдем максимальные касательные напряжения38.
Найдем главные деформации из обобщенного закона Гука:39.
4. Найдем эквивалентное напряжение3



















 physics
physics








