Параллельность плоскостей

1. Параллельность плоскостей

2.

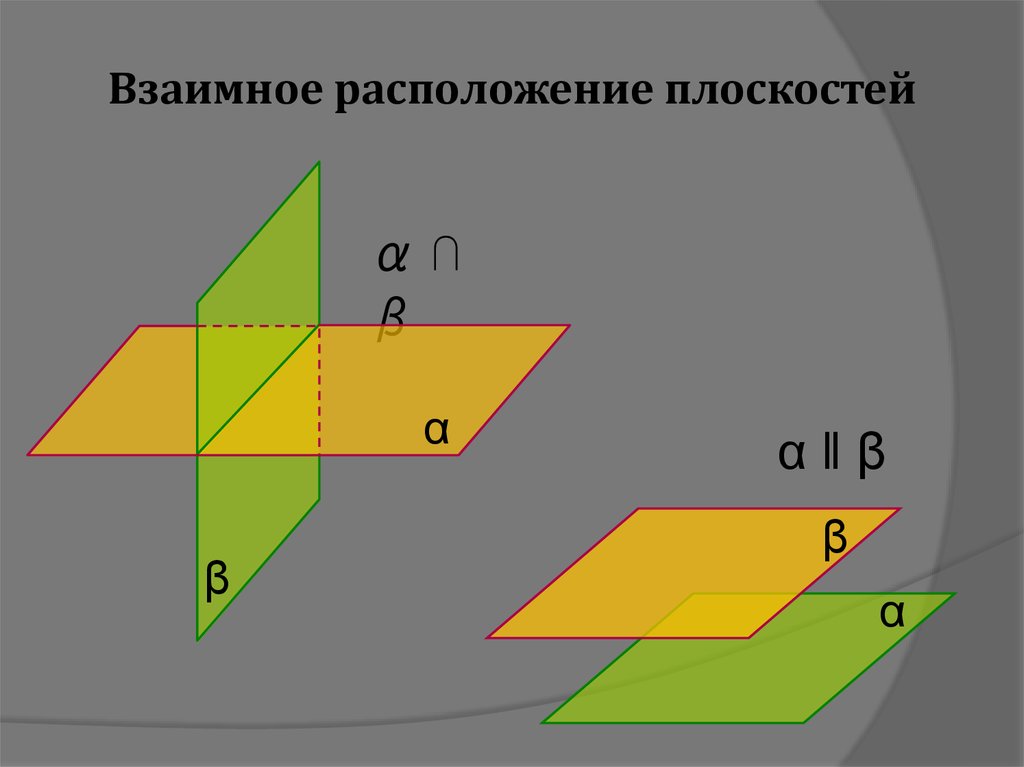
Взаимное расположение плоскостей
α⋂
β
α
β
α‖β
β
α

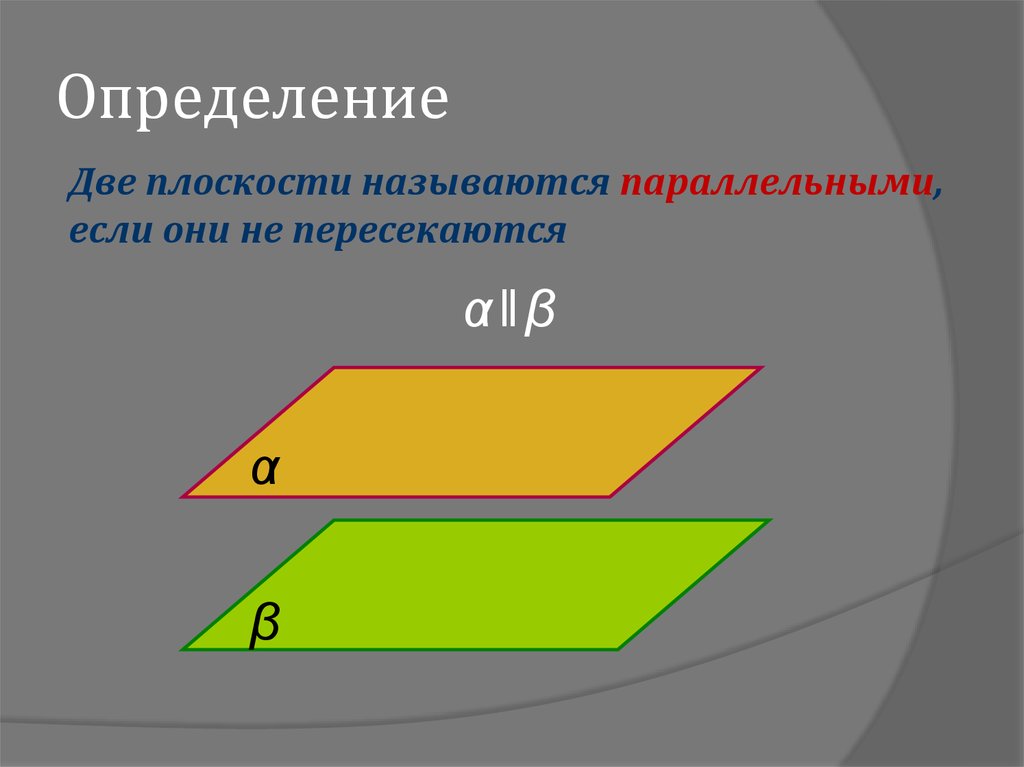
3. Определение

Две плоскости называются параллельными,
если они не пересекаются
α‖β
α
β

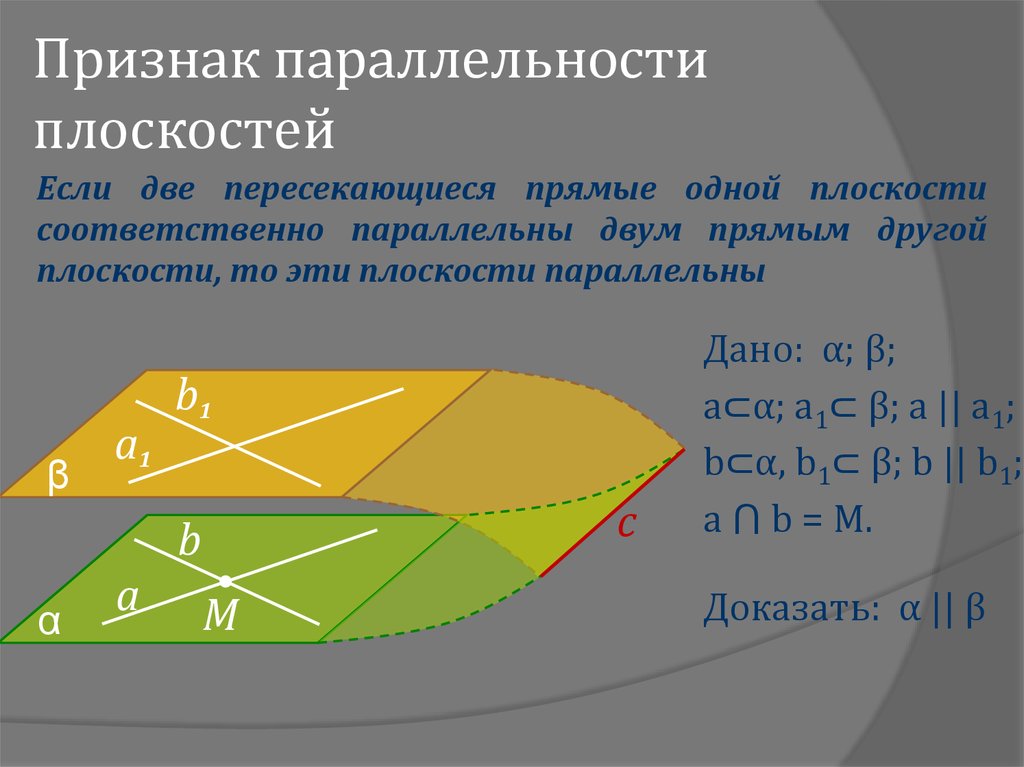
4. Признак параллельности плоскостей

Если две пересекающиеся прямые одной плоскости
соответственно параллельны двум прямым другой
плоскости, то эти плоскости параллельны
β
a1
b1
с
b
α
a
М
Дано: α; β;
a⊂α; a1⊂ β; a || a1;
b⊂α, b1⊂ β; b || b1;
a ⋂ b = M.
Доказать: α || β

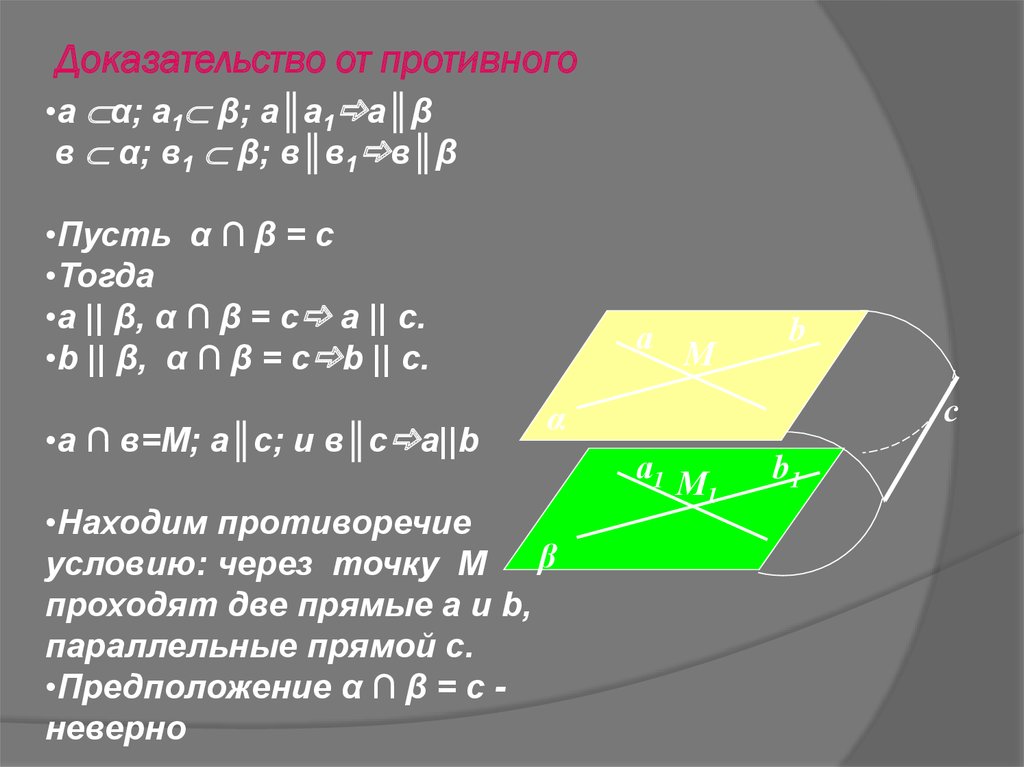
5. Доказательство от противного

•а α; а1 β; а║а1 а║β
в α; в1 β; в║в1 в║β
•Пусть α ∩ β = с
•Тогда
•а || β, α ∩ β = с а || с.
•b || β, α ∩ β = с b || с.
•а ∩ в=М; а║с; и в║с а||b
а М
b
с
α
•Находим противоречие
β
условию: через точку М
проходят две прямые а и b,
параллельные прямой с.
•Предположение α ∩ β = с неверно
а1 М
1
b1

6. Какие теоремы мы использовали при доказательстве признака?

а α; а1 β; а║а1 а║β; в α;
в1 β; в║в1 в║β
Признак параллельности
прямой и плоскости
Пусть α ∩ β = с
Делаем предположение,
противное заключению
Тогда
а || β, α ∩ β = с а || с.
b || β, α ∩ β = с b || с.
Теорема о линии пересечения
плоскостей
а ∩ в=М; а║с; и в║с а||b
Теорема о параллельности
трех прямых в
пространстве
Находим противоречие условию:
через точку М проходят две
прямые а и b, параллельные прямой
с.
Теорема о параллельных
прямых
Предположение
α ∩ β = с - неверно
Делаем вывод, α || β

7. 1 свойство параллельных плоскостей

Если две параллельные плоскости пересечены третьей,
то линии их пересечения параллельны
Дано: α, β, γ, α ‖ β
γ ⋂ α = a, γ ⋂ β = b
γ
a
b
β
α
Доказать: a || b

8. 2 свойство параллельных плоскостей

Отрезки параллельных прямых, заключенные между
параллельными плоскостями, равны
α
β
A
B
γ
C
Дано: α; β; γ;
α ‖ β; γ ⋂ α = AC;
γ ⋂ β = BD; AB ‖ CD.
D
Доказать: AB = CD

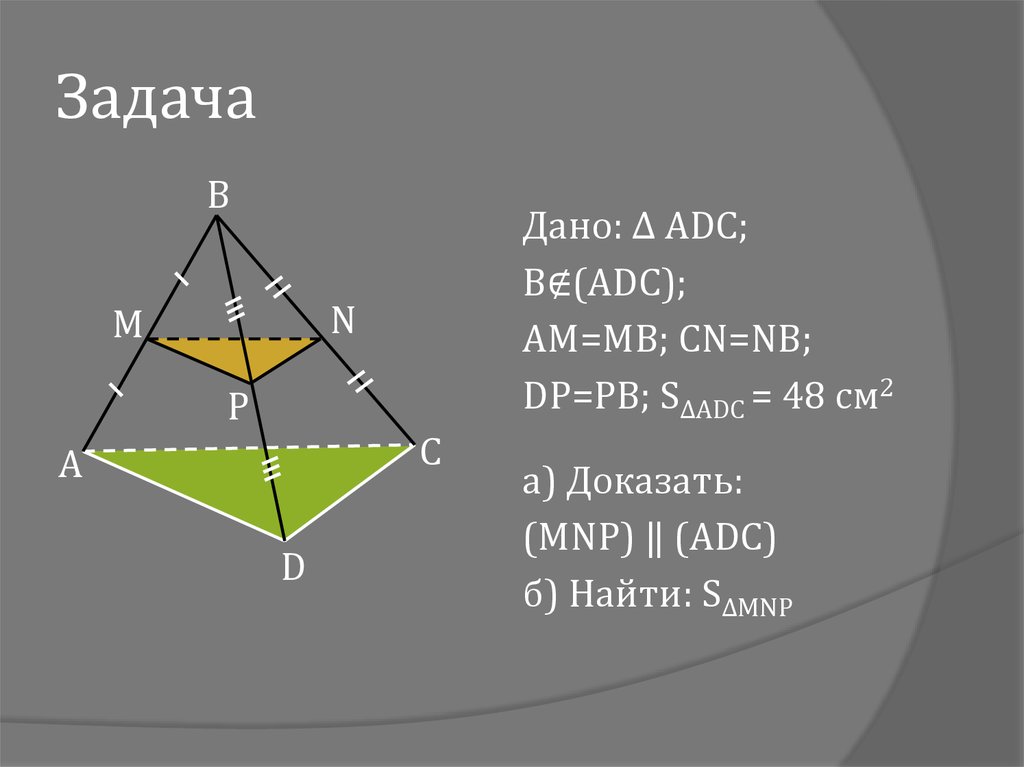
9. Задача

B
Дано: ∆ ADC;
B∉(ADC);
AM=MB; CN=NB;
DP=PB; S∆ADC = 48 см2
N
M
P
C
A
D
а) Доказать:
(MNP) ‖ (ADC)
б) Найти: S∆MNP

10. Отвечаем на вопросы

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Могут ли прямая и плоскость не иметь общих точек?
Верно ли, что если две прямые не пересекаются, то они
параллельны?
Плоскости и β параллельны, прямая m не лежит в
плоскости . Верно ли, что прямая m параллельна плоскости
β?
Верно ли, что если прямая а параллельна одной из двух
параллельных плоскостей, с другой плоскостью прямая а
имеет одну общую точку?
Боковые стороны трапеции параллельны плоскости . Верно
ли, что плоскость трапеции параллельна плоскости ?
Две стороны трапеции лежат в параллельных плоскостях.
Могут ли эти стороны быть боковыми сторонами трапеции?
Верно ли, что плоскости параллельны, если прямая,
лежащая в одной плоскости, параллельна другой плоскости?
Верно ли, что линия пересечения двух плоскостей
параллельна одной из этих плоскостей?
Верно ли, что любые четыре точки лежат в одной плоскости?
Верно ли, что если две стороны треугольника параллельны
плоскости , то и третья сторона параллельна плоскости ?

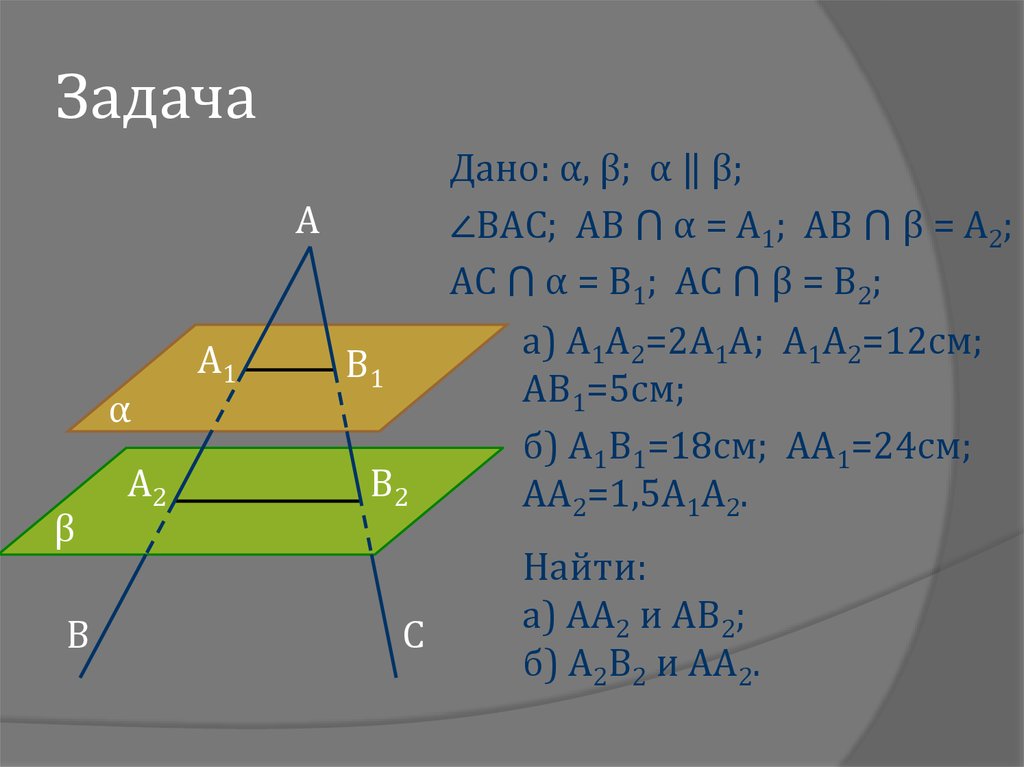
11. Задача

A
α
β
B
A2
A1
B1
B2
C
Дано: α, β; α ‖ β;
∠BAC; AB ⋂ α = A1; AB ⋂ β = A2;
AC ⋂ α = B1; AC ⋂ β = B2;
а) A1A2=2A1A; A1A2=12см;
AB1=5см;
б) A1B1=18см; AA1=24см;
AA2=1,5A1A2.
Найти:
а) AA2 и AB2;
б) A2B2 и AA2.