Векторный анализ. Лекция 4

1. Векторный анализ

Лекция 4

2.

§4 Поверхности второго порядка
Поверхности второго порядка описываются
уравнениями второго порядка относительно
переменных x, y, z.
Среди поверхностей второго порядка выделим
цилиндрические поверхности.

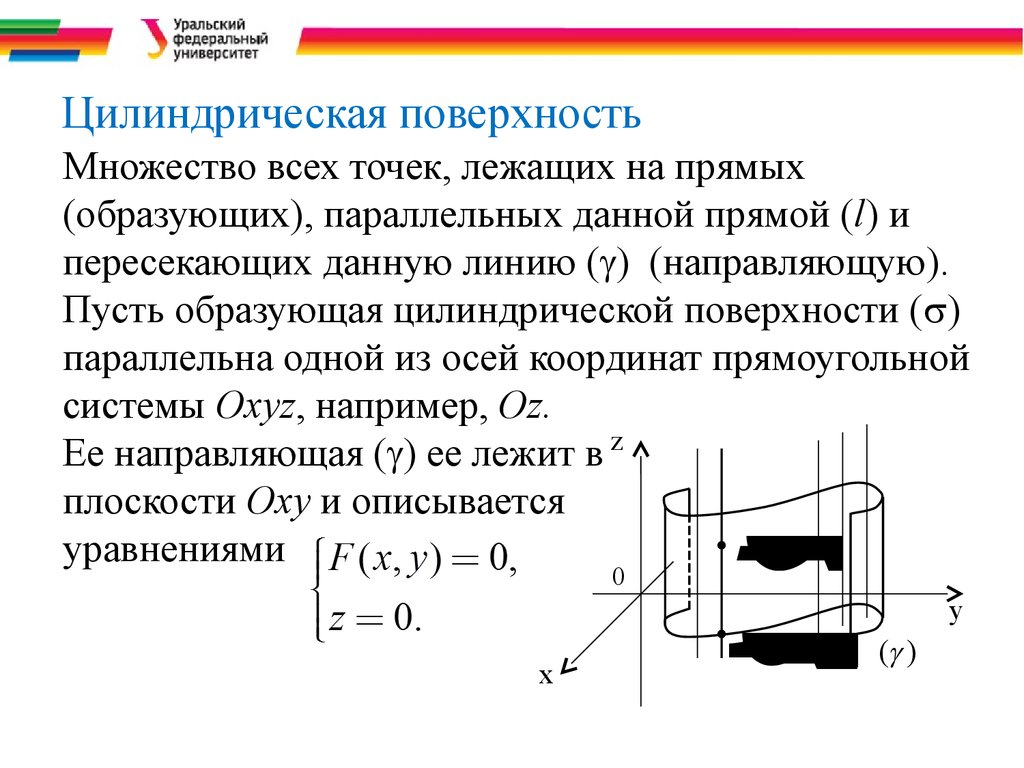
3. Цилиндрическая поверхность

(
)
(l)N(xxN,,yyz)0)
M
Множество всех точек, лежащих на прямых
(образующих), параллельных данной прямой (l) и
пересекающих данную линию ( ) (направляющую).
Пусть образующая цилиндрической поверхности ( )
параллельна одной из осей координат прямоугольной
системы Охуz, например, Oz.
Ее направляющая ( ) ее лежит в z
плоскости Оху и описывается
уравнениями
0
y
x
( )

4. Требуется составить уравнение этой цилиндрической поверхности

N
(FxN(x,Ny,y0)) 0
Требуется составить уравнение этой цилиндрической
поверхности
Точка
, где (l) – одна из
образующих цилиндрической поверхности ( ), которая
пересекает направляющую ( ) в точке
.
Т.к. точка N ( ), то
. (*)
Точки М и N принадлежат одной и той же прямой (l),
параллельной оси Oz, и, следовательно,
.

5.

Подставив в равенство (*) вместо хN и yN
соответственно х и у, получим равенство F(x,y)=0,
которое является уравнением цилиндрической
поверхности ( ).
Итак, F(x,y)=0 есть уравнение цилиндрической
поверхности с образующими, параллельными оси Oz,
и направляющей, расположенной в плоскости Оху.

6. Замечания

1.Уравнение цилиндрической поверхности, подобной
рассмотренной, совпадает с уравнением ее
направляющей, расположенной в одной из
координатных плоскостей прямоугольной системы
Охуz.
2. Уравнение не содержит одной переменной,
одноименной с осью, параллельной образующей
0
цилиндрической поверхности.

7.

Пример.
уравнение цилиндрической
поверхности с образующей, параллельной оси Oz
(в уравнении отсутствует переменная z), с
направляющей, расположенной в плоскости Оху и
представляющей параболу с тем же самым
z
уравнением.
0
x
y

8. Поверхности второго порядка

Общее уравнение поверхности 2-го порядка имеет
вид:
где
.

9. Поверхности второго порядка

Теорема.
Общее уравнение поверхности 2-го порядка с
помощью симметрии относительно плоскости,
поворота оси и параллельного переноса
прямоугольной системы координат может быть
приведено к одному из следующих канонических
уравнений:

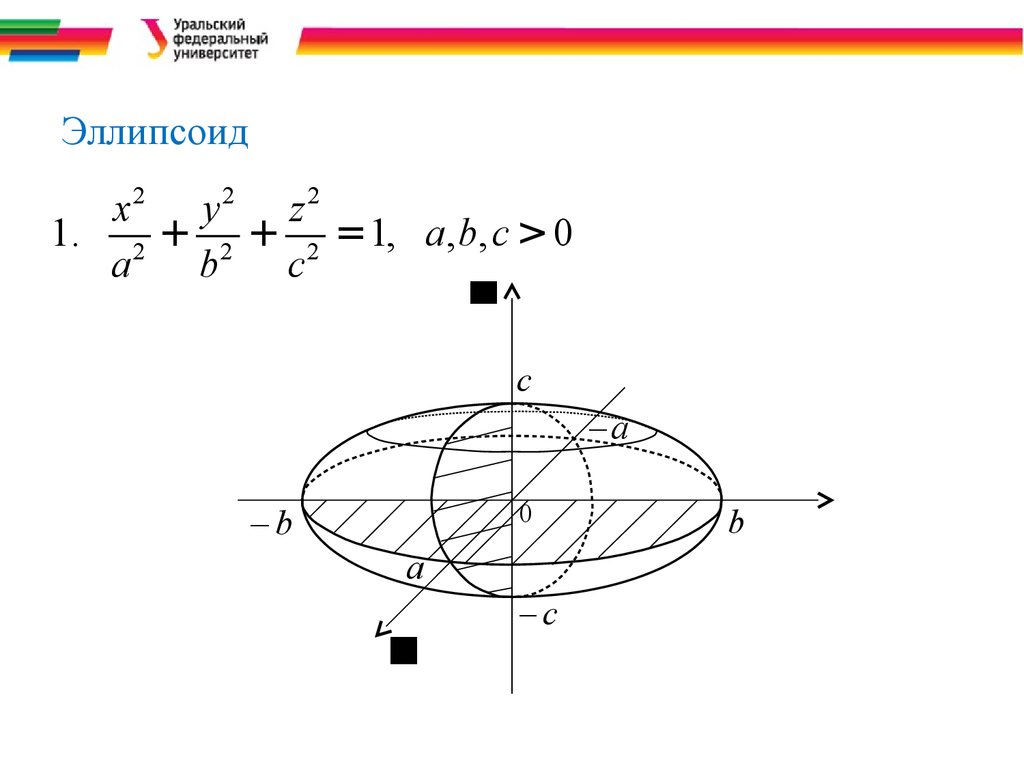
10. Эллипсоид

zxy
x2 y2 z 2
1. 2 + 2 + 2 = 1, a, b, c > 0
a
b
c
с
a
b
0
a
с
b

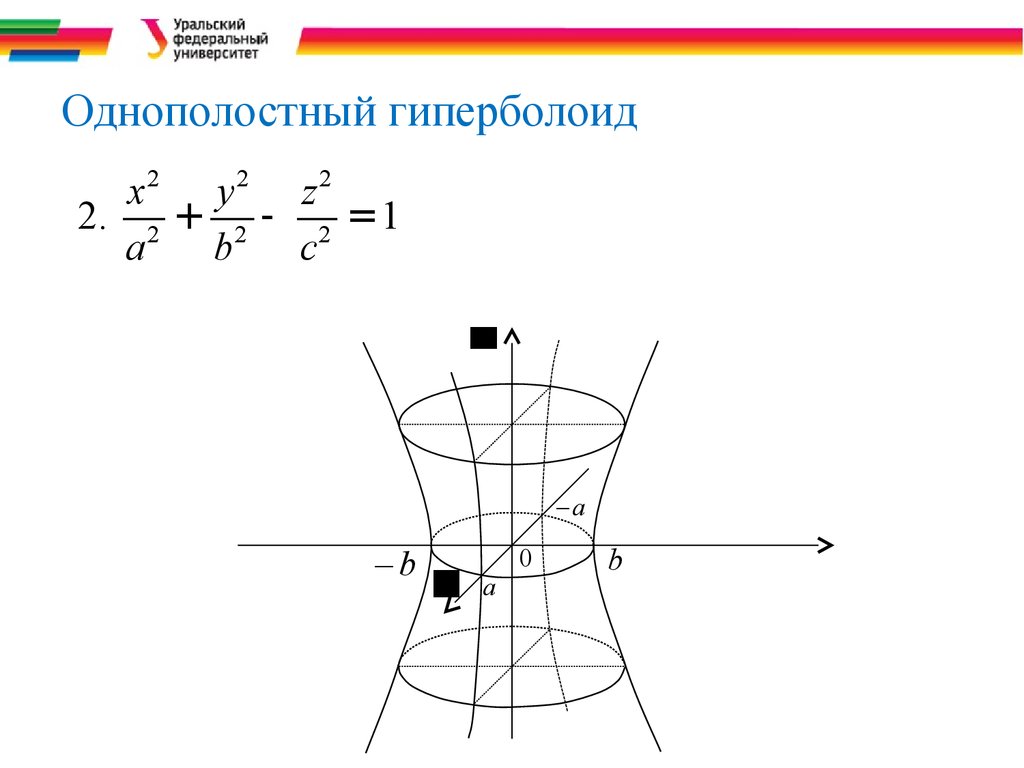
11. Однополостный гиперболоид

zxy
Однополостный гиперболоид
x2 y 2 z 2
2. 2 + 2 - 2 = 1
a
b
c
a
b
a
0
b

12. Двухполостный гиперболоид

zxy
Двухполостный гиперболоид
x2 y 2 z 2
3. 2 + 2 2 = 1
a
b
c
с
a
b
a
0
с
b

13. Коническая поверхность второго порядка (конус)

zxy
Коническая поверхность второго порядка
(конус)
x2 y 2 z 2
4. 2 + 2 2 = 0
a
b
c
с
a
b a
0
с
b

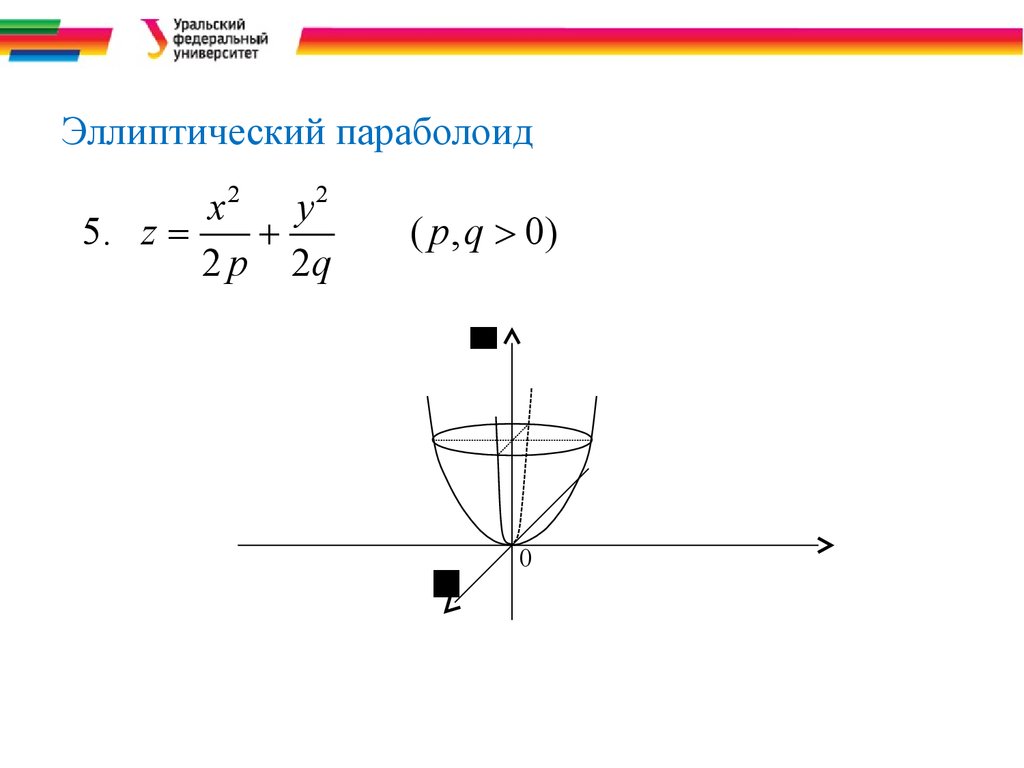
14. Эллиптический параболоид

zxy
Эллиптический параболоид
x2 y2
5. z =
+
2 p 2q
( p , q > 0)
0

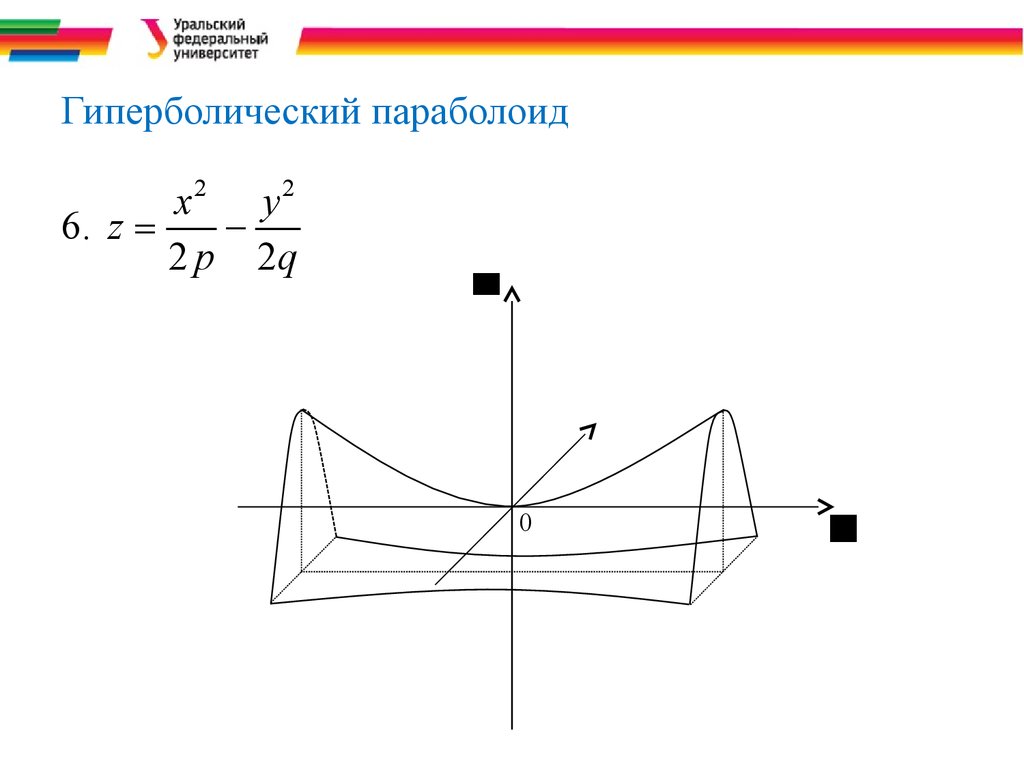
15. Гиперболический параболоид

zyx
Гиперболический параболоид
x2 y 2
6. z =
2 p 2q
0

16.

7.
8.
xa22+
y b22=1
(a,b>0) – эллиптический цилиндр
- гиперболический цилиндр

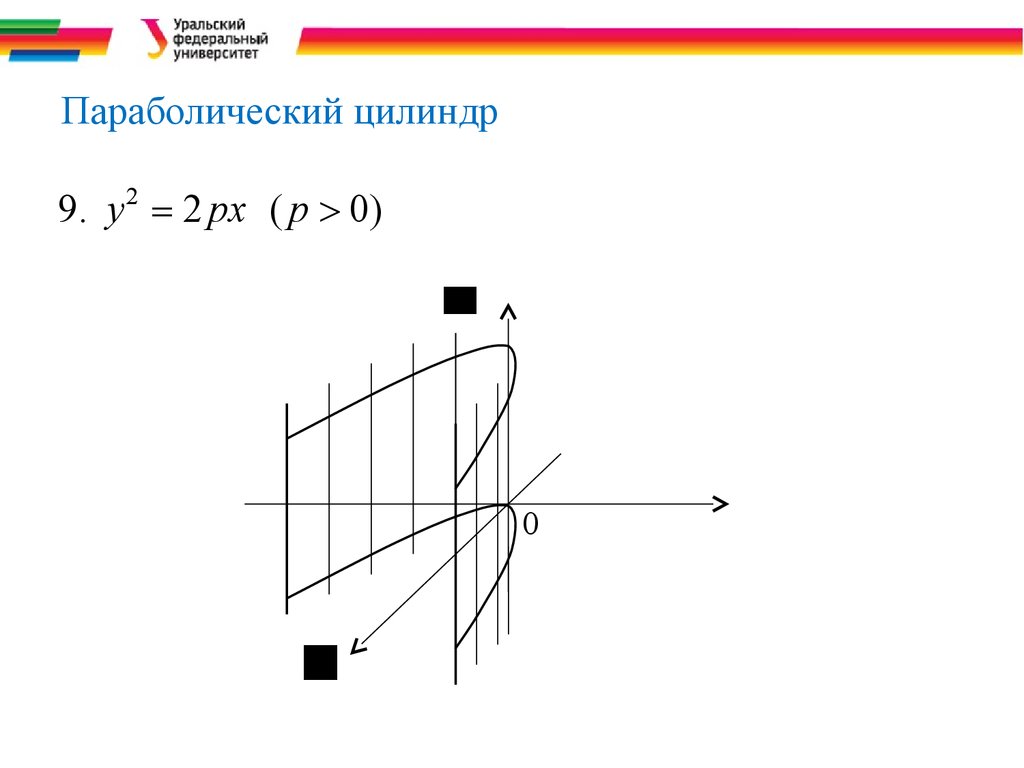
17. Параболический цилиндр

zxy
Параболический цилиндр
9. y = 2 px ( p > 0)
2
0

18.

10.
11.
12.
13.
2
xaxax222+
y=
=
0
bby0
22=
0
- пара пересекающихся плоскостей,
- пара параллельных плоскостей,
- пара совпадающих плоскостей,
- прямая х=у=0 (пара мнимых
пересекающихся плоскостей),

19.

14.
15.
16.
xa22+by22cz22=0 1
- точка (0, 0, 0) (мнимый конус),
- (мнимый эллипсоид),
- (мнимый эллиптический цилиндр),
17. 2 2
- (пара мнимых параллельных плоскостей).
x +a =0
Указанное в теореме преобразование системы координат
называется приведением к главным осям.

20. Метод сечений

xa2+by2cz2=1
Метод сечений
Пересечение исследуемой поверхности с плоскостью
дает плоскую кривую. Ряд таких пересечений (называемых
сечениями) позволяет выяснить строение поверхности.
1. Эллипсоид.
Каноническое уравнение эллипсоида имеет вид:
(a>0,b>0,c>0).
Исследуем форму эллипсоида по его уравнению.

21. Метод сечений

|x a,y|bz c
Из уравнения видно, что эллипсоид представляет собой
ограниченную поверхность, заключенную в параллелепипеде
Координатные плоскости являются плоскостями симметрии
эллипсоида, оси координат – его осями симметрии (все оси
эллипсоида вещественны, т.е. их эллипсоид пересекает),
начало координат – центром симметрии эллипсоида.

22. Эллипсоид

z
2
zax2=
y+
,0.bxy
=
1
Эллипсоид
Дальше исследуем форму эллипсоида по его сечениям
плоскостями. Рассмотрим сечение эллипсоида координатной
плоскостью Оху. В сечении получается линия:
с
a
Эта линия представляет собой
эллипс с полуосями a и b.
0
b
a
с
b

23. Эллипсоид

2
ayxxb2=
z2=
+
,0+
=
1
c0cz2=
1,
Эллипсоид
Аналогично устанавливается сечение данного эллипсоида
с плоскостью Oxz
- эллипс с полуосями a и с,
и с плоскостью Оуz
- эллипс с полуосями b и с.

24. Эллипсоид

z =zax2=h+h.(by2 =10) hc2, za2=(1x .2hc)+b2(1y 2hc)=1,
Эллипсоид
Рассмотрим теперь сечение эллипсоида с плоскостями
, параллельными плоскости Оху.
Уравнения линий пересечения будут
или

25. Эллипсоид

Если положить
2,b
2
~a
h
~a=1 hc~
=b
1~
| czax
2=
2
yc+
,h.b
=
1
~
,
то уравнения запишутся в виде
Отсюда видно, что полуоси
и являются
действительными числами лишь при
и линия
пересечения эллипсоида с плоскостью z=h представляет
собой эллипс с полуосями и .

26. Эллипсоид

h= c
Эллипсоид
При
эллипсоид и плоскость пересекаются в
одной точке (вырожденный эллипс).
Если |h|>c, то эллипсоид и плоскость не имеют общих
точек (пересекаются по мнимому эллипсу).
Аналогично находим, что в пересечении эллипсоида с
плоскостями, параллельными координатным плоскостям
Oxz и Oyz, получаются также эллипсы.

27. Эллипсоид

Таким образом, эллипсоид представляет собой
ограниченную поверхность, линиями пересечения которой
с координатными плоскостями и им параллельными
являются эллипсы. Числа a,b,c называются полуосями
эллипсоида. Если все они различны, то эллипсоид
называется трехосным. Если a=b=c, то эллипсоид
превращается в сферу.
Замечание. Эллипсоид может быть получен равномерным
сжатием сферы относительно двух перпендикулярных его
плоскостей симметрии.

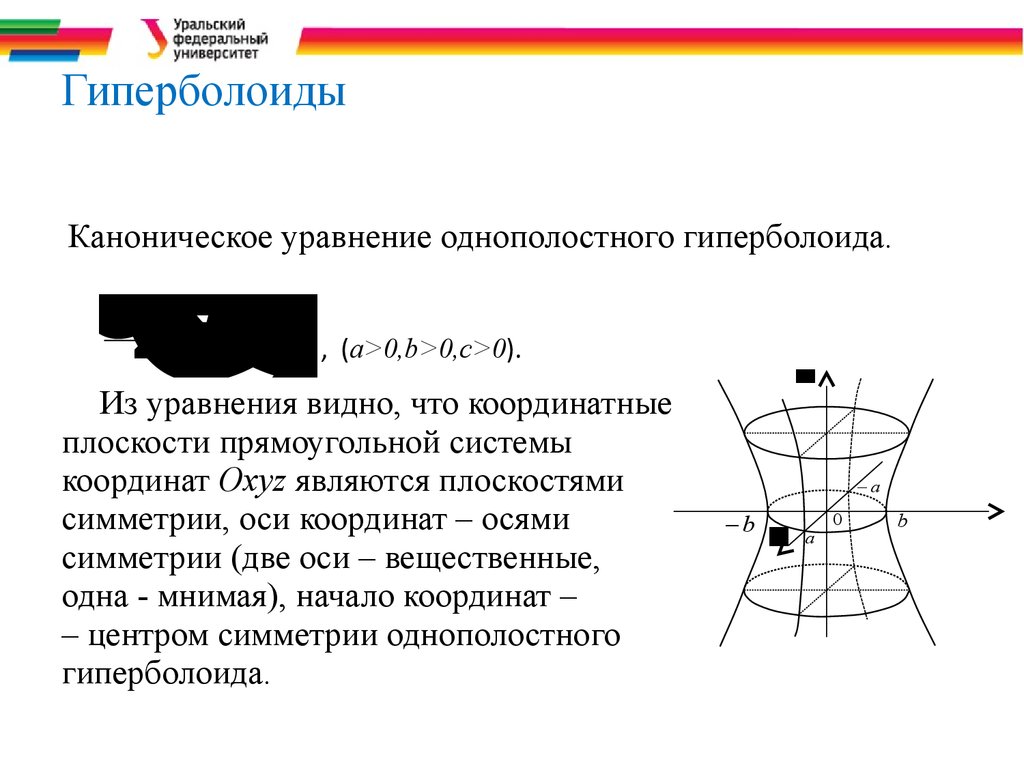
28. Гиперболоиды

xa2+by2 cz2=1 x
zy
Гиперболоиды
Каноническое уравнение однополостного гиперболоида.
, (a>0,b>0,c>0).
Из уравнения видно, что координатные
плоскости прямоугольной системы
координат Охуz являются плоскостями
симметрии, оси координат – осями
симметрии (две оси – вещественные,
одна - мнимая), начало координат –
– центром симметрии однополостного
гиперболоида.
a
b
a
0
b

29. Гиперболоид

2
zax2=
y+
,0.b
=
1
Гиперболоид
Исследуем форму этого гиперболоида по его сечениям
координатными и параллельными им плоскостями.
Линия пересечения гиперболоида с плоскостью Оху имеет
уравнения:

30. Гиперболоид

2
2
2
2
zax2=
y+
h
x
y
,hba~=c1+hc2,b~= za1=
=
1
+
,+hcb2
+
=
1
~
Гиперболоид
Эти уравнения определяют эллипс с полуосями а и b.
Линиями пересечения данного гиперболоида с плоскостями
z=h (h R), параллельными координатной плоскости Оху,
будут эллипсы
или
с полуосями
Полуоси
|h|.
и
неограниченно увеличиваются с увеличением

31. Гиперболоид

2
2
x
z
=
1
,
a
c
y
=
0
2
xby2=
z
,0c
=
1
Гиперболоид
Линией пересечения данного гиперболоида с плоскостью
Oxz будет гипербола
с действительной полуосью Ox и мнимой осью Oz, а и с –
полуоси гиперболы, с плоскостью Оуz - гипербола
с полуосями b и с.
Числа a,b,c называются полуосями однополостного
гиперболоида.

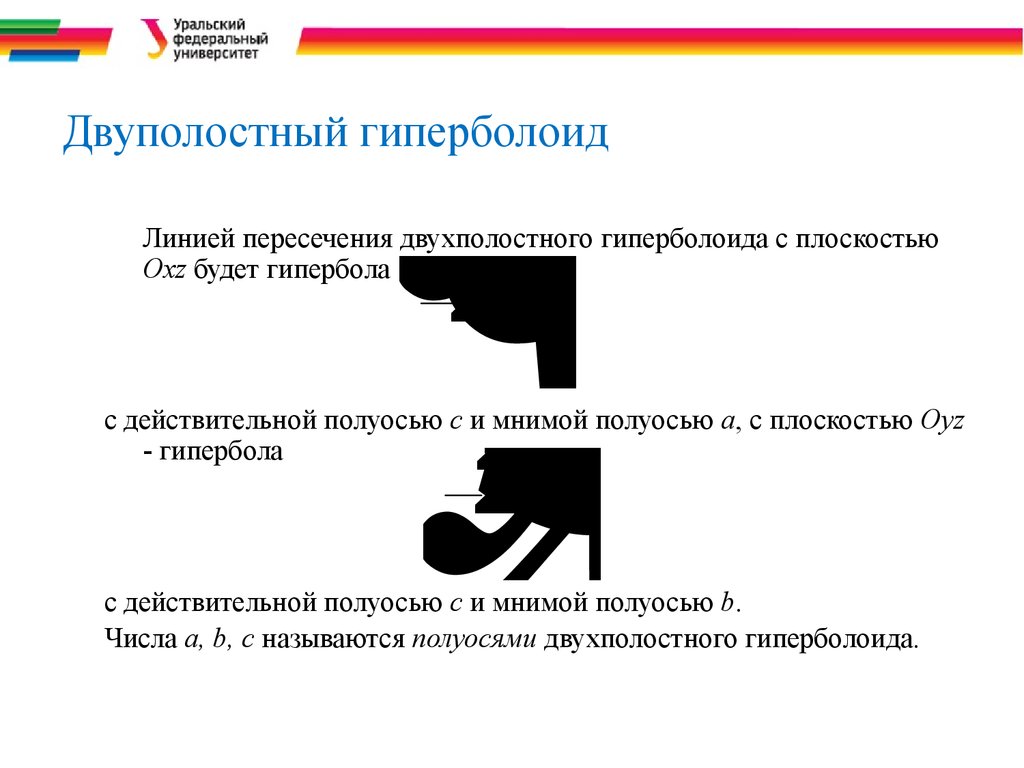
32. Двуполостный гиперболоид

xa2+by2 cz2= 1xzy
Двуполостный гиперболоид
, (a>0, b>0, c>0).
Из этого уравнения видно, что
координатные плоскости являются
плоскостями симметрии, оси
координат – осями симметрии
(одна ось – вещественная, две оси –
– мнимые), а начало координат –
– центром симметрии двухполостного
гиперболоида.
с
0
с

33. Двуполостный гиперболоид

2
zax2=
y+
,0.b
=
1
Двуполостный гиперболоид
В сечении данного гиперболоида с координатной
плоскостью Оху получается мнимый эллипс:
Это значит, что плоскость z=0 не пересекает гиперболоид.

34. Двуполостный гиперболоид

2
2
2
2
x
y
zax2=
y+
h
,a1=
+
=
1
,ha~;bhcc2 1,b~=hc2 z
=
1
~
b
h.
Двуполостный гиперболоид
Линии пересечения данного гиперболоида с
плоскостями z=h представляют собой эллипсы, уравнения
которых имеют вид:
или
где

35. Двуполостный гиперболоид

~
a
b
|h c.
Двуполостный гиперболоид
Полуоси и
являются действительными числами
лишь при
Это означает, что в пространстве между
плоскостями z=с и z= – с не содержится точек
рассматриваемой поверхности.
Эта поверхность состоит из двух полостей, расположенных
так, как показано на рисунке.

36. Двуполостный гиперболоид

2
ayx 2x=
zb
,2=
=
1
c0
z0c2=
1,
Двуполостный гиперболоид
Линией пересечения двухполостного гиперболоида с плоскостью
Oxz будет гипербола
с действительной полуосью с и мнимой полуосью а, с плоскостью Оуz
- гипербола
с действительной полуосью с и мнимой полуосью b.
Числа a, b, c называются полуосями двухполостного гиперболоида.

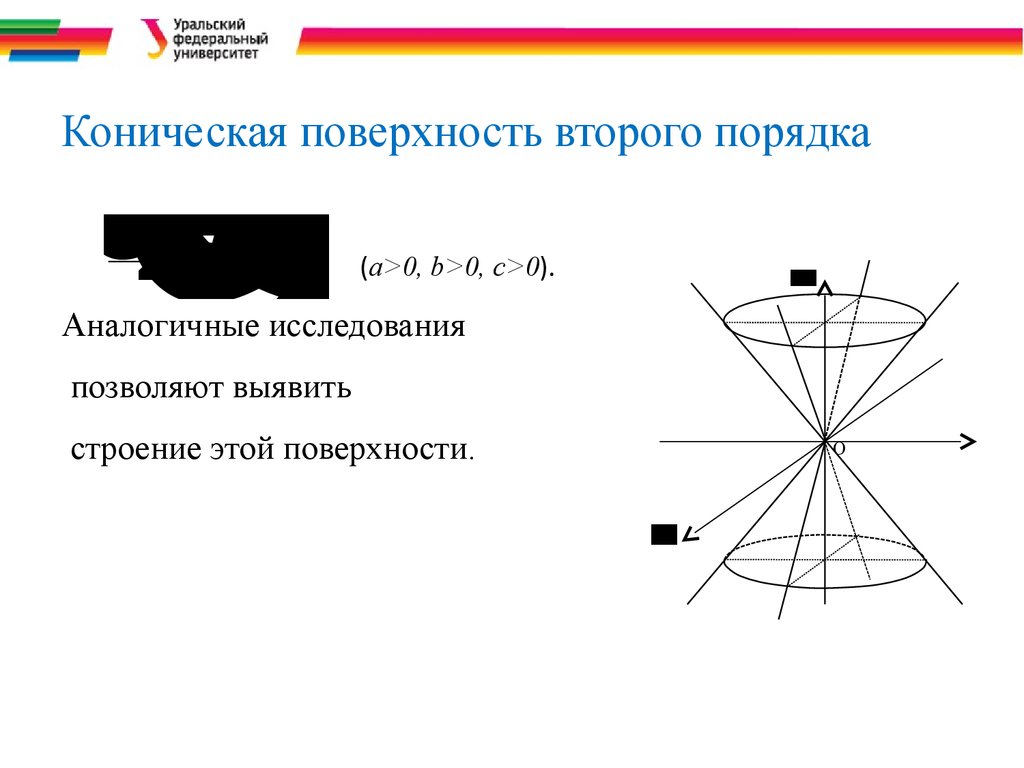
37. Коническая поверхность второго порядка

xa2+by2 cz2=0x
zy
Коническая поверхность второго порядка
(a>0, b>0, c>0).
Аналогичные исследования
позволяют выявить
строение этой поверхности.
0

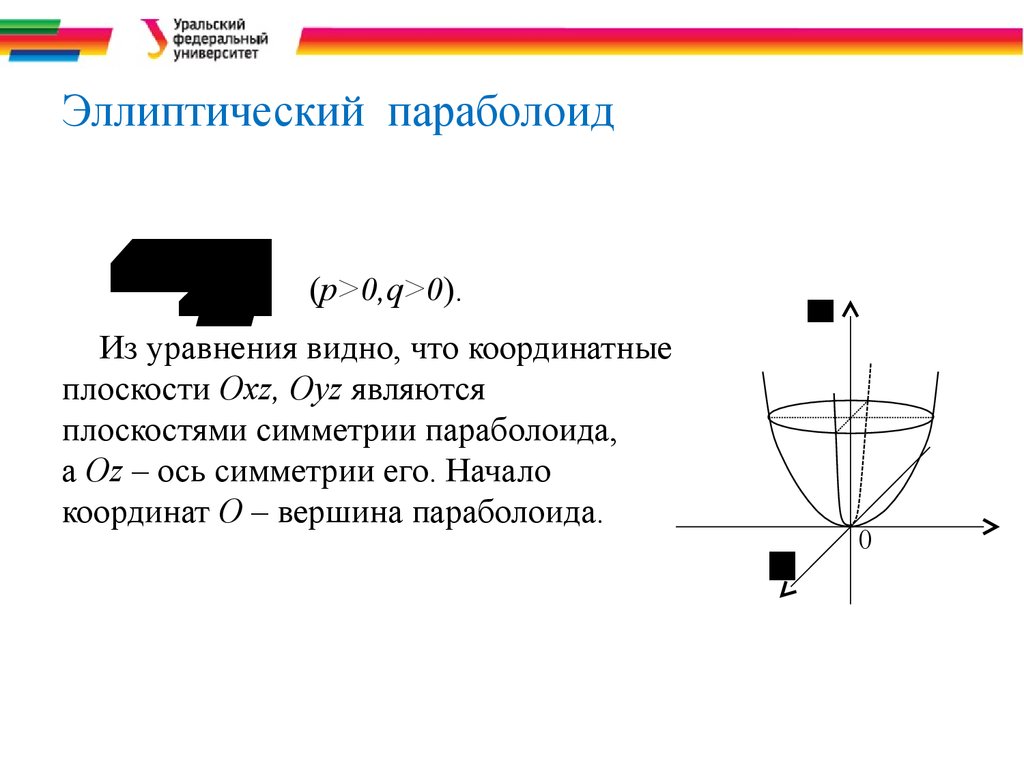
38. Эллиптический параболоид

z
xz=2p2+yq2 x
y
Эллиптический параболоид
(p>0,q>0).
Из уравнения видно, что координатные
плоскости Охz, Оуz являются
плоскостями симметрии параболоида,
а Oz – ось симметрии его. Начало
координат О – вершина параболоида.
0

39.

https://www.youtube.com/watch?v=qBeBPl6N2p0