Аналитическая геометрия Поверхности второго порядка. Раздел 3

1. Раздел 3 Аналитическая геометрия Поверхности второго порядка

Общее уравнение ПВП
Эллипсоид
Гиперболоиды
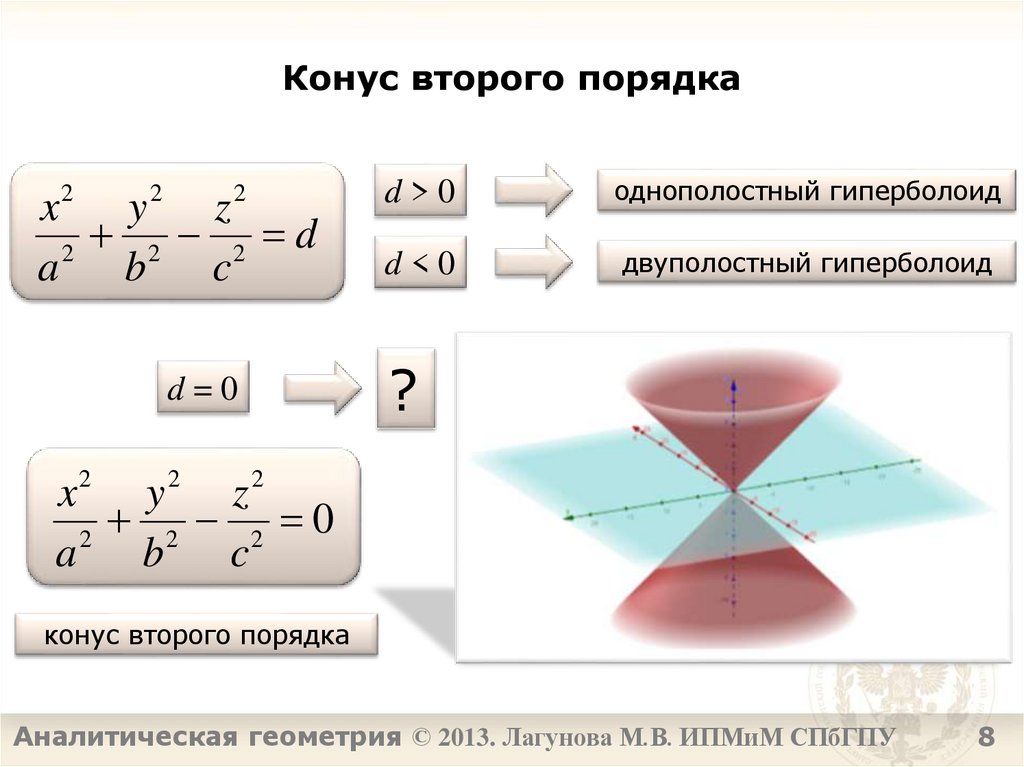
Конус второго порядка
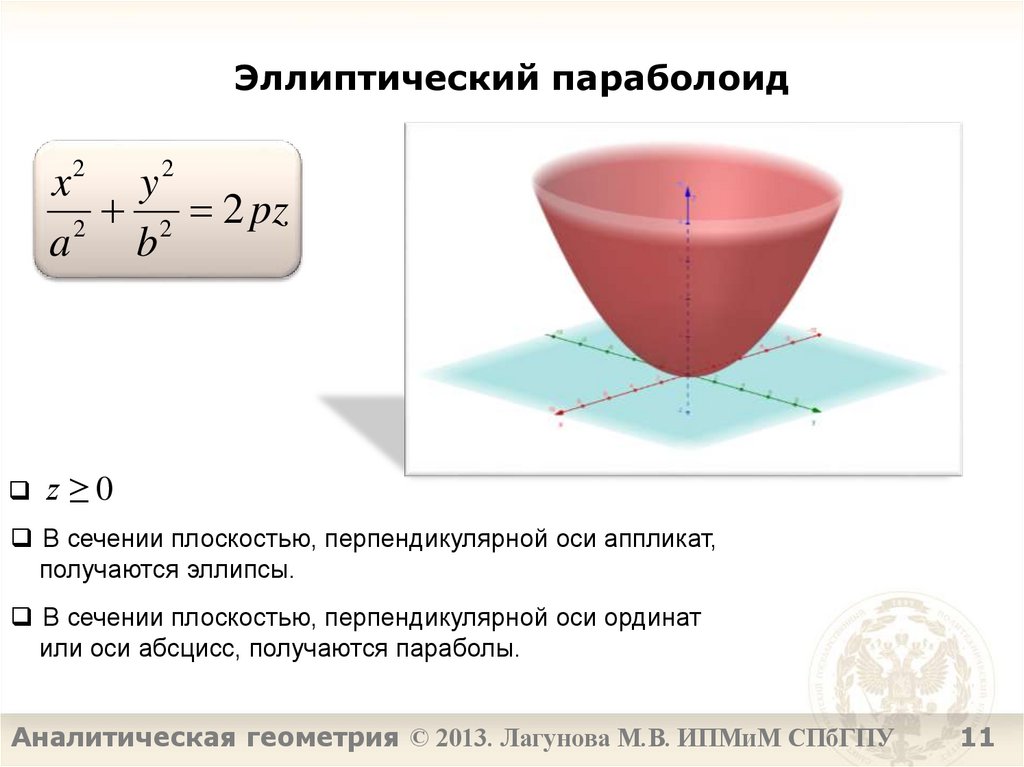
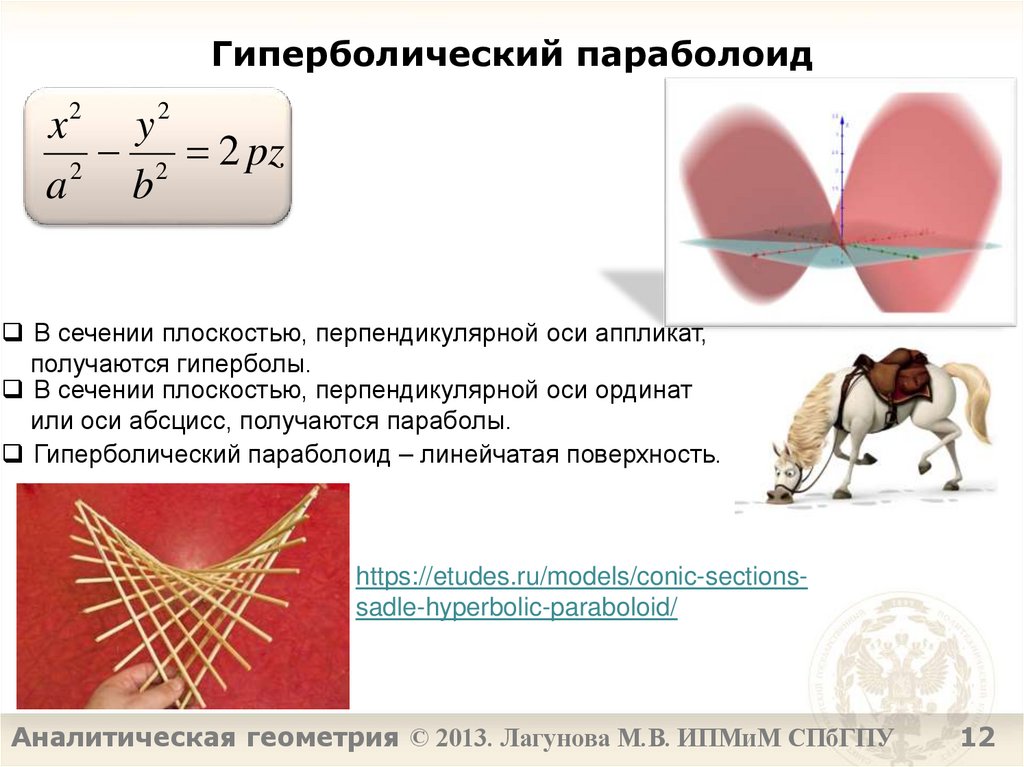
Параболоиды
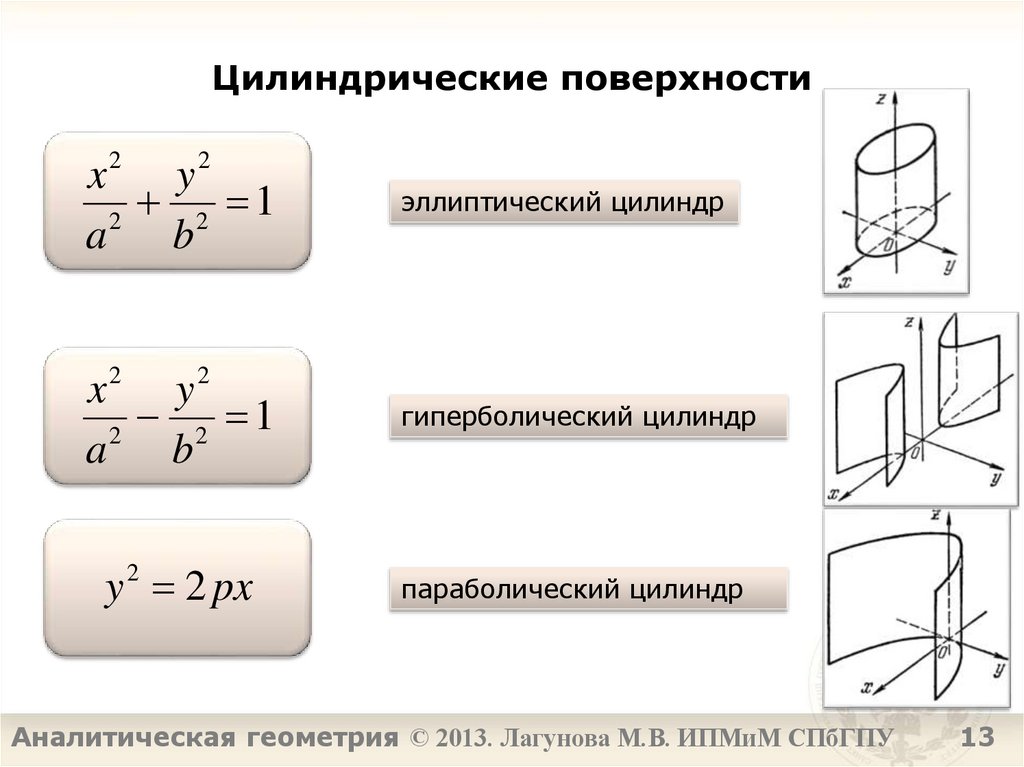
Цилиндрические поверхности
© 2013. Лагунова М.В. СПбГПУ

2. Общее уравнение поверхности второго порядка

Уравнение
Ax2 + 2By2+2Cz2+2Dxy+ 2Exz+2Fyz+
+2Gx+2Hy + 2Iz + J=0,
где A2+B2+C2+D2+E2+F2>0, является уравнением
поверхности второго порядка (ПВП).
Примеры
x2 y 2 z 2 1 0
уравнение сферы
x2 y 2 1 0
уравнение прямого
кругового цилиндра
Аналитическая геометрия © 2013. Лагунова М.В. ИПМиМ СПбГПУ
2

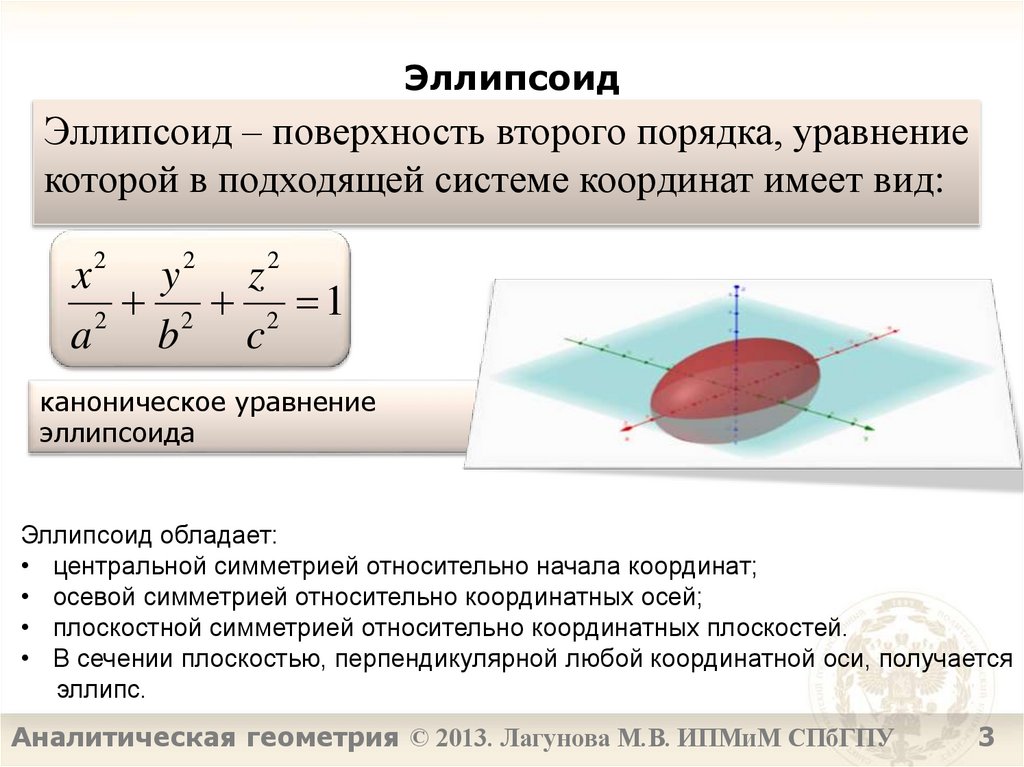
3. Эллипсоид

Эллипсоид – поверхность второго порядка, уравнение
которой в подходящей системе координат имеет вид:
x2 y 2 z 2
2 2 1
2
a
b
c
каноническое уравнение
эллипсоида
Эллипсоид обладает:
• центральной симметрией относительно начала координат;
• осевой симметрией относительно координатных осей;
• плоскостной симметрией относительно координатных плоскостей.
• В сечении плоскостью, перпендикулярной любой координатной оси, получается
эллипс.
Аналитическая геометрия © 2013. Лагунова М.В. ИПМиМ СПбГПУ
3

4. Гиперболоиды

Гиперболоиды – поверхности второго порядка,
уравнение которых в подходящей системе координат
имеют вид:
2
2
2
x
y
z
2 2 1
2
a
b
c
однополостный гиперболоид
2
2
2
x
y
z
2 2 1
2
a
b
c
двуполостный гиперболоид
Гиперболоиды обладают:
центральной симметрией относительно начала координат;
осевой симметрией относительно координатных осей;
плоскостной симметрией относительно координатных плоскостей.
Аналитическая геометрия © 2013. Лагунова М.В. ИПМиМ СПбГПУ
4

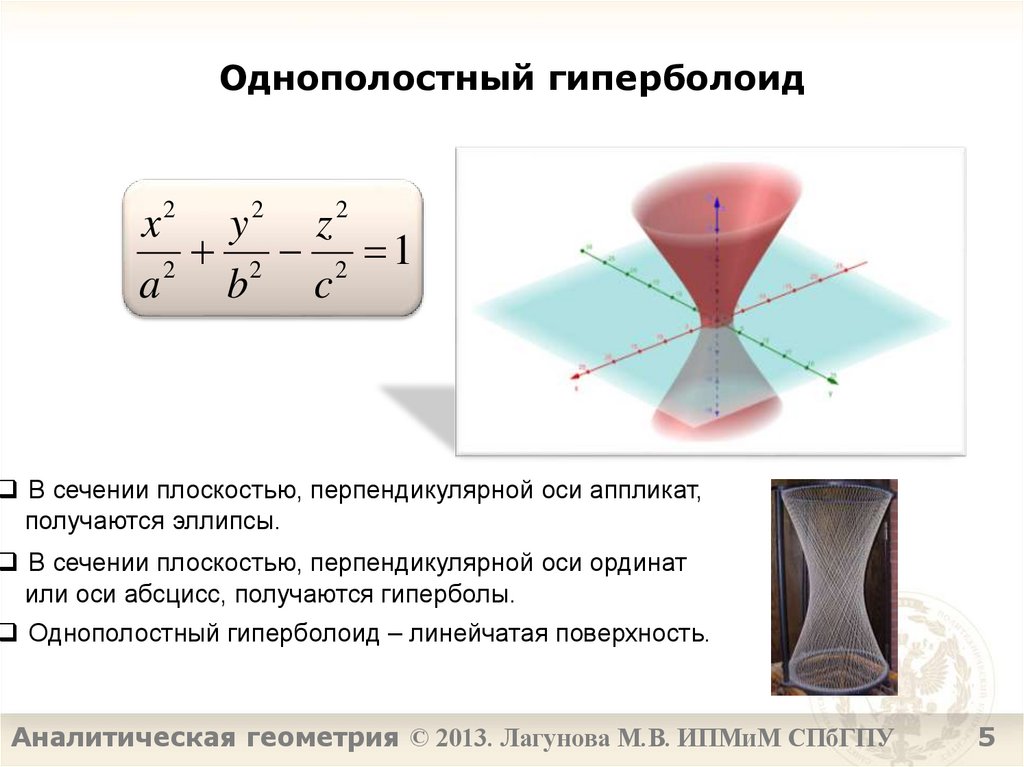
5. Однополостный гиперболоид

x2 y 2 z 2
2 2 1
2
a
b
c
В сечении плоскостью, перпендикулярной оси аппликат,
получаются эллипсы.
В сечении плоскостью, перпендикулярной оси ординат
или оси абсцисс, получаются гиперболы.
Однополостный гиперболоид – линейчатая поверхность.
Аналитическая геометрия © 2013. Лагунова М.В. ИПМиМ СПбГПУ
5

6.

Шуховская башня в Москве
строительство 1920 – 1922
высота 160 м
Телебашня в Гуанчжоу (Китай)
строительство 2005 – 2009
высота 600 м
https://etudes.ru/models/conic-sectionshyperboloid-pencil-holder/
Аналитическая геометрия © 2013. Лагунова М.В. ИПМиМ СПбГПУ
6

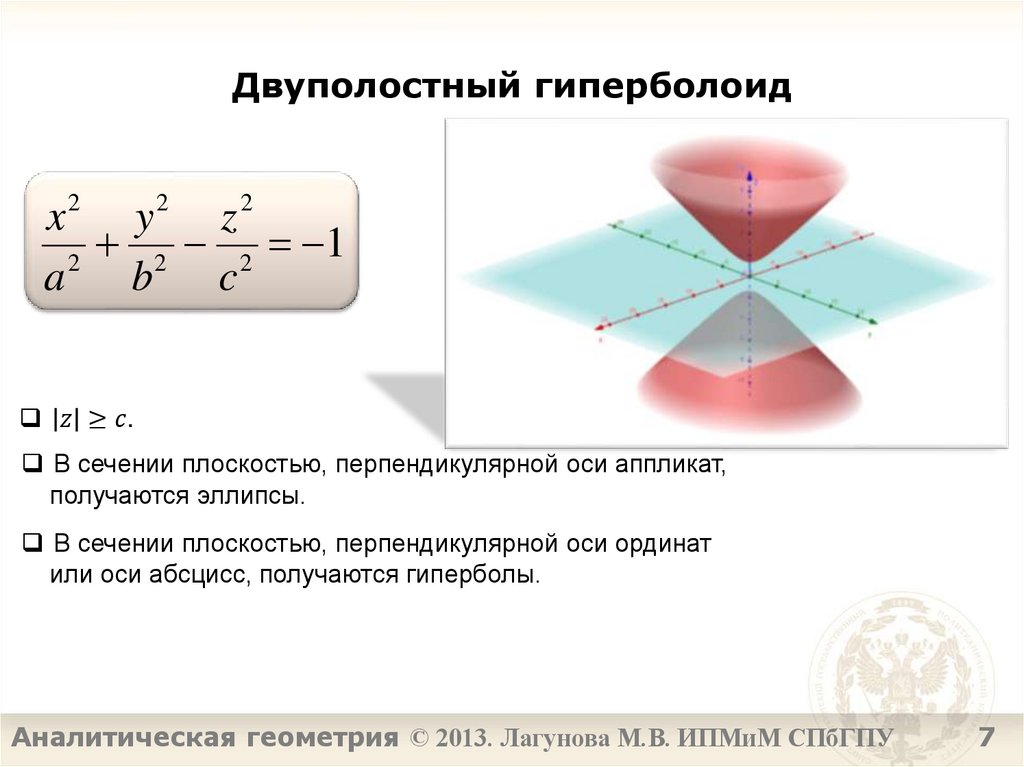
7. Двуполостный гиперболоид

x2 y 2 z 2
2 2 1
2
a
b
c