Similar presentations:
Поверхности второго порядка
1. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
2. 1. Сферическая поверхность (сфера)
x2 y 2 z 2 r 2Z
r
О(0;0;0) – центр сферы.
Горизонтальные сечения
– окружности;
О
r
У
Х
вертикальные сечения
– окружности.
3. Сфера со смещенным центром
Z( x x0 ) ( y y0 ) ( z z0 ) r
2
r
r
2
2
М0(х0;у0;z0)
М0(х0;у0;z0) – центр сферы.
О
Х
У
2
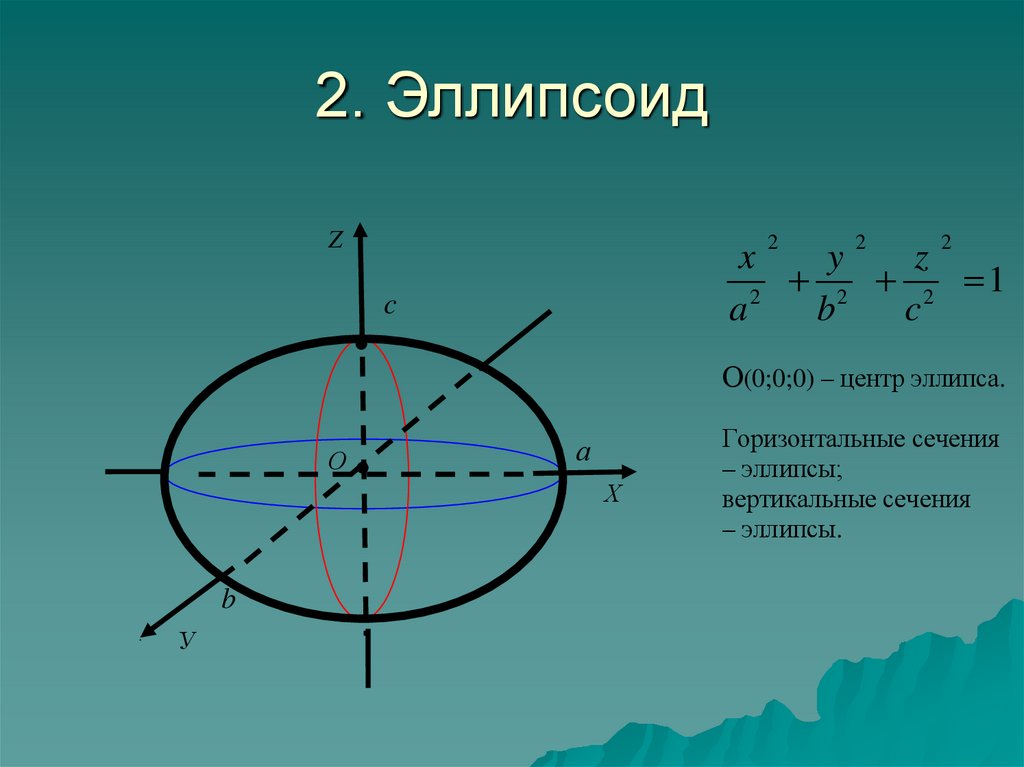
4. 2. Эллипсоид
Z2
2
2
x
y
z
2 2 1
2
a
b
c
c
О(0;0;0) – центр эллипса.
О
а
Х
b
У
Горизонтальные сечения
– эллипсы;
вертикальные сечения
– эллипсы.
5. Эллипсоид со смещенным центром
( x x0 ) ( y y0 ) ( z z0 )1
2
2
2
a
b
c
2
2
2
М0 (х0;у0;z0) – центр эллипса.
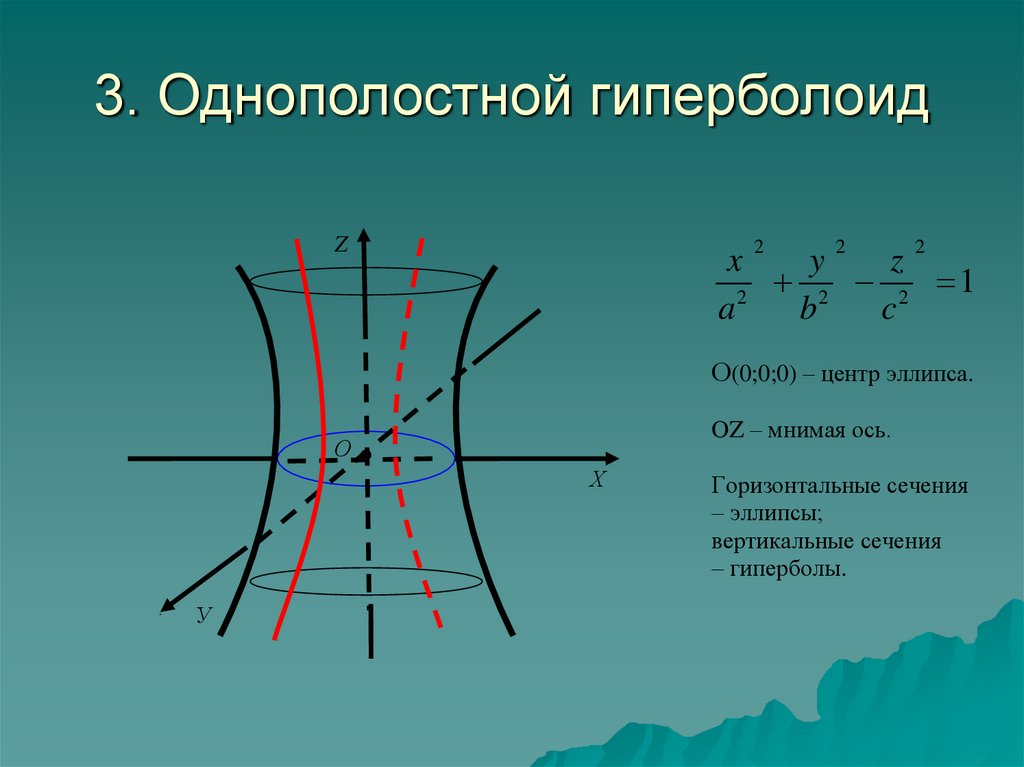
6. 3. Однополостной гиперболоид
Z2
2
2
z
y
x
2 2 1
2
c
b
a
О(0;0;0) – центр эллипса.
OZ – мнимая ось.
О
Х
У
Горизонтальные сечения
– эллипсы;
вертикальные сечения
– гиперболы.
7. Однополостной гиперболоид со смещенным центром
( x x0 ) ( y y0 ) ( z z0 )1
2
2
2
a
b
c
2
2
2
М0 (х0;у0;z0) – центр гиперболоида,
Мнимая ось параллельна оси OZ.
В частности:
- мнимая ось параллельна оси ОУ
( x x0 ) ( y y0 ) ( z z0 )
1.
2
2
2
a
b
c
2
2
2
-мнимая ось параллельна оси ОХ
( x x0 )
( y y0 )
( z z0 )
1.
2
2
2
a
b
c
2
2
2
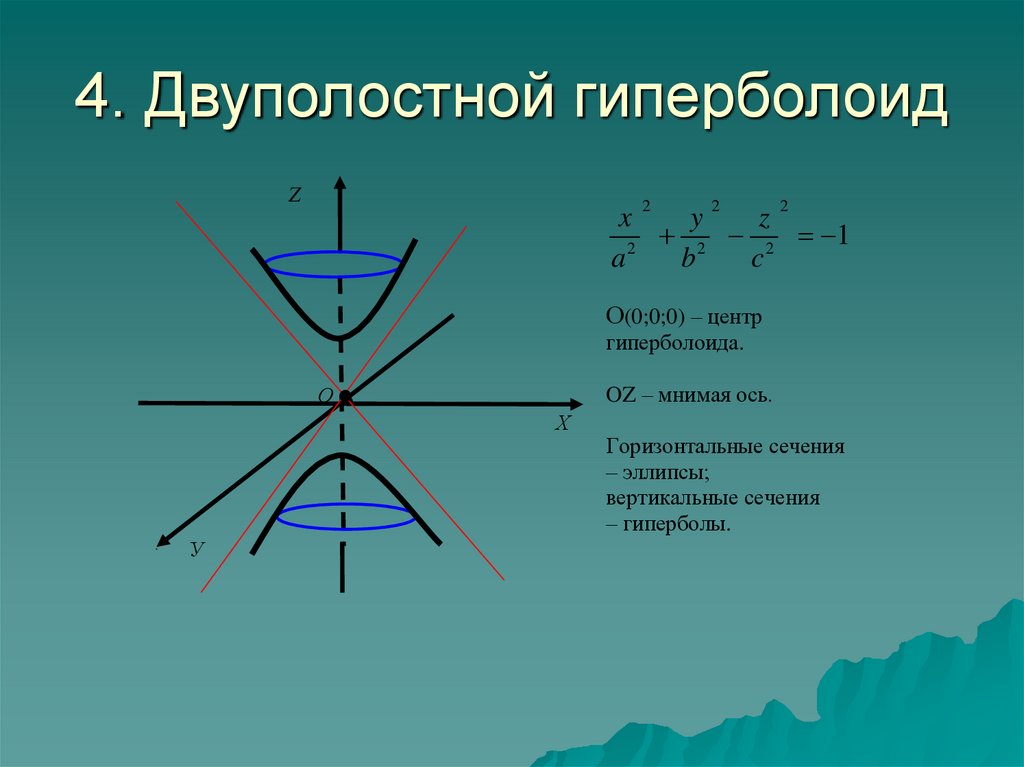
8. 4. Двуполостной гиперболоид
Z2
2
2
x
y
z
2 2 1
2
a
b
c
О(0;0;0) – центр
гиперболоида.
OZ – мнимая ось.
О
Х
У
Горизонтальные сечения
– эллипсы;
вертикальные сечения
– гиперболы.
9. Двуполостной гиперболоид со смещенным центром
( x x0 )( y y0 )
( z z0 )
1
2
2
2
a
b
c
2
2
2
М0 (х0;у0;z0) – центр гиперболоида,
Мнимая ось параллельна оси OZ.
В частности:
мнимая ось параллельна оси ОУ
( x x0 )
( y y0 )
( z z0 )
1
2
2
2
a
b
c
2
2
2
мнимая ось параллельна оси ОХ
( x x0 )
( y y0 )
( z z0 )
1
2
2
2
a
b
c
2
2
2
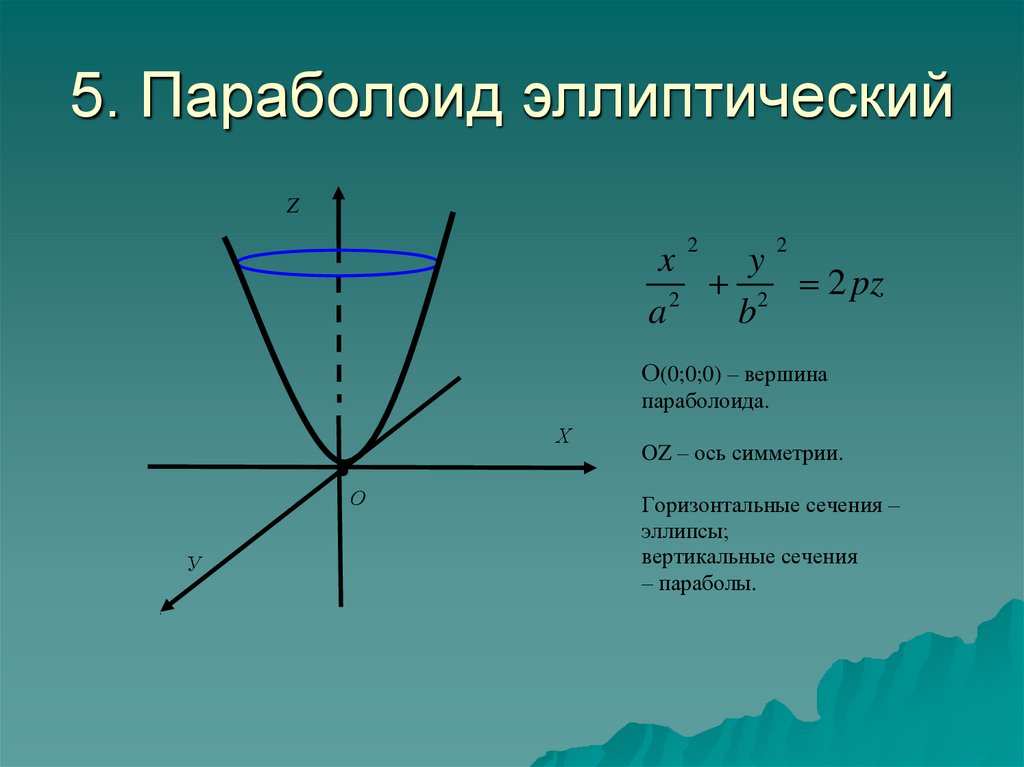
10. 5. Параболоид эллиптический
Z2
2
x
y
2 2 pz
2
a
b
О(0;0;0) – вершина
параболоида.
Х
О
У
OZ – ось симметрии.
Горизонтальные сечения –
эллипсы;
вертикальные сечения
– параболы.
11. Параболоид эллиптический со смещенной вершиной
( y y0 )( x x0 )
2 p ( z z0 )
2
2
b
a
2
2
М0 (х0;у0;z0) – вершина параболоида,
OZ – ось симметрии.
В частности:
ОУ – ось симметрии
( z z0 )
( x x0 )
2 p( y y0 )
2
2
c
a
2
2
ОХ – ось симметрии
( z z0 )
( y y0 )
2 p( x x0 )
2
2
c
b
2
2
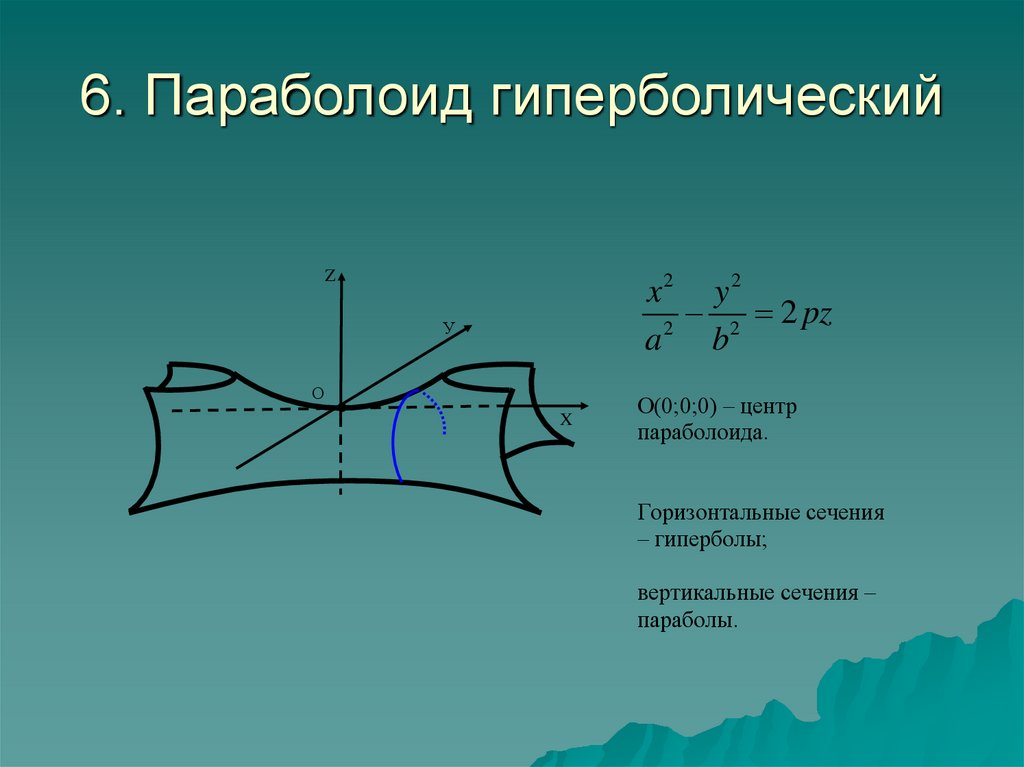
12. 6. Параболоид гиперболический
Zx2 y 2
2 2 pz
2
a b
У
О
X
О(0;0;0) – центр
параболоида.
Горизонтальные сечения
– гиперболы;
вертикальные сечения –
параболы.
13. Параболоид гиперболический со смещенным центром
( x x0 ) ( y y0 )( x x0 ) ( y y0 )
2 p ( z z0 )
2
p
(
z
z
)
0 или
a2
b2
a2
b2
2
2
2
2
М0 (х0;у0;z0) – центр параболоида, OZ – ось симметрии.
В частности:
ОУ – ось симметрии
2
2
( x x0 ) ( z z0 )
( x x0 ) ( z z0 )
2 p( y y0 ) или
2 p( y y0 )
a2
c2
a2
c2
2
2
ОХ – ось симметрии
2
2
( y y0 ) ( z z0 )
( y y0 ) ( z z0 )
2 p( x x0 ) или
2 p( x x0 )
b2
c2
b2
c2
2
2
14. 7. Конус эллиптический
Z2
2
2
x
y
z
2 2 0
2
a
b
c
О(0;0;0) – центр конуса.
О
У
Х
OZ – ось симметрии.
15. 8. Цилиндрические поверхности 1) эллиптический
Z2
2
x
y
2 1
2
a
b
OZ – ось симметрии.
Горизонтальные сечения – эллипсы.
О
У
В частности:
2
2
x
z
2 1 - ось симметрии ОУ,
a2
c
2
Х
2
y
z
2 1 - ось симметрии ОХ.
2
b
c
16. 2) гиперболический
Z2
2
x
y
2 1
2
a
b
У
OZ – ось симметрии.
Горизонтальные сечения – гиперболы.
О
Х
В частности:
2
2
x
z
2 1 - ось симметрии ОУ,
2
a
c
2
2
y
z
2 1 - ось симметрии ОХ.
b2
c
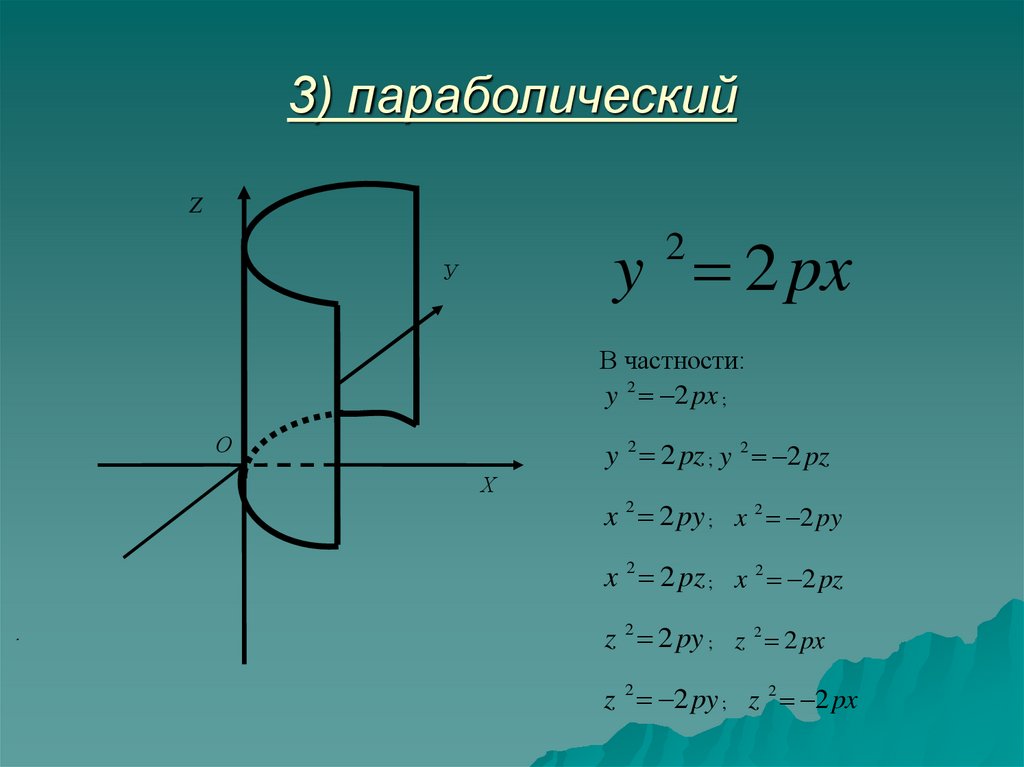
17. 3) параболический
Zy 2 px
2
У
В частности:
y 2 2 px ;
О
y 2 2 pz ; y 2 2 pz
Х
x 2 2 py ; x 2 2 py
x 2 2 pz ; x 2 2 pz
z 2 2 py ; z 2 2 px
z 2 2 py ; z 2 2 px












 mathematics
mathematics








