Similar presentations:
Сложное сопротивление. Общий случай действия сил
1.
Сложноесопротивление.
Общий случай действия сил
2.
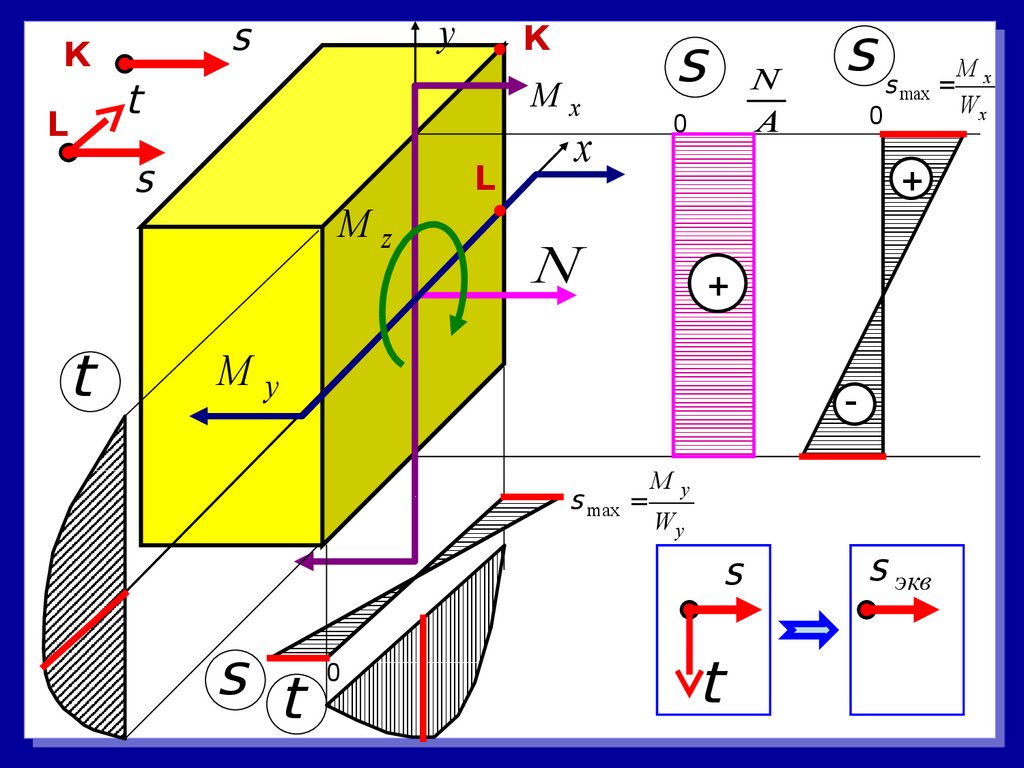
ys
К
К
Mx
t
L
s
t
s
L
Mz
M
N
A
0
x
0
max
+
N
+
y
s max =
M
y
Wy
s
s t
ss
0
t
s экв
=
Mx
Wx
3.
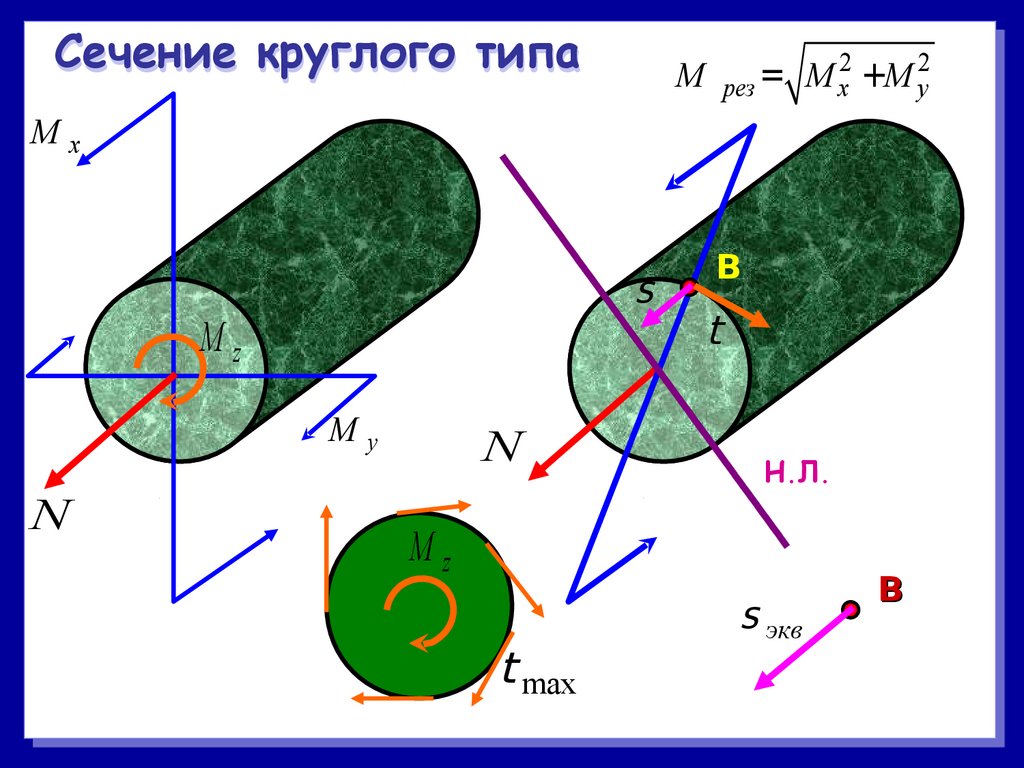
Сечение круглого типа2
2
=
M
+
M
рез
x
y
M
Mx
s
Mz
M
N
N
y
В
t
Н.Л.
Mz
t max
s экв
В
4.
Условие прочностиs экв R
Формулы для подсчета
эквивалентных напряжений
зависят от теории прочности.
5.
Основныетеории
прочности.
6.
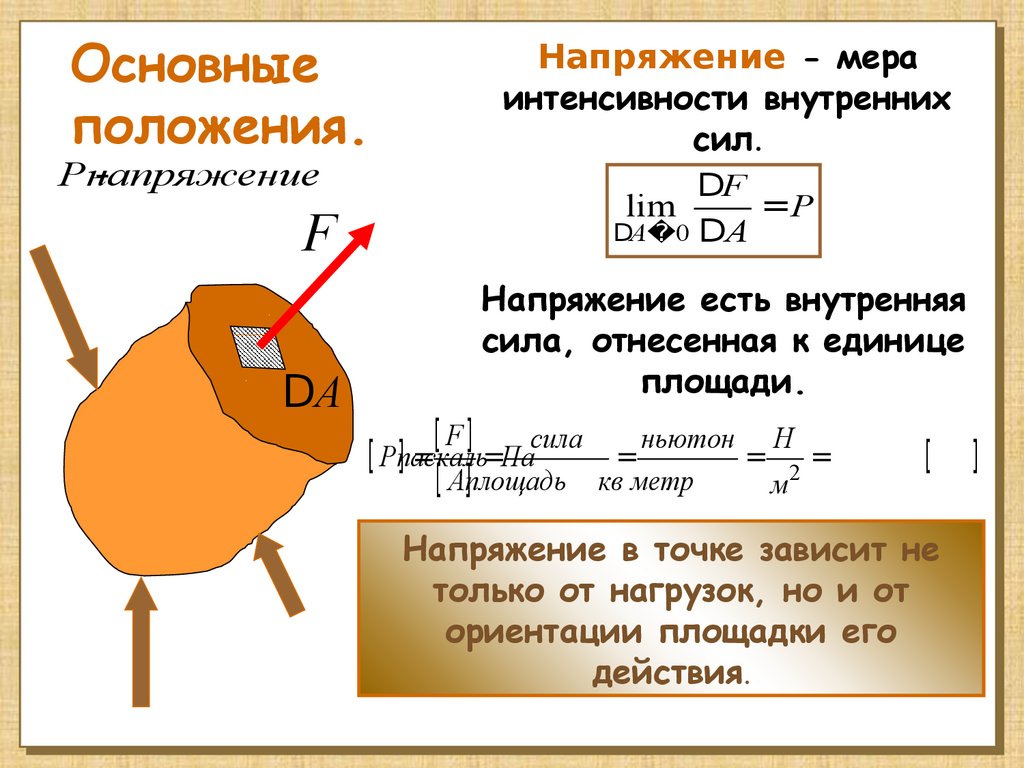
Основныеположения.
Pнапряжение
-
Напряжение - мера
интенсивности внутренних
сил.
DF
lim
=P
DA 0 DA
F
DA
Напряжение есть внутренняя
сила, отнесенная к единице
площади.
F]
[
сила
[ Pпаскаль
] = =Па
[ Aплощадь
]
ньютон Н
=
= 2=
кв метр
.
м
[
Напряжение в точке зависит не
только от нагрузок, но и от
ориентации площадки его
действия.
]
7.
Совокупность всех нормальных и касательныхнапряжений на бесконечном множестве площадок,
проведенных через данную точку тела, называется
напряженным состоянием в точке.
Напряженное состояние можно описать
с помощью тензора напряжений Ts :
s x t xy t xz
Ts =
t yx s y t yz
t
t
s
zy
z
zx
8.
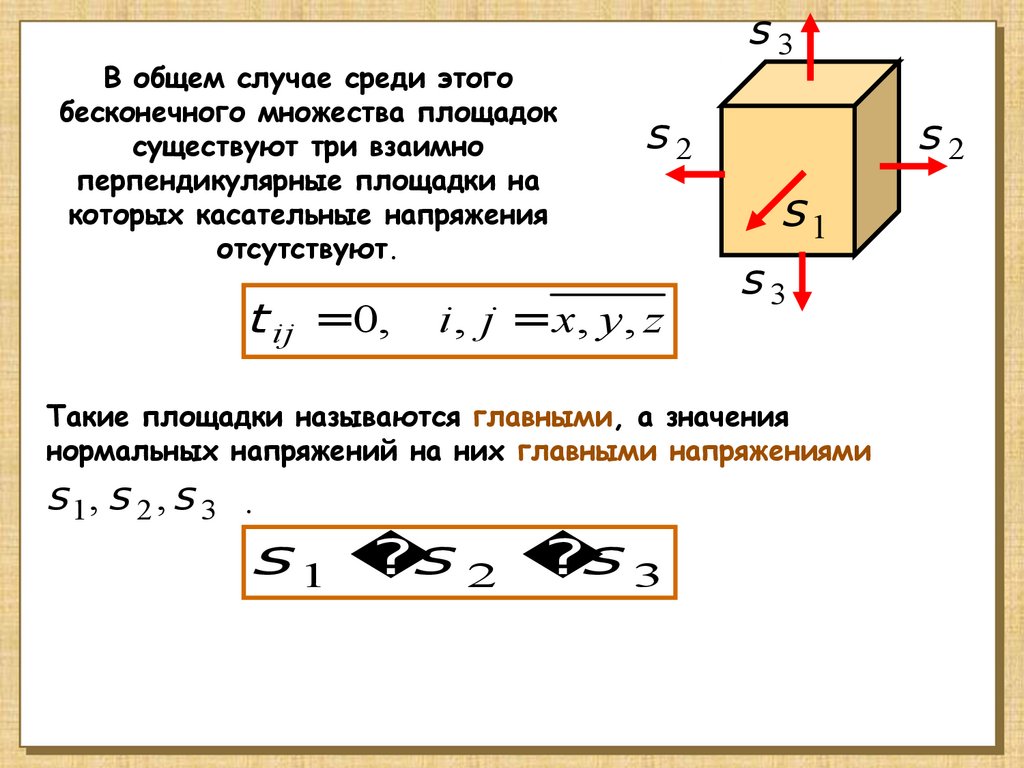
В общем случае среди этогобесконечного множества площадок
существуют три взаимно
перпендикулярные площадки на
которых касательные напряжения
отсутствуют.
t ij =0,
s3
s2
i, j =x, y , z
s2
s1
s3
Такие площадки называются главными, а значения
нормальных напряжений на них главными напряжениями
s 1, s 2 , s 3
.
s 1 s 2 s 3
9.
Виды напряженного состоянияОДНООСНОЕ
(ЛИНЕЙНОЕ)
s1
s1
s 1 0,
s 2 =0,
s 3 =0.
ДВУХОСНОЕ
(ПЛОСКОЕ)
s2
ТРЕХОСНОЕ
(ОБЪЕМНОЕ)
s1
s1
s2
s1
s 1 0,
s 2 0,
s 3 =0.
s2
s2
s1
s 1 0,
s 2 0,
s 3 0.
10.
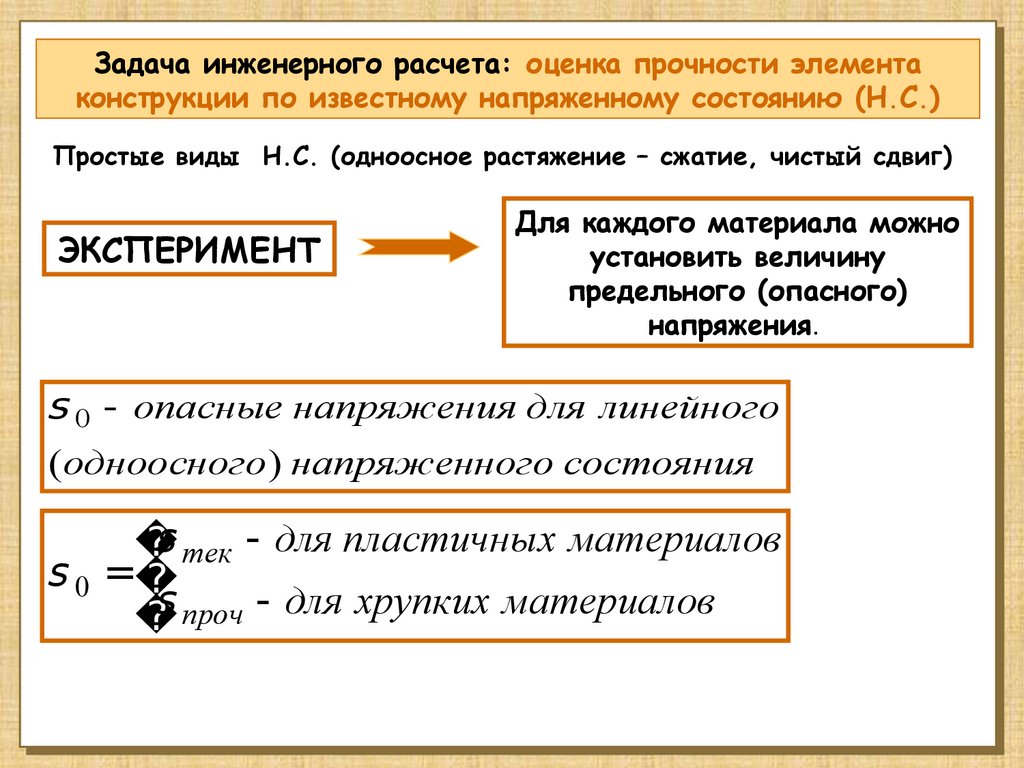
Задача инженерного расчета: оценка прочности элементаконструкции по известному напряженному состоянию (Н.С.)
Простые виды Н.С. (одноосное растяжение – сжатие, чистый сдвиг)
ЭКСПЕРИМЕНТ
Для каждого материала можно
установить величину
предельного (опасного)
напряжения.
s 0 - опасные напряжения для линейного
(одноосного) напряженного состояния
s тек - для пластичных материалов
s 0 =
s проч - для хрупких материалов
11.
Задача инженерного расчета: оценка прочности элементаконструкции по известному напряженному состоянию (Н.С.)
?
Сложное напряженное состояние
ЭКСПЕРИМЕНТ
?
ДРУГОЙ ПУТЬ
Экспериментальные данные при
одноосном растяжении-сжатии
Гипотеза о преимущественном
влиянии на прочность какоголибо фактора
Необходимо большое количество
испытаний, отсутствие
испытательных машин и
измерительной техники для
создания любого напряженного
состояния в образце и получения
достоверных результатов.
s экв = f ( s 1, s 2 , s 3 )
s экв R
12.
Основная задача критериев (теорий)прочности –свести сложное напряжённое состояние к линейному.
Два напряжённых состояния считаются равноопасными, если
увеличивая главные напряжения в одно и то же число раз
материал одновременно переходит в опасное состояние.
В этом случае коэффициент запаса прочности будет одинаковым.
Эквивалентное напряжение – напряжение, при котором образец
материала в условиях одноосного напряжённого состояния
оказывается в равноопасном состоянии с рассматриваемым
сложным напряжённым состоянием в точке.
13.
Первая теория прочности( критерий прочности понаибольшим нормальным напряжениям).
ГИПОТЕЗА: Предельное состояние
материала наступает тогда, когда
наибольшее рабочее напряжение
достигает опасного значения
Галилео
Галилей
(15.02.1564
–
08.01.1642)
математик,
механик,
астроном.
s max =s 1 <s 0
s0
s max
K
=R
Kкоэффициент
запаса прочности
14.
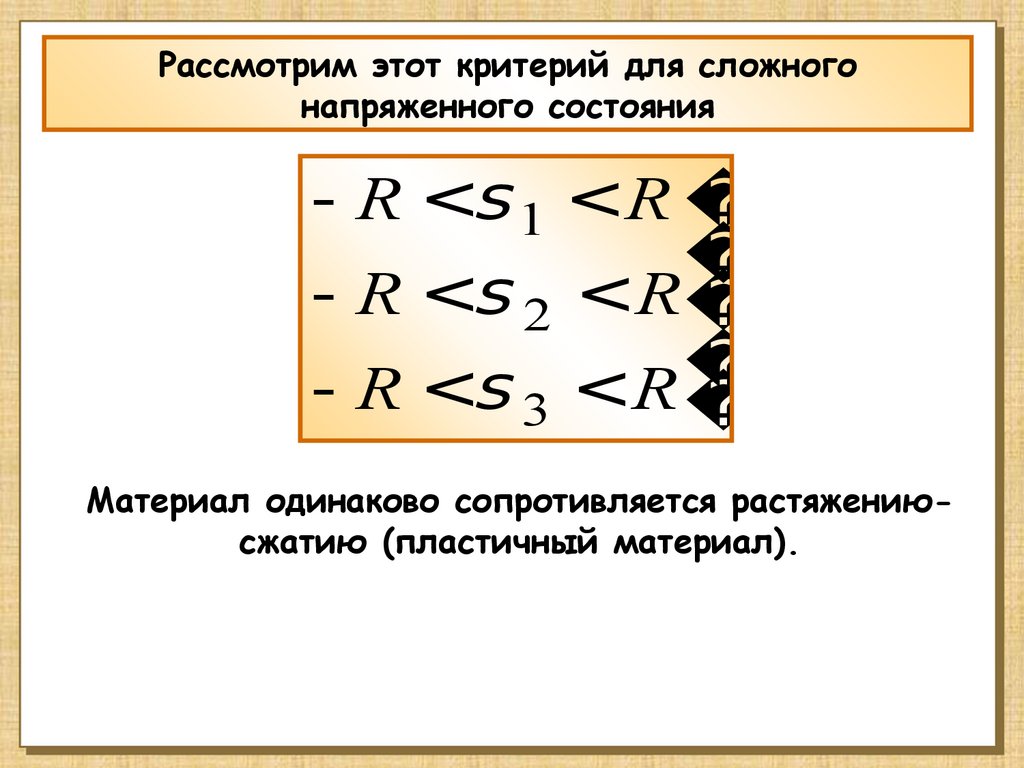
Рассмотрим этот критерий для сложногонапряженного состояния
- R <s 1 <R
- R <s 2 <R
- R <s 3 <R
Материал одинаково сопротивляется растяжениюсжатию (пластичный материал).
15.
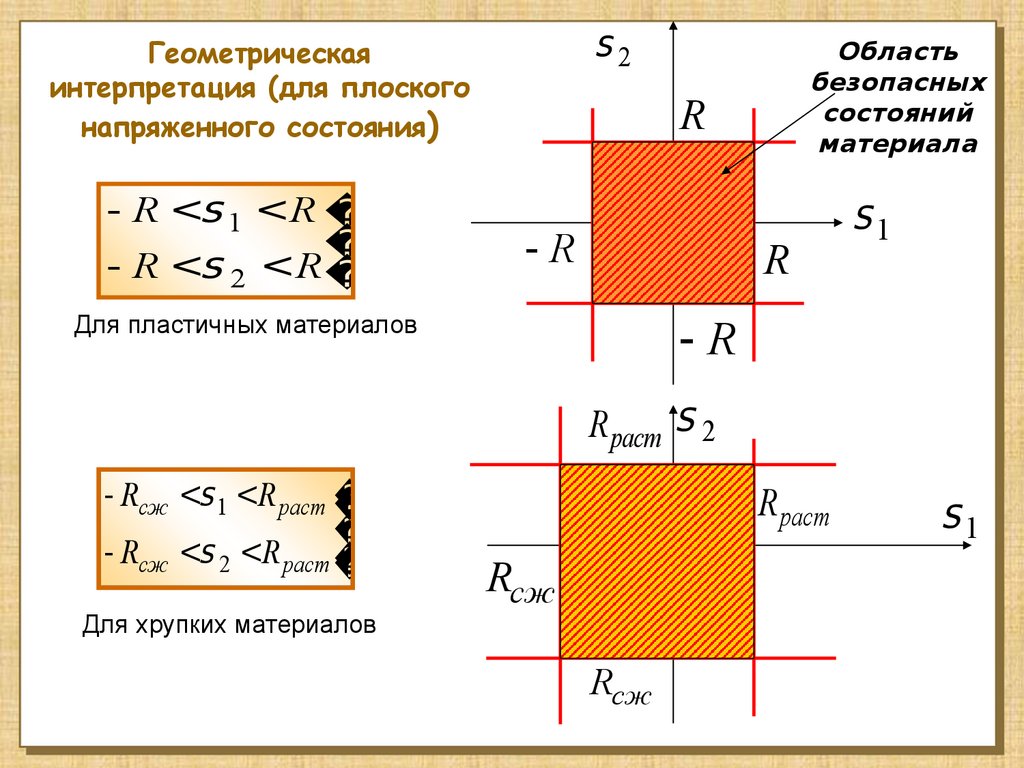
s2Геометрическая
интерпретация (для плоского
напряженного состояния)
- R <s 1 <R
- R <s 2 <R
Область
безопасных
состояний
материала
R
-R
R
s1
-R
Для пластичных материалов
R раст s 2
- Rсж <s 1 <R раст
- Rсж <s 2 <R раст
Для хрупких материалов
R раст
Rсж
Rсж
s1
16.
«-» (Недостаток теории): не учитывается взаимноевлияние главных напряжений при переходе
материала в опасное состояние
Первая теория прочности удовлетворительно
подтверждается лишь для некоторых весьма хрупких
материалов (кирпич, стекло и т.п.)
По этой причине в современных инженерных
расчетах гипотеза Галилея не используется.
17.
Вторая теория прочности( критерий прочности понаибольшим относительным удлинениям).
ГИПОТЕЗА:
При наступлении
предельного состояния наибольшее
удлинение достигает предельного
значения, равного относитель-ному
удлинению при одноосном растяжении.
Условие разрушения:
Эдме
Мариотт
(1620 –
12.05.1684)
физик,
механик.
emax =e1 <e0
emax =e1 = E1
s1 - n
II
s экв
(
s0
s 2 +s 3
< E
)
=s 1 - n ( s 2 +s 3 ) R
18.
Рассмотрим этот критерий для сложного напряженногосостояния
- R <s 1 - n ( s 2 +s 3 ) <R
- R <s 2 - n ( s 3 +s 1 ) <R
- R <s 3 - n ( s 1 +s 2 ) <R
Материал одинаково сопротивляется растяжениюсжатию (пластичный материал).
19.
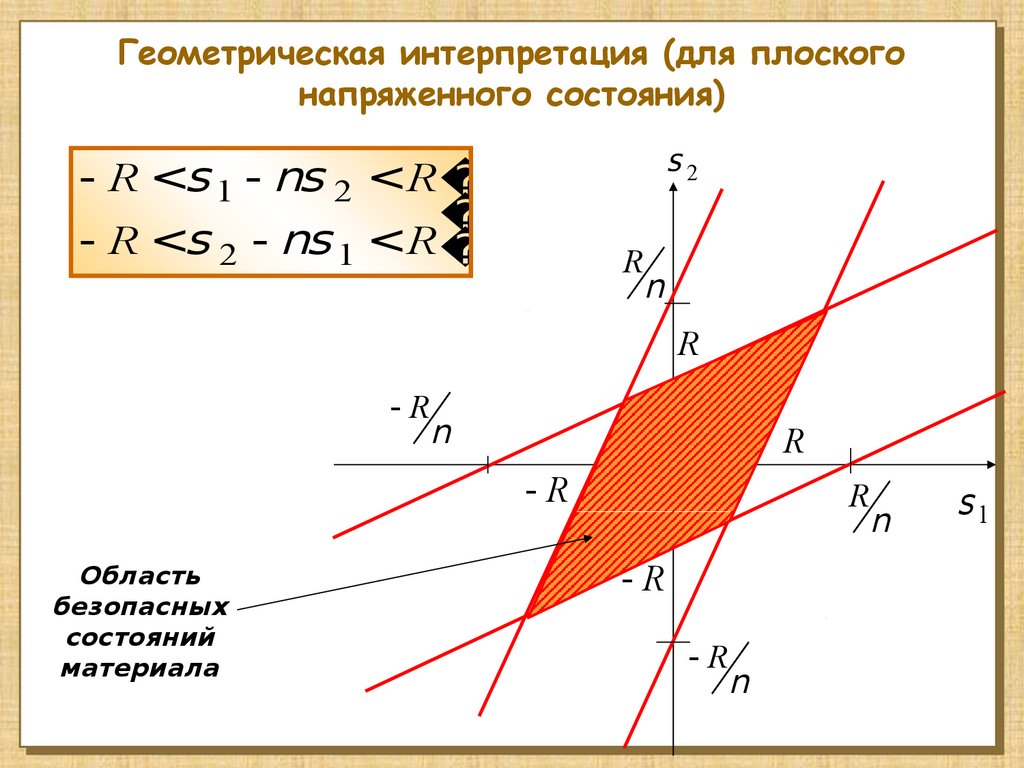
Геометрическая интерпретация (для плоскогонапряженного состояния)
s2
- R <s 1 - ns 2 <R
- R <s 2 - ns 1 <R
R
n
R
-R
n
R
-R
Область
безопасных
состояний
материала
R
-R
-R
n
n
s1
20.
«-» : не учитывается взаимное влияние главныхдеформаций при переходе материала в опасное
состояние
«+» : Вторая теория учитывает взаимное
влияние главных напряжений при переходе
материала в опасное состояние
Вторая теория прочности удовлетворительно
подтверждается лишь для немногих хрупких
материалов (легированный чугун, высокопрочные
стали после низкого отпуска и т.п.)
Для большинства материалов она не применима,
поэтому в практике современных инженерных
расчетов не используется.
21.
Третья теория прочности( критерий пластичности понаибольшим касательным напряжениям).
Анри Эдуард Треска
(1814 –1885) механик,
инженер.
Шарль
Огюстен
Кулон
(14.06.1736 –
23.08.1806)
физик,
механик,
инженер.
1864г
Разрез установки
А. Треска для
изучения течения
металлов
Сечение набора
десяти свинцовых
пластин после
выдавливания на
установке.
Адемар ЖанКлод Барре
Сен-Венан
(23.08.1797 –
06.01.1886)
механик,
инженер.
1871г
22.
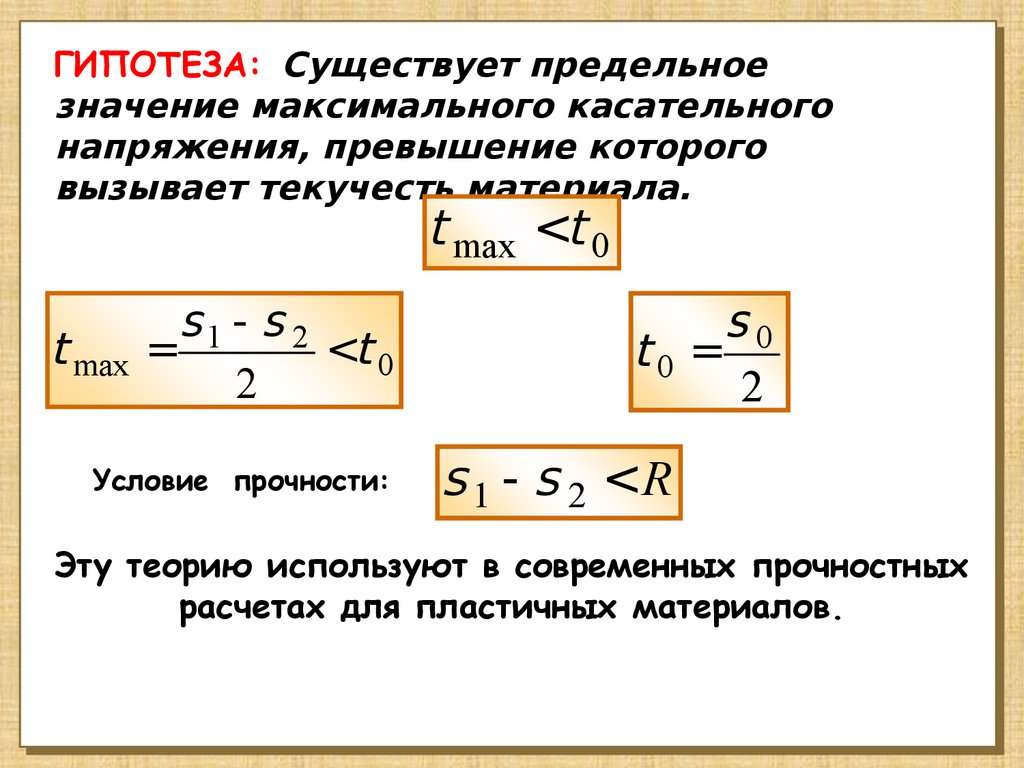
ГИПОТЕЗА: Существует предельноезначение максимального касательного
напряжения, превышение которого
вызывает текучесть материала.
t max <t 0
t max
s1 - s 2
=
<t 0
2
Условие прочности:
s0
t0 =
2
s 1 - s 2 <R
Эту теорию используют в современных прочностных
расчетах для пластичных материалов.
23.
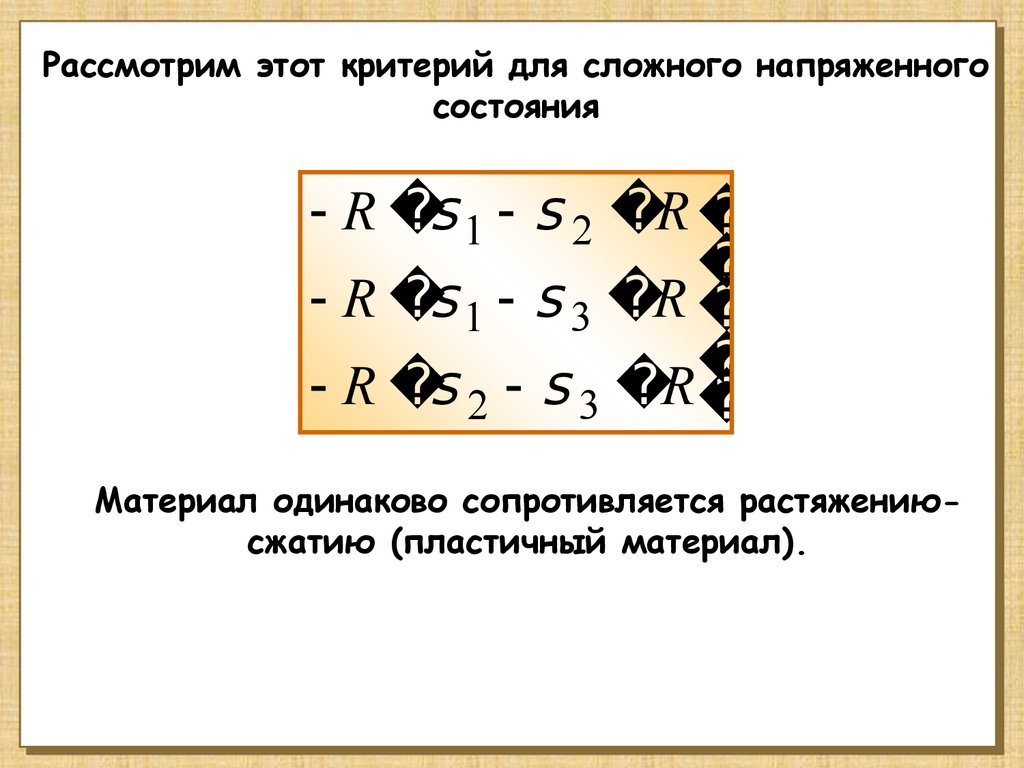
Рассмотрим этот критерий для сложного напряженногосостояния
- R s 1 - s 2 R
- R s 1 - s 3 R
- R s 2 - s 3 R
Материал одинаково сопротивляется растяжениюсжатию (пластичный материал).
24.
- R s 1 - s 2 R- R s 1 R
- R s 2 R
Геометрическая интерпретация (для
плоского напряженного состояния)
s2
R
s1
-R
R
Область
безопасных
состояний
материала
-R
25.
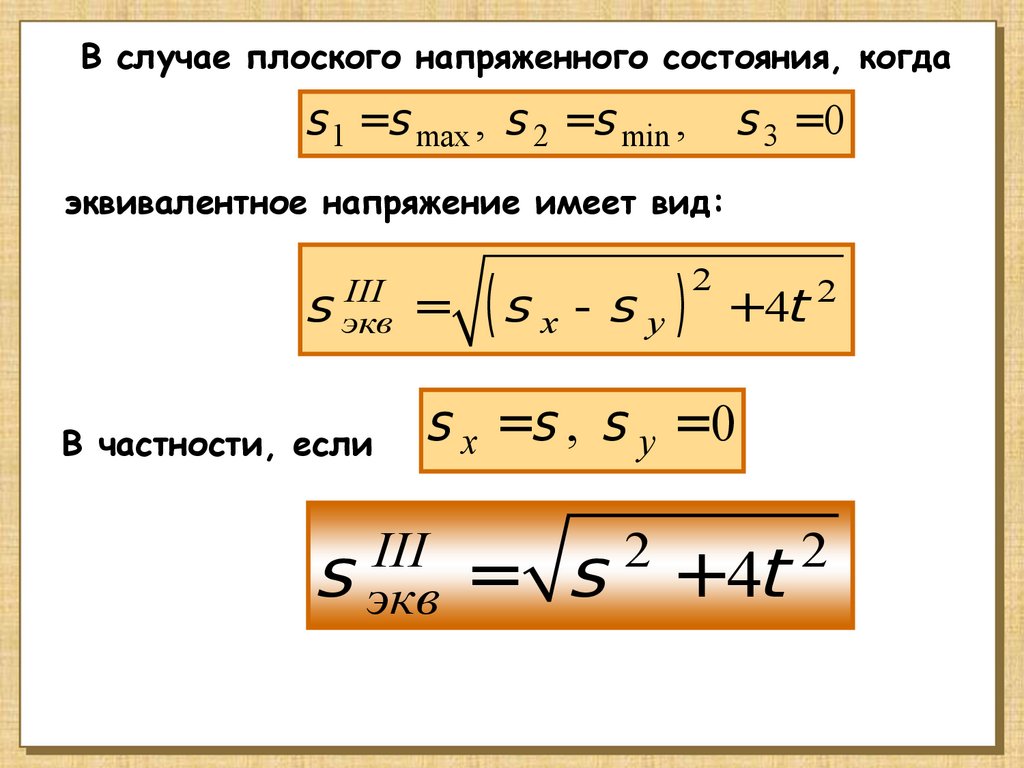
В случае плоского напряженного состояния, когдаs 1 =s max , s 2 =s min ,
s 3 =0
эквивалентное напряжение имеет вид:
s
III
экв
В частности, если
=
2
2
s
s
+
4
t
( x y)
s x =s , s y =0
III
s экв
= s
2
+4t
2
26.
Четвертая теория прочности( критерий потенциальнойэнергии изменения формы).
Эудженио
Бельтрами
(16.11.183518.02.1900)
математик
1885г
Джеймс Клерк
Максвелл
(13.06.1831 –
05.11.1879)
физик,
механик.
1856г
Максимилиан
Тытус Хубер
(04.01.1872 –
09.12.1950)
механик,
инженер.
1904г
Рихард Мизес
(19.04.1883 –
14.07.1953)
механик,
инженер.
1913г
27.
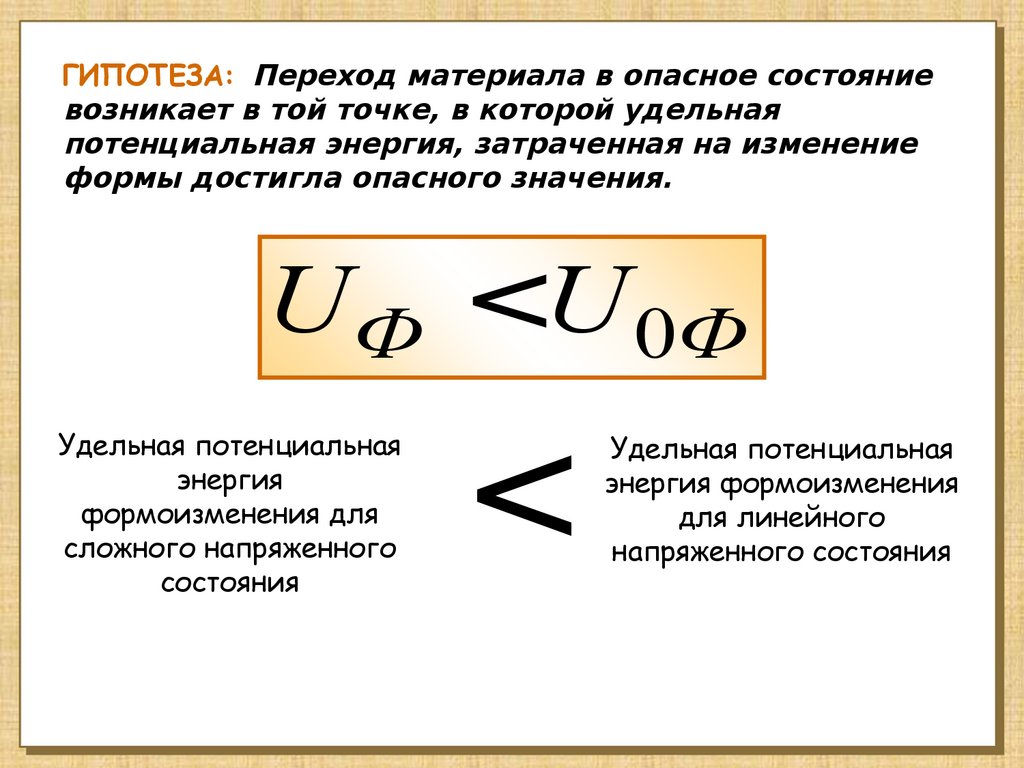
ГИПОТЕЗА: Переход материала в опасное состояниевозникает в той точке, в которой удельная
потенциальная энергия, затраченная на изменение
формы достигла опасного значения.
UФ <U 0Ф
Удельная потенциальная
энергия
формоизменения для
сложного напряженного
состояния
<
Удельная потенциальная
энергия формоизменения
для линейного
напряженного состояния
28.
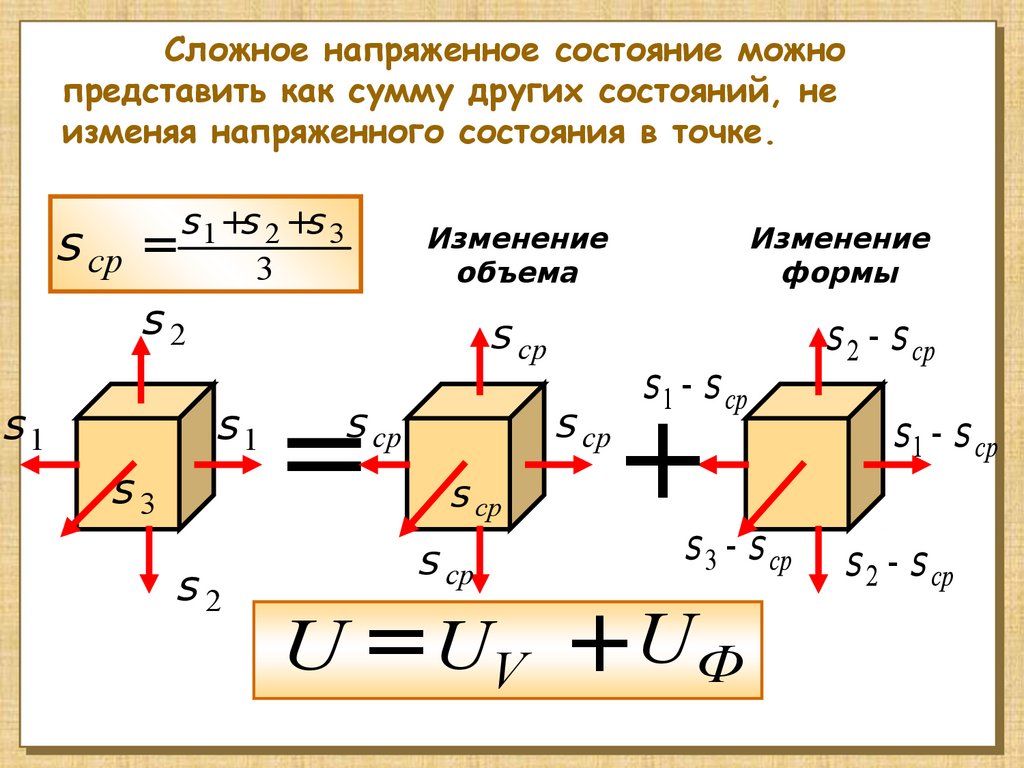
Сложное напряженное состояние можнопредставить как сумму других состояний, не
изменяя напряженного состояния в точке.
s 1 +s 2 +s 3
s ср =
3
Изменение
объема
s2
s1
s ср
s1
s3
s2
=
s ср
s ср
s ср
s ср
U = UV
Изменение
формы
s 1 - s ср
+
s 3 - s ср
+UФ
s 2 - s ср
s 1 - s ср
s 2 - s ср
29.
U =UVФ+UUФ =U - UV
(*)
s 1 ,s 2 ,s 3 - главные напряжения
U =1
s
e
+
s
e
+
s
e
[
1
1
2
2
3
3]
2
U
2
2
2
1
=2 E s 1 +s 2 +s 3
2n ( s 1s 2 +s 2s 3 +s 1s 3 ) (**)
30.
Определим из (**) выражение для энергии, связаннойс изменением объема.
s 1 =s 2 =s 3 =s ср
3 ( 1 - 2n ) 2
UVср=
s (***)
2E
(**) и (***) подставим в (*)
UФ =U - UV =
2
2
2
1
=2 E s 1 +s 2 +s 3
3 ( 1 - 2n ) 2
2n ( s 1s 2 +s 2s 3 +s 1s 3 ) s
ср
2E
31.
22
2
UФ =21E
s
+
s
+
s
- 2n ( s 1s 2 +s 2s 3 +s 1s 3 ) 1
2
3
-
(
)
3( 1- 2n ) s 1 +s 2 +s 3 2
;
2E
3
UФ =13+En
2
2
2
s
+s 2 +s 3 - ( s 1s 2 +s 2s 3 +s 1s 3 )
1
UФ =16+En
2
2
2
( s 1 - s 2 ) +( s 1 - s 3 ) +( s 2 - s 3 ) (1)
32.
Определим удельную потенциальную энергию,затраченную на изменение формы, для линейного
напряжённого состояния.
UФ =16+En s 1
(
2
2
s 2 ) +( s 1 - s 3 ) +( s 2 - s 3 )
Полагаем в (1)
2
(1)
s 2 =s 3 =0, s 0 =s 1
2
1
+
n
U 0Ф = 3 E s 0
(2)
33.
(1) и (2) подставим в неравенство(s1 - s 2 )
2
UФ <U 0Ф
2
2
2
2s 0
2
2
2
+( s 1 - s 3 ) +( s 2 - s 3 )
Условие прочности
2
( s 1 - s 2 ) +( s 1 - s 3 ) +( s 2 - s 3 )
2R
34.
«+»: Четвертая теория учитывает
взаимное влияние всех трех главных
напряжений при переходе материала в
опасное состояние
Этот критерий пластичности даёт хорошие
результаты для пластичных материалов,
одинаково работающих при растяжении и
сжатии.
35.
Геометрическая интерпретация (дляплоского напряженного состояния)
s 3 =0
2
2
2
2
s
s
+
s
+
s
2R
( 1 2)
1
2
s 12 - s 1s 2 +s 2 2 R 2
s2
R
эллипс
Область безопасных
состояний материала
-R
R
-R
s1
36.
В случае плоского напряженного состоянияусловие прочности имеет вид:
IV
s экв
2
2
= s +3t R
37.
Пятая теория прочности (теория прочности Мора).Эту теорию прочности удобно интерпретировать
с помощью кругов напряжений.
Рассмотрим осевое растяжение.
F
F
s 1 0
Отто
Христиан Мор
(08.10.1835 –
03.10.1918)
механик,
инженер.
ta
sa
a
n
s 2 =0, s 3 =0
t
ta
Круг Мора
a
z
s1
0
sa
s
38.
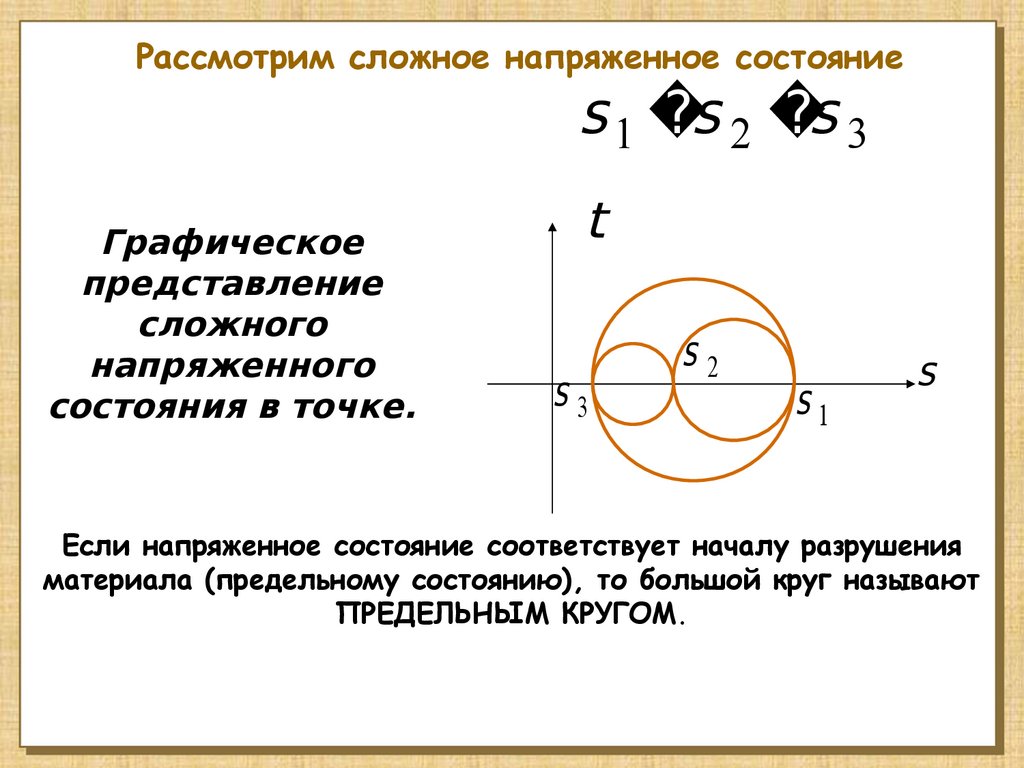
Рассмотрим сложное напряженное состояниеs 1 s 2 s 3
Графическое
представление
сложного
напряженного
состояния в точке.
t
s3
s2
s1
s
Если напряженное состояние соответствует началу разрушения
материала (предельному состоянию), то большой круг называют
ПРЕДЕЛЬНЫМ КРУГОМ.
39.
Опишем напряженное состояние с помощью кругов Мора дляосевого растяжения-сжатия
Для пластичных
материалов
Для хрупких
материалов
касательная
t
t
s
s
s 1 =s 0раст
s 3 =s 0сж
s 1 =s 0раст
40.
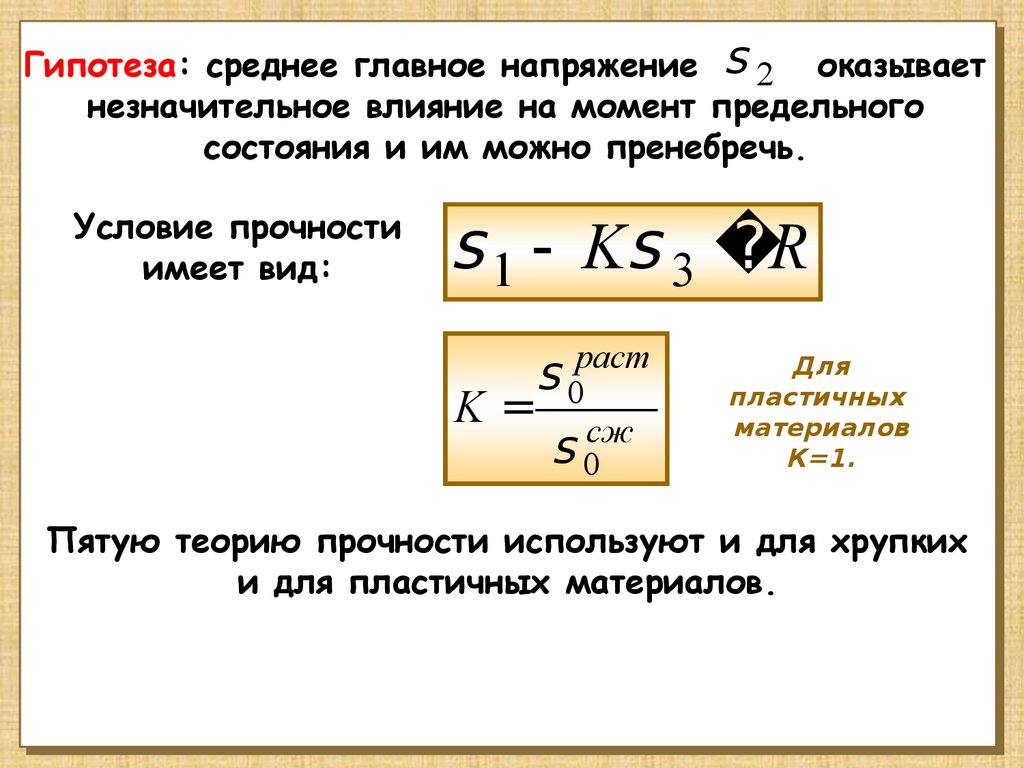
Гипотеза: среднее главное напряжение s 2 оказываетнезначительное влияние на момент предельного
состояния и им можно пренебречь.
Условие прочности
имеет вид:
s 1 - Ks 3 R
K
раст
s0
= сж
s0
Для
пластичных
материалов
К=1.
Пятую теорию прочности используют и для хрупких
и для пластичных материалов.
41.
Понятие оновых теориях
прочности
42.
КритерииКритерии прочности
прочности ии пластичности
пластичности справедливы
справедливы для
для
традиционных
традиционных конструкционных
конструкционных материалов
материалов -- однородных
однородных ии
изотропных.
изотропных.
Материал
Материал однороден,
однороден,
т.е.
т.е.
характеристики
характеристики
материала
материала во
во всех
всех
точках
точках одинаковы.
одинаковы.
Материал
Материал изотропен,
изотропен,
т.е.
т.е. обладает
обладает
одинаковыми
одинаковыми
свойствами
свойствами во
во всех
всех
направлениях.
направлениях.
ff ( ss11,,ss 22,,ss 33) =
=00
Eмодуль
-Юнга
Eмодуль
Юнга
m
m-- коэффициент
коэффициент Пуассона
Пуассона
43.
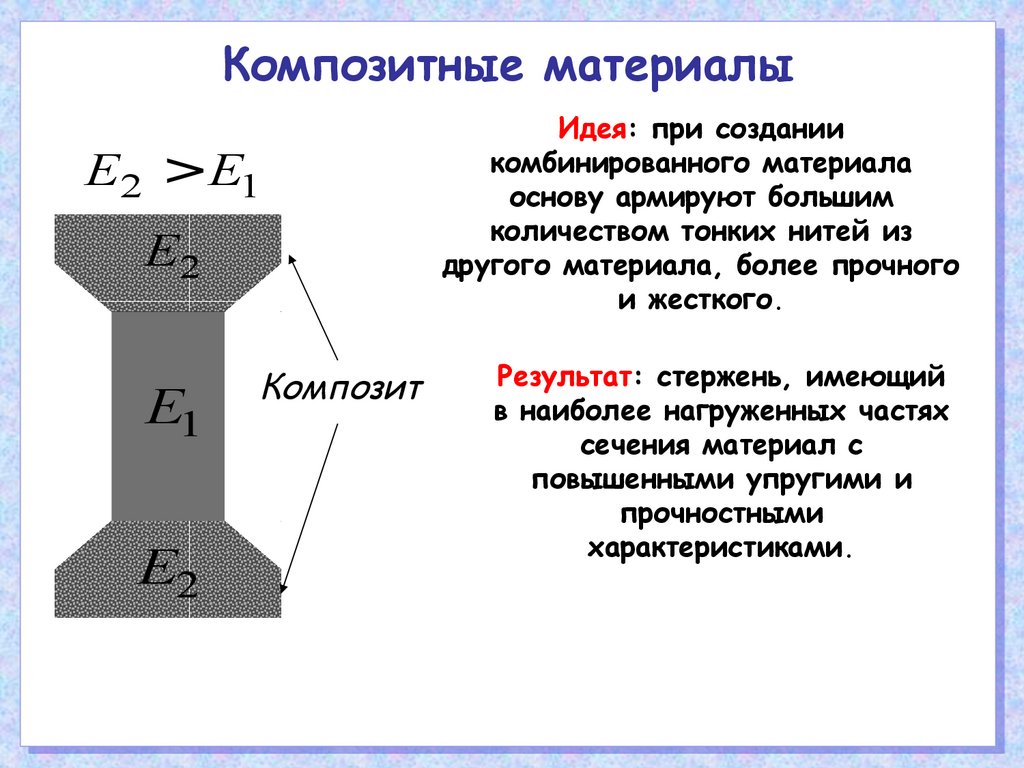
Композитные материалыE2 >E1
E2
E1
E2
Композит
Идея: при создании
комбинированного материала
основу армируют большим
количеством тонких нитей из
другого материала, более прочного
и жесткого.
Результат: стержень, имеющий
в наиболее нагруженных частях
сечения материал с
повышенными упругими и
прочностными
характеристиками.
44.
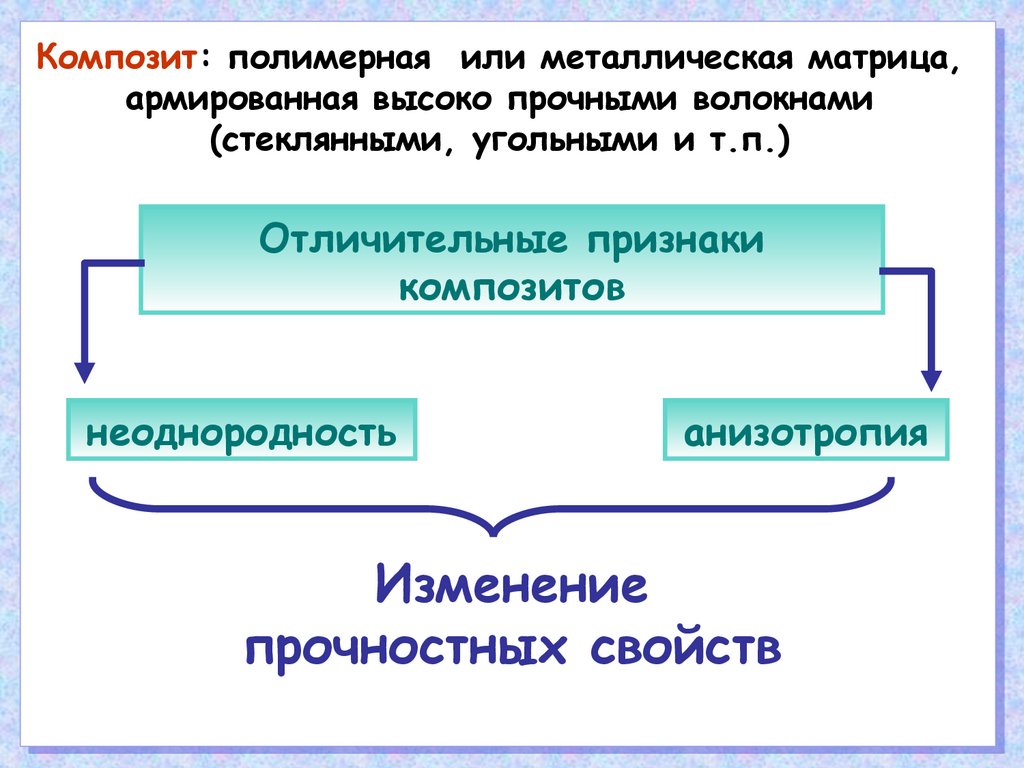
Композит: полимерная или металлическая матрица,армированная высоко прочными волокнами
(стеклянными, угольными и т.п.)
Отличительные признаки
композитов
неоднородность
анизотропия
Изменение
прочностных свойств
45.
Армирование композитаоднонаправленное
ортогональное
Симметричное в
нескольких направлениях
46.
Условие прочности для ортотропного материала(свойства в продольном и поперечном направлении
различны).
f ( s 1 ,s 2 ,s 3 , E1 , Eуглы
наклона
2,
,...) =0
Пример.
Пример.
Обобщение критерия
текучести по удельной
энергии
формоизменения в
случае плоского
напряженного
состояния:
2
2
s z t z
+ 1
s 0z
t 0z
47.
Условие прочности для полимерных материалов(
0
)
f s 1 ,s 2 ,s 3 , Ei , tвремя
(
),Т температура
(
) =0
Теории, которые учитывают изменение свойств и
деформаций с течением времени называют
теориями вязкоупругости.
Для любого материала и для любого
напряженного состояния можно
записать условие прочности.






























 mechanics
mechanics