Сложное сопротивление. Лекция 2.5.2

1.

«Прикладная механика»
раздел 2 Сопротивление материалов
Лекция 2.5.2 Сложное сопротивление.

2.

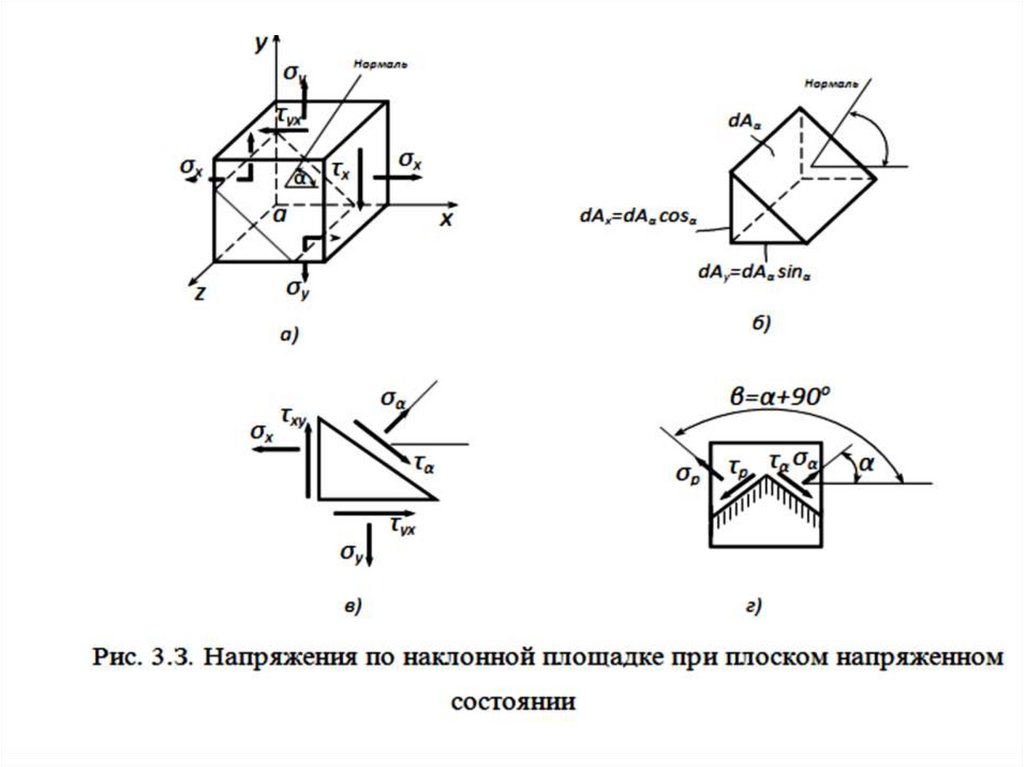
Вопрос 1. Анализ напряжённого и деформированного состояния в точке тела
Компоненты напряжений в точке. Если твердое тело нагружено системой сил,
то через любую его точку можно провести бесчисленное множество различно
ориентированных площадок, по которым действуют нормальные и
касательные напряжения. Совокупность напряжений, действующих на этих
площадках, характеризует напряженное состояние в данной точке.
Исследование напряженного состояния в теле связано с получением
зависимостей, позволяющих определить напряжения по любой площадке в
любой точке тела.
В теле, нагруженном произвольной системой сил (рис. 3.1, а) выделим в
окрестности некоторой точки элементарный объем в виде параллелепипеда, по
граням которого действуют внутренние силы, заменяющие действие
отброшенных частей тела (рис. 3.1, б).
Полное напряжение, возникающее на гранях элемента, можно разложить на
три составляющие. В обозначении нормального напряжения индекс указывает
ось, параллельно которой оно направлено. В обозначении касательного
напряжения два индекса: первый показывает, к какой оси перпендикулярна
площадка, на которой действует напряжение, второй — направление действия
напряжения.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

Вопрос 2. Сложное сопротивление.
В общем случае нагрузка на брус может быть такой, что в его поперечных сечениях
возникает одновременно несколько внутренних силовых факторов (поперечная и
продольная силы, изгибающий и крутящий моменты). Такой случай принято называть
сложным сопротивлением бруса.
Расчеты на прочность и жесткость бруса при сложном сопротивлении основываются
обычно на принципе независимости действия сил. Опыт показывает, что, пока
деформации малы, этот принцип может быть использован. Поэтому для определения
полных напряжений и деформаций, возникающих в упругой системе в результате
действия на нее любой системы нагрузок, можно геометрически суммировать
напряжения и перемещения, соответствующие различным видам простейших
деформаций.
При простом напряженном состоянии элемента все напряжения одного вида (например,
нормальные) суммируют алгебраически, а при сложном напряженном состоянии (имеют
место и нормальные, и касательные напряжения) используют различные теории
прочности.
Необходимо отметить, что в некоторых случаях расчета деталей можно пренебречь
второстепенными деформациями и привести, таким образом, сложное сопротивление к
более простому.
При расчете на жесткость определяют в общем виде деформацию от каждого силового
фактора и, найдя суммарную деформацию, оценивают жесткость элемента.

16.

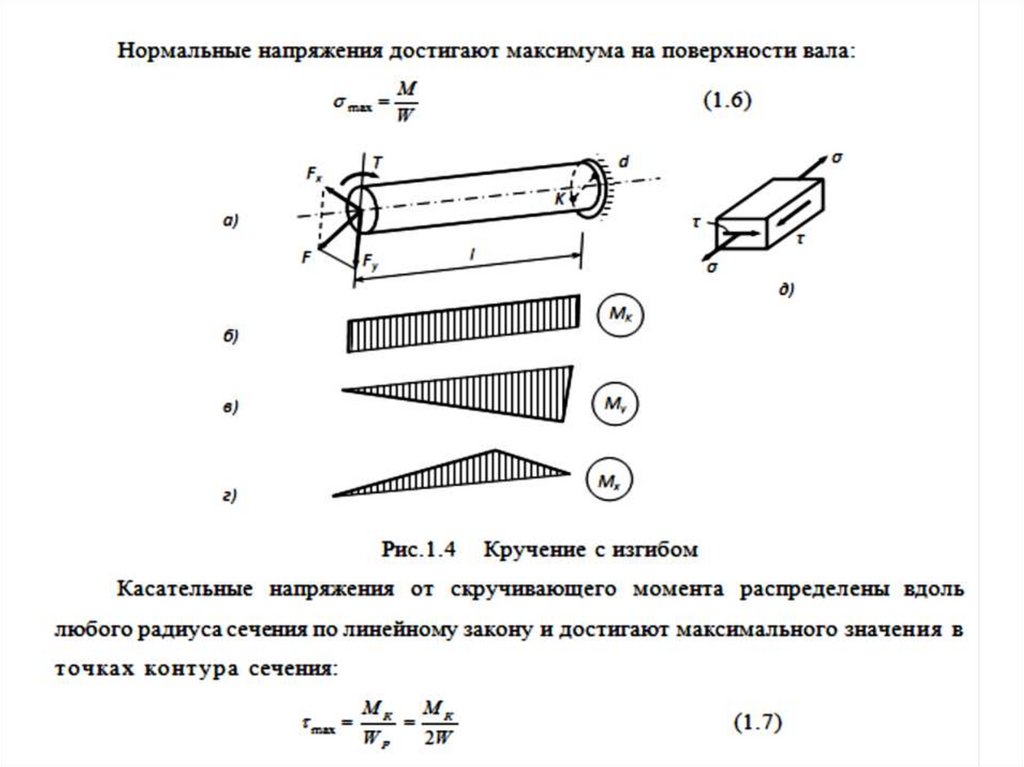
Изгиб с растяжением (сжатием). При таком виде сложного сопротивления
внутренние силы в сечении приводятся только к продольной силе N и изгибающему
моменту М, вызывающему либо плоский, либо косой изгиб.
На рис. 1.2 показан случай центрального растяжения бруса в сочетании с косым
изгибом. На консоль действует сила F, составляющая некоторый угол с продольной
осью бруса и не лежащая ни в одной из главных плоскостей инерции сечения. Сила
приложена в центре тяжести торцевого сечения бруса.
Разложим силу F на три составляющие. В данном случае положение опасного
сечения очевидно, и нет необходимости строить эпюры внутренних силовых
факторов. Напряжение в произвольно выбранной точке В с координатами х, у, если
пренебречь действием поперечных сил,

17.

18.

19.

20.

21.

22.

23.

24.

Вывод: В рассмотренном вопросе мы узнали, какой вид
деформации называется сложным сопротивлением. Выяснили,
что косой изгиб имеет место быть, когда плоскость действия
изгибающего момента не совпадает ни с одной из главных
плоскостей инерции сечения бруса. Узнали, что при изгибе с
растяжением (сжатием) внутренние силы в сечении приводятся
только к продольной силе N и изгибающему моменту М,
вызывающему либо плоский, либо косой изгиб. Узнали, что
касательные напряжения от скручивающего момента
распределены вдоль любого радиуса сечения по линейному
закону и достигают максимального значения в точках контура
сечения.

25.

26.

27.

28.

29.

30.

31.

Вопрос 4. Расчёт по теориям прочности
Теории предельных состояний. Предельное напряженное состояние тела
характеризуется началом текучести материала, значительными остаточными
деформациями или появлением трещин, свидетельствующих о начале его
разрушения.
Оценка прочности детали по напряженному состоянию в опасной точке
поперечного сечения является важной задачей сопротивления материалов.
При простейших напряженных состояниях детали, характеризуемых только
одним главным напряжением (растяжение, сжатие) или только касательным
напряжением (чистый сдвиг), оценку ее прочности осуществляют
сравнением действующих в ней напряжений с результатами опытов по
разрушению образцов в лабораторных условиях при таком же напряженном
состоянии.
Большинство деталей при эксплуатации испытывают либо плоское, либо
объемное напряженное состояние. Как показывают исследования, прочность
материала при сложном напряженном состоянии зависит не только от
значений главных напряжений, но и от их соотношения. Из-за
неограниченности вариаций такого соотношения экспериментальное
изучение предельного (опасного) состояния детали при сложном
напряженном состоянии практически невозможно.

32.

Теории предельных состояний используют для определения
условий прочности материала при сложном напряженном
состоянии на основании экспериментальных данных,
полученных при простых видах нагружения: растяжении, сжатии,
чистом сдвиге. Некоторые из этих гипотез (теорий) связывают
прочность материала с нормальными напряжениями, другие —
с касательными напряжениями или с энергией деформации.
Суть их состоит в том, что, определив главную причину
разрушения материала, можно найти эквивалентное
напряжение при сложном напряженном состоянии и составить
условие прочности материала.
Эквивалентное напряжение — это напряжение, которое
следует создать в растянутом образце, чтобы его напряженное
состояние было равноопасно с заданным.

33.

34.

35.

36.

37.

По современным представлениям любой тип разрушения характеризуется
зарождением и образованием микротрещин, их дальнейшим распространением,
приводящим к разрушению тела.
Существование микротрещин в объеме материала обусловлено разными
причинами. Особенно опасными являются трещины в поверхностных слоях
деталей, так как чаще всего на их поверхности и возникают максимальные
напряжения от внешней нагрузки. В то же время наличие микротрещин в объеме
детали не всегда приводит к ее разрушению. Только при определенных условиях
нагружения трещина получает развитие.
Энергия, затраченная на образование и распространение трещины, определяет тип
разрушения. При хрупком разрушении материала эта энергия возрастает до
критической. В критическом состоянии материала трещины распространяются без
дополнительных затрат энергии, происходит внезапное разрушение детали
(конструкции). При пластическом же разрушении имеет место постоянный прирост
энергии до конца разрушения тела.
Понятие о теоретической прочности материалов. Реальная прочность материалов
значительно ниже теоретической, установленной исходя из условий разрушения
идеальной кристаллической решетки. Полагают, что теоретическая прочность
материала при действии на него внешних нагрузок определяется силами связи
между атомами идеальной кристаллической решетки, препятствующими отрыву
или сдвигу одной плоскости атомов относительно другой. Различие между
теоретической и реальной прочностью материалов объясняется наличием
дефектов кристаллической решетки в реальных материалах.

38.

Дефекты структуры материала являются концентраторами
напряжений, способствующими возникновению микротрещин,
которые, развиваясь при росте нагрузки, приводят к разрушению
детали. В пластичных материалах концентрация напряжений
приводит к возникновению пластической деформации в
микрообъемах материала, а затем к ее распространению по всему
его объему.
Вывод: В рассмотренном вопросе мы выяснили, что теории
предельных состояний используют для определения условий
прочности материала при сложном напряженном состоянии на
основании экспериментальных данных, полученных при простых
видах нагружения: растяжении, сжатии, чистом сдвиге. Узнали о
четырех основных теориях прочности, и о теории Мора, которая по
существу является обобщенной теорией: она учитывает влияние на
процесс разрушения и касательных, и нормальных напряжений.