Начертательная геометрия. Лекция 1

1. Начертательная геометрия

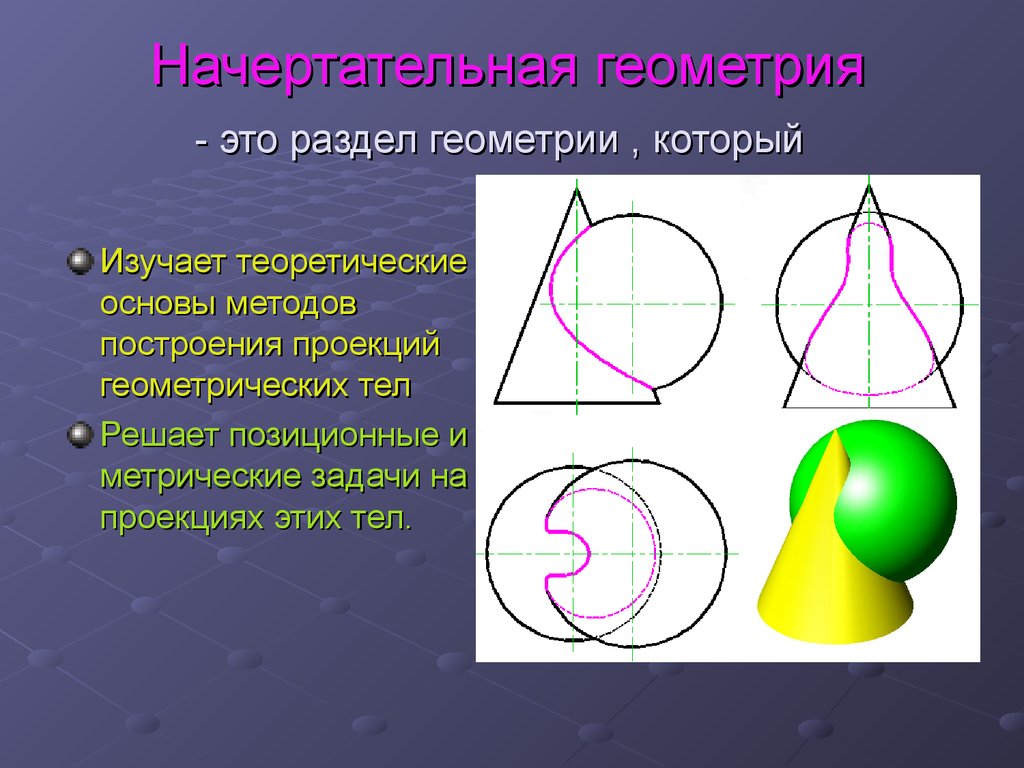
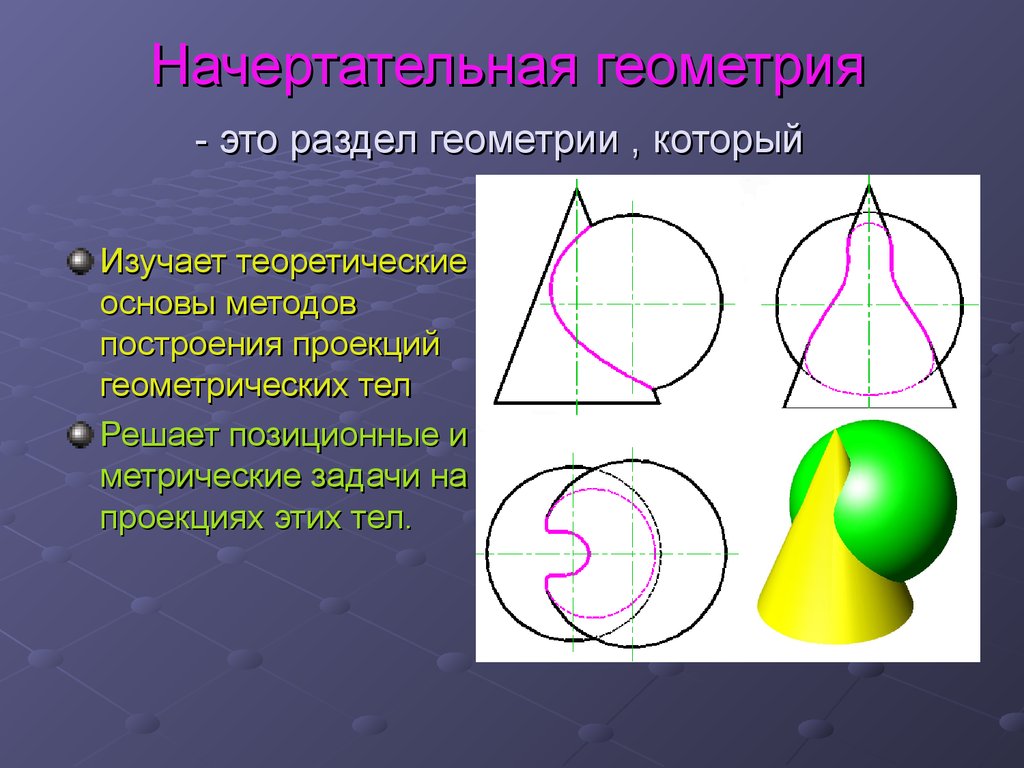
Лекция 1

2. Начертательная геометрия - это раздел геометрии , который

Изучает теоретические
основы методов
построения проекций
геометрических тел
Решает позиционные и
метрические задачи на
проекциях этих тел.

3. Основные понятия

Точка - не имеет размеров, является
результатом пересечения двух прямых или
трех плоскостей (вершина тетраэдра)
Прямая – имеет одно измерение, является
результатом пересечения двух плоскостей
Плоскость – имеет два измерения.
Геометрическая фигура – определяется как
любое множество точек.

4. Обозначения

Ф,Г,∆,∑ А,В,С Поверхности Точки
П1 П2 П3 Плоскости
проекций
а,b,с,d – α,β, γ Линии
Углы
А1,а1,Ф1 – А2,а2,Ф2 – А3,а3,Ф3 –
проекции
точки,
прямой,
поверхности
на П1
проекции
точки,
прямой,
поверхности
на П2
проекции
точки,
прямой,
поверхности
на П3

5. Символы

(АВ) – прямая,
проходящая через
точки А и В
[AB] – отрезок прямой
IADI – расстояние
между точками А и
D
- принадлежность
элемента
- включение
II - параллельные
┴ - перпендикулярные
• - скрещивающиеся
= - результат
построения
- «И»
- если…, то….
- пересечение

6. Начертательная геометрия - это раздел геометрии , который

Изучает теоретические
основы методов
построения проекций
геометрических тел
Решает позиционные и
метрические задачи на
проекциях этих тел.

7. Задачи начертательной геометрии

Прямая задача – создание плоского
чертежа объекта
Обратная задача – возможность по
плоскому чертежу восстановить
пространственный вид объекта

8. Центральное проецирование

S
П
П

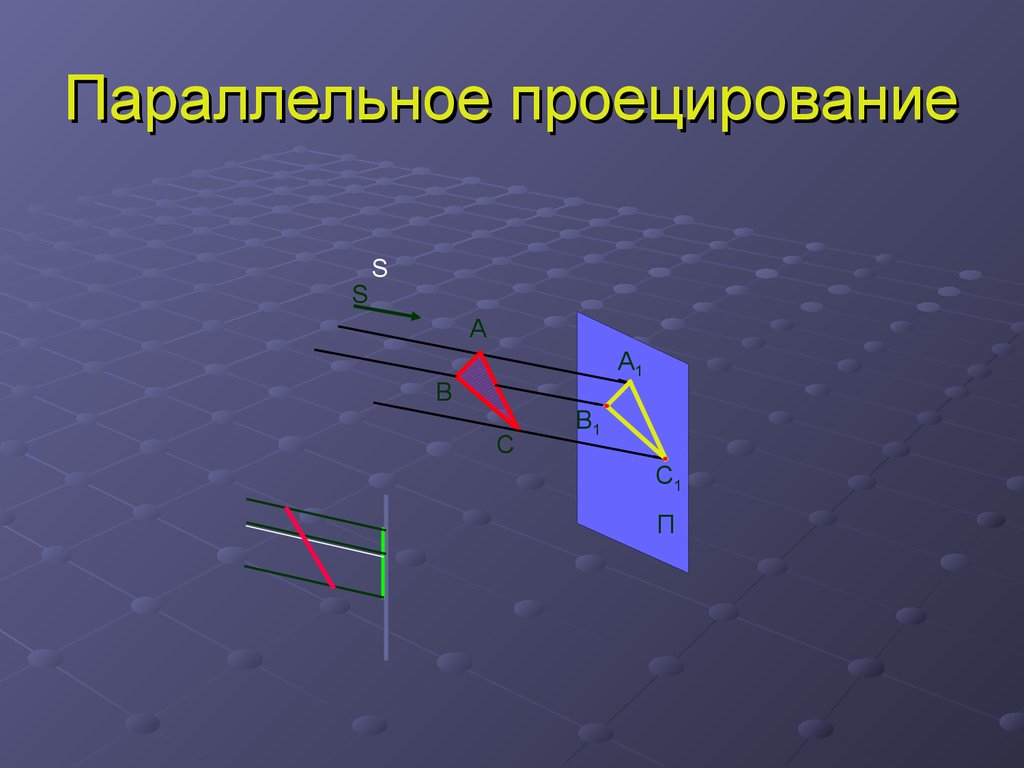
9. Параллельное проецирование

S
S
А
Ï
А1
В
'
'
С
В1
'
С1
П

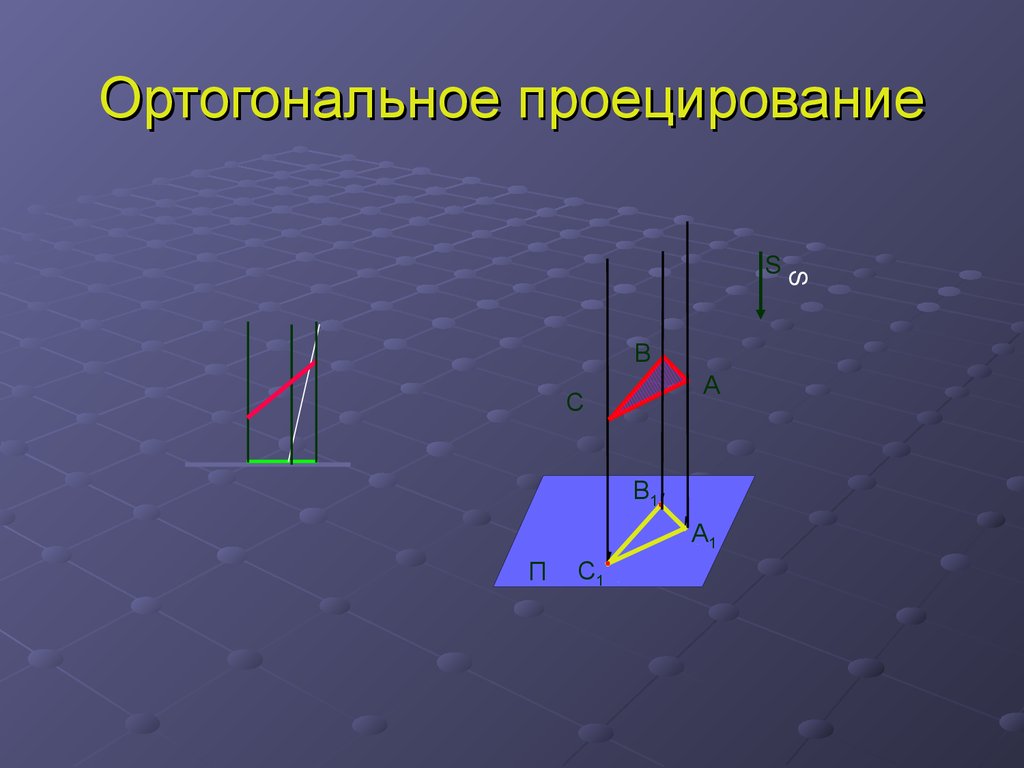
10. Ортогональное проецирование

В
А
С
Ï
В1
'
'
А1
С1
'
П
S
S

11. Свойства ортогонального и параллельного проецирования

1. Проекция точки на плоскость есть
точка
А
А1
А
А1

12. Проекция прямой в общем случае является прямая. Она вырождается в точку, если прямая параллельна направлению проецирования l l1

2.
Проекция прямой в общем случае
является прямая. Она вырождается в
точку, если прямая параллельна
направлению проецирования
l
l1
l
l
l1
l1

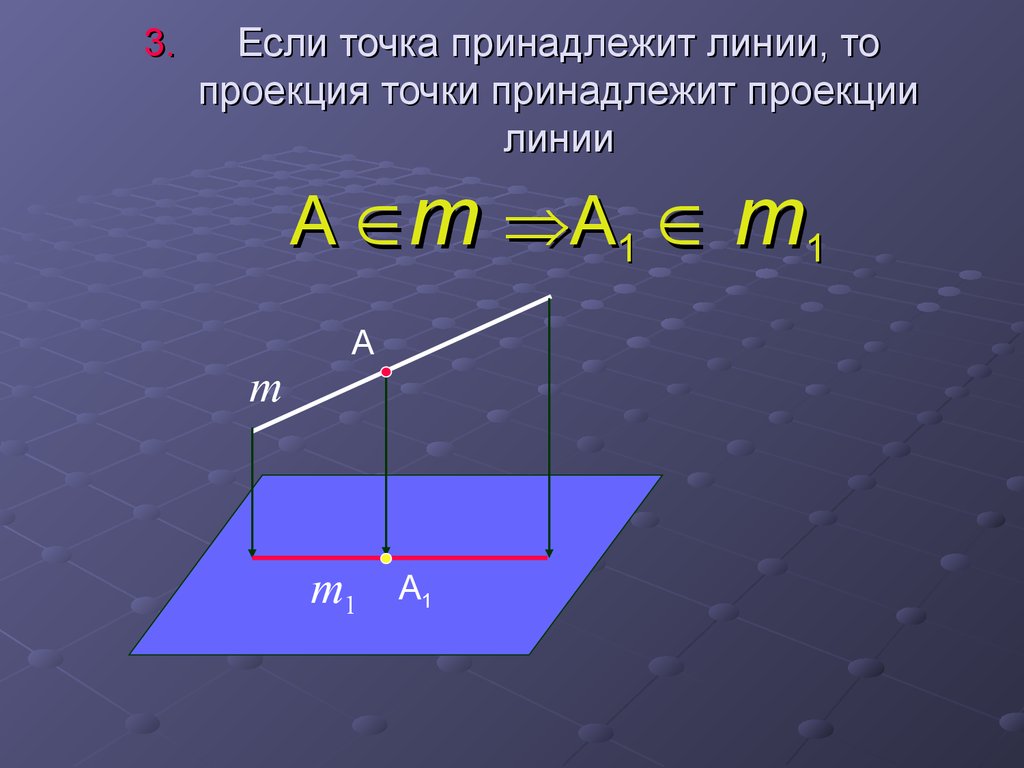
13. Если точка принадлежит линии, то проекция точки принадлежит проекции линии A m A1  m1

3.
Если точка принадлежит линии, то
проекция точки принадлежит проекции
линии
A m A1 m1
m
A
m1
A1

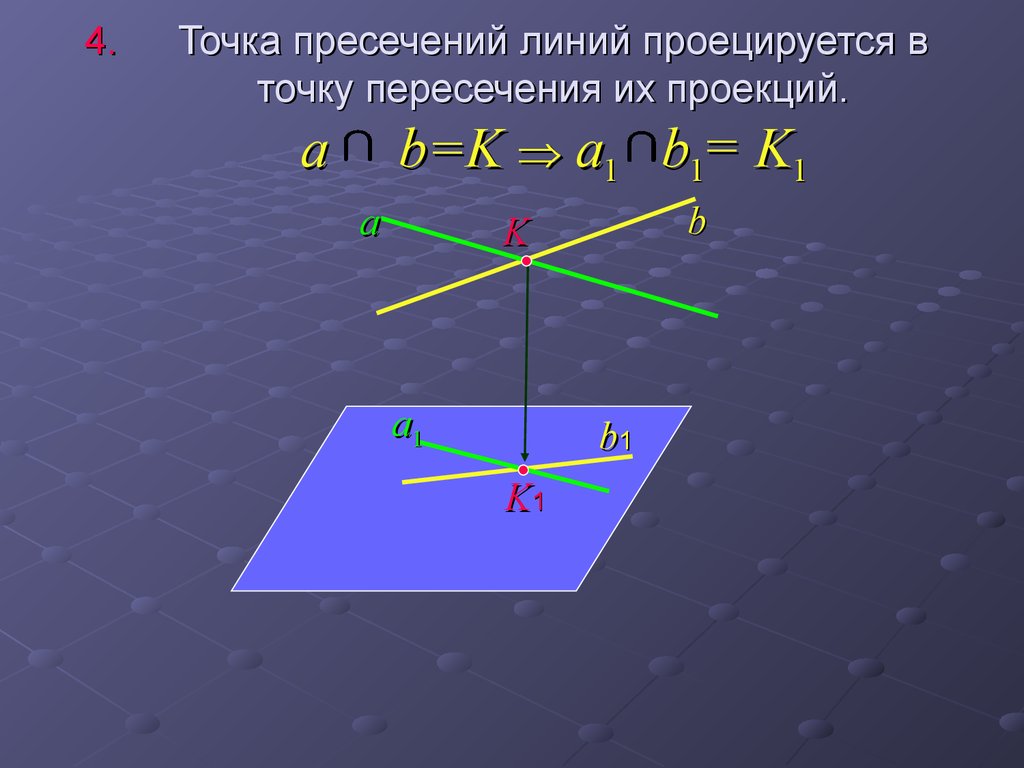
14. Точка пресечений линий проецируется в точку пересечения их проекций. a b=K  a1 b1= K1

4.
Точка пресечений линий проецируется в
точку пересечения их проекций.
a
b=K a1 b1= K1
a
b
K
a1
b1
K1

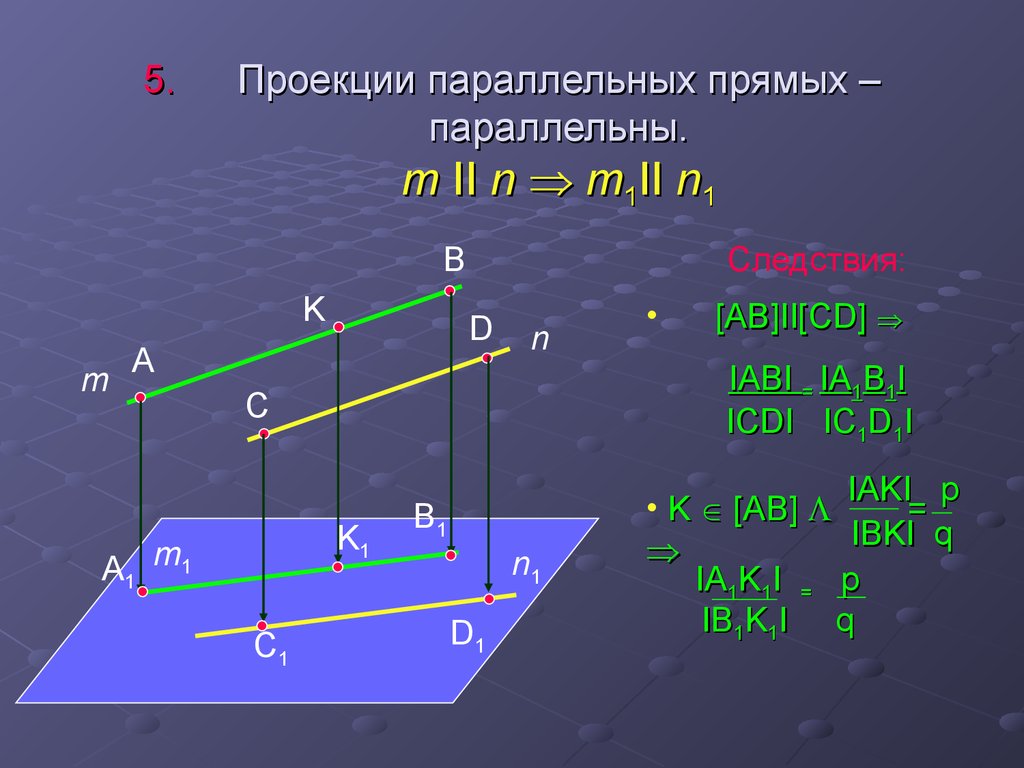
15. Проекции параллельных прямых – параллельны. m II n  m1II n1

5.
Проекции параллельных прямых –
параллельны.
m II n m1II n1
B
K
m
Следствия:
D
A
n
K1
C1
[AB]II[CD]
IABI = IA1B1I
ICDI IC1D1I
C
A1 m1
B1
n1
D1
IAKI p
• K [AB]
=
IBKI q
IA1K1I = p
IB1K1I q

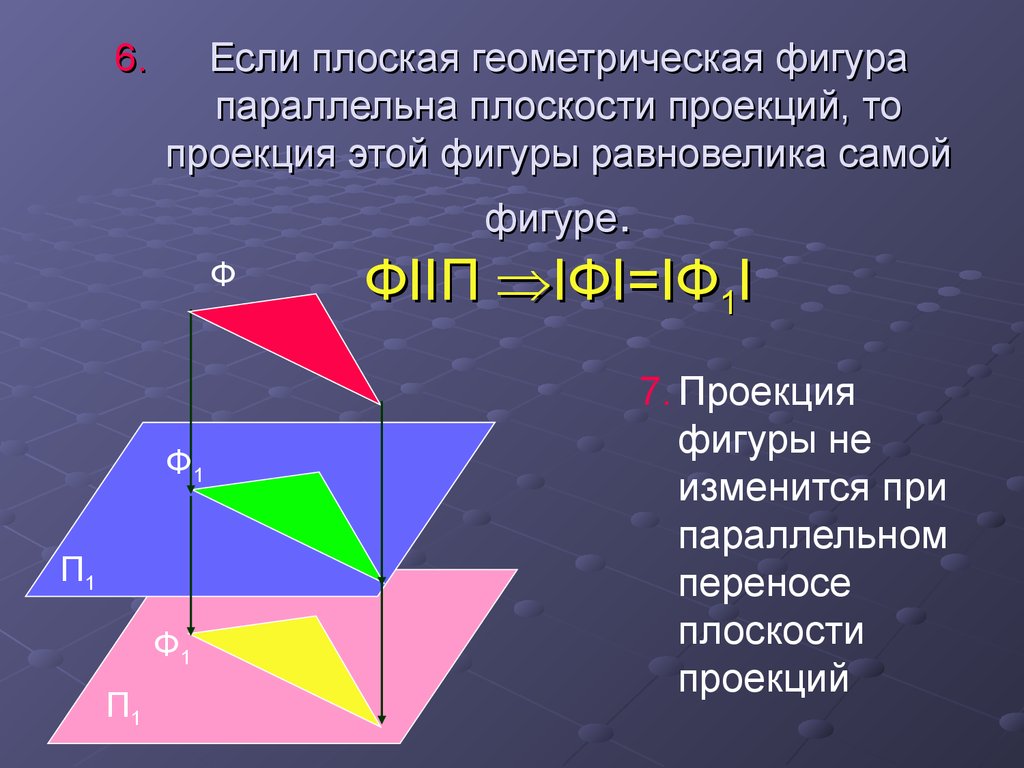
16. Если плоская геометрическая фигура параллельна плоскости проекций, то проекция этой фигуры равновелика самой фигуре. ФIIП IФI=IФ1I

6.
Если плоская геометрическая фигура
параллельна плоскости проекций, то
проекция этой фигуры равновелика самой
фигуре.
Ф
Ф1
П1
Ф1
П1
ФIIП IФI=IФ1I
7. Проекция
фигуры не
изменится при
параллельном
переносе
плоскости
проекций