Similar presentations:
адача нелинейного программирования. Условная оптимизация. Метод проекции градиента
1. Задача нелинейного программирования. Условная оптимизация. Метод проекции градиента
2. Метод проекции градиента
max f X x x 2 x1 4 x2max f X
x1 2 x2 2
A0 X b0
x1 x2 4
1 2
2
x 0
1 1
4
1
b0
x2 0
A0
1 0
0
0 1
0
2 x1 2
2 0
f X
H
0 2
2 x2 4
2
1
2
2
3. Шаг 1. Выбор направления
0X0
0
2
4
A0 X 0 b0
0
Активные ограничения
0
1 0
A
0 1
1 0 2 2 <0
A f X 0
0 1 4 4 <0
2
0
K f X 0
4
Допустимо
градиентное
направление
4. Шаг 1. Определение длины шага
A0 K0
1 2
6
1 1 2 6
1 0 4 2
0 1
4
Ограничения, которые
нарушаются при
движении в выбранном
направлении
Длина шага до нарушаемых ограничений:
0
bk ak X i
2 1 2
tk
i
0 1
0 b1 a1 X 0
ak K
t1
0
i
t2
0
2
a1K
1 2
0
4
4 1 1
0 2
b2 a2 X 0
0
3
2
a2 K
1 1
4
3
5. Шаг 1. Определение длины шага
Максимально возможная длина шага:i
t*
0
t*
f Xi K
T
i
H Xi K
2
2 4
4
1
2 0 2 2
2 4
4
0
2
K
i T
i
Итоговая длина шага:
t
0
0 0 0
min t* , t1 , t2
1 1 2 1
min , ,
2 3 3 3
6. Шаг 1. Координаты новой точки
0X1 X 0 t K
0
0 1 2 2 / 3
0 3 4 4 / 3
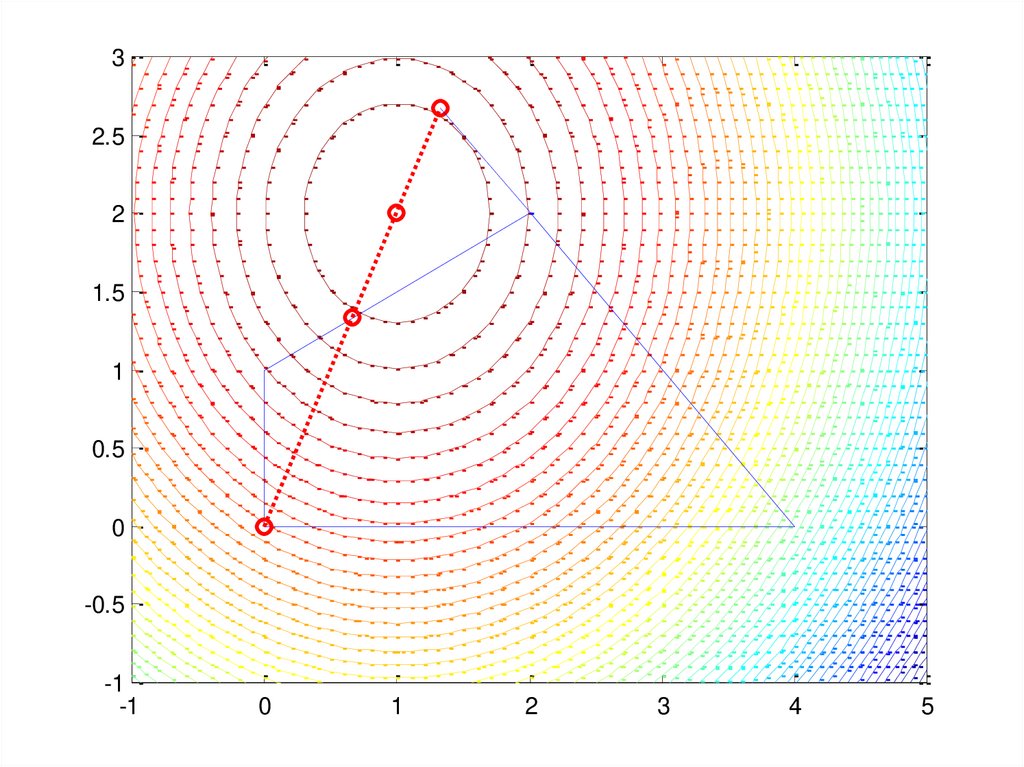
7.
32.5
2
1.5
1
0.5
0
-0.5
-1
-1
0
1
2
3
4
5
8. Шаг 2. Выбор направления
2 x1 2 2 / 3 2 / 32 / 3
f X 1
X1
2
x
4
4
/
3
4
/
3
2
4 / 3
1 2
2 0 Активные
1 1 2 / 3 4 2 ограничения
A0 X 1 b0
1 0 4 / 3 0 2 / 3
A 1 2
0 1
0 4 / 3
2 / 3
A f X 1 1 2
2
4 / 3
>0
Не допустимо
градиентное
направление
9. Шаг 2. Выбор направления
Оператор проекции:P E A
T
AA
T
1
A
1 0 1
1
P
1 2
0 1 2
2
K
1
1
4/ 5 2/ 5
1 2
2/
5
1/
5
4 / 5 2 / 5 2 / 3 16 /15
P f X 1
2
/
5
1/
5
4
/
3
8/15
10. Шаг 2. Определение длины шага
A0 K1
1 2
0
1 1 16 /15 24 /15 Нарушаемые
ограничения
1 0 8/15 16 /15
0 1
8/15
Длина шага
до нарушаемых
ограничений:
1
t2
Максимально возможная
длина шага:
2 / 3
4 1 1
4
/
3
5
16 /15 4
1 1
8/15
1
t
1
t*
1 1
min t* , t2
1
2
1 5 1
min ,
2 4 2
11. Шаг 2. Координаты новой точки
1X 2 X1 t K
1
2 / 3 1 16 /15 6 / 5
4 / 3 2 8/15 8/ 5
12.
32.5
2
1.5
1
0.5
0
-0.5
-1
-1
0
1
2
3
4
5
13. Шаг 3. Выбор направления
2 x1 2 6 / 5 2 / 56 / 5
f X 2
X2
2
x
4
8/
5
4
/
5
2
8/ 5
1 2
2 0 Активные
1 1 6 / 5 4 6 / 5 ограничения
A0 X 2 b0
1 0 8/ 5 0 6 / 5
A 1 2
0 1
0 8/ 5
2 / 5
A f X 2 1 2
2 >0
4/5
Не допустимо
градиентное
направление
14. Шаг 3. Выбор направления
Оператор проекции:1 0 1
1
P
1 2
0 1 2
2
K
2
1
4/ 5 2/ 5
1 2
2/
5
1/
5
4 / 5 2 / 5 2 / 5 0
P f X 2
2 / 5 1/ 5 4 / 5 0
Подозрение на
оптимальность
15. Шаг 3. Проверка останова
AAT
1
A f X 2
1
1 2
2
1
2 / 5
2
<0
1 2
5
4/5
Точка
оптимальна
6 / 5
X
8/ 5
*
16.
32.5
2
1.5
1
0.5
0
-0.5
-1
-1
0
1
2
3
4
5















 programming
programming








