Апертурные искажения. Форма и функция прозрачности развертывающего элемента

1. АПЕРТУРНЫЕ ИСКАЖЕНИЯ

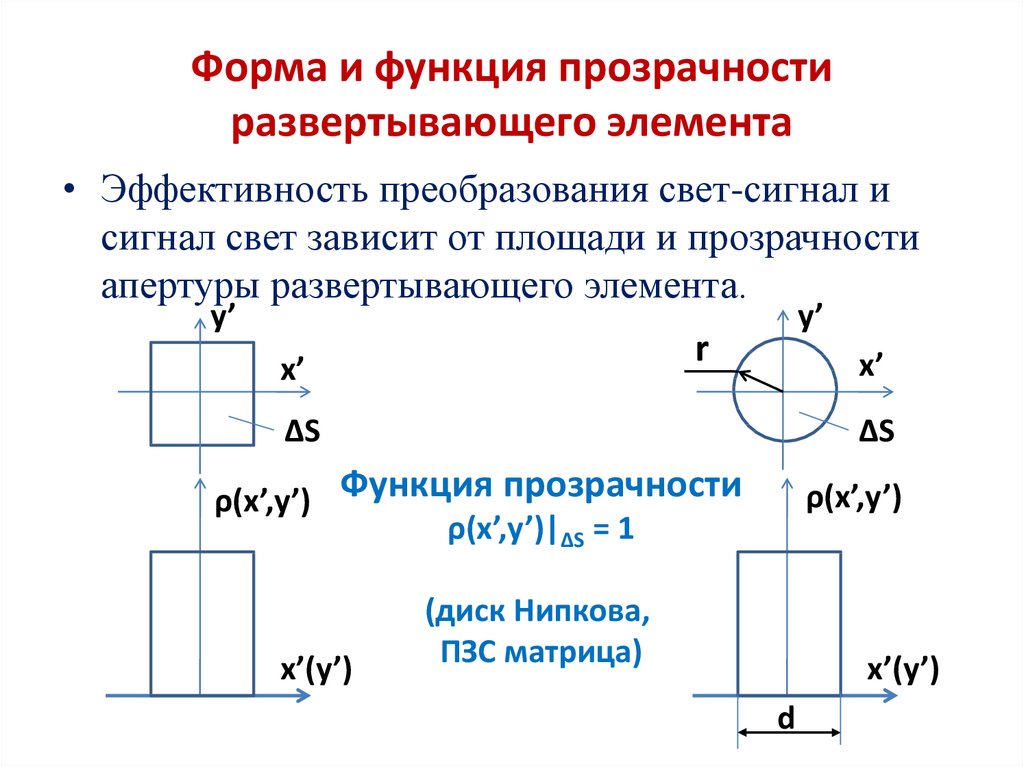
2. Форма и функция прозрачности развертывающего элемента

• Эффективность преобразования свет-сигнал и
сигнал свет зависит от площади и прозрачности
апертуры развертывающего элемента.
y’
y’
r
x’
x’
ΔS
ΔS
ρ(x’,y’) Функция прозрачности
ρ(x’,y’)|ΔS = 1
x’(y’)
ρ(x’,y’)
(диск Нипкова,
ПЗС матрица)
x’(y’)
d

3. Функция прозрачности для электронно-лучевых ФЭП

2
2
x' y '
( x' , y ' ) exp
y’
re re
x’
re – эффективный радиус
1
ρ(x’,y’)
1/e
-re 0 re
Апертурные искажения – искажения,
обусловленные конечными размерами
апертуры и формой функции прозрачности.
Различают
x’(y’) апертурно-временные и
апертурно-частотные искажения.

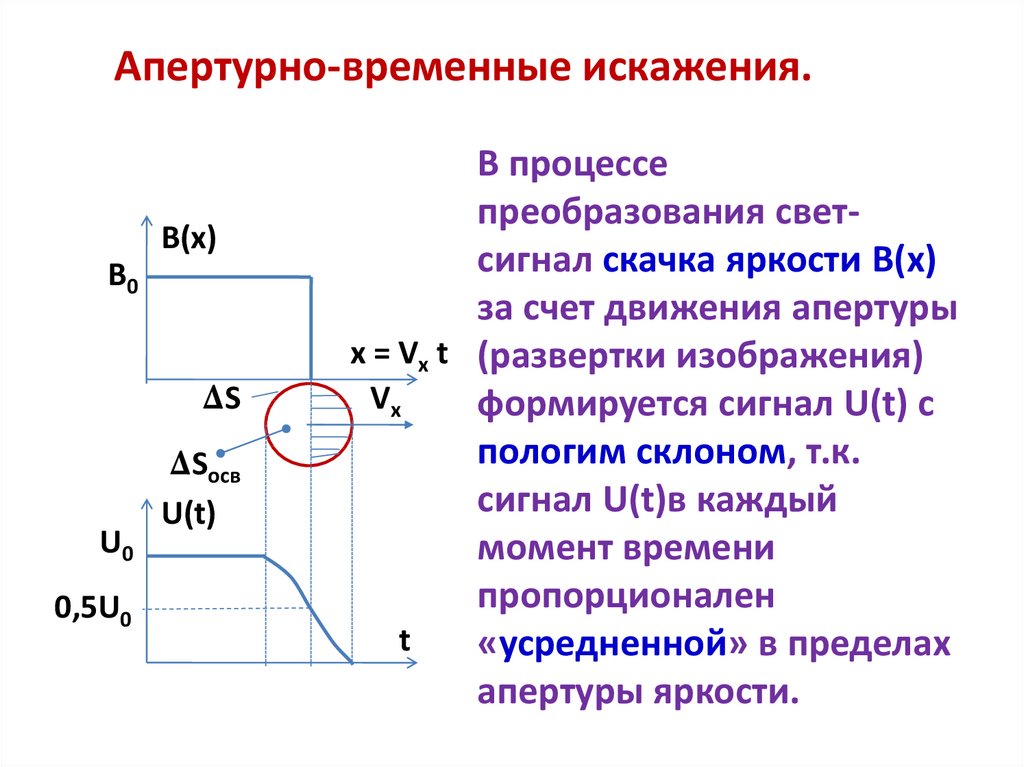
4. Апертурно-временные искажения.

B(x)
B0
ΔS
U0
0,5U0
ΔSосв
U(t)
В процессе
преобразования светсигнал скачка яркости B(x)
за счет движения апертуры
x = Vx t (развертки изображения)
Vx
формируется сигнал U(t) c
пологим склоном, т.к.
сигнал U(t)в каждый
момент времени
пропорционален
t
«усредненной» в пределах
апертуры яркости.

5. Апертурно-временная (переходная) характеристика.

x
0
E(x,y)
y
y
ΔS
E(x,y) = dF/dS – освещенность мишени ФЭП
x
dF = EdS = EdS(x+x`,y+y`)dx`dy` – световой
поток, падающий на dS апертуры.
x’
y’
dS = dx’dy’
x’
dF
y’
ρ(x’, y’) прозрачность
апертуры
dF’
dF` = ρ(x`,y`)dF –световой поток,
прошедший через dS апертуры.
Составляющая фототока, вызванная
световым потоком dF`: di = εdF`,
Тогда, ток ФЭП определяется выражением
i EdS ( x x' , y y ' ) ( x' , y ' )dx' dy'
S

6.

• Пусть E = E0 = const (освещенность постоянна).
Тогда ток на выходе ФЭП также постоянен:
i0 E0 ( x' , y ' )dx' dy ' E0 P0
S
P0 – интегральная прозрачность
• При скачке освещенности в направлении x ток ФЭП
определяется освещенной частью апертуры:
E0 E(x)
-rx’
x’
x
x
ΔSосв
i ( x) E0
y’
rx’
( x' , y' )dx' dy' E P( x)
0
S о св
P(x) – интегральная прозрачность освещенной части апертуры.

7.

• Переходная характеристика:
H(x) = i(x)/i0 = P(x)/P0
• Распределение прозрачности в сечении x’ = cons
rx '
R( x' )
( x' , y' )dy'
rx '
r
• Тогда
P( x)
R( x' )dx',
rx '
r
P0 R( x' )dx'
r
И учитывая симметрию апертуры получаем:
x
1
2
H ( x) P( x) / P0 1 R( x' )dx'
2 P0 0

8.

• Для нормальной ТВ системы с квадратной
апертурой: ρ(x`,y`) = 1 в пределах квадрата.
• Тогда площадь сечения функции прозрачности
R(x`) = d, а интегральная прозрачность P0 = d2 .
• Учитывая, что
получаем
x
x
0
0
R( x' )dx' d dx' d x,
1
x
H ( x) (1 2 )
2
d
Так как x= vt, d = vτ, то
1
t
h(t ) (1 2 )
2
(при
r x r)
(при / 2 t / 2)

9.

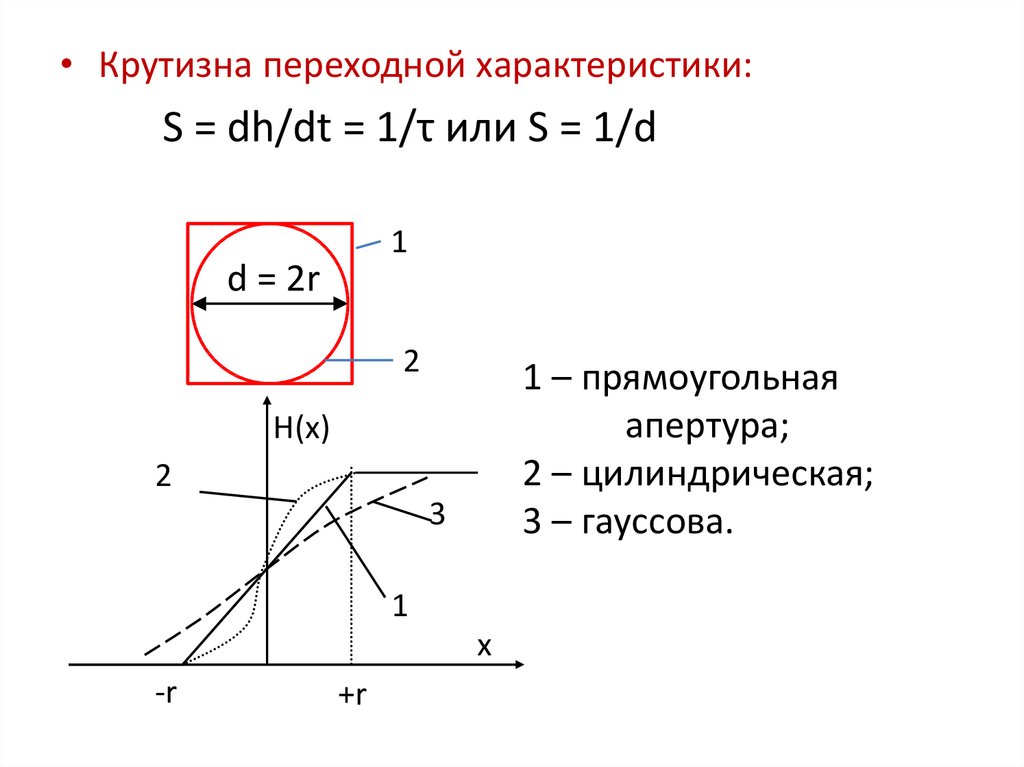
• Крутизна переходной характеристики:
S = dh/dt = 1/τ или S = 1/d
1
d = 2r
2
1 – прямоугольная
апертура;
2 – цилиндрическая;
3 – гауссова.
H(x)
2
3
1
x
-r
+r

10. Апертурно-частотная характеристика ФЭП

B(x)
Bmax
Vx
Bmin

11.

d – размер развертывающей апертуры;
Xi = 2di – переменный шаг штриховой миры;
νi = 1/Xi – пространственная частота миры;
Глубина модуляции видеосигнала
imax imin
M
imax imin
• Если изображение представляет собой
вертикальную штриховую миру с переменным
шагом, то при увеличении пространственной
частоты миры увеличивается частота сигнала и
уменьшается глубина модуляции М (при Xi/2 <d).

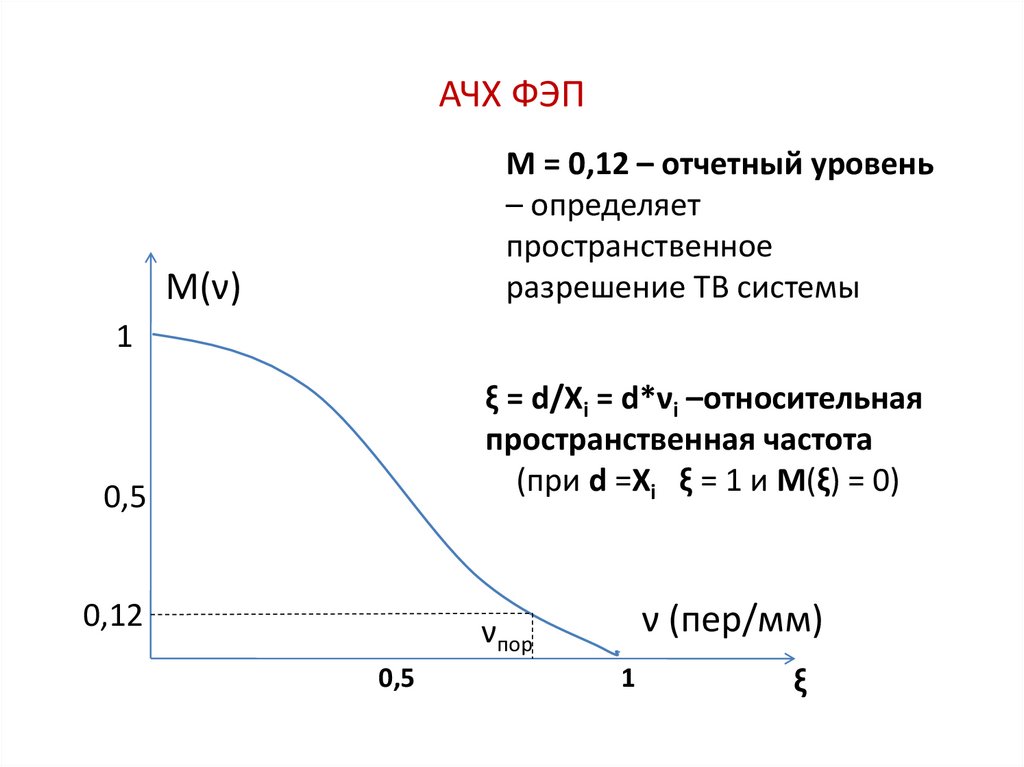
12. АЧХ ФЭП

М = 0,12 – отчетный уровень
– определяет
пространственное
разрешение ТВ системы
М(ν)
1
ξ = d/Xi = d*νi –относительная
пространственная частота
(при d =Xi ξ = 1 и M(ξ) = 0)
0,5
0,12
ν (пер/мм)
νпор
0,5
1
ξ

13.

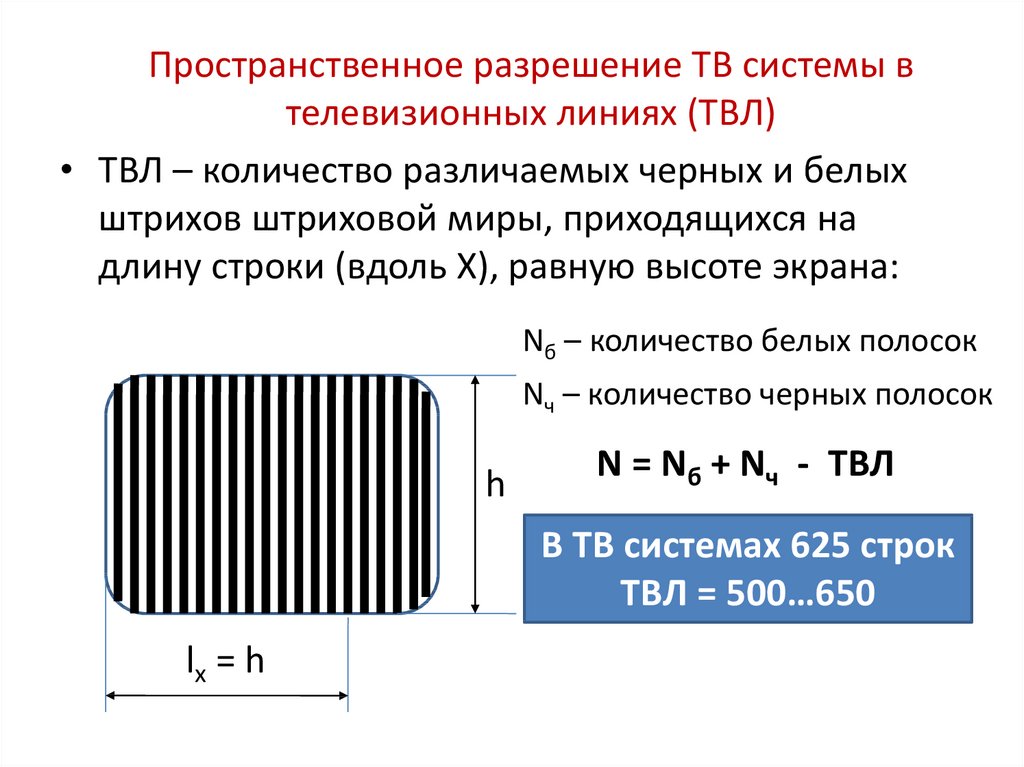
Пространственное разрешение ТВ системы в
телевизионных линиях (ТВЛ)
• ТВЛ – количество различаемых черных и белых
штрихов штриховой миры, приходящихся на
длину строки (вдоль X), равную высоте экрана:
Nб – количество белых полосок
Nч – количество черных полосок
h
N = Nб + Nч - ТВЛ
В ТВ системах 625 строк
ТВЛ = 500…650
lx = h

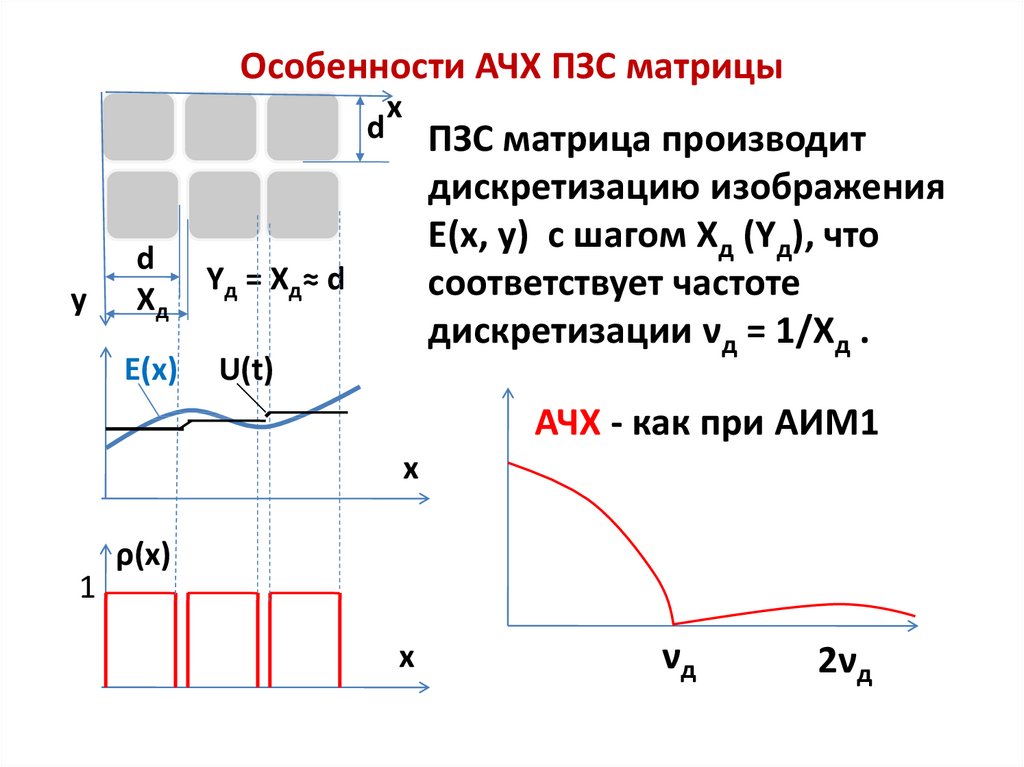
14. Особенности АЧХ ПЗС матрицы

d
y
d
Xд
E(x)
x
ПЗС матрица производит
дискретизацию изображения
E(x, y) с шагом Xд (Yд), что
соответствует частоте
дискретизации νд = 1/Xд .
Yд = Xд≈ d
U(t)
АЧХ - как при АИМ1
x
1
ρ(x)
x
νд
2νд