Similar presentations:
Прямолинейное равноускоренное движение
1. Прямолинейное равноускоренное движение
12. Равноускоренное движение
• Равноускоренным называется такоедвижение, при котором за любые равные
промежутки времени мгновенная скорость
тела изменяется одинаково.
Для любого ∆t₁ = ∆t₂; ∆v₁ = ∆v₂.
• Изменение мгновенной скорости:
∆v = v - v₀.
2
3. Ускорение
• Ускорение – физическая величина,численно равная отношению изменения
мгновенной скорости тела при
равноускоренном движении к промежутку
времени, за которое это изменение
произошло.
v
a ;
t
v v0
или a
; a v .
t
3
4. Единицы измерения
• Единица ускорения – 1 метр в секундуза секунду – 1 м/с2.
м
м
a 1 2 , если за t 1 c, v 1 .
с
с
4
5. Направление вектора ускорения
• Направление вектора ускорениявсегда совпадает с направлением
вектора изменения мгновенной
скорости:
а v
5
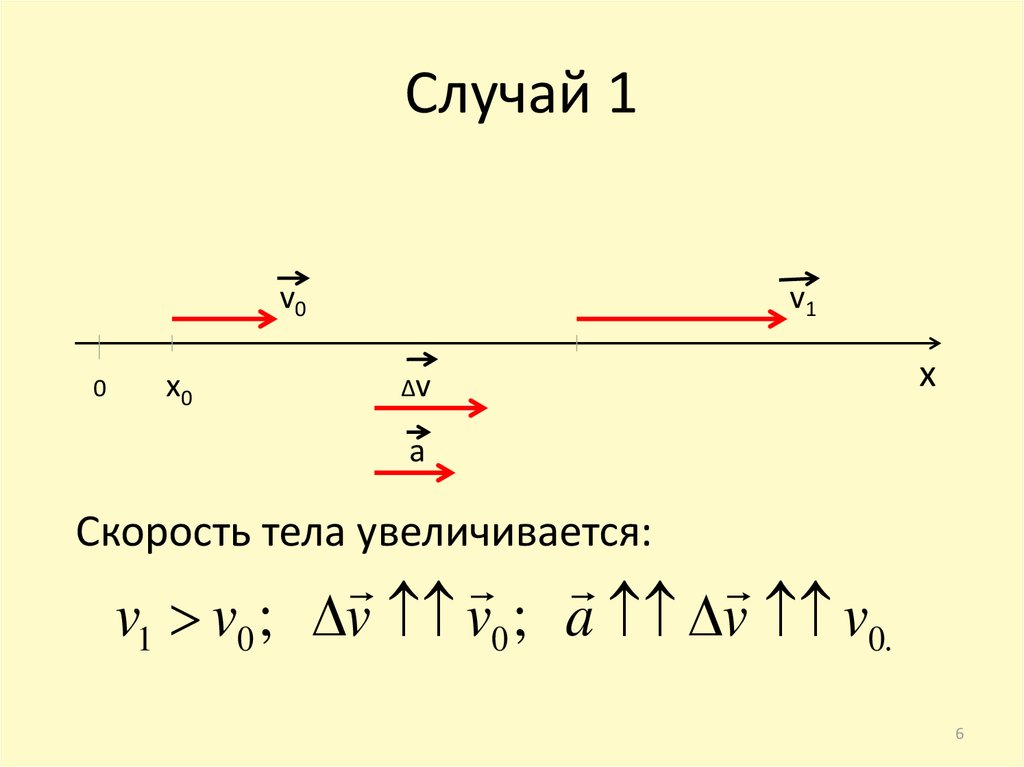
6. Случай 1
v00
x0
v1
∆v
x
a
Скорость тела увеличивается:
v1 v0 ; v v0 ; a v v0.
6
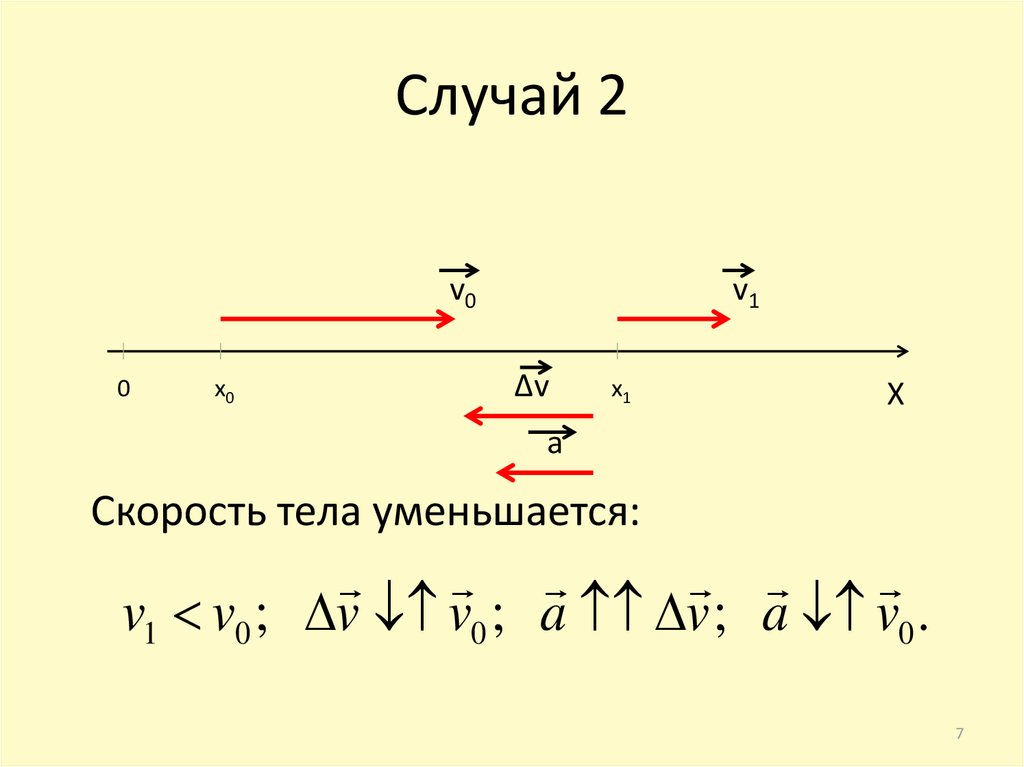
7. Случай 2
v00
x0
v1
∆v
x1
X
a
Скорость тела уменьшается:
v1 v0 ; v v0 ; a v ; a v0 .
7
8. Уравнение скорости при равноускоренном движении
v v0 atvx v0 x a xt
8
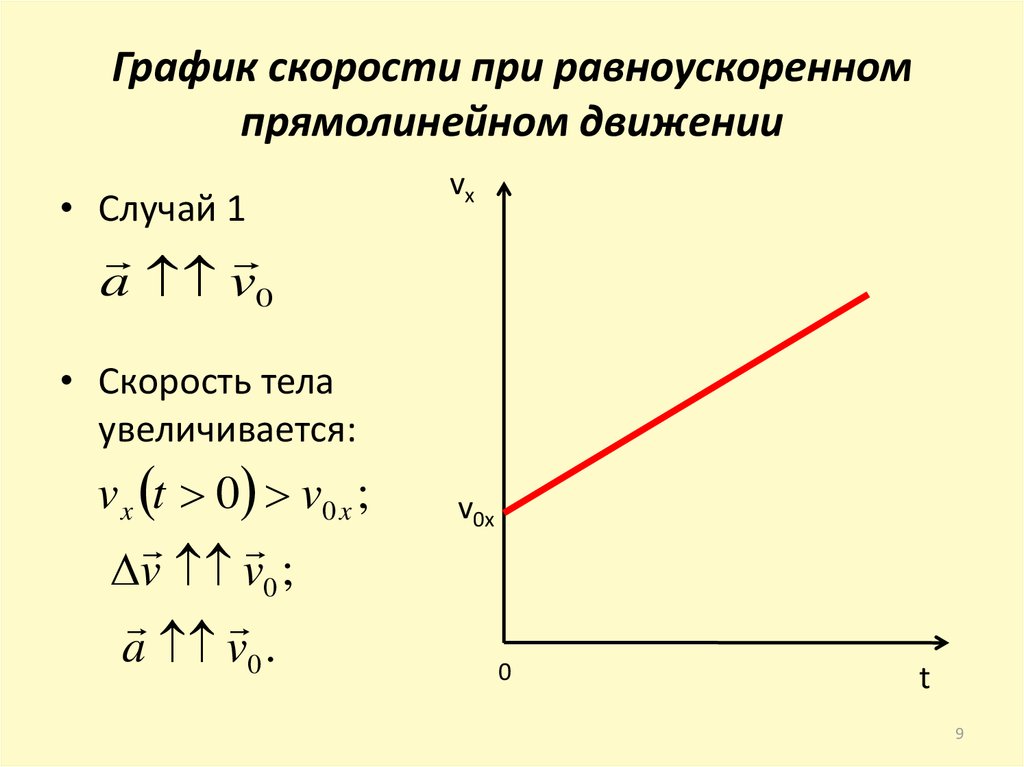
9. График скорости при равноускоренном прямолинейном движении
• Случай 1vx
a v0
• Скорость тела
увеличивается:
v x t 0 v0 x ;
v v0 ;
a v0 .
v0x
0
t
9
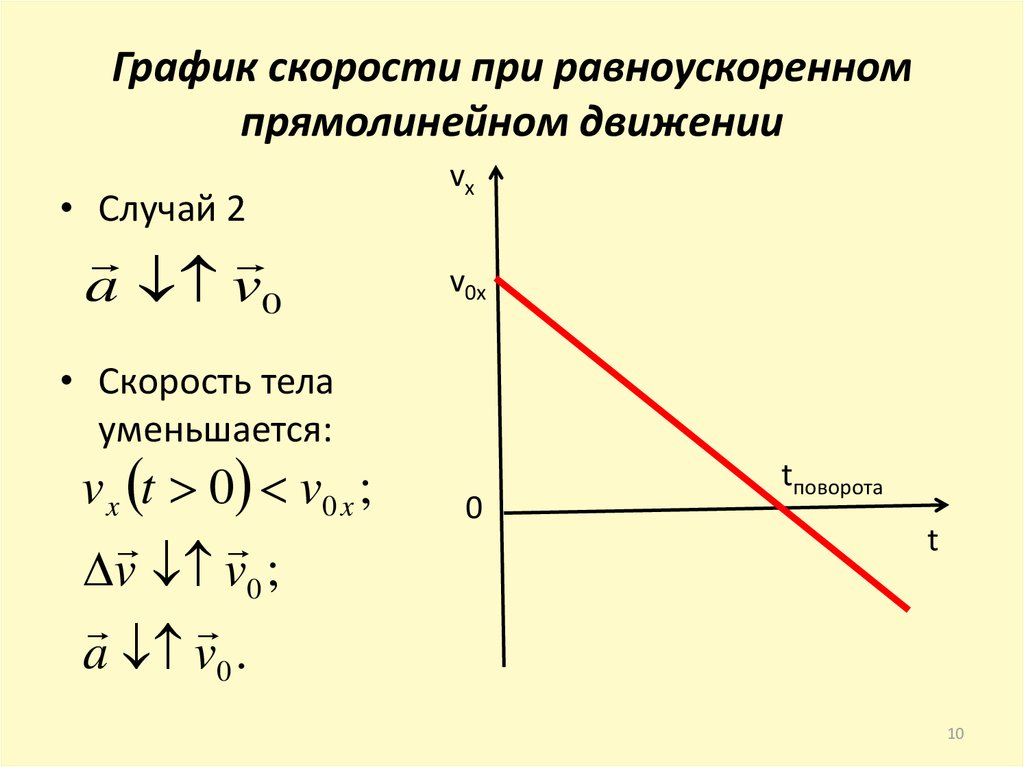
10. График скорости при равноускоренном прямолинейном движении
• Случай 2a v0
vx
v0x
• Скорость тела
уменьшается:
v x t 0 v0 x ;
v v0 ;
a v0 .
0
tповорота
t
10
11. Перемещение при прямолинейном равноускоренном движении
2axt
,
s x v0 x t
2
2
2
v x v0 x
.
sx
2a x
11
12. Координата тела при прямолинейном равноускоренном движении
2axt
x x0 v0 x t
;
2
2
x t ~ t , график - парабола.
2
axt
s x x x0 v0 x t
;
2
2
s x t ~ t , график - парабола.
12
13. Средняя скорость тела при равноускоренном движении
1. При движении в одном направлении:l sx ,
2.
s OX
axt 2
s x v0 x t
;
2
2v0 x t a x t 2
sx
;
2
1
1
s x v0 x t v0 x a x t t v0 x v x t ,
2
2
s
v vx
l
vср x 0 x
.
t
t
2
13
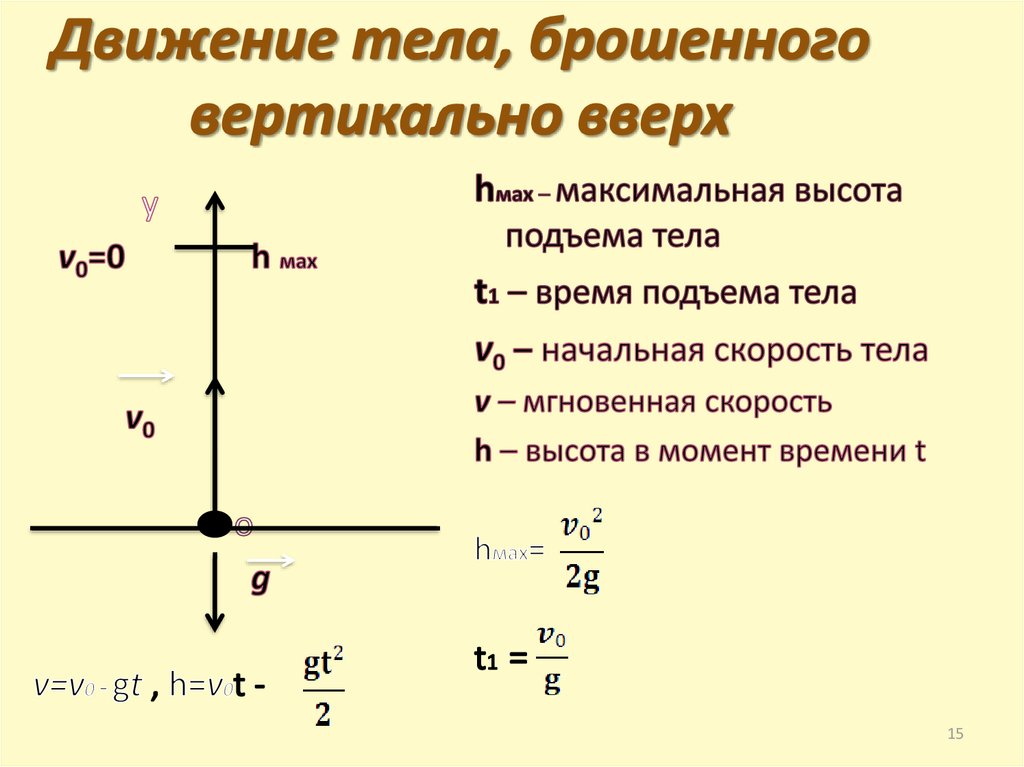
14.
Движение тела,брошенного вертикально
вверх
14
15. Движение тела, брошенного вертикально вверх
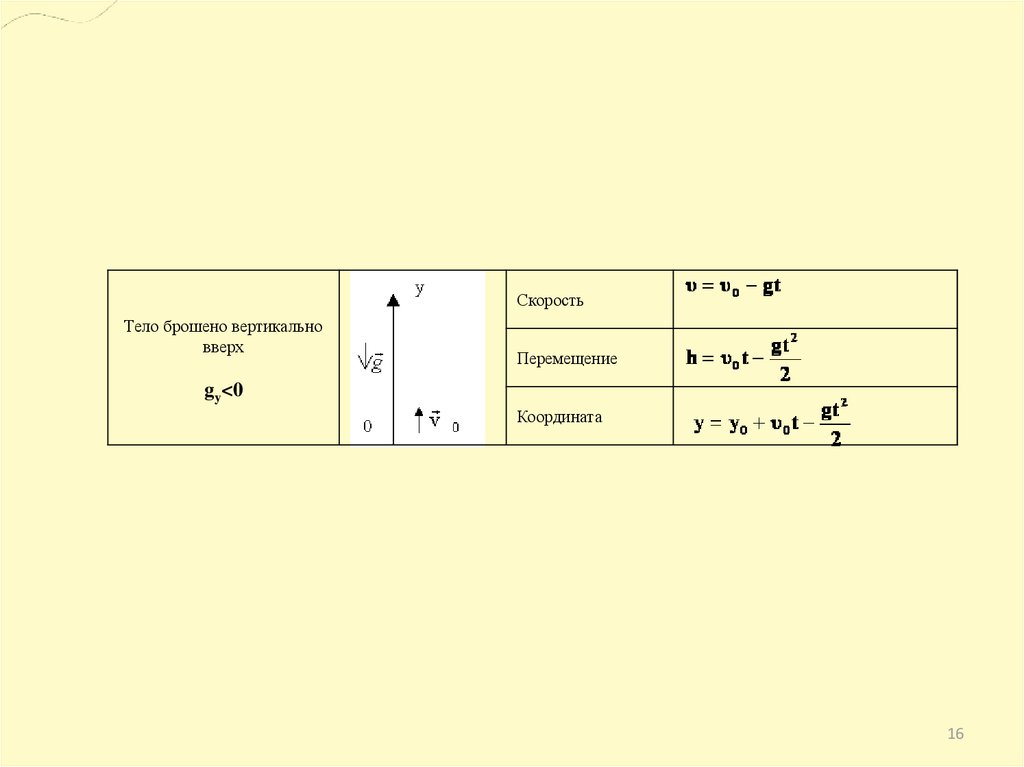
1516.
СкоростьТело брошено вертикально
вверх
Перемещение
gy<0
Координата
16
17.
Понятие об абсолютно твердом теле17
18.
Абсолютно твердое тело – системаматериальных точек, в которой
расстояния между любыми точками не
изменяются при воздействии
любых сил.
Задачи кинематики твердого тела:
1) задание движения и определение
кинематических характеристик
тела в целом;
2) определение кинематических
характеристик движения отдельных
точек тела.
18
19.
• Различают пять видов движения твердоготела:
• 1) поступательное;
• 2) вращательное;
• 3) плоское;
• 4) сферическое;
• 5) свободное.
19
20.
• Поступательное и вращательное движения являютсяпростейшими. Все остальные движения складываются из
простейших в разных сочетаниях и в этом смысле
являются сложными движениями.
• Поступательным движением твердого тела называется
такое движение, при котором любая прямая,
соединяющая две точки тела, движется параллельно
самой себе.
• Поступательное движение твердого тела – это не
обязательно прямолинейное движение. Это может быть
движение тела по любой траектории. Траектории всех
точек тела при поступательном движении совпадают при
наложении. Изучение поступательного движения
сводится, таким образом, к изучению движения одной его
точки, например, центра тяжести. Часто при
поступательном движении твердого тела его принимают
за материальную точку.
20
21.
Плоское движение твердого тела и движение плоскойфигуры в ее плоскости
Определение 1. Плоскопараллельным (или плоским)
движением абсолютно твердого тела называется
такое движение, при котором каждая точка тела
движется в плоскости, параллельной некоторой
неподвижной плоскости.
Определение 2. Плоскопараллельным (или плоским)
движением абсолютно твердого тела называется
такое движение, при котором любая прямая,
проведенная в теле перпендикулярно неподвижной
плоскости, будет оставаться перпендикулярной этой
плоскости.
21
22.
В самом общем случае движение твердоготела может считаться свободным, если оно
может перемещаться каким угодно
образом по отношению к неподвижной
системе отсчета. Свободное тело имеет 6
степеней свободы: 3 поступательных и 3
вращения. Рассматривают такое движение
как поступательное вместе с определенной
точкой вращения и вращательное вокруг
некоторой точки, как неподвижной.
22
23.
Точка совершает относительное движение в некоторойсистеме координат по некоторой траектории. Если эта
система координат движется по отношению к
неподвижной системе отсчета, то в любой момент
времени точка вынуждена совершать движение вместе с
некоторой точкой этой подвижной системы отсчета.
Сложным движением точки называется абсолютное
движение,
составленное из относительного и
переносного движений. По отношению к подвижной
системе координат движение точки будет относительным,
движение подвижной системы координат по отношению к
неподвижной
–
переносным.
Для
обозначения
относительного движения используются индексы «отн»
или «r», для обозначения переносного движения «пер»
или «e».
23
24.
2425.
Если тело совершает относительноедвижение в некоторой системе
координат, которая движется по отношению к
неподвижной системе отсчета, то
результирующее движение тела называют
сложным.
Задачей кинематики в этом случае является
нахождение зависимости между
характеристиками относительного,
переносного и абсолютного движений.
25



















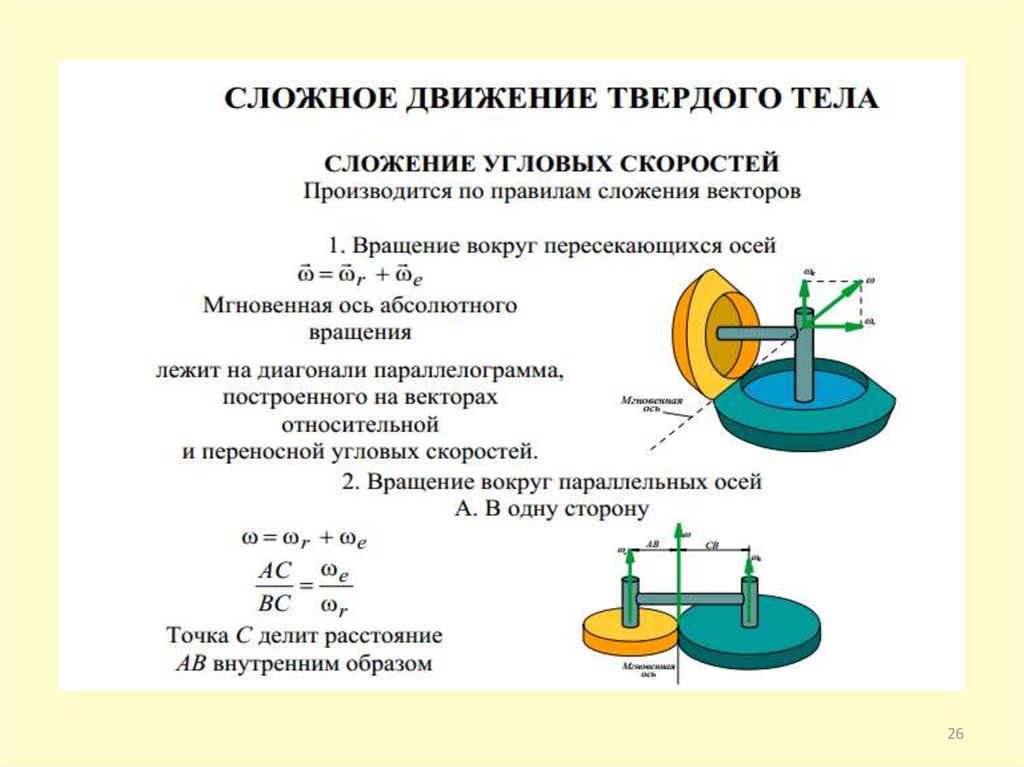
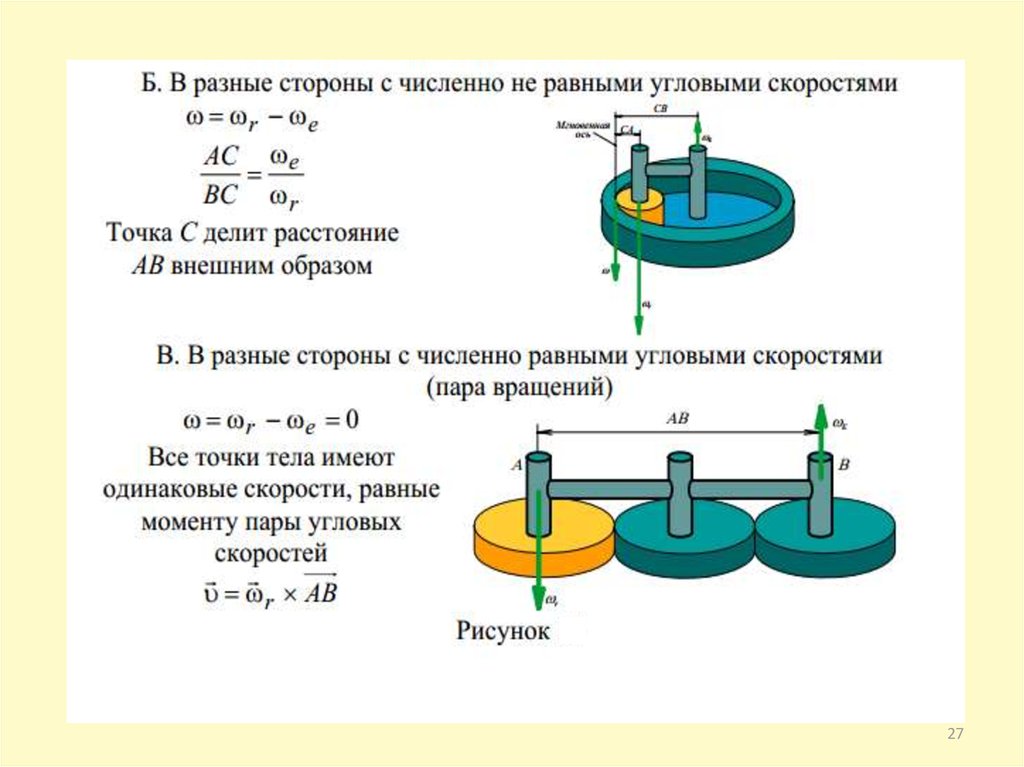

 physics
physics