Логарифм и ОДЗ. Решения

1. Логарифм и ОДЗ

Loga b=Х
х
а
=b
b?
a?
Логарифм и
ОДЗ
ВМЕСТЕ
трудятся
везде!

2.

Тест№1
log1/2 4
-2
log5 5
1/2
log 3 27 3
1
log 2 -2
4
5
2log 5 3 =
log2 3
8
lg 0,1=
9
= 27
-1
log2 (-8)
не существует
42+log45 = 80

3.

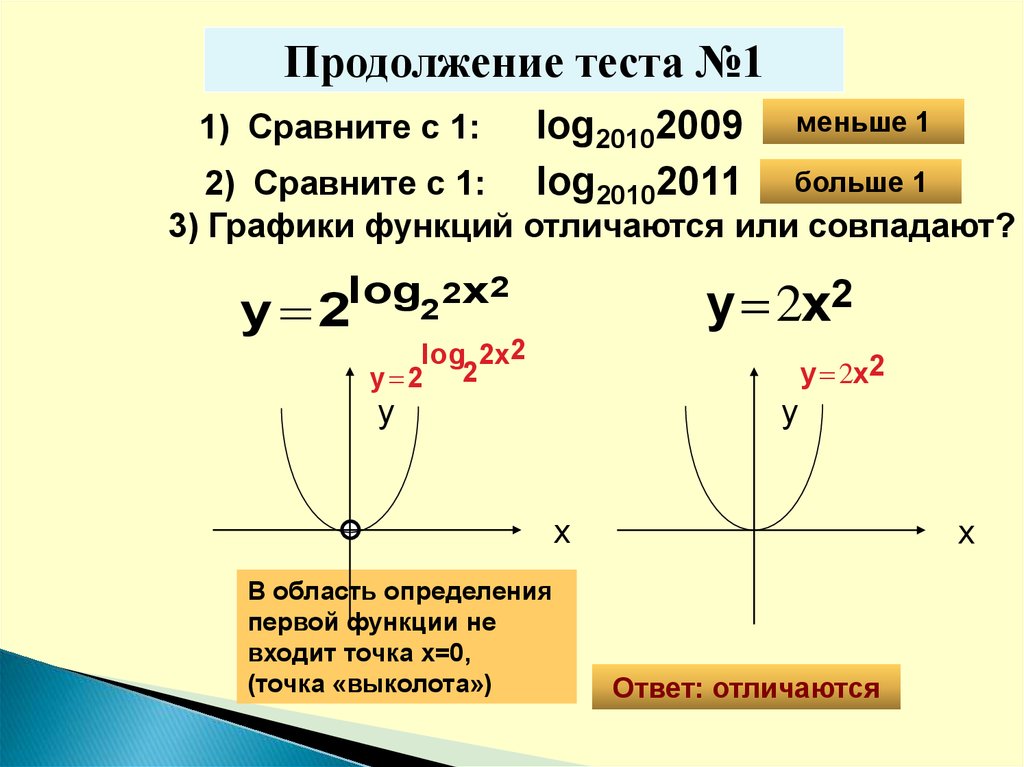
Продолжение теста №1
1) Сравните с 1:
log20102009
log20102011
меньше 1
больше 1
2) Сравните с 1:
3) Графики функций отличаются или совпадают?
y 2x2
log2 2x2
y 2
log 2x2
y 2 2
y 2x2
y
y
x
В область определения
первой функции не
входит точка х=0,
(точка «выколота»)
x
Ответ: отличаются

4.

Методы решения
1) по определению логарифма;
2)функционально-графический метод;
3)метод потенцирования;
4)метод введения новой переменной;

5.

Пути решения уравнений
1
2
•Решить уравнение,
выбрав метод
решения
•Найти область
допустимых значений
(ОДЗ) переменной
•Проверить
найденные корни
непосредственной
подстановкой в
исходное уравнение
•Решить уравнение,
выбрав метод решения
•Выяснить,
удовлетворяют ли
корни решённого
уравнения ОДЗ
3
•Заменить
уравнение
равносильным
уравнением или
равносильной
системой

6. Метод решения с помощью определения ЛОГАРИФМА

7. Метод решения с помощью определения ЛОГАРИФМА

8. Метод потенцирования:

9. 2. Решите уравнения методом потенцирования:

а) log2 (3x – 6) = log2 (2x – 3);
б) log6 (14 – 4x) = log6 (2x + 2);
в) log0,5 (7x – 9) = log0,5 (x – 3);
г) log0,2 (12x + 8) = log0,2 (11x +
7).

10. Метод введения вспомогательной переменной:

11. 3.Решите уравнения методом введения вспомогательной переменной:

lg 2 x 3 10 lg x 1 0
lg x 10 lg x 1 0
2
3
log 22 x 4 log 2 x 3 0;
3 log x 5 log 0,5 x 2 0;
2
05
2 log 20,3 x 7 log 0,3 x 4 0.

12. Рецензирование.

1
4
lg 2 x lg x 15
4
1
lg 2 x 4 lg x 15
4
lg 2 x lg x 15
2 x x 15
x 15
Ответ: корней нет

13.

Гимназия № 8
Сочи
уравнения
Работа Решите
в группах.
Решите уравнения.
log 2 ( x 8) 4
lg x 2
2
X=24
X=-10 и X=10
log2x+4log4x=12
X=16
log log log x 0
x=64
2
3
xlgx=100x;
4

14. Тест №3. Укажите метод решения

log7 ( 4 3 x ) log7 ( 6 5 x )
log3 ( x 1 ) log3 ( x 1 )4 2
2
log3 x log9 x log27 x 5 ,5
log9 x log x 9 0 ,5
x
1 lg x
100

15.

Продолжение теста №3.
Найдите лишнее уравнение и
назовите метод решения
Логарифмирование
Логарифмирование
Лишнее
Квадратное относительно логарифма. Замена
Лишнее
Квадратное относительно логарифма. Замена

16. Логарифмы в ЕГЭ (часть 2)

log 10 x log
x
log
x
...
log
x
5
,
5
3
10
10
10
10
lоg10x + 2log10x + 3 log10x + …+ 10 log10x = 5,5
(1 + 2 + 3 + …+ 10) log10x = 5,5
∑ = 55
55 lgx = 5,5
lgx = 0,1
х = 10 0,1
Ответ: 10 0,1

17.

Логарифмическая
спираль
Подготовила Крутякова Кристина

18.

полюс
- расстояние от полюса до
произвольной точки на спирали
– угол поворота относительно
полюса
– постоянная
или
Спираль называется
логарифмической, т.к. логарифм
расстояния (
) возрастает
пропорционально углу поворота

19.

Если вращать спираль
вокруг полюса по
часовой стрелке, то
можно наблюдать
кажущееся растяжение
спирали.

20.

Если вращать спираль
вокруг полюса против
часовой стрелки, то
можно наблюдать
кажущееся сжатие
спирали.

21.

Спирали широко проявляют себя в
живой природе. Спирально
закручиваются усики растений, по
спирали происходит рост тканей в
стволах деревьев.

22.

В подсолнухе
семечки расположены
по дугам, близким к
логарифмической
спирали

23.

Рога животных растут
лишь с одного конца.
Этот рост осуществляется
по логарифмической
спирали. Например, рога
баранов, коз, антилоп и
других рогатых
животных.

24.

Раковины морских животных могут расти лишь в одном
направлении. Чтобы не слишком вытягиваться в длину,
им приходится скручиваться, причем каждый следующий
виток подобен предыдущему. Поэтому раковины многих
моллюсков, улиток, закручены по логарифмической
спирали.

25.

По логарифмической спирали
формируется тело циклона

26.

По логарифмическим спиралям закручены и
многие галактики, в частности – Галактика
Солнечной системы.

27.

Потребность в сложных расчетах XVI века
быстро росла. В конце века нескольким
математикам, почти одновременно, пришла
в голову идея: заменить трудоемкое
умножение на простое сложение, а деление
автоматически заменяется на более простое
и надежное вычитание.

28.

Здесь лежит результат
деятельности многих
ученых . То, что здесь
находится
использовалось в
учебных заведениях и
инженерных расчетах
до конца прошлого
века.
В. Брадис

29.

30.

Здесь лежит, то что еще
в 20 годах 17 века
придумал английский
математик Уильям
Отред.
«Считать на ней можно
быстро, места почти не
занимает, её можно
всюду носить с собой в
кармане.»

31.

32. Домашнее задание

Выполнить
индивидуальный мини-проект
«Уравнение с изнанки»

33. Рефлексия (итог урока)

Какую цель ставили перед собой на уроке?
Cмогли ли её достичь?
Оцените свою деятельность на уроке.
Какой вид деятельности вам больше
понравился?

34.

Спасибо за работу на уроке!

35. Использованная литература

Виленкин Н. Я. Функции в природе и технике – М.:
Просвещение, 1978.
Кочагин В. В., Кочагина М. Н. ЕГЭ Математика, 2007 –
М.: «Эксмо», 2007.
Лиман М. М. Школьникам о математике и математиках.
4 - 8 кл. – М.: Просвещение, 1981.
Мерзляк А. Г. и др. Алгебраический тренажер – М.:
«Илекса», 2005.
Перельман Я. И. Занимательная алгебра – М.:
Госиздат технико-теоретической литературы, 1955.
Рурукин А. Н. Интенсив. Математика – М.: «ВАКО»,
2006.