Similar presentations:
Шарики на нити
1. 9. Шарики на нити
Докладчик - Хорошко ИльяНаденьте шарик со сквозным отверстием
на нить так, чтобы он мог свободно
двигаться вдоль нити. На конце нити
закрепите другой шарик. Если периодически
двигать свободный конец нити, то можно
наблюдать сложное движение обоих шаров.
Исследуйте явление.
2. Демонстрация эффекта
Горизонтальныеорбиты
Предварительная часть
Вертикальные
орбиты
IYPT 2019
Team Ukraine 2
Хаотические
решения
3.
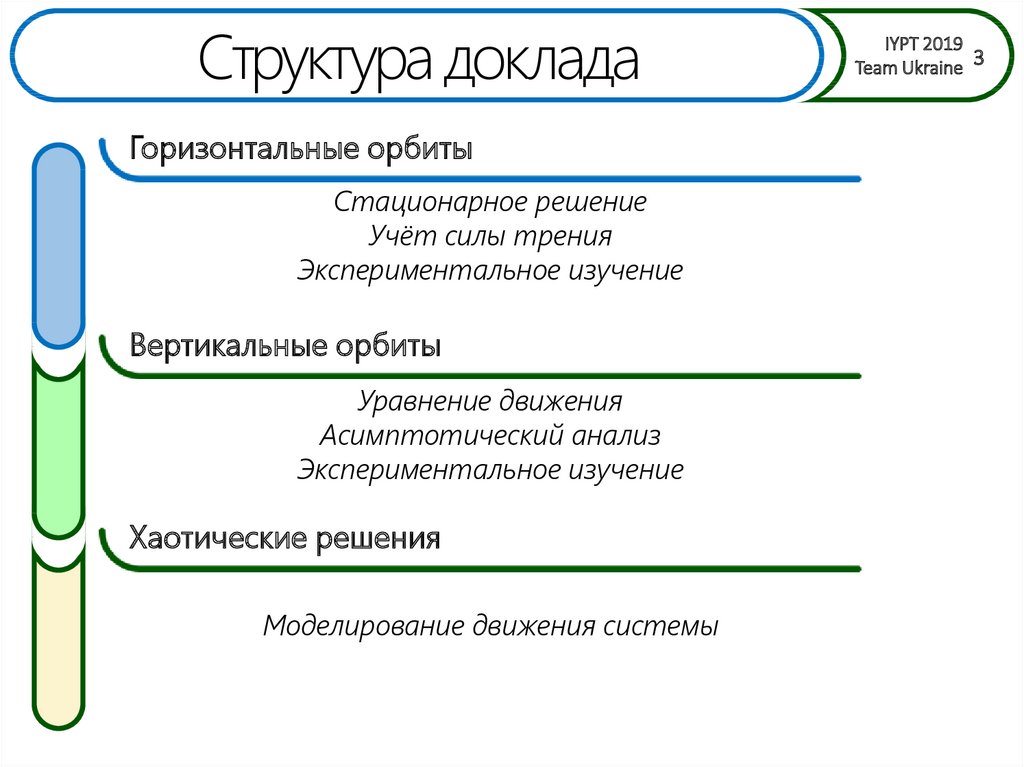
Структура докладаГоризонтальные орбиты
Стационарное решение
Учёт силы трения
Экспериментальное изучение
Вертикальные орбиты
Уравнение движения
Асимптотический анализ
Экспериментальное изучение
Хаотические решения
Моделирование движения системы
IYPT 2019
Team Ukraine 3
4. Горизонтальные решения
IYPT 2019Team Ukraine 4
Горизонтальные решения
Горизонтальные орбиты
Вертикальные орбиты
Хаотические решения
5. Геометрия системы
Горизонтальные орбитыВертикальные орбиты
IYPT 2019
Team Ukraine 5
Хаотические решения
6. Геометрия системы
IYPT 2019Team Ukraine 6
Из геометрии системы следует
Чтобы описать движение
системы найдём:
Горизонтальные орбиты
Вертикальные орбиты
Хаотические решения
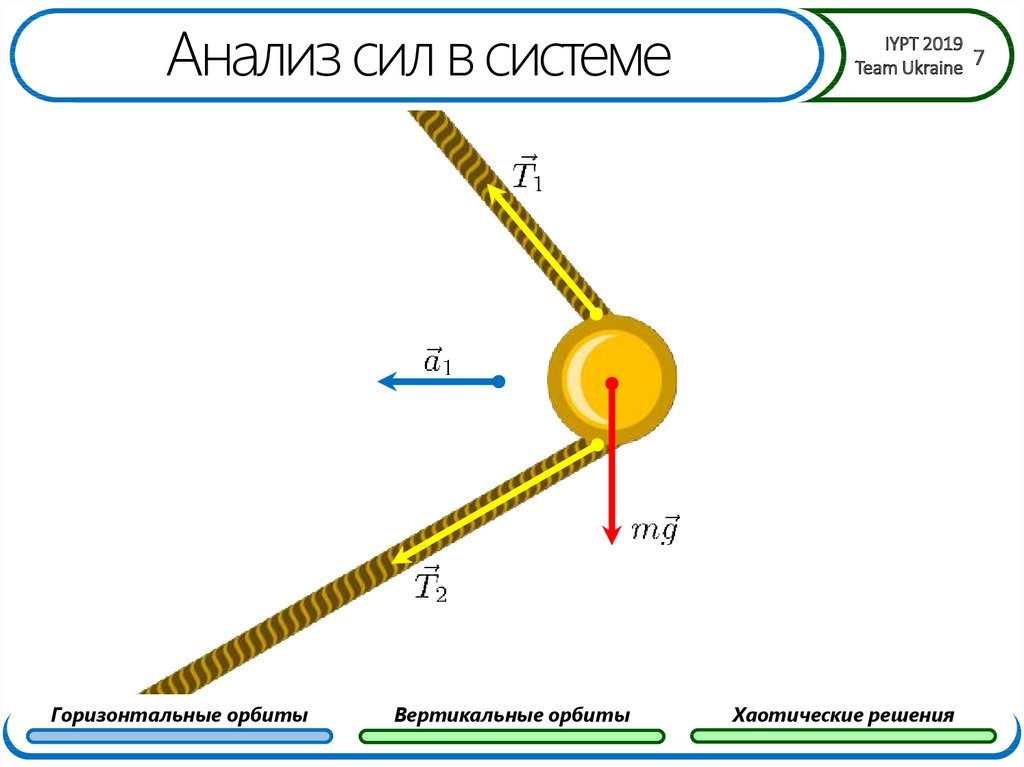
7. Анализ сил в системе
Горизонтальные орбитыВертикальные орбиты
IYPT 2019
Team Ukraine 7
Хаотические решения
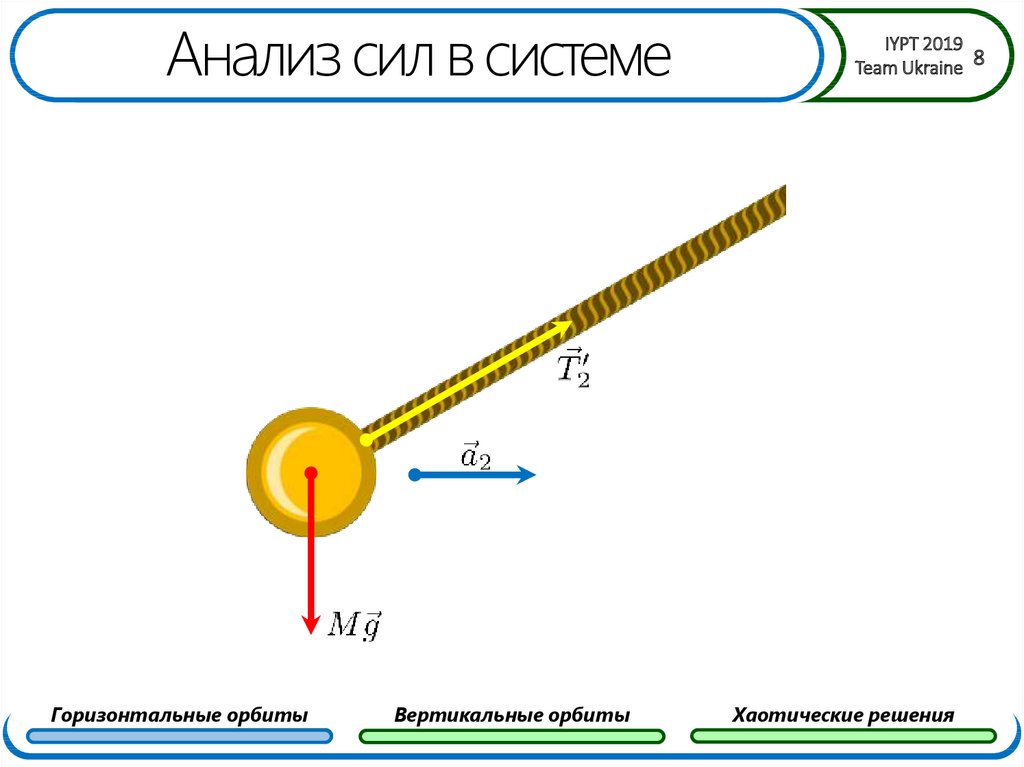
8. Анализ сил в системе
Горизонтальные орбитыВертикальные орбиты
IYPT 2019
Team Ukraine 8
Хаотические решения
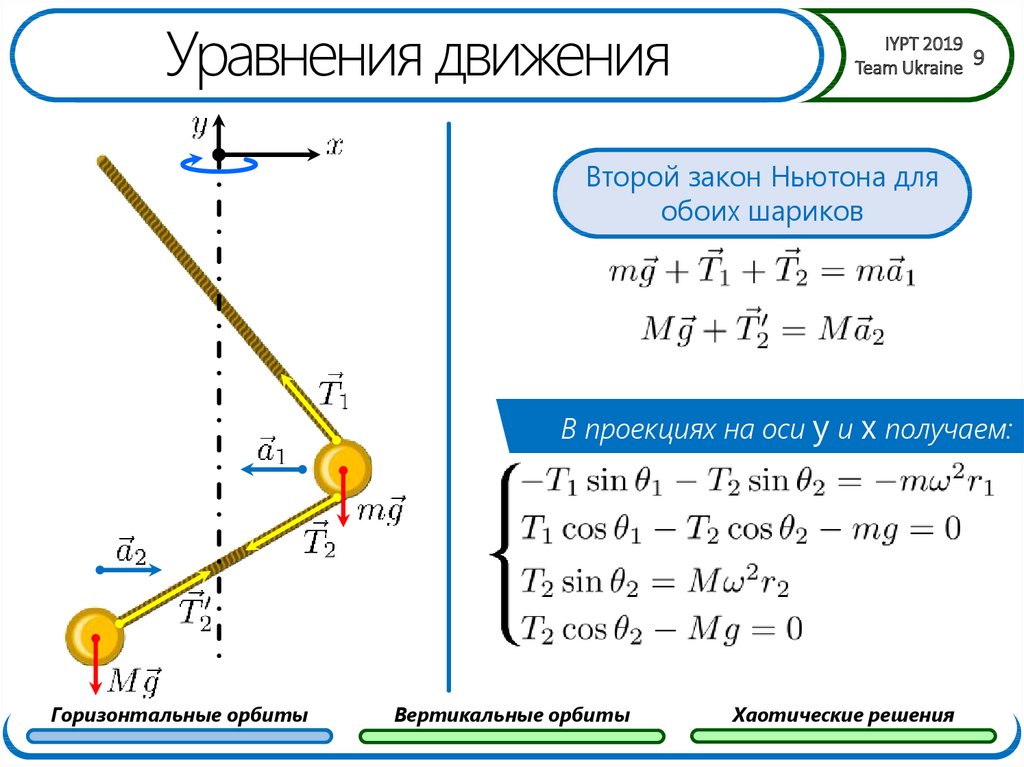
9. Уравнения движения
IYPT 2019Team Ukraine 9
Второй закон Ньютона для
обоих шариков
В проекциях на оси y и x получаем:
Горизонтальные орбиты
Вертикальные орбиты
Хаотические решения
10. Конечная система уравнений
IYPT 2019Team Ukraine 10
Уравнения движения
Переменные системы
Решаем систему в приближении отсутствия сил трения,
тогда силы натяжения нитей считаем равными
Геометрические условия
Горизонтальные орбиты
Вертикальные орбиты
Хаотические решения
11. Численное решение
Горизонтальные орбитыВертикальные орбиты
IYPT 2019
Team Ukraine 11
Хаотические решения
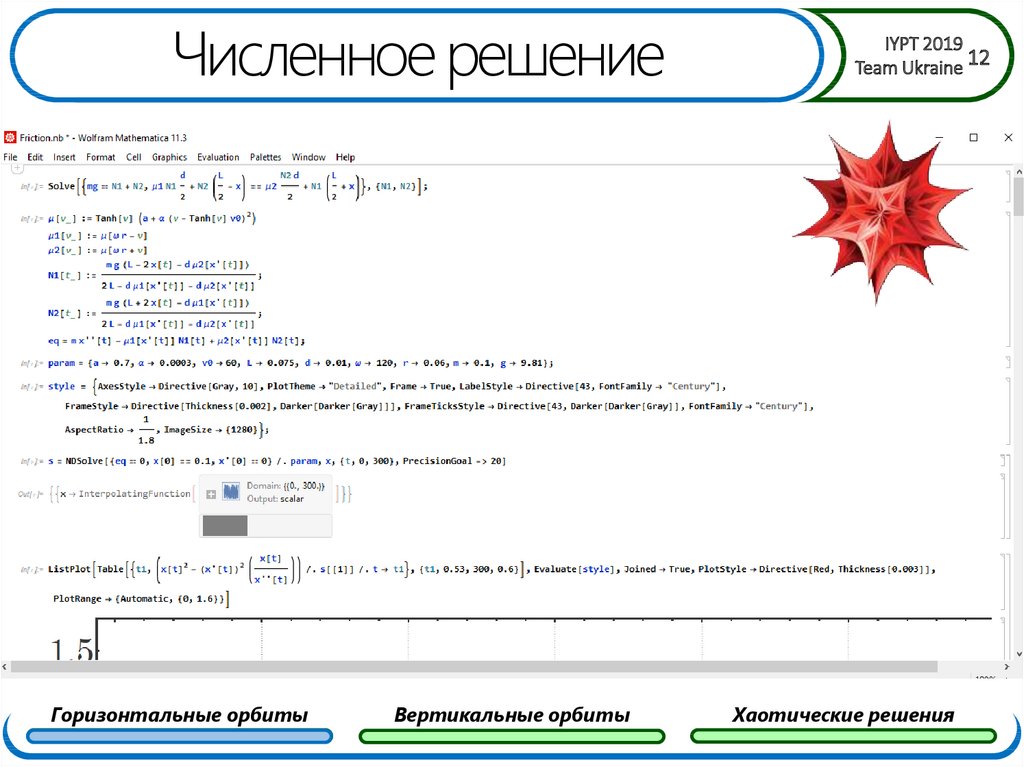
12. Численное решение
Горизонтальные орбитыВертикальные орбиты
IYPT 2019
Team Ukraine 12
Хаотические решения
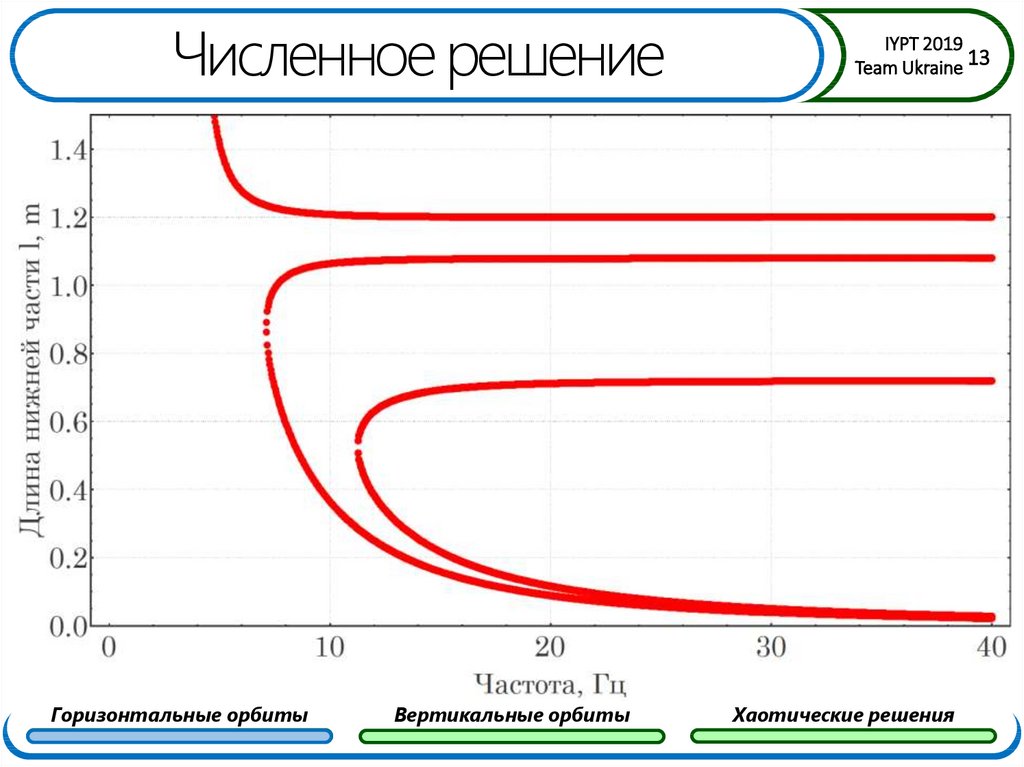
13. Численное решение
Горизонтальные орбитыВертикальные орбиты
IYPT 2019
Team Ukraine 13
Хаотические решения
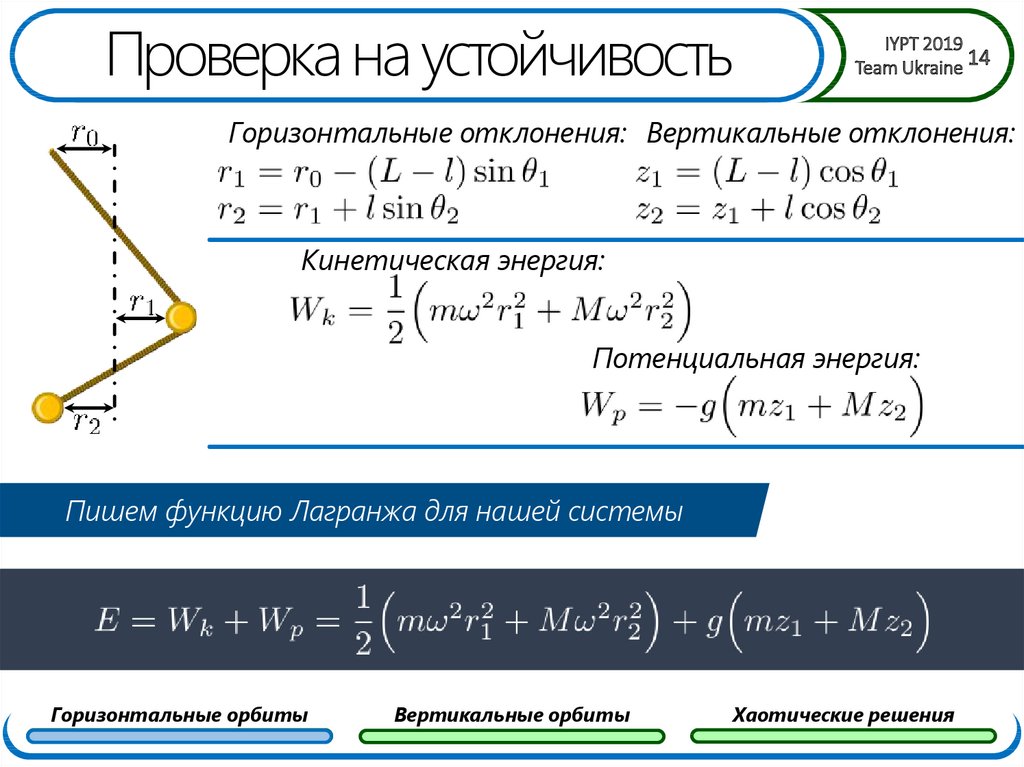
14. Проверка на устойчивость
IYPT 2019Team Ukraine 14
Горизонтальные отклонения: Вертикальные отклонения:
Кинетическая энергия:
Потенциальная энергия:
Пишем функцию Лагранжа для нашей системы
Горизонтальные орбиты
Вертикальные орбиты
Хаотические решения
15. Проверка на устойчивость
IYPT 2019Team Ukraine 15
Горизонтальные отклонения: Вертикальные отклонения:
Кинетическая энергия:
Потенциальная энергия:
Условия равновесия системы:
Выпуклость энергии вблизи точки равновесия говорит об устойчивости
Эффективная энергия: данного положения
Горизонтальные орбиты
Вертикальные орбиты
Хаотические решения
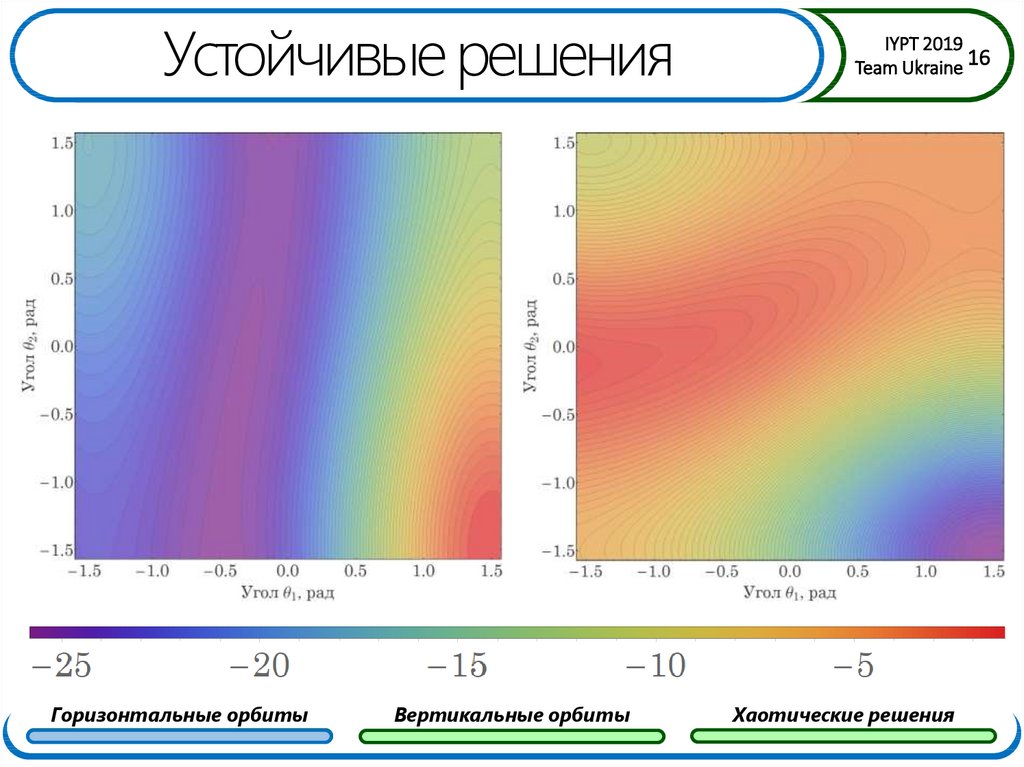
16. Устойчивые решения
Горизонтальные орбитыВертикальные орбиты
IYPT 2019
Team Ukraine 16
Хаотические решения
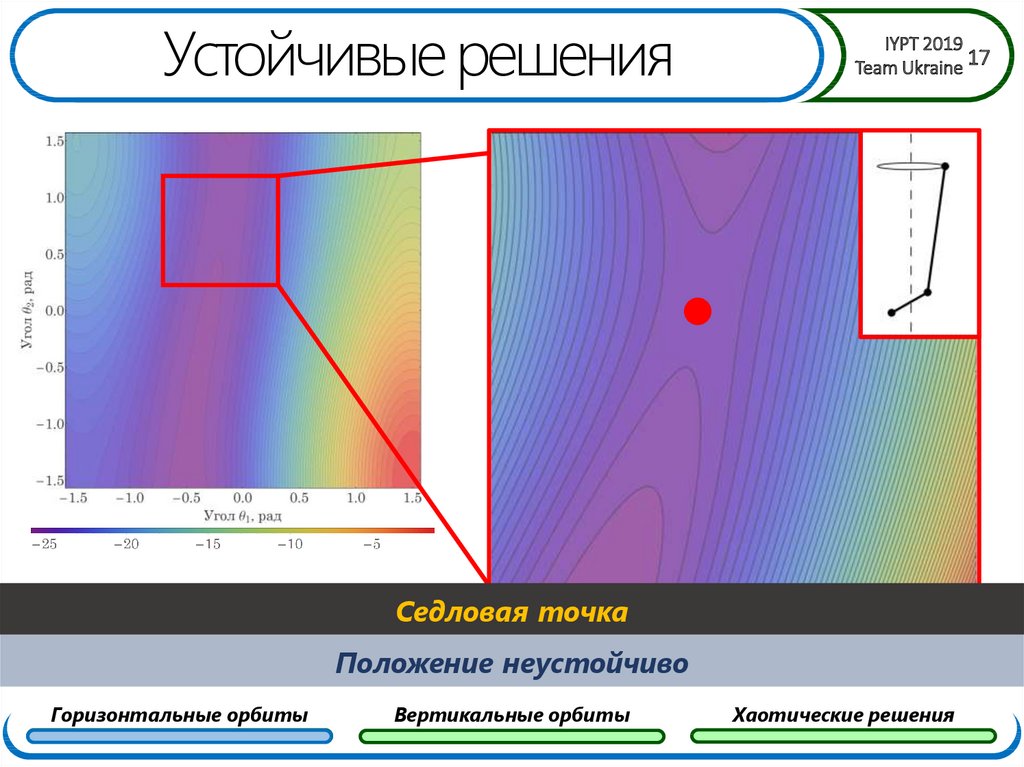
17. Устойчивые решения
IYPT 2019Team Ukraine 17
Седловая точка
Положение неустойчиво
Горизонтальные орбиты
Вертикальные орбиты
Хаотические решения
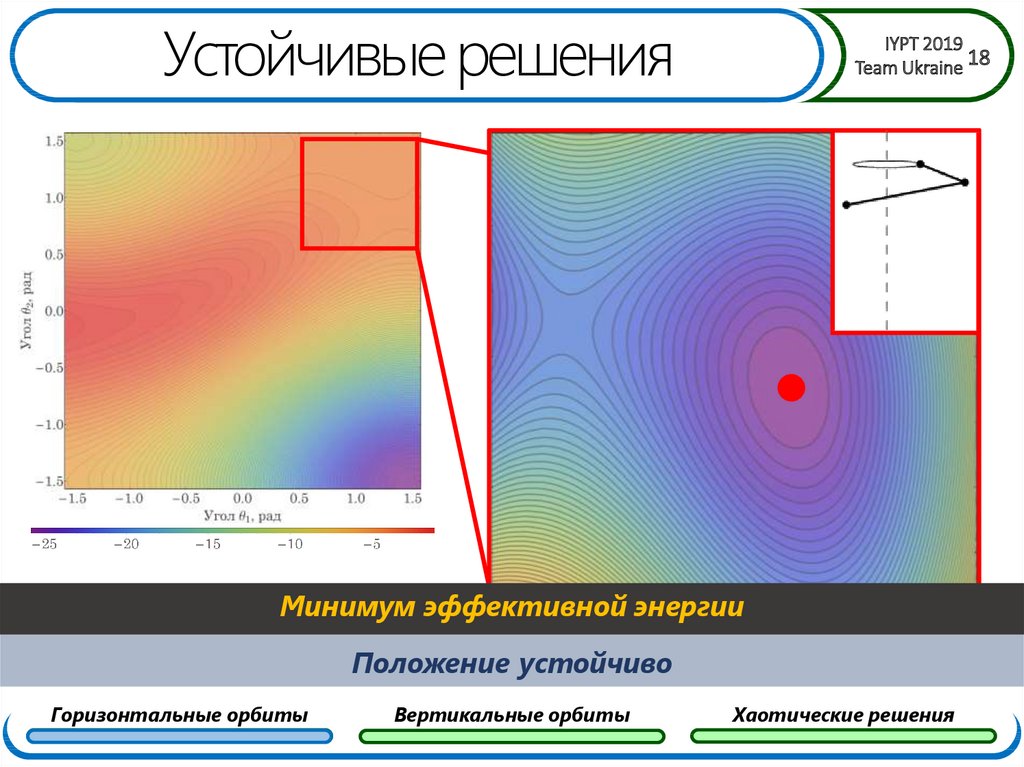
18. Устойчивые решения
IYPT 2019Team Ukraine 18
Минимум эффективной энергии
Положение устойчиво
Горизонтальные орбиты
Вертикальные орбиты
Хаотические решения
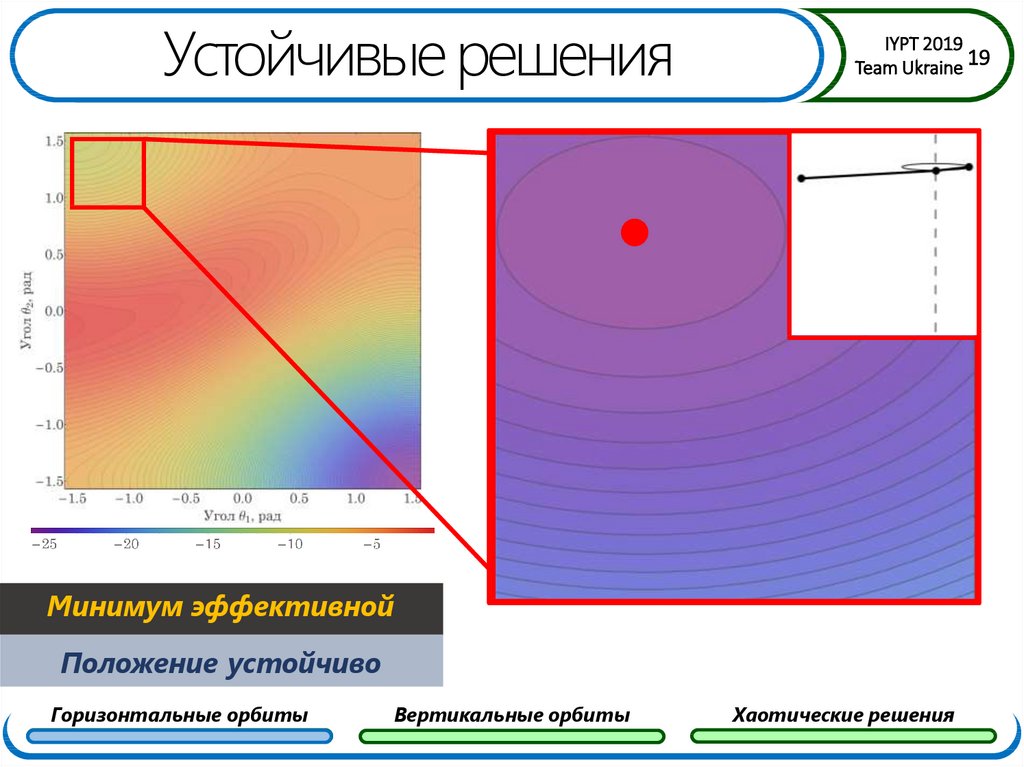
19. Устойчивые решения
IYPT 2019Team Ukraine 19
Минимум эффективной
энергии
Положение устойчиво
Горизонтальные орбиты
Вертикальные орбиты
Хаотические решения
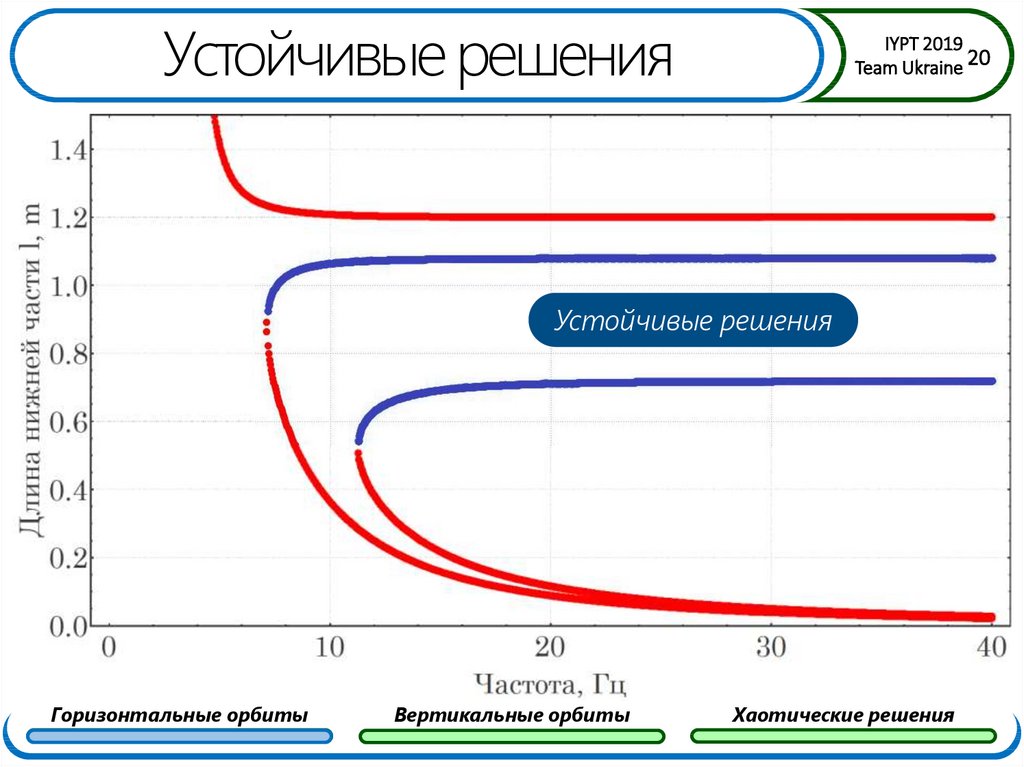
20. Устойчивые решения
IYPT 2019Team Ukraine 20
Устойчивые решения
Горизонтальные орбиты
Вертикальные орбиты
Хаотические решения
21. Сила трения в системе
IYPT 2019Team Ukraine 21
Уравнения движения
Переменные системы
Решаем систему в приближении отсутствия сил трения,
тогда силы натяжения нитей считаем равными
Геометрические условия
Горизонтальные орбиты
Вертикальные орбиты
Хаотические решения
22. Решение с учётом сил трения
Горизонтальные орбитыВертикальные орбиты
IYPT 2019
Team Ukraine 22
Хаотические решения
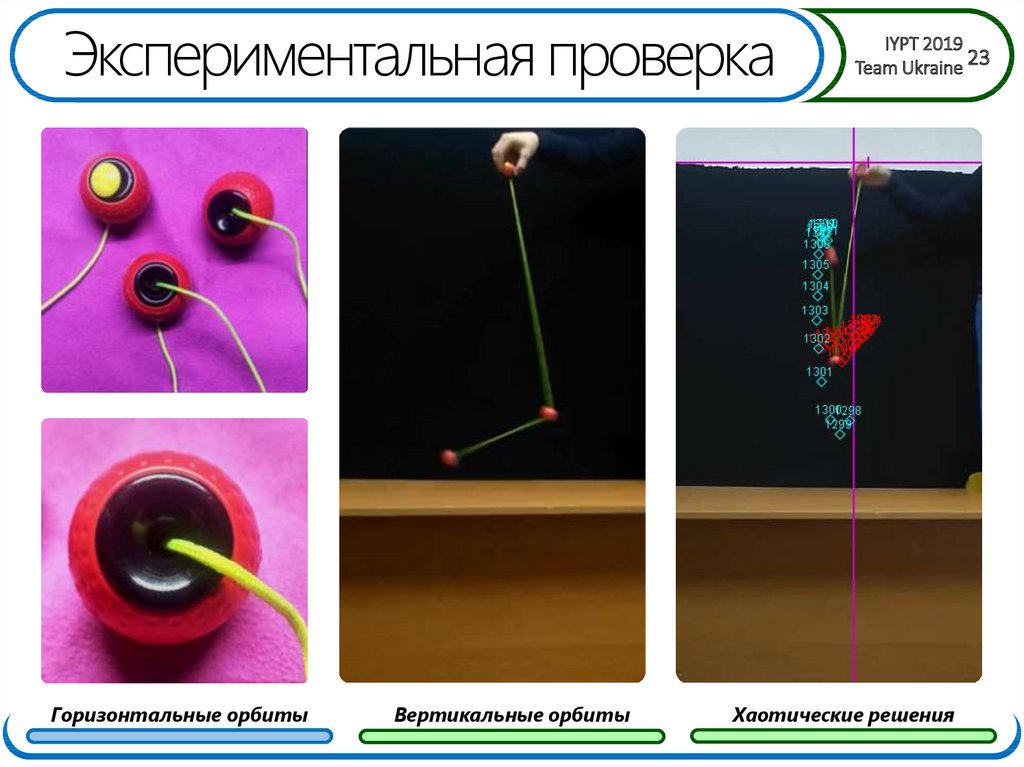
23. Экспериментальная проверка
Горизонтальные орбитыВертикальные орбиты
IYPT 2019
Team Ukraine 23
Хаотические решения
24. Экспериментальная проверка
Горизонтальные орбитыВертикальные орбиты
IYPT 2019
Team Ukraine 24
Хаотические решения
25. Вертикальные орбиты
IYPT 2019Team Ukraine 25
Вертикальные орбиты
Горизонтальные орбиты
Вертикальные орбиты
Хаотические решения
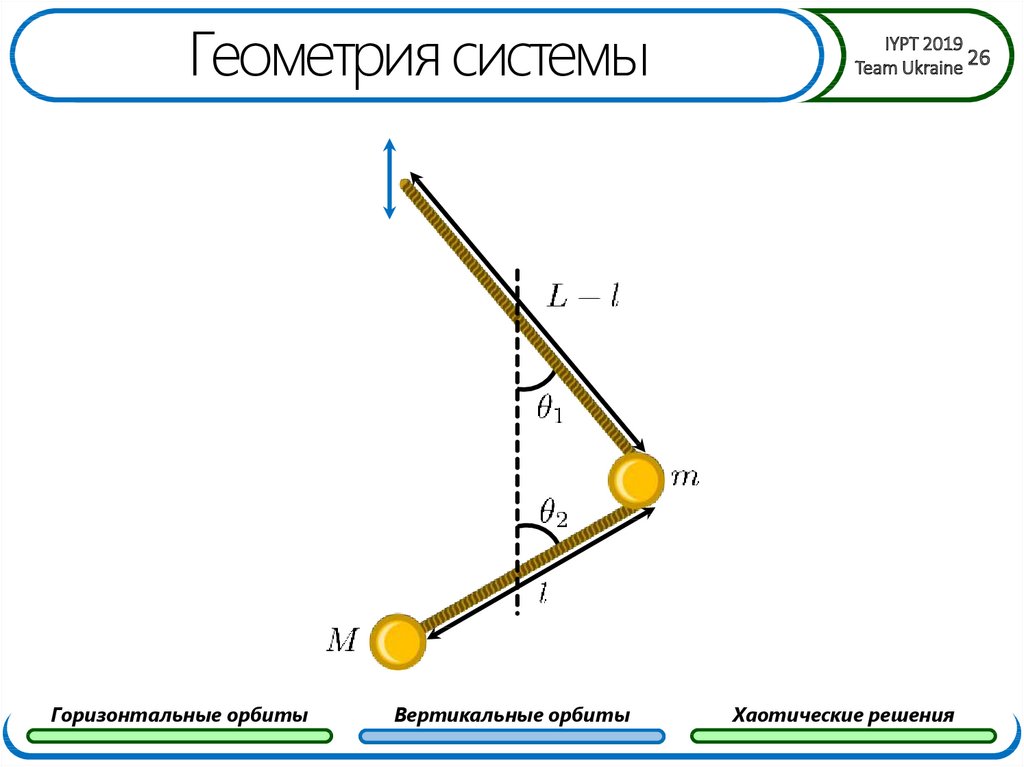
26. Геометрия системы
Горизонтальные орбитыВертикальные орбиты
IYPT 2019
Team Ukraine 26
Хаотические решения
27. Геометрия системы
Горизонтальные орбитыВертикальные орбиты
IYPT 2019
Team Ukraine 27
Хаотические решения
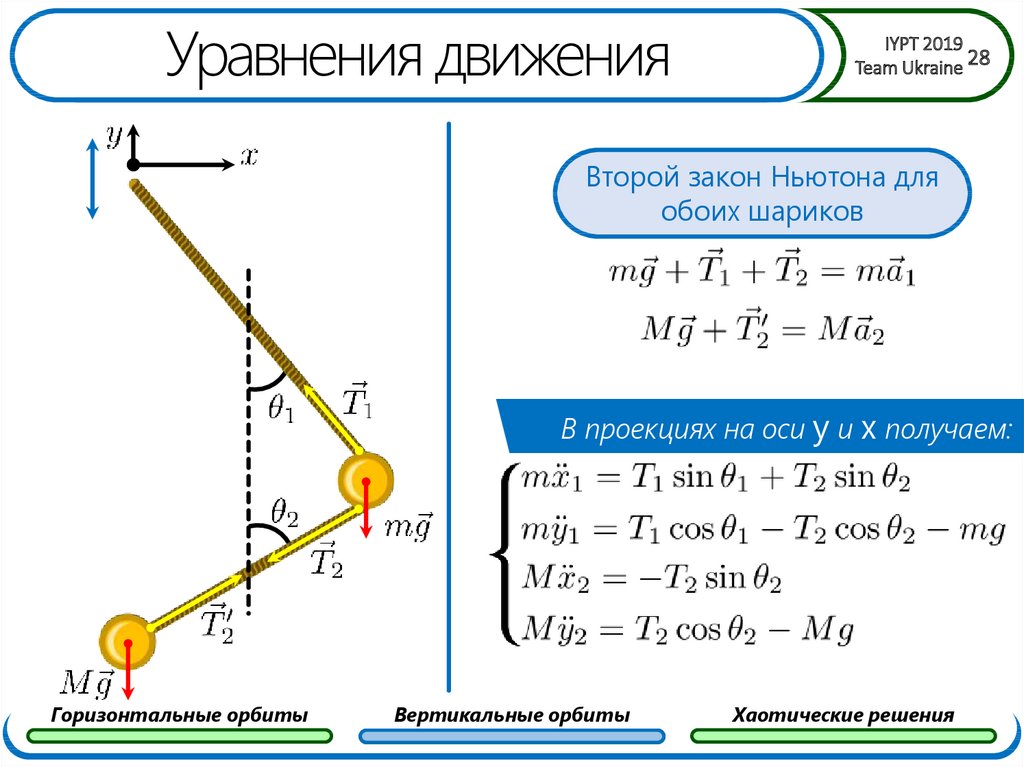
28. Уравнения движения
IYPT 2019Team Ukraine 28
Второй закон Ньютона для
обоих шариков
В проекциях на оси y и x получаем:
Горизонтальные орбиты
Вертикальные орбиты
Хаотические решения
29. Полная система уравнений
Горизонтальные орбитыВертикальные орбиты
IYPT 2019
Team Ukraine 29
Хаотические решения
30. Численное решение
Горизонтальные орбитыВертикальные орбиты
IYPT 2019
Team Ukraine 30
Хаотические решения
31. Экспериментальная проверка
Горизонтальные орбитыВертикальные орбиты
IYPT 2019
Team Ukraine 31
Хаотические решения
32. Хаотические решения
IYPT 2019Team Ukraine 32
Хаотические решения
Горизонтальные орбиты
Вертикальные орбиты
Хаотические решения
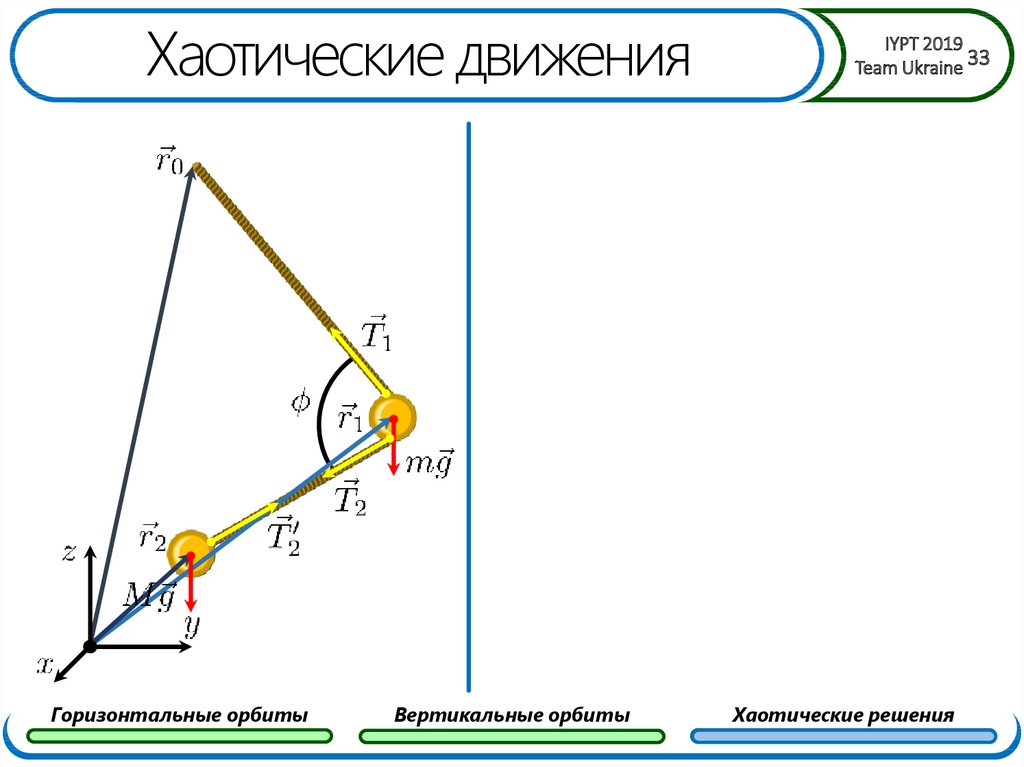
33. Хаотические движения
Горизонтальные орбитыВертикальные орбиты
IYPT 2019
Team Ukraine 33
Хаотические решения
34. Что-то теоретическое…
Горизонтальные орбитыВертикальные орбиты
IYPT 2019
Team Ukraine 34
Хаотические решения
35. Что-то экспериментальное…
Горизонтальные орбитыВертикальные орбиты
IYPT 2019
Team Ukraine 35
Хаотические решения
36. 9. Шарики на нити
IYPT 2019Team Ukraine 36
Наденьте шарик со сквозным отверстием на нить так, чтобы он мог свободно
двигаться вдоль нити. На конце нити закрепите другой шарик. Если
периодически двигать свободный конец нити, то можно наблюдать сложное
движение обоих шаров. Исследуйте явление.
Вертикальные орбиты
• Качественное и
теоретическое изучение
динамики движения системы
• Изучение устойчивости
решений
• Экспериментальное изучение
Результаты и выводы
37. 9. Шарики на нити
IYPT 2019Team Ukraine 37
Наденьте шарик со сквозным отверстием на нить так, чтобы он мог свободно
двигаться вдоль нити. На конце нити закрепите другой шарик. Если
периодически двигать свободный конец нити, то можно наблюдать сложное
движение обоих шаров. Исследуйте явление.
Горизонтальные орбиты
• Теоретическое изучение
динамики движения системы
• Экспериментальная
проверка решений
Результаты и выводы
38. 9. Шарики на нити
IYPT 2019Team Ukraine 38
Наденьте шарик со сквозным отверстием на нить так, чтобы он мог свободно
двигаться вдоль нити. На конце нити закрепите другой шарик. Если
периодически двигать свободный конец нити, то можно наблюдать сложное
движение обоих шаров. Исследуйте явление.
Хаотические решения
• Универсальная
теоретическая модель для
численной симуляции
движения системы
Результаты и выводы
39.
Докладчик – Хорошко ИльяСпасибо за внимание!





















 physics
physics








