Линейная функция и её график

1.

2.

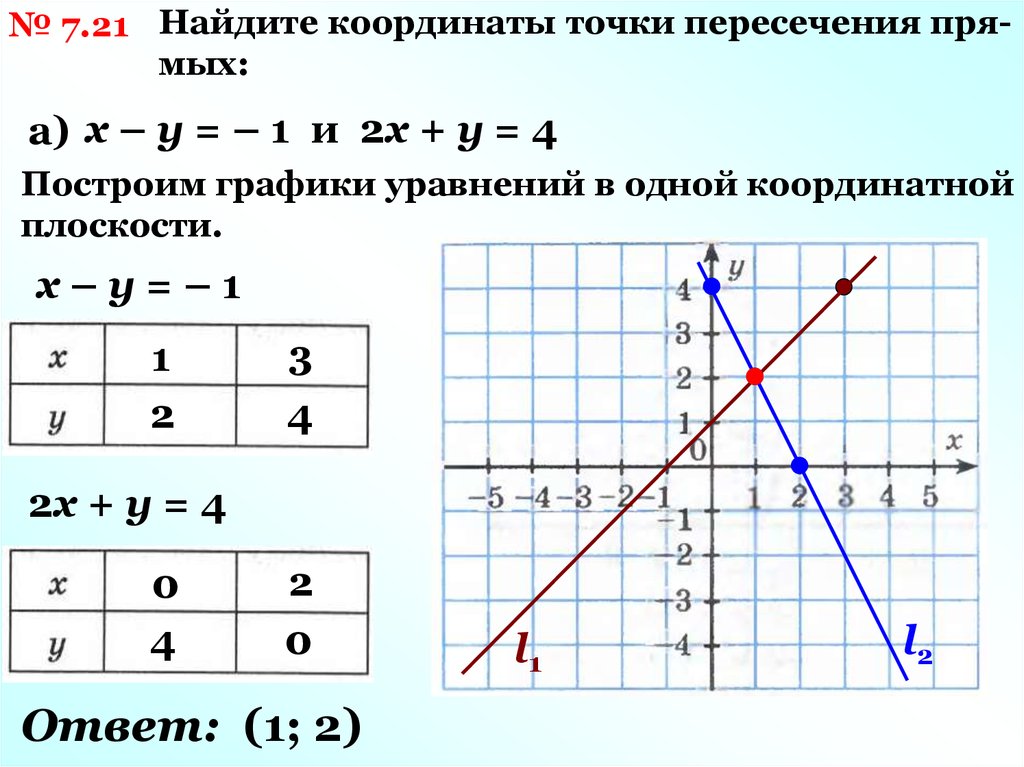
№ 7.21 Найдите координаты точки пересечения прямых:
а) х – у = – 1 и 2х + у = 4
Построим графики уравнений в одной координатной
плоскости.
х–у=–1
1
2
3
4
2х + у = 4
0
4
2
0
Ответ: (1; 2)
l1
l2

3.

№ 7.21 Найдите координаты точки пересечения прямых:
б) 4х + 3у = 6 и 2х + 3у = 0
Построим графики уравнений в одной координатной
плоскости.
4х + 3у = 6
0
2
1,5
0
2х + 3у = 0
0
0
3
–2
Ответ: (3; – 2)
l2
l1

4.

№ 7.23(а,б) Дано линейное уравнение с двумя переменными. Используя его, выразите каждую из переменных через другую:
а) 3а + 8b = 24
а через b
3a = – 8b + 24 : 3
8
a= b+8
3
b через a
8b = – 3а + 24 : 8
3
b= a+3
8

5.

№ 7.23(а,б) Дано линейное уравнение с двумя переменными. Используя его, выразите каждую из переменных через другую:
б) 6с + 5d = 30
с через d
6с = – 5d + 30 : 6
5
с= d +5
6
d через c
5d = – 6с + 30 : 5
6
d= c+6
5

6.

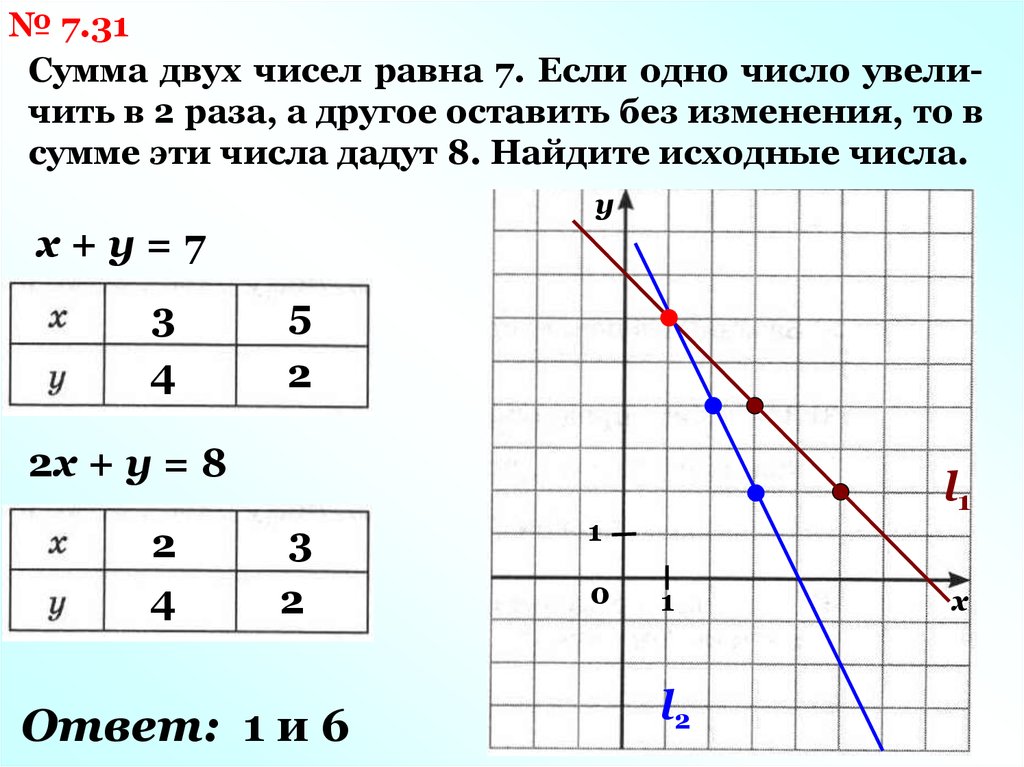
№ 7.31
Сумма двух чисел равна 7. Если одно число увеличить в 2 раза, а другое оставить без изменения, то в
сумме эти числа дадут 8. Найдите исходные числа.
I число – х
х+у=7
II число – у
2х + у = 8
Построим графики уравнений в одной координатной
плоскости.

7.

№ 7.31
Сумма двух чисел равна 7. Если одно число увеличить в 2 раза, а другое оставить без изменения, то в
сумме эти числа дадут 8. Найдите исходные числа.
у
х+у=7
3
4
5
2
2х + у = 8
2
4
3
2
Ответ: 1 и 6
l1
1
0
1
l2
х

8.

20.10.2019
Классная
р а б о т а.
Линейная функция и её график

9.

РТ № 8.1 1) Выразите у из уравнения:
а) – 6х + 3у – 9 = 0
3у = 6х + 9 : 3
у = 2х + 3
б) – 2х + 3у – 10 = 0
3у = 2х + 10 : 3
2
10
у= x+
3
3
в) 3х + 4у + 8 = 0
4у = – 3х – 8 : 4
у = – 0,75х – 2
г) ах + bу + c = 0
bу = – aх – c : b
с
а
у= x
b
b
у = kx + m

10.

РТ № 8.1
у = kx + m
а) – 6х + 3у – 9 = 0
3у = 6х + 9 : 3
у = 2х + 3
б) – 2х + 3у – 10 = 0
3у = 2х + 10 : 3
2
10
у= x+
3
3
у
в) 3х + 4у + 8 = 0
4у = – 3х – 8 : 4
у = – 0,75х – 2
г) ах + bу + c = 0
bу = – aх – c : b
с
а
у= x
b
b
линейной функцией

11.

РТ № 8.1
у = kx + m
а) – 6х + 3у – 9 = 0
3у = 6х + 9 : 3
у = 2х + 3
б) – 2х + 3у – 10 = 0
3у = 2х + 10 : 3
2
10
у= x+
3
3
а) k = 2
m=3
2
10
б) k =
m=
3
3
в) 3х + 4у + 8 = 0
4у = – 3х – 8 : 4
у = – 0,75х – 2
г) ах + bу + c = 0
bу = – aх – c : b
с
а
у= x
b
b
в) k = – 0,75 m = – 2

12.

№ 8.4(г) Преобразуйте уравнение к виду ли-
нейной функции у = kx + m и выпишите коэффициенты k и m.
9 x 11
у=
5
9 x 11
у=
5
5
у = 1,8х – 2,2
k =1,8
m = – 2,2

13.

№ 8.5(г) Преобразуйте уравнение к виду ли-
нейной функции у = kx + m и выпишите коэффициенты k и m.
16 4 x
у=
8
16 4 x
у=
8
8
у = – 2 – 0,5х
у = – 0,5х – 2
k = – 0,5 m = – 2

14.

РТ № 8.2 Дана линейная функция у = 2х + 3
1) Заполните таблицу:
–1
1
3
5
7
9
11
у = 2 · (– 2) + 3 = – 4 + 3 = – 1
2) Значения у из второй строчки называют
значениями линейной функции
3) х – независимая переменная (или аргумент)
у – зависимая переменная

15.

РТ № 8.3 Найдите значение линейной функ-
ции у = 3х – 1 при данном значении
аргумента.
х=5
Образец.
у = 3х – 1
у=3·5–1
у = 14
Ответ: 14
а) х = 4;
б) х = – 2;
в) х = 2,5

16.

РТ № 8.3 Найдите значение линейной функ-
ции у = 3х – 1 при данном значении
аргумента.
а) х = 4
у = 3х – 1
у=3·4–1
у = 11
Ответ: 11
б) х = – 2; у = 3х – 1
у = 3 · (– 2) – 1
у=–7
Ответ: – 7

17.

РТ № 8.3 Найдите значение линейной функ-
ции у = 3х – 1 при данном значении
аргумента.
в) х = 2,5
у = 3х – 1
у = 3 · 2,5 – 1
у = 6,5
Ответ: 6,5

18.

РТ № 8.4 Дана линейная функция у = 5х – 2,5.
Найдите значение х, которому соответствует данное значение у.
Образец.
у=7
7 = 5х – 2,5
5х – 2,5 = 7
5х = 7 + 2,5
5х = 9,5 : 5
х = 1,9
Ответ: 1,9
а) у = 8,5;
в) у = – 12,5;

19.

РТ № 8.4 Дана линейная функция у = 5х – 2,5.
Найдите значение х, которому соответствует данное значение у.
а) у = 8,5
8,5 = 5х – 2,5
5х – 2,5 = 8,5
5х = 8,5 + 2,5
5х = 11 : 5
х = 2,2
Ответ: 2,2

20.

РТ № 8.4 Дана линейная функция у = 5х – 2,5.
Найдите значение х, которому соответствует данное значение у.
в) у = – 12,5
– 12,5 = 5х – 2,5
5х – 2,5 = – 12,5
5х = – 12,5 + 2,5
5х = – 10 : 5
х=–2
Ответ: – 2

21.

У: стр. 47 § 8
З: § 8 № 1 – 2(а,б); 4(а);
5(б); 8(а,б);
11(а,б); 14(а,б);
16(а,б).

22.

В – 1 № 8.2(в); 8.9(в);
8.14(в); 8.16(в).
В – 2 № 8.2(г); 8.9(б);
8.14(г); 8.16(г).