Координатная прямая. Урок 14

1.

2.

№ 5.7(а,б)
а) (3; + ∞)
IIIIIIIIIIIIII
х
3
Открытый луч
x>3
б) (– ∞; – 5)
IIIIIIIIIIII
–5
Открытый луч
x< –5
х

3.

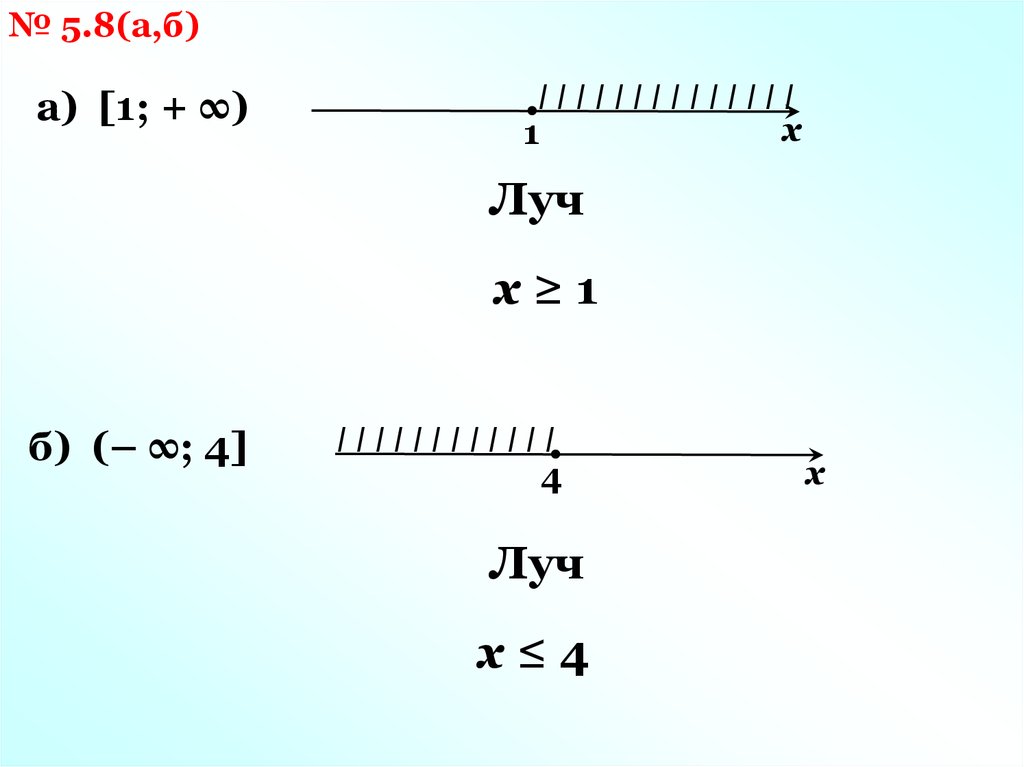
№ 5.8(а,б)
а) [1; + ∞)
IIIIIIIIIIIIII
х
1
Луч
x≥1
б) (– ∞; 4]
IIIIIIIIIIII
4
Луч
x≤4
х

4.

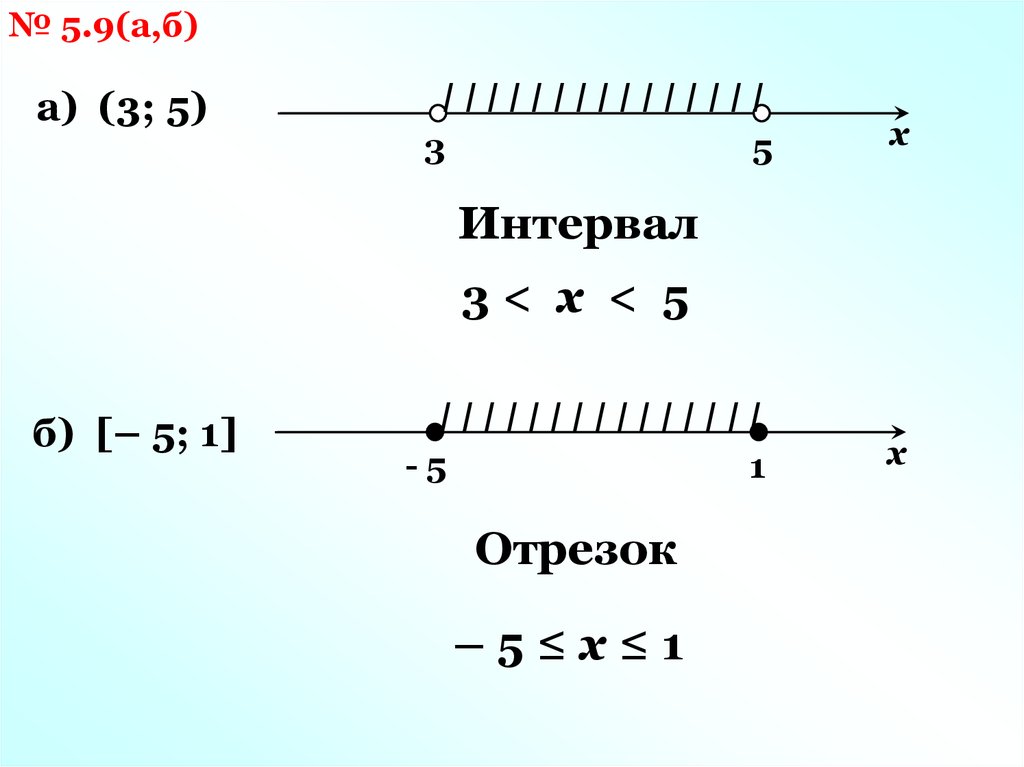
№ 5.9(а,б)
а) (3; 5)
IIIIIIIIIIIIIII
3
5
х
Интервал
3< x < 5
б) [– 5; 1]
IIIIIIIIIIIIIII
-5
1
Отрезок
–5≤x≤1
х

5.

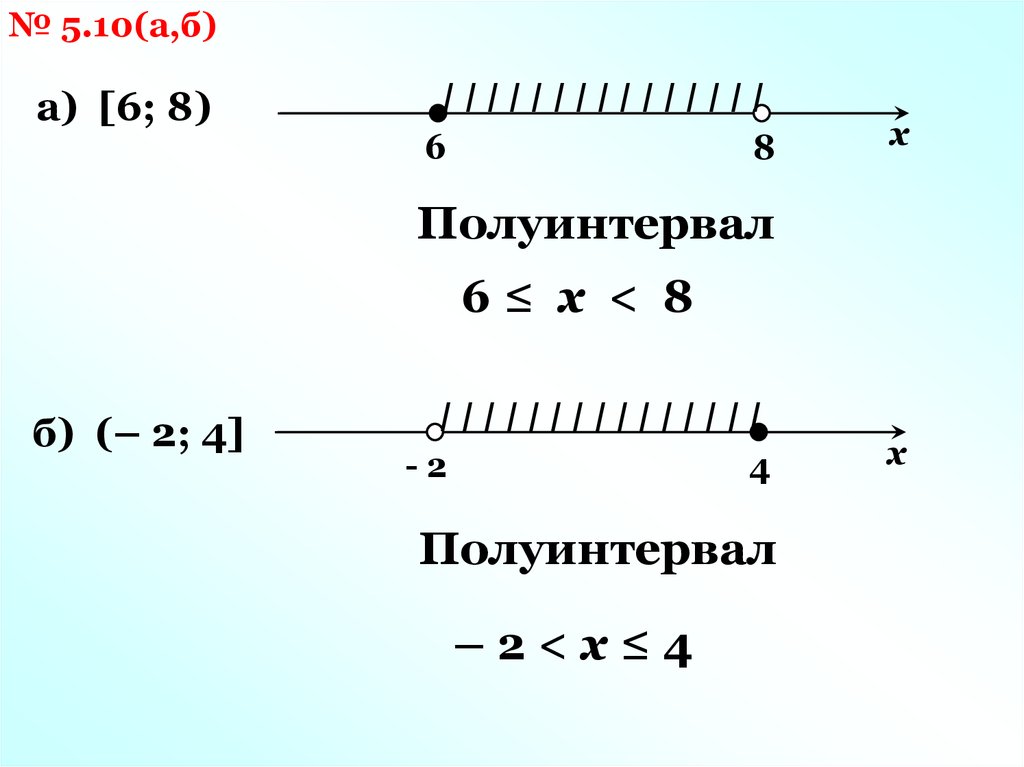
№ 5.10(а,б)
а) [6; 8)
IIIIIIIIIIIIIII
6
8
х
Полуинтервал
6≤ x < 8
б) (– 2; 4]
IIIIIIIIIIIIIII
-2
4
Полуинтервал
–2<x≤4
х

6.

№ 5.11(а,б)
Открытый луч
(5; +∞)
x>5
Открытый луч
(– ∞; – 7)
x< –7

7.

№ 5.12(а,б)
Луч
[2; +∞)
y≥2
Луч
(– ∞; 1]
y≤1

8.

№ 5.13(а,б)
Интервал
(3; 5)
3< а < 5
Отрезок
[3; 5]
3≤ а ≤ 5

9.

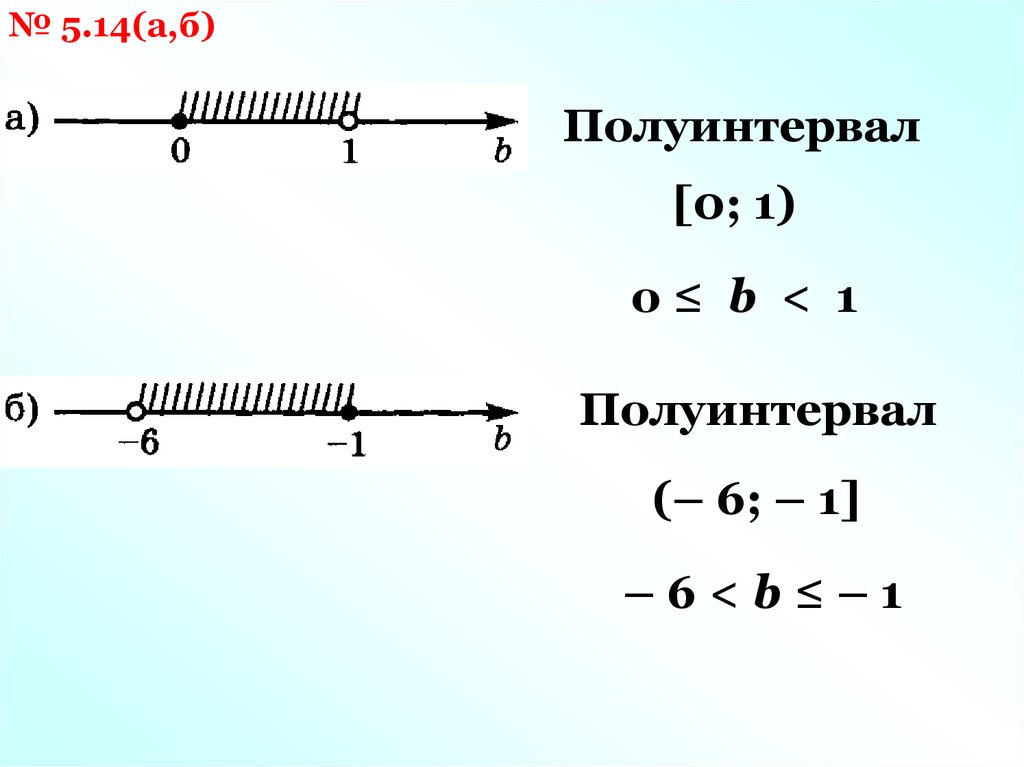
№ 5.14(а,б)
Полуинтервал
[0; 1)
о≤ b < 1
Полуинтервал
(– 6; – 1]
–6<b≤–1

10.

№ 5.17(а,б)
а) x > 3
IIIIIIIIIIIIII
х
3
Открытый луч
(3; +∞)
б) x ≥ 3
IIIIIIIIIIIIII
х
3
Луч
[3; +∞)

11.

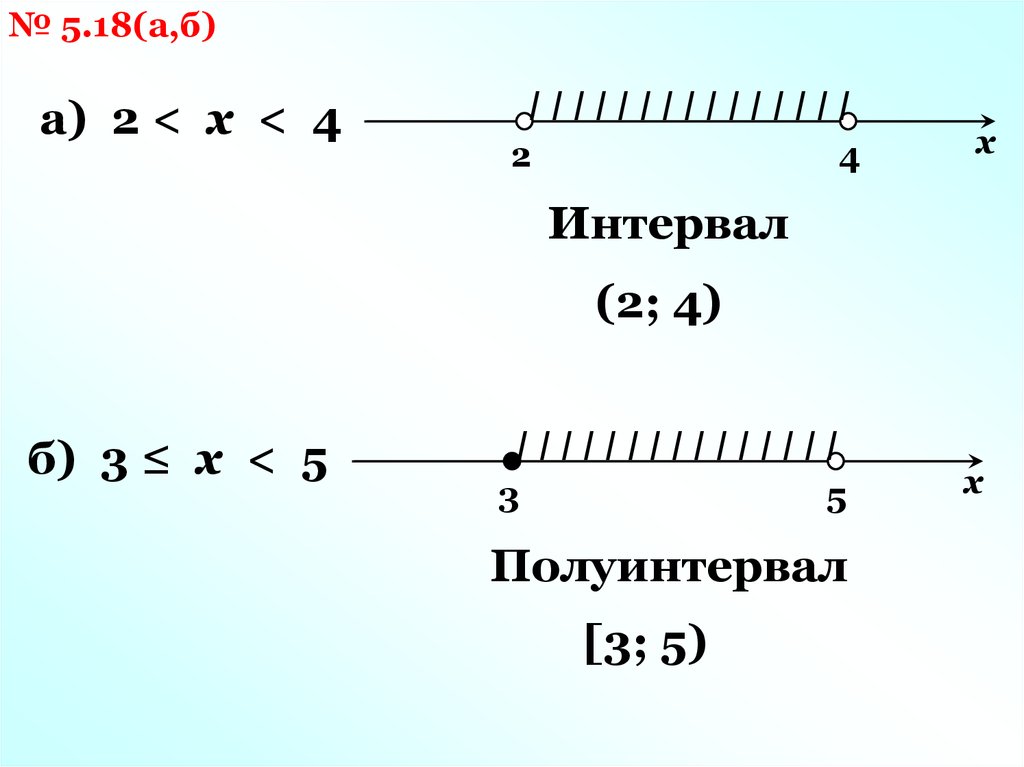
№ 5.18(а,б)
а) 2 < х < 4
IIIIIIIIIIIIIII
2
4
х
Интервал
(2; 4)
б) 3 ≤ х < 5
IIIIIIIIIIIIIII
3
5
Полуинтервал
[3; 5)
х

12.

№ 5.19(а,б)
а) x ≥ 2
IIIIIIIIIIIIII
х
2
Луч
[2; +∞)
б) - 5 < х < - 2
IIIIIIIIIIIIIII
-5
-2
Интервал
(- 5; - 2)
х

13.

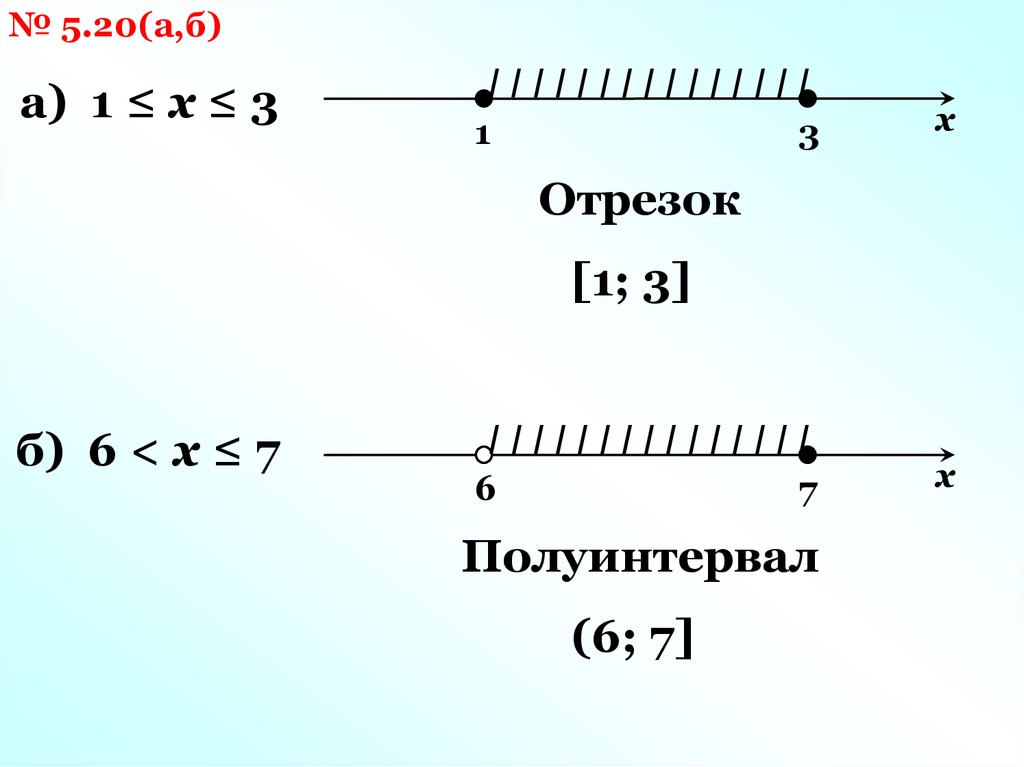
№ 5.20(а,б)
а) 1 ≤ х ≤ 3
IIIIIIIIIIIIIII
1
3
х
Отрезок
[1; 3]
б) 6 < х ≤ 7
IIIIIIIIIIIIIII
6
7
Полуинтервал
(6; 7]
х

14.

13.10.2019
Классная
р а б о т а.
Координатная прямая

15.

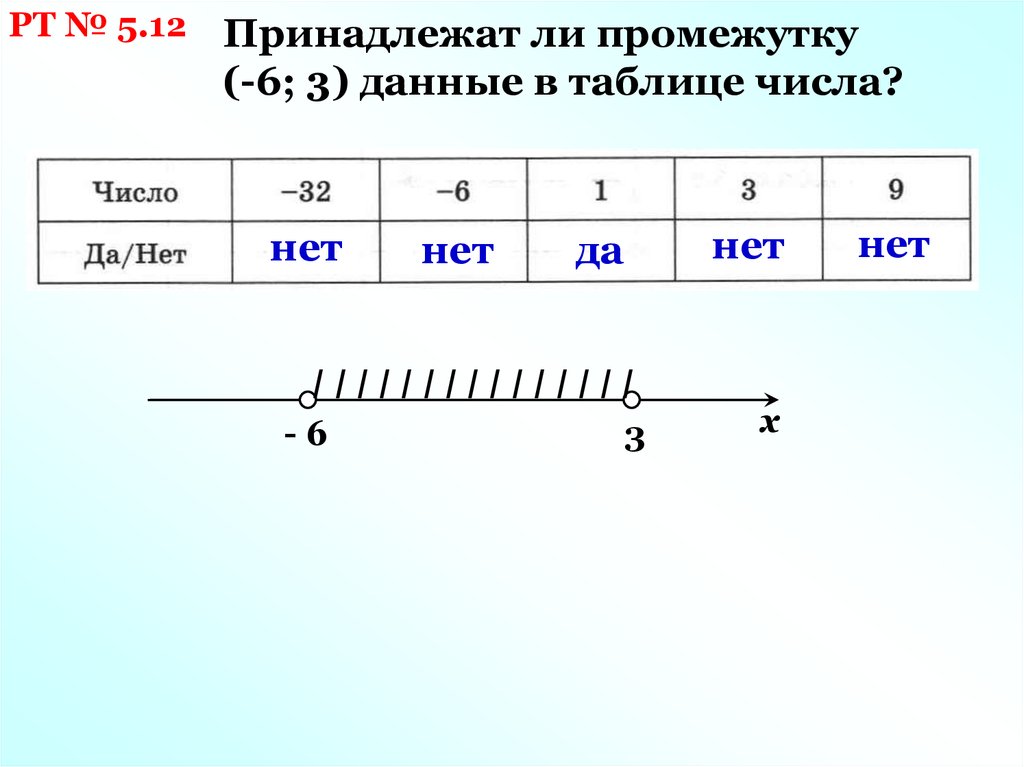
РТ № 5.12
Принадлежат ли промежутку
(-6; 3) данные в таблице числа?
нет
нет
нет
да
IIIIIIIIIIIIIII
-6
3
х
нет

16.

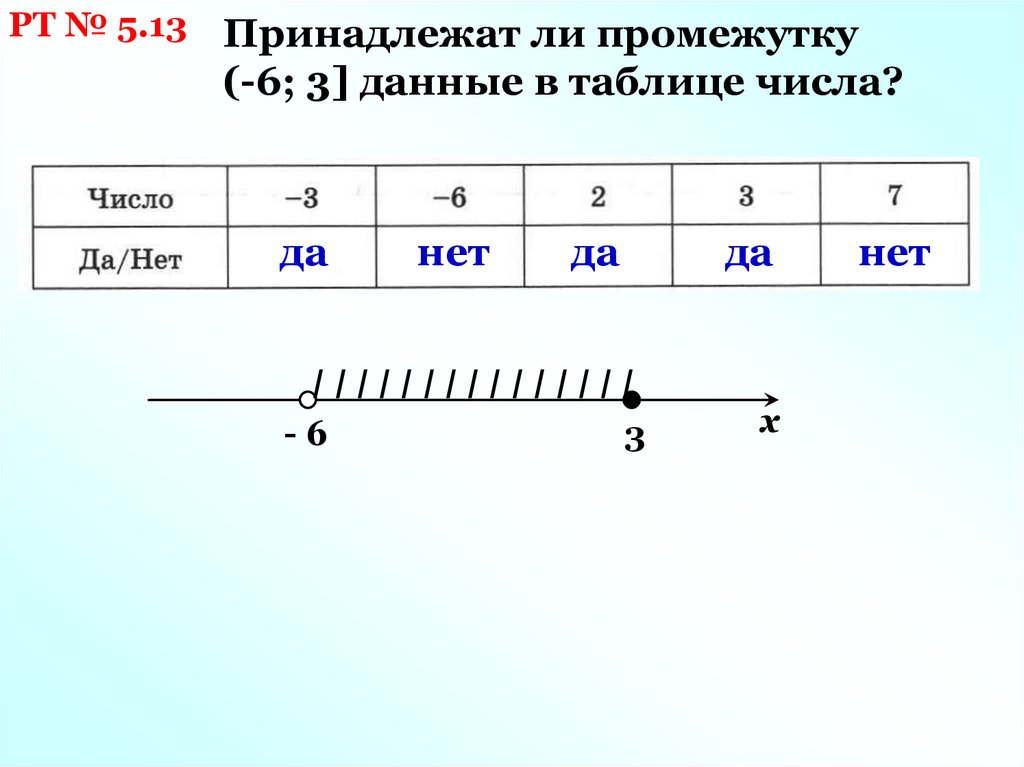
РТ № 5.13
Принадлежат ли промежутку
(-6; 3] данные в таблице числа?
да
нет
да
да
IIIIIIIIIIIIIII
-6
3
х
нет

17.

РТ № 5.14
Принадлежат ли промежутку
(6; +∞) данные в таблице числа?
нет
нет
нет
да
IIIIIIIIIIIIII
х
6
да

18.

РТ № 5.15
Принадлежат ли промежутку
[5; +∞) данные в таблице числа?
нет
нет
да
да
IIIIIIIIIIIIII
х
5
да

19.

РТ № 5.16
Запишите все целые числа
принадлежащие промежутку:
6, 7, 8
7, 8
7
6, 7

20.

РТ № 5.17
Запишите все натуральные числа
принадлежащие промежутку:
1; 2
1
1
2

21.

№ 5.15 По названию числового промежутка запишите его обозначение, постройте геометрическую и аналитическую модели:
а) Открытый луч с началом в точке 5;
IIIIIIIIIIIIII
х
5
(5; + ∞)
x>5

22.

№ 5.15 По названию числового промежутка запишите его обозначение, постройте геометрическую и аналитическую модели:
б) Луч с началом в точке – 2;
IIIIIIIIIIIIII
х
–2
[– 2; + ∞)
x≥–2

23.

№ 5.15 По названию числового промежутка запишите его обозначение, постройте геометрическую и аналитическую модели:
в) Интервал с началом в точке 1 и концом в точке 3;
IIIIIIIIIIIIIII
1
3
(1; 3)
1< x < 3
х

24.

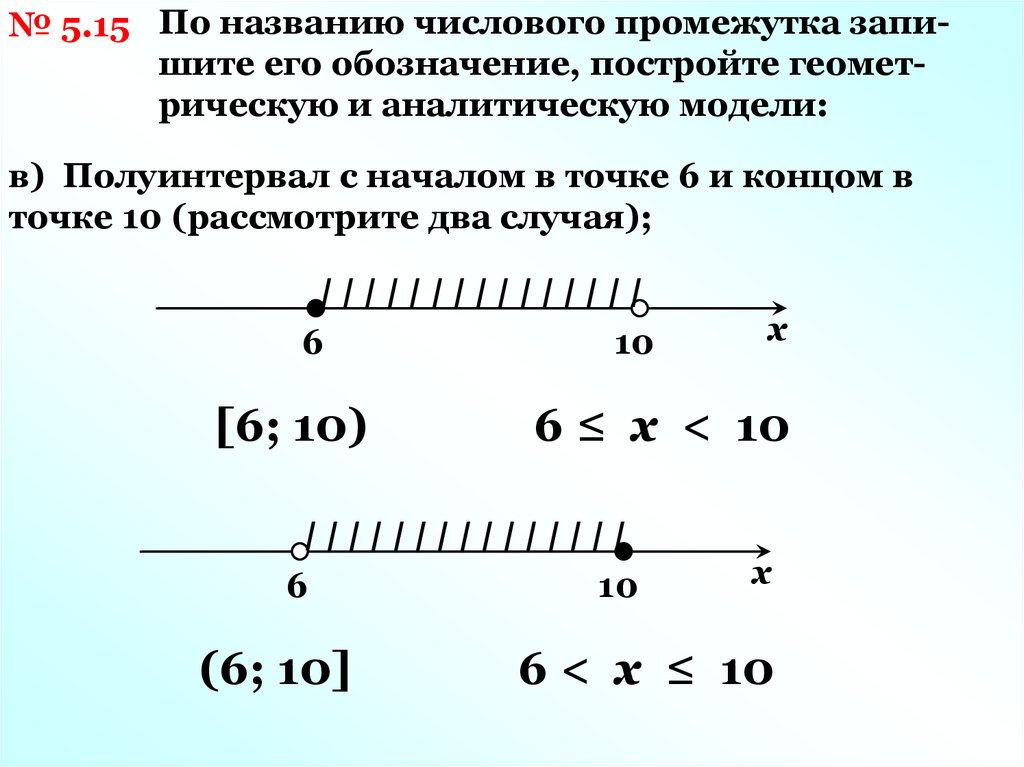
№ 5.15 По названию числового промежутка запишите его обозначение, постройте геометрическую и аналитическую модели:
в) Полуинтервал с началом в точке 6 и концом в
точке 10 (рассмотрите два случая);
IIIIIIIIIIIIIII
6
[6; 10)
10
6 ≤ x < 10
IIIIIIIIIIIIIII
6
(6; 10]
х
10
х
6 < x ≤ 10

25.

№ 1.16(в,г)
в) – 1,06 + 0,04 – 7,04 + 2,16 = 1,1 – 7 =
= – 5,9
г) 18,9 – 6,8 – 5,2 + 4,1 = 23 – 12 = 11

26.

№ 1.17(б,г)
3
3 3
б) 42,4 2,4 = (42,4 2,4) =
4
4 4
10
3
3 40
= 40 =
= 30
4
4
1
1
1
г) 6 4,8+6 5,2 = 6 (4,8+ 5,2) =
5
5
5
2
31
31 10
=
10 =
= 62
5
5

27.

№ 1.25(а)
Упростите выражение и найдите его
значение:
3(2х + у) – 4(2у – х) = 6х + 3у – 8у + 4х =
= 10х – 5у
2
если х = 0,5, у = , то 10х – 5у =
5
2
5 2
= 10 0,5 5 = 5
=5+2=7
5
5

28.

Решите уравнение:
а) – 12х + 9 = 37
– 12х = 37 – 9
7х – 15х = – 60 + 2
– 12х = 28
– 12 – 12
– 8х = – 58
–8
–8
7
х=
3
29
х=
4
7
Ответ:
3
1
Ответ: 7
4

29.

№ 3.35 Решите задачу, выделяя три этапа математического моделирования:
В жилом доме всего 215 квартир. Сколько из них
однокомнатных, если известно, что трёхкомнатных квартир на 10 меньше, чем двухкомнатных,
и на 5 больше, чем однокомнатных?
I
Квартиры
1-комн.
2-комн.
3-комн.
Кол-во
x
x + 5 + 10
x+5
x + x + 15 + x + 5 = 215
215 кв

30.

№ 3.35 Решите задачу, выделяя три этапа математического моделирования:
В жилом доме всего 215 квартир. Сколько из них
однокомнатных, если известно, что трёхкомнатных квартир на 10 меньше, чем двухкомнатных,
и на 5 больше, чем однокомнатных?
II 3x + 20 = 215
3x = 215 – 20
3x = 195
x = 65
III Ответ: 65 квартир
Квартиры
1-комн.
2-комн.
3-комн.
Кол-во
x
x + 5 + 10
x+5

31.

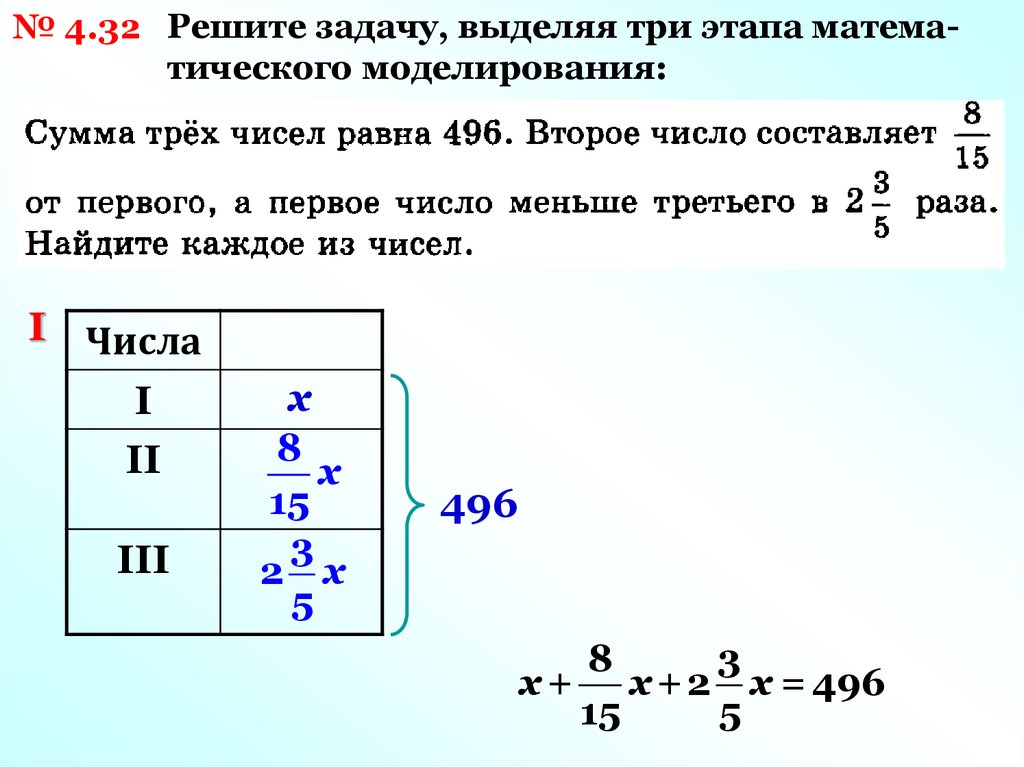
№ 4.32 Решите задачу, выделяя три этапа математического моделирования:
I Числа
I
II
III
x
8
х
15
3
2 х
5
496
8
3
х + х + 2 х = 496
15
5

32.

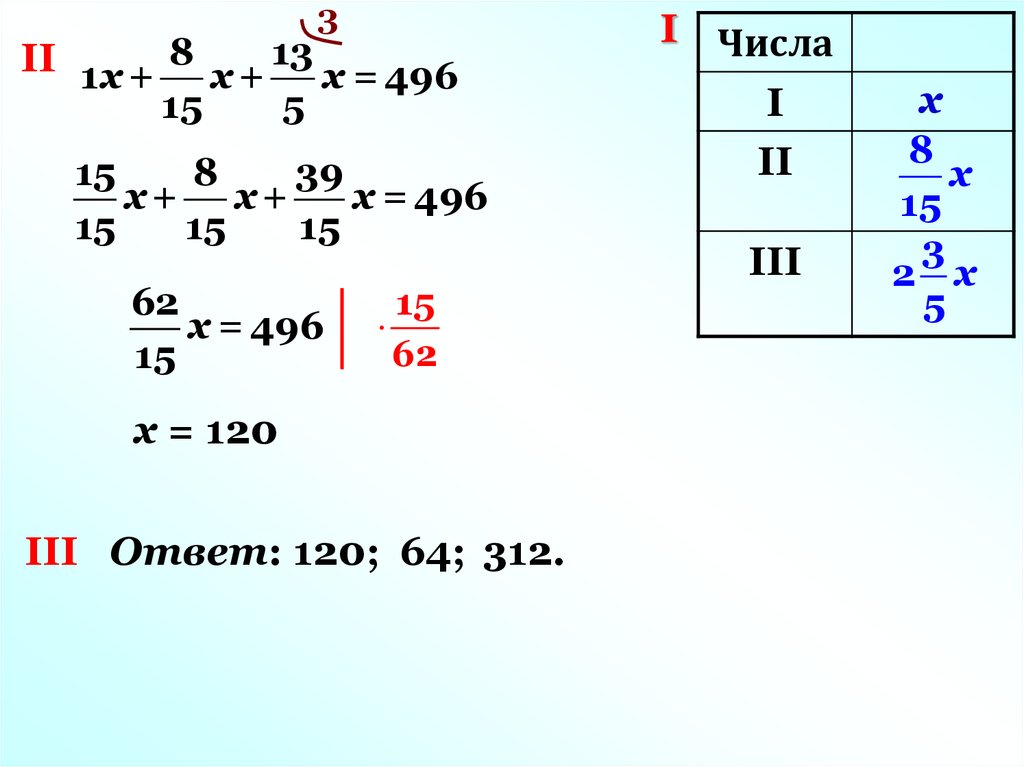
3
II 1 х + 8 х + 13 х = 496
15
5
15
8
39
х+ х+
х = 496
15
15
15
62
х = 496
15
15
62
x = 120
III Ответ: 120; 64; 312.
I Числа
I
II
III
x
8
х
15
3
2 х
5

33.

З: § 5 № 21 – 34(а,б).