Расположение прямых на плоскости. Расстояние от точки до прямой на плоскости

1.

РАЗДЕЛ II
ВЕКТОРНАЯ АЛГЕБРА.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
ЛЕКЦИЯ 3
РАСПОЛОЖЕНИЕ ПРЯМЫХ
НА ПЛОСКОСТИ.
РАССТОЯНИЕ ОТ ТОЧКИ
ДО ПРЯМОЙ НА ПЛОСКОСТИ

2.

Найдём
на
который
надо
вокруг
Дано:
l1:угол,
y=k1x+b
l2: y=k
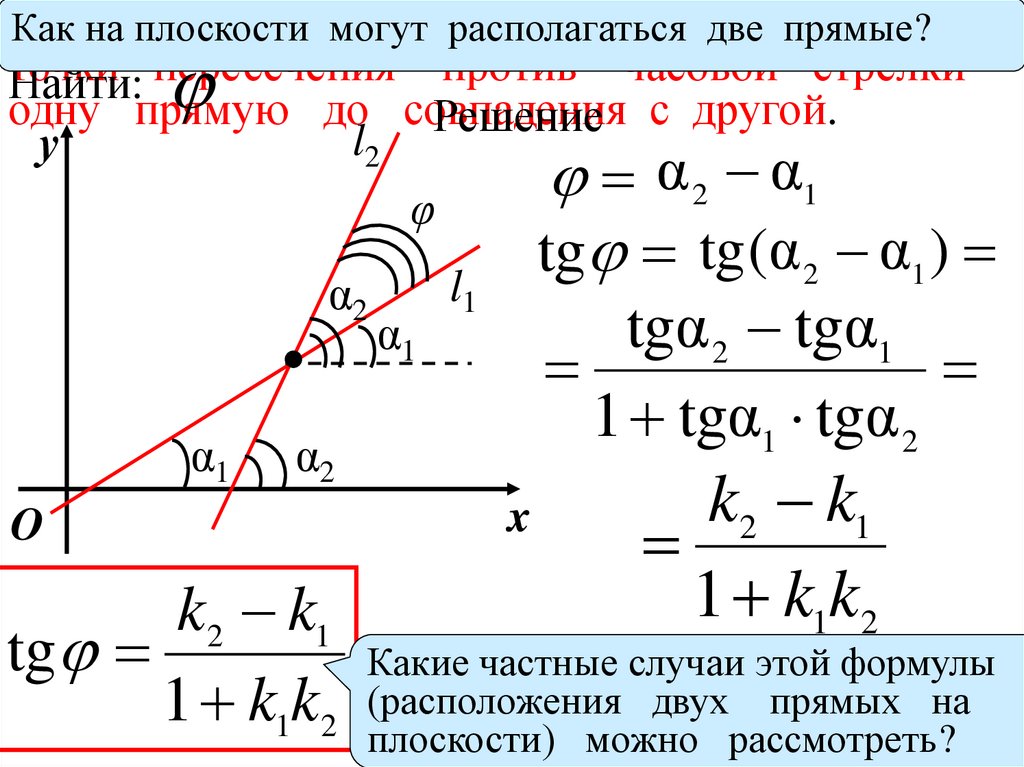
Как
на плоскости
могут
1 , располагаться
2x+bповернуть
2 две прямые?
точки
Найти: пересечения против часовой стрелки
одну прямую до совпадения
Решение с другой.
l2
у
α 2 α1
φ
α2
α1
α1
tg tg (α 2 α1 )
tgα 2 tgα1
1 tgα1 tgα 2
l1
α2
O
k2 k1
tg
1 k1k2
x
k2 k1
1 k1k2
Какие частные случаи этой формулы
(расположения двух прямых на
плоскости) можно рассмотреть?

3.

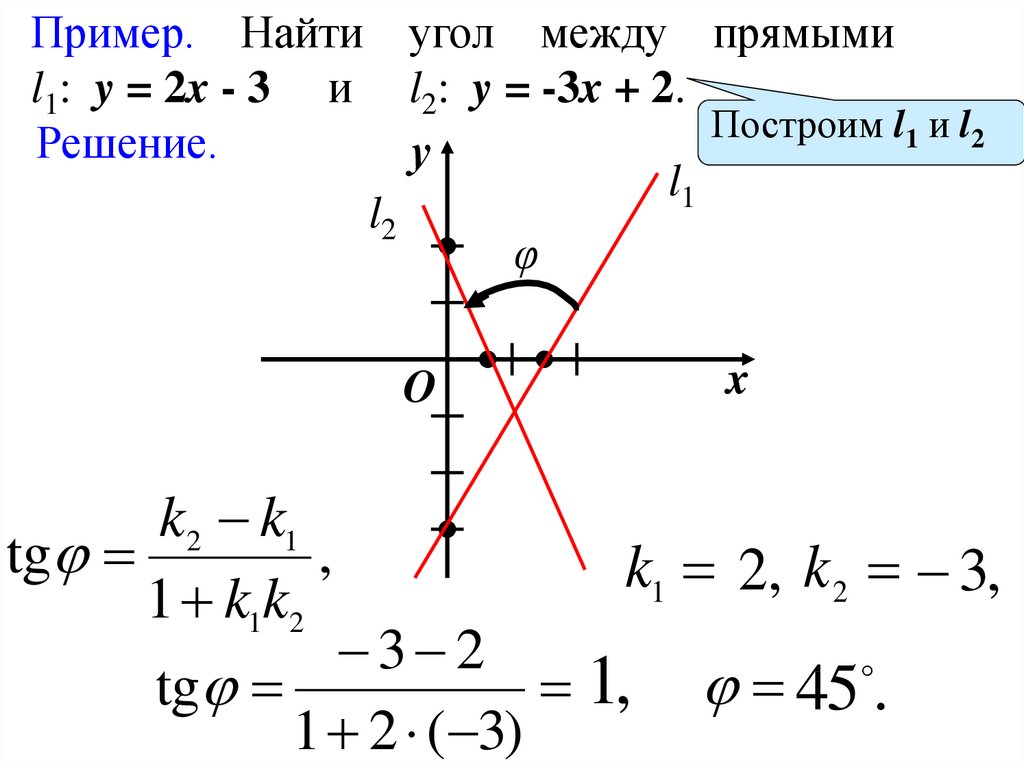
Пример. Найти угол между прямыми
l1: y = 2x - 3 и l2: y = -3x + 2.
Построим l1 и l2
Решение.
у
l1
l2
φ
O
x
k2 k1
tg
,
k1 2, k 2 3,
1 k1k2
3 2
tg
1, 45 .
1 2 ( 3)

4.

π не существует
π
l1 l2 tg
2 1 k k
2
1 2
Рассмотрим сtg
Условие перпендикулярности
k2 k1
двух прямых с известными угловыми
коэффициентами
1
π
сtg 0 1 k1k2 0 k 2
k1
2
l1 || l2 0 tg 0 0 k 2 k1 0
k1 k 2
Условие параллельности двух прямых
с известными угловыми коэффициентами

5.

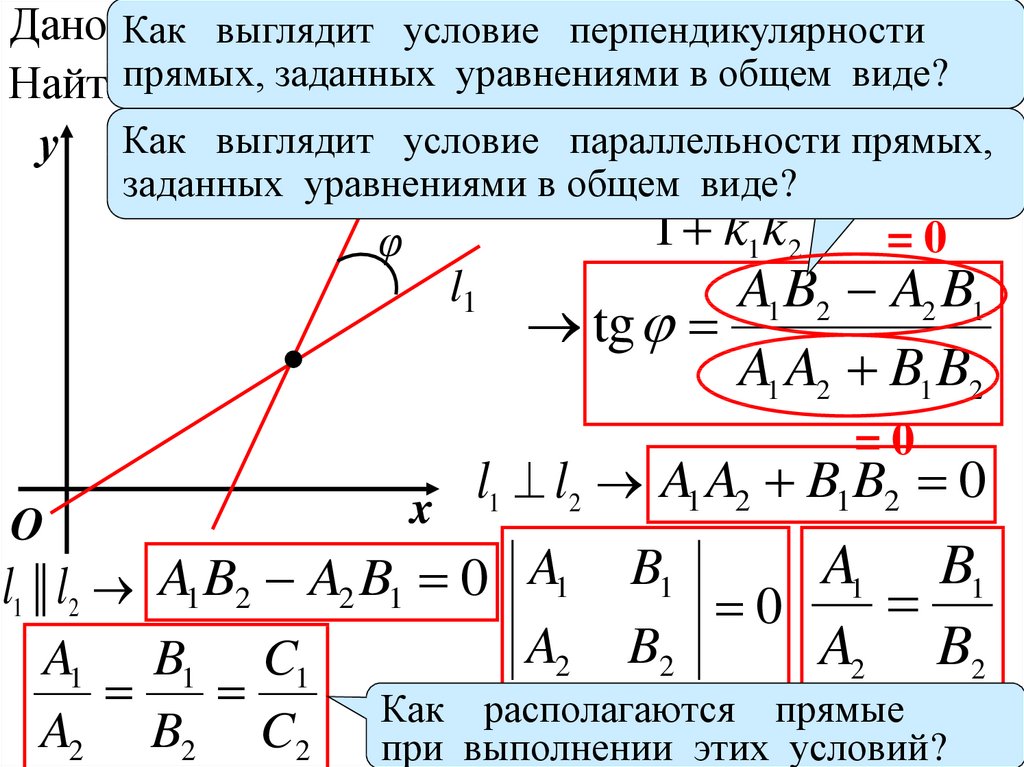
Дано: Как
l1: A
l2: A2 x эту
C1 0, перпендикулярности
выглядит
условие
Получите
B2 yформулу
C2 0
1 x B1 y
самостоятельно
в общем виде?
Найти:прямых, заданных уравнениями
Решение
у Как выглядитl2 условие параллельности
k 2 k1 прямых,
заданных уравнениямиtg
в
общем
виде?
φ
l1
1 k1k 2
=0
A1 B2 A2 B1
tg
A1 A2 B1 B2
=0
A
A
B
B
0
l
l
1
2
1
2
1
2
x
O
l1 || l2 A1 B2 A2 B1 0 A1 B1 0 A1 B1
A2 B2
A2 B2
A1 B1 C1
Как располагаются прямые
A2 B2 C2 при выполнении этих условий?

6.

Пример. Указать, какие из следующих прямых
l1: 3x - 15y +16=0,
l2: 3x + 15y -8=0,
l3: 6x - 30y +13=0,
l4: 30x + 6y -7=0
параллельны или перпендикулярны.
Пример. Составить уравнение прямой,
проходящей через точку M(2;3)
а) параллельно прямой l: 2x +5y +1=0;
б) перпендикулярно к этой прямой.
Пример. Определить, пересекает ли прямая
l: 2x - 2y + 5 = 0 отрезок, концами которого
являются точки
а) A(1;2), B(-2;3);
б) C(1;1), D(19;-1).

7.

Расстоянием от точки до прямой называется
длина перпендикуляра, опущенного из этой
точки на данную прямую.
у
Теорема 3.1. Расстояние d
М1(х1; y1) от данной точки M (x ;y )
1
O
1
1
до прямой l, заданной
d ( M1;l ) уравнением Ax+By+C=0,
на плоскости
определяется формулой:
l x
d
Ax1 By1 C
A B
2
2
.

8.

Пример. Найти расстояние от точки M1(2;3)
до прямой l: 3x + 4y – 22 = 0.
Пример. Найти расстояние между параллельными
прямыми l1: 4x + 3y – 15 = 0 и l2: -8x - 6y + 5 = 0.