Similar presentations:
Степенная функция и ее свойства и график
1.
26.09.19Классная работа
Степенная функция,
её свойства и график
2.
Определение функцииЕсли каждому значению х из
некоторого множества чисел Х
поставлено в соответствие число у,
то говорят, что на этом множестве
задана функция у(х).
х–
у–
независимая переменная или
аргумент
зависимая переменная или
функция
3.
Областью определения функцииназывают множество всех
значений, которые может
принимать её аргумент.
Графиком функции называется
множество всех точек координатной
плоскости, абсциссы которых равны
значениям независимой переменной,
а ординаты – соответствующим
значениям функции.
4.
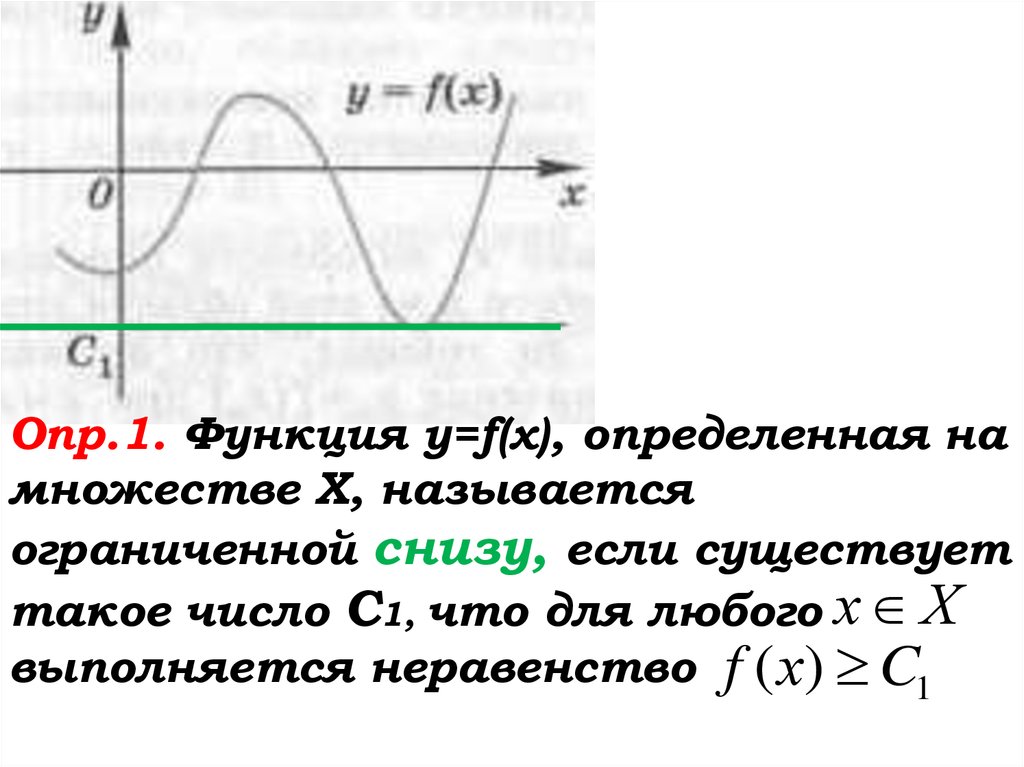
Опр.1. Функция у=f(x), определенная намножестве Х, называется
ограниченной снизу, если существует
такое число С1, что для любого х Х
выполняется неравенство f ( х) C1
5.
Опр.1. Функция у=f(x), определенная намножестве Х, называется
ограниченной сверху, если
существует такое число С2, что для
любого х Хвыполняется неравенство
f ( х) C2
6.
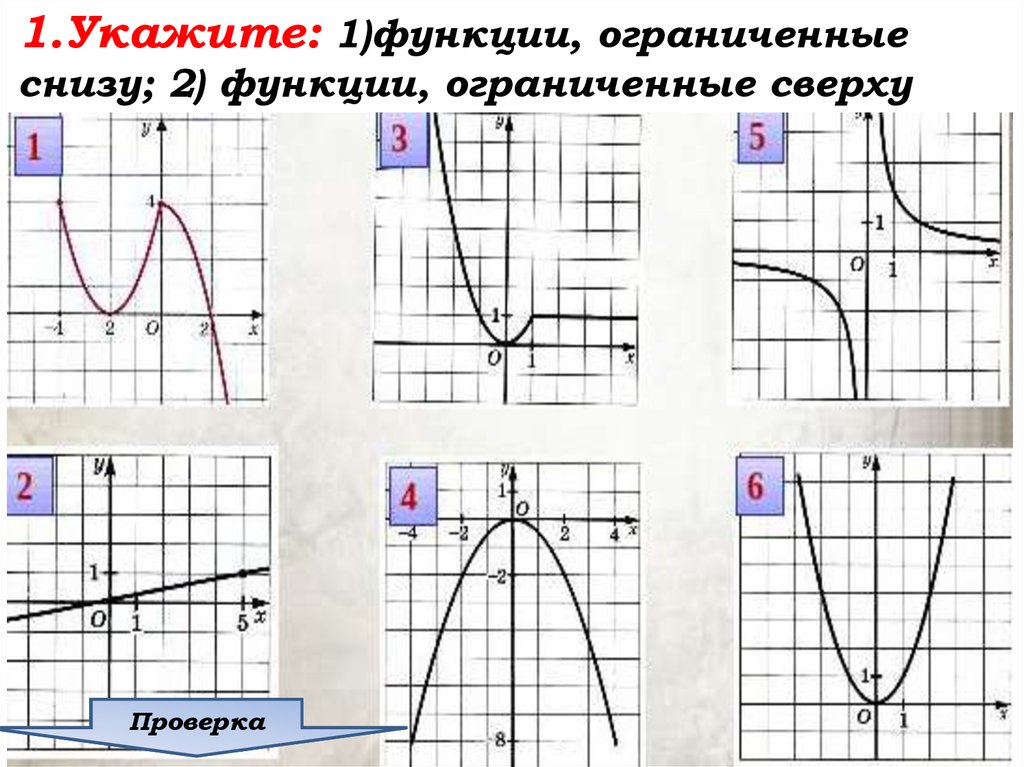
1.Укажите: 1)функции, ограниченныеснизу; 2) функции, ограниченные сверху
Проверка
7.
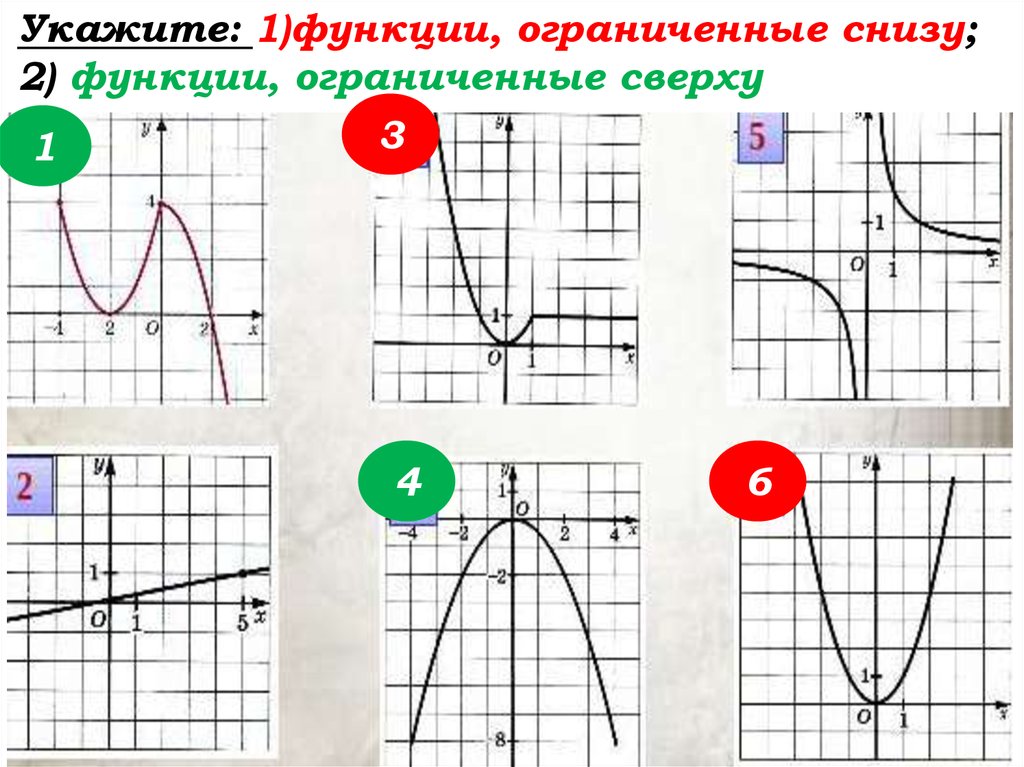
Укажите: 1)функции, ограниченные снизу;2) функции, ограниченные сверху
3
1
4
6
8.
Функция у f (х) , х Х называетсянеограниченной, если для любого С 0
найдется значение хс Х , такое,
что
f ( xС ) C
9.
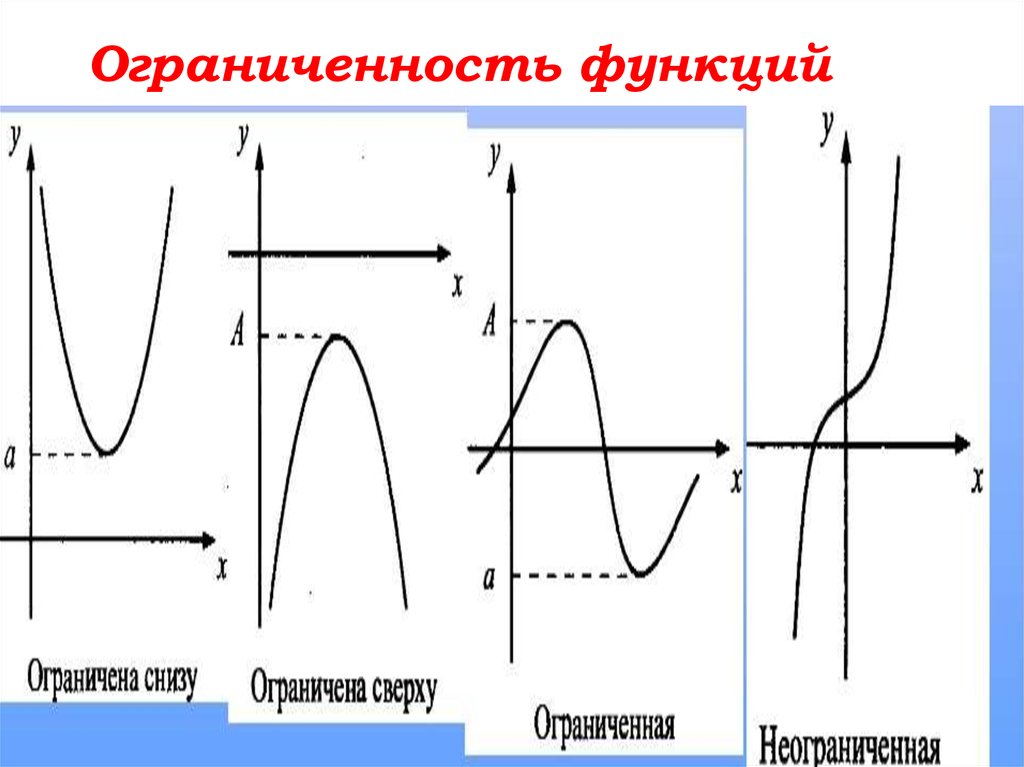
Ограниченность функций10.
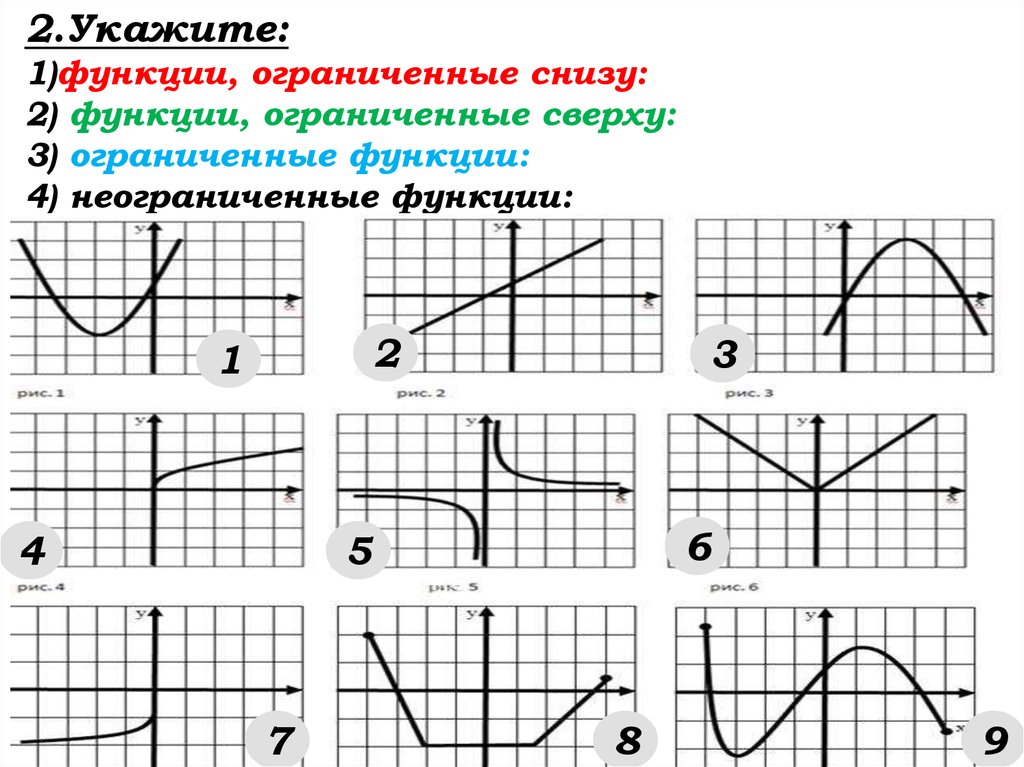
2.Укажите:1)функции, ограниченные снизу:
2) функции, ограниченные сверху:
3) ограниченные функции:
4) неограниченные функции:
2
1
4
3
6
5
7
8
9
11.
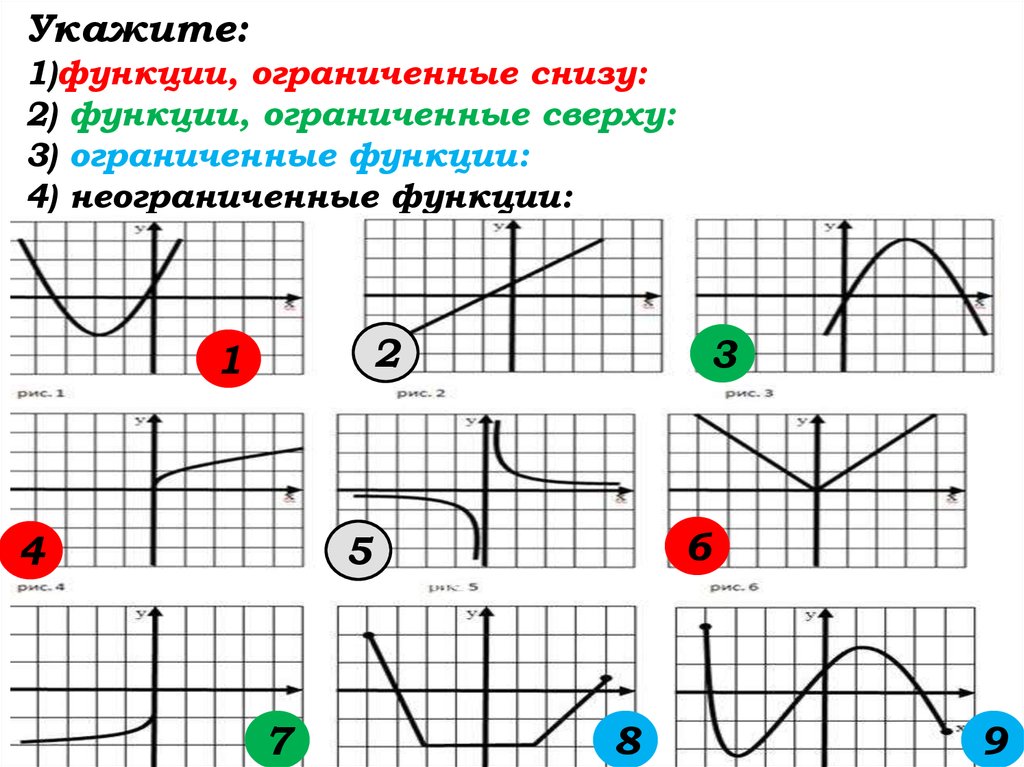
Укажите:1)функции, ограниченные снизу:
2) функции, ограниченные сверху:
3) ограниченные функции:
4) неограниченные функции:
2
1
4
3
6
5
7
8
9
12.
х0у0
Если существует такое значение х0
из области определения Х функции
у f (х), что для любого х из этой
области справедливо неравенство
f ( х) f ( x0 ), то говорят, что
функция у f (х), принимает
наименьшее значение
у0 f ( х0 ) при х х0
13.
у0х0
Если существует такое значение х0
из области определения Х функции
у f (х), что для любого х из этой
области справедливо неравенство
f ( х) f ( x0 ), то говорят, что
функция у f (х), принимает
наибольшее значение
у0 f ( х0 ) при х х0
14.
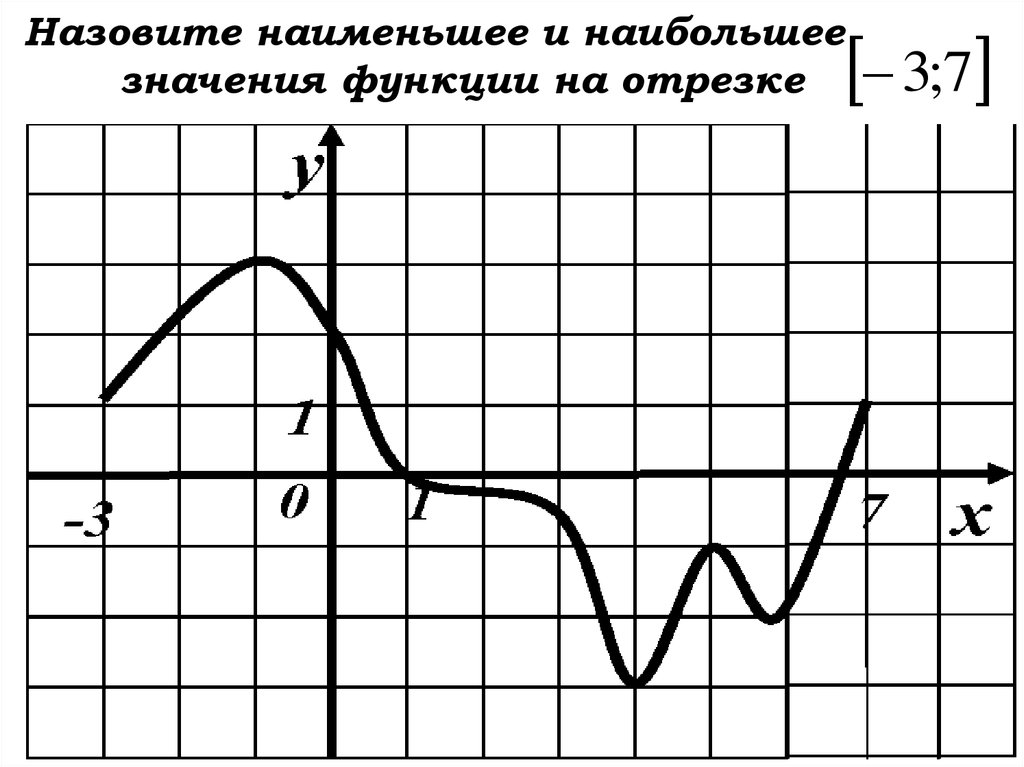
Назовите наименьшее и наибольшеезначения функции на отрезке
3;7
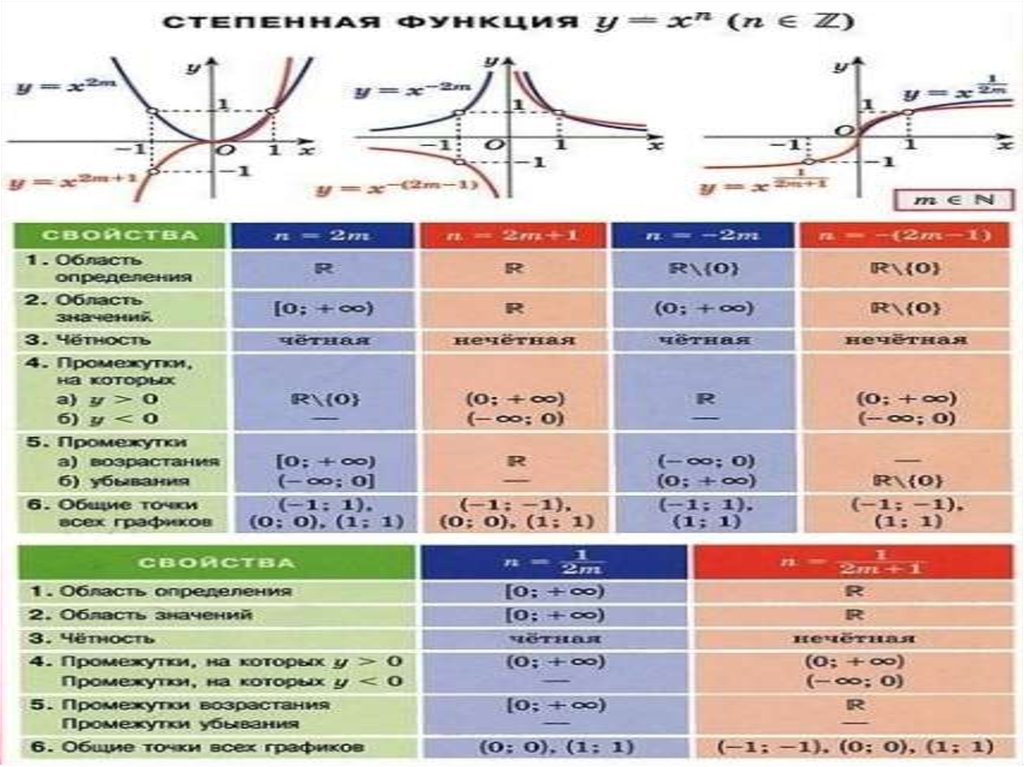
15.
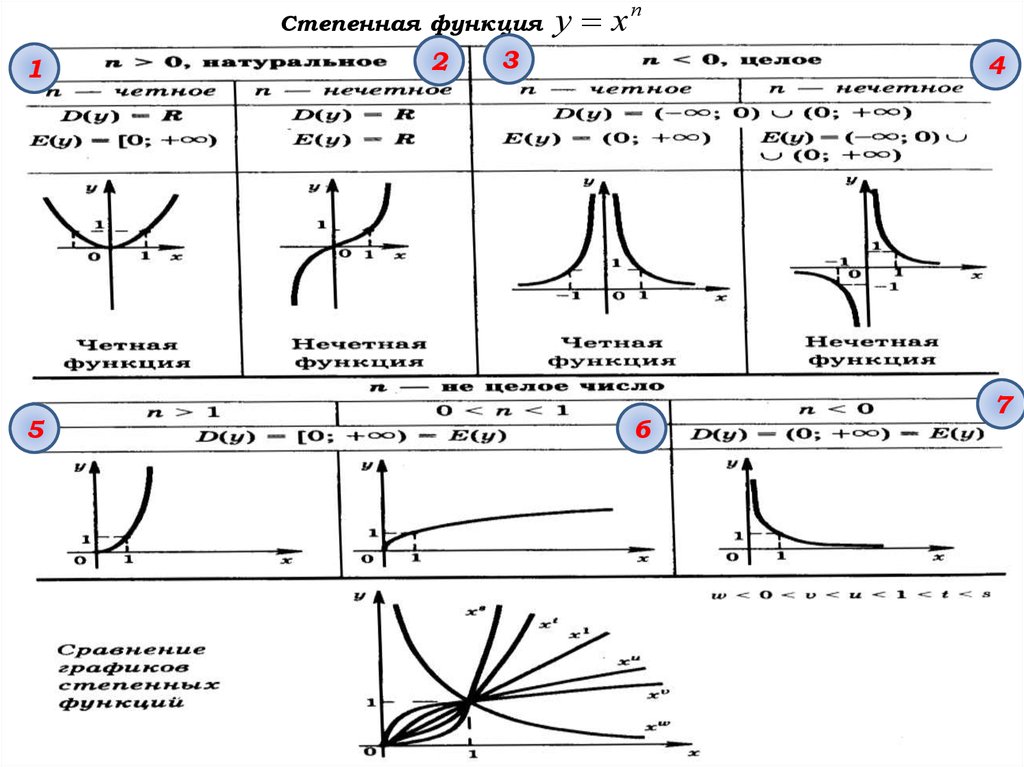
Степенная функция1
5
2
у хп
3
4
6
7
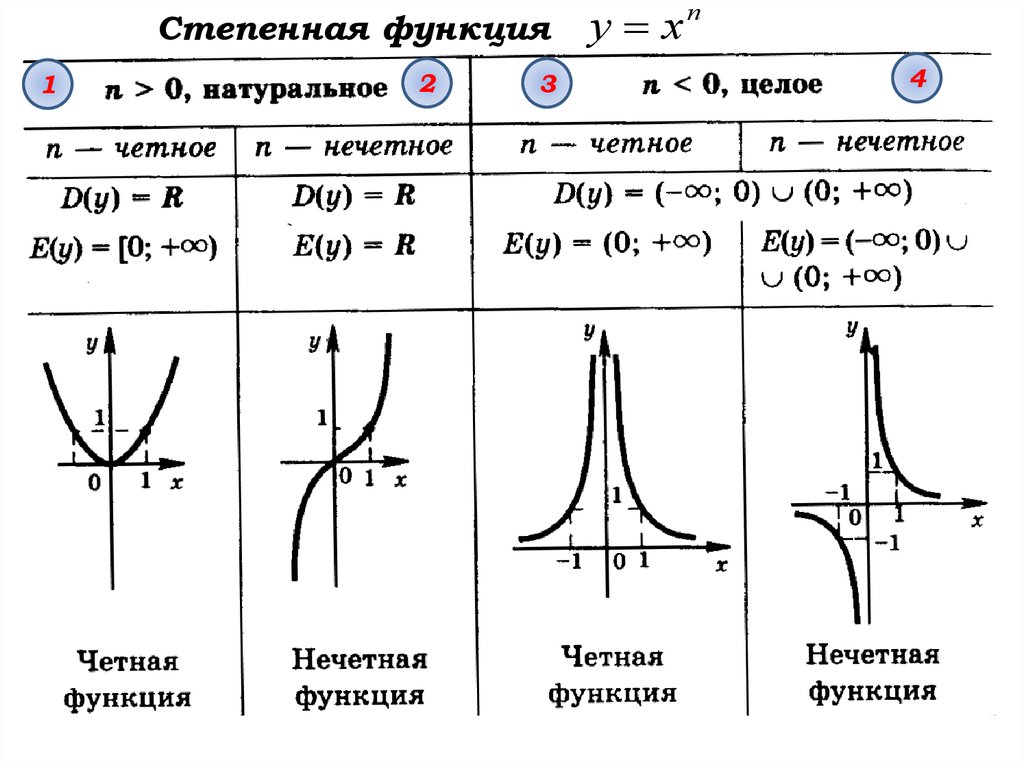
16.
Степенная функция1
2
3
у х
п
4
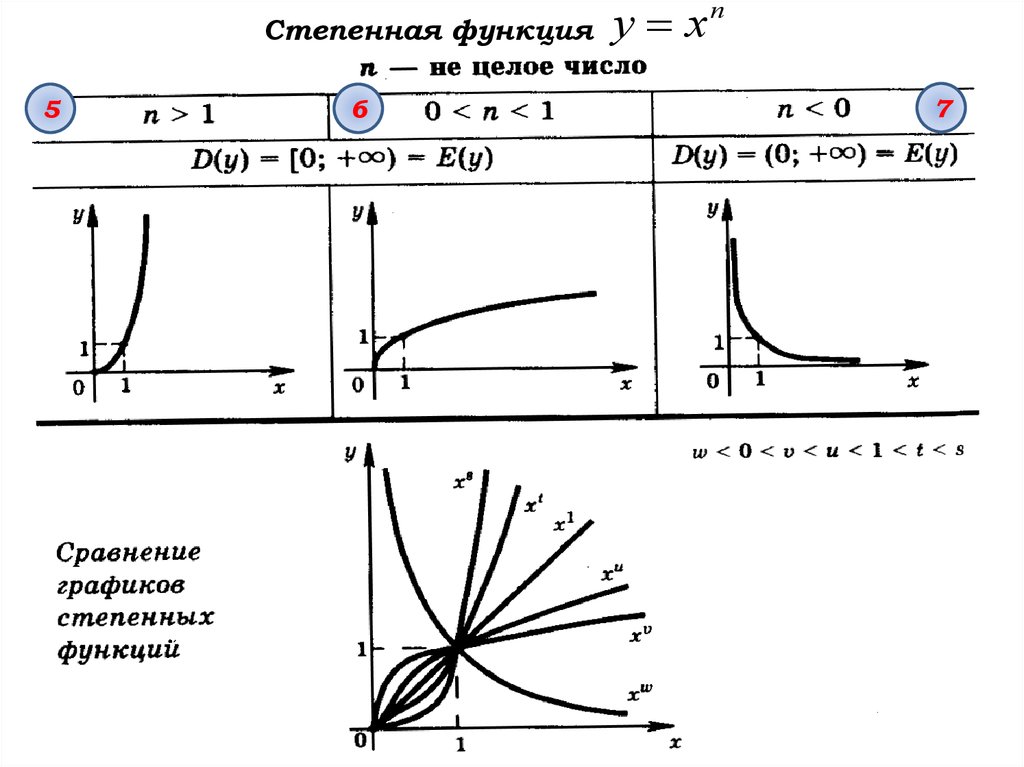
17.
Степенная функция5
6
у хп
7







 mathematics
mathematics








