Эффект Комптона

1. В 1922 – 1923гг американский физик Артур Комптон изучал рассеяние графитом (углерод) монохроматического рентгеновского

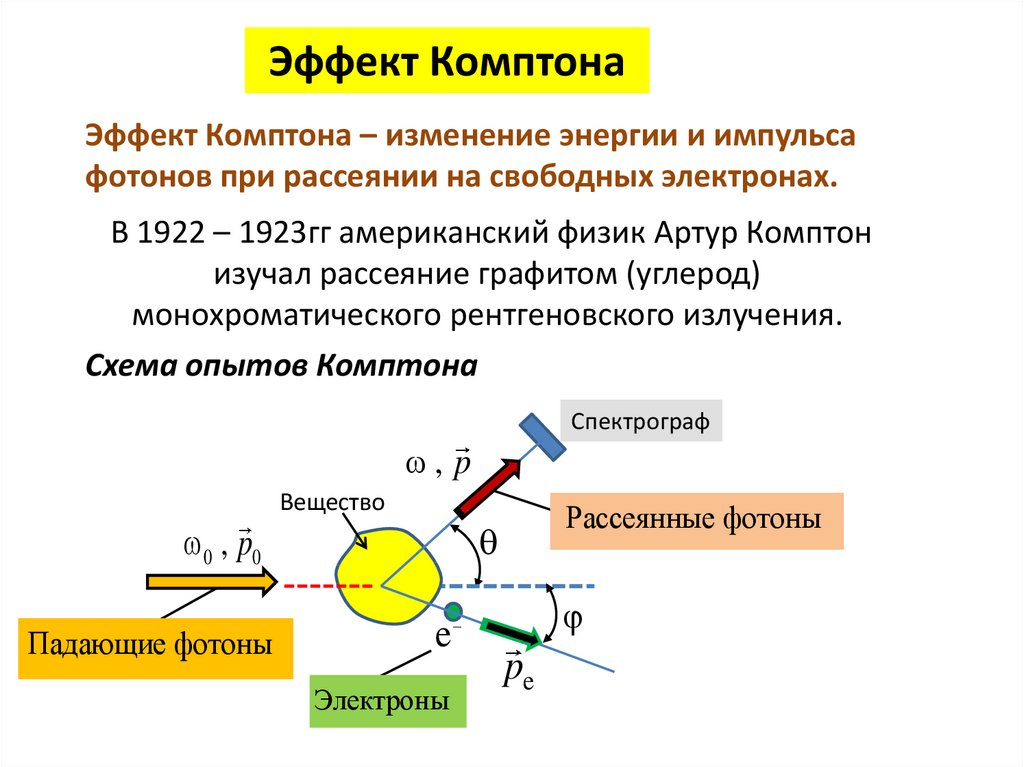
Эффект Комптона
Эффект Комптона – изменение энергии и импульса
фотонов при рассеянии на свободных электронах.
В 1922 – 1923гг американский физик Артур Комптон
изучал рассеяние графитом (углерод)
монохроматического рентгеновского излучения.
Схема опытов Комптона
Спектрограф
, p
Вещество
0 , p0
Падающие фотоны
Рассеянные фотоны
e
Электроны
pe

2.

Результаты опытов
Несмещенная
компонента
450
Смещенная
компонента
На вещество падает узкий пучок
монохроматического рентгеновского излучения
длиной волны 0 0,07 нм и энергией
фотонов 0 20 кэВ . Эта энергия весьма
С
0
900
велика по сравнению с энергией связи Eсв 10 эВ
внешних электронов атома углерода.
В этих условиях можно считать, что процесс
рассеяния происходит на свободных
электронах.
На рисунке представлены результаты
рассеяния рентгеновского излучения на графите,
полученные в опытах Комптона, для трех углов
рассеяния 450, 900 и 1350. По вертикальной оси
отложена интенсивность рассеянного излучения,
по горизонтальной оси – длина волны излучения.
0 - несмещенная компонента
0 -смещенная компонента
0
1350
0
( ) К (1 cos )
К 2, 4 пм

3.

Из экспериментов по рассеянию излучения разными веществами
следовало, что K 2,4 пм и величина смещения не зависит от
того, из каких атомов состоит рассеивающее вещество.
Вывод:
Рассеяние происходит на свободных электронах.
Увеличение длины волны излучения при его рассеянии необъяснимо с
точки зрения волновой теории электромагнитного излучения.
Кроме того, в экспериментах обнаружено, что с увеличением угла
0 уменьшается,
интенсивность несмещенной компоненты с длиной волны
а интенсивность смещенной компоненты увеличивается.
0
С точки зрения классической физики:
*
Электромагнитная волна должна воздействовать сразу на все электроны
вещества. При этом доля энергии и импульса волны, передаваемая одному
электрону, должна быть ничтожно малой.
*
В классической теории рассеяние рассматривается как процесс, в
котором электроны совершают вынужденные колебания под действием
электрического поля падающей волны, излучая вторичные (рассеянные)
электромагнитные волны на частоте падающего излучения.

4.

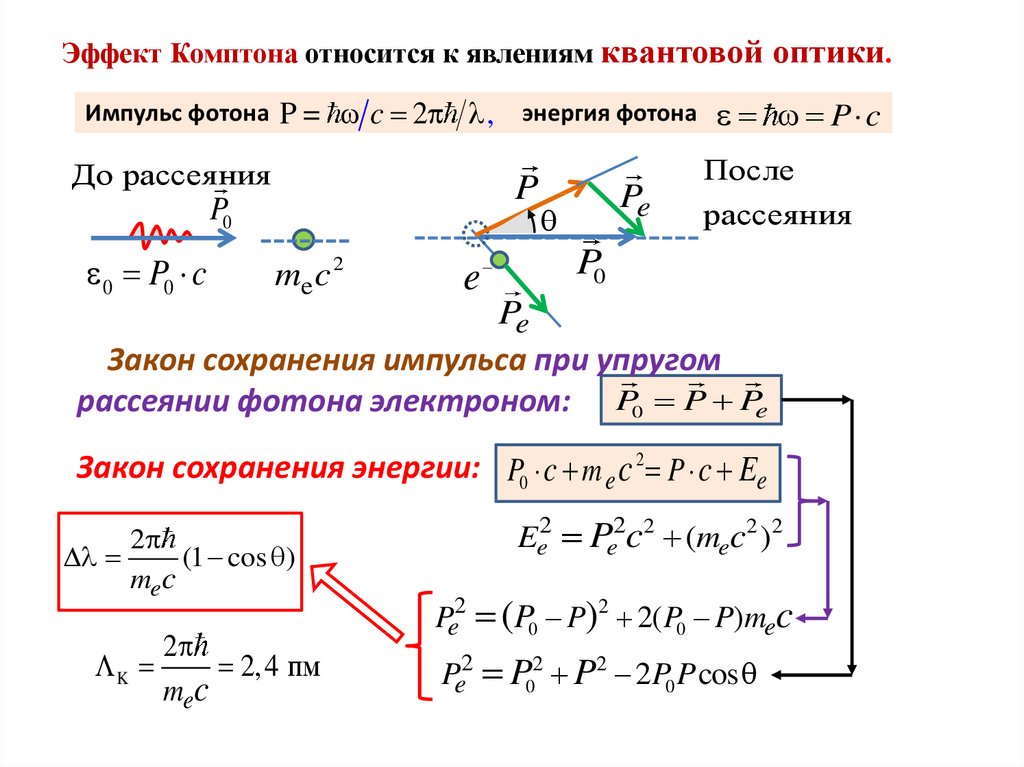
Эффект Комптона относится к явлениям квантовой оптики.
Импульс фотона
P = c 2 , энергия фотона P c
До рассеяния
P
P0
0 P0 c
me c 2
e
Pe
После
рассеяния
P0
Pe
Закон сохранения импульса при упругом
рассеянии фотона электроном: P0 P Pe
Закон сохранения энергии: P0 c m e c 2 P c Ee
2
(1 cos )
mec
K
2
2, 4 пм
mec
Ee2 Pe2c2 (mec2 )2
Pe2 (P0 P)2 2( P0 P)mec
Pe2 P02 P2 2P0 P cos

5.

Энергия рассеянных фотонов в эффекте Комптона
Из тех же уравнений
Pe2 (P0 P)2 2( P0 P)mec
Pe2 P02 P2 2P0 P cos ,
полученных из законов сохранения энергии и импульса, можно получить
формулу для импульса и энергии рассеянного фотона:
P0
P
1
P0
(1 cos )
me c
,
0
1
0
(1 cos )
me c 2
Для электрона me c 0,511 МэВ . Из формул видно, что для эффекта Комптона
требуется рентгеновская область спектра и область гамма диапазона, когда
отношение 0 me c 2 не слишком мало и достаточно для регистрации смещения
длины волны 0 .
2
При рассеянии назад (угол 1800 , cos 1 ), когда 0 me c 2 , энергия
0 3 .
рассеянного фотона в три раза меньше энергии падающего фотона:
2
me c , энергия рассеянного назад
А в случае фотонов большой энергии, когда 0
2
фотона me c 2 0, 255 МэВ .

6.

Формула
K
0 К (1 cos )
, где
2
2, 43 пм - комптоновская длина волны для электрона
mec
получена в предположении, что электрон перед столкновением с
фотоном находился в состоянии покоя.
Формула Комптона содержит постоянную Планка
, и способ, каким
эта величина вошла в эту формулу, является сильным доводом в пользу
фотонных представлений.
Значение эффекта Комптона состоит в том, что он подтверждает
универсальный характер соотношений:
энергия фотона
,
импульс фотона
P k, P c
В опыте Комптона фотон ведет себя как неделимая частица.
В элементарном процессе рассеяния падающий фотон исчезает, и
рождается новый фотон с меньшей энергией и электрон отдачи.