Similar presentations:
Кинематика кривошипно-шатунного механизма. Лекция №1
1. ТЕМА №1: «КИНЕМАТИКА КРИВОШИПНО-ШАТУННОГО МЕХАНИЗМА»
РАССМАТРИВАЕМЫЕ ВОПРОСЫ:1. АНАЛИЗ КШМ
2. КИНЕМАТИКА ПОРШНЯ
2. Цель кинематического анализа КШМ
Исследование законов движения деталей кривошипношатунного механизма (КШМ) ведется с учетом только егоструктуры и геометрическими соотношениями между
звеньями механизма вне зависимости от сил, вызывающих
его движение.
Это позволит:
• оценить возможность функционирования КШМ с заданными
геометрическими размерами;
• получить информацию о компоновочном решении, габаритных
параметрах элементов КШМ и всего ДВС;
• определить влияние кинематических параметров КШМ на
характеристики рабочих процессов ДВС;
• подготовить исходные данные для оценки нагрузок на детали
KШМ.
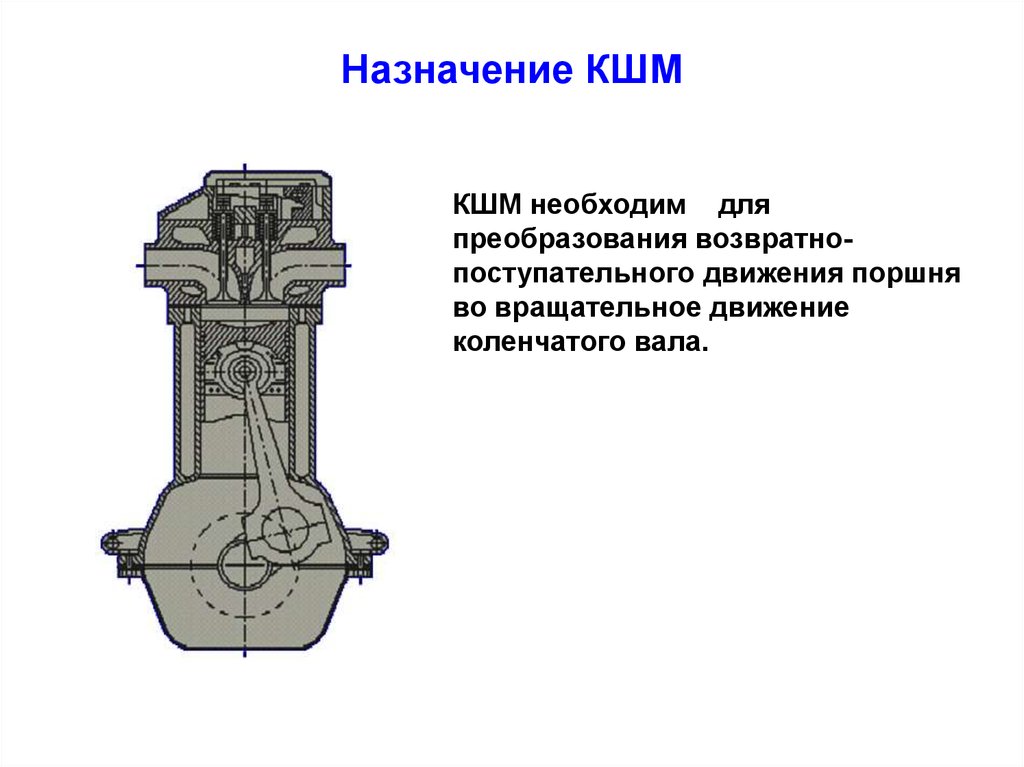
3. Назначение КШМ
КШМ необходим дляпреобразования возвратнопоступательного движения поршня
во вращательное движение
коленчатого вала.
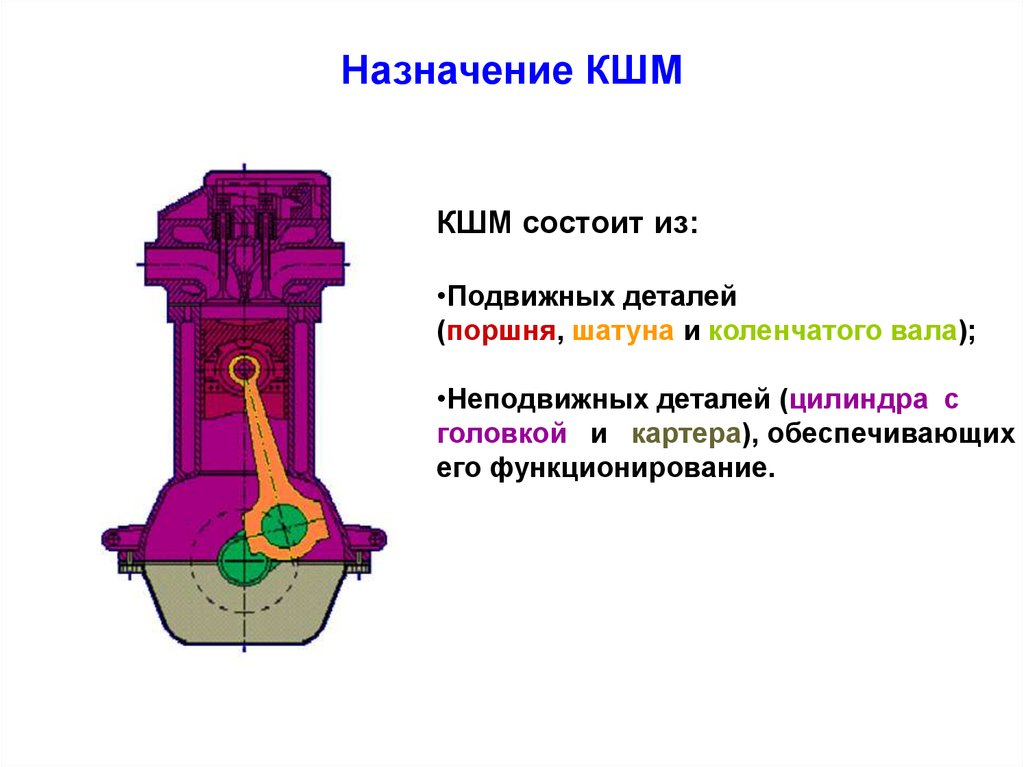
4. Назначение КШМ
КШМ состоит из:•Подвижных деталей
(поршня, шатуна и коленчатого вала);
•Неподвижных деталей (цилиндра с
головкой и картера), обеспечивающих
его функционирование.
5. Упрощенное представление КШМ
6. Поршень совершает возвратно-поступательное движение. При наличии зазоров и соответствующей нагрузке он также совершает
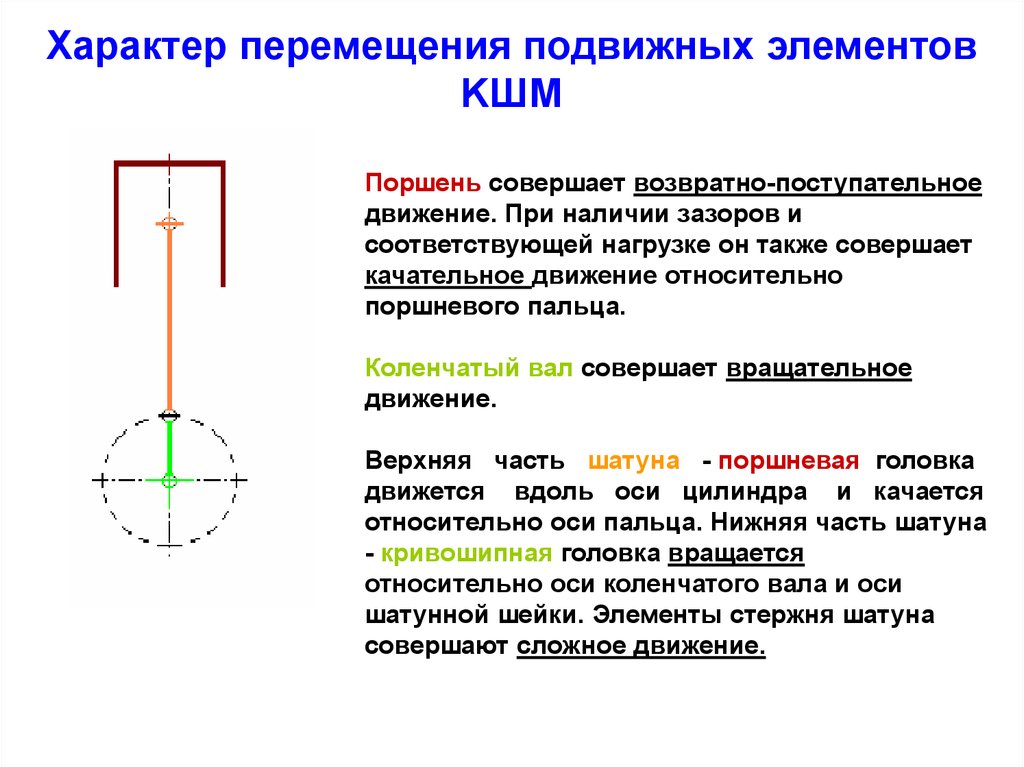
Характер перемещения подвижных элементовKШМ
Поршень совершает возвратно-поступательное
движение. При наличии зазоров и
соответствующей нагрузке он также совершает
качательное движение относительно
поршневого пальца.
Коленчатый вал совершает вращательное
движение.
Верхняя часть шатуна - поршневая головка
движется вдоль оси цилиндра и качается
относительно оси пальца. Нижняя часть шатуна
- кривошипная головка вращается
относительно оси коленчатого вала и оси
шатунной шейки. Элементы стержня шатуна
совершают сложное движение.
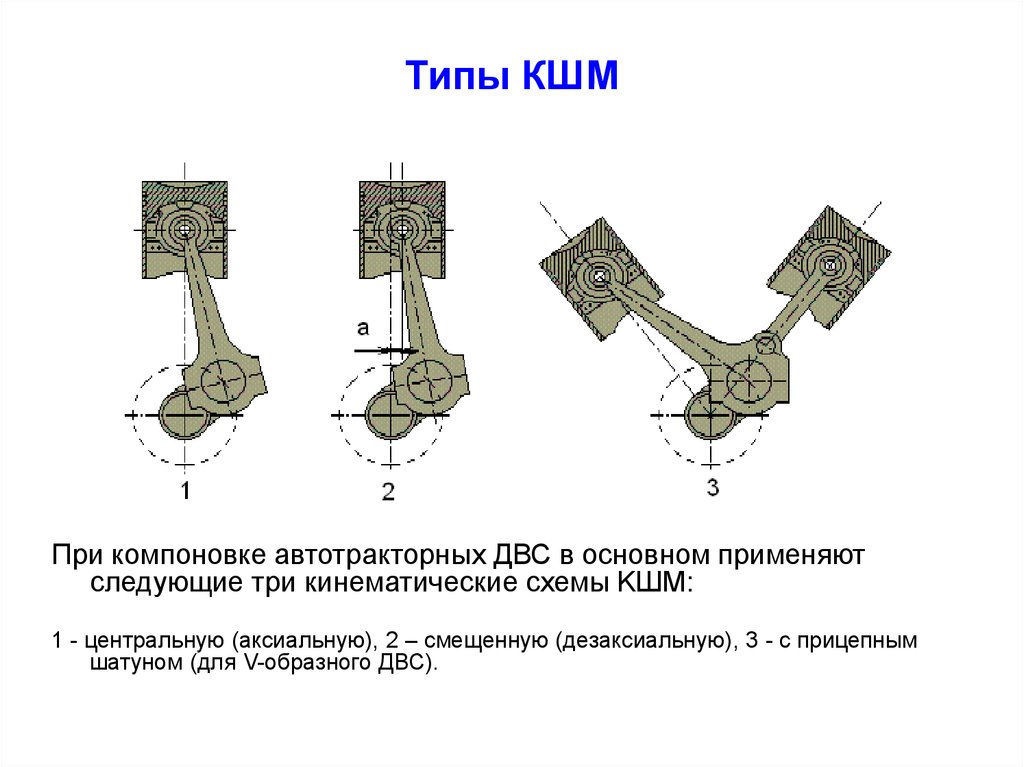
7. Типы КШМ
При компоновке автотракторных ДВС в основном применяютследующие три кинематические схемы KШM:
1 - центральную (аксиальную), 2 – смещенную (дезаксиальную), 3 - с прицепным
шатуном (для V-образного ДВС).
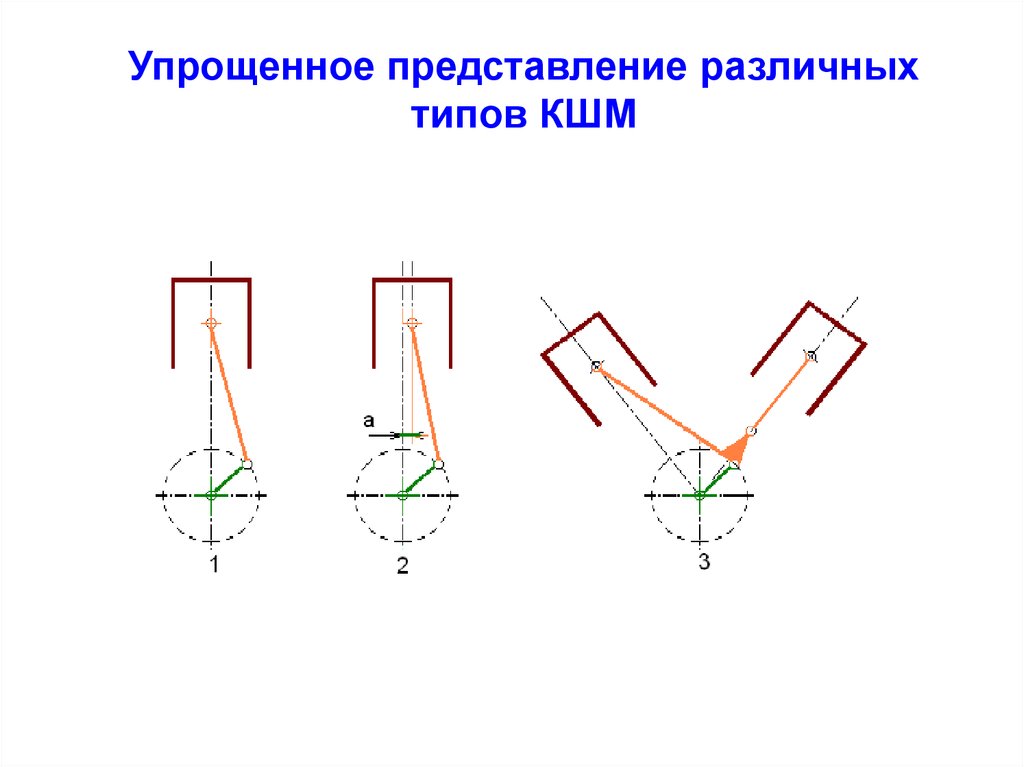
8.
Упрощенное представление различныхтипов КШМ
9.
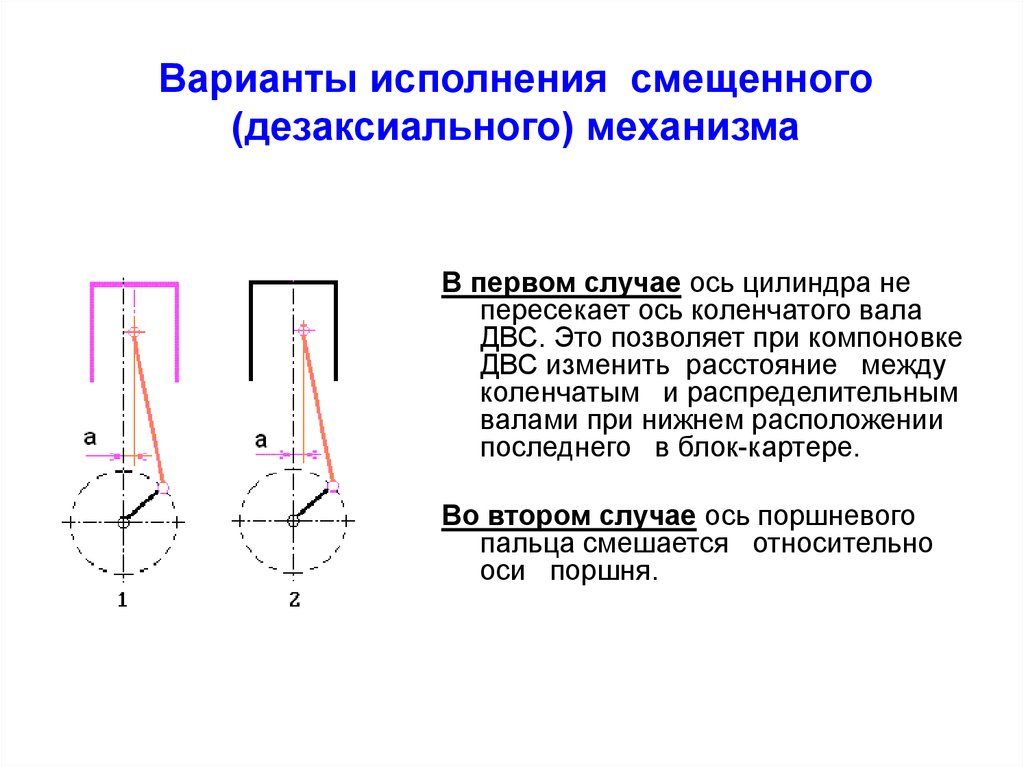
Варианты исполнения смещенного(дезаксиального) механизма
В первом случае ось цилиндра не
пересекает ось коленчатого вала
ДВС. Это позволяет при компоновке
ДВС изменить расстояние между
коленчатым и распределительным
валами при нижнем расположении
последнего в блок-картере.
Во втором случае ось поршневого
пальца смешается относительно
оси поршня.
10.
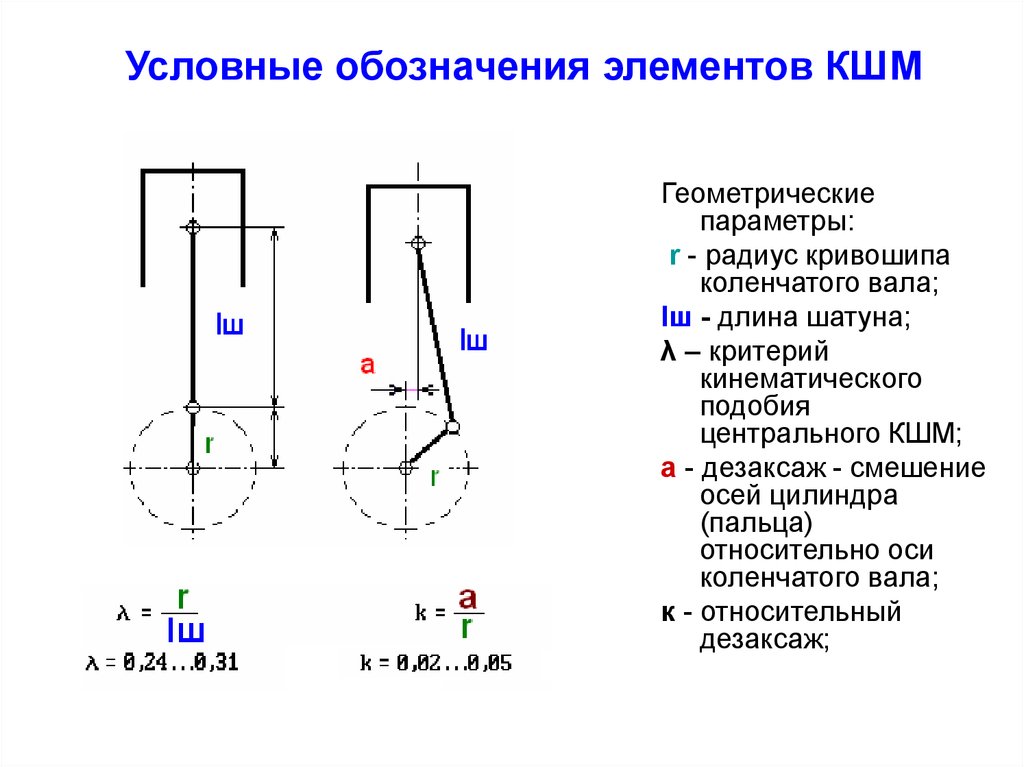
Условные обозначения элементов КШМГеометрические
параметры:
r - радиус кривошипа
коленчатого вала;
lш - длина шатуна;
λ – критерий
кинематического
подобия
центрального КШМ;
a - дезаксаж - смешение
осей цилиндра
(пальца)
относительно оси
коленчатого вала;
к - относительный
дезаксаж;
11.
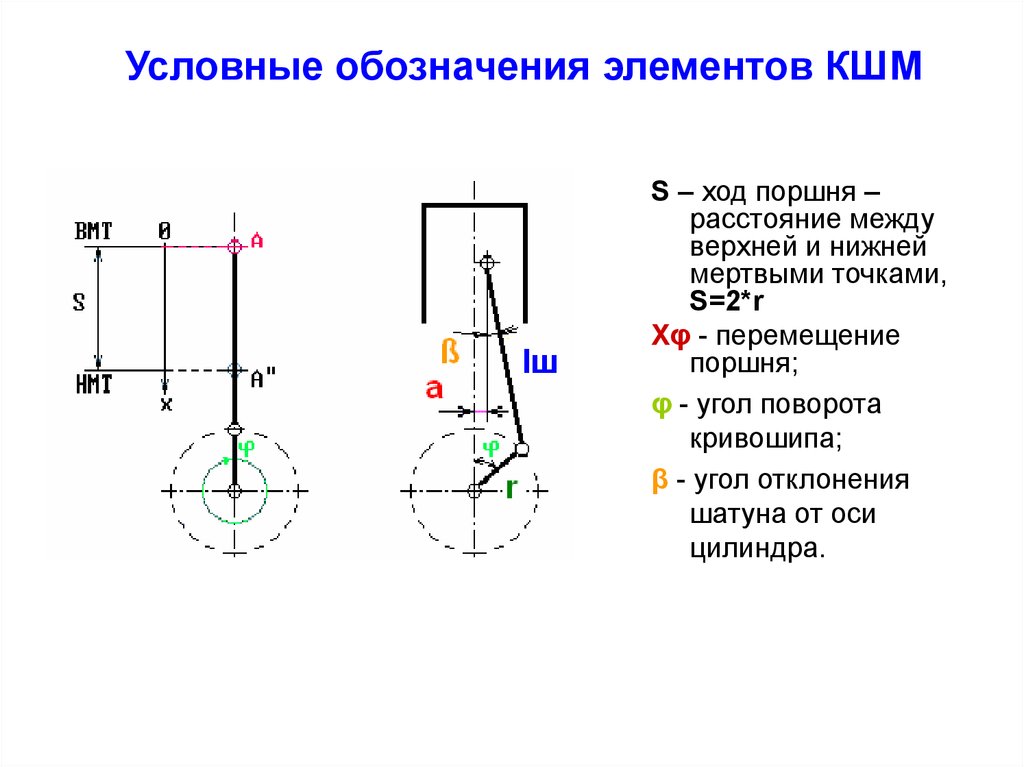
Условные обозначения элементов КШМS – ход поршня –
расстояние между
верхней и нижней
мертвыми точками,
S=2*r
Хφ - перемещение
поршня;
φ - угол поворота
кривошипа;
β - угол отклонения
шатуна от оси
цилиндра.
12.
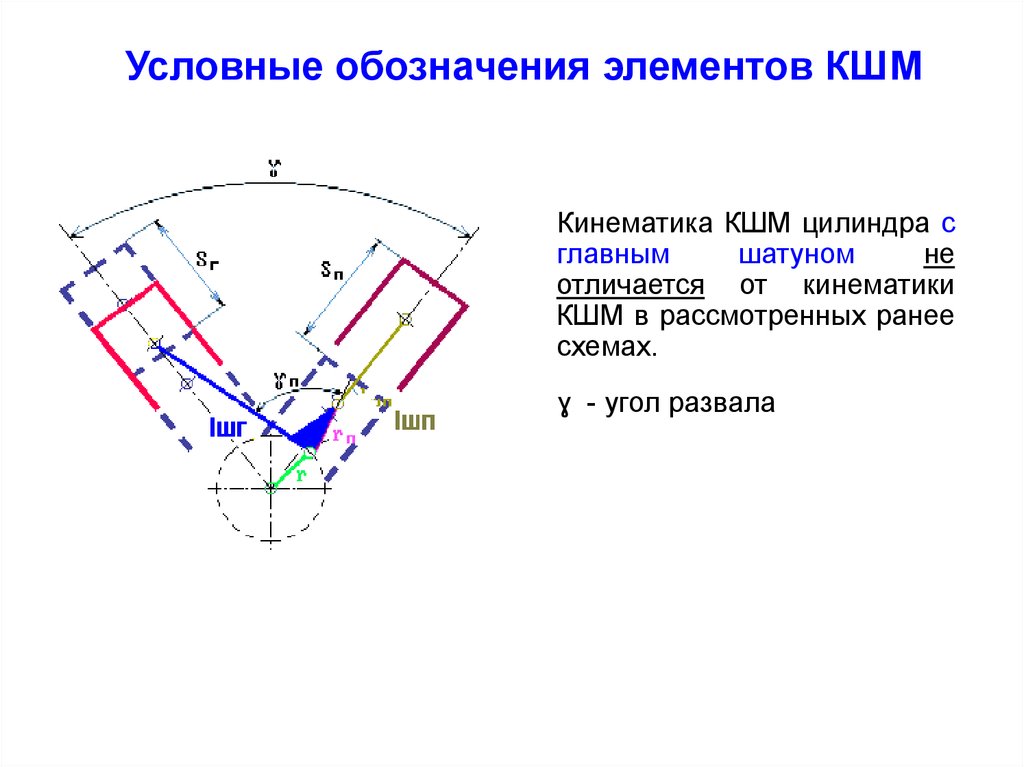
Условные обозначения элементов КШМКинематика КШМ цилиндра с
главным
шатуном
не
отличается от кинематики
КШМ в рассмотренных ранее
схемах.
ɣ - угол развала
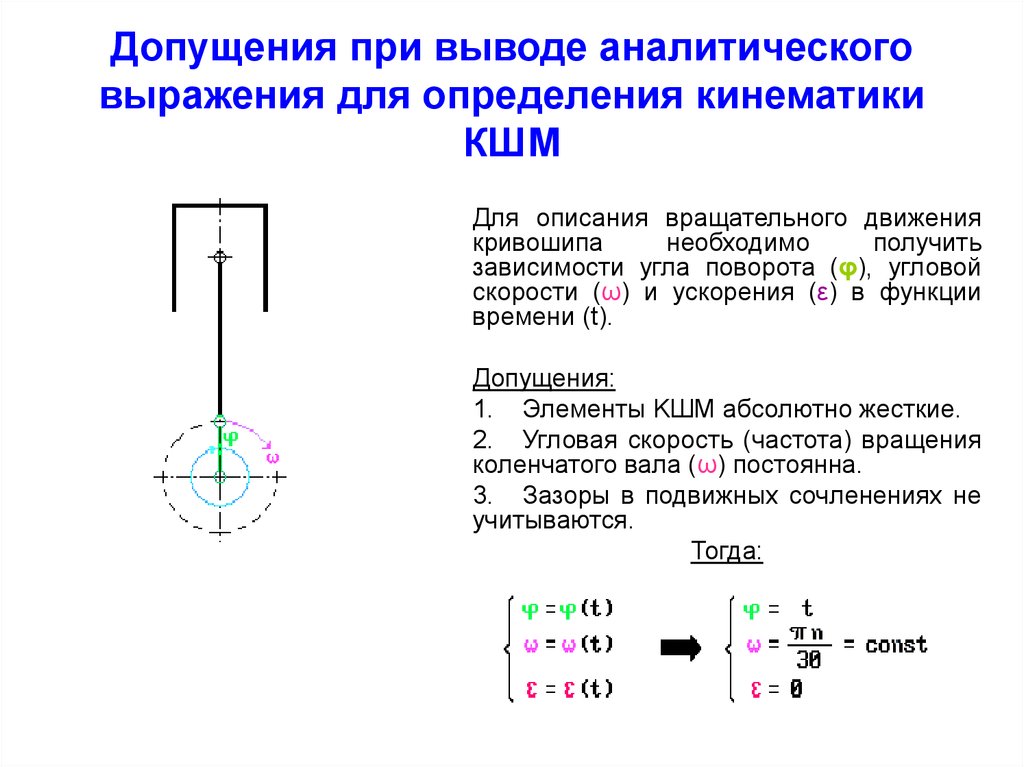
13. Допущения при выводе аналитического выражения для определения кинематики КШМ
Для описания вращательного движениякривошипа
необходимо
получить
зависимости угла поворота (φ), угловой
скорости (ω) и ускорения (ε) в функции
времени (t).
Допущения:
1. Элементы KШМ абсолютно жесткие.
2. Угловая скорость (частота) вращения
коленчатого вала (ω) постоянна.
3. Зазоры в подвижных сочленениях не
учитываются.
Тогда:
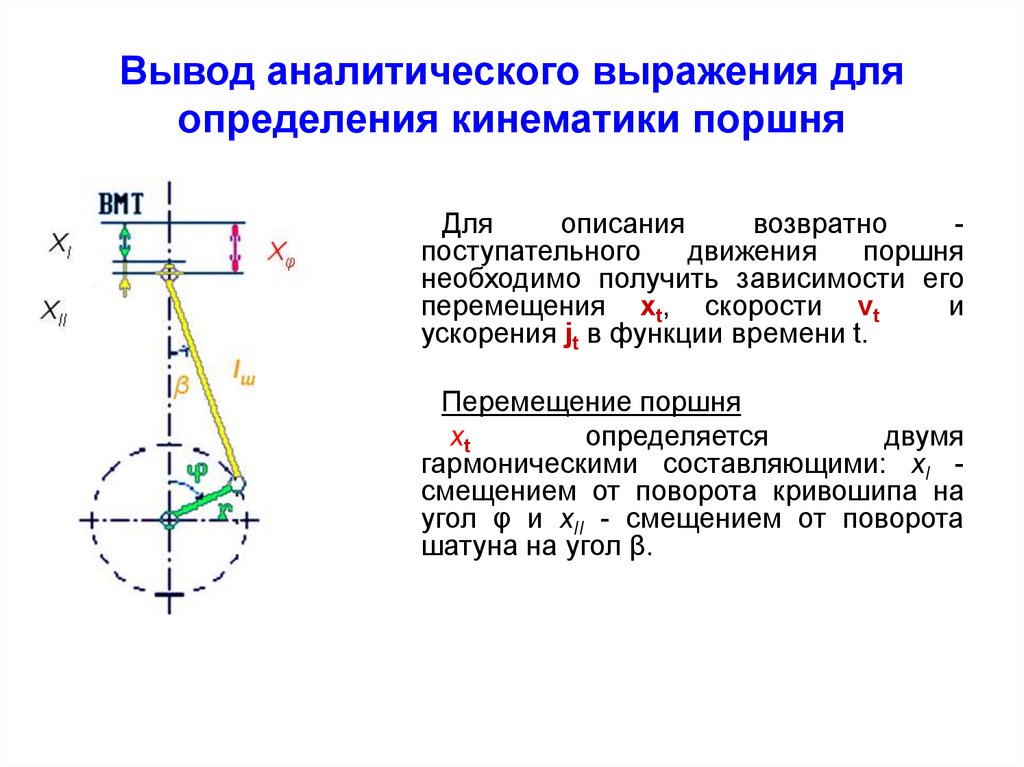
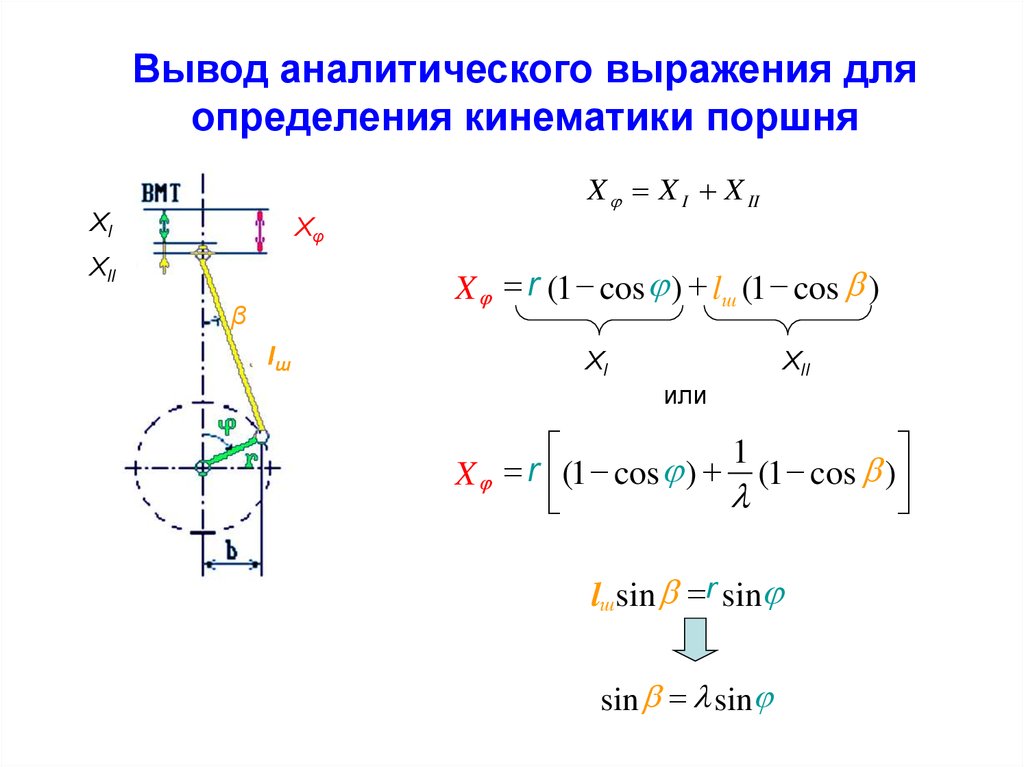
14. Вывод аналитического выражения для определения кинематики поршня
Дляописания
возвратно
поступательного
движения
поршня
необходимо получить зависимости его
перемещения хt, скорости vt
и
ускорения jt в функции времени t.
Перемещение поршня
xt
определяется
двумя
гармоническими составляющими: xI смещением от поворота кривошипа на
угол φ и xII - смещением от поворота
шатуна на угол β.
15. Вывод аналитического выражения для определения кинематики поршня
X j = X I + X IIXI
Xφ
XII
X j = r (1 - cos j ) + lш (1 - cos b )
β
lш
XI
XII
или
1
=
r
j
+
b
Xj
(1 cos ) l (1 cos )
lшsin b =r sinj
sin b = l sinj
16. Вывод аналитического выражения для определения кинематики поршня
sin b = l sinjcos b = 1 - sin 2 b
cos b = 1 - l2 sin 2 j
Точная зависимость перемещения поршня от угла поворота
кривошипа:
1
2
2
r
=
j
+
l
j
Xj
sin )
(1 cos ) l (1 1
17. Вывод аналитического выражения для определения кинематики поршня
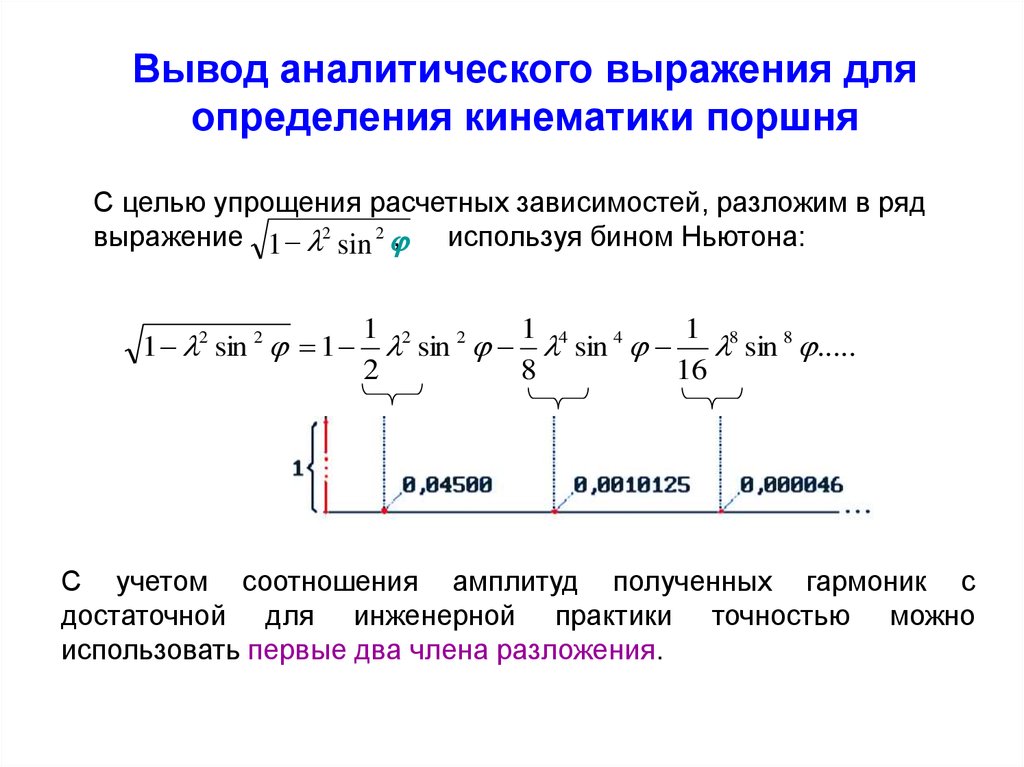
С целью упрощения расчетных зависимостей, разложим в рядвыражение 1 - l2 sin 2 j,
используя бином Ньютона:
1 - l2 sin 2 j = 1 -
1 2
1
1
l sin 2 j - l4 sin 4 j - l8 sin 8 j .....
2
8
16
С учетом соотношения амплитуд полученных гармоник с
достаточной для инженерной практики точностью можно
использовать первые два члена разложения.
18. Вывод аналитического выражения для определения кинематики поршня
Тогда выражение примет вид1
1
1 - l2 sin 2 j 1 - l2 sin 2 j = 1 - l2 cos 2j
2
4
Приближенная зависимость перемещения поршня от угла
поворота кривошипа:
l
j
+
j
X j r (1 cos )
(1 cos 2 )
4
19.
Вывод аналитического выражения дляопределения кинематики поршня
Скорость поршня
Первая производная от перемещения поршня по времени
определяет скорость поршня для любого угла поворота
коленчатого вала:
j =
dxj
dt
=
dxj
dj
dj
dt
Точная зависимость скорости поршня от угла поворота
кривошипа:
j = r
sin( j + b )
cos b
Приближенная зависимость скорости поршня от угла поворота
кривошипа:
l
j r (sin j + sin 2j )
2
Для оценки конструкции ДВС используется средняя скорость
поршня:
Для современных автотракторных ДВС
Сп=8…15м/с
Cп =
2S n S n
=
60
30
20.
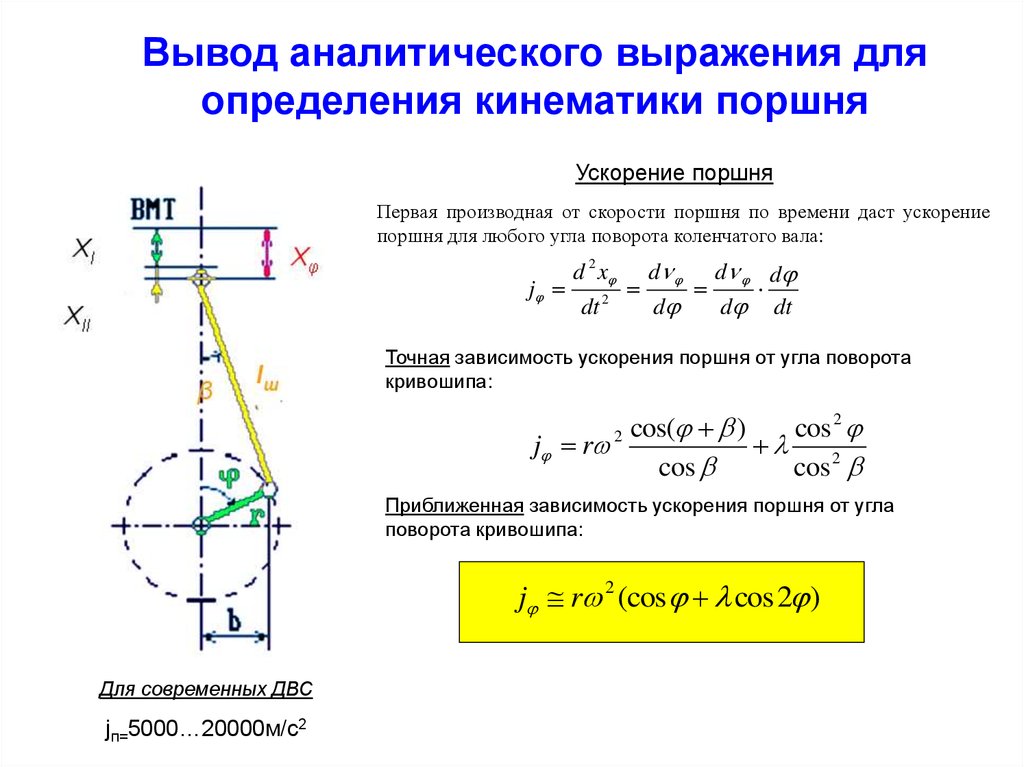
Вывод аналитического выражения дляопределения кинематики поршня
Ускорение поршня
Первая производная от скорости поршня по времени даст ускорение
поршня для любого угла поворота коленчатого вала:
jj =
d 2 xj
dt 2
=
d j
dj
=
d j dj
dj dt
Точная зависимость ускорения поршня от угла поворота
кривошипа:
cos(j + b )
cos 2 j
jj = r
+l
cos b
cos 2 b
2
Приближенная зависимость ускорения поршня от угла
поворота кривошипа:
jj r 2 (cos j + l cos 2j )
Для современных ДВС
jп=5000…20000м/с2
21.
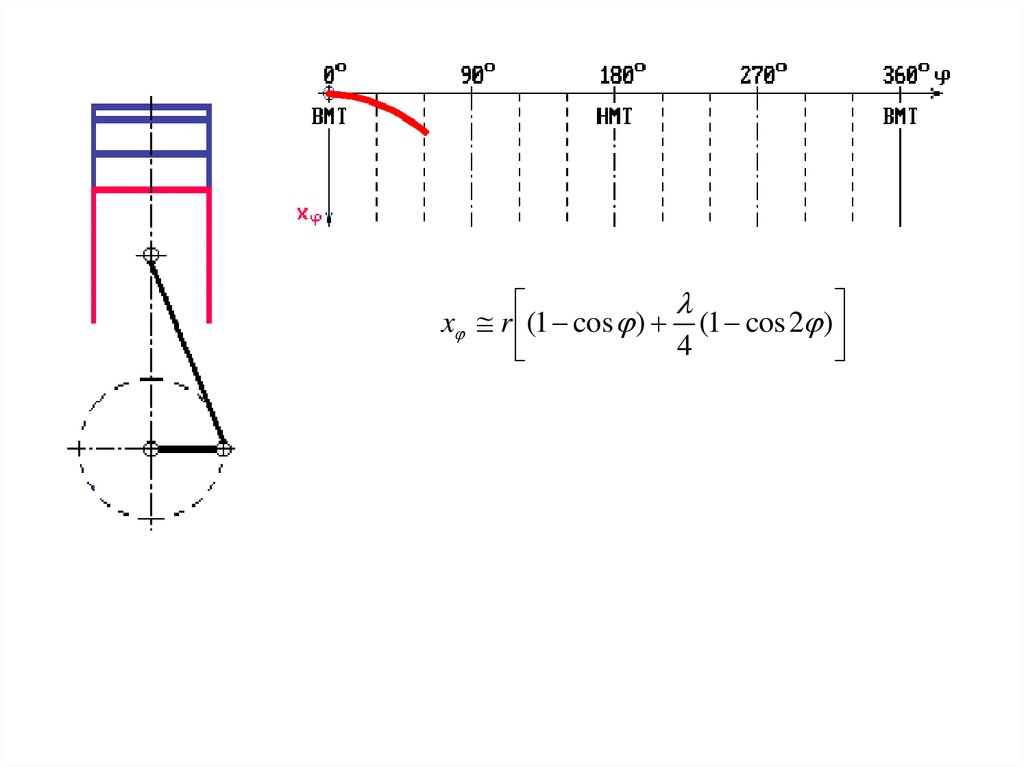
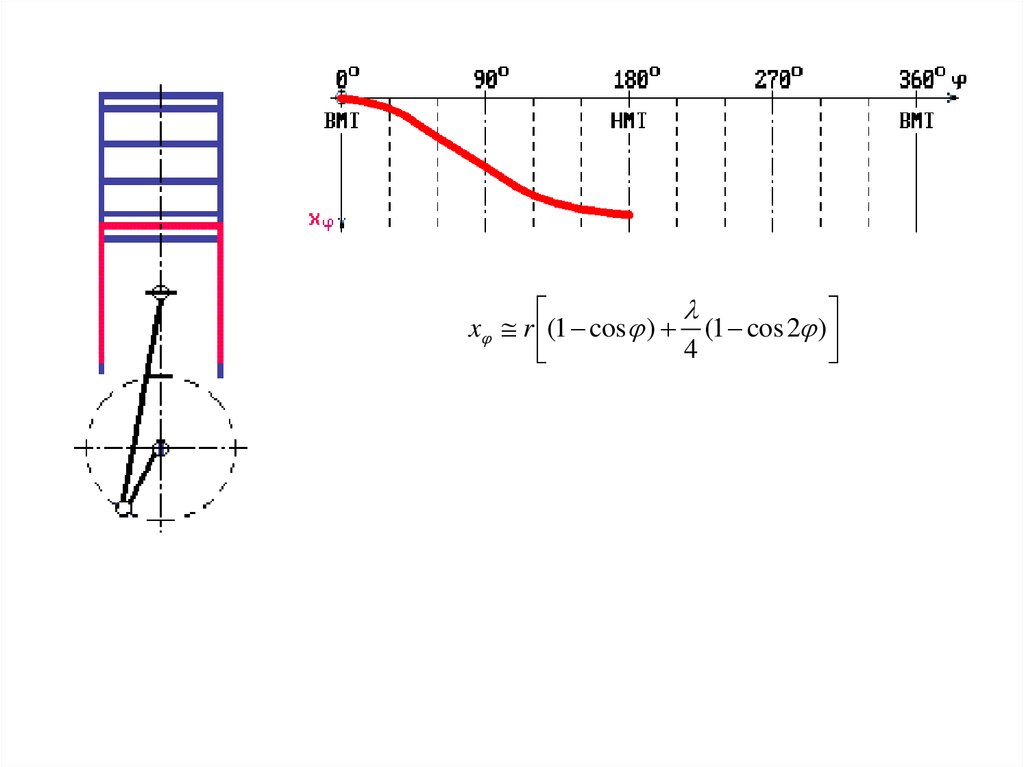
lxj r (1 - cos j ) + (1 - cos 2j )
4
22.
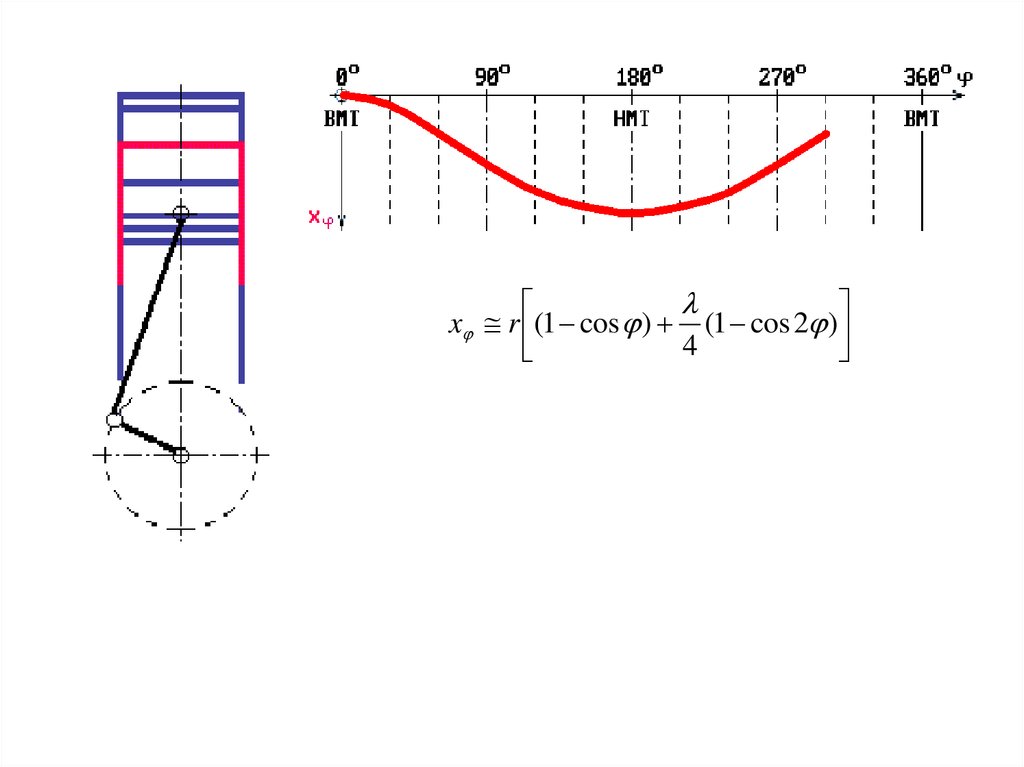
lxj r (1 - cos j ) + (1 - cos 2j )
4
23.
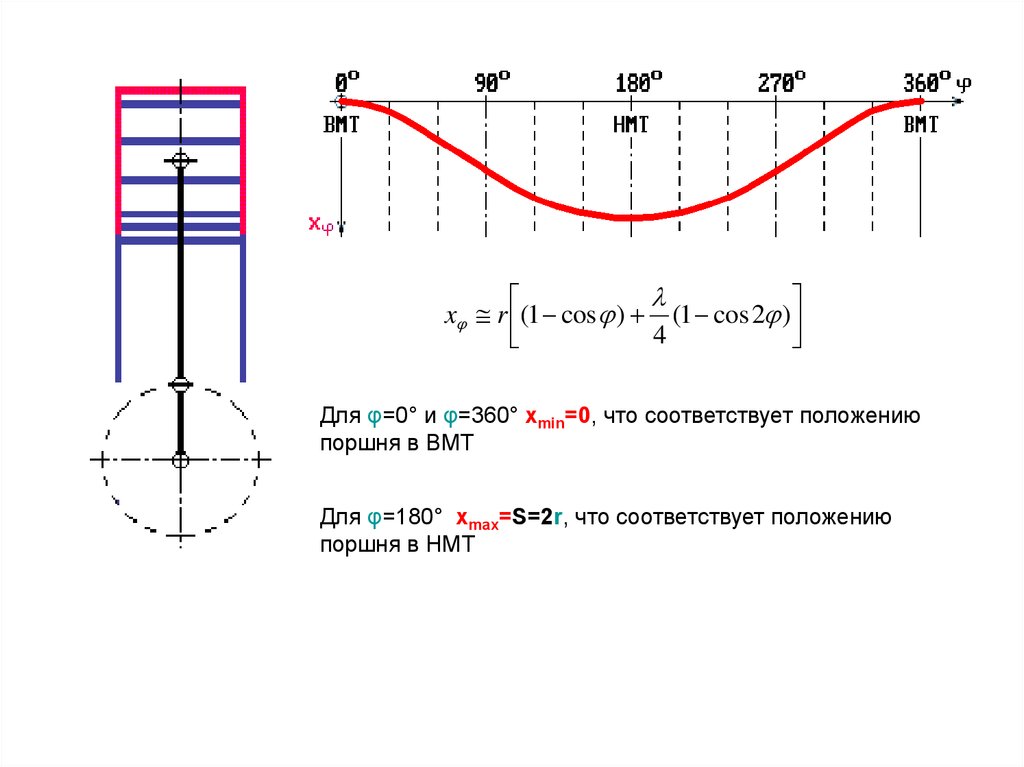
lxj r (1 - cos j ) + (1 - cos 2j )
4
24.
lxj r (1 - cos j ) + (1 - cos 2j )
4
Для φ=0° и φ=360° хmin=0, что соответствует положению
поршня в ВМТ
Для φ=180° хmax=S=2r, что соответствует положению
поршня в НМТ
25.
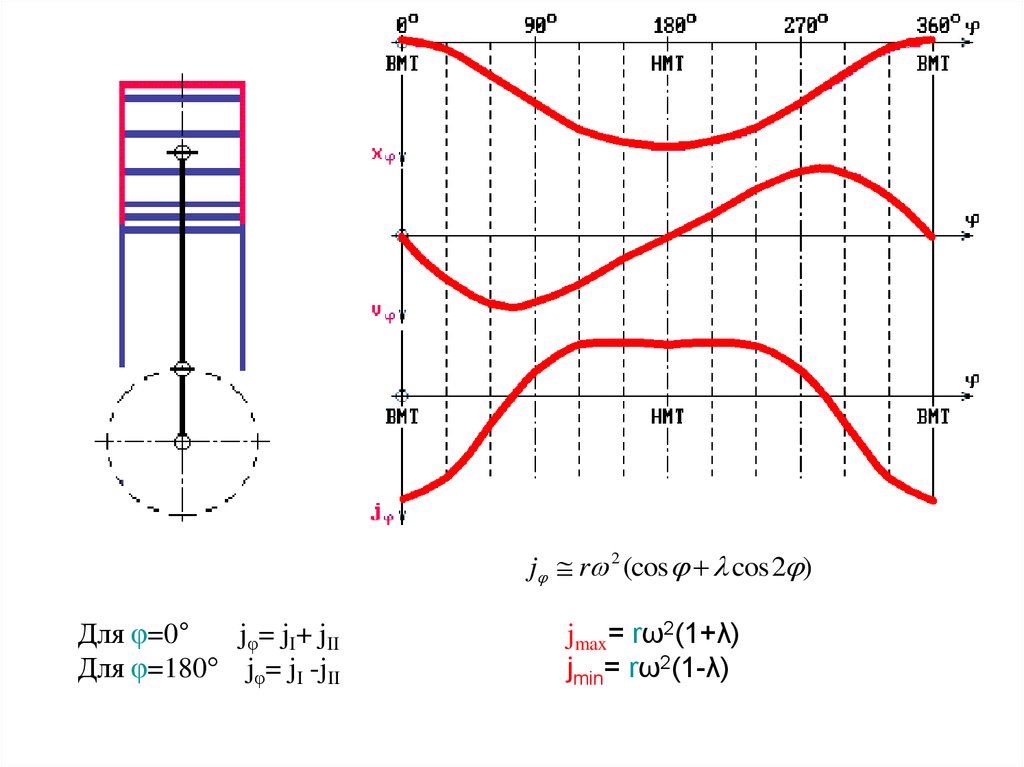
lj r (sin j + sin 2j )
2
Для φ=90° пкв vφ=rω
Максимальное значение скорости в первом приближении
определяется для φ+β =90° , когда ось шатуна перпендикулярна
радиусу кривошипа.
26.
jj r 2 (cos j + l cos 2j )Для φ=0°
jφ= jI+ jII
Для φ=180° jφ= jI -jII
jmax= rω2(1+λ)
jmin= rω2(1-λ)






 physics
physics mechanics
mechanics








