Similar presentations:
Показательные уравнения
1. Показательные уравнения
mathvideourok.moy.su2.
Определение: Показательнымиуравнениями называются уравнения вида
а
f ( x)
a
g ( x)
где а –положительное число ,отличное от 1
Теорема: Показательное уравнение
а
f ( x)
a
g ( x)
, где а 0; а 1
равносильно уравнению
f ( x) g ( x)
так как у а m ( х ) монотонна D( у ) R
3.
Существуют три основных методарешения показательных уравнений
I. Функционально-графический метод.
Он основан на использовании графических
иллюстраций или каких либо свойств
функции
II. Метод уравнивания показателей.
Он основан на использовании теоремы
III. Метод введения новой переменной.
Он основан на использовании введении новой
переменной
а
f ( x)
m, где m 0
4. Решите уравнение:
1)22 х 4 642
2 х 4
2
6
2х 4 6
так как у 2m монотонна
D( y ) R
2 х 10
х 5
Ответ : 5
1
2)
3
2 х 3,5
1
3
2 х 3,5
1
1
3
3
2 х 3,5 0,5
1
2
m
1
так как у монотонна
3
D( y ) R
2х 4
х 2
Ответ : 2
5.
3)5х2 3 х
3 х 8
5
х 3х 3х 8
так как у 5m монотонна
D( y ) R
2
х 6х 8 0
D
2
к ас 9 8 1 0(2к )
4
2
D
к
3 1
4
х1;2
а
1
х1 4; х2 2
Ответ : 4; 2
6.
0, 24)
х 0,5
5 0,04 х 2
5
1
5
5
1
2
5
х 2х 5
х 0,5
1
5
25
1
2
х 2
монотонна
D( y ) R
5 5 5
х 0,5
0,5
2 х 4
5
5 5 5
5 х 5 2 х 5
1 х 0,5
так как у 5m
2 х 2
х 5
Ответ : 5
7.
5)5х 1
25
25 0
Корней нет
у 5m
Е ( у ) (0; )
Ответ : корней нет
6)5
х 1
5
х 1
1
25
5
2
х 1 2
так как у 5m монотонна
D( y ) R
х 1
Ответ : 1
!!!
8.
7)4 2х
х 1
24 0
2 2 2 24 0
п 2 2п 24 0
2х
х
D
1 24 25 0(2к )
4
Пусть 2 п, п 0
х
1 5
п1;2
1
п1 6; п2 4
х
1)если п 6, то 2 6 корней нет
х
2)если п 4, то 2 4
2 2
х
х 2
2
так как у 2m монотонна
D( y ) R
Ответ : 2
9.
8)6х 1 35 6х 1 711
6 6 35 6 71
6
35
х
6 (6 ) 71
6
х
х
35
6 6 71
6
71
6
х
6 71: 71 6
6
71
х
6 6
х 1
х
так как у 6 монотонна
m
D( y ) R
Ответ :1
10.
9) 8 18 2 27х
*
х
х
(2 ) (2 3 ) 2 (3 )
3 х
2 х
3 х
2 2 3 2 3 / : 33 х 0
3х
х
3х
2х
х
2
2
2
3
3
п п 2 0
3
п 1 корень уравнения
(п 1)(п п 2) 0
2
3х
х
2
Пусть п
3
1; 2
п п 2
3
п3 п 2
2
п п
п2 п
п 1
2
п п 2
2п 2
2п 2
0
11.
(п 1)(п2 п 2) 0п2 п 2 0
п 1 0;
п 1
Д 1 8 0
корней нет
х
2
Если п 1, то 1
3
х
0
2 2
3 3
х 0
m
2
так как у монотонна
3
D( y ) R
Ответ : 0
12.
10)* 3х 4 х 5х" Б " х 2, так как 32 42 52
х
х
х
х
3 4 5 /:4 0
" П " х 2 так как
х
х
3
5
1
4 х
4
3
у 1 убывает на D( у ) R
4
х
5
у возрастает на D( у ) R
4
уравнение имеет только один корень 2
Ответ : 2
13.
2 х 3х 2
11) 4
3 4 1
2
х
х
3
2
4
4 3 4 4 1
*
х
Пусть 4 п, п 0
1 3
2
п п 1 0 / 64
64 16
2
п 12п 64 0
6 10
п1;2
1
п1 16; п2 4
D
36 64 100 0(2к )
4
х
1)если п 4, то 4 4 корней нет
х
2)если п 16, то 4 16
14.
х4 4
2
х 2
так как у 4m монотонна
D( y ) R
х 2
12) 15х
2
х 2
х 4
( х2 х 2) х 4
15
Ответ : 2
1
15
0
( х 2 х 2) х 4 0 так как у 15m монотонна
D( y ) R
15.
ОДЗ : х 4 0;х 4
х 4 0
( х х 2) х 4 0
2
х х 2 0;
2
D 1 8 9 0(2к )
1 3
х1;2
2
х1 2; х2 1
х 4 0
х 4
4 4;
2 4;
1 4;
Ответ : 4
16.
sin 2 x*
13)
2
2
cos2 x
1 sin 2 x
2
sin 2 x
2
3
3
sin 2 x
Пусть 2
п, п 0
2
п 3 / п 0
п
п 2 3п 2 0
D 9 8 1 0(2к )
1)если п 1, то 2
sin 2 x
sin2 x
2
3 1
п1;2
2
1
2
0
п1 1; п2 2
17.
sin2 x2
2
sin x 0
2
0
так как у 2m монотонна
sin x 0 D( y) R
x к, к Z
sin 2 x
2)если п 2, то 2
2
sin x 1
2
так как у 2 монотонна
D( y ) R
1 cos 2 x
1
2
1 cos 2x 2
cos 2x 1
2 x 2 m, m Z
m
x
2
m, m Z
Ответ : x к, к Z ;
2
m, m Z
18.
2 х 2 у 1214) 2 х у
3
3
2 х 2 у 12
m
2
х
у
1
так
как
у
3
монотонна
D( y ) R
2 2 12
2 х 1 у
х
у
2 2
х
2 х 1
12
1
2 2 2 12
Пусть 2х п, п 0
2 1
п п 12 / 2
2 2
п 2п 24 0
х
2х
19.
п 2п 24 02
1 5
D
1 24 25 0(2к ) п1;2
1
4
п1 6; п2 4
1)если п 6, 2 -6 корней нет
х
2)если п 4, 2 4
х
2 2
х
х 2
2
так как у 2 монотонна
m
D( y ) R
у 2 2 1 3
Ответ : (2;3)
20.
4 15 8так как 4 15 4 15 1, то
*
15)
4
х
15
4 15
4
1
х
15
1
4 15
х
4 15
Пусть 4 15
х
х
8
п, п 0
1
п 8 / п 0
п
п 2 8п 1 0
21.
п 8п 1 02
4 15
п1;2
1
D
16 1 15 0(2к )
4
п1 4 15; п2 4 15
1)если п 4 15, то 4 15
4
4
15
х 1
4 15
1
4 15 1
4 15
х
15
х
х
так как у 4 15
D( y ) R
m
монотонна
22.
2)если п 4 15, то 4 15х
4 15
х 1 так как у 4 15 монотонна
m
D( y ) R
Ответ : 1
23. Факультативный курс
f ( x)g ( x)
1
Функция является сложнопоказательной.
Основание может равняться 1
f ( x) 1
g
(
x
)
имеет
смысл
g ( x) 0
f ( x) 0
24.
1) х 3х 3
3 х 2 10 х 3
3 х2 10 х 3
1
х 3
х 1 1
х 3 0
2
3 х 10 х 3 0
0
1) х 3 1
х 4; 2
х 3 0
2) 2
3 х 10 х 3 0
а) х 3 0
х 3
25.
б )3х 10 х 3 02
D
25 9 16 0(2к )
4
5 4
х1;2
3
1
х 3;
3
3 не является корнем уравнения
1
Ответ : 4; 2;
3
2)( х х 1)
2
х2 1
1
Ответ : 1;1; 2
26.
Если уравнение содержит переменную какв основании, так и в показателе
степени, то уравнение называется
показательно степенным. Для его
решения нужно рассмотреть три
случая:
1) основание равно 1
2) основание равно 0
3) основание отлично от 0 и 1
27.
3)( х 3)1) х 3 1
х 2
х2 3
( х 3)2 х
Проверка :11 1 4 верно
2 корень уравнения
2) х 3 0
х 3
Проверка : 06 0 6 неверно
0 6 не имеет смысла
3 не корень уравнения
х2 3
( х 3)
( х 3)2 х
3) а)0 x 3 1
2
х 3 2х
3 x 2
так как у х 3 монотонна
m
х 2х 3 0
2
D( y ) R
28.
х 2х 3 02
1 2
D
1 3 4 0(2к ) х1;2
1
4
х 3; 1 не корни т.к. 3 ( 3; 2)
1 ( 3; 2)
б) х 3 1
х 2
х2 3
( х 3)
( х 3)2 х
2
х 3 2х m
так как у х 3 монотонна
х 3; 1 корни т.к.
D( y ) R
3 (-2; )
-1 (-2; )
Ответ : 2; 1;3
29.
4)( х 3) ( х 3)х2
х
Ответ : 0;1;3; 4














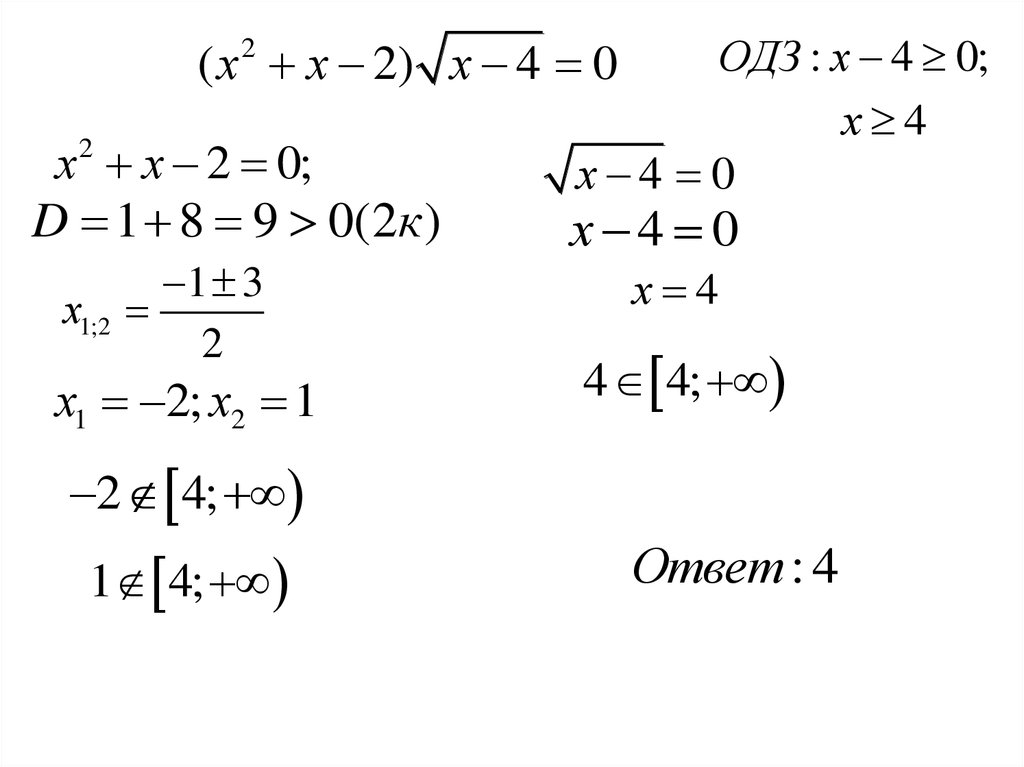
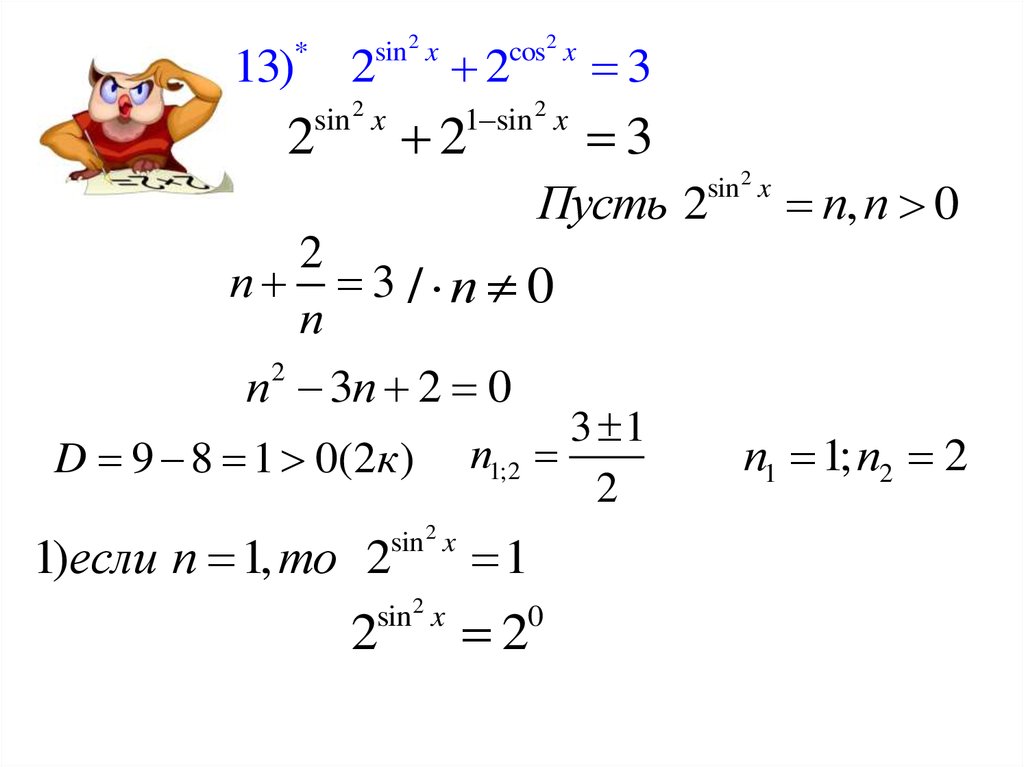
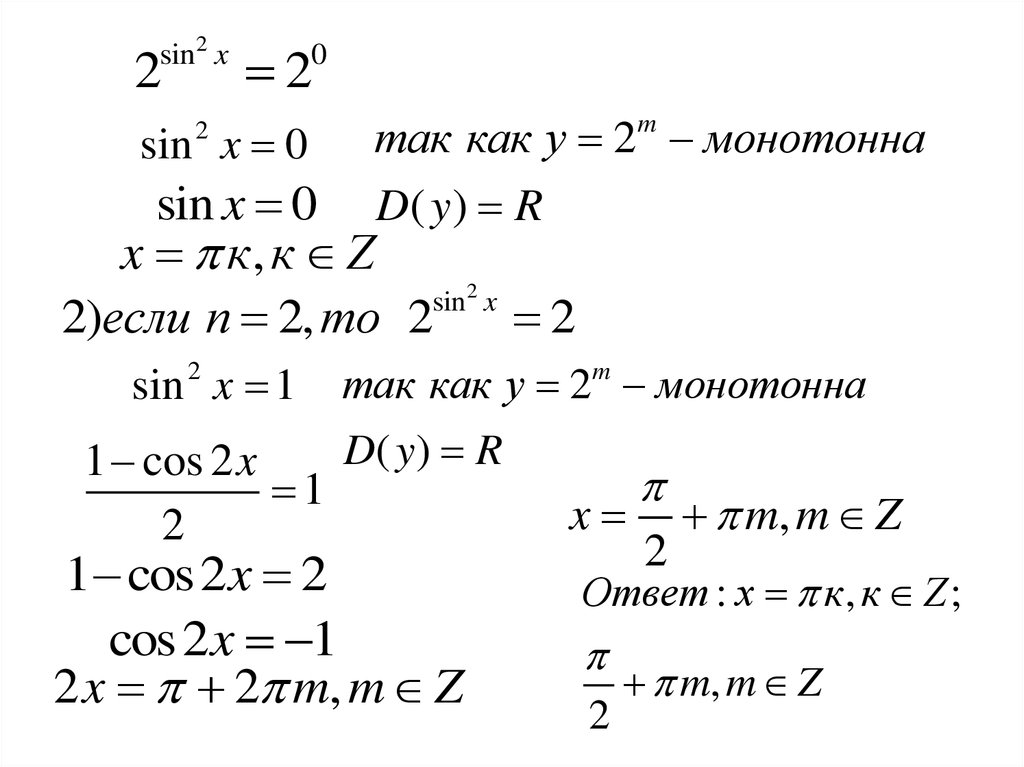
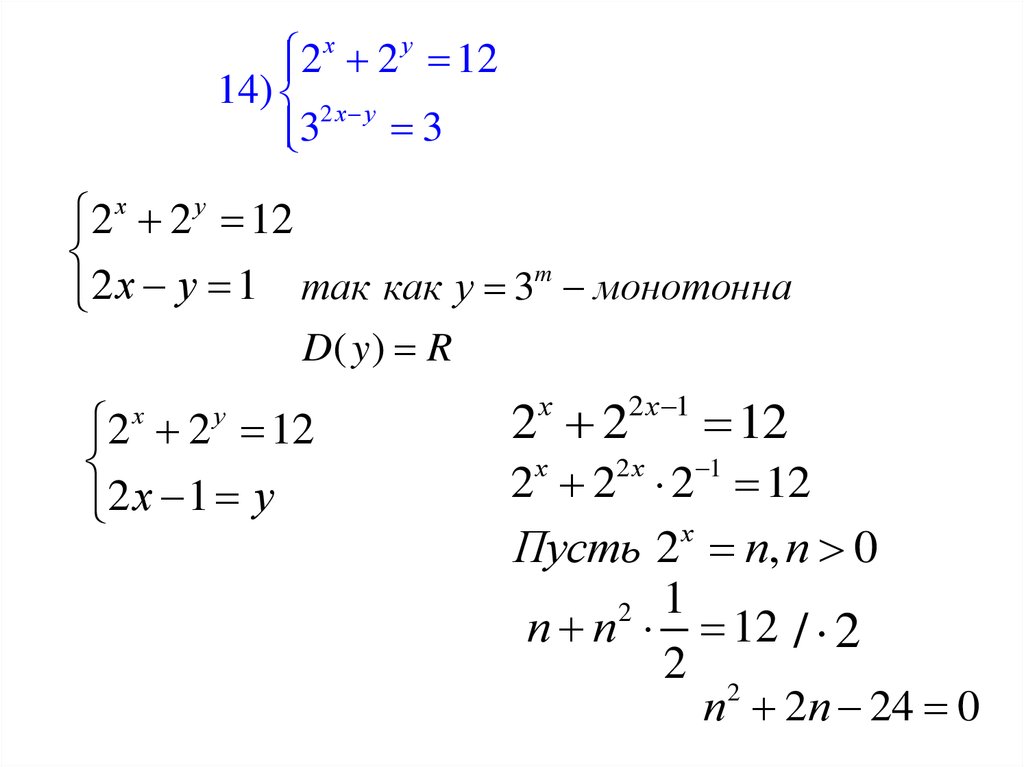


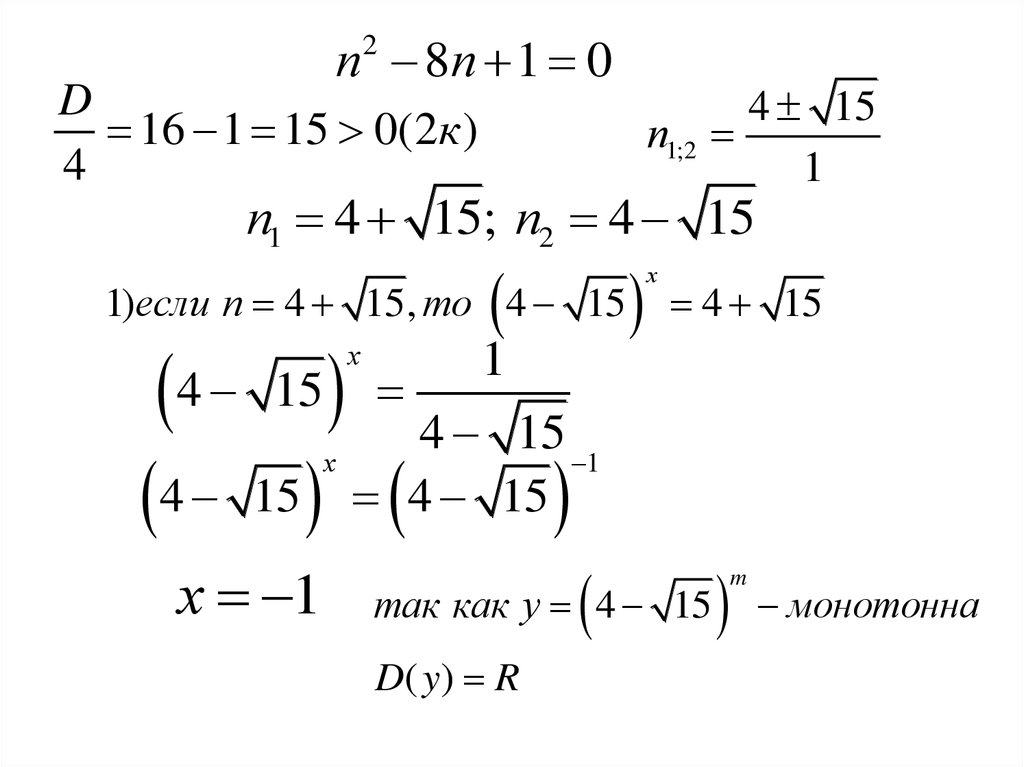








 mathematics
mathematics