Взаимное расположение графиков линейных функций. Блиц-опрос

1. Манькова Ирина Геннадьевна

МАОУ «Тунгусовская СОШ»
2016 г

2.

3.

ЦЕЛЬ:
1
Изучить особенности взаимного
расположения графиков линейных
функций с учетом значения
коэффициентов k и b линейной функции
у = kx + b .
Научиться определять по формулам ,
задающим функции, взаимное
расположение их графиков.

4.

Какую функцию
называют линейной?
Линейной называют
функцию вида y=k x + b,
где k и b – заданные числа.
Что является графиком
линейной функции?
Графиком линейной
функции является
прямая
Какая функция
называется прямой
пропорциональностью?
Прямой
пропорциональностью
называется функция
вида y=kx
В каких координатных
четвертях расположен
график прямой
пропорциональности
при k>0 и при k<0 ?
При k>0 – I и III
координатные четверти
при k<0 – II и IV
координатные четверти

5.

Как получить график функции
у = kx+b из графика функции
у = kx?
Через какую точку обязательно
проходит график прямой
пропорциональности?
Через какую точку обязательно
проходит график линейной
функции?
График функции y=kx+b
получается сдвигом графика
функции y=kx на b единиц
вдоль оси ординат
Через точку (0;0)
Через точку (0;b)

6.

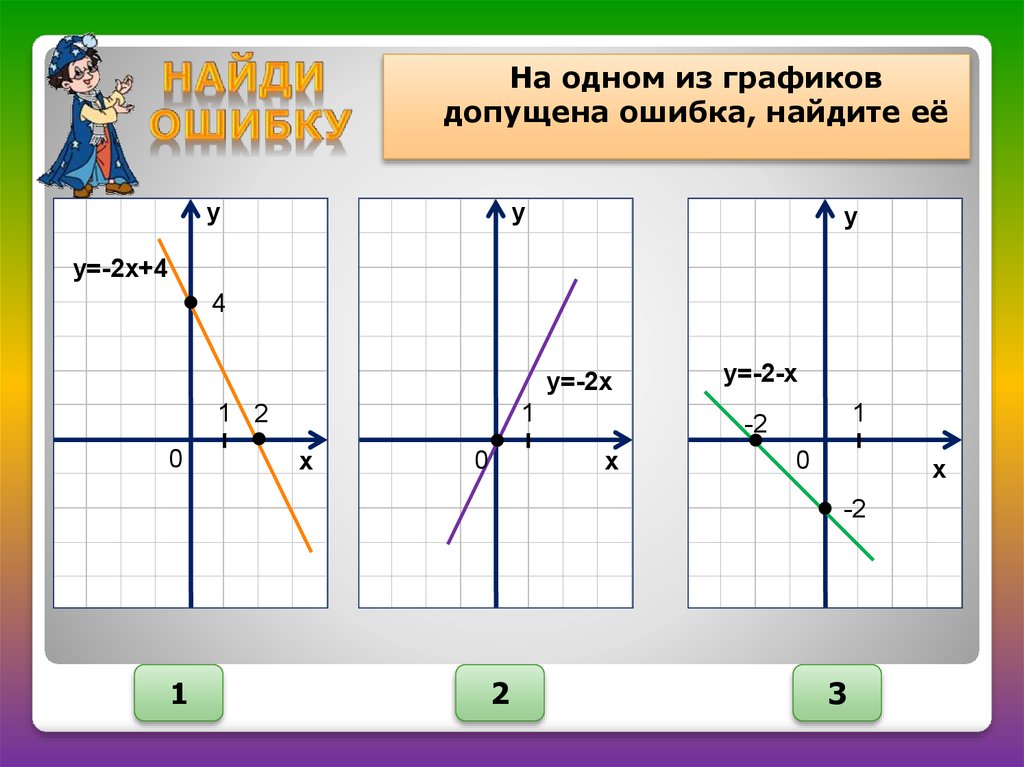
На одном из графиков
допущена ошибка, найдите её
у
у
у
у=-2х+4
4
у=-2х
1 2
0
1
х
1
-2
х
0
у=-2-х
0
х
-2
1
2
3

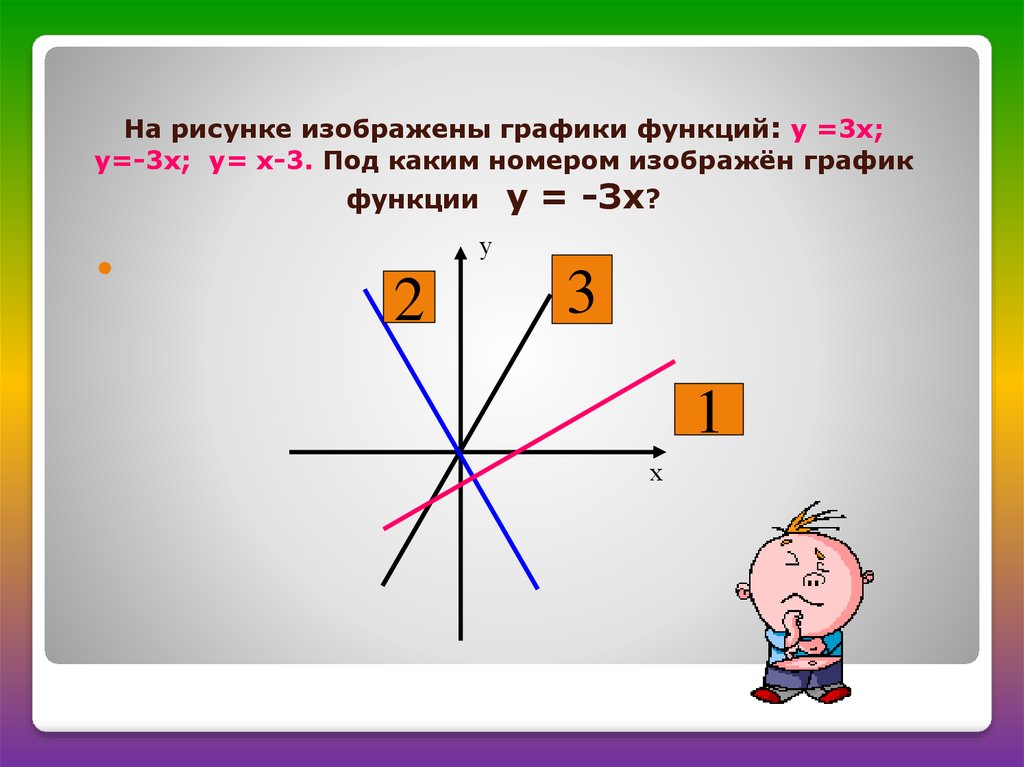
7. На рисунке изображены графики функций: у =3х; у=-3х; у= х-3. Под каким номером изображён график функции у = -3х?

На рисунке изображены графики функций: у =3х;
у=-3х; у= х-3. Под каким номером изображён график
у = -3х?
функции
у
2
3
1
х

8.

9.

Немного истории
17 век. В связи с развитием механики в
математику проникают идеи
функциональной зависимости одной
переменной величины от другой.
Термин «функция» означает
совершение, исполнение (от
латинского слова)
19 век.
Русский математик Н.И.Лобачевский
развил определение понятия
функции.
Немецкий математик Л.Дирихле дал
определение понятия функции очень
близкое к тому, которым пользуются
сегодня.

10.

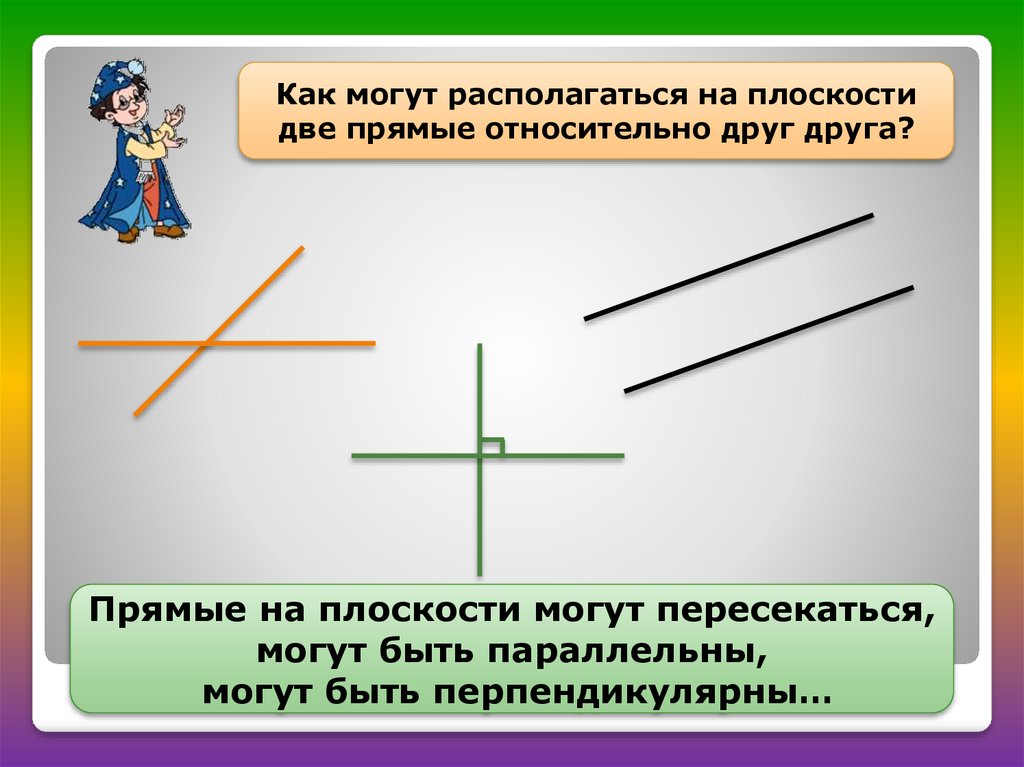
Как могут располагаться на плоскости
две прямые относительно друг друга?
Прямые на плоскости могут пересекаться,
могут быть параллельны,
могут быть перпендикулярны…

11.

12. Проблемы:

1. Постройте в одной системе координат
графики линейных функций.
2. Выяснить при каком значении k и b
графики функций параллельны,
пересекаются.
3. Выяснить существует ли связь между
значением b и координатами точек
пересечения графика с осями
координат.
Проблемы:

13.

Функция
Коэфф. k,
Функция
Число b
у = 3х +2
у = 3х + 4
у = 3х - 3
у = - 3х -2
проверка
Функция
Коэфф. k,
Число b
проверка
Коэфф. k,
Число b
Функция
у = -3х +2
у = - 0,2х +2
у = 5х +2
у = 5х -1
проверка
Коэфф. k,
Число b
проверка
Функция
Коэфф. k,
Число b
у = -2
у=2
проверка
таблица

14.

Функция
Коэффициент
k
Число
у = 3х +2
3
2
у = 3х - 3
3
-3
b
Если коэффициенты
k1 = k2 , b1 ≠ b2,
то прямые параллельны

15.

Функция
Коэффициент k
Число
у = 3х + 4
3
4
у = - 3х - 2
-3
-2
b
Если коэффициенты
k1 ≠ k2 , b1 ≠ b2,
то прямые пересекаются

16.

Функция
Коэффициент k,
Число
у = 5х + 2
5
2
у = - 3х +2
-3
2
b
b
Если коэффициенты
k1 ≠ k2 , b1 = b2,
то прямые пересекаются
в точке (0 ; b)

17.

Функция
у = -0,2х + 2
у = 5х - 1
Коэффициент k,
Число
-0,2
2
5
-1
b
Если коэффициенты
k1 * k2=-1 , b1 ≠ b2,
то прямые перпендикулярны

18.

Функция
Коэффициент k
Число b
у = -2
0
-2
у=2
0
2
Если коэффициенты
k1=k2=0 , b1≠b2 ,
то прямые параллельны и
параллельны оси ОХ

19. Заполните таблицы

Линейные
функции
Алгебраическое
условие
y= k1х+b1
k1 =k2 , b1 ≠ b2
y= k2х+b2
k1 ≠ k2 , b1 ≠ b2
Геометрический
вывод
k1 ≠ k2 , b1=b2
Заполните таблицы
Проверка

20. Заполните таблицы

Линейные
функции
Алгебраическое
условие
Геометрический
вывод
у= k1х+b1
k1 =k2 , b1 ≠ b2
прямые параллельны
у= k2х+b2
k1 ≠ k2 , b1 ≠ b2
прямые пересекаются
k1 ≠ k2 , b1=b2
прямые пересекаются в
точке (0; b)
Заполните таблицы

21. Построить в одной координатной плоскости графики функций

у = 3х +3,
у
х
0
-1
у
3
0
у = 3(х + 1)
3
1
0
х
0
-1
у
3
0
1
х

22.

23.

Найди ошибку:
а) прямые у = 7х -4 и у = 7х +5 – параллельны;
б) прямые у = 10х -3 и у = -10х -6 – параллельны;
в) прямые у = 0,3х -2 и у = 8,1х -2 – пересекаются;
г) прямые у = - 7х +3 и у = -7х -2 – пересекаются;
д) прямые у = 3х +2 и у = 3х – параллельны;
е) прямые у = -2,3х и у = 2,3х – пересекаются

24.

Функции заданы формулами
1
y x 19
3
y 25 3x
y 3x 5
y 0,3x 1
Укажите из них ту,
график которой
параллелен
графику функции
y=3x-19

25.

При каких значениях k и b
график линейной функции
y=kx+b параллелен графику
функции y=6x+14?
k=14 и b=6;
k=8 и b=14;
k=6 и b=14;
k=6 и b=16

26.

Каково взаимное расположение
графиков функций?
у = 5х + 4 и у=5х+8
у = 8х + 10 и у=-8х+6
у = 12х и у=-9х
у = -2х и у=-2х-5
у = 3х+7 и у=-2х+7

27.

Задать формулой функцию, график
которой параллелен прямой
у=-8х+11
и проходит через
начало координат
у=-8х

28. Домашнее задание

№383 (а, в), №384- письменно