Логарифмическая функция

1.

Логарифмы – это все!
Музыка и звуки
И без них никак нельзя
Обойтись науке!

2.

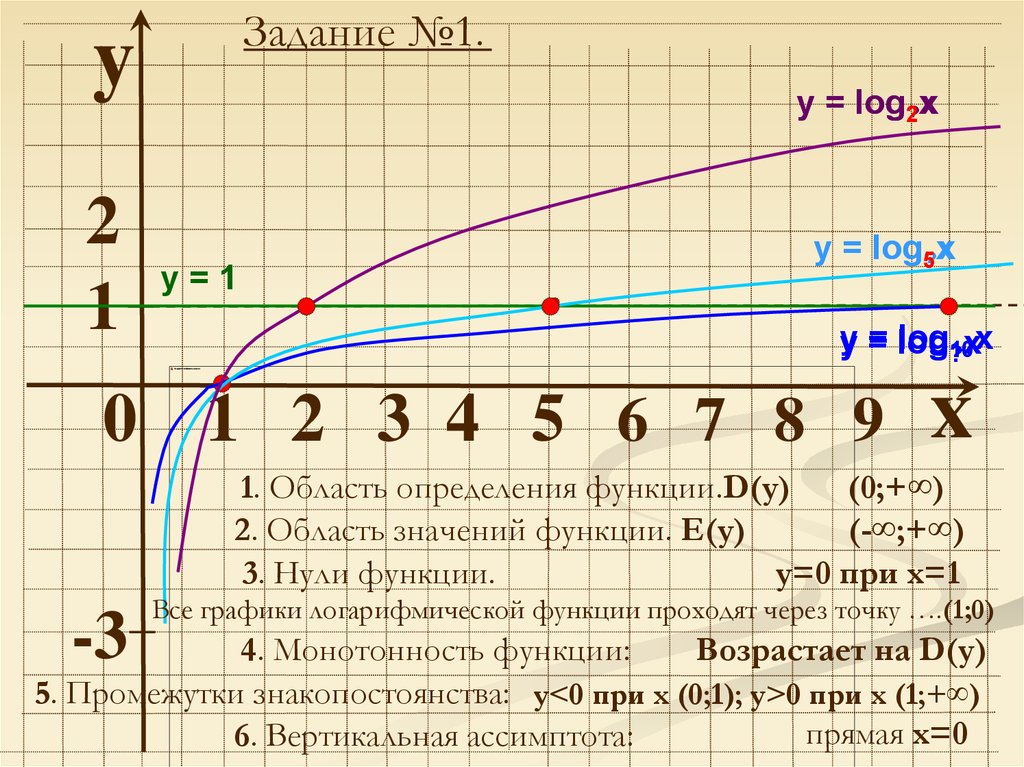
Задание №1.
y
2
1
у = log2?x
у=1
у = log5?x
у = log
lоg?10xx
0 1 2 3 4 5 6 7 8 9
x
1. Область определения функции.D(y)
(0;+∞)
2. Область значений функции. Е(у)
(-∞;+∞)
3. Нули функции.
у=0 при х=1
-3
Все графики логарифмической функции проходят через точку ….(1;0)
4. Монотонность функции:
Возрастает на D(y)
5. Промежутки знакопостоянства: у<0 при х (0;1); у>0 при х (1;+∞)
прямая х=0
6. Вертикальная ассимптота:

3.

y
2
1
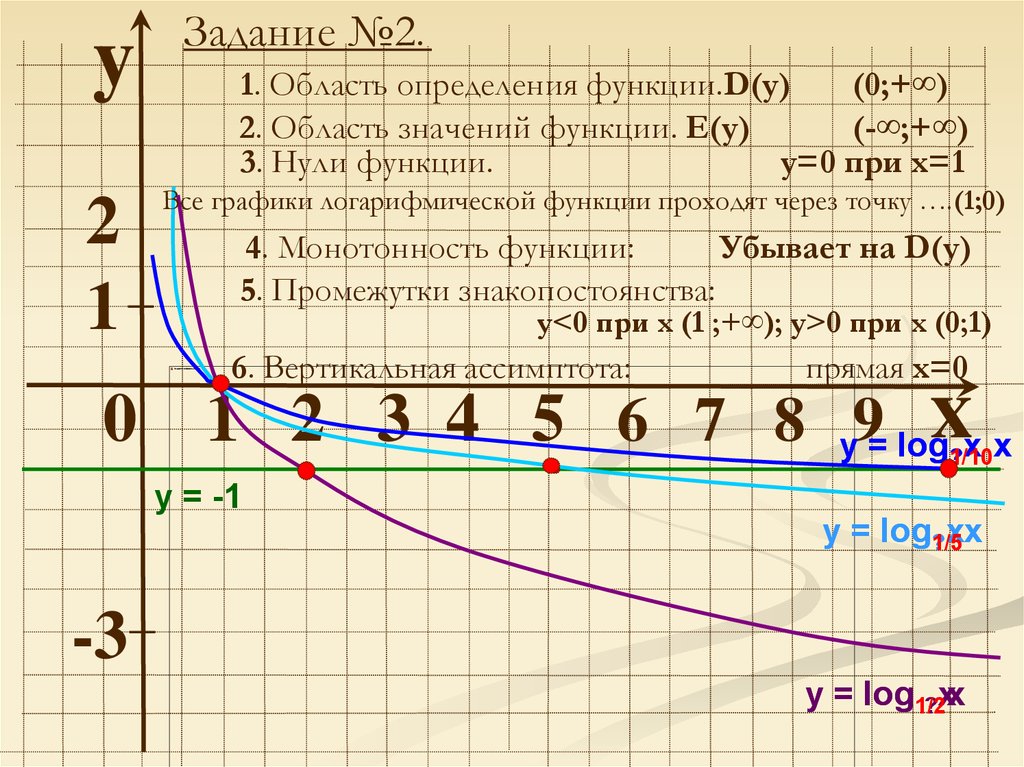
Задание №2.
1. Область определения функции.D(y)
(0;+∞)
2. Область значений функции. Е(у)
(-∞;+∞)
3. Нули функции.
у=0 при х=1
Все графики логарифмической функции проходят через точку ….(1;0)
4. Монотонность функции:
Убывает на D(y)
5. Промежутки знакопостоянства:
у<0 при х (1 ;+∞); у>0 при х (0;1)
6. Вертикальная ассимптота:
прямая х=0
x
0 1 2 3 4 5 6 7 8 у9= lоg
log x x
?
1/10
у = -1
у = log1/5
?xx
-3
у = log1/2
?xx

4.

Задание №3.
Определить вид монотонности функции у=log0,5(3−2х).
Ошибка : т.к. 0<a<1, то функция убывающая.
1.D(у): Х (−∞;1,5) ;
3-2х>0
-2х>0
х<1,5
2.Возьмем из области определения х1 и х2 где х1 < х2.
3.Найдем значение функции в этих точках у1=log0,5(3−2х1), у2=log0,5(3−2х2).
4. Определим знак у2-у1
у2-у1=log0,5(3−2х2)- log0,5(3−2х1)=log0,5 (3−2х2):(3−2х1)
х1 < х2, то
2х1 < 2х2, то
-2х1 >-2 х2, то
3-2х1 >3-2х2,
следовательно (3−2х2):(3−2х1) <1,
значит log0,5 (3−2х2):(3−2х1) >0 ,
т.е. у2>у1.
Вывод: из неравенства х1 < х2 следует у1 < у2.
Доказали, что данная функция возрастающая

5.

Самостоятельная работа
Определите по точкам формулу графика функции и постройте
(1;0);
(1/16;4); (2;1);
(1/4;-2);
(1/2;1);
Х
у1= log2х
Х
у2= log 1/2х
(2;-1); (4;2);
(1/2;-1); (8;3);
(4;-2);
(8;-3);
1/16
1/8
1/4
1/2
-4
-3
-2
-1
1/16
1/8
1/4
1/2
4
3
2
1
(1/8;3);
(16;4);
1
(1/8;-3);
(16;-4); (1/16;-4); (1/4;-2)
2
0
1
4
1
2
0
(1/4;2);
2
4
-1
-2
8
16
3
4
8
16
-3
-4

6.

Практическая работа
Оставьте в таблице возрастающие функции
У=log1,2(х-1) У=log2,5(х-1) У=log√2 (х+2) У=log3/7(2-х)
У=log0,8(1-х) У=log1/2х-1
У=log3/5(х+2) У=log7/3(2-х)
У=log4,2(х-1) У=log1,2(х-1) У=log4/3х+2
У=log1/2х-1
У=log3/4х+2 У=log0,3 (х+2) У=lg(3х+1)
У=log5,3 (х+2) У=log3/2(2-х) У=log√2(2-х)
У=log5,3 х+2
У=lnx
У=ln(х-2)
У=log1/√2(1-х) У=log9,3х+2 Y=log4/3х+2