Модуль. 8 класс

1. Открытый урок по теме:

Никитина И.Г.
ГБОУ Центр образования №173
8 класс
Санкт-Петербург
2014 год

2. х, если х ≥ 0; -х, если х < 0.

Понятие модуля
х =
х, если х ≥ 0;
-х, если х < 0.
Геометрический смысл модуля.
Модулем числа а называется расстояние
(в единичных отрезках)
от 0 до точки, изображающей число а.
-a
O
a
X
5 =5;
-5 = -(-5) = 5

3.

y=IxI+ x2+2x

4.

Свойства модуля
Модуль числа есть число
неотрицательное.
Модули противоположных чисел
равны.
Квадрат модуля равен квадрату
выражения, стоящего под модулем.
Модуль произведения есть
произведение модулей множителей.
Если знаменатель дроби отличен от
0, то модуль дроби равен частному от
деления модуля числителя на модуль
знаменателя.

5.

Пример раскрытия модуля
Чтобы записать выражение без
знака модуля необходимо
знать при каких значениях
неизвестной, выражение
принимает положительное или
отрицательное значение.
Раскройте модуль Х - 5

6.

Пример раскрытия модуля
Х-5
х – 5, если х > 5
= 0,
если х = 5
5 – х, если х < 5

7.

Функция у = IхI и ее график
Свойства:
1.
2.
3.
4.
Область определения функции х – любое число.
Область значений функции у ≥ 0.
Нуль функции у=0 при х = 0.
Функция убывает при х ≤ 0,
функция возрастает при х ≥ 0.
Y
1
-1
O
Х
1

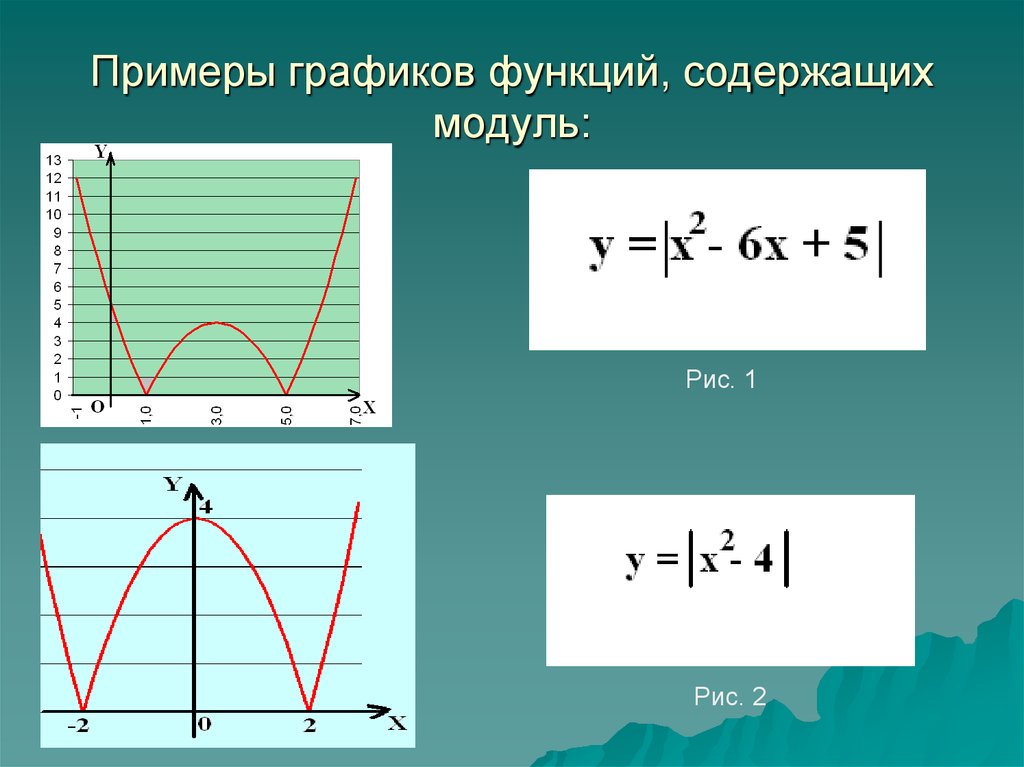
8. Примеры графиков функций, содержащих модуль:

Рис. 1
Рис. 2

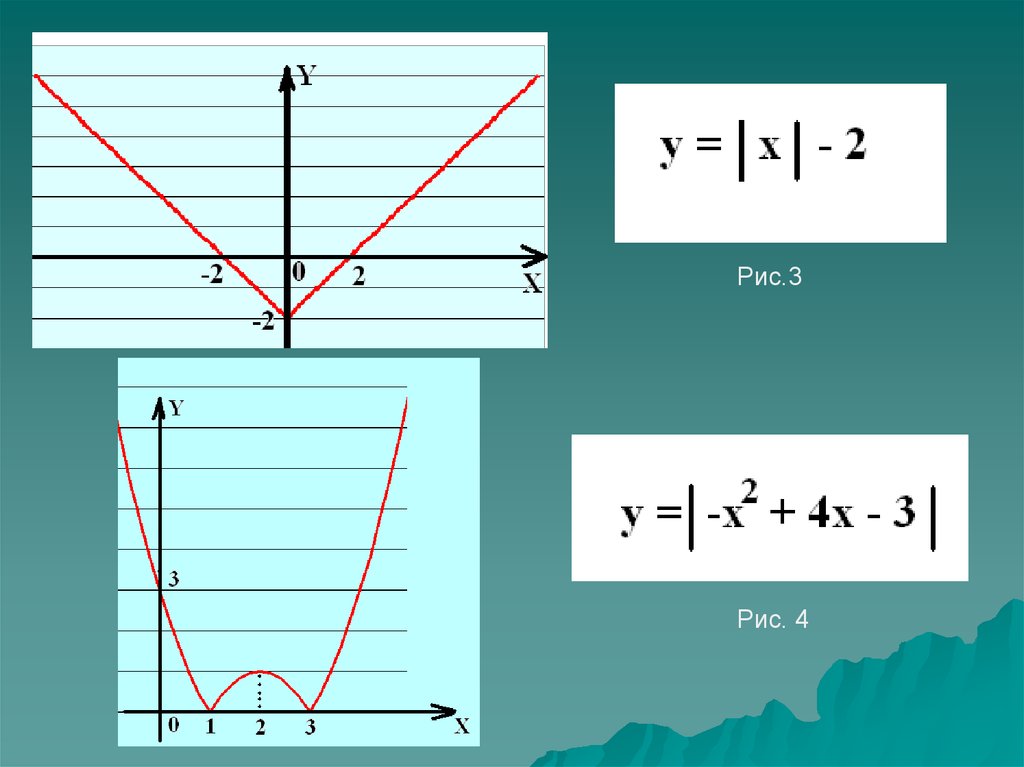
9.

Рис.3
Рис. 4

10.

Построение графиков функции, содержащих
модуль с помощью симметрии относительно
осей координат
• Чтобы построить график функции Y= I f(X) I, надо
построить график функции Y= f(X) и ту часть графика,
которая лежит ниже оси ОХ, симметрично отобразить
относительно этой оси.