Применение тригонометрии в геометрических задачах

1.

Применение тригонометрии в
геометрических задачах
2 1
1 ctg ABC
2
sin BAC
sin
3 ABC
2

2.

1.1
ПРОТОТИП №27327.
1 СПОСОБ РЕШЕНИЯ
2
В треугольнике ABC АС=ВС=27, AH — высота, sin BAC
3
Найдите BH.
1 способ решения:
C
sin BAC sin ABC
2
т .к . ВАС АВС , ∆ АВС - равнобедренный
3
СР – высота в равнобедренном треугольнике.
27
27
ВСР : sin АВС
18
Н
СР СР 2 х
3 х 27 х 9 СР 18
СВ 27 3 х
Используем теорему Пифагора для прямоугольного ∆СРВ :
A
Р
B
РВ 27 2 18 2 ( 27 18)( 27 18) 9 45 9 5 АВ 18 5
АВН : sin АВС
18√5
По теореме
Пифагора:
ВН
АН
АН
2х
х 6 5 АН 12 5
АВ 18 5 3 х
АВ 2 АН 2 (18 5 ) 2 (12 5 ) 2
(6 2 3 2 5) (6 2 2 2 5) (6 2 5) (9 4) 30
СВ˂НВ ═> ∆АВС - тупоугольный
Смотри 2 способ решения:
Ответ: 30

3.

1.1
ПРОТОТИП №27327.
2 СПОСОБ РЕШЕНИЯ
2
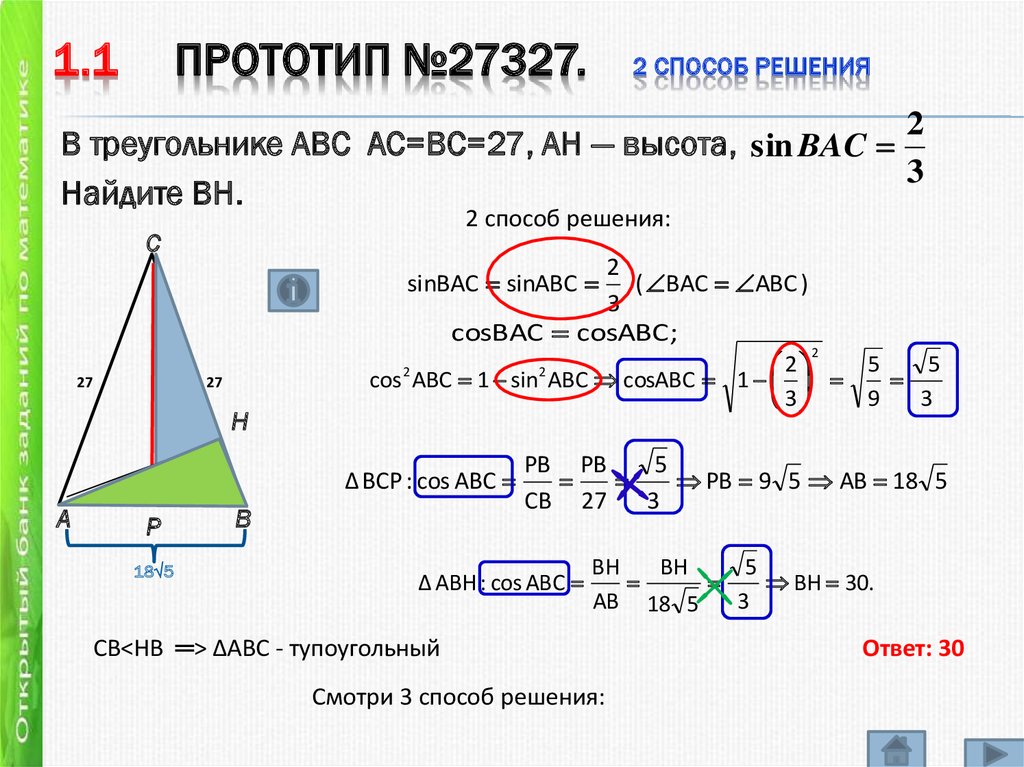
В треугольнике ABC АС=ВС=27, AH — высота, sin BAC
3
Найдите BH.
2 способ решения:
C
2
( ВАС АВС )
3
cosBAC cosABC;
sinBAC sinABC
27
27
Н
Δ ВСР : cos АВС
A
Р
18√5
2
2
cos 2 ABC 1 sin2 ABC cosABC 1
3
B
5
5
9
3
РВ РВ
5
РВ 9 5 АВ 18 5
СВ 27
3
Δ АВН : cos АВС
ВН
ВН
5
ВН 30.
АВ 18 5
3
СВ˂НВ ═> ∆АВС - тупоугольный
Смотри 3 способ решения:
Ответ: 30

4.

1.1
ПРОТОТИП №27327.
3 СПОСОБ РЕШЕНИЯ
В треугольнике ABC АС=ВС=27, AH — высота,
Найдите BH.
3 способ решения:
2
т .к . ВАС АВС;
3
АН 2 х
АН
АВН : sin АВС
х 6 5 АН 12 5
АВ 3 х 18 5
sin BAC sin ABC
C
27
27
Н
1 ctg 2 ABC
1 ctg 2 АВС
A
Р
2
sin BAC .
3
B
ctg 2 ABC
1
sin 2 ABC
1
2
3
2
ctg 2 ABC
5
5
ctgABC
.
4
2
BH
BH
5x
12 5 2 x x 6 5
AH 12 5
2x
BH 5 6 5 30
1
1;
4
9
АВН : ctgАВС
ВН
5х
.
АH
2х
Ответ: 30

5.

1.1
ПРОТОТИП №27327.
4 СПОСОБ РЕШЕНИЯ
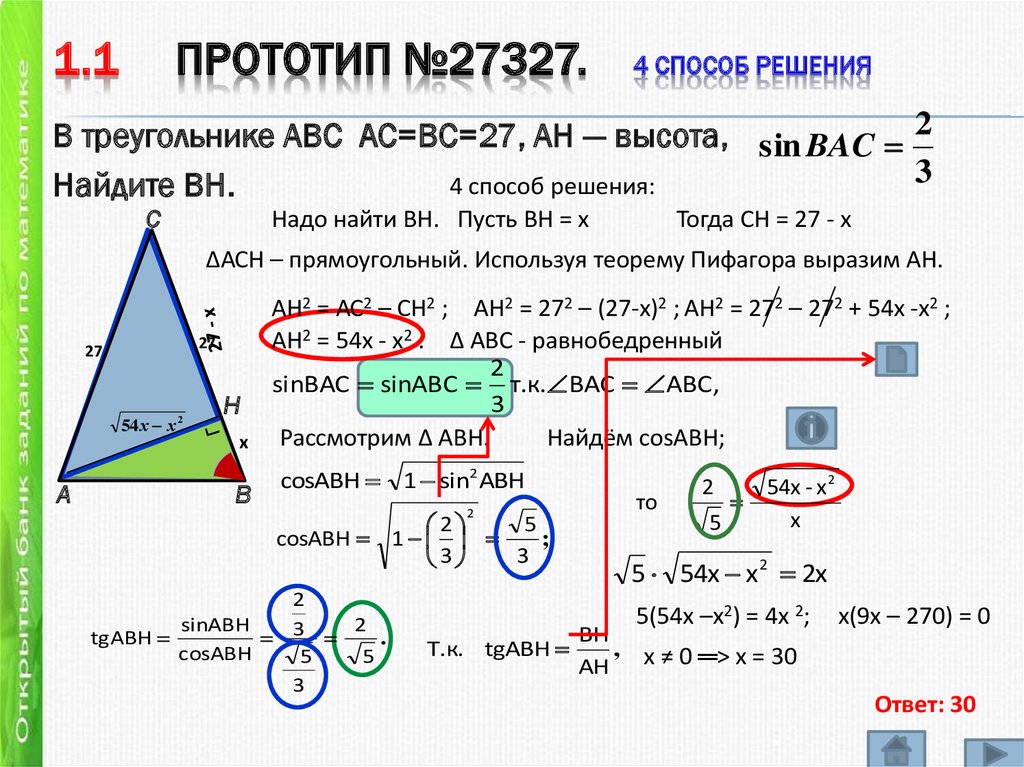
В треугольнике ABC АС=ВС=27, AH — высота, sin BAC 2
3
4 способ решения:
Найдите BH.
C
Надо найти ВН. Пусть ВН = х
Тогда СН = 27 - х
∆АСН – прямоугольный. Используя теорему Пифагора выразим АН.
27
27
54 х х 2
A
Н
х
B
АН2 = АС2 – СН2 ; АН2 = 272 – (27-х)2 ; АН2 = 272 – 272 + 54х -х2 ;
АН2 = 54х - х2 . ∆ АВС - равнобедренный
2
sinBAC sinABC т.к. ВАС АВС,
3
Рассмотрим ∆ АВН.
Найдём соsАВН;
соsABH 1 sin2 ABH
2
5
2
cosABH 1
;
3
3
2
sinABH
2
tgABH
3
.
cosABH
5
5
3
BH
Т.к. tgABH
,
AH
то
2
5
54х - х 2
х
5 54х х 2 2х
5(54х –х2) = 4х 2;
х(9х – 270) = 0
х ≠ 0 ═> х = 30
Ответ: 30

6.

1.1
ПРОТОТИП №27327.
5 СПОСОБ РЕШЕНИЯ
2
В треугольнике ABC АС=ВС=27, AH — высота, sin BAC
3
Найдите BH.
5 способ решения:
В ∆ АСН: АН2 = АС2 – СН2 ;
Пусть СН = х, то ВН = 27 + х ;
АН 729 х 2
АН2 = 729 - х2 ;
Н
2
sinBAC sinABC ; ( ВАС АВС)
АН
АН 3
АВ2 =АН2 + НВ2 ;
sinABC
;
АВ
АВ
АВ2 =729 - х2 + (27 + х)2 ;
х
C
729 х 2
27
АВ2 =729 - х2 + 729 + 54х + х2 ;
АВ2 =54х +1458;
27
729 х 2
АВ
A
54 х 1458
729 х 2
4
;
54х 1458 9
АН2 = 272 – х2 ;
(729-х2)9 =4(54х+1458);
729 - х 2
54х 1458
B
х2 + 24х -81 = 0;
П теореме Виета: х1 = -27(постор.корень) и х2 = 3.
ВН = 27+3 = 30
Ответ: 30
2
;
3

7.

2.1
1
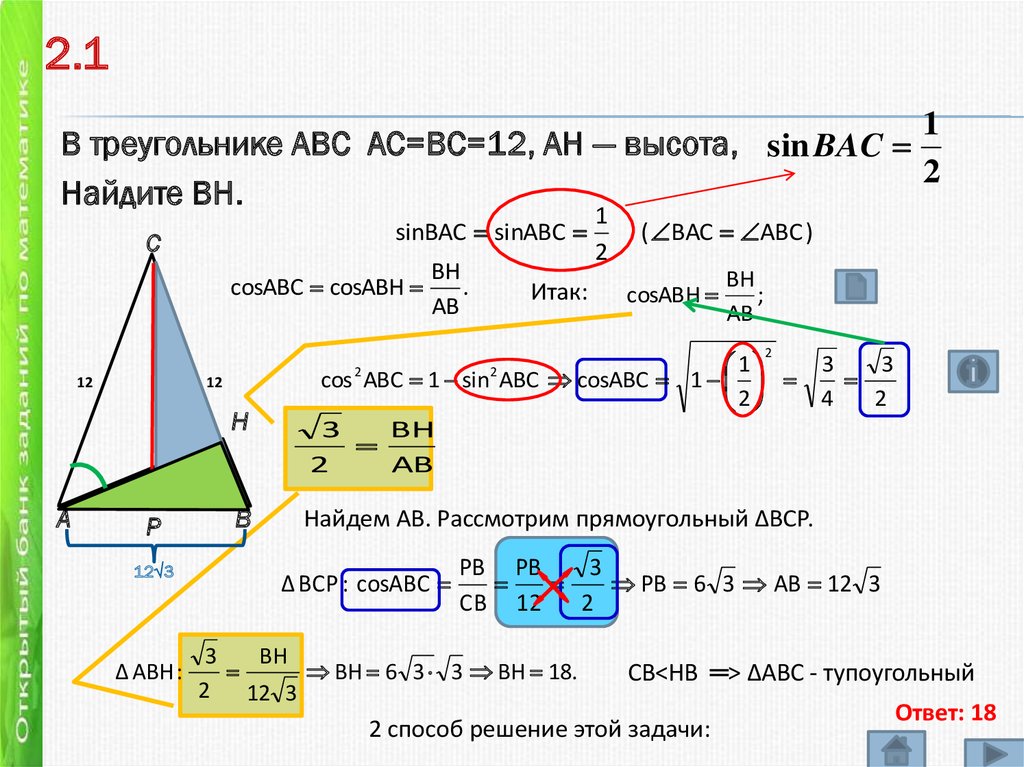
В треугольнике ABC АС=ВС=12, AH — высота, sin BAC
2
Найдите BH.
sinBAC sinABC
C
cosABC cosABH
BH
.
AB
Итак:
1
2
( ВАС АВС )
cosABН
BH
;
AB
2
12
A
Н
1
cos 2 ABC 1 sin2 ABC cosABC 1
2
3
ВH
2
AB
B
Найдем АВ. Рассмотрим прямоугольный ∆ВСР.
12
Р
12√3
Δ АВН :
Δ ВСР : соsАВС
3
3
2
4
2
РВ РВ
3
РВ 6 3 АВ 12 3
СВ 12
2
3
ВН
ВН 6 3 3 ВН 18.
2
12 3
СВ˂НВ ═> ∆АВС - тупоугольный
2 способ решение этой задачи:
Ответ: 18

8.

2.2
1
В треугольнике ABC АС=ВС=12, AH — высота, sin BAC
2
Найдите BH.
2 способ решения:
sinBAC sinABC
6
Н
60о
Следовательно в равнобедренном ∆ АВС
∟САВ = ∟СВА = 30о ;
В ∆ АВС: ∟АСВ = 180о - 2 ∙ 30о = 120о.
Внешний угол: ∟АСН = 180о - 120о = 60о;
C
120о
12
12
∆АСН – прямоугольный: ∟САН = 30о;
30о
30о
30о
B
A
СН = 6;
1
2
ВН = ВС + СН = 12 + 6 =18.
Катет прямоугольного треугольника,
лежащий против угла в 30°, равен
половине гипотенузы
Ответ: 18

9.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ №1
Прямоугольный треугольник – треугольник, один из углов которого прямой.
Сторона с, лежащая против прямого угла, - гипотенуза. Стороны а и в - катеты
А
с
b
C
┐
α
а
В
b
sinα
c
а
соsα
с
b
tgα
a

10.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ №2
1. В равнобедренном треугольнике углы при основании равны.
2. В равнобедренном треугольнике высота, проведенная к основанию,
является и медианой, и биссектрисой.
СР – высота, медиана, биссектриса.
С
Медиана треугольника, проведенная из данной вершины - отрезок
прямой, соединяющий эту вершину с серединой противолежащей
стороны треугольника
А
Р
В
Высота СР разделила ∆ АВС на два равных
прямоугольных треугольника

11.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ №3
Основное тригонометрическое тождество
1.
sin 2 cos 2 1
cos 2 1 sin 2
cos 1 sin 2
2.
1
1 tg
cos 2
1
2
1 ctg
sin 2
2

12.

СКОРО ЕГЭ!
Еще есть время подготовиться!